Космические исследования, 2020, T. 58, № 4, стр. 321-330
Многовитковые перелеты на геостационарную орбиту с обнулением малой тяги в области тени
Р. З. Ахметшин *
Институт прикладной математики им. М.В. Келдыша РАН
г. Москва, Россия
* E-mail: axmetro@yandex.ru
Поступила в редакцию 20.05.2019
После доработки 17.06.2019
Принята к публикации 19.09.2019
Аннотация
Перелеты в центральном ньютоновском поле рассматриваются в предположении, что постоянная по величине малая тяга обнуляется при попадании в тень Земли. С помощью принципа максимума формируется двухточечная краевая задача, в которой, однако, не учитываются условия оптимального пересечения границ тени, которые существенно усложняют задачу. По этой причине краевая задача оказывается “неполной”, а ее решения – неоптимальными. Тем не менее, для перелетов на геостационарную орбиту с высокоэллиптических орбит она позволяет получать “хорошие” траектории, с затратами рабочего вещества меньшими, чем на траекториях без обнуления тяги, или несильно их превышающими. Это показано на примере перелетов с начальной орбиты с наклонением 13° и с расстоянием в перигее ≈15.6 и в апогее ≈83.2 тыс. км.
Вопрос учета влияния тени при проектировании многовитковых перелетов с малой тягой так или иначе затрагивался в различных публикациях. Одной из самых ранних работ, по-видимому, является [1], из более поздних – работы [2–7]. С целью получить хорошие по затратам рабочего вещества траектории используются как прямые методы – с параметрическим заданием функций управления и градиентным спуском в пространстве параметров [7], так и непрямые – с решением краевых задач. Из-за сложности последних обычно применяются какие-либо упрощения – используются локально-оптимальные или “квазиоптимальные” законы управления [4], численное осреднение уравнений движения [1, 4, 5]. В работе [4] предлагается управление с обратной связью, которое способно нивелировать различные возмущения, в том числе влияние тени.
“НЕПОЛНАЯ” КРАЕВАЯ ЗАДАЧА
В данной работе, в отличие от вышеупомянутых, краевая задача решается в исходной постановке, без осреднения уравнений движения, как и в [8]. В работе [8] задача рассматривалась без учета влияния тени (и других возмущающих факторов) в двух постановках: (А) с возможностью многократного включения и выключения тяги, и (Б) с постоянно работающей, постоянной по величине малой тягой. А именно, рассматривалась задача оптимального многовиткового перелета космического аппарата в центральном ньютоновском поле Земли с электроракетными двигателями малой тяги, с питанием от солнечных батарей. Управление КА осуществлялось с помощью вектора малой тяги. На направление тяги не накладывалось никаких ограничений. С использованием принципа максимума Понтрягина задача сводилась к двухточечной краевой задаче. Для этого вводились сопряженные переменные, формировался гамильтониан задачи, с его помощью находились выражения для оптимального направления вектора тяги, как функции фазовых и сопряженных переменных, и дифференциальные уравнения для фазовых и сопряженных переменных
Задача сводилась к поиску начальных значений сопряженных переменных, которые обеспечили бы выполнение краевых условий в конечный момент времени. Таким образом получалась краевая задача в случае (Б). В случае (А), вдобавок к выражениям для оптимального направления тяги, была получена, также с помощью принципа максимума, т.н. функция переключения Sw, которая дает критерий для оптимальных моментов включения и выключения тяги: при Sw < 0 тяга нулевая, при Sw > 0 тяга максимальная (особые случаи не рассматривались).
В данной работе используется постановка (Б), но добавляется условие обнуления тяги в области тени: есть функция тени Sh, при Sh < 0 тяга нулевая, при Sh > 0 тяга максимальная (случаи движения по границе тени рассматривать не будем). Для модели “цилиндрической” тени функция Sh конкретизирована в [9]:
Получающаяся задача очень похожа на задачу (А), но вместо функции переключения Sw величина тяги “задается” функцией Sh. Может возникнуть впечатление, что простой заменой одной функции на другую мы получим новую краевую задачу, решая которую сможем получать искомые траектории. Такая “краевая” действительно дает возможность находить траектории перелета на конечную орбиту с обнулением тяги в области тени, но эти траектории не оптимальны, ибо не учитываются условия оптимального пересечения границ тени. Это т.н. условия скачка в сопряженных переменных [10]:
Без условий скачка краевая задача оказывается “неполной”. Тем не менее, имеет смысл такую задачу исследовать, если поставить цель выяснить, при каких значениях параметров задачи ее решения оказываются “хорошими” по функционалу (в сравнении не с оптимальными, которые нам неизвестны, а с “номинальными”, т.е. перелетами без обнуления тяги), и рассматривая ее как предварительный (или промежуточный) этап на пути к решению “полноценной” краевой задачи.
Основные причины, по которым было решено использовать для поиска траекторий “неполную” краевую задачу, следующие. Во-первых, такая задача существенно проще “полноценной” краевой задачи. На многовитковых траекториях могут быть десятки и сотни участков с тенью [9], и соответственно раза в два больше условий скачка. Во-вторых, предполагалось, что, как и в случае учета влияния других возмущений (гравитационного притяжения Луны, Солнца и вариаций геопотенциала [11–13]), ее решения будут не сильно отличаться от номинальных. А если получаемые решения по функционалу (расходу рабочего вещества) окажутся близки к номинальным траекториям – их можно будет рассматривать как приближенно-оптимальные и, возможно, использовать вместо оптимальных решений.
НАЧАЛЬНЫЕ ОРБИТЫ
Уточним постановку задачи. В качестве конечной орбиты рассматривается геостационарная орбита (ГСО), а в качестве начальной – орбита с наклонением i0 = 13°, высотой перигея Hπ = 9.2 и апогея Hα = 76.8 тыс. км. Эти три параметра задают конфигурацию орбиты. А ее положение в пространстве определяют параметры ω0, Ω0. Как указано в [14], в случае оптимальных по быстродействию перелетов между некомпланарными начальной эллиптической и конечной круговой орбитами со свободной линией апсид начальной орбиты, из условий трансверсальности следует, что линия апсид должна совпадать с линией пересечения плоскостей начальной и конечной орбит. В [4] также отмечено, что задача перелета между такими орбитами типична при выведении КА на высокие круговые орбиты. Поэтому зафиксируем угловое расстояние перицентра от узла ω0 = 0°. Другие характеристики орбиты приведены в табл. 1. Дополнительно полагается, что КА стартует из перигея начальной орбиты, т.е. истинная аномалия θ0 = 0° (следовательно, φ0 = Ω0), а конечный момент времени определяется заданной угловой дальностью перелета, а именно, целым количеством витков N в переменной φ (φк = φ0 + 2πN). Как правило, значение N подбирается оптимальным, для чего приходится решать несколько краевых задач. В результате у нас остается два свободных параметра: долгота восходящего узла Ω0 и время (дата) старта t0 (измеряется в сутках от 00.00 1.I.2018).
НОМИНАЛЬНЫЕ ТРАЕКТОРИИ
Анализ влияния тени будем проводить сравнением многовитковых (с наилучшим количеством витков N) траекторий перелета на геостационарную орбиту с тенью и траекторий номинальных, т.е. оптимальных траекторий перелета без выключения тяги в тени (со своим наилучшим N). Для последних, в силу центральности ньютоновского поля и отсутствия возмущений, имеется симметрия по отношению к параметру Ω0: изменение Ω0 приводит к повороту начальной орбиты и траектории перелета как целого вокруг оси вращения Земли. Параметр t0 также не влияет на траекторию перелета, поскольку от него не зависят ни положение начальной орбиты в пространстве, ни положение КА на орбите в начальный момент времени (в силу принятых выше допущений). Поэтому характеристики номинальных траекторий одинаковы для всех значений параметров Ω0, t0. Они приведены в табл. 2.
ПОЛОЖЕНИЕ УЧАСТКОВ С ТЕНЬЮ НА ТРАЕКТОРИЯХ
В отличие от номинальных, перелеты с нулевой тягой в области тени зависят от положения теневых участков на траектории, а значит, зависят от положения Солнца относительно Земли в небесной системе координат (и, следовательно, от t0), и от положения траектории относительно Солнца (а следовательно, и от Ω0).
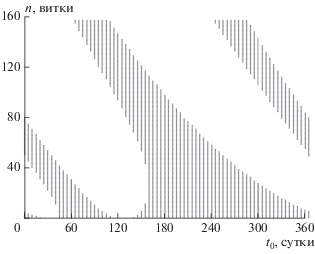
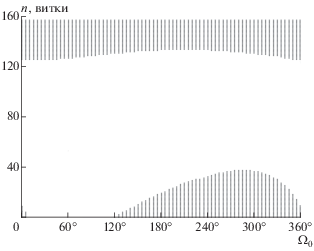
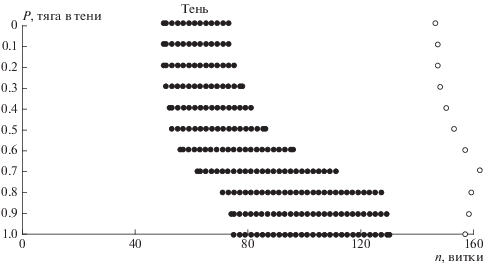
Некоторое общее представление о том, как с изменением параметров меняется количество участков с тенью и на каких витках они расположены, можно получить из т.н. “портретов” номинальных траекторий с тенью (рис. 1, 2). По оси ординат отсчитываются номера витков, по оси абсцисс – либо параметр t0 (при заданном значении Ω0), либо параметр Ω0 (при заданном значении t0), и черными квадратиками отмечены витки с тенью.
Однако, хотя часто с увеличением количества витков с тенью (на номинальных траекториях) растут дополнительные затраты на перелет (на траекториях с обнулением тяги), последние напрямую никак не связаны ни с количеством теневых участков, ни с их общей продолжительностью. Количество витков с тенью на траекториях с обнулением тяги может сильно отличаться от количества витков с тенью на номинальных траекториях. Поэтому спрогнозировать заранее, в какой области параметров дополнительные затраты будут большими, а тем более – насколько большими, проблематично, особенно с учетом того факта, что могут существовать разные ветви решений.
РЕЗУЛЬТАТЫ РАСЧЕТОВ
В табл. 3 приведены результаты решения “неполной” краевой задачи для отдельных значений параметра t0. Дата старта изменяется в интервале года с шагом 1.5 мес., угол Ω0 – в диапазоне [0°–350°] с шагом 10°. Приведены величины “дополнительных” затрат рабочего вещества ∆МРВ на перелет по сравнению с номинальными траекториями в процентах от номинальных затрат МРВ (485.3 кг). Если считать, что дополнительные затраты, не превышающие 2% – это “хороший” результат, то, судя по данным табл. 3, высказанные выше ожидания оправдались на 2/3. В 45 вариантах (≈1/6 часть) затраты на перелет с тенью оказались меньше, чем на номинальной траектории. Но треть результатов превышает 2% (они выделены жирным), причем есть ∆МРВ > 30%.
Таблица 3.
Изменение ∆МРВ массы рабочего вещества МРВ из-за влияния тени
| t0 | 0 | 46 | 91 | 137 | 183 | 228 | 274 | 320 |
|---|---|---|---|---|---|---|---|---|
| Ω0 | ∆МРВ в % от МРВ = 485.3 кг (2% – 9.7 кг) | |||||||
| 0° | 0.2 | 0.5 | 0.6 | 1.7 | 3.5 | 0.9 | 0.5 | 0.1 |
| 10° | 1.4 | 0.8 | 0.5 | 8.8 | 6.9 | 0.3 | 0.2 | 0.5 |
| 20° | 2.4 | 0.8 | 0.7 | 20.4 | 10.6 | 1.0 | 0.0 | 1.2 |
| 30° | 1.1 | 0.5 | 0.8 | 27.2 | 13.3 | 2.4 | –0.1 | 1.1 |
| 40° | 0.1 | –0.0 | 0.8 | 29.7 | 14.7 | 3.4 | –0.2 | 0.4 |
| 50° | –0.2 | –0.2 | 0.8 | 30.3 | 15.0 | 3.7 | –0.2 | –0.1 |
| 60° | 0.1 | –0.3 | 0.7 | 30.0 | 14.7 | 3.4 | –0.3 | –0.2 |
| 70° | 0.9 | –0.2 | 0.4 | 28.9 | 13.0 | 2.7 | –0.1 | 0.3 |
| 80° | 1.9 | –0.0 | 0.1 | 27.5 | 5.5 | 1.8 | 0.2 | 1.5 |
| 90° | 2.9 | 0.2 | –0.1 | 4.9 | 1.6 | 0.1 | 0.6 | 3.0 |
| 100° | 3.8 | 0.4 | –0.2 | 1.3 | 0.0 | –0.3 | 0.9 | 4.5 |
| 110° | 4.5 | 0.6 | –0.2 | –0.2 | 0.3 | –0.2 | 1.1 | 5.8 |
| 120° | 4.9 | 0.8 | –0.2 | 1.2 | 2.9 | 0.2 | 1.0 | 6.5 |
| 130° | 4.8 | 1.0 | –0.2 | 5.9 | 8.2 | 0.5 | 0.8 | 6.4 |
| 140° | 4.2 | 1.0 | –0.1 | 5.0 | 5.9 | 0.6 | 0.7 | 5.4 |
| 150° | 3.2 | 0.9 | –0.1 | 2.8 | 3.4 | 0.5 | 0.5 | 3.6 |
| 160° | 1.9 | 0.8 | –0.1 | 1.2 | 1.6 | 0.4 | 0.5 | 1.8 |
| 170° | 0.8 | 0.5 | –0.1 | 0.3 | 0.5 | 0.3 | 0.5 | 0.7 |
| 180° | 0.4 | 0.2 | –0.1 | 0.1 | 0.2 | 0.2 | 0.5 | 0.6 |
| 190° | 1.7 | 0.1 | –0.1 | 0.3 | 0.4 | 0.3 | 0.6 | 1.7 |
| 200° | 5.1 | 0.7 | –0.1 | 0.7 | 1.0 | 0.5 | 0.7 | 5.2 |
| 210° | 8.8 | 2.1 | –0.1 | 0.9 | 1.3 | 0.8 | 0.8 | 10.9 |
| 220° | 11.9 | 3.7 | –0.1 | 0.7 | 1.2 | 1.0 | 0.9 | 16.2 |
| 230° | 14.5 | 5.2 | –0.1 | 0.2 | 0.7 | 0.8 | 0.8 | 20.0 |
| 240° | 16.4 | 6.6 | 0.0 | –0.1 | 0.2 | 0.4 | 0.7 | 22.8 |
| 250° | 18.0 | 7.8 | 0.4 | –0.2 | –0.2 | –0.0 | 0.5 | 24.8 |
| 260° | 19.0 | 8.7 | 0.9 | 0.1 | –0.1 | –0.2 | 0.1 | 26.2 |
| 270° | 12.3 | 9.2 | 1.4 | 0.8 | 0.4 | –0.1 | –0.3 | 27.0 |
| 280° | 5.9 | 9.4 | 1.8 | 2.0 | 1.5 | 0.4 | –0.5 | 4.1 |
| 290° | 1.9 | 4.4 | 2.0 | 3.4 | 3.0 | 1.3 | –0.4 | 0.7 |
| 300° | –0.1 | 0.9 | 1.8 | 4.8 | 5.0 | 2.2 | –0.2 | –0.2 |
| 310° | 0.7 | –0.2 | 1.0 | 5.7 | 6.0 | 3.0 | 0.1 | 1.7 |
| 320° | 4.8 | 1.4 | 0.2 | 5.5 | 6.0 | 3.5 | 0.4 | 5.7 |
| 330° | 10.4 | 4.6 | 0.2 | 4.0 | 4.8 | 3.6 | 0.7 | 4.0 |
| 340° | 5.0 | 3.1 | 0.4 | 1.9 | 2.8 | 3.1 | 0.7 | 2.0 |
| 350° | 1.5 | 1.3 | 0.5 | 0.6 | 1.8 | 2.0 | 0.6 | 0.5 |
СЛАБОЕ ВЛИЯНИЕ ТЕНИ НА ВИТКАХ В КОНЦЕ ТРАЕКТОРИИ
В табл. 3 особо выделяются два столбца, с t0 = = 91 и 274 суток, в которых все варианты “хорошие”. На первый взгляд, то, что ΔМРВ слабо меняется с изменением Ω0 во всем диапазоне значений, выглядит странно, особенно в сравнении с другими столбцами, в которых изменения большие. Но это частично, а именно в отношении того, почему группа витков в конце траектории с изменением параметра Ω0 почти не влияет на функционал, объясняется просто.
Даты t0 = 91 и 274 суток (от начала года) дней на 10 позже весеннего и осеннего равноденствия. Продолжительность номинального перелета 180 суток – около полугода, поэтому завершение перелетов – лишь на неделю позже осеннего и весеннего равноденствия, когда Солнце находится вблизи экватора. Поэтому витки в конце траектории, имеющие малое наклонение, пересекают цилиндр тени. И это хорошо видно для t0 = 91 на рис. 2: группа витков с тенью в конце траектории состоит из 23–32 витков, в зависимости от Ω0 (для t0 = 274 картина похожая).
Но эти витки имеют и малый эксцентриситет. Изменение параметра Ω0 означает поворот номинальной траектории как целого вокруг оси вращения Земли. На это можно посмотреть по-другому: что Солнце вращается в плоскости экватора вокруг траектории, так что участки тени смещаются по кругу вдоль почти круговых витков. Угловые размеры теневых участков ≈16°. Насколько ситуация близка к симметричной, видно из рис. 3, где показаны “цилиндр” тени и каждый седьмой виток из группы последних витков с тенью со 129-го по 157-й на номинальной траектории с t0 = 274 суток, Ω0 = 0°.
Рис. 3.
Витки 129, 136, 143,150, 157 с тенью на номинальной траектории, наклонение уменьшается с 1° до 0°, эксцентриситет с 0.122 до 0.
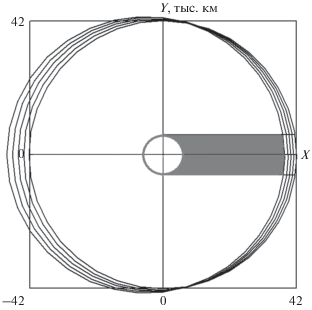
Отметим, что в данном случае группа витков с тенью состоит из 29 витков – это 18.5%, или почти пятая часть от всей угловой дальности перелета, а по продолжительности – 32.4 суток, или 17.7%. На траектории, реализующей такой перелет (с нулевой тягой в области тени), количество витков с тенью увеличивается до 31 (127‑й–157-й витки), ΔМРВ = 0.45% (2.19 кг). А, например, на траектории с Ω0 = 50° группа витков с тенью состоит из 34 витков (124-й–157-й витки), ΔМРВ = –0.24% (–1.15 кг). По угловой дальности это 21.7%, по продолжительности перелета 19.4%.
Из рис. 2 также видно, что почти на трети диапазона изменения Ω0 других витков с тенью, кроме группы конечных, нет. В этом диапазоне ∆МРВ < 0.85%. За пределами этого диапазона количество витков с тенью в начале траектории возрастает до 38 при Ω0 = 275°–295°, причем ∆МРВ достигает максимума 2% при Ω0 ≈ 290°. Были проведены расчеты, в которых влияние тени из первой группы витков было полностью “отключено”, т.е. на этих участках тяга не обнулялась. Они показали, что в таком случае ∆МРВ изменяется в диапазоне –0.146…0.842%. Т.е. вклад в ∆МРВ участков тени на витках в конце траектории действительно невелик, и он не сильно зависит от Ω0.
ОСОБОЕ ПОЛОЖЕНИЕ НАЧАЛЬНОЙ ОРБИТЫ ОТНОСИТЕЛЬНО ОРБИТЫ СОЛНЦА
Из табл. 3 видно, что наряду с “хорошими” столбцами есть несколько строк, в которых также все или почти все варианты “хорошие”. Это строки с Ω0, равным 160°–190°, 350° и 0°. Среди них особо выделяется строка с Ω0 = 180°, в которой значения ΔМРВ не превышают 0.56% (2.7 кг). Ясно, что дело, скорей всего, именно в начальной орбите, представляющей собой сильно вытянутый эллипс с эксцентриситетом e = 0.685 (радиус перигея 15.6, апогея 83.2 тыс. км). К тому же наибольшее наклонение на многовитковой траектории перелета на ГСО именно в начальный момент времени, в данном случае i = 13°.
Еще один аргумент в пользу высказанного предположения – то, что возмущения в начале траектории обычно сильнее влияют на конечные значения, чем возмущения в середине траектории, и тем более в конце. Из общих соображений также можно предположить, что дело не только в параметрах самой начальной орбиты и ее положении относительно орбиты ГСО, но и в ее положении относительно орбиты Солнца.
В чем особенность положения начальной орбиты с Ω0 = 180°, хорошо видно на рис. 4. На нем, в проекции на плоскость 〈Y, Z〉 небесной системы координат, показаны: плоскость эклиптики, в которой находится орбита Солнца, плоскость экватора, в которой находится ГСО, плоскость начальной орбиты для Ω0 = 180° и плоскость начальной орбиты для Ω0 = 0°. Все эти плоскости проходят через ось X (на рисунке в проекции дает точку O на пересечении осей Y, Z, направлена в сторону от зрителя).
Рис. 4.
Проекция плоскостей эклиптики, экватора и начальных орбит на плоскость 〈Y, Z〉 небесной системы координат.
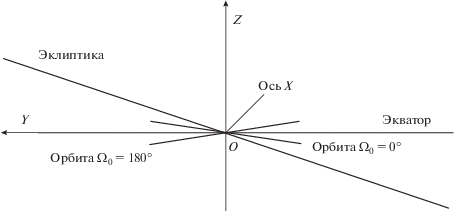
Плоскости начальных орбит с Ω0 = 0° и 180° расположены симметрично относительно плоскости экватора. Большие оси орбит – линии апсид – совпадают с осью X, но направлены противоположно друг другу. При движении Солнца по орбите цилиндр тени заметает окрестность плоскости эклиптики, пересекая начальные орбиты вблизи оси X, т.е. вблизи их линий апсид, в окрестности перигея и апогея. Линии апсид являются осями симметрии эллипса, и именно это является главной особенностью орбит с Ω0 = 0° и 180°, т.к. возмущения от участков тени, расположенных вблизи оси симметрии, по-видимому, легче нивелировать.
Но между двумя этими орбитами есть различия. Во-первых, это противоположные направления больших осей. Во-вторых – разное положение плоскостей орбит по отношению к плоскости эклиптики. Для орбиты с Ω0 = 180° угол между плоскостью орбиты и плоскостью эклиптики равен 23.5° + 13° = 36.5°, для орбиты с Ω0 = 0° он равен 23.5° – 13° = 10.5°. А чем меньше этот угол, тем больший отрезок орбиты заметается цилиндром тени. Например, при наклонении орбиты i = 23.5° угол будет равен 0°, т.е. начальная орбита с Ω0 = 0° будет лежать в плоскости эклиптики, и цилиндр тени будет заметать всю орбиту. В результате по затратам ΔМРВ строка с Ω0 = 0° в табл. 3 оказывается хуже, чем с Ω0 = 180°.
ВОЗМОЖНОСТЬ СУЩЕСТВОВАНИЯ НЕСКОЛЬКИХ РЕШЕНИЙ
Еще одной особенностью задачи является возможность существования разных ветвей решений и, как следствие, нескольких решений для одних и тех же значений параметров.
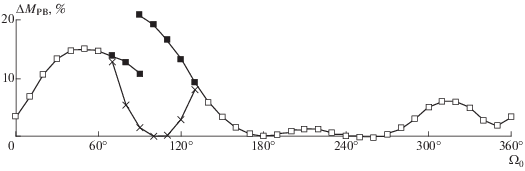
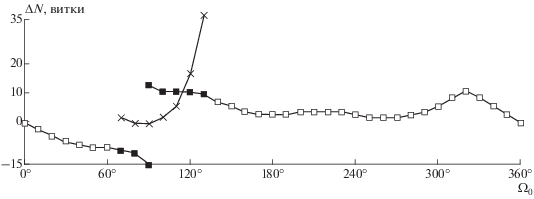
На рис. 5, 6 представлены графики зависимости ∆МРВ и ∆N от Ω0 для двух ветвей решений с t0 = 183. Основная ветвь, решения которой существуют во всем диапазоне изменения параметра Ω0, помечена квадратиками: белыми – на большей части ветви, черными – где функционал больше, чем на второй ветви. Решения второй ветви существуют в небольшом диапазоне углов и дают лучшие решения для Ω0 в диапазоне 70°–130° (помечены крестиками).
Особенностью первой ветви является то, что она не замкнута, хотя ее решения существуют для всех значений Ω0: при приближении Ω0 к 90° слева мы получаем одно решение, при приближении Ω0 к 90° справа – другое решение. В результате для Ω0 = 90° имеем три решения. Они приведены в табл. 4. Причем в данном случае все три решения существуют не только для оптимальных N (помечены звездочкой), но и для N = 157 (как на номинальной траектории).
Таблица 4.
Три решения “неполной” краевой задачи для t0 = 183 суток, Ω0 = 90°
| N, витки | ΔN | T, сутки | ΔT, сутки | TSh, сутки | nSh, витки | kSh | MРВ, кг | ΔМРВ, кг | ΔМРВ, % | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 157 | 0 | 184.67 | 4.68 | 1.73 | 37–79 | 43 | 493.3 | 7.97 | 1.64 |
| 156* | –1 | 184.61 | 4.62 | 1.70 | 37–78 | 42 | 493.2 | 7.87 | 1.62 | |
| 2 | 157 | 0 | 205.07 | 25.08 | 1.29 | 30–58 | 29 | 549.4 | 64.14 | 13.22 |
| 142* | –15 | 200.54 | 20.55 | 1.18 | 31–56 | 26 | 537.5 | 52.23 | 10.76 | |
| 3 | 157 | 0 | 221.08 | 41.09 | 1.40 | 36–68 | 33 | 592.3 | 107.03 | 22.05 |
| 169* | +12 | 219.30 | 39.31 | 1.68 | 37–77 | 41 | 586.8 | 101.47 | 20.91 |
ΔN, ΔT, ΔMРВ – разница в количестве витков N, продолжительности перелета T и затратах рабочего вещества MРВ (в кг и % от 485.31 кг) на траектории с нулевой тягой в тени и на номинальной траектории; TSh – суммарная продолжительность участков с нулевой тягой; nSh, kSh – номера витков с тенью и их количество.
ПРОБЛЕМА НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ
При решении краевых задач возникает проблема выбора хорошего начального приближения. В рассматриваемой задаче это могут быть решения с близкими значениями даты старта t0 или долготы восходящего узла Ω0. Однако, как следует из рис. 5, 6, близость параметров не всегда означает близость решений: имея решение с Ω0 < 90°, принадлежащее левой части первой ветви, получить решение с Ω0 > 90°, принадлежащее правой части этой же ветви, не удастся. Тем более, не удастся получить решение, принадлежащее другой ветви (разве что случайно).
В отсутствие каких-либо решений, либо с целью попытаться найти альтернативное решение, естественно рассмотреть в качестве начального приближения номинальную траекторию. К сожалению, траектории с одинаковыми начальными значениями фазовых и сопряженных переменных, но разными значениями тяги в области тени – номинальной и нулевой, могут отличаться очень сильно, если участков с тенью много. Невязки в перигее и апогее могут достигать десятков тыс. км.
Если бы изменение тяги в области тени было в несколько раз меньше, с номинального (максимального) не до нуля, а, например до 0.9 номинального значения, то и невязки уменьшились бы на порядок, и краевую задачу, возможно, удалось бы решить. Полученное решение затем можно было бы использовать, чтобы получить решение с тягой в 0.8 от номинального значения, и т.д. Т.е. решить серию краевых задач, “выключая” тягу на теневых участках постепенно, пока не получим искомое решение.
На рис. 7 приведен пример серии из 10 краевых задач, с постепенным уменьшением тяги в области тени до нуля с шагом 0.1 (от максимального значения). Учитывая, что решения с количеством витков как у номинальной траектории может не существовать для перелета с нулевой тягой в области тени, в процессе решения каждой краевой задачи оптимизировалось количество витков. Оптимальное количество витков выявлялось прямым перебором, т.е. фактически пришлось решить более трех десятков краевых задач.
На рисунке представлены данные по траекториям с оптимальным количеством витков, последние витки отмечены белыми кружками. Черными кружками отмечены витки с участками тени (при данном масштабе – каждый второй и крайние в группе). В этом примере “эволюция” решения краевой задачи довольно существенна. На траектории с максимальной тягой в области тени количество витков с участками тени – 54 (это витки с 76-го по 129-й), при общем количестве витков 157. На траектории с нулевой тягой в области тени количество витков с тенью – 24 (это витки с 50-го по 73-й), при общем количестве витков 146. То есть общее количество витков уменьшилось на 11 (с 157 до 146), количество витков с тенью – на 30 (с 54 до 24).
Но надо отметить, что это очень “плохой” вариант – различие в затратах рабочего вещества 30.3%, или 147 кг (см. табл. 3 для t0 = 137 и Ω0 = 50°). Если решение краевой задачи очень сильно отличается от номинального, не всегда удается получить решение таким образом. В “хороших” случаях различие невелико и по функционалу – затратам рабочего вещества, и по другим характеристикам траекторий.
ТЕНЬ КАК БАРЬЕР
В отличие от других возмущающих факторов – гравитационного влияния Луны, Солнца, вариаций геопотенциала, которые представляют собой поле сил, рассматриваемое влияние тени таковым не является. Тень ведет себя, скорее, как барьер. А проявляется это, в частности, в незамкнутости ветви решений и сильном изменении количества витков, как на рис. 5, 6. Каков механизм такого воздействия?
В [8], где рассматривались перелеты без тени, было показано, что существует много решений краевой задачи, различающихся количеством витков. Причем в большом диапазоне изменения количества витков (он тем больше, чем больше наилучшая угловая дальность перелета на ГСО, или, в терминах данной статьи – чем больше угловая дальность номинальной траектории) функционал меняется не сильно. В случае постоянно работающей и постоянной по величине тяги это эквивалентно тому, что в этом диапазоне витков почти постоянна продолжительность перелета. Например, для траекторий перелета на ГСО с рассматриваемой здесь начальной орбиты (табл. 1), с количеством витков N в диапазоне от 151 до 166 (16 траекторий), отличие функционала от номинального (табл. 2) не превышает 1%. Для N из диапазона [149–171] (23 траектории) – менее 2%, из диапазона [144–183] (40 траекторий) – менее 5%, из диапазона [141–201] (61 траектория) – менее 10%.
И здесь напрашивается аналогия со спирально закрученной пружиной будильника. Только в случае с пружиной постоянна ее длина. При скручивании пружины увеличивается количество витков, а так как общая длина не изменяется – уменьшаются длина каждого витка и его размеры. Аналогично и с многовитковой траекторией: с увеличением количества витков при почти постоянной общей продолжительности перелета продолжительность каждого витка и его размеры уменьшаются. С уменьшением количества витков их размеры, наоборот, увеличиваются. Частично за счет этого можно “обогнуть” препятствие в виде цилиндра тени. А в зависимости от того, с наружной или внутренней стороны витков находится большая часть цилиндра тени, количество витков будет уменьшаться или увеличиваться. Именно этим, по-видимому, можно объяснить эффекты, проявляющиеся на рис. 5, 6. Хотя в реальности все сложнее, поскольку витков с тенью много, цилиндр тени от витка к витку смещается в пространстве, и продолжительность перелета может изменяться очень сильно.
МИНИМИЗАЦИЯ ЗАТРАТ ПО ПАРАМЕТРУ Ω0
Определим для каждого t0 наилучшее значение Ω0 и соответствующее ΔМРВ.
Изменяя время старта tС ракетоносителя в интервале одних суток, можно получить весь спектр значений параметра Ω0. Подобрать tС можно так, чтобы момент t(Ω0) выхода КА на нужную начальную орбиту лежал в диапазоне t0 ± 0.5. После чего может потребоваться пауза Δt продолжительностью от 0 до 1.264 суток, чтобы старт с начальной орбиты был в перигее. В зависимости от значений t(Ω0) и Δt можно скорректировать время tС так, чтобы время старта с орбиты отличалось от t0 не более чем на 0.5 суток. Например, если t(Ω0) = 0.5, а Δt = 0.25, 0.5, 0.75, 1.0 или 1.25 – можно уменьшить tС на сутки или двое, и время старта с орбиты будет соответственно t0 – 0.25, t0, t0 + 0.25, t0 ± 0.5, t0 – 0.25. Из-за таких изменений времени старта значения ΔМРВ будут отличаться от табличных не сильно, и совсем немного – для хороших вариантов.
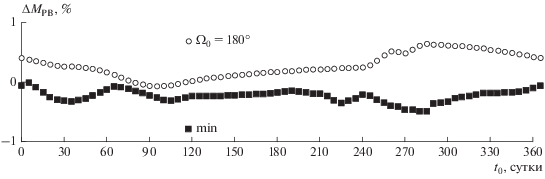
На рис. 8 приведен график минимальных по параметру Ω0 значений ΔМРВ. Расчеты проводились для t0 с шагом 5 суток и Ω0 с шагом 10°. Как видно, во всем диапазоне изменения даты старта t0 затраты ΔMРВ < 0, т.е. затраты на перелет с обнулением тяги в области тени меньше, чем на номинальной траектории. Однако выигрыш в затратах небольшой – менее 0.5%. Для сравнения приведен также график ΔМРВ для Ω0 = 180°: для большинства значений t0 затраты ΔМРВ > 0, но не превышают 0.62%.
Т.о., для перелетов на ГСО с рассмотренных здесь начальных орбит “неполная” краевая задача позволила получить траектории с нулевой тягой в области тени с затратами рабочего вещества меньшими, чем на траекториях номинальных – с постоянно работающей малой тягой. При этом перелеты с начальной орбиты с фиксированным значением параметра Ω0 = 180° лишь ненамного хуже номинальных.
Список литературы
Sackett L.L., Malchow H.L., Edelbaum T.N. Solar Electric Geocentric Transfer with Attitude Constraints. 1975 Analysis, NASA CR 134927, Washington, DC.
Салмин В.В. Оптимизация космических перелетов с малой тягой. М.: Машиностроение, 1987.
Lundberg B.N. An Adjoint Jump Shooting Method for Parametric Low Thrust Orbit Transfer Problems with Eclipsing // Proceedings of the Fourth International Conference on Astrodynamics Tools and Techniques (WPP-308), ESAC, Madrid, Spain. 2010.
Петухов В.Г. Квазиоптимальное управление с обратной связью для многовиткового перелета с малой тягой между некомпланарными эллиптической и круговой орбитами // Космич. исслед. 2011. Т. 49. № 2. С. 128–137. (Cosmic Research. P. 121).
Tarzi Z., Speyer J., Wirz R. Fuel Optimum Low-Thrust Elliptic Transfer Using Numerical Averaging // Acta Astronautica. 2013. V. 86. P. 95–118.
Mazzini L. Finite Thrust Orbital Transfers // Acta Astronautica. 2014 V. 100. P. 107–128.
Graham K.F., Rao A.V. Minimum-Time Trajectory Optimization of Low-Thrust Earth-Orbit Transfers with Eclipsing // J. Spacecraft and Rockets. 2016. V. 53. P. 289–303.
Ахметшин Р.З. Плоская задача оптимального перелета космического аппарата с малой тягой с высокоэллиптической орбиты на геостационар // Космич. исслед. 2004. Т. 42. № 3. С. 248–259. (Cosmic Research. P. 238).
Ахметшин Р.З. Многовитковые траектории с учетом пауз в работе ЭРД малой тяги при попадании КА в тень Земли. Препринты ИПМ им. М.В. Келдыша. 2018. № 266.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1976.
Ахметшин Р.З. Возмущения от Луны при многовитковых перелетах на геостационарную орбиту космического аппарата с малой тягой. Препринты ИПМ им. М.В. Келдыша. 2015. № 107.
Ахметшин Р.З. Возмущения от Солнца при многовитковых перелетах на геостационарную орбиту космического аппарата с малой тягой. Препринты ИПМ им. М.В. Келдыша. 2016. № 77.
Ахметшин Р.З. Влияние вариаций геопотенциала при многовитковых перелетах на геостационарную орбиту космического аппарата с малой тягой. Препринты ИПМ им. М.В. Келдыша. 2016. № 111.
Петухов В.Г. Оптимизация многовитковых перелетов между некомпланарными эллиптическими орбитами // Космич. исслед. 2004. Т. 42. № 3. С. 260–279. (Cosmic Research. P. 250).
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования