Космические исследования, 2021, T. 59, № 3, стр. 218-234
Исследование колебаний элементов конструкции космической станции по видеоинформации
Н. Д. Беклемишев 1, А. А. Богуславский 1, М. Ю. Беляев 2, О. Н. Волков 2, В. В. Сазонов 1, *, С. М. Соколов 1, А. Н. Софинский 2
1 Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
2 Ракетно-космическая корпорация “Энергия” им. С.П. Королёва
Королёв, Россия
* E-mail: sazonov@keldysh.ru
Поступила в редакцию 27.03.2020
После доработки 02.05.2020
Принята к публикации 29.05.2020
Аннотация
Результаты космического эксперимента “Среда – МКС” показали, что зрительные данные о колебаниях элементов конструкции МКС позволяют получить количественные характеристики этих колебаний. Такие характеристики были найдены в результате анализа временных рядов, полученных прослеживанием на видеопоследовательностях некоторых объектов в конструкции МКС. Числовые данные представляют собой выраженные в пикселях вертикальные и горизонтальные координаты в кадре выделенной точки элемента конструкции. Анализ полученных временных рядов позволяет восстановить реальную зависимость указанных координат от времени. Эта зависимость в ряде случаев носит колебательный характер и может быть представлена суммой конечного числа гармоник, амплитуды и частоты которых определяются с помощью спектрального анализа.
ВВЕДЕНИЕ
Результаты космического эксперимента “Среда – МКС” показали [1], что зрительная информация о колебаниях элементов конструкции станции позволяет получить содержательные количественные характеристики этих колебаний. В этой работе приведены результаты обработки временных рядов, полученных оцифровкой четырех видеофильмов, снятых фотоаппаратом Nikon D5 в 2018 году: 4.IV, 31.V и 26.VII. Длительность каждого фильма около получаса. Объектом съемки служили внешние элементы конструкции МКС со сравнительно малыми инерционными параметрами (массами и моментами инерции). Ниже приведены некоторые результаты [1] по определению характеристик колебаний, которые можно рассматривать как установившиеся.
Фотоаппарат располагался рядом с одним из иллюминаторов Российского сегмента (РС) МКС и крепился к корпусу станции с помощью специального кронштейна. На объектах съемки выделялись характерные точки, движение которых прослеживалось в течение практически всего видеофильма. Метод межкадрового прослеживания описан в [2]. Координаты выделенных точек в кадре определялись в цифровом виде. Их значения задавались на равномерной временной сетке с шагом 0.04 с. Полученные временные ряды служили объектом последующего анализа. Такой анализ позволяет восстановить реальную зависимость указанных координат от времени и получить сведения о движении снятых объектов.
Найденные движения представляют собой колебания, характер которых со временем меняется. Однако на большом числе продолжительных по времени отрезков эти колебания можно считать установившимися и представить в виде суммы конечного числа гармоник (циклических трендов). Параметры гармоник (частоты, амплитуды и фазы) определяются методами спектрального анализа [3]. В результате удается получить количественные характеристики колебаний объектов. Ниже основное внимание уделено выявлению и исследованию таких многочастотных колебаний.
Заметим, что видеосъемка – наиболее практичный способ получения такого рода данных для малоинерционных объектов. В случае массивных объектов похожую (и более точную) информацию можно получить, анализируя данные бортовых акселерометров [4–6], но в случае внешних малоинерционных объектов использовать акселерометры гораздо сложнее.
ПОЛУЧЕНИЕ И ПОДГОТОВКА ВИДЕОИНФОРМАЦИИ
Видеосъемка производилась фотоаппаратом Nikon D5 с объективом AFZoom-Nikkor 80–400 мм f/4.5-f/5.6. Объектив имеет фокусное расстояние 400 мм, скорость видеосъемки – 25 кадров в секунду, размер кадра – 3840 × 2160 пикселей. Размер матрицы фотоаппарата – 35.9 × × 23.9 мм. Отсюда находим значения фокусного расстояния объектива в пикселях видео – $f = 42{\kern 1pt} 785.5$. Масштаб съемки – длина стороны одного пикселя изображения объекта, находящегося на расстоянии d от фотоаппарата, – определяется как отношение ${d \mathord{\left/ {\vphantom {d f}} \right. \kern-0em} f}$. При расстоянии до объекта 10 м размер пикселя равен примерно $0.23$ мм.
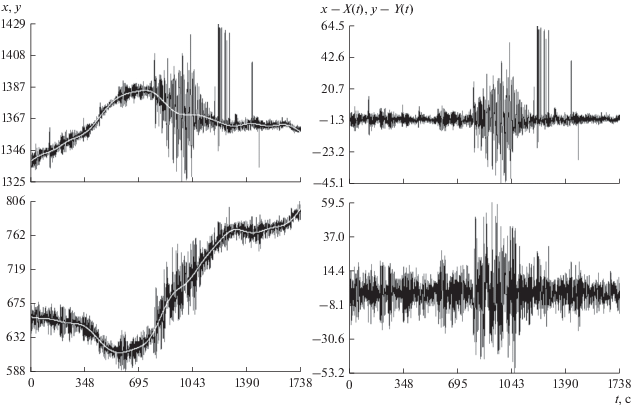
В качестве примера рассмотрим съемку 31.V.2018 (более детально результаты съемок и их обработки приведены в [1]). Объект съемки – край правого трехполосного радиатора (рис. 1). Фотоаппарат закреплен кронштейном УПК LIV/106/20 к поручню выходного люка МИМ2 у иллюминатора № 8. Расстояние до объекта съемки – примерно 8 м, масштаб съемки – 1 пиксель ≈0.19 мм. Начало съемки – 12.37 Мск. Продолжительность видео – 28 мин 25 с, всего обработано 42627 кадров. По данной видеопоследовательности прослеживались семь точек, показанных на рис. 2. Графики зависимости пиксельных координат точки 7 от времени приведены в правой части рис. 3. Здесь и ниже время отсчитывается от начала съемки.
Объектом съемки 4.IV.2018 был край левого трехполосного радиатора, если смотреть из РС в направлении Американского сегмента (АС) МКС. Фотоаппарат закреплен кронштейном УПК LIV/106/20 к поручню выходного люка СО1 у иллюминатора № 2. Расстояние до объекта съемки – около 10 м, масштаб съемки – 1 пиксель ≈0.23 мм. Начало съемки – 13.34 Мск. Продолжительность видео – 28 мин 8 с, всего обработано 42200 кадров. По данной видеопоследовательности прослеживались 8 точек. Графики зависимости пиксельных координат одной из точек от времени приведены в левой части рис. 3. За время съемки происходило постепенное смещение объекта съемки в кадре на величину примерно 700 пикселей ≈16 см. По-видимому, это связано с долгопериодическими колебаниями конструкции с периодом, большим, чем время съемки видео. В некоторые моменты наблюдались резкие толчки с амплитудой до 150 пикселей ≈35 мм.
26.VII.2018 выполнялась одновременная видеосъемка двумя фотоаппаратами Nikon D5 из двух модулей РС МКС. Во время съемки была проведена коррекция орбиты МКС. Съемка началась в 18.55 Мск, корректирующие двигатели работали 199 с на интервале 19.10.17–19.13.36.
Первым фотоаппаратом проводилась съемка через иллюминатор № 7 Служебного модуля (СМ) РС. Объект съемки – оконечность солнечной батареи корабля Прогресс. Вторым фотоаппаратом проводилась съемка через иллюминатор № 2 модуля МИМ2. Объект съемки: оконечность радиатора МКС, расположенного справа от корпуса станции по ходу ее движения по орбите. Расстояние до объекта съемки – около 10 м, масштаб съемки – 1 пиксель ≈0.23 мм. По данной видеопоследовательности прослеживались 9 точек. 43 452 кадра (28 мин 58 с). Графики пиксельных координат одной из точек приведены в левой части рис. 4. Смещение объекта за время съемки относительно первого кадра находилось в пределах 200 пикселей (~46 мм) по каждой координате. Во время коррекции орбиты вид колебаний не менялся.
ПОДГОТОВКА ДАННЫХ ДЛЯ СПЕКТРАЛЬНОГО АНАЛИЗА
Как видно из графиков на рис. 3, 4, колебания выделенных точек на элементах конструкции МКС описываются функциями времени специального вида. Эти функции представляют собой сумму двух слагаемых. Одно из них имеет характерное время изменения несколько минут, другое с характерным временем изменения несколько секунд похоже на сумму конечного числа гармоник (в ряде случаев гармоник, умноженных на экспоненты). Слагаемое первого типа характеризует медленные движения элементов конструкции станции, вызванные тепловыми деформациями, колебаниями станции как твердого тела, поворотом солнечных батарей (СБ) и другими аналогичными причинами. Такие движения происходят с частотами менее 0.001 Гц. Гармоники, входящие во второе слагаемое, имеют частоты в пределах 0.05–0.3 Гц. Второе слагаемое обусловлено собственными колебаниями элементов конструкции станции. Именно эти колебания изучаются ниже.
При изучении таких колебаний указанное выше первое слагаемое из функций, описывающих изменение координат выделенных точек, следует исключить. Исключение выполнялось с использованием дискретных рядов Фурье. Смещения выделенных точек на ПЗС матрице фотоаппарата обозначим $x$, $y$ и будем выражать в пикселях, т.е. размер стороны пикселя примем в качестве единицы измерения длины. Значения смещений заданы в узлах равномерной временной сетки ${{t}_{n}} = {{t}_{0}} + nh$, $h = 0.04$ с, $n = 0,\;1,\, \ldots ,\,N$. Эти значения обозначим ${{x}_{n}}$, ${{y}_{n}}$ и полагаем их измерениями реальных смещений $x(t),\;y(t)$: ${{x}_{n}} \approx x({{t}_{n}}),\;{{y}_{n}} \approx y({{t}_{n}})$.
По данным $\{ ({{t}_{n}},{{x}_{n}}{\kern 1pt} )\} _{{n = 0}}^{N}$ методом наименьших квадратов построим выражение
(1)
$X(t) = \alpha + \beta (t - {{t}_{0}}) + \sum\limits_{m = 1}^M {{{a}_{{m}}}\sin \frac{{\pi m(t - {{t}_{0}})}}{{{{t}_{N}} - {{t}_{0}}}}} .$По данным $\{ ({{t}_{n}},{{y}_{n}}{\kern 1pt} )\} _{{n = 0}}^{N}$ – аналогичное выражение $Y(t)$. Каждое выражение – сумма линейной функции и отрезка ряда Фурье по синусам. Выражения вида (1) удобно использовать для аппроксимации произвольных гладких функций, заданных на отрезке ${{t}_{0}} \leqslant t \leqslant {{t}_{N}}$ [7]. При подходящем значении $M$ эти выражения аппроксимируют слагаемые указанного выше первого типа в функциях $x(t),\;y(t)$. Разности ${{x}_{n}} - X({{t}_{n}})$, ${{y}_{n}} - Y({{t}_{n}})$ уже не содержат таких слагаемых и представляют собой сумму конечного числа гармоник и, возможно, гармоник, умноженных на экспоненты.
Пример исключения слагаемых первого типа приведен на рис. 4. В левой части этого рисунка изображены графики исходных данных и выражений $X(t)$, $Y(t)$. Графики исходных данных представляют собой пилообразные ломаные линии. Звенья верхних ломаных соединяют соседние по времени точки $({{t}_{n}},\;{{x}_{n}})$, нижние ломаные имеют вершины в точках $({{t}_{n}},\;{{y}_{n}})$. Плавные кривые на фоне ломаных – графики выражений $X(t)$, $Y(t)$. В данном примере эти выражения построены при $M = 20$.
В правой части рис. 4 приведены графики ломаных с вершинами в точках $({{t}_{n}},\;{{x}_{n}} - X({{t}_{n}})),$ $({{t}_{n}},\;{{y}_{n}} - Y({{t}_{n}}))$. Как видно из этих графиков, слагаемые первого типа в соответствующих кусочно-линейных функциях отсутствуют. Ниже для упрощения записи разности ${{x}_{n}} - X({{t}_{n}})$, ${{y}_{n}} - Y({{t}_{n}})$ будем обозначать ${{x}_{n}}$ и ${{y}_{n}}$ соответственно.
СПЕКТРАЛЬНЫЙ АНАЛИЗ
Основные приемы спектрального анализа изложим на примере данных $\{ ({{t}_{n}},{{x}_{n}}{\kern 1pt} )\} _{{n = 0}}^{N}$. Данные $\{ ({{t}_{n}},{{y}_{n}}{\kern 1pt} )\} _{{n = 0}}^{N}$ анализируются аналогично. Более подробно эти приемы описаны в [3]. Спектральный анализ начинался с попытки выделить из данных ${{x}_{n}}$ отдельные гармонические составляющие (их еще называют циклическими трендами). С этой целью данные аппроксимировались функцией
где ${{a}_{0}}$, $a$, $b$ и $f$ – параметры. Значения параметров искались методом наименьших квадратов. Составим выражениеСогласно методу наименьших квадратов определение параметров ${{a}_{0}}$, $a$, $b$ и $f$ сводится к минимизации по ним выражения (3). Функция $\Psi = \Psi ({{a}_{0}},\,a,\,b,\,f)$ имеет, как правило, много локальных минимумов, поэтому ее минимизация проводилась поэтапно. Сначала в результате решения ряда одинаковых линейных задач наименьших квадратов вычислялись значения функции ${{\Psi }_{1}}(f) = \mathop {\min }\limits_{{{a}_{0}},a,b} \Psi ({{a}_{0}},a,b,f)$ в узлах достаточно мелкой равномерной сетки на отрезке $0 \leqslant f \leqslant F = {{(2h)}^{{ - 1}}}$ (смысл величины $F$ пояснен ниже), строился график этой функции. Затем перебором по сетке находились приближенные значения точек минимума ${{\Psi }_{1}}(f)$. Абсциссы значимых (с достаточно малыми ординатами) точек минимума могут быть частотами искомых гармоник. Значения параметров ${{a}_{0}}$, $a$, $b$ и $f$, отвечающие значимым сеточным минимумам функции ${{\Psi }_{1}}$, уточнялись посредством минимизации функционала (2), (3). Задача одновременного уточнения параметров ${{a}_{0}}$, $a$, $b$ и $f$ является нелинейной. Ее решение находилось методом Гаусса–Ньютона [8].
Для проверки значимости найденных частот другим способом наряду с функцией ${{\Psi }_{1}}(f)\,$ рассматривалась функция
(4)
$x(t) = {{a}_{0}} + \sum\limits_{k = 1}^K {({{a}_{k}}\cos 2\pi {{f}_{k}}t + {{b}_{k}}\sin 2\pi {{f}_{k}}t} ),$Его можно преобразовать к виду
В выражении для $\Delta {{I}_{1}}(f)$ частоты ${{\Omega }_{m}}$ и $\Omega _{m}^{'}$ принадлежат множеству чисел $\{ \pm {{f}_{1}}, \pm {{f}_{2}}, \ldots , \pm {{f}_{K}}\} ,$ коэффициенты ${{A}_{m}}$ и ${{B}_{m}}$ выражаются через ${{\alpha }_{k}}$ и ${{\beta }_{k}}$ $(k = 1,\;2,\; \ldots ,\;K)$.
Функция $W(f)$ называется функцией окна [3]. Она – четная, периодическая с периодом 2F = ${{h}^{{ - 1}}}$ и удовлетворяет соотношениям $0 \leqslant W(f) \leqslant 1$, $W(0) = 1$. Ее наименьший положительный нуль равен ${{[(N + 1)h]}^{{ - 1}}}$. Значимые максимумы (пики) функции окна равны 1 и достигаются в точках ${{F}_{l}} = 2lF$ $(l = 0,\;1,\;2, \ldots )$. Вне малых окрестностей этих точек $W(f) < 0.01$. С увеличением $N$ ширина пиков этой функции сужается. В силу четности и периодичности функция окна полностью определяется своими значениями на отрезке $0 \leqslant f \leqslant F$.
Для $\Delta {{I}_{1}}(f)$ не удается найти простых эффективных оценок, но при большом $N$ вкладом этого слагаемого в значения функции ${{I}_{1}}(f)$ вблизи точек ее значимых максимумов можно пренебречь и принять
Здесь необходимо отметить следующее. Корректная интерпретация частот в данных на равномерной временной сетке с шагом $h$ возможна лишь в том случае, если в этих данных отсутствуют частоты, превышающие частоту Найквиста $F = {{0.5} \mathord{\left/ {\vphantom {{0.5} h}} \right. \kern-0em} h}$. Если в данных присутствует гармоническая составляющая частотой $f > F$, то она либо исказит составляющие с частотами $\left| {f \pm {{F}_{l}}} \right|$ при значениях $l$, для которых $0 \leqslant \left| {f \pm {{F}_{l}}} \right| \leqslant F$, либо проявится как дополнительная частота. Этот эффект называется наложением частот. Чтобы избежать его, регистрируемые данные перед оцифровкой подвергают фильтрации. В случае обрабатываемых видеоданных фильтрации не было, анализ их спектров показывает, что сколько-нибудь значимых гармонических составляющих с частотами из диапазона $2{\kern 1pt} - {\kern 1pt} 12.5\,\,{\text{Гц}}$ в них нет. Колебания с частотами более 12.5 Гц в случае МКС имеют весьма малую амплитуду и в видеофильмах не проявляются. Это обстоятельство служит обоснованием корректности проводимого спектрального анализа.
Периодограмма Шустера используется следующим образом. Если функция ${{I}_{1}}(f)$ имеет значимый максимум в точке $f{\text{*}}$, то $f{\text{*}}$ близка одной из частот выражения (3). При $f{\text{*}} \approx {{f}_{k}}$ величина ${{2\sqrt {{{I}_{1}}(f{\text{*}})} } \mathord{\left/ {\vphantom {{2\sqrt {{{I}_{1}}(f{\text{*}})} } {(N + 1)}}} \right. \kern-0em} {(N + 1)}} \approx \sqrt {\alpha _{k}^{2} + \beta _{k}^{2}} $, т.е. является оценкой амплитуды гармоники с частотой ${{f}_{k}}$. Так как погрешность соотношения ${{\alpha }_{0}} = x{\text{*}}$ обычно весьма мала, в выписанных соотношениях функцию ${{I}_{1}}(f)$ можно заменить функцией $I(f)$.
Ниже для удобства вместо графиков функций ${{\Psi }_{1}}(f)\,$ и $I(f)$ приводятся графики функций
Минимумы функции $E(f)$ дают оценки средней квадратичной ошибки аппроксимации функции $x(t)$ выражением (1), максимумы функции $A(f)$ – оценки амплитуды $\sqrt {{{a}^{2}} + {{b}^{2}}} $. Функцию $A(f)$ называют еще амплитудным спектром. Ниже функции E( f) и A( f), построенные по данным $\{ ({{t}_{n}},{{x}_{n}}{\kern 1pt} )\} _{{n = 0}}^{N}$, снабжены нижним индексом $x$, функции, построенные по данным $\{ ({{t}_{n}},{{y}_{n}}{\kern 1pt} )\} _{{n = 0}}^{N}$, снабжены индексом $y$.
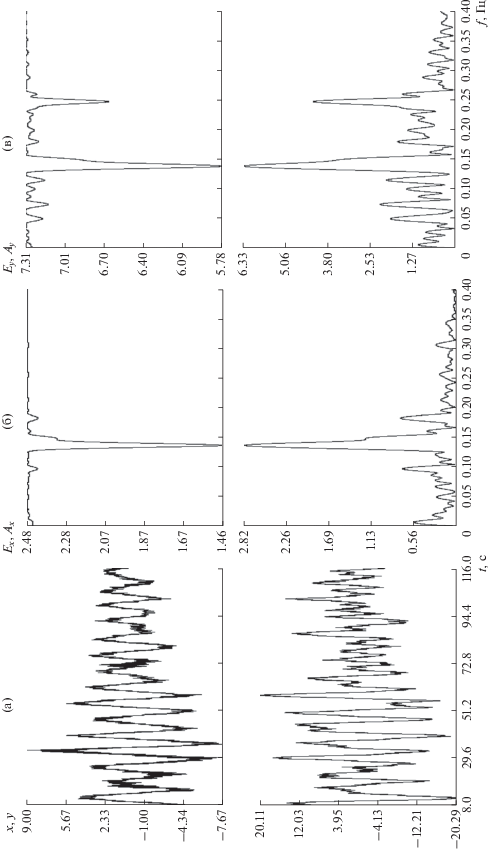
Результаты спектрального анализа фрагмента данных, выделенного из данных на рис. 4, приведен на рис. 5. В левой части этого рисунка представлены графики анализируемого фрагмента – ломаные с вершинами в точках $({{t}_{n}},\;{{x}_{n}})$, $({{t}_{n}},\;{{y}_{n}})$. В средней и правой частях рисунков приведены соответствующие периодограммы (спектры) ${{E}_{x}}(f)$, ${{A}_{x}}(f)$ и ${{E}_{y}}(f)$, ${{A}_{y}}(f)$. Спектры построены на отрезке $0 \leqslant f \leqslant 0.4$ Гц. При $f > 0.4$ Гц значимых экстремумов периодограмм не обнаружено. Ниже приведены частоты $f$ и амплитуды $A = \sqrt {{{a}^{2}} + {{b}^{2}}} $ циклических трендов, отвечающих значимым и с подозрением на значимость минимумам функции ${{\Psi }_{1}}(f)$. Частоты приведены в герцах, амплитуды – в пикселях. Нижние индексы $x$ и $y$ указывают, к каким данным $\{ {{x}_{n}}\} $ или $\{ {{y}_{n}}\} $ эти частоты и амплитуды относятся:
(5)
$\begin{gathered} {{f}_{{x,1}}} = 0.00506,\,\,\,\,{{A}_{{x,1}}} = 0.57,\,\,\,\,{{f}_{{x,2}}} = 0.09692,\,\,\,\,{{A}_{{x,2}}} = 0.72, \hfill \\ {{f}_{{x,3}}} = 0.13656,\,\,\,\,{{A}_{{x,3}}} = 2.85,\,\,\,\,{{f}_{{x,4}}} = 0.18249,\,\,\,\,{{A}_{{x,4}}} = 0.74, \hfill \\ {{f}_{{x,5}}} = 0.25639,\,\,\,\,{{A}_{{x,5}}} = 0.23,\,\,\,\,{{f}_{{x,6}}} = 0.30595,\,\,\,\,{{A}_{{x,6}}} = 0.28, \hfill \\ {{f}_{{y,1}}} = 0.05010,\,\,\,\,{{A}_{{y,1}}} = 1.94,\,\,\,\,{{f}_{{y,2}}} = 0.07429,\,\,\,\,{{A}_{{y,2}}} = 2.25, \hfill \\ {{f}_{{y,3}}} = 0.11527,\,\,\,\,{{A}_{{y,3}}} = 2.06,\,\,\,\,{{f}_{{y,4}}} = 0.13878,\,\,\,\,{{A}_{{y,4}}} = 6.33, \hfill \\ {{f}_{{y,5}}} = 0.18002,\,\,\,\,{{A}_{{y,5}}} = 1.72,\,\,\,\,{{f}_{{y,6}}} = 0.24759,\,\,\,\,{{A}_{{y,6}}} = 4.27. \hfill \\ \end{gathered} $Рис. 5.
Фрагмент съемки 26.VII.2018: а – колебания выделенной точки; б, в – спектры координат $x$, $y$.
Анализ найденных частот обнаруживает их повторяемость и локализацию в нескольких достаточно узких диапазонах [1]. Например, частоты из окрестностей значений 0.09, 0.14, 0.18, 0.22 Гц и др. встречаются в разные дни съемки.
Вообще, поиск гармонических составляющих в данных измерений является коварной задачей. Если амплитуда найденной гармоники мала и нет априорной уверенности в существовании такой гармоники, то вывод о ее обнаружении может оказаться ошибочным [3]. Гармоники с малыми амплитудами могут порождаться случайными ошибками в данных. Для гармоник с большими амплитудами таких сомнений не возникает. Еще одна сложность, которая может возникнуть в спектральном анализе, это – разрешение близких частот. В приведенных фрагментах этот эффект встречается неоднократно (см. ниже). Чтобы проверить правильность и оценить значимость найденных гармонических составляющих решалась задача синтеза – построение аппроксимации выбранного отрезка данных в виде линейной комбинации этих составляющих.
Пусть с использованием периодограммы ${{\Psi }_{1}}(f)$ описанным выше способом найдены частоты $f_{k}^{^\circ }$ $(k = 1,2, \ldots ,K;K \ll N)$. Отвечающий этим частотам тренд (сумму циклических трендов) ищем в виде
(6)
${{x}_{{{\text{ap}}}}}(t) = {{a}_{0}} + \sum\limits_{k = 1}^K {({{a}_{k}}\cos 2\pi {{f}_{k}}t + {{b}_{k}}\sin 2\pi {{f}_{k}}t} ),$Уточненные частоты ${{f}_{k}}$ обычно оказывались близкими к исходным частотам первого приближения $f_{k}^{^\circ }$, но если частоты первого приближения были близкими, то соответствие между исходными и уточненными частотами, как правило, нарушалось. Построение аппроксимирующего выражения (6) проводилось в несколько этапов (почти всегда в два этапа). Опишем это построение на примере данных $\{ {{x}_{n}}\} $. На первом этапе в (6) включались гармоники с основными частотами спектра исходных данных. Построенное по этим частотам выражение использовалось для расчета остатков $\Delta {{x}_{n}} = {{x}_{n}} - {{x}_{{{\text{ap}}}}}({{t}_{n}})$ $(n = 0,\;1,\, \ldots ,\,N)$. Остатки подвергались спектральному анализу. Для них по описанным выше правилам строились периодограммы ${{E}_{{\Delta x}}}(f)$, ${{A}_{{\Delta x}}}(f)$, находились наиболее значимые частоты, и эти частоты добавлялись к частотам, найденном на первом этапе. Для расширенного набора частот по исходным данным $\{ {{x}_{n}}\} $ строилось новое выражение (6), вычислялись новые остатки $\Delta {{x}_{n}}$, которые затем подвергались спектральному анализу и т.д.
На каждом этапе точность построения аппроксимирующего выражения (5) характеризовалась отношением среднеквадратичных значений
Полученные таким способом результаты для фрагмента на рис. 5. представлены на рис. 6, 7. На рис. 6 представлены результаты двухэтапного построения выражения (6) по данным $\{ {{x}_{n}}\} $. График этого выражения изображен плавной кривой в верхней системе координат в левой части рисунка. Рядом с ним маркерами отмечены точки $({{t}_{n}},\;{{x}_{n}})$. В данном случае $K = 7$. График ошибок аппроксимации приведен в нижней системе координат левой части рисунка. Этот график представляет собой ломаную, последовательно соединяющую точки $({{t}_{n}},\;\Delta {{x}_{n}})$, $n = 0,\;1,\, \ldots ,\,N$. Частоты и амплитуды гармоник построенного выражения (6):
Рис. 6.
Фрагмент съемки 26.VII.2018: а – аппроксимация координаты $x$ и ее ошибка, 7 гармоник; б – спектр ошибки аппроксимации.
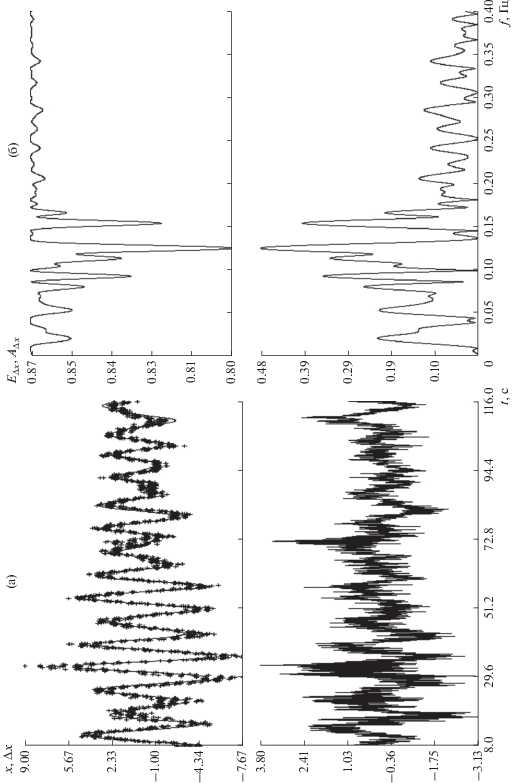
Рис. 7.
Фрагмент съемки 26.VII.2018: а – аппроксимация координаты $y$ и ее ошибка, 7 гармоник; б – спектр ошибки аппроксимации.

Процесс построения выражения (6) практически не изменил основную гармонику с номером $k = 3$. Частоты остальных гармоник изменились в 3–4 цифре после запятой, что для частоты с номером $k = 1$ оказалось существенным. Амплитуды изменились несколько больше – сказалось распределение энергии данных по разным гармоникам. Построенная аппроксимация выглядит правдоподобной. Периодограммы ${{E}_{{\Delta x}}}(f)$, ${{A}_{{\Delta x}}}(f)$ приведены в правой части рис. 6. В них нет существенно доминирующих пиков, а отвечающие им амплитуды малы.
Рис. 7 иллюстрирует результат двухэтапного процесса построения аппроксимирующего выражения вида (6) при $K = 7$ для данных $\{ {{y}_{n}}\} $.
По описанной схеме были обработаны еще несколько фрагментов съемок, выполненных 26.VII.2018, 4.IV.2018 и 31.V.2018. Построение аппроксимирующих выражений во всех случаях, кроме данных $\{ {{y}_{n}}\} $ одной из съемок 26.VII.2018 (рис. 8), потребовало проведения второго этапа. В примере на рис. 8 для аппроксимации данных $\{ {{x}_{n}}\} $ использованы 7 гармоник с частотами и амплиудами
Рис. 8.
Фрагмент съемки 26.VII.2018. Слева – аппроксимация координаты $x$, 7 гармоник; справа – аппроксимация координаты $y$, 10 гармоник.
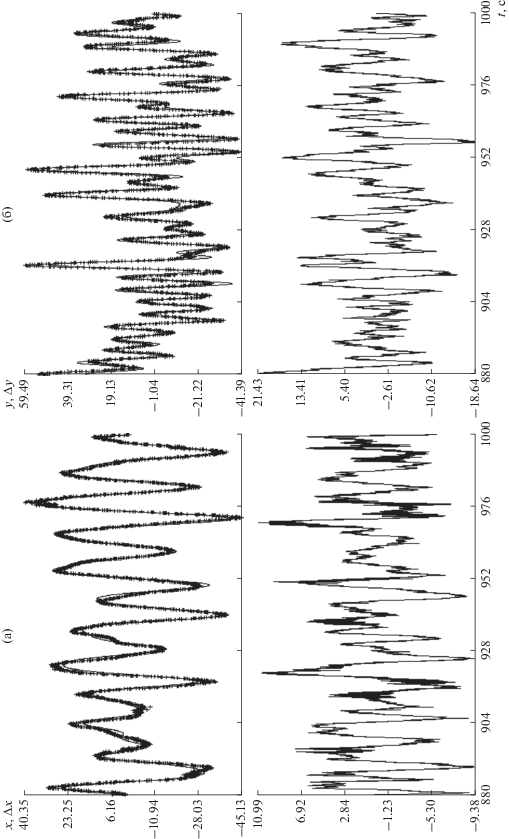
В верхней части рис. 8 сплошными линиями изображены графики аппроксимирующих тригонометрических полиномов, маркерами указаны данные измерений. В нижней части рисунка приведены графики ошибок аппроксимации.
Аналогичным образом организованы рис. 9, 10. В примере на рис. 9 для аппроксимации данных $\{ {{x}_{n}}\} $ использованы 7 гармоник с частотами и амплиудами
Рис. 9.
Фрагмент съемки 4.IV.2018: слева – аппроксимация координаты $x$, 7 гармоник; справа – аппроксимация координаты $y$, 8 гармоник.
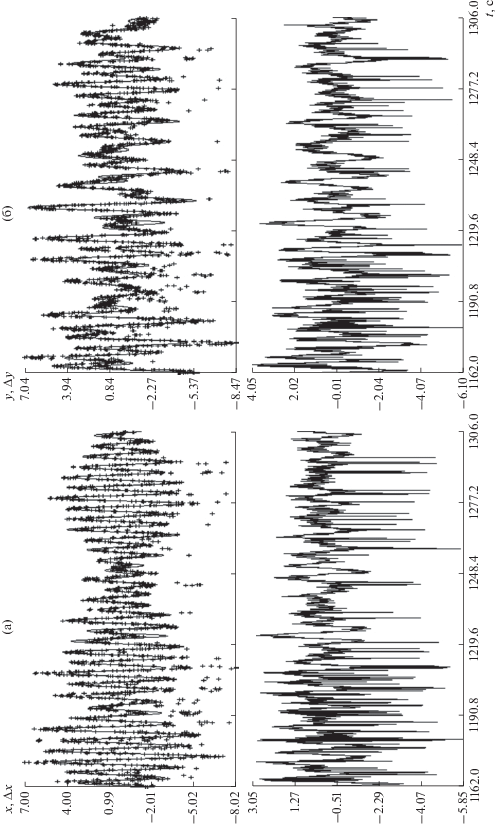
Рис. 10.
Фрагмент съемки 31.V.2018: слева – аппроксимация координаты $x$, 8 гармоник; справа – аппроксимация координаты $y$, 9 гармоник.
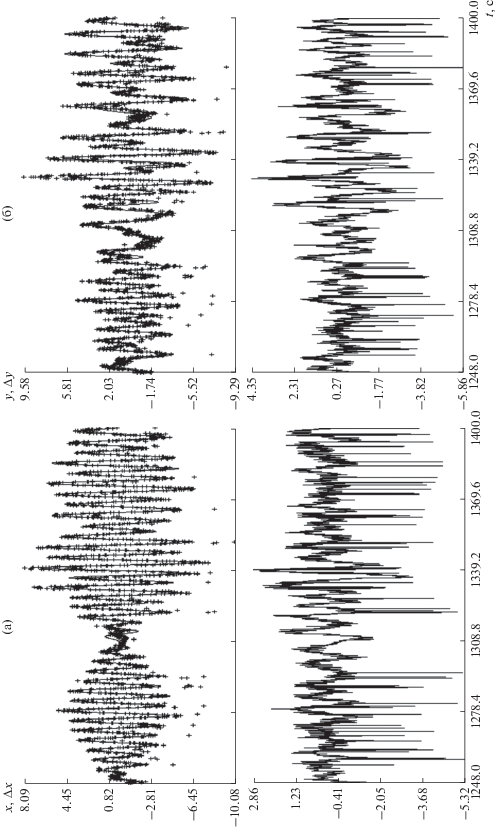
В примере на рис. 10 использованы соответственно 8 и 9 гармоник:
О ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ЦИКЛИЧЕСКИХ ТРЕНДОВ
Поскольку отыскание параметров циклических трендов в оцифрованных видеоданных выполнялось методом наименьших квадратов, точность определения этих параметров удобно характеризовать обычными оценками точности метода наименьших квадратов – соответствующими стандартными отклонениями. Хотя теоретико-вероятностные условия применимости таких оценок в данном случае не выполнены, некоторое представление о точности полученных результатов эти оценки дают. Приведем используемые в соответствующих расчетах формулы.
Начнем с задачи поиска циклических трендов в данных $\{ {{x}_{n}}\} $. Формулы (2), (3) запишем в виде
Параметр $\alpha $ введен вместо $f$ для простоты письма. Уточнение параметров ${{a}_{0}}$, $a$, $b$ и $\alpha $ в окрестности значимых максимумов функции ${{\Psi }_{1}}(f)$, найденных на некоторой равномерной сетке $\{ {{f}_{m}}\} \subset [0,\;F]$, выполнялось методом Гаусса–Ньютона [8]. На каждой итерации этого метода поправки $\Delta {\kern 1pt} {{a}_{0}}$, $\Delta {\kern 1pt} a$, $\Delta {\kern 1pt} b$ и $\Delta \alpha $ к имеющимся значениям ${{a}_{0}}$, $a$, $b$ и $\alpha $ определяются переопределенной системой уравнений
Ее решение находится методом наименьших квадратов. Матрицу, вектор неизвестных и правую часть этой системы обозначим соответственно $B$, $\xi $ и $\beta $. Тогда $\xi = {{({{B}^{{\text{T}}}}B)}^{{ - 1}}}{{B}^{{\text{T}}}}\beta $. Итерации заканчиваются, когда норма вектора поправок $\xi $ становится достаточно малой. Ковариационная матрица найденных оценок параметров ${{a}_{0}}$, $a$, $b$ и $\alpha $ имеет вид
Для примера приведем оценки точности циклических трендов с частотами ${{f}_{{x,2}}}$, ${{f}_{{x,3}}}$, ${{f}_{{x,4}}}$ и ${{f}_{{y,2}}}$, ${{f}_{{y,3}}}$, ${{f}_{{y,4}}}$ для фрагмента на рис. 5 (см. (4а)):
Аналогичным образом можно получить оценки точности параметров аппроксимирующего выражения (6). Величины ${{x}_{{{\text{ap}}}}}({{t}_{n}})$ представим в виде
(9)
$\begin{gathered} {{x}_{{{\text{ap}}}}}({{t}_{n}}) = {{a}_{0}} + \sum\limits_{k = 1}^K {({{a}_{k}}\cos n{{\alpha }_{k}} + {{b}_{k}}\sin n{{\alpha }_{k}}} ) \equiv \chi (n), \\ {{\alpha }_{k}} = 2\pi {{f}_{k}}h. \\ \end{gathered} $Минимизация функционала (8), (9) выполняется методом Гаусса–Ньютона. Схема вычислений была описана выше. Дальнейшая ее детализация приводит к системе линейных уравнений
Смысл использованных здесь обозначений, такой же, как в системе, использованной при минимизации функционала (7), (8). Новая система так же решается методом наименьших квадратов, описанным выше способом, и по существу по тем же формулам вычисляются стандартные отклонения ${{\sigma }_{{{{f}_{{x,k}}}}}}$ и ${{\sigma }_{{{{A}_{{x,k}}}}}}$. Ниже приведены параметры трендов из примера на рис. 6, рядом с ними в скобках указаны их стандартные отклонения:
Параметры трендов из примера на рис. 7, в скобках указаны стандартные отклонения:
Примерно такие же величины имеют стандартные отклонения остальных найденных циклических трендов.
Приведенные выше оценки характеризуют так называемую точность по внутренней сходимости, т.е. точность методики средствами самой методики. Представляет интерес сравнить описанные выше результаты с аналогичными результатами, полученными другими методами. При анализе колебаний конструкции МКС похожую информацию можно получить, анализируя данные бортовых акселерометров [4–6]. Акселерометр регистрирует кажущиеся ускорения, поэтому из его показаний напрямую можно использовать только частоты колебаний (и другие параметры, выражаемые в единицах времени, например, характеристики переходных процессов). Частоты, найденные разными методами, можно сравнивать непосредственно. Сравнение амплитуд требует привлечения сложных математических моделей, поскольку речь идет о разных физических величинах. По этой причине сравнение амплитуд практически невозможно. Кроме того, акселерометры на борту МКС “чувствуют” колебания только достаточно массивных объектов, которые в случае малоинерционных объектов проявляются как вынужденные колебания.
Частоты, приведенные в [4–6] и в данной статье, относятся к разным конфигурациям МКС, поэтому априори нельзя было ожидать очень точного совпадения. Однако все указанные выше частоты оказались весьма близкими некоторым частотам, приведенным в [6].
В видеофильме, содержащем эпизод с коррекцией орбиты, также не зафиксировано заметного изменения характера колебаний вследствие этой коррекции. По-видимому, это обстоятельство отражает существо дела. Ускорение МКС при коррекции весьма точно регистрируется акселерометром [4]. Это ускорение вызывает смещение станции как твердого тела, а видеоданные позволяют найти только смещения одних элементов ее конструкции относительно других элементов. Более того, видеоинформация о смещениях такого рода вместе с полезными данными может содержать мешающие данные о колебаниях фотоаппарата на фиксирующем его устройстве. Тем не менее, в настоящее время видеосъемка наиболее практичный и, возможно, единственный способ получения количественных характеристик относительных смещений малоинерционных элементов конструкции МКС.
Список литературы
Беклемишев Н.Д., Богуславский А.А., Беляев М.Ю. и др. Исследование колебаний элементов конструкции космической станции по видеоинформации. Препринты ИПМ им. М.В. Келдыша. 2019. № 43. С. 46. https://doi.org/10.20948/prepr-2019-43
Беклемишев Н.Д. Оценка среднего параллакса стереоизображений // Препринты ИПМ им. М.В. Келдыша. 2016. № 88. С. 12. https://doi.org/10.20948/prepr-2016-88
Теребиж В.Ю. Анализ временных рядов в астрофизике. М.: Наука, 1992.
Завалишин Д.А., Беляев М.Ю., Сазонов В.В. Определение характерных частот упругих колебаний конструкции МКС // Космич. исслед. 2010. Т. 48. № 4. С. 362–370. (Cosmic Research. P. 352–361).
Завалишин Д.А., Беляев М.Ю., Сазонов В.В. Оценка динамических характеристик Международной космической станции по измерениям микроускорений // Космич. исслед. 2009. Т. 47. № 2. С. 193–203. (Cosmic Research. P. 173–184).
Беляев М.Ю., Волков О.Н., Рябуха С.Б. Микровозмущения на Международной космической станции // Космическая техника и технологии. 2013. № 2. С. 1–11.
Ланцош К. Практические методы прикладного анализа. М.: Физматгиз, 1961.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. М.: Мир, 1985.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования