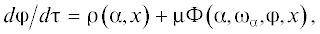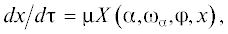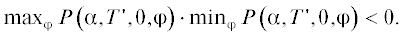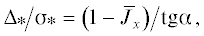Космические исследования, 2021, T. 59, № 4, стр. 339-352
Резонансные эффекты при движении малого космического аппарата вокруг центра масс в составе развертываемой тросовой системы
Ю. М. Заболотнов *
Самарский национальный исследовательский университет им. академика С.П. Королева
Самара, Россия
* E-mail: yumz@yandex.ru
Поступила в редакцию 12.02.2020
После доработки 08.01.2021
Принята к публикации 22.01.2021
Аннотация
Анализируются резонансные движения малого космического аппарата относительно центра масс при развертывании тросовой системы. Развертывание тросовой системы осуществляется с базового космического аппарата, совершающего движение по околоземной орбите. Малый космический аппарат совершает угловые движения относительно направления троса, причем сила натяжения троса изменяется по заданной программе. Малый космический аппарат представляет собой тело вращения и характеризуется малой статической и динамической асимметриями. Анализируется резонанс низшего порядка, при реализации которого имеет место “лунное” движение космического аппарата относительно направления троса. Для исследования резонансных эффектов используются приближенные нелинейные уравнения движения космического аппарата, полученные методом интегральных многообразий с использованием асимптотического подхода. Получены необходимые условия “захвата” системы в резонанс, то есть условия, при которых возможна реализация длительных резонансных режимов движения космического аппарата. Оценивается величина вероятности “захвата” в резонанс и определены условия, при которых вероятность “захвата” близка к единице. Рассматривается характерная программа выпуска троса, которая анализируются с точки зрения реализации возможных резонансных эффектов. Результаты, полученные с использованием приближенных уравнений движения, подтверждаются численным моделированием по исходным уравнениям углового движения космического аппарата.
ПОСТАНОВКА ЗАДАЧИ
Несмотря на наличие в настоящее время большого количества публикаций, связанных с анализом динамики космических тросовых систем (КТС) различных назначений и конфигураций, исследованиям углового движения космических аппаратов в составе КТС не уделялось достаточного внимания. Хотя понятно, что полное исследование движения систем твердых тел, соединенных тросами, на орбите должно включать в себя как анализ поведения системы в целом (сохранение ее конфигурации с точки зрения положений центров масс твердых тел), так и анализ угловых колебаний тел относительно своих центров масс [1]. Особенно это важно для концевых тел, соединенных с КТС одиночным тросом, для которых устойчивость угловых колебаний относительно направления троса требует отдельного исследования. Кроме того, если в состав КТС входят малые космические аппараты (МКА) или наноспутники (НС), то для них обеспечение устойчивости углового движения усложняется, так как действие любых малых возмущений (в сочетании с небольшими величинами их моментов инерции) может привести к потере устойчивости их углового движения, когда угол между продольной осью МКА (линией, соединяющей точку крепления троса и центр масс МКА) и направлением троса превысит, по крайней мере, ${{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 2}} \right. \kern-0em} 2}$. Это в свою очередь может привести к ослаблению троса (его провисанию) и соответственно к потере возможности управлять натяжением троса, например, при его выпуске по заданной программе. С другой стороны, использование математических моделей, наиболее полно описывающих движение КТС как распределенных систем [2], предполагает более точное задание граничных условий для описания поперечных и продольных колебаний троса, что естественно зависит от углового движения концевых тел, входящих в состав КТС.
В настоящей работе рассматривается угловое движение МКА в составе КТС при ее развертывании. Тросовая система состоит из базового космического аппарата (БКА), масса которого много больше массы остальной части системы (троса и МКА). Выпуск троса осуществляется по заданной номинальной программе, которая реализуется с помощью управляющего механизма, расположенного на БКА. Малый космический аппарат, который представляет собой твердое тело, близкое к телу вращения, совершает угловые колебания относительно направления троса. Основными факторами, влияющими на движение МКА относительно направления троса, являются: начальные условия отделения МКА от БКА, программа выпуска троса, наличие малой статической и динамической асимметрий у МКА.
Здесь необходимо отметить, что движение МКА относительно направления троса близко к движению несимметричного волчка Лагранжа относительно неподвижной точки (в данном случае центра масс) [3, 4]. То есть имеется основной восстанавливающий момент от силы натяжения троса (предполагается, что трос натянут), а другие моменты и влияние асимметрии рассматриваются как малые возмущения. При совпадении характерных частот системы (частоты вращения МКА относительно продольной оси и частот, характеризующих прецессию МКА вокруг направления троса) влияние асимметрии усиливается. Это приводит к интенсивному перераспределению энергии колебаний в угловом движении МКА. Например, уменьшение угловой скорости вращения МКА вокруг его продольной оси приводит к увеличению амплитуды колебаний по углу нутации, и наоборот. Особенно опасными является случаи реализации “захватов” в резонанс, когда резонансные соотношения частот поддерживаются длительной время в силу действующих возмущений. Особенностью рассматриваемой задачи является то, что частоты системы зависят от программы выпуска троса, точнее, от изменения силы натяжения троса. Это дает возможность прогнозировать моменты прохождения системы через резонансы, а в некоторых случаях избежать резонансных эффектов. Наличие резонансных эффектов было подтверждено в численных расчетах, представленных в работах [5, 6], однако никакого анализа этих явлений не было сделано.
Для анализа резонансов в рассматриваемой задаче используется приближенная нелинейная система уравнения движения МКА, полученная методом интегральных многообразий, которая в отличие от уравнений, приведенных в [6], получена при наиболее полном учете асимметрий и в форме, удобной для анализа поведения системы в резонансных областях. Уравнения, полученные методом интегральных многообразий, описывают “медленные” (близкие к прецессионным) движения МКА. Такой подход при исследовании резонансных режимов использовался ранее в задаче о движении КА в атмосфере [7, 8], которая также близка к задаче о движении тяжелого твердого тела вокруг неподвижной точки в случае Лагранжа. С помощью построенных уравнений “медленного” движения обнаружены и исследованы основные резонансные эффекты в угловом движении МКА при развертывании КТС для типичной программы выпуска троса [5, 9]. Получены и проанализированы необходимые и достаточные условия “захвата” системы в резонанс, и выявлены случаи, когда вероятность “захвата” близка к нулю, и когда создаются благоприятные условия для реализации длительных резонансных режимов движения МКА. Полученные оценки и выводы подтверждаются численными результатами по исходным уравнениям движения МКА на тросе.
УРАВНЕНИЯ ДВИЖЕНИЯ МКА НА ТРОСЕ
Уравнения углового движения МКА на тросе записываются в виде, удобном для применения асимптотических методов [6]
(1)
${{\tilde {d}{{K}_{x}}} \mathord{\left/ {\vphantom {{\tilde {d}{{K}_{x}}} {dt}}} \right. \kern-0em} {dt}} = \Delta M_{x}^{s} + \Delta M_{x}^{d},\,\,\,\,{{\tilde {d}{{K}_{{xt}}}} \mathord{\left/ {\vphantom {{\tilde {d}{{K}_{{xt}}}} {dt}}} \right. \kern-0em} {dt}} = \Delta {{M}_{{xt}}},$(2)
$\begin{gathered} {{d{{{{\omega }}}_{{zn}}}} \mathord{\left/ {\vphantom {{d{{{{\omega }}}_{{zn}}}} {dt}}} \right. \kern-0em} {dt}} = {{M_{{zn}}^{t}} \mathord{\left/ {\vphantom {{M_{{zn}}^{t}} J}} \right. \kern-0em} J} + \\ + \,\,\frac{{\left( {{{K}_{x}}\cos {{\alpha }} - {{K}_{{xt}}}} \right)\left( {{{K}_{x}} - {{K}_{{xt}}}\cos {{\alpha }}} \right)}}{{{{J}^{2}}{{{\sin }}^{3}}{{\alpha }}}} + \frac{{\Delta M_{{zn}}^{d}\, + \,\Delta M_{{zn}}^{s}}}{J}, \\ \end{gathered} $(3)
${{d{{\alpha }}} \mathord{\left/ {\vphantom {{d{{\alpha }}} {dt}}} \right. \kern-0em} {dt}} = {{{{\omega }}}_{{zn}}} + \Delta {{\dot {\alpha },}}$(4)
$\begin{gathered} {{d{{\varphi }}} \mathord{\left/ {\vphantom {{d{{\varphi }}} {dt}}} \right. \kern-0em} {dt}} = {{{{K}_{x}}} \mathord{\left/ {\vphantom {{{{K}_{x}}} {{{J}_{x}}}}} \right. \kern-0em} {{{J}_{x}}}} + \\ + \,\,\frac{{{{K}_{x}}\cos {{\alpha }} - {{K}_{{xt}}}}}{{J{{{\sin }}^{2}}{{\alpha }}}}\cos {{\alpha }} + \Delta {{{{{\dot {\varphi }}}}}_{d}} + \Delta {{\dot {\varphi },}} \\ \end{gathered} $(5)
${{d\psi } \mathord{\left/ {\vphantom {{d\psi } {dt}}} \right. \kern-0em} {dt}} = \frac{{{{K}_{{xt}}} - {{K}_{x}}\cos {{\alpha }}}}{{J{{{\sin }}^{2}}{{\alpha }}}} + \Delta {{\dot {\psi }}_{d}} + \Delta \dot {\psi }{\text{,}}$Правая система координат $c{{x}_{t}}{{y}_{t}}{{z}_{t}}$ введена следующим образом [5]: ось $c{{x}_{t}}$ параллельна направлению троса и направлена в сторону БКА, плоскость $c{{x}_{t}}{{y}_{t}}$ параллельна плоскости, проходящей через геоцентрический радиус-вектор точки крепления троса к БКА и натянутый трос. Углы Эйлера определяют положение связанной системы координат $cxyz$ относительно системы координат $c{{x}_{t}}{{y}_{t}}{{z}_{t}}$. Последовательность поворотов: по углу прецессии ψ – вокруг оси $c{{x}_{t}}$, по углу нутации ${{\alpha }}$ – вокруг повернутой на угол ψ оси $c{{z}_{t}}$, по углу собственного вращения ${{\varphi }}$ – вокруг оси $cx$.
Форма уравнений (1)–(5) использовалась во многих задачах, в которых рассматривалось вращение твердого тела относительно центра масс для случаев, близких к случаю Лагранжа, например, при движении КА в атмосфере [7, 8]; при движении наноспутников относительно центра на низких орбитах [10]; при развертывании космической тросовой системы [6], и, наконец, при исследовании резонансных движений волчка Лагранжа [4]. При записи уравнений движения (1)–(5) действием гравитационного момента на движение МКА относительно центра масс пренебрегается.
ПРИБЛИЖЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
Для применения асимптотических методов при анализе движения МКА на тросе уравнения (1)–(5) представляются в виде
(6)
${{{{d}^{2}}{{\alpha }}} \mathord{\left/ {\vphantom {{{{d}^{2}}{{\alpha }}} {d{{t}^{2}}}}} \right. \kern-0em} {d{{t}^{2}}}} + F({{\alpha }},x) = {{\varepsilon }}f\left( {{{\alpha }},{{\varphi }},x} \right),$(7)
${{d{{\varphi }}} \mathord{\left/ {\vphantom {{d{{\varphi }}} {dt}}} \right. \kern-0em} {dt}} = {{{{\omega }}}_{{{\varphi }}}}\left( {{{\alpha }},x} \right) + {{\varepsilon }}\Phi \left( {{{\alpha }},{{d{{\alpha }}} \mathord{\left/ {\vphantom {{d{{\alpha }}} {dt}}} \right. \kern-0em} {dt}},{{\varphi }},x} \right),$(8)
${{dx} \mathord{\left/ {\vphantom {{dx} {dt}}} \right. \kern-0em} {dt}} = {{\varepsilon }}X\left( {{{\alpha }},{{d{{\alpha }}} \mathord{\left/ {\vphantom {{d{{\alpha }}} {dt}}} \right. \kern-0em} {dt}},{{\varphi }},x} \right),$$x = \left( {{{K}_{x}},{{K}_{{xt}}},r} \right)$ – вектор медленных переменных системы, $r$ – вектор медленных переменных, который определяет изменение силы натяжения троса $T\left( r \right)$, ${{\varepsilon }}$ – малый параметр. Вектор $r$ определяется по-разному в зависимости от принятой номинальной программы выпуска троса. В системе (6)–(8) уравнение (5) не рассматривается, так как правые части остальных уравнений не зависят от угла прецессии, и изменение угла прецессии может быть получено после определения асимптотического решения через другие переменные системы.
Малый параметр ${{\varepsilon }}$ введен в систему (1)–(5) формально посредством масштабирования слагаемых, которые определяют действие возмущений. Причем за невозмущенную систему принимается система, описывающая движение статически и динамически симметричного МКА при постоянной силе натяжения троса $T = {\text{const}}$. В невозмущенном движении компоненты вектора кинетического момента ${{K}_{x}},{{K}_{{xt}}}$ постоянны, то есть являются интегралами движения системы, что соответствует движению симметричного волчка Лагранжа.
Резонанс низшего порядка системы характеризуется условием ${{{{\omega }}}_{{{\varphi }}}}\left( {{{\alpha }},x} \right) = 0$, при этом реализуется так называемое “лунное” движение, когда МКА повернут одной стороной к линии троса. Для применения метода интегральных многообразий в резонансном случае, то есть, когда ${{{{\omega }}}_{{{\varphi }}}}\left( {{{\alpha }},x} \right) = O\left( {\sqrt {{\varepsilon }} } \right)$, система (6)–(8) приводится к сингулярной форме [11]
(10)
${{{{\mu }}d{{\alpha }}} \mathord{\left/ {\vphantom {{{{\mu }}d{{\alpha }}} {d{{\tau }}}}} \right. \kern-0em} {d{{\tau }}}}\,\,{\text{ = }}\,\,{{{{\omega }}}_{{{\alpha }}}},$Методика построения асимптотических решений системы (9)–(12) изложена в работах [4, 11], где осуществляется асимптотическое разделение движений на “медленную” (прецессионную) и “быструю” (нутационную) составляющие. Там же приведены соответствующие теоремы, обосновывающие данную процедуру. Теоремы основываются на теоретическом материале, изложенном в монографии [12], и адаптированы применительно к системе (9)–(12). В работе [6] на основании асимптотического разделения движений для системы (9)–(12) выделены характерные частоты и определены резонансы, возможные при движении КА на тросе. Там же на основе асимптотического анализа получены приближенные аналитические решения для “быстрых” (нутационных) движений относительно центра масс КА.
Для анализа влияния резонанса ${{{{\omega }}}_{{{\varphi }}}}\left( {{{\alpha }},x} \right) = 0$ на движение асимметричного МКА на тросе здесь используется “медленная” составляющая решения системы (9)–(12). Такой подход не является новым, так как он использовался ранее для аналогичной системы при движении КА в атмосфере [8]. Наиболее простой вариант “медленных” составляющих решений уравнений движения твердого тела в атмосфере, так называемых квазистатических решений, для малых углов нутации (углов атаки) использовался также для анализа влияния резонансов низшего порядка в работе [7].
Уравнения “медленного” движения системы (9)–(12) с точностью до членов $O\left( {{\mu }} \right)$ включительно определяются из выражений
(15)
${{dx} \mathord{\left/ {\vphantom {{dx} {d{{\tau }}}}} \right. \kern-0em} {d{{\tau }}}} = {{\mu }}X\left( {{{\alpha ,0,\varphi }},x} \right).$В уравнениях (13)–(15) для простоты используются те же обозначения, что и в системе (9)–(12), хотя она описывает лишь “медленную” составляющую ее решений. Предполагается, что алгебраическое уравнение $F({{\alpha }},x) = 0$ имеет изолированный корень по ${{\alpha }}$ при каждом $x$, и в системе имеется малая диссипация энергии, обеспечивающая убывание амплитуд колебаний “быстрых” движений, соответствующих отклонениям от решений уравнений (13)–(15). Малая диссипация энергии может быть обусловлена, например, трением в специальном шарнире, обеспечивающем связь между МКА и тросом и предназначенном для исключения (или уменьшения) явления скручивания троса. Система (13)–(15) описывает движения МКА на тросе, близкие к его прецессии вокруг направления троса, хотя эти движения отличны от регулярной прецессии симметричного волчка Лагранжа. Это связано с влиянием асимметрии МКА, которая является причиной периодических возмущений при изменении угла ${{\varphi }}$, причем это влияние усиливается при более медленном изменении угла ${{\varphi }}$, то есть при прохождении системы через резонансные области ее движения ${{{{\omega }}}_{{{\varphi }}}}\left( {{{\alpha }},x} \right) = O\left( {\sqrt {{\varepsilon }} } \right)$.
Для приведения системы (13)–(15) к стандартному виду системы с одной фазой и для удобства последующего анализа поведения системы в резонансной области получим дифференциальное уравнение для угла нутации, соответствующее “медленному” движению системы. Тогда дифференцируя выражение (13), найдем
(16)
$\frac{{\partial F}}{{\partial {{\alpha }}}}\frac{{d{{\alpha }}}}{{d{{\tau }}}} = - \frac{{\partial F}}{{\partial x}}\frac{{dx}}{{d{{\tau }}}}.$При использовании выражения (16) уравнение (13) решается только в начальный момент времени для определения начального условия по углу ${{\alpha }}$.
Для анализа поведения системы в окрестности резонанса система уравнений (14)–(16) с быстрой фазой (которая аналогична по форме частично усредненной системе метода усреднения) стандартным образом приводится к уравнениям движения “маятника” с действующими на него возмущениями [13, 14]
(18)
$\begin{gathered} \frac{{d{{\varphi }}}}{{d{{\tau }}}} = {{\rho }} - {{\mu }}\frac{{{{f}_{{{\alpha }}}}}}{{{{F}_{{{\alpha }}}}}} \times \,\, \\ \times \,\,\left[ {\frac{{{{{{\omega }}}^{2}}}}{{\sin {{\alpha }}\cos {{\alpha }}}}{{\sigma }}\,{\text{cos}}\left( {{{\varphi }} + {{{{\varphi }}}_{1}}} \right) + {{\omega }}_{1}^{2}\Delta {\text{cos}}\left( {2\left( {{{\varphi }} + {{{{\varphi }}}_{2}}} \right)} \right)} \right], \\ \end{gathered} $НЕОБХОДИМЫЕ УСЛОВИЯ “ЗАХВАТА” В РЕЗОНАНС
Уравнения (18)–(19) описывают движения “маятника” в переменных  при действии малых возмущений. Невозмущенные движения “маятника” описываются уравнением
при действии малых возмущений. Невозмущенные движения “маятника” описываются уравнением
“Захвату” в резонанс соответствует переход “маятника” из области вращений в области его колебательных движений. Следовательно, необходимыми условиями существования “захватов” в резонанс является наличие областей колебательных движений “маятника”. Это условие имеет вид [7]
Условие (21) обеспечивает существование положений равновесия “маятника”. При этом
на фазовом портрете “маятника” на плоскости $\left( {{{\rho ,\varphi }}} \right)$, который определяется видом его “потенциальной” энергии  ($C$ – произвольная постоянная), имеются, как известно, особые точки двух типов: “центр”
и “седло”. Конкретный вид фазового портрета “маятника” зависит от значений параметров
асимметрии МКА ${{\sigma , }}\Delta $ и переменных ${{\alpha , }}T{\kern 1pt} '$ в момент прохода через резонанс $\left( {{{\rho }} = 0} \right)$. Функция
($C$ – произвольная постоянная), имеются, как известно, особые точки двух типов: “центр”
и “седло”. Конкретный вид фазового портрета “маятника” зависит от значений параметров
асимметрии МКА ${{\sigma , }}\Delta $ и переменных ${{\alpha , }}T{\kern 1pt} '$ в момент прохода через резонанс $\left( {{{\rho }} = 0} \right)$. Функция  в данном случае имеет вид
в данном случае имеет вид
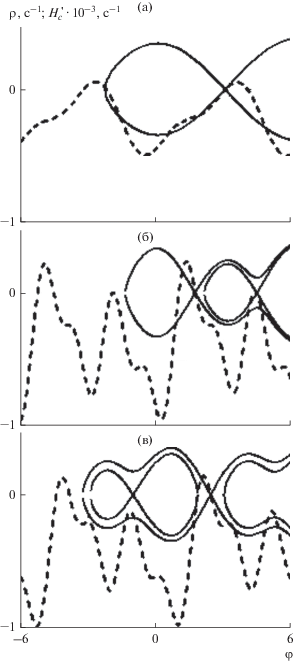
При записи выражения (22) полагается ${{{{\varphi }}}_{1}} = 0$, то есть формально изменяется начало отчета угла ${{\varphi }}$. Структура функции (22) такая же, как для аналогичной функции, которая используется при анализе резонансных движений волчка Лагранжа при малых углах нутации [3], где в зависимости от значений коэффициентов, стоящих перед тригонометрическими функциями угла ${{\varphi }}$ (их отношений), приводятся все возможные фазовые портреты для невозмущенного “маятника” (20). На рис. 2 изображены положения сепаратрис для типичных фазовых портретов, возможных в рассматриваемой системе (за исключением переходных случаев) в случае, когда выполняется условие (21). Здесь рассматриваются МКА с вытянутыми вдоль оси $cx$ эллипсоидами инерции ${{\bar {J}}_{x}} < 1$. Рис. 2 построен для $T{\kern 1pt} ' < 0$, ${{\bar {J}}_{x}} = 0.5$, ${{\alpha }} = 0.3$, если $T{\kern 1pt} ' > 0$, то положение сепаратрис аналогично, только их петли, ограничивающие области колебательных движений “маятника”, повернуты в другую сторону. При этом рис. 2а соответствует простой асимметрии, когда ${{\sigma }} = 0.05$ и $\Delta = 0$, рис. 2б, 2в – сложной асимметрии, когда ${{\sigma }} = 0.05$, $\Delta = 0.2$. Причем рис. 2б и рис. 2в отличаются лишь фазой ${{\varphi }_{2}} = 0$ и ${{\varphi }_{2}} = {{ - {{\pi }}} \mathord{\left/ {\vphantom {{ - {{\pi }}} 4}} \right. \kern-0em} 4}$ соответственно.
В частных случаях, когда ${{\sigma }} = 0$ или $\Delta = 0$, условие (21) можно записать в аналитическом виде
(23)
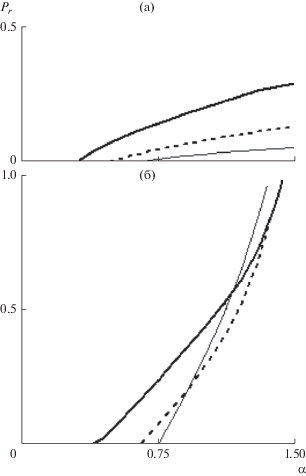
$\left| {\frac{{T{\kern 1pt} '}}{{2\mu \omega T\sigma }}\frac{{{{K}_{2}}\left( \alpha \right)}}{{{{K}_{1}}\left( \alpha \right)}}} \right| < 1,\,\,\,\,\left| {\frac{{T{\kern 1pt} '\left( {1 - {{{\bar {J}}}_{x}}} \right)}}{{2\mu \omega T\Delta {\text{ tg}}\alpha {\text{ }}}}\frac{{{{K}_{2}}\left( \alpha \right)}}{{{{K}_{1}}\left( \alpha \right)}}} \right| < 1.$Из условий (23) можно получить критические значения обобщенных параметров асимметрии ${{\sigma *}},\Delta {\text{*}}$, если левые части соотношений (23) приравнять к 1. В этом случае можно также найти отношение критических значений параметров асимметрии
из которого следует, что при малых углах нутации влияние асимметрии ${{\sigma }}$ является определяющим при формировании фазового портрета системы. Однако влияние параметра $\Delta $ становится больше, если эллипсоид инерции МКА приближается к сфере ${{\bar {J}}_{x}} \to 1$.О ВЕРОЯТНОСТИ “ЗАХВАТА” В РЕЗОНАНС
Выполнение условия (21) не гарантирует “захвата” системы в резонанс, когда фазовая траектория “маятника”, попадая в область колебаний, остается в этой области достаточно длительное время в силу действующих в системе возмущений. В общем случае, как известно, явление “захвата” в резонанс имеет вероятностный характер [15, 16]. Вероятность “захвата” определяется по начальным условиям как предел [16]
(25)
${{P}_{r}}\left( {{{M}_{0}}} \right) = \mathop {\lim }\limits_{{{\delta }} \to {\text{0}}} \mathop {\lim }\limits_{{{\mu }} \to 0} \frac{{{\text{mes}}U_{v}^{{({{\delta }})}}}}{{{\text{mes}}{{U}^{{({{\delta }})}}}}},$где ${{M}_{0}}\left( {{{\alpha }_{0}},{{\rho }_{0}},{{\varphi }_{0}}} \right)$ – некоторая начальная точка, взятая в области вращений “маятника” (17)–(19),  – δ-окрестность точки ${{M}_{0}}$, $U_{v}^{{({{\delta }})}}$ – множество точек из
– δ-окрестность точки ${{M}_{0}}$, $U_{v}^{{({{\delta }})}}$ – множество точек из  , для которых траектория системы попадает в области колебаний “маятника”, ${\text{mes}}$ – объем соответствующих областей.
, для которых траектория системы попадает в области колебаний “маятника”, ${\text{mes}}$ – объем соответствующих областей.
Для оценки вероятности (25) используются величины, связанные с приращениями энергии “маятника”, вычисленные на сепаратрисе ${{l}_{c}}$ невозмущенной задачи [15]
где $H_{c}^{'} = {{d{{H}_{c}}} \mathord{\left/ {\vphantom {{d{{H}_{c}}} {d{{\tau }}}}} \right. \kern-0em} {d{{\tau }}}}$ – производная энергии “маятника”, определенная в силу возмущенной системы (17)–(19). Причем энергия определяется как ${{H}_{c}} = {{{{\rho }^{2}}} \mathord{\left/ {\vphantom {{{{\rho }^{2}}} 2}} \right. \kern-0em} 2} + \Pi - {{\Pi }_{с}}$, где потенциальная энергия “маятника” ${{\Pi }_{с}}$ определяется на сепаратрисе невозмущенной системы в момент пересечения траектории резонанса $\rho = 0$.“Захват” в резонанс возможен только, если ${{\Theta }_{v}} > 0$. В противном случае траектория возмущенной системы покидает область колебаний “маятника” и вероятность “захвата” в резонанс близка к нулю. Если ${{\Theta }_{v}} > 0$, то вероятность “захвата” в резонанс оценивается по формуле [15]
(27)
${{P}_{r}} = \frac{{{{\Theta }_{v}}}}{{2\pi \left| {{{M}_{p}}} \right| + {{{{\Theta }_{v}}} \mathord{\left/ {\vphantom {{{{\Theta }_{v}}} 2}} \right. \kern-0em} 2}}},$Вероятность (27) представляет собой отношение фазового объема траекторий “маятника”, входящего в его область колебаний, к полному фазовому объему траекторий, пересекающих резонанс ${{\rho }} = 0$. Формула (27) может быть применена для любого фазового портрета системы, изображенного на рис. 2. Если на отрезке $\left[ { - \pi ,\pi } \right]$ имеется две области колебаний (петель сепаратрис, рис. 2б), то величина представляет собой сумму интегралов (26), соответствующих каждой области колебаний. Если одна область колебаний охватывает две других (рис. 2в), то интеграл (26) берется по внешней сепаратрисе.
Два характерных случая прохода через резонанс ($T{\kern 1pt} ' > 0$ и $T{\kern 1pt} ' < 0$) существенно отличаются с точки зрения величины вероятности (27). Для оценки величины вероятности необходимо найти производную
(28)
$H_{c}^{'} = \frac{{\partial {{H}_{c}}}}{{\partial \alpha }}\frac{{d\alpha }}{{d\tau }} + \frac{{\partial {{H}_{c}}}}{{\partial \varphi }}\frac{{d\varphi }}{{d\tau }} + \frac{{\partial {{H}_{c}}}}{{\partial \rho }}\frac{{d\rho }}{{d\tau }}.$В момент пересечения резонанса ${{\rho }} = 0$ поведение производной (28) как функции $H_{c}^{'}(\varphi )$ зависит от значений ${{\alpha }},{{\bar {J}}_{x}},T{\kern 1pt} '$, а также от обобщенных параметров асимметрии ${{\sigma }},\Delta $. На рис. 2 показаны функции $H_{c}^{'}\left( {{\varphi }} \right)$ (штриховые линии), соответствующие значениям параметров ${{\sigma }},\Delta $,${{\alpha }},{{\bar {J}}_{x}},T{\kern 1pt} ' < 0$, для которых построены сепаратрисы. В этом случае, очевидно, что ${{\Theta }_{v}} > 0$, и вероятность “захвата” может быть вычислена по формуле (27). Однако если пересечение резонанса ${{\rho }} = 0$ происходит при $T{\kern 1pt} ' > 0$ (значения параметров ${{\sigma }},\Delta $,${{\alpha }},{{\bar {J}}_{x}}$ не изменяются), то знак производной (28) меняется на противоположный. Рис. 3 иллюстрирует влияние параметра $T{\kern 1pt} '$ на вид функции $H_{c}^{'}\left( {{\varphi }} \right)$ (рис. 3 отличается от рис. 2в только знаком $T{\kern 1pt} '$), из которого следует, что у функции $H_{c}^{'}\left( {{\varphi }} \right)$ изменяется знак, и она симметрично отражается относительно оси ординат. В этом случае ${{\Theta }_{v}} < 0$ и вероятность “захвата” близка к нулю Параметры ${{\sigma }},\Delta ,{{\bar {J}}_{x}}$ качественно не изменяют поведение функции $H_{c}^{'}\left( {{\varphi }} \right)$, если для них выполняется необходимое условие существования областей колебаний (21). Так при увеличении значений обобщенных параметров асимметрии ${{\sigma }},\Delta $ в силу вида уравнений движения (17)–(19) и вида функции $P\left( {\alpha ,0,\varphi } \right)$ (22) увеличивается объем областей колебаний “маятника”, а для функции $H_{c}^{'}\left( {{\varphi }} \right)$ эти параметры выступают как масштабные коэффициенты, от которых функция $H_{c}^{'}\left( {{\varphi }} \right)$ зависит линейно. Здесь необходимо отметить, что если $T{\kern 1pt} ' > 0$ (рис. 3), то никакое увеличение асимметрии ${{\sigma }},\Delta $ не может привести к выполнению условия возможности “захвата” в резонанс, так как ${{\Theta }_{v}} < 0$, и модуль величины ${{\Theta }_{v}}$ увеличивается.
Однако зависимость вероятности “захвата” в резонанс от значения угла нутации ${{\alpha }}$ более сложная, что иллюстрируется рис. 4, 5. Рис. 4 соответствует случаю $T{\kern 1pt} ' > 0$, а рис. 5 – $T{\kern 1pt} ' < 0$. Причем на рис. 4а и рис. 5а показаны зависимости, когда $\sigma = 0.05,\,\,\Delta = 0$, а рис. 4б и рис. 5б соответствуют более сложной асимметрии $\sigma = 0.05,\,\,\Delta = 0.2$. В последнем случае имеют место более сложные варианты фазовых портретов (рис. 2б, 2в). На рис. 4, 5 жирные линии соответствуют значению параметра ${{\bar {J}}_{x}} = 0.25$, штриховые линии – ${{\bar {J}}_{x}} = 0.5$, тонкие линии – ${{\bar {J}}_{x}} = 0.8$. Как следует из результатов, представленных на рис. 4, если $T{\kern 1pt} ' > 0$, то вероятность захвата увеличивается с увеличением угла нутации ${{\alpha }}$, причем когда ${{\alpha }} < 0.3$, то вероятность “захвата” близка к нулю. Это связано с тем, что при малых углах нутации для этого случая величина ${{\Theta }_{v}} < 0$. Наоборот, при $T{\kern 1pt} ' < 0$ (рис. 5) наблюдается тенденция уменьшения вероятности “захвата” с увеличением угла нутации ${{\alpha }}$, при этом, если ${{\alpha }} > 0.8$, то вероятность “захвата” также близка к нулю. Из приведенных результатов следует, что влияние асимметрии $\Delta $ на резонансное движение МКА существенно меньше, чем асимметрии ${{\sigma }}$. Влияние асимметрий ${{\sigma }},\,\Delta $ примерно становится одинаковым, если асимметрия $\Delta $ в несколько раз превышает асимметрию ${{\sigma }}$. Поэтому рис. 4б и рис. 5б построены при $\sigma = 0.05,\,\Delta = 0.2$.
Здесь необходимо отметить, что графики, представленные на рис. 4 и рис. 5, лишь качественно отражают зависимость вероятности “захвата” от рассматриваемых параметров, так как они соответствуют мгновенному значению интеграла ${{\Theta }_{v}}$. Это связано, прежде всего, с уравнением, которое описывает изменение угла нутации (17). При приближении к резонансу ${{\rho }} = 0$ его влияние приводит к возмущению угла нутации, причем это влияние может проявляться даже за пределами резонансной области, размеры которой обычно оценивают величиной $O\left( {{\mu }} \right) = O(\sqrt {{\varepsilon }} )$ [13]. Это так называемый вторичный резонансный эффект [17, 18], который обнаруживается во втором приближении метода усреднения в нерезонансных областях движения колебательных систем. Причем данный эффект может привести как к увеличению угла нутации, так и к его уменьшению. В первом случае возникает так называемая “положительная обратная связь”, так как увеличение угла нутации приводит к увеличению областей колебаний “маятника”, что естественно увеличивает вероятность “захвата”, с другой стороны во втором случае уменьшение угла нутации наоборот уменьшает вероятность “захвата”. Ниже будет показано, что эти два варианта возмущений угла нутации ${{\alpha }}$ также определяются знаком производной $T{\kern 1pt} '$: при $T{\kern 1pt} ' < 0$ угол нутации увеличивается, а при $T{\kern 1pt} ' > 0$ – уменьшается. Это увеличивает асимметрию обоих рассматриваемых случаев с точки зрения величины вероятности “захвата” в резонанс.
ПРИМЕР АНАЛИЗА РЕЗОНАНСНЫХ “ЭФФЕКТОВ” ДЛЯ ТИПИЧНОЙ ПРОГРАММЫ РАЗВЕРТЫВАНИЯ КТС
В настоящее время предложено большое количество программ развертывания КТС, например, [2, 19, 20] и др. Анализ известных программ развертывания КТС показывает, что все они имеют одну особенность, которая существенно влияет на реализацию явления “захвата” в резонанс. Это связано с тем, что при увеличении длины троса его натяжение, как правило, увеличивается, что связано с увеличение расстояния между концевыми телами в системе. Увеличение расстояния соответственно приводит к увеличению разности гравитационных сил, действующие на концевые тела, и соответственно увеличивает натяжение в тросе. Исключение могут составлять небольшие по протяженности участки развертывания КТС, которые имеют место или в начале процесса развертывания, или при переходе от одной программы выпуска троса к другой. Поэтому случай, когда $T{\kern 1pt} ' > 0$, является доминирующим при рассмотрении вопросов, связанных с рассматриваемыми резонансными эффектами при развертывании КТС.
При анализе резонансных эффектов условие пересечение резонансов удобно представить в другом виде, вычислив резонансные значения угловой скорости ${{\omega }}_{x}^{{\left( r \right)}}$ исходя из равенства ${{\rho }} = 0$, тогда
(29)
$\omega _{x}^{{\left( r \right)}} = {{ \pm \omega } \mathord{\left/ {\vphantom {{ \pm \omega } {\sqrt {1 - {{{\bar {J}}}_{x}}} }}} \right. \kern-0em} {\sqrt {1 - {{{\bar {J}}}_{x}}} }},$Поэтому при проходе через резонансы имеем $\omega _{x}^{{\left( r \right)}} = {{\omega }_{x}}$, а функция ${{\omega }}_{x}^{{\left( r \right)}}\left( {T,{{\alpha }}} \right)$ на плоскости переменных $\left( {T,{{\alpha }}} \right)$ задает резонансные кривые, при пересечении которых угловой скоростью ${{{{\omega }}}_{x}}$ возникают резонансные эффекты. Если пренебречь ошибками регулирования при реализации программ развертывания КТС, то сила натяжения троса играет роль медленного времени [6]. Изменение угла нутации в соответствии с приведенными выше математическими моделями (1)–(5) и (17)–(19) является более сложным. Так в соответствии с приближенными уравнениями движения (17)–(19) угол нутации ${{\alpha }}$ в нерезонансных областях движения системы является медленно изменяющейся переменной, однако при пересечении резонансов это уже не выполняется, так как при этом имеют место возмущения, которые формируются в течение достаточно небольшого промежутка времени. Аналогично ведет себя угловая скорость ${{{{\omega }}}_{x}}$.
Для анализа влияния резонансных эффектов рассматривается динамическая программа выпуска троса, состоящая из участков “медленного” и “быстрого” развертывания, близкая к программе, которая была реализована в реальном тросовом эксперименте YES2 [5, 9]. Данная программа включает в себя ряд характерных участков, влияющих на реализацию резонансных эффектов. Эти участки отличаются величиной и знаком производной $T'$: 1) $T{\kern 1pt} ' > 0$ (${{\omega }}{\kern 1pt} ' > 0$); 2) $T{\kern 1pt} ' < 0$ (${{\omega }}{\kern 1pt} ' < 0$); 3) $T{\kern 1pt} ' \approx 0$. Причем, как было сказано выше, участки, соответствующие $T{\kern 1pt} ' < 0$, являются не продолжительными.
Рассматривается развертывание КТС с базового КА, масса которого много раз больше массы остальных частей системы (6000 кг). Нижний концевой груз – малый КА (20 кг). Уравнений движения, которые описывают номинальное движение центра масс МКА и, следовательно, изменение силы натяжения троса, решаются независимо и имеют известный вид: можно использовать, например, уравнения, приведенные в [2, 5]. Как показано в [5], влияние гравитационного момента на движение МКА для рассматриваемой программы развертывания КТС) пренебрежимо мало, даже если рассматривается МКА с вытянутом эллипсоидом инерции (${{\bar {J}}_{x}} = 0.1$).
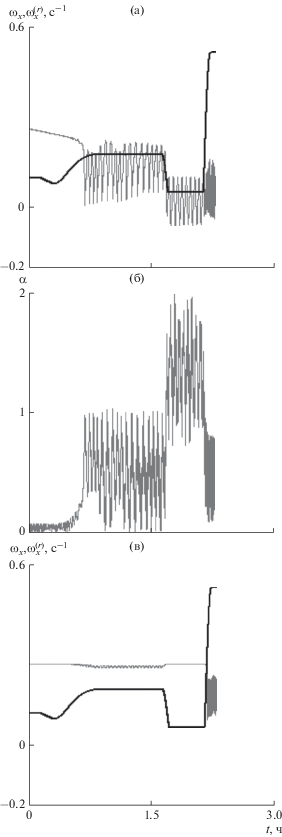
Так как резонансные угловые скорости (29) симметричны, то, не ограничивая общности, можно рассматривать движение системы, когда ${{{{\omega }}}_{x}} > 0$. Изменение резонансной скорости (${{\omega }}_{x}^{{\left( r \right)}} > 0$) для рассматриваемой программы развертывания КТС приводится на рис. 6 и 8 (полужирные линии). На рис. 6–9 приводятся также зависимости ${{{{\omega }}}_{x}}\left( t \right)$ и ${{\alpha }}\left( t \right)$, определенные в соответствии с моделями (1)–(5) (а) и (17)–(19) (б). Рис. 6, 7 соответствуют случаю, когда в момент отделения МКА начальный угол нутации мал $\alpha (0) = 0.01$, а для рис. 8, 9 – достаточно большой ${{\alpha (0)}} = 1$. При малом начальном угле нутации (рис. 6, 7) “захват” в резонанс имеет место только на участках, когда $T{\kern 1pt} ' < 0$ (${{\omega }}{\kern 1pt} ' < 0$). С другой стороны при достаточно больших начальных углах нутации (рис. 8, 9) угловая скорость ${{{{\omega }}}_{x}}\left( t \right)$ находится в окрестности резонансной кривой ${{\omega }}_{x}^{{\left( r \right)}}\left( t \right)$ практически на всей траектории развертывания КТС. Это соответствует оценкам вероятности “захвата” в резонанс, полученным ранее (рис. 4, 5), то есть при малых углах нутации вероятность “захвата” близка к нулю, когда $T{\kern 1pt} ' > 0$ (рис. 4). Автору не удалось найти траектории системы, для которых имеет место явление “захвата” в резонанс при малых начальных углах нутации, изменяя, например, начальную фазу $\varphi \left( 0 \right) \in \left[ {0,2\pi } \right)$ или с помощью изменения ${{\alpha }}\left( 0 \right)$ (до $0.3$), хотя при достаточно больших значений $\alpha \left( 0 \right) > 0.7$ такие траектории легко находятся. Зависимости, приведенные на рис. 6–9, построены при ${{\bar {J}}_{x}} = 0.5$, ${{\sigma }} = 0.14$, $\Delta = 0.1$. Как следует из результатов, приведенных на рис. 6–9, приближенные уравнения движения МКА относительно центра масс (17)–(19) качественно правильно описывают процесс “захвата” в резонанс в рассматриваемой системе (1)–(5). Отличие в зависимостях для угла нутации ${{\alpha }}\left( t \right)$ (рис. 7 и 9) объясняется наличием в исходной системе нутационных колебаний (пограничных членов), которые отсутствуют в приближенных уравнениях (17)–(19), описывающих движение системы по интегральному многообразию (прецессионное движение МКА).
Здесь необходимо отметить характерную особенность зависимостей, представленных на рис. 6–9, а именно: увеличение угловой скорости ${{{{\omega }}}_{x}}$, например, при реализации явления “захвата” в резонанс, как правило, сопровождается уменьшением угла нутации ${{\alpha }}$, и наоборот. Причем данный эффект усиливается в резонансных областях движения системы. Поэтому, если “захват” в резонанс происходит при $T{\kern 1pt} ' > 0$, то есть когда резонансная угловая скорость ${{\omega }}_{x}^{{\left( r \right)}}$ (а значит и ${{{{\omega }}}_{x}}$) увеличивается, то это приводит к уменьшению угла нутации, то есть реализуется “отрицательная обратная связь”. Если “захват” в резонанс реализуется при $T{\kern 1pt} ' < 0$, то имеет место обратная картина. Естественно, если “захват” в резонанс происходит при $T{\kern 1pt} ' \approx 0$, то угол нутации совершает колебания с почти постоянными амплитудой (рис. 7, 9). Отмеченная зависимость наиболее выражена для случая, когда движение МКА происходит с малыми начальными углами нутации (рис. 6, 7).
Анализ резонансных эффектов для случая ${{{{\omega }}}_{x}} < 0$, которые возникают при пересечении резонансной кривой ${{\omega }}_{x}^{{\left( r \right)}} < 0$ (29) осуществляется аналогично и приводит к тем же выводам. Только здесь необходимо иметь в виду, что участкам, например, когда $T{\kern 1pt} ' < 0$ (${{\omega }}{\kern 1pt} ' < 0$), соответствуют наоборот участки увеличения значений ${{\omega }}_{x}^{{\left( r \right)}}$ (по модулю значения уменьшаются). В этом случае зависимости для угловой скорости ${{{{\omega }}}_{x}}\left( t \right)$, определенные для обоих случаев (${{{{\omega }}}_{x}} > 0$ и ${{{{\omega }}}_{x}} < 0$), симметричны относительно оси времени, если изменить знаки начальной угловой скорости ${{{{\omega }}}_{x}}\left( 0 \right)$ и производной угла прецессии ${{d{{\psi }}} \mathord{\left/ {\vphantom {{d{{\psi }}} {dt\left( 0 \right)}}} \right. \kern-0em} {dt\left( 0 \right)}}$.
При анализе угловых колебаний МКА относительно направления троса надо иметь в виду неизбежное наличие в рассматриваемой системе малых диссипативных моментов. Это связано, во-первых, в использовании специальных шарниров в точках крепления троса для исключения его скручивания; во-вторых, в применении пассивных демпфирующих устройств [1, 9] для гашения колебаний в системе; в-третьих, в естественном трении между волокнами троса [2]. С одной стороны наличие диссипативных моментов (даже малых) в системе является теоретическим обоснованием использования метода интегральных многообразий [4, 12, 21]. С другой стороны, возникающие диссипативные моменты влияют на реализацию резонансных “эффектов” в угловом движении МКА. В данной работе оценка влияния диссипативных моментов осуществлялась на примере демпфирующего момента, действующего в точке крепления троса к МКА. Демпфирующий момент задавался в связанной с МКА системе координат пропорционально угловым скоростям $M_{{x,y,z}}^{{{\omega }}} = m_{{x,y,z}}^{{{\omega }}}{{{{\omega }}}_{{x,y,z}}}$. Расчеты проводились по исходной модели движения МКА (1)–(5). Было установлено, что достаточно малая диссипация (отношение модуля демпфирующего момента к модулю восстанавливающего момента от силы натяжения троса не превышала 0.1) качественно не изменяет поведение системы в резонансных областях ее движения. Однако наличие поперечных демпфирующих моментов $M_{{y,z}}^{{{\omega }}} < 0$ всегда уменьшает угол нутации, что ведет соответственно к уменьшению вероятности “захвата” в резонанс. Влияние малого диссипативного момента $M_{x}^{{{\omega }}} < 0$, действующего относительно продольной оси МКА $cx$, неоднозначно, и в ряде случаев может привести к увеличению вероятности “захвата” в резонанс. Это может иметь место, когда начальная угловая скорость $\left| {{{{{\omega }}}_{x}}\left( 0 \right)} \right| > \left| {{{\omega }}_{x}^{{\left( r \right)}}} \right|$. В этом случае диссипативный момент уменьшает модуль угловой скорости ${{{{\omega }}}_{x}}$ и приближает траекторию системы к резонансной области. Кроме того, если при этом угловая скорость ${{{{\omega }}}_{x}}$ пересекает резонансную кривую ${{\omega }}_{x}^{{\left( r \right)}}\left( t \right)$ при $T{\kern 1pt} ' < 0$ (резонансная угловая скорость ${{\omega }}_{x}^{{\left( r \right)}}\left( t \right)$ приближается к оси абсцисс), то знаки производных функций ${{\omega }}_{x}^{{\left( r \right)}}\left( t \right)$ и ${{{{\omega }}}_{x}}\left( t \right)$ по времени совпадают, и создаются благоприятные условия для “захвата” в резонанс. На рис. 10 приводится пример, который соответствует случаю, когда МКА в момент отделения от базового КА стабилизируется вращением, то есть имеет расчетную не нулевую угловую скорость ${{{{\omega }}}_{x}}\left( 0 \right) = 0.25\,\,{{{\text{с}}}^{{ - 1}}}$. Наличие малого диссипативного момента $m_{x}^{{{\omega }}} = - {{10}^{{ - 5}}}$ приводит не только к пересечению траектории системы резонансной области, но и к реализации длительного резонансного режима движения системы (рис. 10а), то есть к “захвату” в резонанс. При этом угол нутации увеличивается и превышает ${{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 2}} \right. \kern-0em} 2}$ (рис. 10б). С другой стороны, если формально провести моделирование движения при $m_{x}^{{{\omega }}} = 0$, то система ведет себя совершенно по-другому, и “захвата” не наблюдается (рис. 10в). Причем угол нутации в последнем случае остается малым (зависимости на рис. 10 построены для начального значения ${{\alpha }}\left( 0 \right) = 0.01$) и увеличивается только в конце процесса развертывания КТС (до 0.2) при проходе через резонансную область без “захвата” (рис. 10в).
ЗАКЛЮЧЕНИЕ
Представленные в работе исследования движения МКА относительно центра масс в составе развертываемой КТС показывают, что наличие резонансных эффектов может существенно повлиять на угловое движение МКА. Это проявляется в нерегулярном поведении угла нутации ${{\alpha }}$ (угла между направлением троса и продольной осью МКА) и угловой скорости ${{{{\omega }}}_{x}}$ при пересечении траекторией системы резонансных областей ее движения. Задание динамической программы развертывания КТС определяет закон изменения силы натяжения троса, от которого в свою очередь зависят значения резонансных угловых скоростей ${{\omega }}_{x}^{{\left( r \right)}}$. Резонансные области движения системы характеризуются условием ${{\omega }}_{x}^{{\left( r \right)}} \approx {{{{\omega }}}_{x}}$. При пересечении системы резонансных областей возможно два варианта ее поведения: “быстрый” проход через резонансную область и “захват”, при котором в течение достаточно длительного времени выполняется условие ${{\omega }}_{x}^{{\left( r \right)}} - {{{{\omega }}}_{x}} \approx 0$ в силу действующих возмущений. “Захват” в резонанс, как правило, приводит, и это показано на примере типичной программы развертывания КТС, к недопустимому увеличению угла нутации, когда его значение достигает и даже превосходит ${{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 2}} \right. \kern-0em} 2}$. Данный эффект может привести в общем случае к ослаблению троса (его провисанию), что в свою очередь приведет к потере управляемости при развертывании КТС.
В работе с помощью приближенной математической модели движения, описывающей поведение системы с учетом резонансов низшего порядка, получены необходимые условия существования длительных резонансных режимов и проведен параметрический анализ вероятности “захвата” системы в резонанс, если необходимые условия выполняются. На основании проведенных исследований может быть построена методика выбора параметров КТС и начальных условий отделения МКА, с помощью которой можно минимизировать влияние резонансных эффектов на его угловой движение, в частности, уменьшить вероятность явления “захвата” в резонанс.
Можно сформулировать следующие выводы, которые непосредственно влияют на реализацию резонансных режимов движения в рассматриваемой системе для заданной программы развертывания КТС (силы натяжения троса $T\left( t \right)$):
1. Естественным способом уменьшения влияния резонансных эффектов на движение МКА является уменьшение величин его асимметрий (параметров ${{\sigma }}$ и $\Delta $), что ведет соответственно к уменьшению объема областей колебаний “маятника” и, следовательно, к уменьшению вероятности “захвата” в резонанс.
2. Обеспечение ограниченных значений угла нутации и угловых скоростей при отделении МКА в общем случае ведет к уменьшению вероятности “захвата”, что непосредственно следует из результатов, представленных на рис. 4 и соответствующих случаю, когда $T{\kern 1pt} ' < 0$, имея в виду, что участки, когда $T{\kern 1pt} ' < 0$, как правило, не продолжительны.
3. При обеспечении ограниченных значений угла нутации и угловых скоростей МКА при отделении вероятность “захвата” уменьшается, когда параметр ${{\bar {J}}_{x}}$ увеличивается и приближается к 1 (рис. 4), то есть эллипсоид инерции МКА как тела вращения приближается к сфере.
4. Изменяя положение центра масс МКА ($\Delta x$) можно соответственно изменять значения резонансной угловой скорости ${{\omega }}_{x}^{{\left( r \right)}}$ (изменяются значения частоты ${{\omega }}$), однако такой вариант, конечно, имеет естественные ограничения.
5. Если при отделении МКА будет выполнено условие $\left| {{{\omega }_{x}}\left( 0 \right)} \right| < \left| {\omega _{x}^{{\left( r \right)}}} \right|$, то наличие даже малого диссипативного момента $m_{x}^{{{\omega }}} < 0$ может обеспечить отсутствие резонансных эффектов в угловом движении МКА.
6. Начальная стабилизация МКА вращением также может быть положительным фактором, уменьшающим влияние резонансных эффектов, если, например, обеспечить выполнение неравенства $\left| {{{\omega }_{x}}\left( 0 \right)} \right| > \left| {\omega _{x}^{{\left( r \right)}}} \right|$ в процессе развертывания КТС.
В заключение необходимо отметить, что изложенный подход для анализа резонансных эффектов может быть использован для многих задач, близких к задаче о движении тяжелого твердого тела вокруг неподвижной точки (близких к случаю Лагранжа) при медленном изменении частот системы.
Исследование выполнено при финансовой поддержке РФФИ и Государственного фонда естественных наук Китая в рамках научного проекта № 21-51-53001.
ПРИЛОЖЕНИЕ
Слагаемые, входящие в исходные уравнения движения МКА (1)–(5).
Список литературы
Алпатов А.П., Белецкий В.В., Драновский В.И. и др. Динамика космических систем с тросовыми и шарнирными соединениями. Москва-Ижевск: НИЦ “Регулярная и хаотическая динамика”, Институт компьютерных исследований, 2007.
Белецкий В.В., Левин Е.М. Динамика космических тросовых систем. М.: Наука, 1990.
Заболотнов Ю.М. Резонансные движения статически устойчивого волчка Лагранжа при малых углах нутации // Прикладная математика и механика. 2016. Т. 80. № 4. С. 432–443.
Заболотнов Ю.М. Резонансные движения статически устойчивого волчка Лагранжа // Прикладная математика и механика. 2019. Т. 83. № 4. С. 615–635.
Заболотнов Ю.М., Наумов О.Н. Движение спускаемой капсулы относительно центра масс при развертывании орбитальной тросовой системы // Космич. исслед. 2012. Т. 50. № 2. С. 177–187. (Cosmic Research. P. 177–187).
Заболотнов Ю.М. Применение метода интегральных многообразий для анализа пространственного движения твердого тела на тросе // Механика твердого тела. Известия РАН. 2016. № 4. С. 3–18.
Ярошевский В.А. Движение неуправляемого тела в атмосфере. М: Машиностроение, 1978.
Заболотнов Ю.М., Любимов В.В. Применение метода интегральных многообразий для построения резонансных кривых в задаче входа КА в атмосферу // Космич. исслед. 2003. Т. 41. № 5. С. 481–487. (Cosmic Research. P. 481–487).
Kruijff M. Tethers in Space. Netherlands: Delta-Utec Space Research, 2011.
Белоконов И.В., Тимбай И.А., Николаев П.Н. Анализ и синтез движения аэродинамически стабилизированных космических аппаратов нанокласса формата CUBESAT // Гироскопия и навигация. 2018. Т. 26. № 3(102). С. 69–91.
Заболотнов Ю.М. Метод исследования резонансного движения одной нелинейной колебательной системы // Механика твердого тела. Известия РАН. 1999. № 1. С. 33–45.
Стрыгин В.В., Соболев В.А. Разделение движений методом интегральных многообразий. М.: Наука, 1988.
Арнольд В.И., Козлов В.В., Нейштадт А.И. Математические аспекты классической и небесной механики. Т. 3. М.: ВИНИТИ, 1985.
Журавлев В.Ф., Климов Д.М. Прикладные методы в теории колебаний. М.: Наука, 1988.
Нейштадт А.И. Вопросы теории возмущений нелинейных систем. М.: МГУ, 1988.
Neishtadt A. Averaging method for systems with separatrix crossing // Nonlinearity. 2017. V. 30. № 5. P. 2871–2917.
Садов Ю.А. Вторичный резонансный эффект в двухчастотной системе с быстрыми фазами / Устойчивость движения. Новосибирск: Наука, 1985.
Заболотнов Ю.М., Любимов В.В. Вторичный резонансный эффект при движении КА в атмосфере // Космич. исслед. 1998. Т. 36. № 2. С. 206–213. (Cosmic Research. P. 194–201).
Ишков С.А., Наумов С.А. Управление развертыванием орбитальной тросовой системы // Вестник Самарского государственного аэрокосмического университета. 2006. № 1. С. 81–90.
Заболотнов Ю.М. Управление развертыванием орбитальной тросовой системы, состоящей из двух малых космических аппаратов // Космич. исслед. 2017. Т. 55. № 3. С. 236–246. (Cosmic Research. P. 224–233).
Митропольский Ю.А., Лыкова О.Б. Интегральные многообразия в нелинейной механике. М.: Наука, 1973.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования