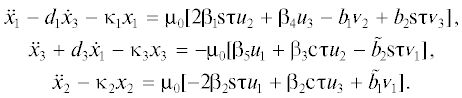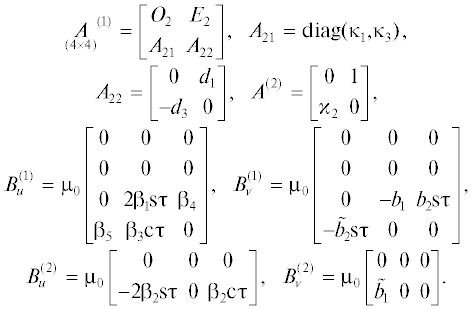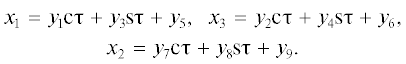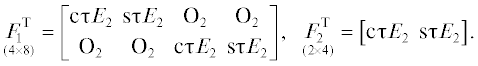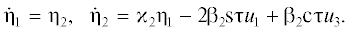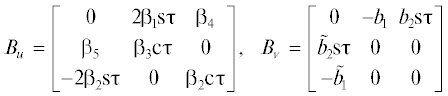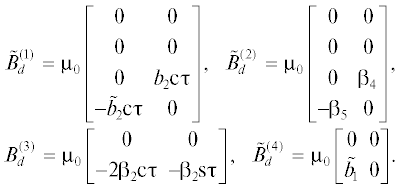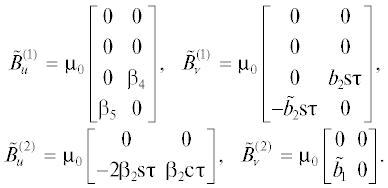Космические исследования, 2021, T. 59, № 5, стр. 393-407

ВВЕДЕНИЕ

Электродинамическое взаимодействие спутника с магнитным полем Земли оказывает существенное влияние на динамику вращательного движения спутника относительно центра масс и может быть использовано при построении системы управления ориентацией. Магнитные системы ориентации и стабилизации широко применяются в практике космических исследований, в частности, для малых спутников.

Методы создания управляющих моментов основаны на различных типах указанного взаимодействия. При одном методе используется эффект взаимодействия внутреннего магнитного момента спутника, создаваемого магнитными катушками, с геомагнитным полем. Другой метод управления основан на использовании электродинамического эффекта влияния лоренцевых сил, действующих на заряженную часть поверхности спутника. Первому методу посвящено большое число публикаций [1–19]. Обзор работ этого направления, выполненных до 2003 г., содержится в [20], а более поздних работ в [21, 22]. Второй метод был предложен в работе А.А. Тихонова [23]. Он был развит и модифицирован в работах А.А. Тихонова и его соавторов [24–29], в которых наряду с моментами сил Лоренца используются внутренние магнитные моменты. Обзор полученных в этих работах результатов содержится в [30, 31]. Использование момента лоренцевых сил для управления космическим аппаратом рассмотрено также в [32–37].

Во многих работах отмечается, что как магнитные системы управления, так и системы, основанные на применении моментов лоренцевых сил, имеют ограничения, связанные с направлениями указанных управляющих моментов. В [24] показано, что имеющиеся ограничения применения обеих систем исчезают при создании единой электродинамической системы управления ориентацией спутника, использующей одновременно управляющие моменты магнитных и лоренцевых сил. На это обстоятельство указано также в работах [36–40], в которых рассматривалось совместное действие магнитных и лоренцевых моментов.

При применении обоих методов управления управляющий момент является функцией геомагнитного поля, которое изменяется во время движения спутника по орбите вокруг Земли. В большинстве работ предполагается, что это изменение носит периодический характер, если орбита спутника – круговая. Как отмечено в [20], это предположение вполне оправдано. Поэтому математические модели рассматриваемых задач представляют собой системы дифференциальных уравнений с периодическими коэффициентами. Это обстоятельство вносит существенные трудности как в изучение управляемости системы, так и в разработку эффективных алгоритмов управления.

Вопрос об управляемости в указанных задачах является важным, но во многих работах, в которых предлагаются алгоритмы управления, эта проблема вообще не обсуждается.

Управляемость спутников с магнитной системой ориентации в периодическом геомагнитном поле без учета гравитационного момента рассмотрена в [37]. В работе [16] показано, что система, линеаризованная в окрестности положения равновесия спутника, снабженного магнитной системой, управляема при любых моментах инерции, если орбита спутника не является экваториальной. Достаточные условия управляемости в этой задаче были получены в [38], а при учете аэродинамических сил в [39]. Необходимые и достаточные условия управляемости при действии моментов лоренцевых сил сформулированы в [45]. Вопросы управляемости “в среднем” как при действии магнитных моментов, так и при действии моментов лоренцевых сил рассмотрены в [4, 5, 12, 30].

При построении алгоритмов управления с обратной связью используются два подхода. Один основан на применении метода Ляпунова [23, 28, 29], другой приводит к численному анализу линейной периодической системы на основании теории Флоке [7–11].

Как отмечено в [20], выбор коэффициентов усиления в законе управления с обратной связью – центральный вопрос в этой задаче. Оказалось, что при этом методе управления алгоритм особенно чувствителен к точности информации о тензоре инерции спутника [7–10]. Следует подчеркнуть, что при обоих указанных подходах выбор коэффициентов обратной связи не алгоритмизован, и способ их выбора не указан.

Цель предлагаемой статьи – представить строгий аналитический подход к изучению этой проблемы, заключающийся в приведении исходной нестационарной системы к стационарной. Этот подход был развит для линейных нестационарных систем (ЛНС) определенного класса и ранее применялся для решения ряда прикладных задач [40–44], в том числе для задачи стабилизации ориентации спутника при использовании магнитных моментов [15, 16] и при использовании моментов лоренцевых сил [45].

Факт приводимости системы к стационарной эффективно используется как при анализе управляемости, так и при построении алгоритмов стабилизации. При наличии свойства управляемости приведенной стационарной системы для нее строится оптимальный алгоритм стабилизации, основанный на LQR-методе на бесконечном интервале времени, который приводит к управлению в виде обратной связи с постоянными коэффициентами. Это управление обеспечивает асимптотическую устойчивость стационарной системы. Построенное стабилизирующее управление вводится в исходную нестационарную систему при помощи введения дополнительных переменных и соответствующего ограниченного преобразования, при этом коэффициенты обратной связи оказываются переменными. Исходная система, замкнутая таким управлением, также асимптотически устойчива.

Следует подчеркнуть, что выбор коэффициентов обратной связи, имеющий важное и принципиальное значение, при указанном подходе хорошо алгоримизован и состоит из определения коэффициентов для стационарной системы из стандартной процедуры LQR (при этом требуется задать лишь параметры функционалов) и преобразования к исходным переменным, которое строится конструктивным способом.

ПОСТАНОВКА ЗАДАЧИ

Рассматривается движение спутника около центра масс в гравитационном и магнитном полях Земли. Предполагается, что центр масс спутника движется по круговой орбите. Спутник снабжен магнитными катушками и экраном, обладающим электрическим зарядом.

Системы координат и уравнения движения

Используются две правые системы координат:

$OXYZ$ – орбитальная система координат с началом в центе масс спутника: ось $OZ$ направлена по радиус-вектору центра масс относительно притягивающего центра (центра Земли); $OY$ – по нормали к плоскости орбиты, $OX$ дополняет систему до правой тройки;

$Oxyz$ – связанная система координат (подвижная), оси которой направлены по главным центральным осям инерции спутника.

Ориентация системы $Oxyz$ относительно орбитальной задается с помощью углов Эйлера θ₁, θ₂, θ₃. Матрица перехода от системы $OXYZ$ в системе $Oxyz$ имеет вид [46]

$\begin{gathered} \Theta = \left\| {{{\Theta }_{{ij}}}} \right\|;\,\,\,\,{{\Theta }_{{11}}} = \cos {{{{\theta }}}_{1}}\cos {{{{\theta }}}_{3}} - \sin {{{{\theta }}}_{1}}\sin {{{{\theta }}}_{2}}\sin {{{{\theta }}}_{3}}, \\ {{\Theta }_{{12}}} = - \sin {{{{\theta }}}_{1}}\cos {{{{\theta }}}_{2}},\,\,\,\,{{\Theta }_{{13}}} = \cos {{{{\theta }}}_{1}}\sin {{{{\theta }}}_{3}} + \\ + \,\,\sin {{{{\theta }}}_{1}}\sin {{{{\theta }}}_{2}}\cos {{{{\theta }}}_{3}},\,\,\,\,{{\Theta }_{{21}}} = \sin {{{{\theta }}}_{1}}\cos {{{{\theta }}}_{3}} + \\ + \,\,\cos {{{{\theta }}}_{1}}\sin {{{{\theta }}}_{2}}\sin {{{{\theta }}}_{3}},\,\,\,\,{{\Theta }_{{22}}} = \cos {{{{\theta }}}_{1}}\cos {{{{\theta }}}_{2}}, \\ {{\Theta }_{{23}}} = \sin {{{{\theta }}}_{1}}\sin {{{{\theta }}}_{3}} - \cos {{{{\theta }}}_{1}}\sin {{{{\theta }}}_{2}}\cos {{{{\theta }}}_{3}}, \\ {{\Theta }_{{31}}} = - \cos {{{{\theta }}}_{2}}\sin {{{{\theta }}}_{3}},\,\,\,\,{{\Theta }_{{32}}} = \sin {{{{\theta }}}_{2}}, \\ {{\Theta }_{{33}}} = \cos {{{{\theta }}}_{2}}\cos {{{{\theta }}}_{3}}. \\ \end{gathered} $

Компоненты абсолютной угловой скорости спутника ${\mathbf{\omega }}$ в проекциях на оси системы координат $Oxyz$ имеют вид [46]

(1)

$\begin{gathered} {{{{\omega }}}_{1}} = - {{{{{\dot {\theta }}}}}_{1}}\cos {{{{\theta }}}_{2}}\sin {{{{\theta }}}_{3}} + {{{{{\dot {\theta }}}}}_{2}}\cos {{{{\theta }}}_{3}} + {{{{\omega }}}_{0}}{{{{\theta }}}_{{21}}}, \\ {{{{\omega }}}_{2}} = {{{{{\dot {\theta }}}}}_{3}} + {{{{{\dot {\theta }}}}}_{1}}\sin {{{{\theta }}}_{2}} + {{{{\omega }}}_{0}}{{{{\theta }}}_{{22}}}, \\ {{{{\omega }}}_{3}} = {{{{{\dot {\theta }}}}}_{1}}\cos {{{{\theta }}}_{2}}\cos {{{{\theta }}}_{3}} + {{{{\theta }}}_{2}}\sin {{{{\theta }}}_{3}} + {{{{\omega }}}_{0}}{{{{\theta }}}_{{23}}}, \\ \end{gathered} $

где ${{{{\omega }}}_{0}}$ – величина угловой скорости орбитального движения.

Динамические уравнения движения спутника около центра масс имеют вид [46]

(2)

${\mathbf{J}}\frac{{d{\mathbf{\omega }}}}{{dt}} + {\mathbf{\omega }} \times {\mathbf{J\omega }} = 3{{\omega }}_{0}^{2}\left( {{{\Theta }^{{\text{T}}}}{{{\mathbf{e}}}_{r}} \times {\mathbf{J}}{{\Theta }^{{\text{T}}}}{{{\mathbf{e}}}_{r}}} \right) + {\mathbf{M}}.$

Здесь ${\mathbf{J}} = {\text{diag(}}\begin{array}{*{20}{c}} {{{J}_{1}}}&{{{J}_{2}}}&{{{J}_{3}}} \end{array}{\text{);}}$ ${{J}_{1}},{{J}_{2}},{{J}_{3}}$ – главные центральные моменты инерции спутника, ${{{\mathbf{e}}}_{r}}$ – единичный вектор оси $OZ,$ ${\mathbf{M}}$ – управляющий момент, который создается как за счет взаимодействия собственного дипольного магнитного момента спутника с магнитным полем Земли (${{{\mathbf{M}}}_{{\text{M}}}}$), так и силами Лоренца, действующими на заряженную поверхность КА (${{{\mathbf{M}}}_{{\text{L}}}}$). ${\mathbf{M}} = {{{\mathbf{M}}}_{{\text{M}}}} + {{{\mathbf{M}}}_{{\text{L}}}}.$

Управляющие моменты ${{{\mathbf{M}}}_{{\text{M}}}}$ и ${{{\mathbf{M}}}_{{\text{L}}}}$ имеют вид [1, 7, 22, 30]

(3)

${{{\mathbf{M}}}_{{\text{M}}}} = {\mathbf{m}} \times {{\Theta }^{{\text{T}}}}{\mathbf{b}},\,\,\,\,{{{\mathbf{M}}}_{{\text{L}}}} = q{{{\mathbf{\rho }}}_{{\mathbf{0}}}} \times {{\Theta }^{{\text{T}}}}({{{\mathbf{V}}}_{C}} \times {\mathbf{b}}).$

Здесь ${\mathbf{m}} = {{[\begin{array}{*{20}{c}} {{{m}_{1}}}&{{{m}_{2}}}&{{{m}_{3}}} \end{array}]}^{{\text{T}}}}$ ‑ магнитный дипольный момент спутника, ${\mathbf{b}}(t)$ – вектор индукции геомагнитного поля, которое аппроксимируется прямым магнитным диполем в орбитальной системе координат [47]

${\mathbf{b}}(t) \approx \frac{{{{{{\mu }}}_{{\text{E}}}}}}{{{{R}^{3}}}}\left[ {\begin{array}{*{20}{c}} {\cos {{{{\omega }}}_{0}}t\sin I} \\ { - \cos I} \\ {2sin{{{{\omega }}}_{0}}t\sin I} \end{array}} \right],$

где $I$ – угол наклона плоскости орбиты спутника к плоскости экватора; μ_E – постоянная магнитного поля Земли, $R$ – радиус орбиты центра масс спутника; $q$ – электростатический заряд; ${{{\mathbf{\rho }}}_{{\mathbf{0}}}} = {{\left[ {{{x}_{0}}\,{{y}_{0}}\,{{z}_{0}}} \right]}^{{\text{T}}}}$ – радиус-вектор центра заряда спутника относительно его центра масс; ${{{\mathbf{V}}}_{C}}$ – скорость центра масс спутника относительно геомагнитного поля, ${{{\mathbf{V}}}_{c}} = R({{{{\omega }}}_{0}} - {{{{\omega }}}_{{\text{E}}}}\cos I){{{\mathbf{e}}}_{{{\tau }}}}$ + $R{{{{\omega }}}_{{\text{E}}}}\sin I\cos {{{{\omega }}}_{0}}t{{{\mathbf{e}}}_{n}};$ ${{{{\omega }}}_{{\text{E}}}}$ – величина угловой скорости суточного вращения Земли; $R$ – радиус орбиты; ${{{\mathbf{e}}}_{{{\tau }}}},{{{\mathbf{e}}}_{n}}$ – единичные вектора осей $OX$ и $OY.$ В рамках принятого приближения будем пренебрегать величиной ${{{{\omega }}}_{{\text{E}}}}$ по сравнению с ${{{{\omega }}}_{0}}$ (${{{{{{\omega }}}_{{\text{E}}}}} \mathord{\left/ {\vphantom {{{{{{\omega }}}_{{\text{E}}}}} {{{{{\omega }}}_{0}}}}} \right. \kern-0em} {{{{{\omega }}}_{0}}}} \approx {{10}^{{ - 2}}}$). Поэтому далее ${{{\mathbf{V}}}_{c}} = R{{{{\omega }}}_{0}}{{{\mathbf{e}}}_{{{\tau }}}}.$

Величины ${{m}_{1}},{{m}_{2}},{{m}_{3}}$ и ${{x}_{0}},{{y}_{0}},{{z}_{0}}$ далее считаются управляющими параметрами: ${\mathbf{m}} = {\mathbf{u}}({{m}_{1}},{{m}_{2}},{{m}_{3}}),$ ${{{\mathbf{\rho }}}_{0}} = {\mathbf{v}}({{x}_{0}} = {{\nu }_{1}},{{y}_{0}} = {{{v}}_{2}},{{z}_{0}} = {{{v}}_{3}}).$

Для более сложных моделей магнитного поля предлагаемый метод также применим.

Линеаризованные уравнения движения. Уравнения движения (1), (2) при ${\mathbf{M}} = 0$ допускают стационарные решения, отвечающие положениям относительного равновесия спутника, в которых оси связанной системы координат $Oxyz$ совпадают с осями орбитальной системы координат $OXYZ$ [46]. Углы поворота ${{{{\theta }}}_{i}}(i = 1,2,3)$ выбраны таким образом, что в положении относительного равновесия все углы и относительные угловые скорости спутника равны нулю

(4)

Управление ${\mathbf{M}}$ формируется в виде линейной обратной связи по компонентам вектора состояния ${{{{\theta }}}_{i}},{{{{\dot {\theta }}}}_{i}}$ $(i = 1,2,3).$ При линеаризации уравнений движения (1), (2) в окрестности относительного равновесия (4), очевидно, линеаризуются и выражения для моментов (3), в которых можно считать $\Theta = {{E}_{3}}$ (${{E}_{k}}$ – единичная матрица ($k \times k$)).

Тогда линеаризованные уравнения управляемого движения при введении безразмерного времени ${{\tau }} = {{{{\omega }}}_{0}}t$ имеют вид

(5)

Здесь “точка” по-прежнему обозначает производную по времени τ;

Для круговой орбиты ${{\omega }}_{0}^{2} = \frac{{{\mu }}}{{{{R}^{3}}}},$ μ – гравитационный параметр Земли. Тогда величина ${{{{\mu }}}_{{\text{0}}}} = \frac{{{{{{\mu }}}_{{\text{E}}}}}}{{{\mu }}}$ не зависит от радиуса орбиты.

В Приложении приведены нелинейные уравнения с точностью до членов второго порядка включительно.

Систему (5) можно представить в виде системы первого порядка

$\dot {\xi } = {{A}_{\xi }}\xi + {{B}_{\xi }}(\tau ){{U}_{\xi }}.$

Введя

$\begin{gathered} \mathop \xi \limits_{(6 \times 1)} = \left[ {\begin{array}{*{20}{c}} {{{\xi }^{{(1)}}}} \\ {{{\xi }^{{(2)}}}} \end{array}} \right],\,\,\,\,{{\xi }^{{(1)}}} = {{\left[ {\begin{array}{*{20}{c}} {{{x}_{1}}}&{{{x}_{3}}}&{{{{\dot {x}}}_{1}}}&{{{{\dot {x}}}_{3}}} \end{array}} \right]}^{{\text{T}}}},\,\,\,\,{{\xi }^{{(2)}}} = {{\left[ {\begin{array}{*{20}{c}} {{{x}_{2}}}&{{{{\dot {x}}}_{2}}} \end{array}} \right]}^{{\text{T}}}}, \\ \mathop {{{U}_{\xi }}}\limits_{(6 \times 1)} = \left[ {\begin{array}{*{20}{c}} {\mathop u\limits_{(3 \times 1)} } \\ {\mathop {v}\limits_{(3 \times 1)} } \end{array}} \right],\,\,\,\,{{A}_{\xi }} = {\text{diag}}({{A}^{{(1)}}},{{A}^{{(2)}}}),\,\,\,\,{{B}_{\xi }}(\tau ) = \left[ {\begin{array}{*{20}{c}} {{{{\mathop B\limits_{(4 \times 6)} }}^{{(1)}}}} \\ {{{{\mathop B\limits_{(2 \times 6)} }}^{{(2)}}}} \end{array}} \right], \\ \end{gathered} $

эту систему удобно представить в виде двух подсистем

(6)

${{\dot {\xi }}^{{(1)}}} = {{A}^{{(1)}}}{{\xi }^{{(1)}}} + B_{u}^{{(1)}}u + B_{{v}}^{{(1)}}{v};$

(7)

${{\dot {\xi }}^{{(2)}}} = {{A}^{{(2)}}}{{\xi }^{{(2)}}} + B_{u}^{{(2)}}u + B_{{v}}^{{(2)}}{v},$

где матрицы имеют вид

Здесь $\mathop {{{O}_{2}}}\limits_{(2 \times 2)} $ – нулевая матрица.

Требуется построить управление, обеспечивающее асимптотическую устойчивость положения относительного равновесия (4), основываясь либо на системе уравнений (5), либо (6), (7). Аналитически построить стабилизирующее управление непосредственно для исходной системы затруднительно из-за ее существенной нестационарности. Для преодоления указанных трудностей предлагается подход, ранее применявшийся для решения ряда прикладных задач [40–43], в том числе для решения задач стабилизации движения спутников при использовании магнитных катушек [15, 16] и моментов сил Лоренца [45].

Этот подход основан на том, что рассматриваемые системы, нестационарные по управлению, относятся к классу линейных нестационарных систем (ЛНС), приводимых к стационарным [40]. Он состоит из ряда этапов:

1) построение конструктивного преобразования исходной нестационарной системы к стационарной системе;

2) проведение анализа управляемости полученной стационарной системы;

3) при наличии управляемости построение для стационарной системы оптимального алгоритма управления на основе квадратичного критерия качества на бесконечном интервале времени, что позволяет получить линейную обратную связь с постоянными коэффициентами;

4) осуществление обратного перехода к исходным переменным нестационарной системы.

ПРЕОБРАЗОВАНИЕ К СТАЦИОНАРНОЙ СИСТЕМЕ

Системы (5) и (6), (7) относятся к классу ЛНС, содержащих управление, которые допускают приведение к стационарным системам в расширенном пространстве состояний [40–42]. Напомним, что этот класс систем характеризуется тем, что функции, входящие в выражение для матрицы $B(\tau )$ при управлении, являются решениями линейной однородной системы с постоянными коэффициентами. В системах уравнений (5) и (6), (7) матрицы коэффициентов при управлении, имеют вид

Коэффициенты матриц $B({{\tau }})$ являются элементами вектора $f({{\tau }})$

Преобразование системы (5) к стационарной системе. Согласно [40], введем новые переменные ${{y}_{j}}(j = 1,...9)$ по формулам

Дважды дифференцируя эти соотношения, подставляя их в систему (5) и приравнивая коэффициенты при функциях $\cos \tau ,\sin \tau ,1,$ получим

Стационарная система (8)–(11) состоит из двух независимых систем (8), (9) и (10), (11), в которые входят управления ${{u}_{2}},{{{v}}_{1}},{{{v}}_{3}}$ и ${{u}_{1}},{{u}_{3}},{{{v}}_{2}}.$

Преобразование системы (6), (7) к стационарной системе. Введем векторы

Переменные ${{{{\xi }}}_{j}}(j = 1,2,...6),$ удовлетворяющие системе (6), связаны с переменными ${{z}_{j}}(j = 1,...,18)$ соотношениями

Здесь

В переменных ${{z}_{j}}(j = 1,...,18)$ система стационарна и имеет вид

Эта стационарная система состоит из двух независимых групп (13), (14) с управлением ${{V}_{1}}$ и (15), (16) с управлением ${{U}_{1}}.$

Замечание. Если системы (8)–(11) представить в виде системы первого порядка, то нетрудно показать, что полученная система будет связана с системой (13)–(16) невырожденным преобразованием с постоянной матрицей.

УПРАВЛЯЕМОСТЬ

Управляемость в рассматриваемой задаче можно исследовать как исходя из нестационарной системы (6), так и анализируя стационарные системы (8)–(11) или (13)–(16). Как уже указывалось, стационарные системы являются избыточными по отношению к исходной системе. Если стационарная система управляема, то управляема и исходная нестационарная система. Однако неуправляемость стационарной системы может и не повлечь неуправляемость исходной нестационарной системы.

Управляемость нестационарной системы (6). Применяя критерий Красовского [48], нетрудно показать, что нестационарная система (6) управляема при наличии всех шести управляющих воздействий ${{u}_{j}},{{{v}}_{j}}(j = 1,2,3)$ и если орбита не является ни полярной ($I = {{\pi /}}2$), ни экваториальной ($I = 0$).

1. Если орбита экваториальная ($I = 0$), то система (6) становится стационарной (${{{{\beta }}}_{j}} = 0$ $(j = 1,2,3),$ ${{b}_{2}} = {{\tilde {b}}_{2}} = 0$). В этом случае управления ${{u}_{2}},{{{v}}_{3}}$ в систему не входят; на переменную ${{x}_{2}}$ действует управление ${{{v}}_{1}},$ а для переменных ${{x}_{1}},{{x}_{3}}$ – управления ${{u}_{1}},{{u}_{3}},{{{v}}_{2}}.$ Необходимым условием управляемости является наличие управления ${{{v}}_{1}},$ т.е. если лоренцевых сил нет, то система неуправляема.

Если магнитные моменты отсутствуют (${{u}_{j}} = 0$), то сиcтема управляема только при наличии лоренцевых сил, если выполнены условия ${{J}_{2}} \ne {{J}_{1}} + {{J}_{3}}$ и ${{J}_{1}} \ne {{J}_{2}}.$

2. Если орбита полярная ($I = {{\pi /}}2$), то система (6) расщепляется на две независимые группы: уравнения для переменных ${{x}_{1}},{{x}_{3}}$ с управлениями ${{u}_{2}},{{{v}}_{1}},{{{v}}_{3}};$ уравнения для ${{x}_{2}}$ с управлениями ${{u}_{1}},{{u}_{3}}.$ Управление ${{{v}}_{3}}$ в систему не входит.

Рассмотрим следующую систему, представив уравнение для переменной ${{x}_{2}}$ системы (5) в виде системы уравнений первого порядка

Применяя критерий [48], нетрудно получить, что эта система управляема при наличии хотя бы одного управления ${{u}_{1}}$ или ${{u}_{3}}.$ Это означает, что на полярной орбите при отсутствии магнитного управления (${{u}_{1}} = {{u}_{3}} = 0$) система неуправляема.

Аналогично, для переменных ${{x}_{1}},{{x}_{3}}$ можно показать, что система управляема при наличии всех управлений ${{u}_{2}},{{{v}}_{1}},{{{v}}_{3}}.$ В [15] показано, что при отсутствии лоренцевых моментов (${{{v}}_{1}} = {{{v}}_{3}} = 0$), система также управляема (${{u}_{2}} \ne 0$).

Итак, на экваториальной орбите система неуправляема при отсутствии моментов лоренцевых сил. На полярной орбите система неуправляема при отсутствии магнитных моментов.

Замечание. Ранги матриц коэффициентов при магнитных моментах и при лоренцевых моментах

Если положить ${{u}_{2}} = 0,$ ${{{v}}_{2}} = 0,$ то на переменные подсистемы (13), (14) действуют только моменты лоренцевых сил, а на переменные подсистемы (15), (16) – только момент, создаваемый магнитными катушками. Тогда нетрудно показать, что нестационарная система также управляема, если. $I \ne 0,$ $I \ne {{\pi /}}2.$

Управляемость стационарных систем. Управляемость стационарной системы удобнее исследовать на основе системы (8)–(11), состоящей из двух подсистем (8), (9) и (10), (11), на которые действуют независимые управления ${{V}_{1}} = {{u}_{2}},{{{v}}_{1}},{{{v}}_{3}}$ и ${{U}_{1}} = {{u}_{1}},{{u}_{3}},{{{v}}_{2}}.$

Согласно критерию [49] система (8), (9) управляема тогда и только тогда, когда

Нетрудно показать, что условиями неуправляемости в этом случае будут условия

Неуправляемость в этих случаях подтверждается наличием первых интегралов систем (8), (9) или (13), (14).

Система (10), (11) управляема тогда и только тогда, когда

Нетрудно показать, что условиями неуправлемости в этом случае будут условия

Это также подтверждается наличием первого интеграла, не зависящего от управления у систем (10), (11) или (15), (16)

В случае, когда ${{u}_{2}} = {{{v}}_{2}} = 0,$ возникают новые условия неуправлямости.

Для систем (8), (9) – условие неуправляемости ${{J}_{2}} = {{J}_{1}} + {{J}_{3}};$ соответствующие первые интегралы

Для систем (10), (11) – условие неуправляемости ${{J}_{2}} = {{J}_{3}},$ ${{J}_{1}} = \frac{4}{3}{{J}_{3}};$ соответствующие первые интегралы

В случаях неуправляемости стационарных систем можно, используя соответствующие интегралы, выделить управляемые подсистемы.

АЛГОРИТМ ПОСТРОЕНИЯ СТАБИЛИЗИРУЮЩЕГО УПРАВЛЕНИЯ

Одна из основных идей предлагаемого метода состоит в использовании стационарной системы для выбора стабилизирующего управления. Это хорошо разработанный и алгоритмизированный, устойчивый в работе, способ удобный для применения. Алгоритм строится на основе стационарной системы (13)–(16). Задача стабилизации стационарной управляемой системы (13)–16) состоит в том, чтобы построить управление, обеспечивающее стремление к нулю компонент вектора состояния системы при ${{\tau }} \to \infty .$

Как было отмечено система (13)–16) состоит из двух независимых подсистем: (13), (14) (десятого порядка) с управлением ${{V}_{1}}$ и (15), (16) (восьмого порядка) с управлением ${{U}_{1}}.$ Далее будем полагать ${{u}_{2}} = 0,$ ${{{v}}_{2}} = 0,$ $U = {{\left[ {\begin{array}{*{20}{c}} {{{u}_{1}}}&{{{u}_{3}}} \end{array}} \right]}^{{\text{T}}}},$ $V = {{\left[ {\begin{array}{*{20}{c}} {{{{v}}_{1}}}&{{{{v}}_{3}}} \end{array}} \right]}^{{\text{T}}}}.$

Стабилизирующее управление строится для каждой подсистемы независимо в виде обратной связи по состоянию, а матрица коэффициентов управления выбирается из условия минимума квадратичных функционалов

Оптимальное управление имеет вид [50]

Матрицами ${{\tilde {B}}^{{(i)}}}$ обозначены матрицы ${{B}^{{(i)}}}$ с исключенными вторыми столбцами.

Матрицы $\mathop {{{P}^{{(1)}}}}\limits_{(10 \times 10)} ,$ $\mathop {{{P}^{{(2)}}}}\limits_{(8 \times 8)} $ являются положительно определенными решениями соответствующих матричных алгебраических уравнений Риккати

Синтезированные управляющие воздействия $V({{\tau }})$ и $U({{\tau }})$ являются функциями переменных ${{Z}^{{(1)}}}({{\tau }})$ и ${{Z}^{{(2)}}}({{\tau }})$ стационарной системы (13)–(16) более высокого порядка, чем исходная нестационарная система (6), (7). Для введения этих управлений непосредственно в исходную систему следует выразить векторы ${{Z}^{{(1)}}}({{\tau }})$ и ${{Z}^{{(2)}}}({{\tau }})$ через векторы состояния $\mathop {{{\xi }^{{(1)}}}}\limits_{(4 \times 1)} $ и $\mathop {{{\xi }^{{(2)}}}}\limits_{(2 \times 1)} ,$ дополненные вспомогательными векторами $\mathop {{{\xi }^{{'(1)}}}}\limits_{(6 \times 1)} $ и $\mathop {{{\xi }^{{'(2)}}}}\limits_{(6 \times 1)} ,$ которые введем, учитывая формулы (12)

Уравнения для вспомогательных векторов $\mathop {{{\zeta }^{{(1)}}}}\limits_{(4 \times 1)} ,\mathop {{{\zeta }^{{(2)}}}}\limits_{(4 \times 1)} ,\mathop {{{\zeta }^{{(3)}}}}\limits_{(4 \times 1)} ,\mathop {{{\zeta }^{{(4)}}}}\limits_{(2 \times 1)} $ имеют вид

Векторы состояния ${{\tilde {\xi }}^{{(1)}}},{{\tilde {\xi }}^{{(2)}}},$ содержащие векторы исходной нестационарной системы и вспомогательные векторы ${{\tilde {\xi }}^{{'(1)}}},{{\tilde {\xi }}^{{'(2)}}},$ связаны с векторами ${{Z}^{{(1)}}},{{Z}^{{(2)}}}$ стационарной системы следующими преобразованиями

Исходная система (6), (7) при ${{u}_{2}} = 0,$ ${{{v}}_{2}} = 0$ имеет вид

Тогда нестационарную систему для моделирования составляют системы (24), (20), (23) и (25), (21), (24)

Управления (18), построенные для стационарной системы (13)–(16), можно вводить в систему (26) в виде

Замкнутая управлением система имеет вид

Решения $\tilde {\xi }(\tau )$ системы (28), содержащие компоненты исходного вектора $\xi (\tau ),$ стремятся к нулю при ${{\tau }} \to \infty $ в силу выбора матрицы ${{K}_{Z}},$ так как они связаны с асимптотически стремящимися к нулю компонентами вектора $Z$ ограниченным преобразованием T.

МОДЕЛИРОВАНИЕ

Моделирование проводилось при помощи стандартного пакета Matlab 7.1. Коэффициенты управления выбирались при помощи стандартной программы LQR для стационарных систем (13), (14) десятого порядка и (15), (16) восьмого порядка. Матрицы в функционале (17) имеют вид

Радиус орбиты $R = 7000\,\,{\text{км}}{\text{.}}$ Величина заряда $q = 5.0 \cdot {{10}^{{ - 3}}}\,\,{\text{Кл}}$ [28].

Параметр, определяющий величину собственного магнитного момента ${{{{\mu }}}_{{\text{0}}}}\, = \,\frac{{{{{{\mu }}}_{{\text{E}}}}}}{{{\mu }}},$ ${{{{\mu }}}_{{\text{E}}}} = 7.812$ · $ \cdot \,\,{{10}^{6}}\,{\text{к}}{{{\text{м}}}^{3}}\, \cdot \,{\text{кг}}\, \cdot \,{{{\text{с}}}^{{ - 2}}}\, \cdot \,{{{\text{А}}}^{{ - 1}}},$ ${{\mu }} = 3.986 \cdot {{10}^{5}}\,\,{\text{к}}{{{\text{м}}}^{{\text{3}}}}{{{\text{с}}}^{{ - {\text{2}}}}}.$

Значения параметров функционалов (17)

Начальные условия по углам: ${{{{\theta }}}_{1}}(0) = 0.1,$ ${{{{\theta }}}_{2}}(0) = 0.15,$ ${{{{\theta }}}_{3}}(0) = 0.2;$ по скоростям: ${{{{\dot {\theta }}}}_{1}}(0) = 0.15,$ ${{{{\dot {\theta }}}}_{2}}(0) = 0.1,$ ${{{{\dot {\theta }}}}_{3}}(0) = 0.1.$ По дополнительным переменным начальные условия принимались нулевыми.

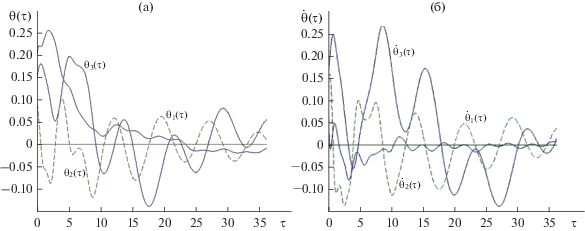
На рис. 1 представлено поведение переменных ${{{{\theta }}}_{{\text{1}}}}{\text{,}}{{{{\theta }}}_{{\text{2}}}}{\text{,}}{{{{\theta }}}_{{\text{3}}}}$ и их производных ${{{{\dot {\theta }}}}_{{\text{1}}}}{\text{,}}{{{{\dot {\theta }}}}_{{\text{2}}}}{\text{,}}{{{{\dot {\theta }}}}_{3}}$ в зависимости от безразмерного времени ${{\tau }}$ для спутника с тензором инерции $J = [115.0,120.0,135.0]\,\,{\text{кг}} \cdot \,{{{\text{м}}}^{2}}$ [32]. Угол наклона плоскости орбиты $I = 60^\circ .$

Рис. 1.

(a) ${{\theta }_{i}}(\tau ),$ (б) ${{\dot {\theta }}_{i}}(\tau ).$

Процесс стабилизации практическим завершился к моменту времени ${{\tau }} = 20 \approx 4.5\,{\text{ч}}{\text{.}}$

На рис. 2 представлено поведение компонент управлений ${{u}_{j}}({{\tau }}),{{{v}}_{j}}({{\tau }})\,\,(j = 1,3)$ в сравнении с гравитационным моментом ${{M}_{g}}({{\tau }}).$

Рис. 2.

(a) $u(\tau ),{{M}_{g}}(\tau ),$ (б) ${v}(\tau ),{{M}_{g}}(\tau ).$

Если моменты инерции спутника не являются близкими к “критическим” (не удовлетворяют условиям неуправляемости стационарной системы), то их изменение на 10–15% не приводит к изменению характера кривых.

Чувствительность алгоритма к изменению тензора инерции проявляется только в окрестности условий неуправляемости.

Было проведено моделирование алгоритмов “вблизи” выполнения условий неуправляемости ${{J}_{1}} = {{J}_{2}} = {{J}_{3}};$ и ${{J}_{1}} = {{J}_{3}},$ ${{J}_{2}} = 2{{J}_{3}}.$

На рис. 3, 4 продемонстрировано, как влияет близость моментов инерции к соотношениям, удовлетворяющим условиям неуправляемости стационарной системы.

Рис. 3.

(a) ${{\theta }_{i}}(\tau ),$ (б) ${{\dot {\theta }}_{i}}(\tau ).$

Рис. 4.

(a) ${{\theta }_{i}}(\tau ),$ (б) ${{\dot {\theta }}_{i}}(\tau ).$

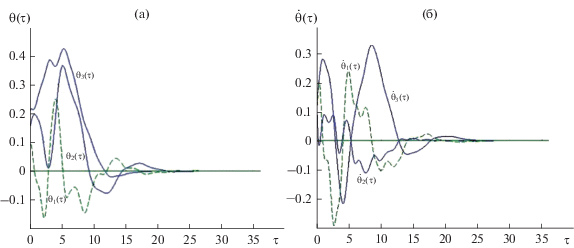
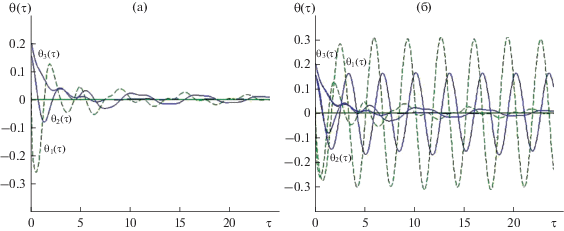
На рис. 3 показано поведение переменных ${{{{\theta }}}_{{\text{1}}}}{\text{,}}{{{{\theta }}}_{{\text{2}}}}{\text{,}}{{{{\theta }}}_{{\text{3}}}}$ и их производных ${{{{\dot {\theta }}}}_{{\text{1}}}}{\text{,}}{{{{\dot {\theta }}}}_{{\text{2}}}}{\text{,}}{{{{\dot {\theta }}}}_{{\text{3}}}}$ в зависимости от времени для спутника с тензором инерции ${{J}_{1}} = [210.0,190.0,210.0]\,\,{\text{кг}}\, \cdot {{{\text{м}}}^{2}}$ (тензор инерции отличается от шарового на ~5%).

Процесс стабилизации требует большего времени по сравнению с кривыми, представленными на рис. 1.

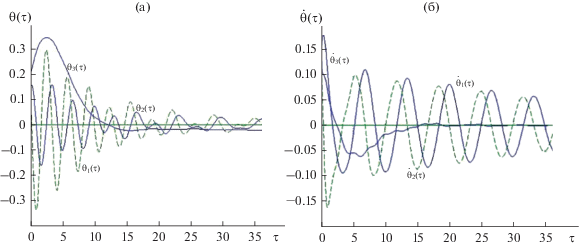
Если тензор инерции отличается от шарового на ~10% ${{J}_{1}} = [220.0,180.0,230.0]\,\,{\text{кг}}\, \cdot {{{\text{м}}}^{2}},$ поведение переменных ${{{{\theta }}}_{{\text{1}}}}{\text{,}}{{{{\theta }}}_{{\text{2}}}}{\text{,}}{{{{\theta }}}_{{\text{3}}}},$ ${{{{\dot {\theta }}}}_{{\text{1}}}}{\text{,}}{{{{\dot {\theta }}}}_{{\text{2}}}}{\text{,}}{{{{\dot {\theta }}}}_{{\text{3}}}}$ показано на рис. 4.

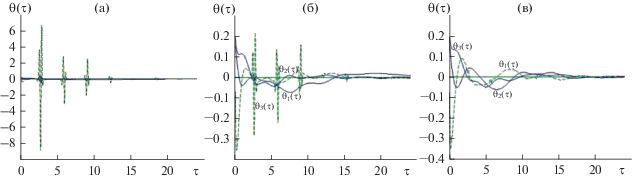
Как проявляется чувствительность алгоритма в окрестности условий неуправляемости для малого спутника продемонстрировано на рис. 5.

Рис. 5.

${{\theta }_{i}}(\tau )$ (a) $J = [3.2;3.4;3.0]\,\,{\text{кг}}\, \cdot {{{\text{м}}}^{2}},$ (б) $J = [3.2;3.6;3.0]\,\,{\text{кг}}\, \cdot {{{\text{м}}}^{2}},$ (в) $J = [3.2;4.0;3.0]\,\,{\text{кг}}\, \cdot {{{\text{м}}}^{2}}.$

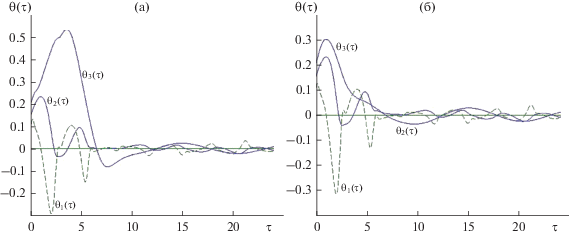
Процесс стабилизации переменных вектора состояния в том случае, когда моменты инерции спутника ${{J}_{1}} = [220.0,420.0,220.0]\,\,{\text{кг}}\, \cdot {{{\text{м}}}^{2}}$ (тензор инерции почти удовлетворяют второму условию неуправляемости стационарной системы ${{J}_{1}} = {{J}_{3}},$ ${{J}_{2}} = 2{{J}_{3}}$) представлен на рис. 6.

Рис. 6.

(a) ${{\theta }_{i}}(\tau ),$ (б) ${{\dot {\theta }}_{i}}(\tau ).$

Характер кривых, отображающих процесс стабилизации на рис. 6, отличается от варианта, представленного на рис. 3.

Для сравнения процесса стабилизации переменных 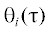в тех случаях, когда интегрировалась линейная система и когда в исходной системе учитывались нелинейные члены (см. Приложение (П-1)), было проведено моделирование при движении по орбите, близкой к полярной $I = 87.0^\circ $ спутника [51] с моментами инерции $J = [27.0,17.0,25.0]\,\,{\text{кг}}\, \cdot {{{\text{м}}}^{2}}.$ Результаты моделирования на рис. 7.

Рис. 7.

${{\theta }_{i}}(\tau )$ (a) линейная система, (б) нелинейная система.

На рис. 8 представлено поведение переменных в процессе стабилизации линейной и нелинейной (см. Приложение (П-II)) систем при движении по экватору ($I = 0.0^\circ $) для спутника [32] с моментами инерции $J = [110.0,130.0,155.0]\,\,{\text{кг}}\, \cdot {{{\text{м}}}^{2}}.$

Рис. 8.

${{\theta }_{i}}(\tau )$ (a) линейная система, (б) нелинейная система.

Времена установления процессов стабилизации в линейной и нелинейной системах примерно одинаковые, но величина перерегулирования в нелинейной системе немного больше.

Моделирование показало, что управления, построенные для линейных систем, применимы для нелинейных, если начальные условия по углам не превышают ${{{{\theta }}}_{1}}(0) = {{{{\theta }}}_{2}}(0) = 0.3\,\,{\text{рад}};$ ${{{{\theta }}}_{3}}(0) = 0.5\,\,{\text{рад}};$ а по скоростям не превышают ${{{{\dot {\theta }}}}_{1}}(0) = {{{{\dot {\theta }}}}_{2}}(0)$ = $ = {{{{\dot {\theta }}}}_{3}}(0) = 0.2\,\,{{{\text{рад}}} \mathord{\left/ {\vphantom {{{\text{рад}}} \tau }} \right. \kern-0em} \tau }.$

На рис. 9 приведено сравнение процессов стабилизации в тех случаях, когда применяется гибридное управление (управление при помощи моментов магнитных катушек и моментов сил Лоренца) и когда используется лишь управление от моментов магнитных катушек. Тензор инерции спутника $J = [3.6,5.8,2.5]\,\,{\text{кг}}\, \cdot {{{\text{м}}}^{2}}$ [7]. Орбита, близкая к полярной.

Рис. 9.

${{\theta }_{i}}(\tau )$($I = 82.5^\circ ;$ $u \ne 0$) (a) ${v} \ne 0,$ (б) ${v} = 0.$

Алгоритм стабилизации при использовании только собственных моментов, очевидно, результатов не дает, т.к. как показано в [16], соответствующая стационарная система в этом случае неуправляема.

ЗАКЛЮЧЕНИЕ

Показано, что если для стабилизации ориентации спутника используются одновременно моменты сил Лоренца и собственные моменты, создаваемые, находящимися на спутнике магнитными катушками, линеаризованная в окрестности положения относительного равновесия система уравнений движения относится к специальному классу линейных нестационарных систем, допускающих приведение к стационарным системам.

Система приведена к стационарной системе большей размерности, чем исходная система. На основе полученной стационарной системы исследована управляемость и построены работоспособные алгоритмы стабилизации.

Проведено обстоятельное моделирование, подтверждающее эффективность предложенной методики, в том числе при учете нелинейности исходных нестационарных систем на экваторе и вблизи полярных орбит. Показано, что алгоритмы чувствительны к малым изменениям тензоров инерции только вблизи условий неуправляемости стационарной системы. Моделирование подтвердило бóльшую эффективность предлагаемых алгоритмов при использовании гибридного способа управления – управления при помощи магнитных катушек и управления за счет электромагнитного влияния сил Лоренца по сравнению с вариантом использования для управления только магнитных катушек.

ПРИЛОЖЕНИЕ

При движении по полярной орбите $I = {{\pi /}}2$ уравнения (5) с учетом нелинейных членов имеют вид

Уравнения движения спутника (5) при движении по экватору с учетом членов второго приближения имеют вид

Здесь ${{\delta }_{1}} = {{J}_{1}} + {{J}_{2}} - {{J}_{3}},$ ${{\delta }_{2}} = {{J}_{2}} + {{J}_{3}} - {{J}_{1}},$ ${{\delta }_{3}}\, = \,{{J}_{3}}\, - \,{{J}_{1}},$ ${{\delta }_{4}} = {{J}_{3}} - {{J}_{2}}.$