1. На главную
  2. Электронные версии
  3. Космические исследования
  4. T. 59, № 5, 2021

Космические исследования, 2021, T. 59, № 5, стр. 385-392

Оценка вероятности столкновения околоземных космических объектов с учетом формы и ориентации

М. О. Каратунов 1, 2, *, А. А. Баранов 1, 3, А. Р. Голиков 3

1 Российский университет дружбы народов
Москва, Россия

2 Астрономический научный центр
Москва, Россия

3 Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия

* E-mail: maksim_karatunov@mail.ru

Поступила в редакцию 30.07.2020
После доработки 17.10.2020
Принята к публикации 10.12.2020

Полный текст (PDF)

Аннотация

Предлагается метод оценки вероятности столкновения двух наблюдаемых космических объектов в околоземном космическом пространстве. Решение основано на методе статистического моделирования, что позволило учесть форму и ориентацию сближающихся объектов. Разработанный метод предусматривает автоматическую остановку вычислений при достижении требуемой точности и достоверности решения. Приводится анализ существующих подходов к оценке вероятности столкновения. Произведен расчет для реального сближения аппаратов CHINASAT-20 и SHIJIAN-17.

ВВЕДЕНИЕ

Операторы современных КА в процессе своей деятельности вынуждены учитывать угрозу столкновения с объектами в околоземном космическом пространстве (ОКП). С целью заблаговременного предупреждения об опасных ситуациях в разных странах были созданы специализированные системы АСПОС (Роскосмос), CRASS (ESOC), SOCRATES (Analytical Graphics Inc.), STK Advanced CAT (Analytical Graphics Inc.) и др. Ежегодно центры управления космическими полетами регистрируют до 70 потенциально опасных сближений с отдельными активными КА [1].

Помимо выявления факта предстоящего сближения для принятия решения о реализации маневра уклонения необходимо оценить степень угрозы. Наиболее походящим критерием является вероятность столкновений. Известно несколько методов, позволяющих определить вероятность в рамках следующих допущений:

1) КО имеют сферическую форму.

2) В пределах интервала сближения движение прямолинейно.

3) Составляющие скоростей КО определены без ошибок.

4) Ошибки определения параметров движения распределены по нормальному закону.

В исследовании [2] задача сводится к нахождению вероятности попадания вектора относительного положения в точке максимального сближения в сферу заданного радиуса. Вероятность определяется на основе вычисления объемного интеграла при помощи аппроксимации кубами малого размера, либо с использованием асимптотических рядов.

В работах [3, 4] выводится аналитическая формула расчета вероятности, при этом общие допущения дополняются следующим пунктом:

5) Размер эллипсоида рассеивания СКО значительно превосходит габариты ЗКО.

Данное допущение не позволяет применять метод к крупногабаритным ЗКО, таким как МКС. В исследовании [5] авторы предлагают альтернативный подход к решению задачи, заменяя допущение 5 на допущение:

6) Линейные размеры защищаемого КА много больше размеров сближающихся объектов.

Здесь потенциально опасные КО аппроксимируются материальными точками. В рамках исследования демонстрируется, что для момента максимального сближения в направлении вектора относительной скорости неопределенность вектора относительного положения равна 0. Этот факт позволяет свести решение трехмерной задачи к двумерному случаю путем выбора новой системы координат, одна из осей которой коллинеарна вектору относительной скорости.

Допущения упомянутых подходов могут существенным образом влиять на величину вероятности столкновения, как будет показано далее учет реальной формы и ориентации КО изменяет результат вычисления в несколько раз. Допущение 2) не позволяет оценивать сближения, длительность которых занимает продолжительно время. Остальные допущения также вносят существенный вклад в погрешность вычислений. Снять данные ограничения можно, прибегнув к методам статистического моделирования (Монте-Карло). Использование метода Монте-Карло для расчета вероятности столкновения в ОКП встречается в нескольких работах, например, в работах [6–8], однако алгоритм учета формы и ориентации КО используется только в исследовании [9]. В этой связи была поставлена задача в следующей формулировке.

ПОСТАНОВКА ЗАДАЧИ И ОБЩИЙ ПОДХОД К РЕШЕНИЮ

Пусть на временном интервале $\left[ {{{t}_{1}},{{t}_{2}}} \right]$ выявлен факт сближения двух КО. На момент начала сближения известны векторы состояния ${{{\mathbf{X}}}_{{\text{I}}}}\left( {{{t}_{1}}} \right),$ ${{{\mathbf{X}}}_{{{\text{II}}}}}\left( {{{t}_{1}}} \right),$ ковариационные матрицы ${{{\mathbf{K}}}_{{\text{I}}}}\left( {{{t}_{1}}} \right),$ ${{{\mathbf{K}}}_{{{\text{II}}}}}\left( {{{t}_{1}}} \right),$ закон изменения ориентации и геометрическая форма объектов. Необходимо найти оценку вероятности столкновения $\overline {\Pr \left( A \right)} ,$ удовлетворяющую заданному уровню точности $\varepsilon $ и достоверности $\alpha {\text{:}}$

$\Pr \left( {\left| {\Pr (A) - \overline {\Pr (A)} } \right| \leqslant \varepsilon } \right) \geqslant 1 - \alpha .$

Как было отмечено, решить задачу, не прибегая к классическим допущениям возможно при помощи метода моделирования случайных величин и статистической оценки их характеристик. В данном случае моделируемой случайной величиной является индикатор события столкновения двух КО:

${{I}_{A}}\left( \omega \right) = \left\{ \begin{gathered} 1,\,\,\omega \in A \hfill \\ 0,\,\,\omega \notin A \hfill \\ \end{gathered} \right.,$
где $\omega $ – элементарное событие, A – событие столкновения объектов.

Математическое ожидание индикатора события ${{I}_{A}}$ равно вероятности события, следовательно, получая оценку математического ожидания (${{\bar {m}}_{n}}$) на основе ряда стохастических симуляций процесса сближения, можно рассчитать приближенное значение вероятности столкновения: $\Pr \left( A \right) = M\left[ {{{I}_{A}}} \right]$ ≈ ≈ ${{\bar {m}}_{n}} = {{\sum\nolimits_{i = 1}^N {{{I}_{{Ai}}}} } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^N {{{I}_{{Ai}}}} } N}} \right. \kern-0em} N},$ $\Pr \left( A \right)\xrightarrow[{n \to \infty }]{}{{\bar {m}}_{n}}.$

Необходимое число симуляций n может быть найдено на основе неравенства (1), конкретные способы расчета n и оценки точности решения будут представлены далее.

Алгоритм вычисления вероятности столкновения состоит из следующих этапов:

– генерация массива псевдослучайных шестимерных векторов состояния $\left\{ {{{{\mathbf{\chi }}}_{{{{{\text{I}}}_{1}}}}},{{{\mathbf{\chi }}}_{{{{{\text{I}}}_{2}}}}}, \ldots ,{{{\mathbf{\chi }}}_{{{{{\text{I}}}_{k}}}}}} \right\},$ $\left\{ {{{{\mathbf{\chi }}}_{{{\text{I}}{{{\text{I}}}_{1}}}}},{{{\mathbf{\chi }}}_{{{\text{I}}{{{\text{I}}}_{2}}}}},\,\, \ldots \,\,,{{{\mathbf{\chi }}}_{{{\text{I}}{{{\text{I}}}_{l}}}}}} \right\}$ КО в соответствии с ${{{\mathbf{X}}}_{{\text{I}}}}\left( {{{t}_{1}}} \right),$ ${{{\mathbf{X}}}_{{{\text{II}}}}}\left( {{{t}_{1}}} \right),$ ${{{\mathbf{K}}}_{{\text{I}}}}\left( {{{t}_{1}}} \right),$${{{\mathbf{K}}}_{{{\text{II}}}}}\left( {{{t}_{1}}} \right);$

– выявление факта пересечения трехмерных моделей КО для потенциально опасных комбинаций на интервале $\left[ {{{t}_{1}},{{t}_{2}}} \right];$

– расчет $\overline {\Pr \left( A \right)} $ и оценка точности полученного значения.

ГЕНЕРАЦИЯ МАССИВА ПСЕВДОСЛУЧАЙНЫХ ВЕКТОРОВ

На данном этапе необходимо получить k реализаций шестимерного вектора кинетических параметров КО $\left\{ {{{{\mathbf{\chi }}}_{1}},{{{\mathbf{\chi }}}_{2}}, \ldots ,{{{\mathbf{\chi }}}_{k}}} \right\},$ распределенных по нормальному закону в соответствии с математическим ожиданием ${\mathbf{X}}$ и ковариационной матрицей K.

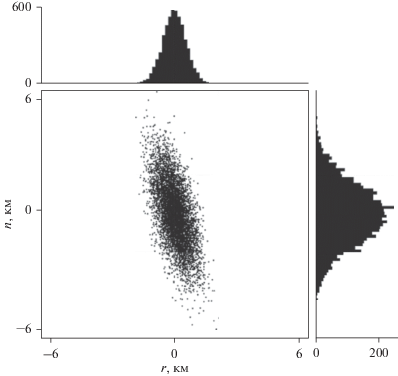
Первым шагом является генерация набора псевдослучайных величин $\{ {{\vartheta }_{1}},{{\vartheta }_{2}}, \ldots ,{{\vartheta }_{n}}\} ,$ распределенных равномерно на интервале $[0,1]$ (U(0, 1)). От выбора генератора равномерного распределения зависит скорость работы алгоритма и качество получаемых случайных векторов. Принимая во внимание работы по данной теме [10], [11], [12], был выбран алгоритм Вихря Мерсенна (Mersenne Twister – MT). На рис. 1 изображено равномерное распределение U(0, 1) точек в двумерном пространстве, полученное в результате работы программного модуля генерации псевдослучайных величин, основанного на алгоритме MT. Далее при помощи преобразования Бокса-Мюллера получается набор независимых реализаций векторов состояния, распределенных по нормальному закону $\mathcal{N}$(0, 1) с нулевым математическим ожиданием и единичной ковариационной матрицей. На рис. 2 представлен результат перехода от U(0, 1) к $\mathcal{N}$(0, 1). Диаграммы, расположенные сверху и справа, показывают суммарное количество точек, находящихся в соответствующем диапазоне координат. На основе данных диаграмм можно получить визуальное представление о законе распределения.

Рис. 1
Рис. 2

Для получения вектора ${{{\mathbf{\chi }}}^{1}},$ учитывающего дисперсию и взаимную зависимость своих составляющих, необходимо осуществить следующее линейное преобразование: ${{{\mathbf{\chi }}}^{1}} = {{{\mathbf{\lambda }}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{\mathbf{\Phi }}{{{\mathbf{\chi }}}^{0}},$ где $\lambda $ – диагональная матрица, составленная из собственных чисел ковариационной матрицы K, ${\mathbf{\Phi }}$ – матрица, составленная из собственных векторов ковариационной матрицы K.

На рис. 3 представлено распределение точек возможного положения реального КА (CHINASAT-20) в проекции на плоскость ${\mathbf{r}},{\mathbf{n}}$ орбитальной СК. Заключительным этапом генерации случайных векторов ${\mathbf{\chi }}$ является параллельный перенос в соответствии с заданным математическим ожиданием.

Рис. 3

ВЫЯВЛЕНИЕ ФАКТА ПЕРЕСЕЧЕНИЯ ТРЕХМЕРНЫХ МОДЕЛЕЙ КО

Перед выявлением факта столкновения объектов сложной формы для каждой пары траектории $\left\{ {{{{\mathbf{\chi }}}_{{{{{\text{I}}}_{i}}}}},{{{\mathbf{\chi }}}_{{{\text{I}}{{{\text{I}}}_{j}}}}}} \right\},$ $i = 1 \ldots k,$ $j = 1 \ldots l$ целесообразно произвести отбор таких траекторий, при движении по которому происходит сближение на расстояние меньшее чем $R = {{R}_{{\text{I}}}} + R{}_{{{\text{II}}}},$ где ${{R}_{{\text{I}}}},R{}_{{{\text{II}}}}$ – радиусы сфер описывающих реальную форму КО. В силу того, что количество симуляций в рамках поставленной задачи $N = lk$ может достигать значений порядка 106, быстродействие данного участка алгоритма является критичным. Учитывая данный факт, а также то, что объекты на интервале сближения находятся на относительно небольшом расстоянии друг от друга и испытывают одинаковое воздействие возмущающих факторов, в рамках предварительной фильтрации пар применяются упрощенные математические модели:

– линеаризованная модель движения для околокруговых орбит [13];

– кеплерова модель движения для орбит с существенной эллиптичностью.

В результате отсева остается множество пар траекторий, при движении по которым имеет место столкновение объектов сферической формы. Далее для данного множества необходимо выявить факт пересечения трехмерных моделей на интервале $\left[ {{{t}_{1}},{{t}_{2}}} \right].$

Задача создания быстрого и эффективного алгоритма обнаружения пересечения двух трехмерных фигур заданной формы является одной из центральных проблем робототехники и компьютерных игр. Как следствие, на данный момент существует ряд проверенных методов и алгоритмов решения данной задачи. Общим подходом является разбиение процесса расчета на две фазы: широкую и узкую.

В широкой фазе все объекты представляются в виде ограничивающих параллелепипедов, стороны которых параллельны осям координат. Данное упрощение позволяет очень быстро отобрать объекты потенциального столкновения. В качестве алгоритма широкой фазы был выбран алгоритм Sweep-and-Prune [14].

В качестве алгоритма узкой фазы был выбран алгоритм Гилберта–Джонсона–Кѐрти (Gilbert–Johnson–Keerthi, GJK), который в силу своей стабильности, скорости и занимаемому объему памяти получил широкое распространение [15]. GJK использует такие математические понятия, как сумма Минковского, опорная функция и симплекс [16]. Кратко работу данного алгоритма можно описать следующим образом. Выполняется проверка принадлежности центра СК произвольному начальному симплексу, если результат проверки положительный, то фигуры пересекаются, иначе при помощи опорной функции вычисляется экстремальная точка в направлении противоположном радиус-вектору ближайшей к центу СК точки симплекса. Далее найденная точка добавляется в симплекс, а самая дальняя от центра СК точка удаляется. Если экстремальная точка является одной из ранее удаленных или одной из тех, которые входят в текущий симплекс, то вычисления завершаются.

ОЦЕНКА ТОЧНОСТИ И УСЛОВИЕ АВТОМАТИЧЕСКОЙ ОСТАНОВКИ РАСЧЕТА

Оценка математического ожидания стремится по вероятности к истинному значению при стремлении количества симуляций n к бесконечности. При этом абсолютная погрешность $\varepsilon ,$ полученной оценки пропорциональна ${{n}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ Так как IA принимает одно из двух возможных значений $\left\{ {0,1} \right\},$ можно отнести данную случайную величину к классу чисел Бернулли, для которых в свою очередь возможен непосредственный расчет необходимого числа реализаций N*, гарантирующих выполнение неравенства (1). Существует несколько подходов к определению N* [17].

Наиболее грубую оценку сверху можно по-лучить на основе неравенства Чебышева: $\Pr \left( {\left| {X - m} \right| \geqslant \varepsilon } \right) \leqslant {{{{D}_{x}}} \mathord{\left/ {\vphantom {{{{D}_{x}}} {{{\varepsilon }^{2}}}}} \right. \kern-0em} {{{\varepsilon }^{2}}}},$ здесь X – случайная величина, $m$ – математическое ожидание, ${{D}_{x}}$ – дисперсия. Выберем $X = {{\bar {m}}_{n}},$ при этом ${{D}_{x}} = {{{{D}_{{{{I}_{A}}}}}} \mathord{\left/ {\vphantom {{{{D}_{{{{I}_{A}}}}}} {\sqrt n }}} \right. \kern-0em} {\sqrt n }}.$ Обозначая $\alpha = {{{{D}_{{{{I}_{A}}}}}} \mathord{\left/ {\vphantom {{{{D}_{{{{I}_{A}}}}}} {n{{\varepsilon }^{2}}}}} \right. \kern-0em} {n{{\varepsilon }^{2}}}},$ получим, что неравенство

$\Pr \left( {\left| {{{{\bar {m}}}_{n}} - m} \right| \leqslant \varepsilon } \right) \geqslant 1 - \alpha $

гарантированно выполняется при $n = {{{{D}_{{{{I}_{A}}}}}} \mathord{\left/ {\vphantom {{{{D}_{{{{I}_{A}}}}}} {\alpha {{\varepsilon }^{2}}}}} \right. \kern-0em} {\alpha {{\varepsilon }^{2}}}}.$ Для чисел Бернулли дисперсия не превосходит значение 0.25, следовательно, верхняя граница требуемого числа симуляций:

$N_{{Cheb}}^{*} = {1 \mathord{\left/ {\vphantom {1 {4\alpha {{\varepsilon }^{2}}}}} \right. \kern-0em} {4\alpha {{\varepsilon }^{2}}}}.$

Альтернативный подход к определению N* базируется на центральной предельной теореме: если ${{X}_{1}}, \ldots ,{{X}_{n}}$ независимые случайные величины, распределенные по одинаковому закону, то $\frac{{{{{\bar {m}}}_{n}} - m}}{{\sqrt {{{{{D}_{Y}}} \mathord{\left/ {\vphantom {{{{D}_{Y}}} n}} \right. \kern-0em} n}} }}\xrightarrow[{n \to \infty }]{}\mathcal{N}\left( {0,1} \right).$ Исходя из этого, можно записать следующее приближенное неравенство: $\Pr \left( {\left| {{{{\bar {m}}}_{n}} - m} \right| \leqslant \varepsilon } \right)$ ≈ $1 - \frac{{{{z}_{{{{{\alpha }} \mathord{\left/ {\vphantom {{{\alpha }} 2}} \right. \kern-0em} 2}}}}{{D}_{Y}}}}{{n{{\varepsilon }^{2}}}},$ которое выполняется для $n = {{{{z}_{{{{{\alpha }} \mathord{\left/ {\vphantom {{{\alpha }} 2}} \right. \kern-0em} 2}}}}{{D}_{Y}}} \mathord{\left/ {\vphantom {{{{z}_{{{{{\alpha }} \mathord{\left/ {\vphantom {{{\alpha }} 2}} \right. \kern-0em} 2}}}}{{D}_{Y}}} {\alpha {{\varepsilon }^{2}}}}} \right. \kern-0em} {\alpha {{\varepsilon }^{2}}}},$ здесь ${{z}_{{{{{\alpha }} \mathord{\left/ {\vphantom {{{\alpha }} 2}} \right. \kern-0em} 2}}}}$ – квантиль нормального распределения для вероятности $1 - {\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0em} 2}.$

Используя верхнюю границу для дисперсии чисел Бернулли, получаем, что неравенство (2) приближенно выполняется для

$N_{{CLT}}^{*} = {{{{z}_{{{{{\alpha }} \mathord{\left/ {\vphantom {{{\alpha }} 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{{z}_{{{{{\alpha }} \mathord{\left/ {\vphantom {{{\alpha }} 2}} \right. \kern-0em} 2}}}}} {4{{\varepsilon }^{2}}}}} \right. \kern-0em} {4{{\varepsilon }^{2}}}}.$

Сравнивая (4) и (3), можно сделать вывод о том, что из-за отсутствия коэффициента достоверности в знаменателе (4) величина $N_{{CLT}}^{*}$ возрастает гораздо медленнее чем $N_{{Cheb}}^{*}.$ С другой стороны, не стоит забывать, что в данном случае неравенство (2) является асимптотически верным.

Третий способ нахождения N* основан на неравенстве Хефдинга для случайных величин, лежащих в диапазоне $\left[ {0,1} \right]{\text{:}}$ $\Pr \left( {\left| {{{{\bar {m}}}_{n}} - m} \right| \geqslant \varepsilon } \right) \leqslant 2\exp \left( { - 2n{{\varepsilon }^{2}}} \right),$ следовательно, N* может быть найдено из уравнения:

$N_{{Hoeff}}^{*} = {{\ln (2{\text{/}}\alpha )} \mathord{\left/ {\vphantom {{\ln (2{\text{/}}\alpha )} {2{{\varepsilon }^{2}}}}} \right. \kern-0em} {2{{\varepsilon }^{2}}}}.$

В табл. 1 представлен расчет количества симуляций N* необходимого для гарантированного достижения точности $\varepsilon = {{10}^{{ - 4}}}$ при различных подходах.

Таблица 1.

Количество реализаций, гарантирующее точность решения $\varepsilon = {{10}^{{ - 4}}}$

$1 - \alpha $ $N_{{Cheb}}^{*}$ $N_{{CLT}}^{*}$ $N_{{Hoeff}}^{*}$
0.95 $5.000 \cdot {{10}^{8}}$ $5.000 \cdot {{10}^{7}}$ $1.844 \cdot {{10}^{8}}$
0.99 $2.500 \cdot {{10}^{9}}$ $6.450 \cdot {{10}^{7}}$ $2.649 \cdot {{10}^{8}}$
0.9973 $9.259 \cdot {{10}^{9}}$ $7.500 \cdot {{10}^{7}}$ $3.303 \cdot {{10}^{8}}$

Минимальное значение N* получается при использовании метода, основанного на выводах центральной предельной теоремы. Даже при использовании формулы (4) порядок количества симуляций равен 109, что ставит под сомнение применимость метода Монте-Карло для расчета вероятности столкновения. В то же время, стоит отметить, что в формулах (3)–(5) используется предположение о максимально возможном значении дисперсии ${{D}_{{{{I}_{A}}}}} = {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}.$ В реальных расчетах дисперсия принимает гораздо меньшее значение и, как следствие, необходимая точность достигается при меньшем числе симуляций. Данный вывод подтверждает график на рис. 4, показывающий зависимость оценки вероятности $\overline {\Pr \left( A \right)} $ от количества симуляций N для нескольких прогонов алгоритма. Запуски производились на одинаковых начальных данных, в качестве трехмерной модели использовалась сфера. На основе графика можно сделать приблизительный вывод о скорости сходимости метода, точность $\varepsilon = {{10}^{{ - 4}}}$ достигается при $N = 1.6 \cdot {{10}^{6}}.$

Рис. 4

Исходя из этого, предлагается использовать условие автоматической остановки расчета при достижении требуемой точности и достоверности решения. Начиная с некоторого количества симуляций N0, производится оценка текущего значения дисперсии $\overline {{{D}_{{{{I}_{A}}}}}} $ и проверка условия (2), если условие выполняется, то вычисления прекращаются.

ПРИМЕР РАСЧЕТА ВЕРОЯТНОСТИ СТОЛКНОВЕНИЯ

Событие сближения между спутником C-INASAT-20 (28082, 2003-052А) и спутником SHI-JIAN-17 (41838, 2016-065А) произошло 16.III.2018 в 18:35:49.63 (UTC). Минимальное расстояние между математическими ожиданиями положения центров масс составило 286.3 м. В целях тестирования было произведено сравнение результатов работы алгоритма З.Н. Хуторовского [3] и алгоритма Монте-Карло для сферических объектов с радиусом 15 м.

В табл. 2 представлены результаты трех серий запусков алгоритма Монте-Карло для различных значений требуемой точности $\varepsilon ,$ при этом коэффициент достоверности имеет постоянное значение – 99%. Каждая серия состоит из трех запусков отличающихся только набором сгенерированных псевдослучайных векторов. Здесь ${{\bar {P}}_{{{\text{сф}}}}}$ – оценка вероятности столкновения сферических объектов, ${{\Delta }_{Х}}$ – абсолютное значение разности результатов, полученных аналитическим методом З.Н. Хуторовского и численным методом Монте-Карло, N – фактическое количество симуляций.

Таблица 2.  

Результаты расчета вероятности столкновения сферических объектов

№ $\varepsilon $ ${{\bar {P}}_{{{\text{сф}}}}}$ ${{\Delta }_{Х}}$ N, тыс. Время расчета, с
1.1 $5 \cdot {{10}^{{ - 5}}}$ $1.608 \cdot {{10}^{{ - 4}}}$ $3.3 \cdot {{10}^{{ - 5}}}$ 429 30
1.2 $5 \cdot {{10}^{{ - 5}}}$ $1.366 \cdot {{10}^{{ - 4}}}$ $0.9 \cdot {{10}^{{ - 5}}}$ 366 24
1.3 $5 \cdot {{10}^{{ - 5}}}$ $1.122 \cdot {{10}^{{ - 4}}}$ $1.5 \cdot {{10}^{{ - 5}}}$ 303 19
2.1 $3 \cdot {{10}^{{ - 5}}}$ $1.485 \cdot {{10}^{{ - 4}}}$ $2.1 \cdot {{10}^{{ - 5}}}$ 1098 94
2.2 $3 \cdot {{10}^{{ - 5}}}$ $1.414 \cdot {{10}^{{ - 4}}}$ $1.4 \cdot {{10}^{{ - 5}}}$ 1047 89
2.3 $3 \cdot {{10}^{{ - 5}}}$ $1.235 \cdot {{10}^{{ - 4}}}$ $0.4 \cdot {{10}^{{ - 5}}}$ 915 76
3.1 $1 \cdot {{10}^{{ - 5}}}$ $1.253 \cdot {{10}^{{ - 4}}}$ $0.2 \cdot {{10}^{{ - 5}}}$ 8346 690
3.2 $1 \cdot {{10}^{{ - 5}}}$ $1.307 \cdot {{10}^{{ - 4}}}$ $0.3 \cdot {{10}^{{ - 5}}}$ 8700 730
3.3 $1 \cdot {{10}^{{ - 5}}}$ $1.336 \cdot {{10}^{{ - 4}}}$ $0.6 \cdot {{10}^{{ - 5}}}$ 8892 745

На основе проведенных расчетов можно утверждать, что численный алгоритм работает стабильно, величины оценок вероятности в рамках одной серии запусков лежат в диапазоне $ \pm \varepsilon .$ В то же время расхождение результатов ${{\Delta }_{Х}}$ двух методов также лежит в приделах заданной погрешности $ \pm \varepsilon ,$ что свидетельствует о согласованности аналитического и численного подхода в рамках классических допущений. Время расчета в однопоточном режиме вычислений на процессоре AMD Phenom IIХ4 975 для $\varepsilon = 1 \cdot {{10}^{{ - 5}}}$ составило приблизительно 13 мин.

В табл. 3 приведены результаты расчета вероятности столкновения с учетом формы и ориентации КО. В рамках тестирования была использована обобщенная трехмерная модель геостационарных спутников, представленная на рис. 5. Данная модель может быть вписана в сферу радиусом 15 м. Так как солнечные панели, как правило, имеют одну степень свободы, их форма была аппроксимирована цилиндрами. При этом предполагалось, что объекты имеют типичную для геостационарных спутников ориентацию: ось солнечных панелей перпендикулярна плоскости орбиты, главная ось направлена на центр Земли.

Таблица 3.  

Результаты расчета вероятности столкновения объектов сложной формы

№ $\varepsilon $ $\bar {P}$ N, тыс. Время расчета, с
1.1 $6 \cdot {{10}^{{ - 6}}}$ $2.30 \cdot {{10}^{{ - 5}}}$ 4260 389
1.2 $6 \cdot {{10}^{{ - 6}}}$ $2.56 \cdot {{10}^{{ - 5}}}$ 4730 433
1.3 $6 \cdot {{10}^{{ - 6}}}$ $2.85 \cdot {{10}^{{ - 5}}}$ 5270 484
2.1 $4 \cdot {{10}^{{ - 6}}}$ $2.11 \cdot {{10}^{{ - 5}}}$ 8780 812
2.2 $4 \cdot {{10}^{{ - 6}}}$ $2.22 \cdot {{10}^{{ - 5}}}$ 9240 853
2.3 $4 \cdot {{10}^{{ - 6}}}$ $2.61 \cdot {{10}^{{ - 5}}}$ 10 860 1010
3.1 $2 \cdot {{10}^{{ - 6}}}$ $2.35 \cdot {{10}^{{ - 5}}}$ 39 090 3895
3.2 $2 \cdot {{10}^{{ - 6}}}$ $2.34 \cdot {{10}^{{ - 5}}}$ 39 030 3896
3.3 $2 \cdot {{10}^{{ - 6}}}$ $2.35 \cdot {{10}^{{ - 5}}}$ 39 090 3894
Рис. 5

Аналогично расчетам для сфер было произведено три серии запусков для различных значений требуемой точности $\varepsilon .$ Разброс полученных оценок не превосходит заданную погрешность, при этом значение вероятности столкновения КО сложной формы оказалось приблизительно в пять раз меньше, чем вероятность столкновения описывающих сфер. Время расчета в однопоточном режиме вычислений для $\varepsilon = 2 \cdot {{10}^{{ - 6}}}$ не превысило 65 мин.

ЗАКЛЮЧЕНИЕ

Вероятность столкновения КО является основной величиной, влияющей на принятие решения о применении маневра уклонения. От точности оценки данной величины зависит безопасность космических полетов и скорость расхода рабочего тела КА. В рамках исследования был разработан метод расчета вероятности, позволяющий учесть форму и ориентацию сближающихся объектов, а также снять ряд классических допущений. Было продемонстрировано, что игнорирование реальной формы объектов существенно влияет на точность оценки, для тестового примера было получено пятикратное расхождение результатов. В тоже время при анализе сближения сферических объектов оценки разработанного метода согласуются с оценками классического метода Хуторовского.

В предложенном методе предусмотрен алгоритм автоматической остановки вычислений при достижении заданной точности и достоверности решения. Стоит отметить, что требуемое время расчета нелинейно возрастает при уменьшении величины допустимой погрешности. В целях ускорения работы алгоритма в перспективе планируется заменить ГПСЧ Вихря Мерсенна на последовательности Соболя [18], которые обеспечивают более высокую скорость сходимости методов статистического моделирования. Ускорения также можно добиться, прибегнув к двухэтапной оценке риска, при которой на первом этапе рассчитывается вероятность столкновения описывающих сфер и, если вероятность окажется выше порогового значения, производится учет реальной формы и ориентации сближающихся объектов.

Публикация выполнена при поддержке Программы стратегического академического лидерства РУДН.

Список литературы

  1. Braun V., Flohrer T., Krag H. et al. Operational support to collision avoidance activities by ESA’s space debris office // CEAS Space J. 2016. № 8. P. 177–189.

  2. Козориз А.И., Скорняков В.А. Оценка риска столкновения при сближении МКС с наблюдаемыми космическими объектами // Лесной вестник. 2009. № 2. С. 164–167.

  3. Khutorovsky Z.N., Boikov V.F., Kamensky S.Yu. Direct method for the analysis of collision probability of artificial space objects in LEO: techniques, results and applications // Proceedings of the First Euripean Conference on Space Debris. 1993. P. 491–508.

  4. Fateev V., Sukhanov S., Khutorovsky Z. et al. Collision Prediction for LEO Satellites. Analysis if Characteristics // Proceeding of the 2009 Advanced Maui Optical and Space Surveillance Technologies Conference. 2009. P. 1–4.

  5. Akella M.R., Alfriend K.T. Probability of Collision Between Space Objects // J. Guidence, Control, and Dynamics. 2000. V. 23. № 5. P. 769–772.

  6. Jones B.A., Doostan A., Born G.H. Conjunction assessment using polynomial chaos expansions // Proceedings of the 23rd International Symposium and Space Flight Dynamics. 2012. P. 1–18

  7. Morselli A., Armellin R., Di Lizia P. et al. A high order method for orbital conjunctions analysis: Monte Carlo collision probability computation // Advances in Space Research. 2015. V. 55. № 1. P. 311–333.

  8. Losacco M., Romano M., Di Lizia P. et al. Advanced Monte Carlo Sampling Techniques For Orbital Conjunctions Analysis And Near Earth Objects Impact Probability Computation // 1st NEO and Debris Detection Conference. 2019. P. 1–12.

  9. de Vries W.H., Phillion D.W. Monte Carlo Method for Collision Probability Calculations Using 3D Satellite Models // Advanced Maui Optical and Space Surveillance Technologies Conference. 2010. P. 1–12.

  10. Ding K., Tan Y. Comparison of Random Number Generators in Particle Swarm Optimization Algorithm // IEEE Congress on Evolutionary Computation (CEC). 2014. P. 2664–2671.

  11. Слеповичев И.И. Генератор псевдослучайных чисел. Саратов: СГУ им. Н.Г. Чернышевского, 2017.

  12. L’Ecuyer P. Random number generation. Handbook of Computational Statistics. Berlin: Springer Berlin Heidelberg, 2012.

  13. Эльясберг П.Е. Введение в теорию полета искусственных спутников Земли. М.: Наука, 1965.

  14. Tracy D. Efficient Large-Scale Sweep and Prune Methods with AABB Insertion and Removal // Proceedings of the 2009 IEEE Virtual Reality Conference. 2009. P. 191–198.

  15. Ericson C. Real-time Collision Detection. San Francisco: Morgan Kaufmann Publishers, 2005.

  16. Gilbert E.G., Johnson D.E., Keerthi S.S. A fast procedure for computing the distance between complex objects in three-dimensional space // IEEE J. Robotics and Automation. 1988. V. 4. № 2. P. 193–203.

  17. Jiang L., Hickernell F.J. Guaranteed Monte Carlo Methods for Bernoulli Random Variables // arXiv preprint arXiv:1411.1151 arXiv.org. 2014. URL: https:// arxiv.org/abs/1411.1151

  18. Соболь М. Численные методы Монте-Карло. М.: Наука, 1973.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал