Космические исследования, 2022, T. 60, № 1, стр. 43-56
Оценка низкочастотных микроускорений на борту искусственного спутника Земли в режиме солнечной ориентации
1 Государственный космический научно-производственный центр им. М.В. Хруничева
Москва, Россия
2 Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия
* E-mail: general_z@mail.ru
Поступила в редакцию 12.10.2020
После доработки 26.12.2020
Принята к публикации 22.01.2021
- EDN: YPJQWQ
- DOI: 10.31857/S0023420622010046
Аннотация
Исследованы низкочастотные микроускорения на борту искусственного спутника Земли, предназначенного для микрогравитационных исследований на низкой, почти круговой орбите. Спутник имеет форму цилиндра с двумя панелями солнечных батарей, расположенными в одной плоскости симметрично относительно продольной оси цилиндра. Относительно своего центра масс спутник движется в режиме солнечной ориентации: нормаль к плоскости солнечных батарей направлена на Солнце, угловая скорость вокруг этой нормали мала, продольная ось совершает малые колебания относительно плоскости орбиты. Режим реализуется с помощью системы четырех управляющих двигателей-маховиков. Предложен вариант этого режима с ограничением накопления суммарного кинетического момента системы двигателей-маховиков за счет управления углом поворота спутника вокруг нормали к плоскости солнечных батарей. Рассмотрено движение спутника относительно центра масс в режиме комбинации гравитационной и солнечной ориентации.
1. ВВЕДЕНИЕ
В данной работе рассчитываются низкочастотные (квазистатические) микроускорения на искусственном спутнике Земли типа спутников Бион М-1 и Фотон М-4 [1, 2]. Спутник совершает полет по низкой, почти круговой орбите в режиме солнечной ориентации. Его форма близка к цилиндру, на котором неподвижно закреплены две панели солнечных батарей, расположенные вдоль продольной оси симметрично относительно нее (рис. 1). В режиме солнечной ориентации нормаль к плоскости солнечных батарей направлена на Солнце, продольная ось спутника лежит вблизи плоскости орбиты, угловая скорость мала. Ориентация реализуется с помощью гиросистемы, образованной четырьмя двигателями-маховиками (ДМ). Указанный режим обеспечивает низкий уровень микроускорений и максимальный приток электроэнергии. Недостаток этого режима состоит в необходимости проведения разгрузок кинетического момента гиросистемы, ограничивающих время полета спутника без значительных возмущений. Ниже рассматривается вариант режима солнечной ориентации, при котором накопление суммарного кинетического момента системы ДМ ограничивается за счет управления углом поворота спутника вокруг нормали к светочувствительной стороне солнечных батарей. Исследовано движение спутника в режиме комбинации его гравитационной и солнечной ориентации. С использованием достаточно детальной математической модели движения спутника рассчитаны квазистатические микроускорения, возникающие на борту спутника в указанных режимах.
2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ МИКРОУСКОРЕНИЙ
Квазистатические микроускорения на низкоорбитальном спутнике Земли вызываются четырьмя причинами: 1) движением спутника относительно центра масс как твердого тела, 2) градиентом гравитационного поля, 3) аэродинамическим торможением, 4) действием силы, создаваемой органами управления. Если спутник совершает неуправляемое движение или для управления им используются ДМ, то последняя из перечисленных причин исчезает. В таком случае квазистатическое микроускорение в заданной фиксированной точке борта описывается простой формулой, причем чтобы воспользоваться ею, достаточно знать только орбиту и вращательное движение спутника.
Пусть спутник представляет собой твердое тело, и точка $P$ жестко связана с его корпусом. Микроускорением ${\mathbf{b}}$ в точке $P$ называется разность между напряженностью гравитационного поля в этой точке и абсолютным ускорением последней. Роль вектора ${\mathbf{b}}$ в орбитальных экспериментах аналогична роли ускорения свободного падения в экспериментах на поверхности Земли. В частности, если в точке $P$ закрепить пробное тело с исчезающе малой массой ${{m}_{p}},$ то сила реакции, действующая на это тело со стороны спутника, будет равна $ - {{m}_{p}}{\mathbf{b}}.$ Приближенная формула для расчета микроускорений имеет вид [3]
(1)
$\begin{gathered} {\mathbf{b}} = {{{\mathbf{b}}}_{r}} + {{{\mathbf{b}}}_{g}} + {{{\mathbf{b}}}_{a}},\,\,\,\,{{{\mathbf{b}}}_{r}} = {\mathbf{d}} \times {\mathbf{\dot {\omega }}} + \left( {{\mathbf{\omega }} \times {\mathbf{d}}} \right) \times {\mathbf{\omega }}, \\ {{{\mathbf{b}}}_{g}} = \frac{{{{{{\mu }}}_{{\text{E}}}}}}{{{{r}^{3}}}}\left( {3\frac{{{\mathbf{\rho }} \cdot {\mathbf{r}}}}{{{{r}^{2}}}}{\mathbf{r}} - {\mathbf{\rho }}} \right),\,\,\,\,{{{\mathbf{b}}}_{a}} = c{{{{\rho }}}_{a}}\left| {\mathbf{v}} \right|{\mathbf{v}}. \\ \end{gathered} $Формула (1) выведена для общего случая без каких-либо частотных ограничений. Однако если спутник имеет относительно большие инерционные характеристики и его вращательное движение рассчитывается как движение твердого тела (такое движение обычно очень медленное), то формула (1) дает именно квазистатическое микроускорение.
Формула (1) использовалась для расчета реальных квазистатических микроускорений, имевших место на летавших спутниках [3–8]. Ее можно использовать и для прогноза микроускорений [9, 10]. В этом случае составляются уравнения движения спутника, выбирается режим движения, вычисляется решение уравнений движения, моделирующее этот режим, и вдоль найденного решения микроускорение в заданной точке борта рассчитывается по формуле (1). Именно таким образом формула (1) применяется ниже.
3. УРАВНЕНИЯ ДВИЖЕНИЯ СПУТНИКА
Спутник считаем гиростатом, для описания его движения будем использовать три правых декартовых системы координат.
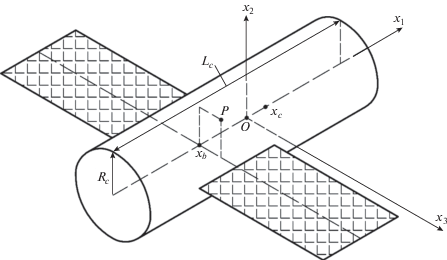
$O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ – связанная система координат, образованная главными центральными осями инерции спутника. Полагаем, что спутник имеет форму прямого кругового цилиндра (рис. 1) радиуса ${{R}_{c}}$ и высоты ${{L}_{c}},$ с двумя прикрепленными к нему одинаковыми прямоугольными пластинами – солнечными батареями суммарной площади Sb. Ось цилиндра совпадает с осью $O{{x}_{1}}.$ Солнечные батареи расположены в плоскости $O{{x}_{1}}{{x}_{3}}$ симметрично относительно оси $O{{x}_{1}},$ стороны батарей параллельны осям $O{{x}_{1}}$ и $O{{x}_{3}},$ ось $O{{x}_{2}}$ перпендикулярна плоскости солнечных батарей. Светочувствительная сторона солнечных батарей обращена к полупространству х2 > 0. Координаты геометрических центров цилиндра и пластин солнечных батарей обозначим (хс, 0, 0) и (xb, 0, 0) соответственно, базисные орты этой системы – e1,e2,e3. Ниже, если не оговорено особо, компоненты векторов и координаты точек относятся к системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}.$
$C{{y}_{1}}{{y}_{2}}{{y}_{3}}$ – гринвичская система координат. Ее начало находится в центре Земли, плоскость $C{{y}_{1}}{{y}_{2}}$ совпадает с плоскостью экватора, ось $C{{y}_{1}}$ пересекает гринвичский меридиан, ось $C{{y}_{3}}$ направлена к Северному полюсу.
$C{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$ – квазиинерциальная система координат. Ось $C{{Z}_{2}}$ параллельна вектору кинетического момента орбитального движения спутника, ось $C{{Z}_{3}}$ лежит в плоскости экватора и направлена в восходящий узел оскулирующей орбиты спутника. Базис этой системы образован ортами ${{E}_{1}}{{E}_{2}}{{E}_{3}}.$
Матрицу перехода от системы $C{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$ к системе $C{{y}_{1}}{{y}_{2}}{{y}_{3}}$ обозначим $C = \left\| {{{c}_{{ij}}}} \right\|_{{i,j = 1}}^{3},$ где ${{c}_{{ij}}}$ – косинус угла между осями $C{{y}_{i}}$ и $C{{Z}_{j}}.$ Элементы этой матрицы выражаются через координаты и компоненты скорости центра масс спутника в гринвичской системе координат. Матрицы перехода от системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ к гринвичской системе координат и системе $C{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$ обозначим соответственно $\left\| {{{u}_{{ij}}}} \right\|_{{i,j = 1}}^{3}$ и $\left\| {{{a}_{{ij}}}} \right\|_{{i,j = 1}}^{3}.$ Здесь ${{u}_{{ij}}}$ и ${{a}_{{ij}}}$ – косинусы углов, которые образует ось $O{{x}_{j}}$ с осями $C{{y}_{i}}$ и $C{{Z}_{i}}.$ Справедливы соотношения ${{a}_{{ij}}} = {{{\mathbf{E}}}_{i}} \cdot {{{\mathbf{e}}}_{j}},$ $U = CA.$
Положение системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ относительно системы $C{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$ будем также задавать углами ψ, θ и φ, которые введем следующим образом. Если точку $C$ перенести в точку O, то систему $C{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$ можно перевести в систему $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ тремя последовательными поворотами: 1) на угол ψ вокруг оси $C{{Z}_{2}},$ 2) на угол π/2 – θ вокруг новой оси $C{{Z}_{1}},$ 3) на угол φ + π вокруг новой оси $C{{Z}_{2}},$ совпадающей с осью $O{{x}_{2}}.$ Элементы матрицы $A$ выражаются через эти углы с помощью следующих формул:
(2)
$\begin{gathered} {{a}_{{11}}} = - \cos {{\varphi }}\cos {{\psi }} + \sin {{\varphi }}\sin {{\psi }}\sin {{\theta ,}} \\ {{a}_{{12}}} = \sin {{\psi }}\cos {{\theta }},\,\,\,\,{{a}_{{21}}} = - \sin {{\varphi }}\cos {{\theta }}, \\ {{a}_{{22}}} = \sin {{\theta }},\,\,\,\,{{a}_{{31}}} = \cos {{\varphi }}\sin {{\psi }} + \sin {{\varphi }}\cos {{\psi }}\sin {{\theta }}, \\ {{a}_{{32}}} = \cos {{\psi }}\cos {{\theta }},\,\,\,\, \\ {{a}_{{13}}} = - \sin {{\varphi }}\cos {{\psi }} - \cos {{\varphi }}\sin {{\psi }}\sin {{\theta }}, \\ {{a}_{{23}}} = \cos {{\varphi }}\cos {{\theta }}, \\ {{a}_{{33}}} = \sin {{\varphi }}\sin {{\psi }} - \cos {{\varphi }}\cos {{\psi }}\sin {{\theta }}. \\ \end{gathered} $Уравнения движения спутника состоят из двух подсистем. Одна подсистема описывает движение центра масс спутника в гринвичской системе координат [11]. В ней учитываются нецентральность гравитационного поля Земли и сопротивление атмосферы. Нецентральность поля учитывается с точностью до членов порядка (16,16) включительно в разложении гравитационного потенциала Земли в ряд по шаровым функциям. Атмосфера считается вращающейся вместе с Землей, ее плотность рассчитывается согласно модели ГОСТ Р 25645.166-2004. Параметры атмосферы и баллистический коэффициент спутника считаются неизменными на всем интервале интегрирования уравнений движения.
Другая подсистема описывает движение спутника относительно центра масс (вращательное движение). Она образована уравнениями, выражающими теорему об изменении кинетического момента спутника в его движении относительно центра масс, кинематическими уравнениями Пуассона для элементов первых двух строк матрицы $U$ и уравнениями, описывающими изменение кинетического момента гиросистемы. В уравнениях, выражающих теорему об изменении кинетического момента спутника, учитываются гравитационный и аэродинамический моменты. Для гравитационного момента существует простое аналитическое выражение [12]. Формула аэродинамического момента имеет вид
Допущения, сделанные при выводе формулы аэродинамического момента, позволяют выписать явное выражение для входящего в формулу (1) баллистического коэффициента спутника. Этот коэффициент имеет вид $c = {{{{S}_{v}}} \mathord{\left/ {\vphantom {{{{S}_{v}}} m}} \right. \kern-0em} m},$ где $m$ – масса спутника, ${{S}_{v}}$ – площадь геометрической фигуры, являющейся проекцией внешней оболочки спутника на плоскость перпендикулярную вектору ${\mathbf{v}}.$ В данном случае
(3)
$\begin{gathered} {{{\mathbf{b}}}_{a}} = c{{{{\rho }}}_{a}}\left| {\mathbf{v}} \right|{\mathbf{v}} = {{{{\rho }}}_{a}} \times \\ \times \,\,\left( {\frac{{\pi R_{c}^{2}}}{m}\left| {{{v}_{1}}} \right| + \frac{{{{S}_{b}}}}{m}\left| {{{v}_{2}}} \right| + \frac{{2{{R}_{c}}{{L}_{c}}}}{m}\sqrt {v_{2}^{2} + v_{3}^{2}} } \right){\mathbf{v}}. \\ \end{gathered} $Все приводимые в данной работе расчеты микроускорений выполнены по формулам (1), (3).
При выводе выражений для аэродинамического момента и баллистического коэффициента не учитывалось возможное взаимное затенение корпуса спутника и солнечных батарей от набегающего аэродинамического потока. Такое упрощение оправдано, поскольку для большинства движений спутника относительная продолжительность отрезков времени, на которых указанное затенение существенно, невелика.
Заметим, что при расчете микроускорений баллистический коэффициент $c$ считался переменным, а в подсистеме уравнений движения центра масс спутника тот же коэффициент принимался постоянным. Сделанное упрощение оправдано тем, что влияние сопротивления атмосферы на движение центра масс весьма мало и достаточно точно описывается с использованием постоянного значения баллистического коэффициента, которое определяется в результате обработки траекторных измерений.
Подсистема уравнений вращательного движения спутника имеет вид
(4)
$\begin{gathered} \hat {I}\frac{{\tilde {d}{\mathbf{\omega }}}}{{dt}} + {\mathbf{\omega }} \times \hat {I}{\mathbf{\omega }} = 3\frac{{{{{{\mu }}}_{{\text{E}}}}}}{{{{r}^{5}}}}({\mathbf{r}} \times \hat {I}{\mathbf{r}}) + p({\mathbf{v}} \times {{{\mathbf{e}}}_{1}}) + {{{\mathbf{M}}}_{c}}, \\ \frac{{\tilde {d}{\mathbf{H}}}}{{dt}} + {\mathbf{\omega }} \times {\mathbf{H}} = - {{{\mathbf{M}}}_{c}},\,\,\,\,\frac{{\tilde {d}{{{\mathbf{u}}}_{1}}}}{{dt}} + {\mathbf{\omega }} \times {{{\mathbf{u}}}_{1}} = {{{{\omega }}}_{{\text{E}}}}{{{\mathbf{u}}}_{2}}, \\ \frac{{\tilde {d}{{{\mathbf{u}}}_{2}}}}{{dt}} + {\mathbf{\omega }} \times {{{\mathbf{u}}}_{2}} = - {{{{\omega }}}_{{\text{E}}}}{{{\mathbf{u}}}_{1}}. \\ \end{gathered} $Чтобы замкнуть подсистему уравнений вращательного движения, надо добавить к уравнениям (4) выражение для ${{{\mathbf{M}}}_{c}}.$ Оно приведено ниже.
В расчетах использовались следующие параметры описанной модели. Параметры спутника: $m$ = 6440 кг, ${{I}_{1}}$ = 2600 кг/м2, ${{I}_{2}}$ = 11 100 кг/м2, ${{I}_{3}}$ = = 10 900 кг/м2, ${{R}_{c}}$ = 1.3 м, ${{L}_{c}}$ = 5.0 м, ${{S}_{b}}$ = 33 м2, ${{x}_{b}}$ = = –1 м, ${{x}_{c}}$ = 0.3 м. Микроускорения рассчитывались в точке $P$ с координатами (–1, 0.7, 0.5 м) (рис. 1). Эта точка находится на внутренней стенке рабочего отсека спутника, примерно на ее середине. Вблизи этой точки возможна установка научной аппаратуры. Параметры модели атмосферы: ${{F}_{{10.7}}}$ = ${{F}_{{81}}}$ = 150, ${{A}_{p}}$ = 12.
Рассматривались два варианта начальных условий движения центра масс спутника. Соответствующие им решения уравнений орбитального движения назовем орбитами I и II. Начальные условия орбиты I задавались в восходящем узле орбиты в момент времени 07.13.07 UTC 5.V.2013. При этом элементы орбиты составляли: высота в апогее 575.2 км, высота в перигее 546.8 км, наклонение 64.87°, аргумент широты перигея – 124.65°, долгота восходящего узла в гринвичской системе координат 343.27°. Начальные элементы орбиты II имели такие же значении, но относились к моменту времени 07.13.07 UTC 21.XII.2013. В случае орбиты I в некоторой точке отрезка времени, на котором моделировалось движение спутника, максимальное значение угла $\vartheta $ между ортом направления “Земля–Солнце” и плоскостью орбиты спутника достигало 47°, для орбиты II максимальное значение угла $\vartheta $ достигало 88°. Таким образом, орбиты I и II по-разному расположены относительно Солнца.
Начальные условия уравнений (4) задавались в тот же момент времени, что и начальные условия орбитального движения. Этот момент служил началом отсчета времени – точкой $t = 0.$
4. СОБСТВЕННЫЙ КИНЕТИЧЕСКИЙ МОМЕНТ СИСТЕМЫ ДМ
Для определенности положим, что гиросистема спутника состоит из четырех ДМ. Векторы ${\mathbf{H}}$ и ${{{\mathbf{M}}}_{c}}$ реализуются в виде суммы четырех векторов, отвечающих соответствующим ДМ. Полагаем, что оси вращения ДМ расположены параллельно боковым ребрам правильной четырехгранной пирамиды. Высота пирамиды параллельна оси $O{{x}_{1}},$ линии пересечения граней пирамиды с плоскостью $O{{x}_{2}}{{x}_{3}}$ параллельны или перпендикулярны осям $O{{x}_{2}},$ $O{{x}_{3}}$ (рис. 2). Орты ${{{\mathbf{g}}}_{k}}$ осей вращения ДМ имеют компоненты
Суммарный кинетический момент системы ДМ выражается формулой
(5)
$\begin{gathered} {\mathbf{H}} = D{\mathbf{G}},\,\,\,\,D = \left( {\begin{array}{*{20}{c}} { - {{d}_{1}}}&{ - {{d}_{1}}}&{{{d}_{1}}}&{{{d}_{1}}} \\ {{{d}_{2}}}&{{{d}_{2}}}&{{{d}_{2}}}&{{{d}_{2}}} \\ { - {{d}_{3}}}&{{{d}_{3}}}&{ - {{d}_{3}}}&{{{d}_{3}}} \end{array}} \right), \\ {\mathbf{G}} = {{({{G}_{1}},{{G}_{2}},{{G}_{3}},{{G}_{4}})}^{T}}, \\ \end{gathered} $При заданном значении ${\mathbf{H}}$ соотношения (5) нельзя единственным образом разрешить относительно ${\mathbf{G}}.$ Для достижения единственности потребуем, чтобы вектор ${\mathbf{G}}$ имел минимальную евклидову норму. Тогда
(6)
${\mathbf{G}} = {{D}^{ + }}{\mathbf{H}},\,\,\,\,{{D}^{ + }} = \frac{1}{4}\left( {\begin{array}{*{20}{c}} { - d_{1}^{{ - 1}}}&{d_{2}^{{ - 1}}}&{ - d_{3}^{{ - 1}}} \\ { - d_{1}^{{ - 1}}}&{d_{2}^{{ - 1}}}&{d_{3}^{{ - 1}}} \\ {d_{1}^{{ - 1}}}&{d_{2}^{{ - 1}}}&{ - d_{3}^{{ - 1}}} \\ {d_{1}^{{ - 1}}}&{d_{2}^{{ - 1}}}&{d_{3}^{{ - 1}}} \end{array}} \right).$5. РЕЖИМ ТРЕХОСНОЙ СОЛНЕЧНОЙ ОРИЕНТАЦИИ СПУТНИКА
Сперва рассмотрим режим трехосной солнечной ориентации спутника, в котором $O{{x}_{2}}$ неизменно направлена на Солнце, ось $O{{x}_{1}}$ лежит в плоскости орбиты, абсолютная угловая скорость спутника мала. Пусть ${\mathbf{s}}$ – орт направления “Земля–Солнце”. Орт ${\mathbf{n}} = {{({\mathbf{s}} \times {{{\mathbf{E}}}_{2}})} \mathord{\left/ {\vphantom {{({\mathbf{s}} \times {{{\mathbf{E}}}_{2}})} {\left| {{\mathbf{s}} \times {{{\mathbf{E}}}_{2}}} \right|}}} \right. \kern-0em} {\left| {{\mathbf{s}} \times {{{\mathbf{E}}}_{2}}} \right|}}$ лежит в плоскости орбиты спутника и ортогонален орту ${\mathbf{s}}.$ Изменение ортов ${\mathbf{s}}$ и ${\mathbf{n}}$ в системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ описывается уравнениями
(7)
${{{\mathbf{M}}}_{c}} = {{{{\xi }}}^{2}}\hat {I}({{{\mathbf{e}}}_{2}} \times {\mathbf{s}} + {{{\mathbf{e}}}_{1}} \times {\mathbf{n}}) - 2{{\xi }}\hat {I}\hat {W}{\mathbf{\omega }},$Ниже принято, что ξ = 0.01 с–1. Полагаем, что закон управления (7) формируется в соответствии с показаниями установленных на спутнике датчиков ориентации и угловой скорости.
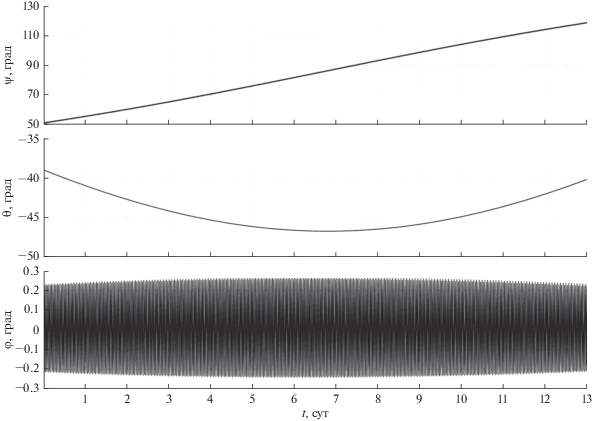
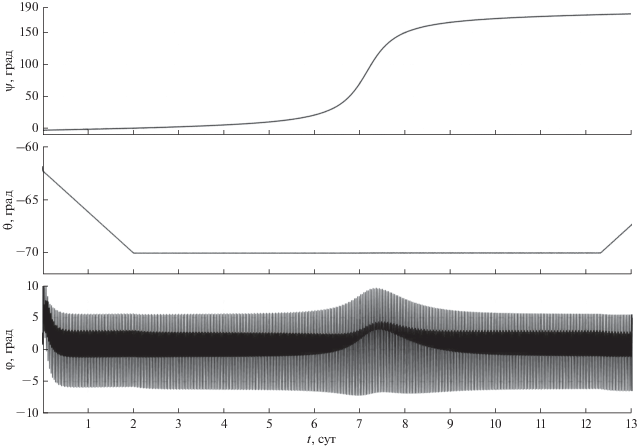
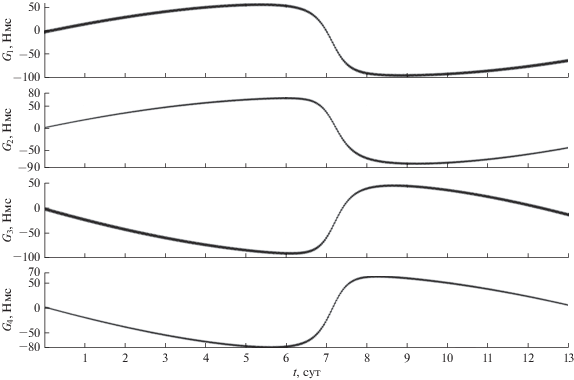
Моделирование режима трехосной солнечной ориентации спутника сводилось к численному интегрированию системы (4), (7) с использованием соотношений (5), (6). Компоненты орта ${\mathbf{s}}$ в гринвичской системе координат рассчитывались по приближенным формулам [17]. Начальные условия системы (4), (7) в момент времени $t$ = 0 задавались следующим образом. Спутник в гринвичской системе координат занимает положение ${{{\mathbf{e}}}_{1}} = {\mathbf{n}},$ ${{{\mathbf{e}}}_{2}} = {\mathbf{s}}.$ Кинетический момент системы ДМ ${\mathbf{H}}$(0) = 0, соответственно ${\mathbf{G}}$(0) = 0. Начальные значения компонент угловой скорости ${{{{\omega }}}_{i}},$ задавались с учетом ошибок в их реализации: ${{{{\omega }}}_{1}}(0) = {{{{\omega }}}_{2}}(0) = {{{{\omega }}}_{3}}(0) = 0.01\,\,{{{\text{град}}} \mathord{\left/ {\vphantom {{{\text{град}}} {\text{c}}}} \right. \kern-0em} {\text{c}}}.$ Результаты расчетов движения спутника, полученные в рамках приятой модели для рассматриваемых орбит приведены на рис. 3, 4 (орбита I) и 5, 6 (орбита II). На рисунках приведены графики зависимости от времени углов ψ, θ, φ и величин собственного кинетического момента каждого из ДМ ${{G}_{k}}.$ Все графики на рис. 3–6 построены на интервале времени 13 сут. Переходной процесс (процесс гашения возмущенного движения), обусловленный ошибками в задании начальной угловой скорости спутника, длится менее 10 мин и из-за масштаба на рисунках не виден.
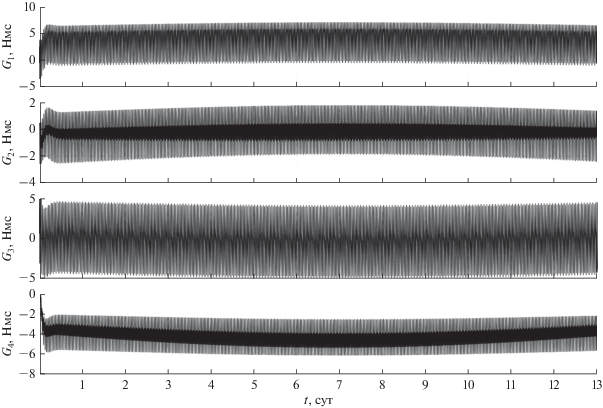
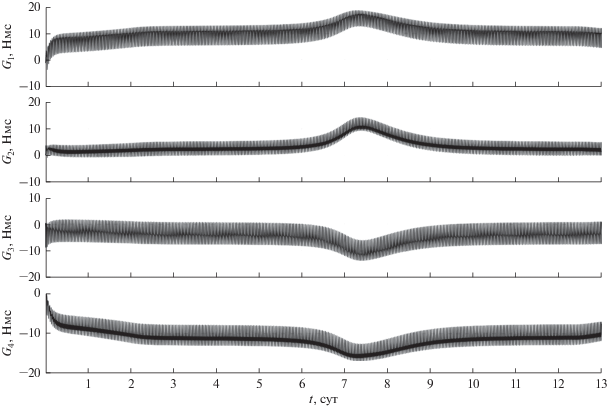
Рис. 4.
Кинетический момент двигателей-маховиков при использовании закона управления (7) (орбита I).
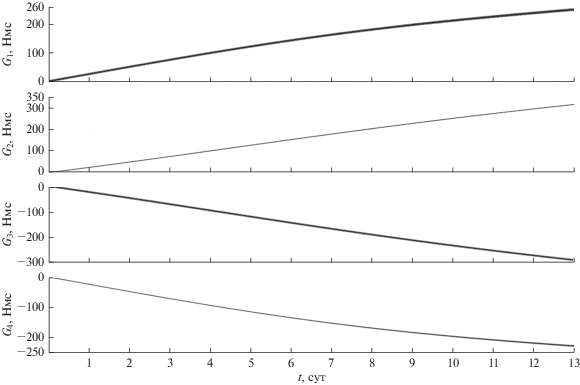
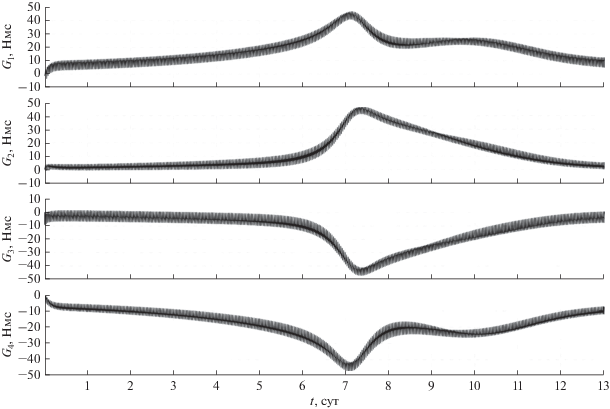
Рис. 6.
Кинетический момент двигателей-маховиков при использовании закона управления (7) (орбита II).
Результаты моделирования показывают, что для двух рассматриваемых вариантов орбит использование закона управления (7) обеспечивает трехосную солнечную ориентацию спутника и затухание его возмущенного движения в окрестности положения ${\mathbf{\omega }} = 0,$ ${{{\mathbf{e}}}_{1}} = {\mathbf{n}},$ ${{{\mathbf{e}}}_{2}} = {\mathbf{s}}.$ Ошибки солнечной ориентации определяются значением угла ${{\sigma }} = \arccos ({\mathbf{s}} \cdot {{{\mathbf{e}}}_{2}})$ (θ = $\vartheta $ при σ = 0), в данном случае σ < 0.4°. Амплитуды установившихся колебаний компонент угловой скорости ограничены значениями:
|ω1| < 1.0 ⋅ 10–4 град/c, |ω2| < 2.0 ⋅ 10–3 град/c,
|ω3| < 7.0 ⋅ 10–4 град/c.
Микроускорения на борту спутника в рассматриваемой точке $P$ по модулю не превышают значения 3.5 ⋅ 10–6 м/с2. Указанный уровень микроускорений является приемлемым для проведения космических экспериментов в области микрогравитации. В работе [18] показано, что наибольший вклад в общий уровень микроускорений ${\mathbf{b}}$ вносит составляющая ${{{\mathbf{b}}}_{g}}$ от действия гравитационного поля Земли, а наименьший – составляющая ${{{\mathbf{b}}}_{r}}$ от вращательного движения спутника относительно центра масс.
На рис. 4 и 6 представлены графики величин ${{G}_{k}}$ $(k = 1,2,3,4),$ на которых видно, что в процессе поддержания солнечной ориентации спутника для всех рассматриваемых орбит кинетический момент каждого из ДМ существенно превысил свое предельно допустимое значение. Разгрузка системы ДМ с помощью магнитных катушек или реактивных двигателей в данной работе не предполагается, поскольку необходимость их проведения сокращает отрезки невозмущенного полета спутника. По этой причине целесообразно рассмотреть возможность использования закона управления, позволяющего не только обеспечить затухание возмущенного движения спутника в окрестности положения покоя с требуемой скоростью, но и дополнительно увеличить продолжительность отрезков полета спутника без проведения разгрузок гиросистемы. Чтобы ограничить рост кинетического момента ДМ не нарушая режим солнечной ориентации спутника в работах [16, 19] предложен соответствующий закон управления, результаты численного моделирования которого будут представлены ниже.
6. РЕЖИМ СОЛНЕЧНОЙ ОРИЕНТАЦИИ СПУТНИКА С ОГРАНИЧЕНИЕМ РОСТА ГИРОСТАТИЧЕСКОГО МОМЕНТА
Рассмотрим возможность использования закона управления, позволяющего не только обеспечить затухание возмущенного движения спутника в окрестности положения ${{{\mathbf{e}}}_{2}} = {\mathbf{s}}$ с требуемой скоростью, но и дополнительно ограничить рост накапливаемого кинетического момента системы ДМ. Чтобы не нарушать режим солнечной ориентации спутника накопление кинетического момента системы ДМ будем контролировать только за счет управления углом φ поворота спутника вокруг орта ${{{\mathbf{e}}}_{2}} = {\mathbf{s}}.$ Закон управления гиросистемой обеспечивающий поддержание режима солнечной ориентации с заданными выше условиями имеет вид [16]:
(8)
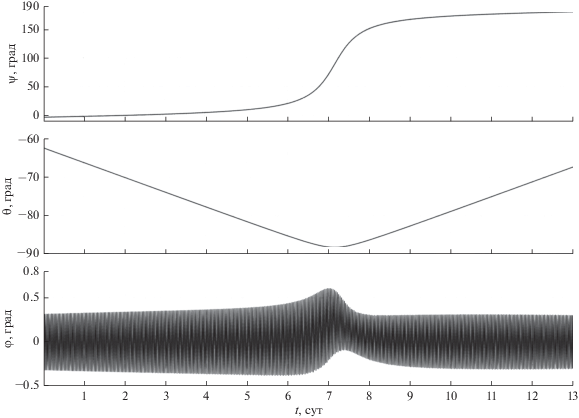
$\begin{gathered} {{{\mathbf{M}}}_{c}} = {{{{\xi }}}^{2}}\hat {I}({{{\mathbf{e}}}_{2}} \times {\mathbf{s}} + {{{\mathbf{e}}}_{1}} \times {\mathbf{n}}) - 2{{\xi }}\hat {I}\hat {W}{\mathbf{\omega }} - \\ - \,\,\hat {I}\left( {{{\chi }}{{{{\omega }}}_{2}} + f} \right){{{\mathbf{e}}}_{2}}, \\ f = - \frac{{3{{\mu }_{{\text{E}}}}}}{{{{r}^{5}}}}\left[ { - \left( {{{{{\kappa }}}_{3}} - {{{{\kappa }}}_{1}}} \right){{{{\gamma }}}_{1}}{{{{\gamma }}}_{2}}{{K}_{1}} + {{{{\kappa }}}_{2}}\left( {{{\gamma }}_{1}^{2} - {{\gamma }}_{3}^{2}} \right){{K}_{2}} + } \right. \\ \left. { + \,\,\left( {{{{{\kappa }}}_{3}} - {{{{\kappa }}}_{1}}} \right){{{{\gamma }}}_{2}}{{{{\gamma }}}_{3}}{{K}_{3}}} \right], \\ \end{gathered} $Покажем, что выбранный закон изменения управляющего момента (8) действительно обеспечивает солнечную ориентацию спутника и при этом ограничивает накопление кинетического момента системы ДМ. С этой целью вычислим решение системы (4), (8) с использованием соотношений (5), (6), приняв χ = 2ξ, ξ = 0.01 с–1, ${{{{\kappa }}}_{1}}$ = = ${{{{\kappa }}}_{2}}$ = 1 (Нмс)–1, ${{{{\kappa }}}_{3}}$ = 3 (Нмс)–1 с начальными условиями в момент времени $t$ = 0 заданными как в п. 5. Результаты расчетов движения спутника для рассматриваемых орбит показывают, что использование закона управления (8) обеспечивает солнечную ориентацию спутника и затухание его возмущенного движения в окрестности положения ${{{\mathbf{e}}}_{2}} = {\mathbf{s}}.$ Графики зависимости от времени углов ψ, θ совпадают с соответствующими графиками представленными на рис. 3, 5. Точность солнечной ориентации спутника σ < 0.4°. Переходной процесс обусловленный ошибками в задании начальной угловой скорости спутника, в данном режиме длится менее 20 мин. После окончания переходного процесса графики угла ${{\varphi }}(t)$ представляют собой установившиеся колебания с доминирующей частотой $4{{f}_{0}} \approx 0.00072$ Гц, где ${{f}_{0}} = {{{{{{\omega }}}_{0}}} \mathord{\left/ {\vphantom {{{{{{\omega }}}_{0}}} {2{{\pi }}}}} \right. \kern-0em} {2{{\pi }}}}$ – орбитальная частота (${{{{\omega }}}_{0}}$ – среднее движение центра масс спутника, для рассматриваемых в данной работе орбит ${{{{\omega }}}_{0}}$ ≈ 1.09 ⋅ 10–3 с–1). Амплитуда установившихся колебаний угла φ ограничена значением $\left| {{\varphi }} \right|$ < 6°. В случае движения спутника по орбите II при значении $\vartheta $ > 70° происходит увеличение амплитуды колебаний угла φ до значений 0° < φ < 15°, максимум которых достигается при максимальном значении угла $\vartheta $ ≈ 88° [16]. В дальнейшем, по мере уменьшения угла $\vartheta ,$ амплитуды колебаний угла φ снижаются до значений $\left| {{\varphi }} \right|$ < 6°. Амплитуды установившихся колебаний компонент угловой скорости ограничены значениями:
|ω1| < 1.2 ∙ 10–4 град/c, |ω2| < 2.2 ∙ 10–3 град/c, |ω3| < 7.0 ∙ 10–4 град/c.
Микроускорения на борту спутника в рассматриваемой точке $P$ по модулю не превышают значения 3.8 ∙ 10–6 м/с2. Указанный уровень микроускорений является приемлемым для проведения космических экспериментов в области микрогравитации.
На рис. 7, 8 на интервале времени 13 сут приведены графики зависимости от величин собственного кинетического момента каждого из ДМ ${{G}_{k}}$ $(k = 1,2,3,4).$ В случае движения спутника по орбите I величины ${{G}_{k}}$ остаются ограниченными значением $\left| {{{G}_{k}}} \right|$ < 10 Нмс $(k = 1,2,3,4)$ (см. рис. 7) на всем интервале движения, что в два раза меньше максимально допустимого значения $\left| {{{G}_{k}}} \right|.$ В случае движения спутника по орбите II, когда Солнце относительно плоскости орбиты поднимается достаточно высоко ($\vartheta $ > 70°$)$, значения $\left| {{{G}_{k}}} \right|$ начинают возрастать (см. рис. 8), достигая своего максимума $\left| {{{G}_{k}}} \right|$ ≈ 48 Нмс при $\vartheta $ ≈ 88°. В дальнейшем, по мере уменьшения $\vartheta ,$ происходит разгрузка системы ДМ до значений $\left| {{{G}_{k}}} \right|$ ≤ 10 Нмс.
7. СПЕКТРАЛЬНЫЙ АНАЛИЗ МИКРОУСКОРЕНИЙ
С целью анализа уровня микроускорений, возникающих на борту спутника в процессе поддержания солнечной ориентации, в работе определены характерные частоты колебаний компонент вектора микроускорений ${\mathbf{b}}$. Частоты были найдены с помощью спектрального анализа, выполнявшегося по следующей схеме [20]. Пусть ${{x}_{n}}$ $(n = 1,\;2,\; \ldots ,\;N)$ – значения какой-либо переменной $x(t)$ исследуемого решения в узлах равномерной временной сетки $\{ {{t}_{n}}\} {\text{:}}$ ${{x}_{n}} = x({{t}_{n}}).$ Во всех рассмотренных ниже примерах шаг сетки $h = {{t}_{{n + 1}}} - {{t}_{n}} = 10$ с. Предположим, что исследуемая функция имеет вид
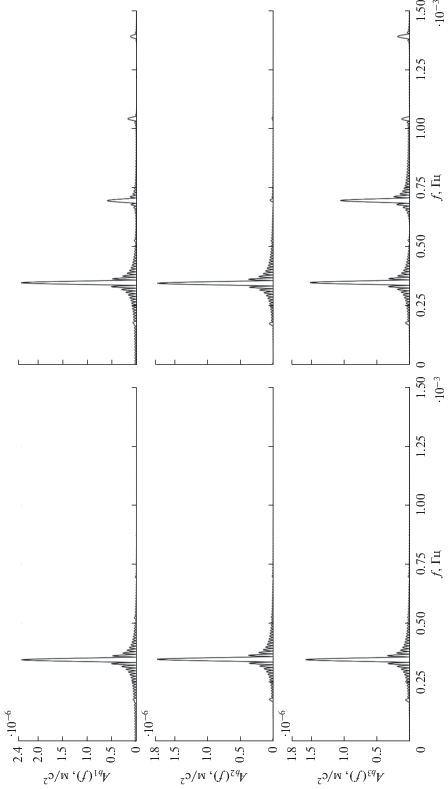
На рис. 9 показаны амплитудные спектры ${{A}_{{bi}}}(f)$ величин суммарных микроускорений ${{b}_{i}}(t)$ $(i = 1,2,3),$ в левой части рисунка в случае использования закона управления (7), в правой – при использовании закона (8). Спектры приведены в диапазоне частот от 0 до 0.0015 Гц, при значениях $h = 10$ с и $N = 8640.$ Как и в случае использования закона управления (7), наибольший вклад в общий уровень микроускорений ${\mathbf{b}}$ на борту спутника при использования закона (8) вносит составляющая ${{{\mathbf{b}}}_{g}}$ с доминирующей частотой $2{{f}_{0}} \approx 0.00036$ Гц. Такие колебания возбуждаются градиентом гравитационного поля. При использовании закона (8) на всех рассматриваемых орбитах движения спутника происходит увеличение амплитуд колебаний величин ${{b}_{1}}(t)$ и ${{b}_{3}}(t)$ на частоте $4{{f}_{0}} \approx 0.00072$ Гц, что соответствует доминирующей частоте колебаний величин угла φ и ${{{{\omega }}}_{2}}.$ Однако такое увеличение амплитуд практически не сказывается на общем уровне микроускорений ${\mathbf{b}}$, возникающих на борту спутника.
8. РЕЖИМ КОМБИНАЦИИ ГРАВИТАЦИОННОЙ И СОЛНЕЧНОЙ ОРИЕНТАЦИИ СПУТНИКА
При движении спутника по орбите II в режиме его солнечной ориентации происходит рост величин $\left| {{{G}_{k}}} \right|$$(k = 1,2,3,4)$ до значений, превышающих максимально допустимое значение $\left| {{{G}_{k}}} \right|$ примерно в два раза (см. рис. 8). Это происходит вследствие уменьшения абсолютной величины действующего на спутник гравитационного момента при достаточно большом значении угла θ. Чтобы ограничить рост величин $\left| {{{G}_{k}}} \right|,$ можно ограничить допустимую величину угла ориентации θ используя следующий сценарий вращательного движения спутника с помощью закона управления (8). До наступления условия θ > η спутник стабилизируется относительного положения ${{{\mathbf{e}}}_{2}} = {\mathbf{s}},$ при выполнении условия θ > η спутник стабилизируется относительно положения ${{{\mathbf{e}}}_{2}} = {\mathbf{\tilde {s}}},$ где η – некоторое наперед заданное значение угла между ортом ${\mathbf{\tilde {s}}} = ({{\tilde {s}}_{1}},\;{{\tilde {s}}_{2}},\;{{\tilde {s}}_{3}})$ и плоскостью $C{{Z}_{1}}{{Z}_{3}}.$ Компоненты орта ${\mathbf{\tilde {s}}}$ в системе координат $C{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$ определяются по следующим формулам:
ЗАКЛЮЧЕНИЕ
В работе показано, что c помощью системы ДМ можно реализовать режим солнечной ориентации спутника с уровнем квазистатических микроускорений, приемлемым для проведения космических экспериментов в области микрогравитации. Стабилизацию режима солнечной ориентации можно обеспечить без накопления кинетического момента ДМ за счет управления углом поворота спутника вокруг направления на Солнце.
Список литературы
Абрашкин В.И., Воронов К.Е., Пияков И.В. и др. Определение вращательного движения спутника Бион М-1 средствами аппаратуры ГРАВИТОН // Космич. исслед. 2015. Т. 53. № 4. С. 306–319.
Абрашкин В.И., Воронов К.Е., Пияков И.В. и др. Вращательное движение спутника Фотон М-4 // Космич. исслед. 2016. Т. 54. № 4. С. 315–322.
Сазонов В.В., Комаров М.М., Полежаев В.И. и др. Микроускорения на орбитальной станции Мир и оперативный анализ гравитационной чувствительности конвективных процессов тепломассопереноса // Космич. исслед. 1999. Т. 37. № 1. С. 86–101.
Сазонов В.В., Чебуков С.Ю., Абрашкин В.И. и др. Анализ низкочастотных микроускорений на борту ИСЗ Фотон-11 // Космич. исслед. 2001. Т. 39. № 4. С. 419–435.
Абрашкин В.И., Волков М.В., Егоров А.В. и др. Анализ низкочастотной составляющей в измерениях угловой скорости и микроускорения, выполненных на спутнике Фотон-12 // Космич. исслед. 2003. Т. 41. № 6. С. 632–651.
Абрашкин В.И., Богоявленский Н.Л., Воронов К.Е. и др. Неуправляемое вращательное движение спутника Фотон М-2 и квазистатические микроускорения на его борту // Космич. исслед. 2007. Т. 45. № 5. С. 450–470.
Бабкин Е.В., Беляев М.Ю., Ефимов Н.И. и др. Определение квазистатической компоненты микроускорения, возникающей на борту Международной космической станции // Космич. исслед. 2004. Т. 42. № 2. С. 162–171.
Бойзелинк Т., Ван Бавинхов К., Сазонов В.В., Чебуков С.Ю. Анализ низкочастотной составляющей в измерениях микроускорения, выполненных на спутнике Фотон М-2 // Космиче. исслед. 2008. Т. 46. № 5. С. 463–483.
Игнатов А.И., Сазонов В.В. Реализация режимов вращательного движения ИСЗ с малым уровнем микроускорений электромеханическими исполнительными органами // Космич. исслед. 2012. Т. 50. № 5. С. 380–393.
Игнатов А.И., Сазонов В.В. Оценка остаточных микроускорений на борту ИСЗ в режиме одноосной солнечной ориентации // Космич. исслед. 2013. Т. 51. № 5. С. 380–388.
Бажинов И.К., Гаврилов В.П., Ястребов В.Д. и др. Навигационное обеспечение полета орбитального комплекса “Салют-6”–“Союз”–“Прогресс”. М.: Наука, 1985.
Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, 1965.
Белецкий В.В., Яншин А.М. Влияние аэродинамических сил на вращательное движение искусственных спутников. Киев: Наук. думка, 1984.
Игнатов А.И., Давыдов А.А., Сазонов В.В. Анализ динамических возможностей систем управления малым космическим аппаратом, построенных на базе двигателей-маховиков. Препринты ИПМ им. М.В. Келдыша РАН. 2005. № 47.
Гантмахер Ф.Р. Теория матриц. М.: Наука, 1988.
Игнатов А.И. Стабилизация режима солнечной ориентации искусственного спутника Земли без накопления кинетического момента гиросистемы // Известия РАН. Теория и системы управления. 2020. № 3. С. 164–176.
Меес Ж. Астрономические формулы для калькуляторов. М.: Мир, 1988.
Игнатов А.И., Сазонов В.В. Оценка уровня квазистатических микроускорений на борту искусственного спутника Земли в режиме солнечной ориентации. Препринты ИПМ им. М.В. Келдыша РАН. 2020. № 54.
Игнатов А.И., Сазонов В.В. Реализация режима солнечной ориентации искусственного спутника Земли без накопления кинетического момента гиросистемы. Препринты ИПМ им. М.В. Келдыша РАН. 2019. № 99.
Теребиж В.Ю. Анализ временных рядов в астрофизике. М.: Наука, 1992.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования