Космические исследования, 2022, T. 60, № 1, стр. 57-72
Нейроадаптивное поддержание формации спутников на низких околоземных орбитах
М. Г. Широбоков 1, *, С. П. Трофимов 1
1 Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
* E-mail: shirobokov@keldysh.ru
Поступила в редакцию 27.11.2020
После доработки 12.02.2021
Принята к публикации 16.06.2021
- EDN: MGENAN
- DOI: 10.31857/S0023420622010101
Аннотация
Работа посвящена разработке и исследованию нейроадаптивного управления формацией из двух спутников на низкой околоземной орбите. Цель управления – поддержание проективной круговой орбиты, при этом считается, что один из аппаратов неуправляемый и его баллистический коэффициент не известен, а другой аппарат – управляемый, при этом есть возможность управлять как его ориентацией (а значит, величиной миделева сечения), так и орбитальным движением с помощью двигателя большой тяги. Искусственные нейронные сети используются для аппроксимации построенных функций управления, а адаптивность системы управления выражается в адаптации управления к неизвестному баллистическому коэффициенту неуправляемого аппарата. В работе детально описывается реализация, архитектура и процесс обучения нейронных сетей, а также способ оценки их качества. Дается описание процедуры адаптации к неизвестному параметру неуправляемого аппарата в режиме реального времени. Показано, что адаптация возможна в течение приемлемого времени. Также приводятся результаты адаптации к двум параметрам модели – баллистическому коэффициенту неуправляемого аппарата и плотности атмосферы. Моделирование производится в рамках возмущенной задачи двух тел с учетом силы атмосферного сопротивления и влияния от второй зональной гармоники геопотенциала.
1. ВВЕДЕНИЕ
В настоящее время методы машинного обучения активно применяются для решения самых разнообразных задач человеческой деятельности. В первую очередь это относится к задачам распознавания образов, прогнозирования эволюции динамических систем и синтеза управления ими, системам искусственного интеллекта, теории принятия решений. Методы машинного обучения сейчас можно обнаружить в экономике, медицине, биохимических исследованиях, системах фильтрации информации и др.
Методы машинного обучения принято делить на три типа: методы обучения с учителем, методы обучения без учителя и методы обучения с подкреплением [1, 2]. Методы обучения с учителем применяются в случаях, когда требуется аппроксимировать зависимость между какими-либо переменными задачи. В этом случае составляется параметрическая модель этой зависимости и множество конкретных пар этих переменных, которое используется для подгонки параметров модели. Процесс такой подгонки называется обучением модели, а множество пар переменных – обучающей выборкой. Методы обучения без учителя используются в случаях, когда дано некоторое множество значений какой-то одной переменной и необходимо определить структуру этого множества (разбиение на подгруппы, принадлежность подпространству меньшей размерности и пр.). Методы обучения с подкреплением созданы для ситуаций, когда исследуемая система может быть формализована как состоящая из среды и агента, действующего в данной среде и получающего от среды скалярный сигнал, который он пытается методом проб и ошибок максимизировать. Поведение агента в среде определяется его стратегией – отображением из множества состояний среды в множество действий. Задача обучения с подкреплением состоит в том, чтобы определить оптимальную стратегию, т.е. стратегию, которая максимизирует суммарный получаемый сигнал подкрепления от среды. Стратегия, как отображение, обычно аппроксимируется какой-либо параметрической моделью.
Уже несколько лет в литературе наблюдается тренд на применение методов машинного обучения для проектирования схем управления космическими аппаратами. Эти работы можно условно разделить на несколько классов: 1) синтез контура управления орбитальным и/или угловым движением космического аппарата, 2) поиск оптимальных управляющих воздействий или оптимальных траекторий перелета на этапе предварительного анализа миссии, 3) распознавание образов для решения задач навигации или дистанционного зондирования, 4) диагностика аппаратуры и 5) все остальные работы, которые трудно классифицировать.
Данная работа относится к первому из перечисленных классов и ставит своей целью оценку возможностей управления формацией спутников на низких околоземных орбитах с помощью искусственных нейронных сетей (далее просто нейронных сетей), а также оценку возможностей адаптации системы управления к меняющимся параметрам аппаратов и среды в режиме полета. Искусственные нейронные сети и выступают, как правило, в роли модели, призванной аппроксимировать зависимость между изучаемыми переменными в методах обучения с учителем или для аппроксимации оптимальной стратегии в методах обучения с подкреплением.
Исследования, в которых методы машинного обучения используются для проектирования оптимальных траекторий или синтеза контура управления, широко представлены в современной литературе. Их можно разбить на два класса: те, что используют методы обучения с учителем, и те, что проводятся с помощью методов обучения с подкреплением. Методы обучения без учителя в задачах управления космическим аппаратом авторам не встречались.
Отметим только ключевые (на взгляд авторов) исследования. Во-первых, упомянем работы [3, 4], в которых строится адаптивное управление вращательным движением космического аппарата с использованием нейронных сетей. Идея состоит в том, чтобы ввести две нейронных сети – прогнозирующую и управляющую. Управляющая нейронная сеть ответственна за выработку управляющих воздействий на аппарат на основе входа – состояния аппарата. Прогнозирующая сеть помогает понять, насколько выбранные управляющие воздействия в текущем состоянии оказываются эффективными: делается это для того, чтобы на основании оценок эффективности скорректировать управляющую нейронную сеть для лучшей работы. Прогнозирующая и управляющая нейронные сети вводятся и в работе [5], где с использованием нейронных сетей решается задача адаптации параметров системы управления реального космического аппарата Solar and Heliospheric Observatory (SOHO) [6].
Надо сказать, что идея использования прогнозирующей сети для коррекции управляющей сети критикуется уже в одной из первых работ [3]. Проблема подобных коррекций связана с тем, что прогнозирующая нейронная сеть должна быть достаточно точной и сама должна корректироваться чаще, чем управляющая сеть. Кроме того, коррекция весов управляющей сети во время полета способна существенно дестабилизировать управление. Поэтому, несмотря на то что в предыдущих наших работах [7, 8] решение задач управления одиночными аппаратами с большой и малой тягой было произведено с помощью управляющей и прогнозирующей нейронных сетей, многочисленные численные эксперименты убедили нас отказаться от этого способа адаптации нейронных сетей в текущей работе.
В работах [9, 10] решается задача аппроксимации функции оптимального управления малой тягой в орбитальном полете. Идея данных работ состоит в замыкании в единый контур нейронных сетей, выдающих значения сопряженных переменных, и обычного метода оптимизации, решающего краевую задачу из принципа максимума Понтрягина. Выход нейронных сетей используется как начальное приближение для метода решения краевой задачи, а выход обычного оптимизационного метода – как правильный пример для коррекции нейронных сетей. Кроме того, интересна идея выделения под каждый аппроксимируемый параметр своей нейронной сети. Этим приемом мы воспользуемся и в данной работе.
В работе [11] решается задача управления формацией с субмиллиметровой точностью с использованием методов детерминированного обучения – т.е. методов обучения с учителем, регулятор которых синтезируется с помощью методов Ляпунова и на основе нейронных сетей, веса которых подчиняются некоторым дифференциальным уравнениям, гарантирующим сходимость к оптимальным (в том или ином смысле) значениям. При этом регулятор на основе нейронных сетей является здесь помощником для основного регулятора (линейно-квадратичный регулятор) и способен подавить возмущения от сил светового давления и гравитации Луны. Основным регулятором в методах детерминированного обучения могут служить и другие регуляторы, например на основе скользящего управления [12].
Все перечисленные выше работы используют методы обучения с учителем для обучения моделей, аппроксимирующих оптимальные управляющие воздействия на космический аппарат. Что касается методов обучения с подкреплением, имеется большая группа работ немецкого специалиста в области прикладной математики Б. Дахвальда и его коллег [13–16]. Все эти работы нацелены на поиск оптимальных траекторий перелета в различных постановках задач. Основная идея состоит в том, чтобы аппроксимировать стратегию поведения агента (функцию управления) с помощью нейронных сетей, а их веса искать генетическими методами оптимизации. Эта связь между машинным обучением и эволюционным программированием особенно подчеркивается и обсуждается в обзорной работе [17]. Похожий метод также описан в работе [18], в которой ставится задача прецизионного управления формацией спутников, где для оптимизации применяется не генетический алгоритм, а метод роя частиц. Предлагаемый подход был протестирован на платформе Synchronized Position Hold Engage Reorient Experimental Satellites (SPHERES) [19] на борту Международной космической станции.
Наконец, отметим еще один крупный класс работ, использующих методы обучения с подкреплением. Это работы американских специалистов Р. Фурфаро и Б. Гаудета [20–24]. Все они посвящены задаче адаптивного управления аппаратом во время спуска на поверхность Марса или другого небесного тела. Оптимальное управление в первых двух работах ищется прямым методом (параметризация функции управления и оптимизация ее параметров). В трех последних работах оптимальное управление ищется непрямыми методами, т.е. таким образом, чтобы оно удовлетворяло уравнению оптимальности Беллмана.
Методы обучения с подкреплением, особенно в задачах с непрерывным множеством состояний и управляющих воздействий, характеризуются повышенной сложностью реализации подобных систем обучения и значительные затраты времени на обучение нейронных сетей даже в сравнительно простых случаях – например, задаче удержания математического маятника в неустойчивом положении равновесия. Многочисленные попытки авторов решить задачу текущей работы методами обучения с подкреплением не увенчались успехом, но результативными оказались методы обучения с учителем.
Итак, в работе разрабатывается адаптивная система управления формацией спутников, движущихся на низких околокруговых орбитах вокруг Земли, на основе нейронных сетей и с использованием силы атмосферного сопротивления. В разделе 2 описывается модель, в рамках которой рассматривается движение космических аппаратов. В разделе 3 ставится задача поддержания спутниковой формации, предлагается метод ее решения, описывается возникающая при этом оптимизационная процедура. В результате решения оптимизационной задачи для различных начальных данных формируется выборка, на которой обучаются две предлагаемые нами управляющие нейронные сети. Способ формирования выборки, метод обучения, архитектура нейронных сетей и результаты расчетов приводятся в разделе 4. В разделе 5 описывается метод адаптации системы управления к меняющимся параметрам спутников и плотности атмосферы, приводятся результаты работы метода. Далее следует заключение, в котором собраны все основные выводы исследования.
2. ОСНОВНЫЕ ОБОЗНАЧЕНИЯ И МОДЕЛИ ДВИЖЕНИЯ
Рассматривается движение двух спутников вблизи круговой орбиты радиуса ${{R}_{{{\text{ref}}}}}$ вокруг Земли. Орбитальную скорость движения по орбите с радиусом ${{R}_{{{\text{ref}}}}}$ обозначим ${{V}_{{{\text{ref}}}}} = \sqrt {{{{{\mu }_{{\text{E}}}}} \mathord{\left/ {\vphantom {{{{\mu }_{{\text{E}}}}} {{{R}_{{{\text{ref}}}}}}}} \right. \kern-0em} {{{R}_{{{\text{ref}}}}}}}} ,$ где ${{\mu }_{{\text{E}}}}$ – гравитационный параметр Земли. Будем считать, что на спутники действует только сила гравитационного притяжения Земли и сила атмосферного сопротивления, а движение спутников определяется дифференциальными уравнениями
(1)
${{{\mathbf{\dot {R}}}}_{i}} = {{{\mathbf{V}}}_{i}},\,\,\,\,{{{\mathbf{V}}}_{i}} = - \frac{{{{\mu }_{{\text{E}}}}}}{{R_{i}^{3}}}{{{\mathbf{R}}}_{i}} + {{{\mathbf{F}}}_{{a,i}}} + {{{\mathbf{F}}}_{{J2,i}}},\,\,\,\,i = 1,2,$Система единиц для обезразмеривания уравнений движения была выбрана следующим образом:
В табл. 1 приведены числовые значения всех используемых параметров. Для первого спутника ($i = 1$) задан диапазон, которому принадлежит отношение площади к массе, это значение зависит от ориентации аппарата. Хотя угловое движение аппаратов не моделируется в данной работе, мы считаем отношение площади к массе первого аппарата переменной величиной, которой можно управлять и создавать таким образом различные возмущающие ускорения, действующие на первый аппарат со стороны атмосферы. Для второго аппарата приводится диапазон возможных значений баллистического коэффициента ${{\beta }_{2}}.$ Истинное значение этого параметра считается неизвестным. Система управления в режиме реального полета должна будет адаптироваться к этому значению.
Таблица 1.
Принятые в данной работе численные значения используемых параметров
| Параметр | Название | Значение |
|---|---|---|
| ${{\mu }_{{\text{E}}}}$ | Гравитационный параметр Земли | $398{\kern 1pt} 600.44$ км$^{3}$/с$^{2}$ |
| ${{R}_{{\text{E}}}}$ | Радиус Земли | $6371$ км |
| ${{R}_{{{\text{ref}}}}} - {{R}_{{\text{E}}}}$ | Высота круговой орбиты | 200 км |
| ${{J}_{2}}$ | Коэффициент при второй зональной гармонике | $1.0826 \cdot {{10}^{{ - 3}}}$ |
| ${{c}_{{x,1}}}$ | Коэффициент аэродинамического сопротивления | 2.1 |
| ${{A}_{1}}{\text{/}}{{m}_{1}}$ | Отношения площади к массе первого спутника | 0.005–0.020 м$^{2}$/кг |
| ${{\beta }_{2}}$ | Баллистический коэффициент второго спутника | 0.01–0.04 м$^{2}$/кг |
| ${\text{DU}}$ | Единица расстояния | $6371$ км |
| ${\text{VU}}$ | Единица скорости | $7.910$ км/с |
| ${\text{TU}}$ | Единица времени | $13.424$ мин |
Введем орбитальную систему координат $Oxyz.$ Начало $O$ поместим на круговую орбиту, радиус которой совпадает с радиусом первого аппарата в некоторый момент времени. Эту орбиту мы будем называть опорной. Каждый раз, когда она нам потребуется, ее параметры будут пересчитываться на основе параметров орбиты первого спутника и фиксироваться до следующего перерасчета. Положение и скорость движущейся точки $O$ на опорной орбите в инерциальной системе координат мы будем обозначать ${{{\mathbf{R}}}_{0}}$ и ${{{\mathbf{V}}}_{0}}$ соответственно. Ось $Ox$ направим вдоль радиус-вектора ${{{\mathbf{R}}}_{0}},$ ось $Oz$ направим вдоль вектора ${{{\mathbf{R}}}_{0}} \times {{{\mathbf{V}}}_{0}},$ а ось $Oy$ выберем дополняющей до правой тройки систему $Oxyz.$ В орбитальной системе координат положение $i$-го аппарата обозначим ${{{\mathbf{r}}}_{i}},$ а скорость – ${{{\mathbf{v}}}_{i}}.$
Фазовый вектор $i$-го аппарата в инерциальной системе координат обозначим как ${{{\mathbf{X}}}_{i}} = [{{{\mathbf{R}}}_{i}},{{{\mathbf{V}}}_{i}}],$ а в орбитальной системе координат – как ${{{\mathbf{x}}}_{i}} = [{{{\mathbf{r}}}_{i}},{{{\mathbf{v}}}_{i}}].$
Уравнения (1) описывают основную модель движения космических аппаратов в формации, именно в рамках этой модели будет впоследствии моделироваться их движение. Кроме этой модели в работе также используются две другие вспомогательные модели движения – невозмущенная линеаризованная модель относительного движения и возмущенная силой атмосферного сопротивления линеаризованная модель относительного движения. А именно, в рамках невозмущенной линеаризованной модели относительного движения вводится понятие проективной круговой орбиты (PCO), а в рамках возмущенной линеаризованной модели относительного движения строится управление одним из спутников для противодействия дрейфу вдоль орбиты. Опишем эти модели подробнее.
В невозмущенной линеаризованной модели уравнения относительного движения линеаризуются относительно опорной кеплеровой орбиты. В данной работе будем полагать ее круговой, тогда соответствующие уравнения движения спутников называются уравнениями Хилла–Клохесси–Уилтшира и имеют вид:
где $\Delta {{{\mathbf{x}}}_{{12}}} = {{{\mathbf{x}}}_{2}} - {{{\mathbf{x}}}_{1}}$ = $[\Delta {{{\mathbf{r}}}_{{12}}},\Delta {{{\mathbf{v}}}_{{12}}}]$ = $[\Delta x,\Delta y,\Delta z,\Delta \dot {x},$ $\Delta \dot {y},\Delta \dot {z}]$ – фазовый вектор второго аппарата относительно первого в орбитальной системе координат, а ${{n}_{0}}$ – среднее движение на опорной орбите. В рамках этой модели считается, что $\left| {\Delta {{{\mathbf{r}}}_{{12}}}} \right| \ll {{R}_{1}}.$ Ограниченные в рамках этой модели траектории отвечают случаю $\Delta \dot {y}({{t}_{0}}) = - 2{{n}_{0}}\Delta x({{t}_{0}})$ (отсутствие дрейфа вдоль орбиты) и принимают следующую форму:(5)
${{\rho }_{x}} = \frac{1}{{{{n}_{0}}}}\sqrt {\Delta {{{\dot {x}}}^{2}}({{t}_{0}}) + n_{0}^{2}\Delta {{x}^{2}}({{t}_{0}})} ,$(7)
${{\rho }_{z}} = \frac{1}{{{{n}_{0}}}}\sqrt {\Delta {{{\dot {z}}}^{2}}({{t}_{0}}) + n_{0}^{2}\Delta {{z}^{2}}({{t}_{0}})} ,$Проективной круговой орбитой называют ограниченную в линейном приближении траекторию с ${{\alpha }_{x}} = {{\alpha }_{z}}$ и ${{\rho }_{z}} = 2{{\rho }_{x}}.$ Заметим, что в этом случае $2{{\rho }_{x}} = {{\rho }_{z}} = {{R}_{{{\text{PCO}}}}}$ – величина, которую мы будем называть радиусом проективной круговой орбиты. Для определенности примем ${{R}_{{{\text{PCO}}}}} = 200$ м.
В рамках возмущенной линеаризованной модели относительного движения в правые части уравнений (2)–(4) добавляются проекции разности ${{{\mathbf{F}}}_{{a,2}}} - {{{\mathbf{F}}}_{{a,1}}}$ сил сопротивления атмосферы, действующих на спутники. В следующем разделе описываются постановка и решение задачи поддержания спутниковой формации в рамках этой модели.
3. ЗАДАЧА ПОДДЕРЖАНИЯ СПУТНИКОВОЙ ФОРМАЦИИ
Задача состоит в синтезе адаптивного нейроуправления орбитальным движением первого аппарата, при котором второй аппарат будет двигаться относительно первого по проективной круговой орбите определенного размера. Предполагается, что данное управление реализуется изменением миделева сечения первого аппарата и с некоторой частотой с помощью серии импульсов. Слово “нейроуправление” означает, что система управления первым аппаратом будет содержать нейронную сеть, а слово “адаптивность” подразумевает, что параметры этой сети будут настраиваться в режиме полета таким образом, чтобы удовлетворить каким-то выбранным изменяющимся условиям. Будем предполагать, что управление вторым аппаратом отсутствует.
Покажем, каким образом задачу синтеза управления для поддержания проективной круговой орбиты можно решить, используя классический подход. Для этого воспользуемся управляемым параметром ${{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}},$ чтобы с помощью атмосферы по возможности максимально сократить относительный дрейф аппаратов вдоль орбиты. Последующая серия импульсов, совершаемых первым аппаратом, направлена на полное устранение дрейфа и нацеливание на требуемые параметры проективной круговой орбиты.
Плотность атмосферы будем считать постоянной и одинаковой всюду и на всем интервале маневрирования.
Приступим непосредственно к постановке оптимизационной задачи, решение которой и дает требуемое управление для поддержания формации в нелинейной модели с возмущениями. Начнем с поиска значения отношения площади к массе ${{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}$ у первого аппарата, такого, чтобы максимально сократить дрейф относительно второго аппарата. С одной стороны, разница в больших полуосях первого и второго аппарата в линейном приближении выражается формулой
(10)
$\Delta {{a}_{0}} = {{a}_{2}}({{t}_{0}}) - {{a}_{1}}({{t}_{0}}) = 4\Delta x({{t}_{0}}) + {{2\Delta \dot {y}({{t}_{0}})} \mathord{\left/ {\vphantom {{2\Delta \dot {y}({{t}_{0}})} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}.$(11)
$\begin{gathered} \Delta {{a}_{1}} = {{a}_{1}}({{t}_{0}} + {{T}_{0}}) - {{a}_{1}}({{t}_{0}}) = - 2a_{0}^{2}{{V}_{0}}{{F}_{{a,1}}}{{T}_{0}}, \\ \Delta {{a}_{2}} = {{a}_{2}}({{t}_{0}} + {{T}_{0}}) - {{a}_{2}}({{t}_{0}}) = - 2a_{0}^{2}{{V}_{0}}{{F}_{{a,2}}}{{T}_{0}}, \\ \end{gathered} $Условие отсутствия дрейфа через виток вдоль опорной орбиты выглядит следующим образом: ${{a}_{1}}({{t}_{0}} + {{T}_{0}}) = {{a}_{2}}({{t}_{0}} + {{T}_{0}}),$ что равносильно условию $\Delta {{a}_{1}} = \Delta {{a}_{2}} + \Delta {{a}_{0}}.$
Выразим в левой части отношение ${{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}$ и получим $\frac{{{{A}_{1}}}}{{{{m}_{1}}}} = \frac{{\Delta {{a}_{0}} + \Delta {{a}_{2}}}}{{ - a_{0}^{2}V_{0}^{3}{{T}_{0}}\rho {{c}_{{x,1}}}}}.$
Если рассчитанное по этой формуле значение оказывается меньше, чем минимально возможное значение ${{({{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}})}_{{min}}},$ то принимаем $({{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}) = {{({{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}})}_{{min}}}.$ Если же это значение оказалось больше, чем максимально возможное значение ${{({{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}})}_{{max}}},$ то принимаем $({{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}) = {{({{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}})}_{{max}}}.$ Поэтому окончательно формула для отношения площади к массе запишется так:
(12)
$\frac{{{{A}_{1}}}}{{{{m}_{1}}}} = max\left( {\mathop {\left( {\frac{{{{A}_{1}}}}{{{{m}_{1}}}}} \right)}\nolimits_{min} ,min\left( {\frac{{\Delta {{a}_{0}} + \Delta {{a}_{2}}}}{{ - a_{0}^{2}V_{0}^{3}{{T}_{0}}\rho {{c}_{{x,1}}}}},\mathop {\left( {\frac{{{{A}_{1}}}}{{{{m}_{1}}}}} \right)}\nolimits_{max} } \right)} \right).$Обращаем внимание на то, что величина $\Delta {{a}_{2}}$ зависит от баллистического коэффициента второго аппарата ${{\beta }_{2}},$ который в режиме реального полета может быть неизвестен. В дальнейшем мы потребуем, чтобы разрабатываемое нейроуправление адаптировалось к этому неизвестному значению.
Итак, формула (12) позволяет вычислить отношение площади к массе для первого аппарата, чтобы с помощью атмосферы сократить дрейф второго аппарата. Соответствующее значение дифференциального ускорения торможения в атмосфере вычисляется по формуле $\Delta F = {{F}_{{a,2}}} - {{F}_{{a,1}}}.$
Теперь перейдем к поиску оптимальной серии импульсов для полного устранения дрейфа и попадания на целевую проективную круговую орбиту.
Ограничимся поиском серии четырех импульсов в пределах одного витка. Можно рассмотреть и иное число импульсов, распределенных на иных интервалах времени, но для определенности мы примем эти значения.
Пусть ${{t}_{1}},$ ${{t}_{2}},$ ${{t}_{3}}$ и ${{t}_{4}}$ – это моменты времени совершения импульсов $\Delta {{{\mathbf{v}}}_{1}},$ $\Delta {{{\mathbf{v}}}_{2}},$ $\Delta {{{\mathbf{v}}}_{3}}$ и $\Delta {{{\mathbf{v}}}_{4}}$ соответственно. По предположению, ${{t}_{0}} \leqslant {{t}_{1}} < {{t}_{2}} < {{t}_{3}} < {{t}_{4}} \leqslant $ $ \leqslant {{t}_{0}} + {{T}_{0}},$ где ${{T}_{0}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ – период опорной орбиты, а ${{t}_{0}}$ – момент начала маневрирования.
В результате применения импульсов скорости $\Delta {{{\mathbf{v}}}_{1}},$ $\Delta {{{\mathbf{v}}}_{2}},$ $\Delta {{{\mathbf{v}}}_{3}}$ и $\Delta {{{\mathbf{v}}}_{4}}$ первым аппаратом в моменты времени ${{t}_{1}},$ ${{t}_{2}},$ ${{t}_{3}}$ и ${{t}_{4}}$ относительный фазовый вектор второго аппарата с учетом воздействия постоянного возмущающего ускорения со стороны атмосферы в линейном приближении будет равен
Теперь, зная $\Delta {\mathbf{x}}({{t}_{0}} + {{T}_{0}}),$ по формулам (5) можно вычислить параметры относительной орбиты ${{\rho }_{x}},$ ${{\rho }_{y}},$ ${{\rho }_{z}},$ ${{\alpha }_{x}},$ ${{\alpha }_{z}}$ и сравнить их с требуемыми параметрами. Это дает четыре уравнения
(13)
${{\rho }_{x}} = {{{{R}_{{{\text{PCO}}}}}} \mathord{\left/ {\vphantom {{{{R}_{{{\text{PCO}}}}}} 2}} \right. \kern-0em} 2},\,\,\,\,{{\rho }_{y}} = 0,\,\,\,\,{{\rho }_{z}} = {{R}_{{{\text{PCO}}}}},\,\,\,\,{{\alpha }_{x}} = {{\alpha }_{z}},$В результате получаются 5 уравнений, играющих роль ограничений-равенств в формулируемой оптимизационной процедуре. Ограничениями-неравенствами служат неравенства
(15)
${{t}_{0}} < {{t}_{1}},\,\,\,\,{{t}_{1}} < {{t}_{2}},\,\,\,\,{{t}_{2}} < {{t}_{3}},\,\,\,\,{{t}_{3}} < {{t}_{4}},\,\,\,\,{{t}_{4}} < {{t}_{0}} + {{T}_{0}}.$В качестве оптимизируемого функционала мы выбрали квадратичный функционал $J = \sum\nolimits_{i = 1}^4 {{{{\left| {\Delta {{{\mathbf{v}}}_{i}}} \right|}}^{2}}} .$
Итак, мы привели основанное на классических подходах решение задачи о поддержании проективной круговой орбиты в линейной модели с возмущениями от силы сопротивления атмосферы. Именно в этих предположениях будет происходить обучение управляющих нейронных сетей, о которых подробно пойдет речь в следующем разделе. Моделирование работы этих нейронных сетей и управления будет производится в основной нелинейной модели движения (1).
4. УПРАВЛЯЮЩИЕ НЕЙРОННЫЕ СЕТИ
Резюмируем в виде алгоритма предложенный в предыдущем разделе метод расчета всех необходимых для управления формацией параметров.
1. В момент времени ${{t}_{0}}$ даны расстояние до первого аппарата ${{R}_{1}},$ его скорость ${{V}_{1}},$ разница фазовых векторов аппаратов в орбитальной системе координат $\Delta {{{\mathbf{x}}}_{{12}}} = {{{\mathbf{x}}}_{2}} - {{{\mathbf{x}}}_{1}},$ плотность атмосферы в точке, где расположен первый аппарат $\rho ,$ и баллистический коэффициент второго аппарата ${{\beta }_{2}}.$
2. На основании этих данных вычисляются большая полуось опорной орбиты ${{a}_{0}},$ скорость движения по опорной орбите ${{V}_{0}},$ среднее движение для опорной орбиты ${{n}_{0}},$ ее период ${{T}_{0}},$ невязка по большим полуосям аппаратов $\Delta {{a}_{0}}$ (10), изменение большой полуоси второго аппарата за период опорной орбиты $\Delta {{a}_{2}}$ (11), отношение площади к массе первого аппарата ${{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}$ (12) и дифференциальное ускорение торможения $\Delta F.$ Величины $\Delta {{a}_{2}},$ ${{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}$ и $\Delta F$ зависят от баллистического коэффициента ${{\beta }_{2}}$ второго аппарата.
3. Ставится задача оптимизации целевой функции ${{J}_{1}}$ или ${{J}_{2}}$ при ограничениях-равенствах (13), (14) и ограничениях-неравенствах (15). В результате решения оптимизационной задачи определяются моменты времени ${{t}_{1}},$ ${{t}_{2}},$ ${{t}_{3}},$ ${{t}_{4}}$ совершения импульсов скорости и сами импульсы $\Delta {{{\mathbf{v}}}_{1}},$ $\Delta {{{\mathbf{v}}}_{2}},$ $\Delta {{{\mathbf{v}}}_{3}},$ $\Delta {{{\mathbf{v}}}_{4}}.$
Оптимизационная задача решается с помощью метода последовательного квадратичного программирования, включающего метод активных множеств и линейный поиск. Для простоты моменты времени было решено зафиксировать и считать ${{n}_{0}}{{t}_{1}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6},$ ${{n}_{0}}{{t}_{2}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-0em} 3},$ ${{n}_{0}}{{t}_{3}} = {{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3},$ ${{n}_{0}}{{t}_{4}} = {{11\pi } \mathord{\left/ {\vphantom {{11\pi } 6}} \right. \kern-0em} 6},$ численные эксперименты показали, что выбор конкретных моментов времени слабо влияет на величину оптимизируемого функционала. Выбор других значений также возможен. Для фиксированных моментов времени необходимость в ограничениях-неравенствах отпадает.
Для управления движением первого аппарата предлагается использовать две управляющие сети. Одна сеть аппроксимирует отображение $[{{R}_{1}},{{V}_{1}},\Delta {\mathbf{x}},\rho ,{{\beta }_{2}}] \to [\Delta {{{\mathbf{v}}}_{1}},\Delta {{{\mathbf{v}}}_{2}},\Delta {{{\mathbf{v}}}_{3}},\Delta {{{\mathbf{v}}}_{4}}]$ и будет обозначаться как функция ${{{\mathbf{N}}}_{{{{\Delta }}{v}}}} = {{{\mathbf{N}}}_{{{{\Delta }}{v}}}}({\mathbf{s}}),$ ${\mathbf{s}} = [{{R}_{1}},{{V}_{1}},\Delta {\mathbf{x}},\rho ,{{\beta }_{2}}].$ Эта функция принимает на вход 10 параметров и выдает 12 параметров. Вторая управляющая сеть аппроксимирует отображение $[{{R}_{1}},{{V}_{1}},\Delta x,\rho ,{{\beta }_{2}}] \to {{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}$ и будет обозначаться как функция ${{N}_{{{A \mathord{\left/ {\vphantom {A m}} \right. \kern-0em} m}}}} = {{N}_{{{A \mathord{\left/ {\vphantom {A m}} \right. \kern-0em} m}}}}({\mathbf{s}}).$ Эта функция принимает на вход 10 параметров и выдает 1 параметр. Аппроксиматор отношения ${{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}$ выделяется в отдельную нейронную сеть для того, чтобы, с одной стороны, упростить аппроксимируемые отображения и тем самым повысить скорость их обучения, а также для того, чтобы выбрать ограниченную активационную функцию на выходном слое этой нейронной сети, так как отношение ${{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}$ может принимать значения в определенном интервале.
Выборка для обучения нейронных сетей ${{{\mathbf{N}}}_{{{{\Delta }}{v}}}}$ и ${{N}_{{{A \mathord{\left/ {\vphantom {A m}} \right. \kern-0em} m}}}}$ формировалась следующим образом. Сначала были случайным образом сформированы значения для входных переменных:
1. ${{R}_{1}} \in U({{R}_{{{\text{ref}}}}} - \Delta R,{{R}_{{{\text{ref}}}}} + \Delta R),$ $\Delta R = 10$ км,
2. ${{V}_{1}} \in U({{V}_{{{\text{ref}}}}} - \Delta V,{{V}_{{{\text{ref}}}}} + \Delta V),$ $\Delta V = 10$ м/с,
3. $\Delta {{{\mathbf{r}}}_{{12}}} \in U({{[ - \Delta r,\Delta r]}^{3}}),$ $\Delta r = 200$ м,
4. $\Delta {{{\mathbf{v}}}_{{12}}} \in U({{[ - \Delta {v},\Delta {v}]}^{3}}),$ $\Delta {v} = 0.2$ м/с,
5. $\rho \in U({{10}^{{ - 12}}},{{10}^{{ - 11}}})$ кг/м3,
6. ${{\beta }_{2}} \in U(0.01,0.04)$ м2/кг.
Здесь $U(a,b)$ означает равномерное распределение на интервале $[a,b],$ $U({{[a,b]}^{n}})$ означает равномерное распределение в гиперкубе ${{[a,b]}^{n}}.$ Для каждой реализации случайных величин было вычислено значение ${{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}$ и найдены оптимальные значения $\Delta {{{\mathbf{v}}}_{1}},$ $\Delta {{{\mathbf{v}}}_{2}},$ $\Delta {{{\mathbf{v}}}_{3}},$ $\Delta {{{\mathbf{v}}}_{4}}.$
Начальные приближения для импульсов скорости выбирались нулевыми векторами. В некоторых случаях оптимизационная процедура не сходилась. В обучающую выборку попадали только те выходы оптимизационной процедуры, которые сигнализировали о сходимости процесса, т.е. когда градиент функции Лагранжа по модулю не превышал ${{10}^{{ - 6}}}.$ В результате была сформирована выборка из 200 тысяч пар вход/выход.
Для обучения нейронных сетей использовалась библиотека Deep Learning Toolbox (Version 13.0) в среде Matlab (R2019b). Были проанализированы как неглубокие, так и глубокие нейронные сети прямого распространения с различным числом нейронов на скрытых слоях. Чтобы отличать нейронные сети с различным числом нейронов, мы будем называть нейронной сетью размера $m \times n$ нейронную сеть, у которой $n$ скрытых слоев и в каждом скрытом слое $m$ нейронов. Графы, которые образуют нейронные сети, являются полносвязными. На всех скрытых слоях активационной функцией был гиперболический тангенс $th(x).$ Другие широко применяемые активационные функции $max(x,0)$ и радиально-базисная функция во всех случаях дали худшую производительность и качество нейронной сети, чем функция $th(x).$ На выходном слое нейронной сети ${{{\mathbf{N}}}_{{{{\Delta }}{v}}}}$ активационная функция является тождественной функцией $\phi (x) = x,$ чтобы не вводить искусственным образом ограничения на выход. На выходном слое нейронной сети ${{N}_{{{A \mathord{\left/ {\vphantom {A m}} \right. \kern-0em} m}}}}$ взята активационная функция $th(x),$ так как эта величина имеет физические ограничения.
Обучение нейронных сетей выполнялось с помощью метода масштабируемых сопряженных градиентов (SCG). В качестве целевого функционала выбрано среднеквадратическое отклонение (MSE) выхода нейронных сетей от целевых значений. Перед обучением выборка была предварительно масштабирована таким образом, чтобы значения входных и целевых параметров лежали в интервале $[ - 1,1].$ Выборка делилась на три части – обучающую, валидационную и тестовую – в соотношении 70/15/15 (обучающая выборка содержит 140 000 элементов, валидационная и тестовая выборки – по 30 000 элементов). Обучение сетей прекращалось только в случае, когда улучшение функционала на валидационной части отсутствовало 50 эпох подряд.
Кроме MSE для оценки качества нейронных сетей ${{{\mathbf{N}}}_{{{{\Delta }}{v}}}}$ различного размера удобно использовать следующий показатель:
В табл. 2 приводятся результаты обучения нейронных сетей для различных архитектур. Также в таблице указаны значения $\mathop {{\text{MSE}}}\nolimits_{tr} ,$ $\mathop {{\text{MSE}}}\nolimits_{v} ,$ $\mathop {{\text{MSE}}}\nolimits_{test} $ среднеквадратичных ошибок, подсчитанных на обучающей, валидационной и тестовой частях выборки соответственно. Горизонтальная черта отделяет результаты для сетей с различным числом скрытых слоев.
Таблица 2.
Качество нейронных сетей ${{{\mathbf{N}}}_{{{{\Delta }}{v}}}}$ различных размеров. Цветами выделены отобранные недефектные и непереобученные сети. По результатам анализа выбрана сеть размера $90 \times 3,$ соответствующая строка выделена оранжевым цветом

Лучшая нейронная сеть отбиралась по следующему правилу. Во-первых, из рассмотрения были удалены все “дефектные” и переобученные нейронные сети, т.е. все сети, у которых ${{{\text{MS}}{{{\text{E}}}_{{test}}}} \mathord{\left/ {\vphantom {{{\text{MS}}{{{\text{E}}}_{{test}}}} {{\text{MS}}{{{\text{E}}}_{{tr}}}}}} \right. \kern-0em} {{\text{MS}}{{{\text{E}}}_{{tr}}}}} < 0.1$ и ${{{\text{MS}}{{{\text{E}}}_{{test}}}} \mathord{\left/ {\vphantom {{{\text{MS}}{{{\text{E}}}_{{test}}}} {{\text{MS}}{{{\text{E}}}_{{tr}}}}}} \right. \kern-0em} {{\text{MS}}{{{\text{E}}}_{{tr}}}}} > 10.$ Во-вторых, были удалены нейронные сети, для которых существуют другие нейронные сети одновременно с меньшими значениями ошибок ${\text{MS}}{{{\text{E}}}_{{tr}}},$ ${\text{MS}}{{{\text{E}}}_{{v}}},$ ${\text{MS}}{{{\text{E}}}_{{test}}}$ на обучающей, валидационной и тестовой частях выборки соответственно. В результате осталось пять нейронных сетей размера $100 \times 2,$ $60 \times 3,$ $80 \times 3,$ $90 \times 3$ и $100 \times 3$ (в табл. 2 соответствующие этим сетям строки выделены цветами). Далее мы объединили валидационную и тестовую части выборки (назовем ее тоже тестовой частью, а соответствующее значение ${\text{MSE}}$ обозначим за ${\text{MS}}{{{\text{E}}}_{{test}}}$) и для каждой нейронной сети получили значения ${\text{MS}}{{{\text{E}}}_{{tr}}}$ и ${\text{MS}}{{{\text{E}}}_{{test}}}.$ Мы исключили нейронную сеть размера $100 \times 3,$ так как по сравнению с другими сетями ${\text{MS}}{{{\text{E}}}_{{tr}}}$ у нее был незаметно лучше, а ${\text{MS}}{{{\text{E}}}_{{test}}}$ сильно хуже. В результате мы оставили только сеть размера $90 \times 3,$ так как для нее оба значения ${\text{MS}}{{{\text{E}}}_{{tr}}}$ и ${\text{MS}}{{{\text{E}}}_{{test}}}$ оказались меньше, чем у остальных сетей.
Итак, в результате анализа среднеквадратичных ошибок мы остановились на сети размера $90 \times 3.$ Именно эта сеть и будет участвовать по всех дальнейших расчетах. Судя по табл. 2, в 2.82% тестовых случаев относительная ошибка исполнения первого импульса превысила 10%. В 12.86% случаев относительная ошибка исполнения второго импульса превысила 10%. В 15.81% случаев относительная ошибка исполнения третьего импульса превысила 10%. И, наконец, в 8.57% случаев относительная ошибка исполнения четвертого импульса превысила 10%.
Что касается сети ${{N}_{{{A \mathord{\left/ {\vphantom {A m}} \right. \kern-0em} m}}}},$ ее качество, помимо ${\text{MS}}{{{\text{E}}}_{{tr}}},$ ${\text{MS}}{{{\text{E}}}_{{v}}},$ ${\text{MS}}{{{\text{E}}}_{{test}}},$ оценивалось аналогичным образом:
где индекс $i$ пробегает все тестовые элементы выборки, индекс $p$ означает выход нейронной сети, $t$ означает целевое значение. Результаты обучения нейронных сетей ${{N}_{{{A \mathord{\left/ {\vphantom {A m}} \right. \kern-0em} m}}}}$ различных размеров приведены в табл. 3.
Таблица 3.
Качество нейронных сетей ${{N}_{{{A \mathord{\left/ {\vphantom {A m}} \right. \kern-0em} m}}}}$ различных размеров. Оранжевым цветом выделена строка с сетью $80 \times 3,$ отобранной по результатам анализа качества

Лучшая нейронная сеть отбиралась тем же способом, что и сеть ${{{\mathbf{N}}}_{{{{\Delta }}{v}}}}{\text{:}}$ сначала были удалены дефектные и переобученные сети, потом все сети, для которых были найдены сети лучше по всем показателям ${\text{MS}}{{{\text{E}}}_{{tr}}},$ ${\text{MS}}{{{\text{E}}}_{{v}}},$ ${\text{MS}}{{{\text{E}}}_{{test}}}.$ Объединять тестовую и валидационную выборку не пришлось, в результате этих двух шагов была обнаружена лучшая сеть – она имеет размер $80 \times 3.$ Как следует из табл. 3, для этой сети относительная ошибка определения ${{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}$ на тестовой части выборки превысила $0.001\% $ только в $3.54\% $ случаев.
5. АДАПТАЦИЯ НЕЙРОННЫХ СЕТЕЙ
Перейдем к процессу адаптации управления к различным значениям баллистического коэффициента ${{\beta }_{2}}$ второго аппарата.
Движение космических аппаратов моделируется согласно уравнениям движения (1). Процесс моделирования состоит из двух циклов: внешнего (эпизоды) и внутреннего (шаги). Каждый эпизод начинался со случайно сгенерированного состояния ${\mathbf{s}} = [{{R}_{1}},{{V}_{1}},\Delta {\mathbf{x}},\rho ,{{\beta }_{2}}],$ где значение баллистического коэффициента ${{\beta }_{2}}$ является оценкой истинного и неизвестного для первого аппарата баллистического коэффициента $\beta _{2}^{{{\text{true}}}}$ второго аппарата. Заметим, что плотность атмосферы $\rho $ мы берем здесь случайной величиной, равномерно распределенной на интервале $[{{10}^{{ - 12}}},{{10}^{{ - 11}}}]$ кг/м3. Это позволит нам, с одной стороны, не привязываться к конкретной модели атмосферы, а с другой стороны, – протестировать нейроуправление в более сложных условиях.
После инициализации состояния системы $s$ шла последовательность шагов, на каждом из которых в течение одного витка выполнялось маневрирование первого аппарата: управляющие нейронные сети выдавали требуемые ${{{{A}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}$ и импульсы скорости. Очередное маневрирование выполнялось сразу после завершения предыдущего маневрирования, хотя можно включить и пассивное движение аппаратов после маневрирования. В начале каждого шага параметры опорной орбиты пересчитывались: большая полуось, наклонение, долгота восходящего узла и истинная долгота брались равными соответствующим значениям для первого аппарата в конце интервала маневрирования, а эксцентриситет опорной орбиты полагался равным нулю.
Истинное значение баллистического коэффициента $\beta _{2}^{{{\text{true}}}}$ второго аппарата неизвестно первому аппарату. На вход ${{\beta }_{2}}$ для управляющих нейронных сетей подавалось фиксированное (тестовое) значение. Для того чтобы понять, насколько хорошо подходит выбранное тестовое значение ${{\beta }_{2}},$ мы накапливали статистику – евклидову норму вектора $\Delta \,\, = \,\,[{{\rho }_{x}}\,\, - \,\,{{{{R}_{{{\text{PCO}}}}}} \mathord{\left/ {\vphantom {{{{R}_{{{\text{PCO}}}}}} 2}} \right. \kern-0em} 2},\,\,{{\rho }_{y}},\,\,{{\rho }_{z}}\,\, - \,\,{{R}_{{{\text{PCO}}}}},\,\,sin{{\alpha }_{x}}\,\, - \,\,sin{{\alpha }_{z}},$ $cos{{\alpha }_{x}} - cos{{\alpha }_{z}}],$ где ${{\rho }_{x}},$ ${{\rho }_{y}},$ ${{\rho }_{z}},$ ${{\alpha }_{x}},$ ${{\alpha }_{z}}$ – параметры относительной орбиты, на которой оказался второй аппарат в результате маневрирования первого аппарата. Эти числа рассчитывались по формулам (5).
Итак, пусть в результате моделирования эпизодов и шагов была собрана выборка из $\left| {{{\Delta }_{i}}} \right|,$ $i = 1, \ldots ,K,$ объема $K.$ Мерой качества управления с выбранным значением ${{\beta }_{2}}$ мы считаем выборочное среднее $\Delta ({{\beta }_{2}}) = \frac{1}{K}\sum\nolimits_{i = 1}^K {\left| {{{\Delta }_{i}}({{\beta }_{2}})} \right|} .$
Задача адаптации управления к истинному значению ${{\beta }_{2}}$ ставится как одномерная оптимизационная задача $\Delta \to mi{{n}_{{{{{{\beta }}}_{2}}}}}.$ Предполагается, что аппарат будет решать эту оптимизационную задачу в режиме полета, поэтому схема оптимизации должна быть по возможности наиболее простой с вычислительной точки зрения.
Численные эксперименты показали, что эту задачу можно решать неградиентным методом оптимизации Хука–Дживса (pattern search, [26]). Ниже приводится алгоритм оптимизационной процедуры.
1. Выбрать какое-либо значение ${{\beta }_{2}}$ из области значений, на которой обучались нейронные сети. В нашем случае это был интервал $[0.01,0.04]$ м$^{2}$/кг.
2. Провести моделирование полета аппаратов с фиксированным значением ${{\beta }_{2}}$ на входе в управляющие нейронные сети. Подавать на вход управляющим нейронным сетям случайное значение плотности атмосферы, распределенное равномерно на интервале $[{{10}^{{ - 12}}},{{10}^{{ - 11}}}]$ кг/м3. Сформировать выборку из $\left| {{{\Delta }_{i}}} \right|,$ $i = 1, \ldots ,K,$ невязок по параметрам относительной орбиты и вычислить выборочное среднее $\Delta ({{\beta }_{2}}) = \tfrac{1}{K}\sum\nolimits_{i = 1}^K {\left| {{{\Delta }_{i}}({{\beta }_{2}})} \right|} .$
3. Выполнить пункт 2 для соседних значений ${{\beta }_{2}} - \delta {{\beta }_{2}}$ и ${{\beta }_{2}} + \delta {{\beta }_{2}},$ где ${{\delta }_{2}}$ можно выбрать, например, равной 0.01. Вычислить таким образом значения $\Delta ({{\beta }_{2}} - \delta {{\beta }_{2}})$ и $\Delta ({{\beta }_{2}} + \delta {{\beta }_{2}}).$
4. В качестве нового значения ${{\beta }_{2}}$ выбрать то значение из ${{\beta }_{2}} - \delta {{\beta }_{2}},$ ${{\beta }_{2}}$ и ${{\beta }_{2}} + \delta {{\beta }_{2}},$ для которого функционал $\Delta $ оказался минимальным. Если таковым оказалось значение $\Delta ({{\beta }_{2}}),$ то шаг $\delta {{\beta }_{2}}$ уменьшается, например, в 2 раза и пункты и 4 выполняются заново. Иначе перейти к пункту 2.
Расчеты прекращаются, если $\delta {{\beta }_{2}} < \varepsilon ,$ где $\varepsilon $ можно взять, например, равным ${{10}^{{ - 3}}}$ м2/кг. Заметим, что в случаях, когда $\delta {{\beta }_{2}}$ не меняется, а ${{\beta }_{2}}$ все время только увеличивается или только уменьшается, то получаются значения функционала $\Delta $ на равномерной сетке. Память значений на этой сетке функционала позволяет не проводить моделирование в уже рассмотренных узлах сетки.
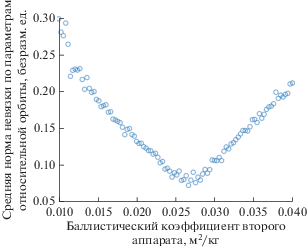
На рис. 1 приведен график функции $\Delta ({{\beta }_{2}})$ на равномерной сетке из 100 значений. Число используемых для расчета эпизодов и шагов равнялось 50. Негладкость функции объясняется тем, что в процессе моделирования используются случайные величины.
В табл. 4 приводятся итерации метода оптимизации для случая, когда $\beta _{2}^{{{\text{true}}}} = 0.03$ м2/кг, начальное значение ${{\beta }_{2}} = 0.015$ м2/кг, начальный шаг $\delta {{\beta }_{2}} = 0.01$ м2/кг, критерием остановки служило значение $\varepsilon = 0.001$ м2/кг, число эпизодов равно 30, число шагов в каждом эпизоде равно 20. В случаях, когда необходимо было обновить шаг $\delta {{\beta }_{2}},$ он уменьшался в 2 раза. Всего было выполнено 8 итераций. Табл. 4 показывает, как быстро происходит сходимость процедуры: после первой итерации получается решение, которое отличается от точного (0.03 м2/кг) на 0.005 м2/кг. После 4 итераций решение отличается от точного на 0.0025 м2/кг.
Таблица 4.
Итерации во время адаптации значения ${{\beta }_{2}}$ в случае, когда $\beta _{2}^{{{\text{true}}}} = 0.03$ м2/кг, начальное значение ${{\beta }_{2}} = 0.015$ м2/кг, начальный шаг $\delta {{\beta }_{2}} = 0.01$ м2/кг. Критерием остановки служило значение $\varepsilon = 0.001$ м2/кг, число эпизодов равно 30, число шагов в каждом эпизоде равно 20
| Номер итерации |
${{\beta }_{2}}$, м$^{2}$/кг | $\delta {{\beta }_{2}}$, м$^{2}$/кг | $\Delta ({{\beta }_{2}} - \delta {{\beta }_{2}})$ | $\Delta ({{\beta }_{2}})$ | $\Delta ({{\beta }_{2}} + \delta {{\beta }_{2}})$ |
|---|---|---|---|---|---|
| 1 | 0.0150 | 0.0100 | 0.38645 | 0.19621 | 0.09407 |
| 2 | 0.0250 | 0.0100 | 0.19631 | 0.09407 | 0.16965 |
| 3 | 0.0250 | 0.0050 | 0.15086 | 0.09407 | 0.10525 |
| 4 | 0.0250 | 0.0025 | 0.12432 | 0.09407 | 0.08629 |
| 5 | 0.0275 | 0.0025 | 0.10068 | 0.08629 | 0.10016 |
| 6 | 0.0275 | 0.0013 | 0.08722 | 0.08629 | 0.10426 |
| 7 | 0.0275 | 0.0006 | 0.08597 | 0.08629 | 0.09406 |
| 8 | 0.0269 | 0.0006 | 0.08810 | 0.08597 | 0.09344 |
На рис. 2 показано распределение нормы вектора невязки по параметрам относительной орбиты, когда оптимизация проводилась для случая ${{\beta }_{2}} = 0.015$ м2/кг (до адаптации) и ${{\beta }_{2}} = 0.0269$ м2/кг (после адаптации). Гистограммы же построены для более объемной выборки – когда число эпизодов и число шагов в каждом из них равно 50. Видно, что доля случаев, когда невязка велика (скажем, 0.25), уменьшилась, а доля случаев, когда невязка мала, – увеличилась.
Рис. 2.
Во время оптимизации число эпизодов равно 30, число шагов в каждом эпизоде равно 20. Оценка распределения до оптимизации (красное) и после оптимизации (синяя) выполняется на 50 эпизодах и 50 шагах в каждом эпизоде.

Число эпизодов и число шагов являются свободными параметрами метода. Эти числа должны быть достаточно велики, чтобы получить репрезентативную выборку невязок по параметрам относительной орбиты и устойчивое значение среднего $\Delta .$ Впрочем, выбор меньших их значений тоже может привести к решению, близкому к истинному значению $\beta _{2}^{{{\text{true}}}}.$ Например, в табл. 5 можно найти примеры итераций для случая, когда число эпизодов и число шагов в каждом из них равно 10. Это значит, что для сбора статистики и оценки $\Delta $ требуется порядка 100 витков вдоль опорной орбиты, т.е. порядка 6.4 дней. Учитывая, что число итераций метода равно 8 и на каждой итерации приходится 1–2 раза собирать статистику, то на адаптацию в целом будет уходить от 50 до 100 дней. Рис. 3 показывает, как меняется распределение невязок по параметрам относительной орбиты до и после адаптации в этом случае. Как и раньше, гистограммы построены для более объемной выборки – когда число эпизодов и число шагов в каждом из них равно 50.
Таблица 5.
Итерации во время адаптации значения ${{\beta }_{2}}$ в случае, когда $\beta _{2}^{{{\text{true}}}} = 0.03$ м2/кг, начальное значение ${{\beta }_{2}} = 0.015$ м2/кг, начальный шаг $\delta {{\beta }_{2}} = 0.01$ м2/кг. Критерием остановки служило значение $\varepsilon = 0.001$ м2/кг, число эпизодов равно 10, число шагов в каждом эпизоде равно 10
| Номер итерации |
${{\beta }_{2}}$, м$^{2}$/кг | $\delta {{\beta }_{2}}$, м$^{2}$/кг | $\Delta ({{\beta }_{2}} - \delta {{\beta }_{2}})$ | $\Delta ({{\beta }_{2}})$ | $\Delta ({{\beta }_{2}} + \delta {{\beta }_{2}})$ |
|---|---|---|---|---|---|
| 1 | 0.0150 | 0.0100 | 0.36112 | 0.21124 | 0.08654 |
| 2 | 0.0250 | 0.0100 | 0.19902 | 0.08654 | 0.16229 |
| 3 | 0.0250 | 0.0050 | 0.17726 | 0.08654 | 0.13510 |
| 4 | 0.0250 | 0.0025 | 0.10291 | 0.08654 | 0.08343 |
| 5 | 0.0275 | 0.0025 | 0.08756 | 0.08343 | 0.09498 |
| 6 | 0.0275 | 0.0013 | 0.08434 | 0.08343 | 0.09998 |
| 7 | 0.0275 | 0.0006 | 0.07863 | 0.08343 | 0.09430 |
| 8 | 0.0269 | 0.0006 | 0.08785 | 0.07863 | 0.09508 |
Рис. 3.
Во время оптимизации число эпизодов равно 10, число шагов в каждом эпизоде равно 10. Оценка распределения до и после оптимизации как на рис. 2.

Гистограммы, показанные на рис. 2 и 3, очень похожи, это объясняется тем, что найденные оптимальные значение ${{\beta }_{2}}$ в обоих случаях оказались одинаковыми. Разница имеет место лишь потому, что во время оптимизации при моделировании были разные последовательности реализаций случайных величин, так как число эпизодов и число шагов отличались.
Отметим, наконец, что адаптация стала возможной даже для случая, когда рассматривался только один эпизод и 5 шагов. Результаты расчетов приводятся в табл. 6 и на рис. 4. Таким образом, для накопления статистики было достаточно сделать 5 витков по орбите. Это значит, что на весь процесс адаптации будет уходить порядка 2.5–5 дней. Кроме того, заметим, что малое число витков для накопления статистики может быть особенно важно на раннем этапе адаптации, чтобы как можно раньше попасть в область значений ${{\beta }_{2}},$ близких к истинному значению.
Таблица 6.
Итерации во время адаптации значения ${{\beta }_{2}}$ в случае, когда $\beta _{2}^{{{\text{true}}}} = 0.03$ м2/кг, начальное значение ${{\beta }_{2}} = 0.015$ м2/кг, начальный шаг $\delta {{\beta }_{2}} = 0.01$ м2/кг. Критерием остановки служило значение $\varepsilon = 0.001$ м2/кг, число эпизодов равно 1, число шагов в каждом эпизоде равно 5
| Номер итерации | ${{\beta }_{2}}$, м$^{2}$/кг | $\delta {{\beta }_{2}}$, м$^{2}$/кг | $\Delta ({{\beta }_{2}} - \delta {{\beta }_{2}})$ | $\Delta ({{\beta }_{2}})$ | $\Delta ({{\beta }_{2}} + \delta {{\beta }_{2}})$ |
|---|---|---|---|---|---|
| 1 | 0.0150 | 0.0100 | 0.32831 | 0.22958 | 0.12593 |
| 2 | 0.0250 | 0.0100 | 0.18645 | 0.12593 | 0.35300 |
| 3 | 0.0250 | 0.0050 | 0.13368 | 0.12593 | 0.32613 |
| 4 | 0.0250 | 0.0025 | 0.05039 | 0.12593 | 0.02982 |
| 5 | 0.0275 | 0.0025 | 0.08887 | 0.02982 | 0.07011 |
| 6 | 0.0275 | 0.0013 | 0.17544 | 0.02982 | 0.14247 |
| 7 | 0.0275 | 0.0006 | 0.09733 | 0.02982 | 0.04134 |
Рис. 4.
Во время оптимизации число эпизодов равно 1, число шагов равно 5. Оценка распределения до и после оптимизации как на рис. 2.

Качество полета можно улучшить, адаптируясь также к истинному неизвестному значению плотности атмосферы ${{\rho }^{{{\text{true}}}}}.$ Будем для простоты считать, что ${{\rho }^{{{\text{true}}}}}$ не зависит от времени, а на вход управляющим нейронным сетям подается тестовое фиксированное значение плотности атмосферы $\rho .$ В таком случае функционал $\Delta = \Delta ({{\beta }_{2}},\rho )$ становится функцией уже двух переменных. Задача адаптации управления к истинным значениям ${{\beta }_{2}}$ и $\rho $ ставится как двумерная задача оптимизации $\Delta \to mi{{n}_{{{{{{\beta }}}_{2}},{{\rho }}}}}.$ Эту задачу можно решать тем же неградиентным методом оптимизации Хука–Дживса, но в этом случае решение ищется уже не на отрезке, а на некотором прямоугольнике в двумерном пространстве. Алгоритм, приведенный выше для одномерной оптимизации, естественным образом обобщается на двумерный (и на любой многомерный) случай, для этого в окрестности каждого вектора $({{\beta }_{2}},\rho )$ на каждой итерации рассматриваются векторы $({{\beta }_{2}} - \delta {{\beta }_{2}},\rho ),$ $({{\beta }_{2}} + \delta {{\beta }_{2}},\rho ),$ $({{\beta }_{2}},\rho - \delta \rho ),$ $({{\beta }_{2}},\rho + \delta \rho ),$ где, как и раньше, $\delta {{\beta }_{2}}$ – шаг по значениям ${{\beta }_{2}},$ а $\delta \rho $ – шаг по значениям $\rho .$
На рис. 5 изображены значения $\Delta ({{\beta }_{2}},{{\rho }_{2}})$ нормы невязки по параметрам относительной орбиты для различных значений параметров ${{\beta }_{2}}$ и ${{\rho }_{2}}.$ Значения $\Delta ({{\beta }_{2}},{{\rho }_{2}})$ рассчитывались для случая, когда $\beta _{2}^{{{\text{true}}}} = 0.03$ м2/кг, ${{\rho }^{{{\text{true}}}}} = 8 \cdot {{10}^{{ - 12}}}$ кг/м3, число эпизодов и число шагов в каждом эпизоде равнялось 50. Хорошо видно, что минимальные значения этой функции сосредоточены в окрестности истинных значений параметров ${{\beta }_{2}}$ и ${{\rho }_{2}}.$
На рис. 6 показано распределение нормы невязки по параметрам относительной орбиты до и после адаптации для случая, когда число эпизодов и шагов равно 10. Моделирование проводилось для значений $\beta _{2}^{{{\text{true}}}} = 0.03$ м2/кг, ${{\rho }^{{{\text{true}}}}} = 8 \cdot {{10}^{{ - 12}}}$ кг/м3, начальные приближения для оптимизационной процедуры выбраны равными ${{\beta }_{2}} = 0.015$ м2/кг, $\rho = 5 \cdot {{10}^{{ - 12}}}$ кг/м3. Для верификации результатов гистограммы построены в результате моделирования 50 эпизодов и 50 шагов в каждом эпизоде. Видно, что адаптация существенно повышает точность управления и, более того, она становится даже выше, чем в случаях, когда плотность атмосферы не адаптируется (ср. с рис. 3).
Следует отметить, что адаптация одновременно двух параметров требует в 2–4 раза больше формирований выборки для невязки $\Delta .$ Кроме того, численные эксперименты показали, что объем выборки из $\Delta $ должен быть в несколько раз больше, чем объем выборки, достаточный для адаптации только коэффициента ${{\beta }_{2}}.$ Например, если взять один эпизод и 5 шагов, то результат адаптации не будет удовлетворительным. Поэтому время полета от момента начала адаптации к параметрам до конца увеличивается в десятки раз. Из рис. 5 видно, что если оценка плотности атмосферы отклонена от истинного значения не более чем на $2 \cdot {{10}^{{ - 12}}}$ кг/м3, то можно адаптировать только ${{\beta }_{2}}.$
ЗАКЛЮЧЕНИЕ
Перечислим основные выводы, которые следуют из проделанной работы.
Задачу построения нейроуправления формацией двух спутников на низких околоземных орбитах лучше выстраивать в рамках методов обучения с учителем, нежели в рамках методов обучения с подкреплением.
Хотя в некоторых задачах идея введения управляющей и прогнозирующей нейронных сетей является естественной, в данном случае эта идея оказалась неэффективной, так как коррекция весов нейронных сетей дестабилизирует управление. В приведенной работе есть только управляющие нейронные сети, а задача адаптации нейроуправления может быть эффективно решена как задача подбора входных параметров управляющих сетей, а не как задача коррекции весов этих сетей.
Чтобы добиться высокой точности аппроксимации нейронными сетями функции управления, потребовалось использовать глубокие нейронные сети – с числом скрытых слоев не менее 3.
Средняя невязка попадания на номинальную относительную орбиту (проективную круговую) оказалась унимодальной функцией баллистического коэффициента неуправляемого аппарата и плотности атмосферы, рассматриваемых как входы в управляющие нейронные сети. Задачу адаптации (как оптимизационную задачу) можно решать неградиентными методами.
Удовлетворительные результаты адаптации получаются даже в случае, когда адаптируется только баллистический коэффициент второго аппарата: на сбор статистики о точности попадания на номинальную орбиту требуется около 8 ч, а вся процедура адаптации занимает от 2.5 до 5 дней. Лучше результаты адаптации получатся в случае, если адаптируются оба параметра – баллистический коэффициент и плотность атмосферы. Однако время для сбора статистики требуется увеличить в десятки раз.
Работа выполнена при поддержке Министерства науки и высшего образования Российской Федерации (Соглашение №075-15-2020-808).
Список литературы
Вьюгин В.В. Математические основы машинного обучения и прогнозирования. М.: МЦНМО, 2014.
Саттон Р.С., Барто Э.Г. Обучение с подкреплением. М.: БИНОМ. Лаборатория знаний, 2011.
KrishnaKumar K., Rickard S., Bartholomew S. Adaptive neuro-control for spacecraft attitude control // Neurocomputing. 1995. V. 9. № 2. P. 131–148. https://doi.org/10.1016/0925-2312(94)00062-W
Biggs J.D., Fournier H. Neural-Network-Based Optimal Attitude Control Using Four Impulsive Thrusters // J. Guidance, Control, and Dynamics. 2020. V. 43. № 2. P. 299–309. https://doi.org/10.2514/1.G004226
Wright W.A. Stochastic tuning of a spacecraft controller using neural networks // Engineering Applications of Artificial Intelligence. 1995. V. 8. № 6. P. 651–656. https://doi.org/10.1016/0952-1976(95)00043-7
Domingo V., Fleck B., Poland A.I. SOHO: The Solar and Heliospheric Observatory // Space Science Reviews. 1995. V. 72. № 1. P. 81–84. https://doi.org/10.1007/BF00768758
Сорокин А.В., Широбоков М.Г. Коррекция и прогнозирование орбитального движения космических аппаратов с помощью искусственных нейронных сетей. Препринты ИПМ им. М.В. Келдыша. 2018. № 198. С. 28. https://doi.org/10.20948/prepr-2018-198
Сорокин А.В., Широбоков М.Г. Разработка нейронных сетей для управления орбитальным движением космического аппарата с двигателем малой тяги. Препринты ИПМ им. М.В. Келдыша. 2018. № 269. С. 31. https://doi.org/10.20948/prepr-2018-269
Cheng L., Wang Z., Jiang F. et al. Real-Time Optimal Control for Spacecraft Orbit Transfer via Multiscale Deep Neural Networks // IEEE Transactions on Aerospace and Electronic Systems. 2018. V. 55. № 5. P. 2436–2450. https://doi.org/10.1109/TAES.2018.2889571
Cheng L., Wang Z., Jiang F. Real-time control for fuel-optimal Moon landing based on an interactive deep reinforcement learning algorithm // Astrodynamics. 2019. V. 3. № 4. P. 375–386. https://doi.org/10.1007/s42064-018-0052-2
Gurfil P., Idan M., Kasdin N.J. Adaptive Neural Control of Deep-Space Formation Flying // J. Guidance, Control, and Dynamics. 2003. V. 26. № 3. P. 491–501. https://doi.org/10.2514/2.5072
Bae J., Kim Y. Adaptive controller design for spacecraft formation flying using sliding mode controller and neural networks // J. Franklin Institute. 2012. V. 349. № 2. P. 578–603. https://doi.org/10.1016/j.jfranklin.2011.08.009
Dachwald B. Optimization of Interplanetary Solar Sailcraft Trajectories Using Evolutionary Neurocontrol // J. Guidance, Control, and Dynamics. 2004. V. 27. № 1. P. 66–72. https://doi.org/10.2514/1.9286
Dachwald B. Optimization of very-low-thrust trajectories using evolutionary neurocontrol // Acta Astronautica. 2005. V. 57. № 2–8. P. 175–185. https://doi.org/10.1016/j.actaastro.2005.03.004
Dachwald B., Ohndorf A. 1st ACT global trajectory optimisation competition: Results found at DLR // Acta Astronautica. 2007. V. 61. № 9. P. 742–752. https://doi.org/10.1016/j.actaastro.2007.03.011
Carnelli I., Dachwald B., Vasile M. Evolutionary Neurocontrol: A Novel Method for Low-Thrust Gravity-Assist Trajectory Optimization // J. Guidance, Control, and Dynamics. 2009. V. 32. № 2. P. 616–625. https://doi.org/10.2514/1.32633
Izzo D., Märtens M., Pan B. A survey on artificial intelligence trends in spacecraft guidance dynamics and control // Astrodynamics. 2019. V. 3. № 4. P. 287–299. https://doi.org/10.1007/s42064-018-0053-6
Izzo D., Simões L.F., de Croon G.C.H.E. An evolutionary robotics approach for the distributed control of satellite formations // Evolutionary Intelligence. 2014. V. 7. P. 107–118. https://doi.org/10.1007/s12065-014-0111-9
Mohan S., Saenz-Otero A., Nolet S. et al. SPHERES flight operations testing and execution // Acta Astronautica. 2009. V. 65. № 7. P. 1121–1132. https://doi.org/10.1016/j.actaastro.2009.03.039
Gaudet B., Furfaro R. Adaptive pinpoint and fuel efficient mars landing using reinforcement learning // IEEE/CAA J. Automatica Sinica. 2014. V. 1. № 4. P. 397–411. https://doi.org/10.1109/JAS.2014.7004667
Furfaro R., Wibben D.R., Gaudet B. et al. Terminal Multiple Surface Sliding Guidance for Planetary Landing: Development, Tuning and Optimization via Reinforcement Learning // J. Astronautical Sciences. 2015. V. 62. № 1. P. 73–99. https://doi.org/10.1007/s40295-015-0045-1
Jiang X., Li S., Furfaro R. Integrated guidance for Mars entry and powered descent using reinforcement learning and pseudospectral method // Acta Astronautica. 2019. V. 163. P. 114–129. https://doi.org/10.1016/j.actaastro.2018.12.033
Gaudet B., Linares R., Furfaro R. Deep Reinforcement Learning for Six Degree-of-Freedom Planetary Landing // Advances in Space Research. 2020. V. 65. № 7. P. 1723–1741. https://doi.org/10.1016/j.asr.2019.12.030
Gaudet B., Linares R., Furfaro R. Adaptive guidance and integrated navigation with reinforcement meta-learning // Acta Astronautica. 2020. V. 169. P. 180–190. https://doi.org/10.1016/j.actaastro.2020.01.007
CIRA-2012: COSPAR international reference atmosphere – 2012. Models of the Earth’s Upper Atmosphere. 2012. P. 20–24. https://spaceweather.usu.edu/ files/chapters_1_3.pdf
Hooke R., Jeeves T.A. “Direct search” solution of numerical and statistical problems // J. ACM. 1961. V. 8. № 2. P. 212–229. https://doi.org/10.1145/321062.321069
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования