Космические исследования, 2022, T. 60, № 2, стр. 167-178

ВВЕДЕНИЕ

Интерес к оптимальным перелетам с участками особого управления возник на самых ранних этапах исследований траекторий перелета космических средств [1, 2]. Он был обусловлен необходимостью исследования важного для практики вопроса о потребности в промежуточной тяге двигательной установки. Несмотря на то, что участки особого управления так и не были найдены на оптимальных траекториях [1–3], возможность появления особого управления требует дальнейшего изучения.

Основной инструментарий при оптимизации траекторий перелетов с малой тягой составляют численные методы, так как немногочисленные аналитические решения охватывают лишь отдельные варианты перелетов [4–6]. На практике используются как прямые [7], так и непрямые методы оптимизации траекторий перелетов [8].

В настоящей работе при оптимизации траекторий межорбитальных перелетов рассматривались только непрямые методы, использующие принцип максимума Понтрягина [9]. При этом в расчетах использовались методы численного интегрирования Рунге–Кутты–Фельберга 7(8) и Рунге–Кутты–Дормана–Принса 7(8) для решения систем дифференциальных уравнений движения КА [10]. Использование принципа максимума Понтрягина позволяет привести вариационную краевую задачу к задаче математического программирования [11] или, другими словами, к задаче оптимизации функции (невязки) нескольких переменных (неизвестных начальных значений сопряженных переменных), которая решалась методами Ньютона и градиентного спуска. Такой подход к оптимизации траекторий перелета предполагает наличие итерационного процесса, последовательно уменьшающего невязку до заданной величины.

Ниже представлены примеры различных перелетов с малой тягой, где итерационный процесс решения сталкивается с вычислительными трудностями. Эти трудности могут быть обусловлены появлением особых точек (точек вырождения базис-вектора Лоудена или касания нулевого уровня функцией переключения). Использование численных методов интегрирования приводит к тому, что в малой окрестности появления особых точек законы управления интерполируются, и появляется методическая погрешность при расчете траектории перелета. Исключение составляют случаи, когда особые точки совпадают с узлами численного интегрирования. При вырождении базис-вектора Лоудена такая ситуация должна приводить к аварийному останову программы расчета. Однако, практика расчетов показывает, что аварийный останов программы расчетов не встречается и не может служить индикатором особых точек.

Методическая погрешность в решении задачи Коши приводит к появлению случайной ошибки в определении невязки. Величина этой ошибки существенным образом зависит от места появления особых точек (чем ближе к началу траектории, тем большее влияние оказывается на величину невязки). Это, в свою очередь, приводит к характерному поведению процесса сходимости – выходу невязки на некоторый уровень, после которого происходит отказ методов решения краевой задачи. Большинство приведенных далее примеров задач характеризуются этим свойством. Причем в рассмотренных задачах в окрестности траектории решенной краевой задачи с хорошим процессом сходимости особых точек, как правило, не наблюдается и, наоборот, плохая сходимость (отказ методов) является признаком их наличия.

Может создаться иллюзия, что применение прямых методов оптимизации траекторий перелета с малой тягой позволяет избавиться от проблемы (и, таким образом, это является еще одним из достоинств прямых методов перед непрямыми). Однако, согласно [12], особые точки можно рассматривать как точки траектории, где вариация критерия качества нечувствительна к любым вариациям управления. Таким образом, при приближении к оптимальной траектории с появлением особых точек даже при использовании прямых методов оптимизации не гарантировано отсутствие вычислительных трудностей. Их наличие отмечается, например, в работе [13], где рассматривается перелет между низкой круговой и вытянутой эллиптической с низким перицентром околоземными орбитами, если эксцентриситет целевой орбиты превышает величину 0.9.

1. МЕТОДИЧЕСКИЙ ПОДХОД К ОПТИМИЗАЦИ ТРАЕКТОРИЙ ПЕРЕЛЕТА

Общий методический подход к рассматриваемым задачам определения траектории движения центра масс КА приведен ниже. Для простоты выражения приведены в векторном виде. В расчетах использовались для разных перелетов декартова и сферическая [4] системы координат, а также равноденственные элементы [8].

В первых пяти примерах рассматривалась задача быстродействия, то есть минимизируемый функционал ${{J}_{1}}{\text{:}}$ ${{J}_{1}} = T,$ где $T$ – продолжительность перелета.

В последнем примере рассматривалась задача максимизации конечной массы $m$ при заданной продолжительности перелета $\tilde {T}$ (минимизируемый функционал ${{J}_{2}}$):${{J}_{2}} = - m(T),$ $T = \tilde {T}.$

Уравнения движения центра масс КА (безразмерные) могут быть записаны в виде

где $r$ – радиус-вектор КА; $V$ – вектор скорости КА; $a$ – вектор ускорения от тяги двигательной установки (ДУ) с модулем $a$ и направлением, определяемым единичным вектором $e;$ $\delta $ – функция включения/выключения (принимает значения: 1 – ДУ включена, 0 – ДУ выключена); ${{a}_{{возм}}}$ – вектор возмущающих ускорений; $\dot {\tilde {m}}$ – расход рабочего тела.

Расход рабочего тела $\dot {\tilde {m}}$ и величина ускорения $a$ могут быть определены через удельный импульс тяги ДУ ${{I}_{{{\text{уд}}}}}$ и начальное ускорение ${{a}_{0}}$ следующим образом (при выборе начальной массы в качестве характерной для обезразмеривания): $\dot {\tilde {m}} = \frac{{{{a}_{0}}}}{{{{I}_{{{\text{уд}}}}}g}},$ $a = \frac{{{{a}_{0}}}}{m},$ где $g$ – стандартное ускорение свободного падения.

Рассмотренные далее примеры перелетов рассчитывались применительно к центральному ньютоновскому гравитационному полю (то есть ${{a}_{{возм}}}$ = 0), кроме перелетов с окололунной орбиты на околоземную (учитывались притяжение Земли и Луны на всей траектории перелета; математическая модель описана в работе [14]) и с околоземной орбиты на околомарсианскую (учитывалось притяжение Солнца, Земли и Марса; подробности в работе [15]).

Тяга ДУ и удельный импульс тяги полагались постоянными в течение всего перелета.

Сопряженная система дифференциальных уравнений:

Здесь под обозначением $\frac{{\partial {{a}_{{возм}}}}}{{\partial {\mathbf{R}}}}$ понимаются соответствующие производные компонентов вектора возмущающего ускорения по компонентам радиус-вектора (для центрального ньютоновского гравитационного поля равны нулю).

В соответствии с принципом максимума Понтрягина можно определить закон управления [9, 11, 12]:

Для задачи быстродействия (функционал ${{J}_{1}}$) $\delta = 1$ на всей траектории движения [16]. В случае функционала ${{J}_{2}}{\text{:}}$ $\delta = \left\{ {\begin{array}{*{20}{c}} {1,}&{\Delta > {\text{0}}} \\ {0,}&{\Delta < {\text{0}}} \end{array}} \right.,$ где функция переключения $\Delta $ определяется как $\Delta = a{{p}_{V}} - \dot {\tilde {m}}{{p}_{m}}.$

Ситуация невозможности определения законов управления на некотором интервале времени с использованием теоремы принципа максимума Понтрягина в случае ${{p}_{V}}$ = 0 или, при равенстве нулю функции переключения $\Delta $, известна как случаи особого управления. При нулевом интервале времени такие ситуации можно определить как особые точки. Для ненулевых участков особого управления известны условия, позволяющие определять оптимальные законы управления [12].

В рассмотренных далее примерах межорбитальных перелетов с ДУ малой тяги обнаружено появление именно особых точек. Так как для решения системы дифференциальных уравнений движения и им сопряженных использовались методы численного интегрирования (Рунге–Кутты–Фельберга и Рунге–Кутты–Дормана–Принса, оба 7(8) порядков [10]), определение направления вектора тяги $e$ производится в узлах интегрирования, а типичный случай вырождения базис-вектора Лоудена между узлами ведет к интерполяции закона управления вектором тяги с квазислучайной ошибкой, величина которой, видимо, определяется длиной шага интегрирования (расстоянием между узлами интегрирования) и близостью узла интегрирования к особой точке. Появление ошибки в определении закона управления ведет к возмущению траектории перелета. Аналогичный эффект возникает при появлении (исчезновении) почти мгновенных включений ДУ при касании функции переключения $\Delta $ нулевой линии уровня.

Для определения направления вектора тяги через орбитальные элементы вместо базис-вектора Лоудена ${{{\mathbf{p}}}_{{\mathbf{V}}}}$ можно использовать его аналог в орбитальной системе координат – вектор $A$ с компонентами (${{A}_{{{\tau }}}},$ ${{A}_{r}},$ ${{A}_{n}}$) в обозначениях работы [8]. Примечательно, что найденные вырождения базис-вектора Лоудена происходят вне зависимости от выбора системы координат для расчетов (как в декартовых, так и в сферических координатах, а также в равноденственных орбитальных элементах) и по времени совпадают с вырождением вектора $A.$ Это демонстрирует проверка с использованием канонических преобразований [17, 18].

Практика расчетов показывает, что применительно к нулю функции переключения вычислительные проблемы, связанные с определением закона управления $\delta ,$ возникают, только если функция переключения $\Delta $ касается, а не пересекает ось. В этом случае неопределенным является наличие на траектории почти мгновенного включения ДУ.

Краевые условия и характеристики ДУ в примерах перелетов, приведенных далее, различны и поэтому конкретизируются при описании каждой задачи.

Решение краевой задачи сводилось к задаче отыскания корней функции (невязки) [11], задаваемой через интегрирование дифференциальных уравнений движения и сопряженных. Непосредственно краевые условия или условия трансверсальности на их основе составляли невязку, неизвестными выступали начальные значения сопряженных, а в некоторых случаях и фазовых переменных. Для минимизации невязки на каждой итерации использовались методы Ньютона [4] и градиентного спуска (выбор метода на каждой итерации определялся из условия минимизации нормы составляющих невязки). Расчет матрицы Якоби и вектора градиента проводился с использованием формулы центральной разности.

Появление квазислучайных возмущений на траектории перелета из-за появления особых точек, как правило, ведет к квазислучайным возмущениям невязки, что обуславливает отказ обоих используемых методов решения краевой задачи по достижению определенного уровня величины нормы невязки.

2. ПЕРЕЛЕТ С НИЗКОЙ КРУГОВОЙ ОРБИТЫ НА ОРБИТУ ТИПА “МОЛНИЯ”

Рассматривался компланарный перелет с круговой околоземной орбиты радиусом 6671 км на полусуточную орбиту с радиусами апоцентра и перицентра 46 452 и 6671 км, соответственно. Начальное ускорение принято равным 10^–4 м/с², а удельный импульс тяги – 2000 с. В качестве функционала выбран ${{J}_{1}}$ (задача быстродействия). Система координат для дифференциальных уравнений движения принята в равноденственных элементах [8]. В качестве характерного расстояния выбрана величина 6671 км (для обезразмеривания, аналогично работе [4]), характерная масса принималась равной массе на левом конце траектории.

Начальная точка выбиралась со свободным значением истинной долготы. На правом конце траектории перелета аргумент перицентра принимался нулевым, а значение истинной долготы – свободным (то есть из условий трансверсальности ${{p}_{F}}$ = 0). Расчет проводился из конечной точки траектории в начальную с положительным расходом (нарастанием) массы. Компоненты невязки $S$ (выражены в равноденственных элементах, обозначения как в работе [8]) следующие (тильдой отмечены заданные значения):

$\tilde {h}$ = 1, $\tilde {m}$ = 1 согласно принятому обезразмериванию.

Неизвестные краевой задачи (на правом конце): ${{p}_{h}},$ ${{p}_{{{{e}_{x}}}}},$ ${{p}_{{{{e}_{y}}}}},$ $F,$ $m.$

Неизвестная продолжительность перелета при каждом расчете траектории (интегрировании уравнений движения и сопряженных) определялась из условия минимума нормы невязки (интервал интегрирования фиксировался). Такой подход представляет собой двухстадийную оптимизацию невязки (первая стадия – на этапе решения задачи Коши, вторая – на этапе применения метода минимизации функции $S$). Общераспространенный альтернативный подход – включение продолжительности перелета в состав неизвестных и использование различных форм нормировок сопряженных переменных для исключения одной из сопряженных из числа неизвестных краевой задачи.

Результаты различных попыток решить поставленную таким образом краевую задачу, в том числе с другими значениями начального ускорения и удельного импульса тяги, демонстрируют отказ методов Ньютона и градиентного спуска при достижении компонентов невязки достаточно малых значений (по радиусам апоцентра и перицентра – менее километра; по массе – менее тысячной доли процента; изменение характеристической скорости для различных решений менее одного м/с). Решению соответствуют следующие значения неизвестных краевой задачи: ${{p}_{h}}$ = –1.00000002, ${{p}_{{{{e}_{x}}}}}$ = = –10.36083482, ${{p}_{{{{e}_{y}}}}}$ = –0.00036115, $F$ = –4.30907220, $m$ = 0.7538, $T$ = 558.9 сут.

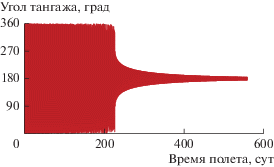
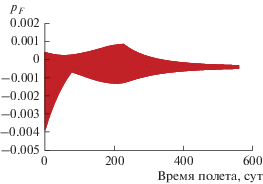
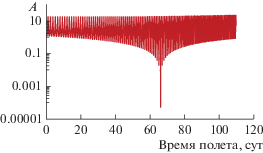
Характер поведения радиусов апоцентра и перицентра полученной траектории по времени полета проиллюстрирован на рис. 1. На рис. 2 показаны соединенные линией расчетные значения в каждом узле интегрирования угла тангажа в зависимости от времени полета, а на рис. 3 и 4 аналогичным образом построены зависимости ${{p}_{F}}$ и величины $A$ от времени полета. Рис. 2–4 содержат зависимости, которые носят колебательный характер с периодом много меньше изображенного интервала времени. Вследствие этого линии зависимостей сливаются в практически полностью заштрихованные области, иллюстрирующие лишь колебательные амплитуды.

Из сопоставления представленных на рис. 1–4 зависимостей видно, что в момент времени полета около 220 сут происходит смена структуры закона управления вектором тяги. Этому же моменту времени соответствует начало уменьшения радиуса перицентра, изменение структуры зависимости угла тангажа, изменение характера зависимости ${{p}_{F}}$ и уменьшение $A$ до малого значения (фактически вырождение). Последнее иллюстрирует особую точку.

Определенный интерес представляет зависимость ${{p}_{F}}$ по времени полета, иллюстрирующая неравенство нулю в начале траектории (невыполнение условия трансверсальности). Попытки найти траекторию, обеспечивающую выполнение условий трансверсальности в начале траектории, оказались безуспешными.

3. ПЕРЕЛЕТ МЕЖДУ ВЫТЯНУТЫМИ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ С НИЗКИМ ПЕРИЦЕНТРОМ

Исследовался компланарный перелет с ДУ малой тяги между эллиптическими орбитами со следующими радиусами апоцентра и перицентра: начальная орбита – 62 932 и 6671 км, конечная орбита – 100 000 и 6671 км. Начальное ускорение, удельный импульс тяги, а также методический подход приняты аналогичными рассмотренному ранее перелету на орбиту типа “Молния”.

Некоторые отличия содержатся в постановке краевой задачи и краевых условиях. Значение истинной долготы на левом конце принималось свободным, конечное значение F_K включалось в вектор неизвестных краевой задачи. Для решения краевой задачи применялась нормировка, при которой сопряженная $p_{h}^{K}$ (на правом конце) принималась равной минус единице. Вектор неизвестных краевой задачи (на правом конце, кроме продолжительности перелета Т, которая справа принимает значение 0): ($p_{{{{e}_{x}}}}^{K},$ $p_{{{{e}_{y}}}}^{K},$ F_K, m_K, T), где $p_{{{{e}_{x}}}}^{K}$ и $p_{{{{e}_{y}}}}^{K}$ – значения сопряженных переменных, F_K – значение истинной долготы, m_K – масса КА.

Компоненты невязки (рассчитывались на левом конце):

где ${{\tilde {h}}_{0}},{{\tilde {e}}_{0}}$ – заданные значения, соответствующие начальной (целевой) орбите, ${{p}_{{{{e}_{x}}}}},{{p}_{{{{e}_{y}}}}},{{p}_{F}}$ – сопряженные переменные в равноденственной системе координат, ${{\tilde {m}}_{0}}$ – заданное значение массы на начальной орбите. Третья и четвертая компоненты вектора невязки соответствуют условиям трансверсальности для свободной линии апсид и свободной угловой дальности [8].

Процесс решения поставленной краевой задачи выявил трудности с нахождением точного решения. Найденное решение характеризуется погрешностью по радиусам перицентра/апоцентра менее 1 км и погрешностью по массе менее 0.01%. Более точное решение не было получено из-за отказа как метода Ньютона, так и метода градиентного спуска. Величина А на траектории решения уменьшается до значения 10^–3. Однако в процессе оптимизации при вычислении шагов методов Ньютона и градиентного спуска периодически выявлялись траектории, характеризующиеся более значительным уменьшением параметра А (менее 10^–4). Таким образом, отказ методов оптимизации может быть связан с наличием в некоторой окрестности решения особых точек. В частности, при изменениях неизвестных относительно ранее найденной траектории по сопряженной ${{p}_{{{{e}_{x}}}}}$ на величину около 10^–2, по сопряженной ${{p}_{{{{e}_{y}}}}}$ на величину около 10^–4, по продолжительности на 0.5% и по массе на 1.4% было получено решение с уменьшением величины А до уровня порядка 4 ⋅ 10^–5. Погрешность решения при этом составила: по радиусу апоцентра 224 км, по радиусу перицентра 310 км; решению соответствуют следующие значения неизвестных краевой задачи: p_h = –1, ${{p}_{{{{e}_{x}}}}}$ = = –5.95629802, ${{p}_{{{{e}_{y}}}}}$ = –0.00077595, F_K = –3.23394357, m_K = 0.9361, T = 109.6 сут.

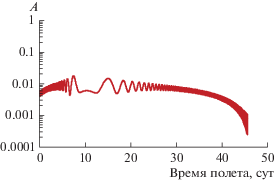
На рис. 5 приведена зависимость функции А (модуль аналога базис-вектора Лоудена в равноденственной системе) от времени полета. В точке, соответствующей примерно 66-м суткам полета, происходит снижение значения функции А до уровня примерно 4 ⋅ 10^–5. Этому же моменту времени соответствует изменение структуры управления по углу тангажа (см. рис. 6). Характер изменения радиусов перицентра и апоцентра приведен на рис. 7 и 8.

Необходимо отметить, что снижение перицентра начинается до момента времени, соответствующего минимальному значению А (возникновению особой точки). Это является отличием рассматриваемого межорбитального перелета от случая перелета на орбиту типа “Молния”.

4. ПЕРЕЛЕТ С НИЗКОЙ КРУГОВОЙ ОРБИТЫ НА ГЕОСТАЦИОНАРНУЮ

В работе [8] выявлено наличие неединственности семейств экстремалей при перелете с круговых орбит на ГСО. Отличительной особенностью экстремалей С-решения являются почти круговые орбиты в процессе перелета на ГСО, в отличие от экстремалей Е-решения, характеризующихся существенным эксцентриситетом орбит в процессе выведения на ГСО.

В той же работе [8] приведены зависимости оптимальных законов управления ориентацией вектора тяги с характерными участками и сменой структуры законов управления между ними для Е-решения. В моменты смены структуры управления угол рысканья достигает величины 90°, что говорит о том, что величины ${{A}_{{{\tau }}}}$ и ${{A}_{r}}$ приближаются к нулю. Характерная картина видна и в предыдущих примерах для компланарных перелетов – в моменты смены структуры законов управления происходит резкое уменьшение значения A, т.е. появляется особая точка.

Учитывая эти аналогии, были предприняты попытки спуска по величине наклонения стартовой круговой орбиты высотой 300 км для получения в конце Е-решения для компланарного перелета на ГСО, хотя в работе [8] утверждается, что с уменьшением наклонения начальной орбиты менее критического значения 47.3° Е-решение переходит в С-решение (в работе [19] также высказывается аналогичное утверждение с точностью до величины критического наклонения 36°, что может объясняться методическими различиями к оптимизации траекторий перелета).

Характеристики ДУ и КА, обезразмеривание и функционал (${{J}_{1}}$) были приняты как в предыдущих примерах межорбитальных перелетов. Краевые условия слева были приняты следующими: $\left( {h,{{e}_{x}},{{e}_{y}},{{i}_{x}},{{i}_{y}},F} \right)$ = $({{\tilde {h}}_{0}},0,0,tg\left( {{{\tilde {i}} \mathord{\left/ {\vphantom {{\tilde {i}} 2}} \right. \kern-0em} 2}} \right),0,0).$

Невязка была составлена из краевых условий справа.

Каждой величине истинной долготы $\tilde {F}$ из некоторого диапазона соответствует своя экстремаль (что показано в работе [20]), причем это справедливо как для семейства Е-решений, так и для семейства С-решений. В проводимых расчетах величина $\tilde {F}$ параметрировалась.

Продолжительность перелета определялась из минимума принятой невязки при каждом интегрировании уравнений движения, а неизвестными краевой задачи выступали начальные значения сопряженных переменных ${{p}_{h}},$ ${{p}_{{{{e}_{x}}}}},$ ${{p}_{{{{e}_{y}}}}},$ ${{p}_{{{{i}_{x}}}}},$ ${{p}_{{{{i}_{y}}}}},$ ${{p}_{F}}.$

Результаты расчетов показали, что если при наклонении 40° еще можно найти Е-решения (максимальный на траектории эксцентриситет ~0.05), то при наклонении 39° полученные решения уже нельзя отнести к Е-классу (максимальный на траектории эксцентриситет ~0.005).

Применительно к семейству С-решений такой подход позволил получить ряд экстремалей с нулевым наклонением начальной орбиты, отличающихся величиной $\tilde {F}.$ Следует заметить, что для компланарного перелета можно сократить размерность краевой задачи на два (отбрасываются из рассмотрения неизвестные ${{p}_{{{{i}_{x}}}}},$ ${{p}_{{{{i}_{y}}}}}$ и соответствующие компоненты невязки, а также среди переменных управления остается только угол тангажа). С-решение компланарного перелета на ГСО с $\tilde {F}$ = 1129400° демонстрирует рост величины $A$ в течение всего перелета, начиная с положительного значения. Таким образом, на этой траектории особых точек не обнаружено. Однако, при увеличении угловой дальности перелета $\tilde {F},$ траектория перелета претерпевает значительные изменения. В частности, уже при $\tilde {F}$ = 1300000° существует С-решение (со следующими значениями неизвестных краевой задачи: ${{p}_{h}}$ = –1.47397227, ${{p}_{{{{e}_{x}}}}}$ = –0.00687022, ${{p}_{{{{e}_{y}}}}}$ = 0.00889361, ${{p}_{F}}$ = 0.00030529, $T$ = 500.0 сут), траектория которого для обеспечения требуемой угловой дальности перелета сначала несколько снижает высоту орбиты, а только потом увеличивает (см. рис. 9). При этом, как показано на рис. 10, в законе управления ориентацией вектора тяги появляется характерная для особых точек смена структуры закона управления. В точке, соответствующей смене этой структуры, величина $A$ испытывает значительное уменьшение (рис. 11), что является признаком особых точек. Расчеты непосредственно в окрестности данной экстремали показывают, что несложно получить траекторию с более значительным уменьшением величины A.

В рассмотренном межорбитальном перелете на ГСО появление особой точки не проявилось в виде отказов методов решения краевых задач. Точность решенных краевых задач – по радиусам апоцентра и перицентра несколько сотен метров, по угловой дальности миллионные доли градуса.

Необходимо отметить, что увеличение угловой дальности перелета $\tilde {F}$ с 1 129 400° до 1 300 000° в настоящем примере малопродуктивно, так как связано с ростом энергетических затрат на перелет (потребная характеристическая скорость увеличивается с 4598 до 4880 м/с). Тем не менее приведенный пример появления особой точки в такой востребованной практикой задаче как перелет на ГСО важен для демонстрации типичности появления особых точек в межорбитальных перелетах с малой тягой.

5. ПЕРЕЛЕТ МЕЖДУ НИЗКИМИ КРУГОВЫМИ ОКОЛОЛУННОЙ И ОКОЛОЗЕМНОЙ ОРБИТАМИ

Рассматривался перелет между круговой окололунной орбитой высотой 100 км с наклонением 90° и круговой околоземной орбитой высотой 800 км с наклонением 51.6° (в качестве опорной плоскости принималась плоскость земного экватора). Оптимизация проводилась с одновременным учетом гравитационных полей Земли и Луны (ограниченная задача трех тел; модель эфемерид – EPM2008 [21]) при сквозном моделировании траектории перелета (то есть непрерывном расчете траектории перелета без введения дополнительных упрощений при переходе от селеноцентрической системы координат к геоцентрической) [14]. Дата старта – 22.VIII.2038. В качестве функционала выбран ${{J}_{1}}$ (задача быстродействия). Для расчета траекторий перелета использовалась система уравнений в равноденственных элементах [8]. В качестве характерного расстояния выбрана величина равная большой полуоси орбиты Луны 384 400 км (для обезразмеривания, аналогично работе [4]). При расчете траектории перелета величина истинной долготы $F(T)$ и положения линий апсид и узлов предполагались свободными.

В этом случае краевые условия будут иметь вид, согласно [8] (обозначения приняты как в работе [14]):

где $\tilde {h}_{{\text{л}}}^{0},$ $\tilde {e}_{x}^{{0{\text{л}}}},$ $\tilde {e}_{y}^{{0{\text{л}}}},$ $\tilde {i}_{x}^{{0{\text{л}}}},$ $\tilde {i}_{y}^{{0{\text{л}}}},$ ${{\tilde {F}}^{0}},$ $\tilde {h}_{{\text{з}}}^{k},$ $\tilde {i}_{{\text{з}}}^{k}$ – зафиксированы.

Неизвестная продолжительность перелета включена в состав невязки и использована нормировка сопряженных переменных (${{\psi }_{h}}$(0) = 1) для исключения одной сопряженной из числа неизвестных краевой задачи.

Применительно к величинам начального ускорения 1.70 ⋅ 10^–3 м/с² и удельного импульса тяги электроракетных двигателей 3000 с на траектории решенной краевой задачи не наблюдается особых точек (резкого уменьшения величины А). Полученному решению соответствуют следующие значения неизвестных краевой задачи: ${{\psi }_{h}}$ = 1, ${{\psi }_{{{{e}_{x}}}}}$ =  –0.00624401, ${{\psi }_{{{{e}_{y}}}}}$ = –0.00115803, ${{\psi }_{{{{i}_{x}}}}}$ = = ‒0.01046849, ${{\psi }_{{{{i}_{y}}}}}$ = 0.00139247, ${{\psi }_{F}}$ = 0.00010290; продолжительность T = 47.9 сут. Точность решения краевой задачи составила: отклонение порядка 80 м радиусов апоцентра и перицентра от заданного значения радиуса круговой орбиты 7171 км и 10^–9° по наклонению от заданного значения 51.6°. Однако расчеты в окрестности полученной экстремали показали, что при изменении начальных значений сопряженных переменных на величину не более 10^–5 в зависимости А от времени полета появляются точки уменьшения А вблизи конца траектории, позволяющие считать их особыми точками. Для одного из расчетов, демонстрирующего признаки наличия особой точки, на рис. 12, 13 и 14 представлены соответственно зависимости величины А¹¹, угла тангажа (угол между проекцией вектора тяги на орбитальную плоскость и трансверсалью) и угла рысканья (угол между вектором тяги и орбитальной плоскостью) от времени полета. Точке минимальной величины А соответствует изменение как в структуре закона управления углом рысканья (рис. 14), так и изменения в структуре закона управления углом тангажа (рис. 13).

Процесс сходимости указанной выше решенной краевой задачи был стабильно сходящимся. Минимальное значение невязки обеспечивалось методом градиентного спуска с периодическими одиночными срабатываниями метода Ньютона, что позволяло получать скачкообразное уменьшение невязки.

Зависимости величин А, углов тангажа и рысканья от времени полета приведены на рис. 15, 16 и 17, соответственно, применительно к решению краевой задачи со значениями начального ускорения 1.27 ⋅ 10^–3 м/с² и удельного импульса тяги электроракетных двигателей 4000 с. Полученному решению соответствуют следующие значения неизвестных краевой задачи: ${{\psi }_{h}}$ = 1, ${{\psi }_{{{{e}_{x}}}}}$ = –0.01777209; ${{\psi }_{{{{e}_{y}}}}}$ = = –0.00146912, ${{\psi }_{{{{i}_{x}}}}}$ = –0.03518325, ${{\psi }_{{{{i}_{y}}}}}$ = = 0.04570219, ${{\psi }_{F}}$ = 0.00038026; продолжительность T = 67.9 сут. Точность решения краевой задачи составила (отклонения): по апоцентру 58 км, по перицентру – 47 км и 10^–3° по наклонению от заданного значения 51.6°.

Как следует из рис. 15 снижение величины А происходит на 16-е сут полета, что условно²² можно считать началом геоцентрического участка, в это же время полета происходит изменение структуры управления (рис. 16, 17).

Из представленных результатов расчетов следует, что при решении задачи перелета с малой тягой с окололунной на околоземную орбиту, по-видимому, могут возникать особые точки на разных этапах полета, а именно: в конце траектории (геоцентрического участка) и в начале геоцентрического участка. Характер зависимостей А от времени полета позволяет предположить возможность появления особой точки и на селеноцентрическом участке (в начале траектории). При этом вычислительные трудности тем более выражены, чем дальше от окончания траектории располагается особое решение.

6. ПЕРЕЛЕТ МЕЖДУ НИЗКИМИ КРУГОВЫМИ ОКОЛОЗЕМНОЙ И ОКОЛОМАРСИАНСКОЙ ОРБИТАМИ

В работе [15] исследовалась задача перелета между низкими околоземной и околомарсианской орбитами. Было найдено единственное решение. Отмечены вычислительные трудности при решении поставленной краевой задачи.

Эти вычислительные трудности могут объясняться наличием особых точек на траекториях вблизи найденного оптимального решения. Для проверки этого предположения были построены зависимости модуля базис-вектора Лоудена ${{p}_{V}}$ (рис. 18) и углов ориентации вектора тяги $\gamma $ и $\alpha $ (рис. 19 и 20, соответственно). Обозначения приняты как в работе [15].

Из рис. 18 следует, что на оптимальной траектории величина базис-вектора Лоудена испытывает провал при смене структуры законов управления ориентацией вектора тяги ДУ (рис. 19 и 20). Величина снижения ${{p}_{V}}$ недостаточна, чтобы вызывать особенности при определении законов ориентации вектора тяги с интегрированием уравнений движения. Однако можно показать, что в непосредственной близости от найденного решения, при изменении неизвестных краевой задачи {$\psi _{{{{e}_{x}}}}^{0},$ $\psi _{{{{e}_{y}}}}^{0},$ $\psi _{{{{i}_{x}}}}^{0},$ $\psi _{{{{i}_{y}}}}^{0}$} на величину не более чем 10^–4, существует траектория (на которой не реализуется выход на орбиту около Марса, а получается пролет планеты назначения с гиперболической скоростью относительно Марса) с уменьшением модуля базис-вектора Лоудена до величины 4 ⋅ 10^–5. При этом вектор тяги ориентируется практически в плоскости эклиптики, а угол $\gamma $ (между опорным направлением и проекцией вектора тяги на плоскость эклиптики) претерпевает разрыв (скачок с –14° до 166°).

Приведенные примеры показывают, что появление случаев точечного вырождения базис-вектора Лоудена не связано со сложностью правых частей дифференциальных уравнений движения. Можно показать, что и в случае задачи расчета гелиоцентрического участка межпланетного перелета Земля-Марс при применении метода транспортирующих траекторий [22], когда компоненты ускорения в правых частях дифференциальных уравнений движения имеют наиболее простую форму записи и определяются только тягой ДУ КА, при определенных условиях возникают вычислительные трудности, подобные приведенным выше.

7. ГЕЛИОЦЕНТРИЧЕСКИЙ УЧАСТОК ПЕРЕЛЕТА МАРС–ЗЕМЛЯ

Задачи межпланетных перелетов с ДУ малой тяги в большинстве случаев рассматриваются с использованием метода грависфер нулевой протяженности. В такой постановке краевые условия гелиоцентрического участка перелета как справа, так и слева состоят в совпадении координат и скоростей КА и соответствующих небесных тел. Эти соотношения составляли основу невязки.

В рассматриваемом далее примере задачи гелиоцентрического участка перелета от Марса к Земле максимизировалась конечная масса при заданной продолжительности перелета (функционал ${{J}_{2}}$). Для уравнений движения применялась сферическая система координат, аналогично [4, 23]. Неизвестными краевой задачи являлись начальные значения сопряженных переменных (шесть – сопряженные координатам и скоростям, седьмая – сопряженная массе). Возможности сокращения размерности краевой задачи при использовании различных видов нормировки сопряженных переменных (как, например, в работе [23]) не использовались. Невязка дополнялась добавочным компонентом – разностью между заданной продолжительностью перелета и текущим временем, а продолжительность перелета определялась из условия минимума невязки для каждого набора искомых начальных значений сопряженных переменных.

Начальное ускорение было принято равным 1.65 ⋅ 10^–3 м/с², а удельный импульс тяги – 7000 с. Принятая дата отлета от Марса 17.II.2051. Эфемериды планет определялись с помощью модели EPM2008 [21].

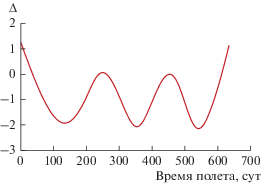
В рассматриваемом примере интересующая особенность (касание функцией переключения $\Delta $ нуля) возникает при продолжении решений путем наращивания продолжительности перелета от некоторого с умеренной величиной (например, 390 сут), где краевая задача решается достаточно стабильно. Однако сходимость теряется при достижении интервала продолжительности около 620–640 сут.

Найденное решение с продолжительностью 631 сут определяется следующими начальными значениями сопряженных переменных (обозначения приняты как в работе [4]): ${{p}_{r}}$ = –9.81002636; ${{p}_{{{\varphi }}}}$ = 0.34203020; ${{p}_{{{\theta }}}}$ = –2.25745484; ${{p}_{u}}$ = –7.74033617; ${{p}_{{{\upsilon }}}}$ = –14.34248610; ${{p}_{{{\omega }}}}$ = –1.75541039; ${{p}_{m}}$ = = 27.51222479. Точность полученного решения недостаточна. Например, разность между требуемым значением и достигнутым составляет: по радиусам апоцентра и перицентра 3.6 ⋅ 10^–6 и 3.4 ⋅ 10^–7 а. е., соответственно, по наклонению 3.4 ⋅ 10^–6 градусов, по долготе восходящего узла 0.06°, по аргументу перицентра 0.07°, по истинной аномалии 0.007°.

Вычислительные трудности, не позволяющие получить более точное решение, по-видимому, обусловлены появлением точки касания функции переключения $\Delta $ линии уровня ноль (рис. 21), что приводит к появлению/исчезновению кратковременного включения ДУ между 400 и 500 сутками полета. Согласно [24], это ведет к скачкам элементов матрицы чувствительности и, как следствие, отказу итерационных методов минимизации невязки.

Вероятно, наличие точки касания функцией переключения нуля не всегда предопределяет появление вычислительных трудностей, а связано, например, с величиной производной функции переключения в окрестности касания. В частности, в работе [24] применительно к перелету по маршруту Земля–Венера–Земля–Юпитер приведены зависимости функции переключения и тяги от времени полета с коротким включением ДУ (почти касанием функции переключения нуля). Однако о возникших в процессе решения вычислительных сложностях не сообщается, что может быть следствием как отсутствия вычислительных трудностей, так и эффективности их преодоления с помощью приведенной в [24] методики расчетов.

ЗАКЛЮЧЕНИЕ

Приведенные выше примеры появления особых точек показывают типичность ситуации для оптимизации перелетов с ДУ малой тяги. Появление этой особенности, как правило, приводит к отказу методов и неудовлетворительной сходимости итерационного процесса решения краевых задач.

В случае, если точное решение краевой задачи не найдено, точность решения в значительной мере определяется моментом появления особых точек – чем ближе к началу траектории, тем точность ниже. Применительно к прямым расчетам с учетом притяжения нескольких тел в течение всего полета (межпланетные перелеты и перелеты в системе Земля–Луна) выявленная особенность оказывает значительное влияние на сходимость итерационного процесса решения краевых задач и требует разработки специальной методики.