1. На главную
  2. Электронные версии
  3. Космические исследования
  4. T. 60, № 2, 2022

Космические исследования, 2022, T. 60, № 2, стр. 151-166

Генерация искусственных гало-орбит в окололунном пространстве с использованием двигателей малой тягой

Ду Чунжуй 1, *, О. Л. Старинова 1, 2

1 Самарский университет
Самара, Россия

2 Нанкинский университет науки и технологий
Нанкин, Китай

* E-mail: ducrui@yandex.ru

Поступила в редакцию 31.12.2020
После доработки 27.06.2021
Принята к публикации 25.08.2021

Полный текст (PDF)

Аннотация

Данная работа посвящена возможности создания искусственных гало-орбит в круговой ограниченной задаче трех тел системы Земля–Луна за счет малого длительно действующего на КА ускорения от двигателей малой тяги в ситуациях, когда естественная гало-орбита не может соответствовать требованиям миссии или занята. В статье с помощью методов коллокации и продолжения по параметру получены два класса искусственных гало-орбит в системе Земля–Луна. Первый класс генерируется за счет постоянного по величине и направлению дополнительного ускорения. Получено полное семейство орбит этого класса, существенно отличающихся от традиционных по периоду и форме. Второй класс орбит генерируется за счет регулируемых электроракетных двигателей. Этот класс орбит получен как решение задачи об оптимальном по расходу рабочего тела формировании орбиты с заданным периодом с использованием принципа максимума Понтрягина и метод продолжения по параметру. Показано, что существуют значительные различия в орбитальных периодах между искусственными гало-орбитами – потомками одной и той же гало-орбиты. Результаты расчетов подтверждают возможность использования двигателей малой тяги для изменения параметров естественных гало-орбит, пригодных для баллистического проектирования будущих лунных миссий.

ВВЕДЕНИЕ

Одним из классов потенциальных рабочих орбит для перспективных лунных миссий являются гало-орбиты – периодические орбиты, как известно, существующие при движении материального тела под действием гравитации двух тел. В настоящее время достигнут значительный прогресс в изучении гало-орбит в рамках задачи трех тел [1–4]. За последние десятилетия множество работ было посвящено изучению гало-орбит, в которых для получения аналитических и численных решений использовались аппроксимация третьего порядка, метод дифференциальной коррекции, гамильтоновы канонические уравнения, теория многообразий и другие методы [5–7].

Параметрами, определяющими характеристики системы трех тел, являются отношение масс первичного и вторичного небесных тел и расстояние между ними [8]. В реальности, для любой конкретной системы трех тел, имеется естественное ограничение на существование периодических орбит. Например, если мы выбираем рабочую гало-орбиту в системе Земля–Луна с периодом 14 дней, т.е. хотим провести двухнедельную миссию, то форма и положение орбиты в пространстве являются строго определенными. Максимальное расстояние между орбитой и Луной и амплитуда отклонения орбиты от плоскости движения Луны также зафиксированы. Таким образом, никакие дополнительные требования к форме и/или положению рабочей орбиты не могут быть выполнены. Кроме того, период рабочей орбиты, который соответствует требуемому положению и фигуре орбиты, также является фиксированным значением. Этот факт будем называть временным и пространственным ограничением на гало-орбиты. Однако, классическая гало-орбита может не являться наилучшим вариантом для проектируемой миссии. Кроме того, выбранное наилучшее местоположение или конкретный орбитальный период будущей рабочей орбиты для перспективной лунной миссии могут оказаться уже использованными другим космическим аппаратом. Преодолению пространственного и временного ограничения за счет использования двигателей малой тяги для создания искусственных гало-орбит посвящена данная статья.

Существуют работы, посвященные генерации искусственных гало-орбит. Например, новое семейство гало-орбит можно получить в системе трех тел за счет естественных возмущений. Обычно такие орбиты незначительно отличаются от классических. Например, в работах [9, 10] рассматривается задача о применении солнечных парусов для создания искусственных периодических орбит в рамках фото-гравитационной задачи трех тел в системе Земля–Солнце. В работах [11, 12] доказывается существование и анализируется устойчивость точек относительного равновесия в ограниченной круговой фото-гравитационной задаче трех тел. В работах [13, 14] дополнительно рассмотрено влияние не центральности гравитационного поля небесного тела и светового давления на фото-гравитационную систему, а также рассчитана периодическая орбита в этой новой модели.

Другим эффективным способом устранения ограничений на орбиты является использование двигателей малой тяги для создания искусственных гало-орбит. Применение дополнительного ускорения позволяет целенаправленно изменять требуемые орбитальные параметры. П.С. Красильников в [15] рассмотрел движение в системе Земля–Луна с учетом дополнительного постоянно действующего ускорения, направленного вдоль оси x. В этой работе для различных уровней дополнительного ускорения вычисляются координаты искусственных точек либрации и представлено распределение кривых нулевой скорости, которое отличается от классического. Некоторые искусственные гало-орбиты в системе Солнце–Земля, полученные за счет малого непрерывного ускорения постоянного направления и величины, вычислены в работе [16]. В этой работе подтверждено существование устойчивых искусственных периодических орбит. Однако, использование метода дифференциальной коррекции для генерации семейства гало-орбит, приводило к разрыву в параметрах орбит и невозможности получения полного семейства искусственных гало-орбит. Кроме того, в практических приложениях непросто организовать постоянный уровень ускорения в течение длительного времени, так как работа двигателя приводит к уменьшению массы космического аппарата, а, следовательно, к возрастанию ускорения.

В данной статье предлагается использовать алгоритм метода продолжения по параметру в сочетании с методом коллокации. В качестве начального приближения, требуемого методом коллокации, используются классические гало-орбиты. Затем для постоянного по величине и направлению ускорения рассчитывается полное семейство искусственных гало-орбит в системе Земля–Луна. На следующем шаге рассчитывается оптимальное по величине и направлению ускорение для формирования искусственной гало-орбиты с заданным периодом и с учетом массовый расхода и возможного регулирования двигателей малой тягой. Этот вычислительный сценарий позволяет применить разработанную методику для устранения ограничений на гало-орбиты с различными уровнями тяги и разными орбитальными периодами. При этом мы ищем оптимальное управление, обеспечивающее формирование заданной гало-орбиты с точки зрения минимума расхода рабочего тела с помощью принципа максимума Понтрягина.

Структура этой статьи следующая: сначала вводятся основные теоретические положения и описывается метод решения; затем анализируется влияние дополнительного ускорения на движение в системе Земля–Луна; и наконец, вычисляется семейство искусственных гало-орбит под действием двигателей малой тяги.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

А) Круговая ограниченная задача трех тел в системе Земля–Луна

Уравнение пассивного движения в синодической системе координат Земля–Луна имеет вид [17]:

(1)
$\ddot {R} = {\mathbf{\omega }} \times ({\mathbf{\omega }} \times R) + 2{\mathbf{\omega }} \times V + A{\text{,}}$
где $\ddot {R}$ – общее ускорение, действующее на КА в системе трех тел; R – расстояние от КА до барицентра системы Земля–Луна; V – относительная скорость КА во вращающей системе координат; A – относительное ускорение во вращающей системе координат; ${\mathbf{\omega }}$ – угловая скорость вращения Земли и Луны, относительно барицентра системы.

В точках либрации A и V равны нулю. Для уменьшения погрешности при численном интегрировании уравнений движения (1), перейдем к безразмерной форме уравнений движения во вращающейся системе координат [18, 19]:

(2)
$\ddot {x} - 2\dot {y} = {{U}_{x}},\,\,\,\,\ddot {y} + 2\dot {x} = {{U}_{y}},\,\,\,\,\ddot {z} = {{U}_{z}},$
где $U = \frac{1}{2}\left( {{{x}^{2}} + {{y}^{2}}} \right) + \frac{{1 - \mu }}{{r1}} + \frac{\mu }{{r2}}$ – псевдопотенциал системы; ${{U}_{x}},$ ${{U}_{y}},$ ${{U}_{z}}$ – его частные производные по координатам; $r_{1}^{2} = {{\left( {x + \mu } \right)}^{2}} + {{y}^{2}} + {{z}^{2}}$ и $r_{2}^{2} = (x - 1 + $ $ + \,\,\mu {{)}^{2}} + {{y}^{2}} + {{z}^{2}}$ – безразмерные расстояния от КА до Земли и Луны соответственно; $\mu = 0.01215$ – отношение масс Земли и Луны.

Преобразование размерных уравнений (1) в безразмерные (2) проводилось по следующим зависимостям для единиц расстояния, скорости и времени в размерной системе координат [20]:

(3)
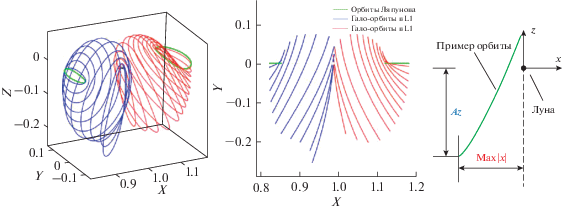
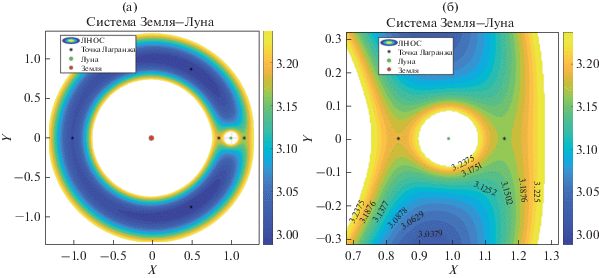
$\begin{array}{*{20}{c}} {{\text{расстояние:}}\,\,R = {{l}_{{\text{*}}}}r,} \\ {{\text{скорость:}}\,\,V {\text{ = }}{{s}_{{\text{*}}}}v,} \\ {{\text{время:}}\,\,T = \frac{{{{\tau }_{*}}}}{{2\pi }}t,} \end{array}$
где ${{l}_{{\text{*}}}}$ – расстояние между Землей и Луной, ${{s}_{{\text{*}}}}$ – орбитальная скорость Луны, ${{\tau }_{{\text{*}}}}$ – орбитальный период Луны.

Известно, что постоянная Якоби J является единственным интегралом в ограниченной кр-уговой задаче трех тел [18]: $J = 2U - {{v}^{2}},$ ${{v}^{2}} = {{\dot {x}}^{2}} + {{\dot {y}}^{2}} + {{\dot {z}}^{2}}.$ Если построить область системы ограниченную линией $v = 0,$ то получится линия нулевой относительной скорости – граница, которую космический корабль может достичь при пассивном движении за счет своей собственной энергии [21]. Рис. 1 показывает пять точек равновесия (Лагранжа) и линии нулевой относительной скорости (ЛНОС) с различными константами интеграла Якоби J. В этой статье мы рассматриваем точки равновесия L1 и L2, которые находятся близко к Луне и имеют в своей окрестности много периодических орбит. Кроме того, пространство вблизи этих точек либрации является перспективным для практического использования в миссиях исследования Луны.

Рис. 1.

(а) Линии нулевой относительной скорости в системе Земля–Луна; (б) ЛНОС в окрестности Луны bc.

В инерциальной системе координат, уравнение движения можно переписать в виде $\ddot {R} = - \frac{{{{\mu }_{{\text{З}}}}}}{{R_{{\text{З}}}^{3}}}{{R}_{{\text{З}}}} = - \frac{{{{\mu }_{{\text{Л}}}}}}{{R_{{\text{Л}}}^{{\text{З}}}}}{{R}_{{\text{Л}}}},$ тогда $\ddot {R}$ представляет собой гравитационное ускорение в системе трех тел [22]. Рис. 2 изображает величину этого гравитационного ускорения в логарифмическом масштабе для системы Земля–Луна $\left( {{\text{lg}}\left| {\ddot {R}} \right|} \right).$ Очевидно, что распределение гравитации вокруг Луны не является однородным, в окрестностях точек либрации существует гравитационное равновесие, которое допускает существование периодических орбит. Пространственные и временные характеристики каждой орбиты связаны только с характеристиками системы гравитирующих тел и не могут быть изменены. Это проводит к ограничениям на временные и пространственные характеристики гало-орбит.

Рис. 2.

(а) Величина гравитационного ускорения в системе Земля–Луна; (б) в окрестности Луны.

Обозначим ${\mathbf{X}} = {{\left[ {x,y,z,\dot {x},\dot {y},\dot {z}} \right]}^{T}}$ – вектор состояния КА во вращающейся системе координат. Тогда уравнение (1) примет наиболее простой вид ${\mathbf{\dot {X}}} = f({\mathbf{X}}).$ Из уравнения (2) выводятся вариационные уравнения первого порядка, которые приводят к следующему векторному дифференциальному уравнению движения КА [19]:

(4)
$\Delta {\mathbf{\dot {X}}} = {\mathbf{A}}(t)\Delta {\mathbf{X}},$
где ${\mathbf{A}}(t)$ – матрица Якоби, соответствующая системе Земля–Луна [19]:

$\begin{gathered} {\mathbf{A}}(t) = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{0}}}_{{3 \times 3}}}}&{{{{\mathbf{I}}}_{{3 \times 3}}}} \\ {{{{\mathbf{U}}}_{{3 \times 3}}}}&{\mathbf{\Omega }} \end{array}} \right],\,\,\,\,{{{\mathbf{U}}}_{{3 \times 3}}} = \left[ {\begin{array}{*{20}{c}} {{{U}_{{xx}}}}&{{{U}_{{xy}}}}&{{{U}_{{xz}}}} \\ {{{U}_{{yx}}}}&{{{U}_{{yy}}}}&{{{U}_{{yz}}}} \\ {{{U}_{{zx}}}}&{{{U}_{{zy}}}}&{{{U}_{{zz}}}} \end{array}} \right], \\ {{U}_{{xx}}} = \frac{{\partial {{U}_{x}}}}{{\partial x}},\,\,\,\,{\mathbf{\Omega }} = \left[ {\begin{array}{*{20}{c}} 0&2&0 \\ { - 2}&0&0 \\ 0&0&0 \end{array}} \right]. \\ \end{gathered} $

Гало-орбита является замкнутым решением с периодическим движением, которая симметрична относительно плоскости x–z во вращающейся системе координат [6]. Эту симметрию можно использовать для создания гало-орбит. Так, если вектор начального состояния имеет вид ${{{\mathbf{X}}}_{0}} = {{\left[ {{{x}_{0}},0,{{z}_{0}},0,{{{\dot {y}}}_{0}},0} \right]}^{T}},$ замкнутые периодические орбиты могут быть получены итерационным путем на базе уравнения (4) [23]. На рис. 3 показаны фигуры южного семейства гало-орбит в системе Земля–Луна, они являются продолжением плоских орбит Ляпунова.

Рис. 3.

Гало-орбиты в системе Земля–Луна.

В этой статье гало-орбита оценивается с точки зрения следующих параметров: орбитальный период, максимальное расстояние от КА до Луны ${\text{Max}}\left| x \right|$ и максимальное отдаление КА от плоскости $Az,$ как показано на рис. 3. Параметры ${\text{Max}}\left| x \right|$ и $Az$ рассматриваются как функции орбитального периода, которые построены на рис. 4.

Рис. 4.

Зависимость параметров Max|x| и $\left| {Az} \right|$ от орбитального периода.

В соответствии с требованиями миссии, с помощью рис. 4 может быть выбрана целевая рабочая орбита. Отметим, что северное семейство орбит имеет положительные значения $Az,$ а южное семейство – отрицательные. Они симметричны относительно плоскости x–y. Для удобства анализа в данной статье рассчитывается только южное семейство орбит.

Б) Устойчивость орбит

Устойчивость точек либрации и периодических орбит в системе трех тел подробно исследованы в работах [23–25]. Линейная устойчивость семейства гало-орбит в этой статье определяется теорией Floquet [26] и зависит от поведения шести собственных значений (помеченных с ${{\lambda }_{1}}$ по ${{\lambda }_{6}}$) матрицы монодромии $\Phi ,$ связанной с уравнением (4):

(5)
$\dot {\Phi } = {\mathbf{A}}\left( t \right)\Phi ,\,\,\,\,\Phi \left( 0 \right) = {\mathbf{I}},$
где ${\mathbf{I}}$ – единичная матрица соответствующего размера.

Этим собственным значениям соответствуют показатели Floquet ${{{{\alpha }}}_{i}},$ определяемые формулой:

(6)
${{\lambda }_{i}} = {{e}^{{{{\alpha }_{i}}T}}},$
где $T$ – орбитальный период. Показатель Ляпунова, обозначенный как ${{{{\varphi }}}_{i}}$ и определяемый как действительная часть ${{\alpha }_{i}},$ чаще используется при оценке устойчивости орбиты. Так, согласно теореме Ляпунова, эти собственные значения находятся во взаимных парах, если они действительны, или в сопряженных парах, если они комплексные. Следовательно, шесть собственных значений для гало-орбит выписываются как $\left\{ {1,1,{{\lambda }_{i}},{{{\bar {\lambda }}}_{r}},{{\lambda }_{r}},1{\text{/}}{{\lambda }_{r}}} \right\},$ соответствующие показатели Floquet и показатели Ляпунова равны $\left\{ {0,0,{{\alpha }_{i}},{{{\bar {\alpha }}}_{i}},{{\alpha }_{r}}, - {{\alpha }_{r}}} \right\}$ и $\left\{ {0,0,0,0,{{\varphi }_{r}}, - {{\varphi }_{r}}} \right\}.$ Условие устойчивости периодической орбиты в линейной форме состоит в том, что все показатели Ляпунова должны быть равны 0 [27]. На рис. 5 показано распределение ${{{{\varphi }}}_{i}}$ в зависимости от орбитальных периодов. Красная часть представляет собой область устойчивых гало-орбит в окололунном пространстве.

Рис. 5.

Распределение показателей Ляпунова по семействам гало-орбит.

В) Метод продолжения по параметру и метод коллокации

Как было сказано ранее, Baig и McInnes [16] использовали метод продолжения по параметру в сочетании с дифференциальной коррекцией для генерации семейства искусственных гало-орбит в системе Солнце–Земля. Однако этот алгоритм при неудачном выборе длины непрерывного шага вызывает разрыв кривой изменения параметров орбиты, и полное семейство орбит не получается. Поэтому, в данной работе, предложено использовать метод продолжения по параметру в сочетании с методом коллокации для получения полных семейств искусственных гало-орбит в системе Земля–Луна с постоянным ускорением, а также для генерации искусственных гало-орбит с минимальным расходом рабочего тела. В этом разделе методы продолжения по параметру и коллокации лишь кратко описаны, а их конкретное применение подробно рассматривается в следующих разделах.

Метод продолжения по параметру является одним из эффективных средств решения серии сложных задач. Обычно определяется непрерывный параметр и существует известное решение задачи при одном из его значений, затем при изменении параметра этот метод позволяет перейти от проблемы с известным решением к новому решению. Например, чтобы автоматически решить задачу об оптимальном переходе в гравитационном поле без знания точных начальных приближений для значений сопряженных переменных, автор [28] использует метод продолжения по гравитационному параметру. В работе [29] применяется метод продолжения по параметру (ньютоновская гомотопия), чтобы постепенно обеспечить требуемые краевые условия.

Метод коллокации [30] – это метод используемый для интегрирования и обновления начальных приближений для генерируемой орбиты. Он обеспечивает альтернативный метод формирования орбит, который доказывает большую надежность даже для случаев крайне неудачных начальных приближений, в которых схема дифференциальной коррекции дает сбой [31]. В отличие от метода Ньютона, который должен обеспечивать только начальные приближения сопряженных векторов, метод коллокации определяет значения вектора состояния и сопряженного вектора в каждой точке дискретизации. В этой статье в качестве начального приближения решения используется орбита, удовлетворяющая определенному условию, а затем используется метод продолжения по параметру для постепенного перехода к окончательному решению. Именно на этом этапе краевая задача на каждом шаге решается методом коллокаций.

MATLAB предоставляет функцию bvp4c, которая использует схему коллокации на основе формулы коллокации Lobatto IIIA. Многочлен коллокации дает C1-непрерывное решение, которое имеет высокий порядок точности равномерно в диапазоне интегрирования. Выбор сетки и контроль ошибок основаны на результатах работы [32]. В методе коллокации используется сетка точек для разделения диапазона интегрирования на подинтервалы. Данный метод позволяет определить численное решение как решение системы глобальных алгебраических уравнений [32, 33], полученных из граничных условий и условий, обеспечивающих требуемую конфигурацию орбиты. Затем решающая программа оценивает ошибку численного решения на каждом подинтервале. Если решение не удовлетворяет критериям допуска, решающая программа корректирует сетку и повторяет процесс.

ИСКУССТВЕННАЯ СИСТЕМА ТРЕХ ТЕЛ

Поскольку орбитальные периоды и формы гало-орбит, которые существуют в естественной системе Земля–Луна, являются фиксированными, они не могут удовлетворить требованиям всех миссий. В этой работе реактивное ускорение, создаваемое двигателем малой тяги, используется для управления параметрами орбит с целью получения искусственных гало-орбит, отличных от классических.

Пусть двигательная установка КА создает ускорение ${{A}_{{{\text{ДУ}}}}},$ тогда в уравнение движения (1) добавится еще одно слагаемое:

(7)
$\ddot {R} = \omega \times (\omega \times R) + 2\omega \times V + A + {{A}_{{{\text{ДУ}}}}},$
или в безразмерном скалярном виде:
(8)
$\ddot {x} - 2\dot {y} = {{U}_{x}} + {{a}_{x}},\,\,\,\,\ddot {y} + 2\dot {x} = {{U}_{y}} + {{a}_{y}},\,\,\,\,\ddot {z} = {{U}_{z}} + {{a}_{z}},$
где $a = {{\left[ {{{a}_{x}},{{a}_{y}},{{a}_{z}}} \right]}^{T}}$ – безразмерное ускорение, соответствующее ${{A}_{{{\text{ДУ}}}}}.$

Обозначаем псевдопотенциал искусственной системы $U* = U + {{a}_{x}}x + {{a}_{y}}y + {{a}_{z}}z,$ где $U$ – псевдопотенциал в естественной системе трех тел в уравнении (2). Различные значения проекций ускорения ${{a}_{x}},{{a}_{y}}$ и ${{a}_{z}}$ будут обеспечивать различные положения точек равновесия системы, т.е. приведут к созданию искусственных точек либрации. В соответствии с формулой (4) вторые производные от потенциальной функции при существовании реактивного ускорения не изменяться: ${{{\mathbf{U}}}_{{3 \times 3}}} = {\mathbf{U}}_{{3 \times 3}}^{*},$ поэтому устойчивость точек либрации сохраняется.

Рассмотрим КА массой 1500 кг движущийся под действием ускорения от регулируемого электроракетного двигателя (ЭРД) с максимальной тягой 200 мН, что соответствует безразмерному ускорению 0.05 единиц. Соответственно, рассматривается диапазон изменения корректирующих ускорений ${{a}_{x}},{{a}_{y}}$ и ${{a}_{z}}$ от –0.05 до 0.05. Большее ускорение не может поддерживаться современными двигательными установками продолжительное время и поэтому здесь не рассматривается.

На рис. 6 показаны изменения координат положения точек L1 и L2 при изменении величина и направления дополнительного ускорения $a,$ некоторые результаты представлены в табл. 1.

Рис. 6.

Положение искусственных точек либрации L1 и L2 при ${{a}_{x}},{{a}_{y}}$ и ${{a}_{z}}$от –0.05 до 0.05: (а) дополнительное ускорение параллельно оси OX $a = \left( {\begin{array}{*{20}{c}} {{{a}_{x}},}&{0,}&0 \end{array}} \right);$ (б) дополнительное ускорение параллельно оси OY $a = \left( {\begin{array}{*{20}{c}} {0,}&{{{a}_{y}},}&0 \end{array}} \right);$ (в) дополнительное ускорение параллельно оси OZ $a = \left( {\begin{array}{*{20}{c}} {0,}&{0,}&{{{a}_{z}}} \end{array}} \right);$ (г) дополнительное ускорение параллельно плоскости XOY $a = \left( {\begin{array}{*{20}{c}} {{{a}_{x}},}&{{{a}_{y}},}&0 \end{array}} \right).$

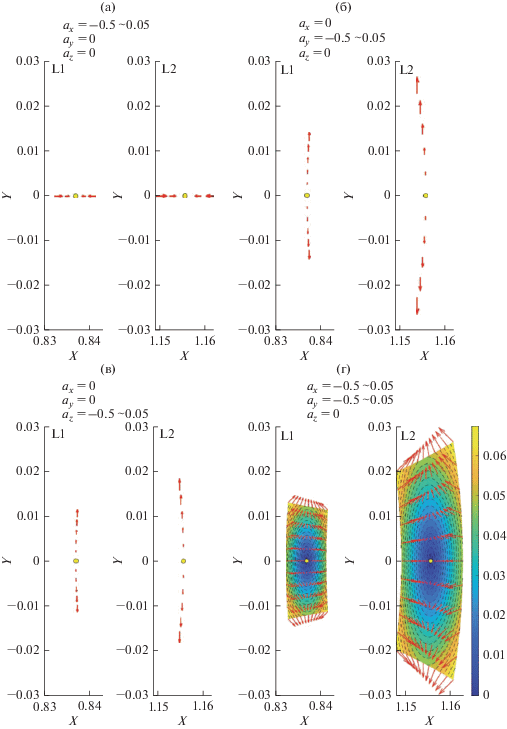
Таблица 1.  

Положения искусственных точек либрации L1 и L2 при некоторых значениях дополнительного ускорения

α L1 L2
${{a}_{x}}$ ${{a}_{y}}$ ${{a}_{z}}$ x y z x y z
0 0 0 0.836918 0 0 1.155680 0 0
0.01 0 0 0.836028 0 0 1.154337 0 0
–0.01 0 0 0.837799 0 0 1.157047 0 0
0 0.01 0 0.836935 0.002411 0 1.155613 0.004565 0
0 –0.01 0 0.836935 –0.002411 0 1.155613 –0.004565 0
0 0 0.01 0.836929 0 0.001943 1.155648 0 0.003134
0 0 –0.01 0.836929 0 –0.001943 1.155648 0 –0.003134
0.05 0 0 0.832379 0 0 1.149191 0 0
–0.05     0.841234 0 0 1.162760 0 0
0 0.05 0 0.837335 0.012077 0 1.154005 0.022742 0
0 –0.05 0 0.837335 –0.012077 0 1.154005 –0.022742 0
0 0 0.05 0.837188 0 0.009723 1.154889 0 0.015653
0 0 –0.05 0.837188 0 –0.009723 1.154889 0 –0.015653

На рис. 6а–6в показаны результаты изменения составляющих ускорения по одной координате, а на рис. 6г показан результат совместного действия составляющих ускорения ${{a}_{x}}$ и ${{a}_{y}}.$ Начальная точка каждой стрелки соответствует положению определенной искусственной точки либрации, а направление и размер стрелки содержит информацию о дополнительном ускорении, генерирующем эту точку. Разные цвета на рис. 6г соответствуют разным величинам дополнительного ускорения в окрестностях точек либрации L1 и L2.

В соответствии с данными табл. 1 можно сделать следующие выводы о влиянии дополнительного ускорения на положение искусственных точек либрации:

1) Положительное значение ${{a}_{x}}$ приводит к уменьшению x-координаты точек L1 и L2. Отрицательное значение ${{a}_{x}}$ увеличивает x-координаты, ${{a}_{x}}$ не влияет на координаты y и z. Если составляющие ${{a}_{x}}$ равны по размеру и противоположны по направлению, то координаты искусственных точек L1 и L2 примерно симметрично распределены относительно соответствующих точек либрации.

2) Положительные значения ${{a}_{y}}$ или ${{a}_{z}}$ увеличивают y-координату или z-координату точек L1 и L2, отрицательные координаты ускорения уменьшают соответствующие координаты. Наличие ${{a}_{y}}$ и ${{a}_{z}}$ заставит x-координаты приближаться к Луне и не влияют на соответствующие координаты точек либрации. Если ${{a}_{y}}$ или ${{a}_{z}}$ равны по размеру и противоположны по направлению, то координаты искусственных L1 и L2 симметричны относительно оси x.

3) Составляющая ${{a}_{z}}$ определяет положение поверхности гравитационного равновесия. В этой плоскости, одинаковые значения величины ускорения, приложенные в разных направлениях, заставляют перемещаться точки L1 и L2 вокруг исходного положения по эллипсу.

4) Точка либрации L2 чувствительнее к приложению дополнительного ускорения по сравнению с L1. При одно и том же ускорении отклонение точки L2 от классического положения примерно вдвое больше, чем у точки L1.

СЕМЕЙСТВО ИСКУССТВЕННЫХ ГАЛО-ОРБИТ В СИСТЕМЕ ЗЕМЛЯ–ЛУНА

Реактивное ускорение может изменить положения точек либрации системы трех тел, а также генерировать искусственные гало-орбиты относительно этих точек. Дополнительное ускорение можно создать с помощью двигателя малой тяги.

А) Генерация искусственных гало-орбит с постоянным ускорением

Дополнительное ускорение постоянной величины и направления, как показано в [16] позволяет создавать искусственные гало-орбиты. Проведем качественный анализ возможного диапазона изменения параметров орбит в системе Земля–Луна. В работе [16] используется ускорение, направленное параллельно оси x, как показано на рис. 6а. В данной работе используется метод коллокации для создания семейства искусственных гало-орбит, генерируемых дополнительным ускорением в соответствии со следующей вычислительной процедурой:

1. Классическая гало-орбита дискретизируется по времени от 0 до ${{t}_{f}}$ в соответствии с периодом обращения T, ${{t}_{f}}$ = T. Затем используются векторы состояний каждой из дискретных точек в качестве начальных приближений, требуемых функцией bvp4c (метод коллокации).

2. Пусть ${{a}_{x}} = (1 - \zeta ){{a}_{{x1}}} + \zeta {{a}_{{x2}}},$ $\zeta \in [0,1].$ Предположим, что замкнутая орбита получилась при некотором маленьком ускорении (${{a}_{x}} = {{a}_{{x1}}}$). Тогда, применяя метод продолжения по параметру $\zeta ,$ постепенно увеличивая параметр $\zeta $ от 0 до 1, будет рассчитана орбита при большем ускорении (${{a}_{x}} = {{a}_{{x2}}}$).

3. На этапе 2 процесса решения для нового значения $\zeta $ метод коллокации требует, чтобы предыдущее сходящееся решение использовалось в качестве начального приближения в текущей ситуации для итеративного решения до тех пор, пока не выполнится $\zeta = 1.$

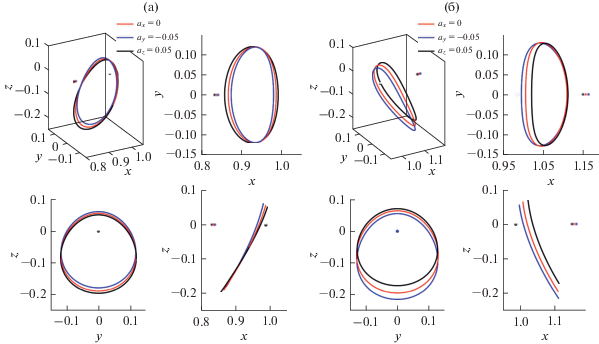
Таким образом, начиная с ${{a}_{{x1}}} = 0$ (естественная гало-орбита), рассчитываются искусственные гало-орбиты при различных условиях ускорения. Например, на рис. 7 показаны искусственные орбиты вокруг точек либрации L1 и L2, с орбитальным периодом равным десяти дням при ${{a}_{x}}$ = –0.05, 0 и 0.05. Звездочкой отмечены соответствующие точки либрации. Для гало-орбит относительно точки L2, при изменении генерирующего ускорения ${{a}_{x}}$ от –0.05 до 0.05, максимальное расстояние от КА до Луны Max|x| меняется от 35 500 до 34 700 км, амплитуда вне плоскости $\left| {Az} \right|$ меняется от 84 000 до 72 000 км. Для гало-орбиты относительно точки L1, Max|x| меняется от 43 360 до 49 660 км, $\left| {Az} \right|$ от 68300 до 75 000 км.

Рис. 7.

Гало-орбиты с орбитальным периодом 10 дней. (а) относительно точки либрации L1; (б) относительно точки либрации L2.

На рис. 8 показана связь изменения параметра Max|x| и $\left| {Az} \right|$ с периодом орбиты в точках либрации L1 и L2 при ${{a}_{x}}$ = –0.05, 0 и 0.05. Можно видеть, что дополнительное ускорение вызывает смещение характеристической кривой орбиты, так что в пределах определенного диапазона ограничения на период и пространственное положение гало-орбиты снимаются. Для гало-орбит относительно точки либрации L1, отрицательная проекция дополнительного ускорения ${{a}_{x}}$ заставляют характеристические кривые двигаться вниз, а положительная – вверх. В точке L2 наоборот, отрицательная проекция ускорения ${{a}_{x}}$ заставляют характеристическую кривую $\left| {Az} \right|$ двигаться вверх, а кривую Max|x| вниз. Положительная величина ${{a}_{x}}$ заставляет кривые изменяться в противоположном направлении. Сплошной квадратный маркер на кривой указывает, что данная точка является линейной устойчивой гало-орбитой. Дополнительное ускорение может изменить диапазон устойчивых орбит, а также может привести к исчезновению некоторых устойчивых орбит.

Рис. 8.

Зависимость параметров $\left| {Az} \right|$ и Max|x| от периода гало-орбит относительно точек либрации L1 (а) и L2 (б) при ${{a}_{x}}$ = –0.05, 0 и 0.05.

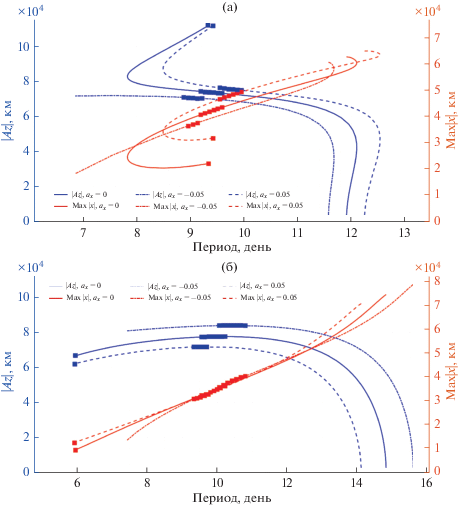
Рис. 8 показывает изменение орбитальных параметров только для граничных случаев изменения генерирующего ускорения ${{a}_{x}}$ и демонстрирует экстремальные значения, которых могут достигать орбитальные параметры. Для формирования промежуточных значений орбитальных параметров согласно расчетной базы данных и кривой зависимости орбитальных параметров могут быть выбраны соответствующие потребные дополнительные ускорения.

В табл. 2 приведен диапазон изменения орбитальных периодов семейства искусственных гало-орбит для рассматриваемого диапазона генерирующего ускорения.

Таблица 2.  

Диапазон изменения периодов гало-орбит (дней)

${{a}_{x}}$ –0.05 0 0.05
min max min max min max
L1 6.86 11.68 7.83 12.10 8.49 12.53
L2 7.43 15.60 5.96 14.82 5.93 14.11

Б) Генерация гало-орбит с переменным дополнительным ускорением

Хотя искусственные гало-орбиты получаются с использованием постоянного ускорения, на практике трудно реализовывать одну и ту же величину ускорения в течение длительного времени. Поэтому рассмотрим генерацию искусственных гало-орбит с учетом расхода топлива и регулирования двигателя.

В ограниченной круговой задаче трех тел, уравнение (8) можно переписать в следующей векторной форме, учитывающей массовый расход и регулирование двигателя [34]:

(9)
$\dot {x}{ = }f{\text{(}}x,\alpha ,u{\text{)}} \Rightarrow \left[ \begin{gathered} {\dot {r}} \hfill \\ {\dot {v}} \hfill \\ {\dot {m}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} v \\ g{\text{(}}r{\text{)}}{ + }h{\text{(}}v{\text{)}} + {{u{{T}_{{\max }}}\alpha } \mathord{\left/ {\vphantom {{u{{T}_{{\max }}}\alpha } m}} \right. \kern-0em} m} \\ {{ - u{{T}_{{\max }}}} \mathord{\left/ {\vphantom {{ - u{{T}_{{\max }}}} {{{I}_{{sp}}}{{g}_{0}}}}} \right. \kern-0em} {{{I}_{{sp}}}{{g}_{0}}}} \\ \end{gathered} \right],$
где $r = {{\left[ {x,y,z} \right]}^{T}}$ и $v = {{\left[ {{{v}_{x}},{{v}_{y}},{{v}_{z}}} \right]}^{T}}$ – положение и скорость КА; m – масса КА; ${{T}_{{\max }}}$ – величина тяги; ${{I}_{{sp}}}$ – удельный импульс двигателя; ${{g}_{0}} = 9.8\;{\text{м/}}{{{\text{с}}}^{{\text{2}}}}$ – стандартное ускорение свободного падения; $u \in [0,1]$ – коэффициент регулирования двигателя; α – единичный вектор направления тяги; g(r) и h(v) – гравитационное и инерциальное ускорение:

(10)
$\left\{ \begin{gathered} g\left( r \right) = - {{\left( {\frac{{\partial U}}{{\partial x}},\frac{{\partial U}}{{\partial y}},\frac{{\partial U}}{{\partial z}}} \right)}^{T}} \hfill \\ h\left( v \right) = {{\left( {2{{v}_{y}}, - 2{{v}_{x}},0} \right)}^{T}} \hfill \\ \end{gathered} \right..$

Параметры КА, рассматриваемого в данной статье, перечисляются в табл. 3.

Таблица 3.  

Параметры КА

Параметры Значение
Начальная масса КА m* 1500 кг
Удельный импульс ${{I}_{{sp}}}$ 2000 с
Max тяга ${{T}_{{\max }}}$ до 0.2 Н

Стратегия использования переменного ускорения для создания искусственной гало-орбиты состоит в том, чтобы КА из начальной фазовой точки P на классической гало-орбите под действием двигателя малой тяги КА вернется в ту же точку P через некоторое время ${{t}_{f}}.$ Таким образом, получается замкнутая искусственная гало-орбита с орбитальным периодом ${{t}_{f}},$ или орбитальная фазовая модуляция завершена.

Будем искать оптимальное управление, доставляющее минимум расходу рабочего тела, согласно критерию:

(11)
${{J}_{f}} = \frac{{{{T}_{{\max }}}}}{{{{I}_{{sp}}}{{g}_{0}}}}\int\limits_0^{{{t}_{f}}} {udt} .$
Для того, чтобы избежать разрывов непрерывных функций из-за дихотомии параметра u, используется метод продолжения по параметру [34] для сглаживания профиля управления. С учетом определения гомотопического параметра ${{\varepsilon ,}}$ задача оптимального энергопотребления и задача оптимального расхода топлива связаны между собой соотношением [35]:

(12)
${{J}_{{ef}}} = \frac{{{{T}_{{\max }}}}}{{{{I}_{{sp}}}{{g}_{0}}}}\int\limits_0^{{{t}_{f}}} {[u - {{\varepsilon }}u(1 - u)]} dt,\,\,\,\,{{\varepsilon }} \in [0,1].$

Гомотопический метод – это тоже своего рода метод продолжения по параметру [28], который следует методике: сначала получается решение задачи о минимизации энергии при $\varepsilon = 1$ $\left( {{{J}_{e}} = \frac{{{{T}_{{\max }}}}}{{{{I}_{{sp}}}{{g}_{0}}}}\int_0^{{{t}_{f}}} {{{u}^{2}}} dt} \right),$ затем с использованием алгоритма продолжения параметр $\varepsilon $ постепенно уменьшается от 1 до 0, и получается требуемая орбита с минимальным расходом топлива.

Введем вектор сопряженных переменных ${\mathbf{\lambda }} = {{\left[ {{{{\mathbf{\lambda }}}_{r}}{\text{,}}{{{\mathbf{\lambda }}}_{v}}{\text{,}}{{{{\lambda }}}_{m}}} \right]}^{T}},$ тогда Гамильтониан системы (9) и критерия (12) задается следующим образом:

(13)
$\begin{gathered} H = {\mathbf{\lambda }}_{r}^{T}v{ + }{\mathbf{\lambda }}_{v}^{T}\left[ {g{\text{(}}r{\text{)}}{ + }h{\text{(}}v{\text{)}}{ + }\frac{{{{T}_{{\max }}}u}}{m}\alpha } \right] - {{{{\lambda }}}_{m}}\frac{{{{T}_{{\max }}}u}}{c} + \\ + \,\,\frac{{{{T}_{{\max }}}}}{c}[u - {{\varepsilon }}u(1 - u)], \\ \end{gathered} $
где ${{{\mathbf{\lambda }}}_{r}} = {{\left[ {{{{{\lambda }}}_{x}}{\text{,}}{{{{\lambda }}}_{y}}{\text{,}}{{{{\lambda }}}_{z}}} \right]}^{T}}$ и ${{{\mathbf{\lambda }}}_{v}} = {{\left[ {{{{{\lambda }}}_{{{{v}_{x}}}}}{\text{,}}{{{{\lambda }}}_{{{{v}_{y}}}}}{\text{,}}{{{{\lambda }}}_{{{{v}_{z}}}}}} \right]}^{T}}.$

Согласно теории оптимального управления, получаем следующую систему для сопряженных переменных:

(14)
$\left\{ \begin{gathered} {{{{\mathbf{\dot {\lambda }}}}}_{r}} = - {{\left( {\frac{{\partial g(r)}}{{\partial r}}} \right)}^{T}}{{{\mathbf{\lambda }}}_{v}} \hfill \\ {{{{\mathbf{\dot {\lambda }}}}}_{v}} = - {{{\mathbf{\lambda }}}_{r}} - {{\left( {\frac{{\partial h(v)}}{{\partial v}}} \right)}^{T}}{{{\mathbf{\lambda }}}_{v}} \hfill \\ {{{{{\dot {\lambda }}}}}_{m}} = \frac{{u{{T}_{{\max }}}}}{{{{m}^{2}}{{{\mathbf{\lambda }}}_{v}}}}{\mathbf{\alpha }} \hfill \\ \end{gathered} \right..$

Применяя принцип максимума Понтрягина получим следующие оптимальные выражения ${\mathbf{\alpha }}{\text{*}}$ и $u{\text{*}}$ [34]:

(15)
$\begin{gathered} {\mathbf{\alpha }}* = - \frac{{{{{\mathbf{\lambda }}}_{v}}}}{{\left\| {{{{\mathbf{\lambda }}}_{v}}} \right\|}}, \\ u{\text{*}} = \left\{ \begin{gathered} 0\,\,\,\,S > \varepsilon \hfill \\ {{(\varepsilon - S)} \mathord{\left/ {\vphantom {{(\varepsilon - S)} {2\varepsilon }}} \right. \kern-0em} {2\varepsilon }}\,\,\,\, - \varepsilon \leqslant S \leqslant \varepsilon \hfill \\ 1\,\,\,\,S < - \varepsilon \hfill \\ \end{gathered} \right., \\ \end{gathered} $
где $S = 1 - \frac{{\left\| {{{{\mathbf{\lambda }}}_{v}}} \right\|c}}{m} - {{\lambda }_{m}}$ – функция переключения.

Таким образом, получается 14-мерная система уравнений управляемого движения КА с двигателем малой тягой в системе Земля–Луна:

(16)
$\begin{gathered} {\mathbf{\dot {\Phi }}} = {\text{F(}}{\mathbf{\Phi }}{\text{)}} \Rightarrow \\ \Rightarrow \left[ \begin{gathered} {\dot {r}} \hfill \\ {\dot {v}} \hfill \\ {\dot {m}} \hfill \\ {{{{\mathbf{\dot {\lambda }}}}}_{r}} \hfill \\ {{{{\mathbf{\dot {\lambda }}}}}_{v}} \hfill \\ {{{{{\dot {\lambda }}}}}_{m}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} v \\ g{\text{(}}r{\text{)}}{ + }{{h{\text{(}}v{\text{)}} - ({{{{{\mathbf{\lambda }}}_{v}}} \mathord{\left/ {\vphantom {{{{{\mathbf{\lambda }}}_{v}}} {{{{{\lambda }}}_{v}}}}} \right. \kern-0em} {{{{{\lambda }}}_{v}}}})u{{T}_{{\max }}}} \mathord{\left/ {\vphantom {{h{\text{(}}v{\text{)}} - ({{{{{\mathbf{\lambda }}}_{v}}} \mathord{\left/ {\vphantom {{{{{\mathbf{\lambda }}}_{v}}} {{{{{\lambda }}}_{v}}}}} \right. \kern-0em} {{{{{\lambda }}}_{v}}}})u{{T}_{{\max }}}} m}} \right. \kern-0em} m} \\ {{ - u{{T}_{{\max }}}} \mathord{\left/ {\vphantom {{ - u{{T}_{{\max }}}} c}} \right. \kern-0em} c} \\ - {{\partial g{\text{(}}r{\text{)}}} \mathord{\left/ {\vphantom {{\partial g{\text{(}}r{\text{)}}} {\partial r \cdot {{{\mathbf{\lambda }}}_{v}}}}} \right. \kern-0em} {\partial r \cdot {{{\mathbf{\lambda }}}_{v}}}} \\ - {{{\mathbf{\lambda }}}_{r}} - {{\partial h{\text{(}}v{\text{)}}} \mathord{\left/ {\vphantom {{\partial h{\text{(}}v{\text{)}}} {\partial v \cdot {{{\mathbf{\lambda }}}_{v}}}}} \right. \kern-0em} {\partial v \cdot {{{\mathbf{\lambda }}}_{v}}}} \\ {{ - {{{{\lambda }}}_{v}}u{{T}_{{\max }}}} \mathord{\left/ {\vphantom {{ - {{{{\lambda }}}_{v}}u{{T}_{{\max }}}} {{{m}^{2}}}}} \right. \kern-0em} {{{m}^{2}}}} \\ \end{gathered} \right], \\ \end{gathered} $
где ${\mathbf{\Phi }}$ – вектор состояния, который складывается из векторов координат, массы КА и сопряженных векторов: ${\mathbf{\Phi }} = {{\left[ {x,m,{\mathbf{\lambda }}} \right]}^{T}},$ $x = {{\left[ {r,v} \right]}^{T}}.$

После определения точки P $\left( {{{x}_{p}} = {{{\left[ {{{r}_{p}},{{v}_{p}}} \right]}}^{T}}} \right)$ строятся следующие условия трансверсальности:

(17)
$\begin{gathered} {\text{начальные}}\,\,{\text{условия:}}\,\,r({{t}_{0}}) = {{r}_{p}}, \\ v({{t}_{0}}) = {{v}_{p}},\,\,\,\,m({{t}_{0}}) = m* \\ {\text{конечные}}\,\,{\text{условия:}}\,\,r({{t}_{f}}) = {{r}_{p}}, \\ v({{t}_{f}}) = {{v}_{p}},\,\,\,\,{{\lambda }_{m}}({{t}_{f}}) = 0. \\ \end{gathered} $

Таким образом задача о генерации искусственных гало-орбит преобразуется в двухточечную краевую задачу. Решение данной задачи также выполняется с использованием метода коллокации и следующей методики:

1. В качестве начального приближения, требуемого методом коллокации, используется траектория КА движущемся от точки P по классической гало-орбите с периодом ${{t}_{f}}$ равным исходному орбитальному периоду T0, а максимальная величина тяги ${{T}_{{\max }}}$ считается равной нулю. При этом параметр регулирования $u \equiv 0,$ как для случая с $\varepsilon = 1,$ так и для $\varepsilon = 0.$

2. В случае $\varepsilon = 1$ используется метод продолжения по тяге двигателя для постепенного увеличения ${{T}_{{\max }}}$ до T1 без изменения ${{t}_{f}}.$ Поскольку начальным приближением решения является классическая гало-орбита, коэффициент регулирования двигателя u все еще остается постоянным и равным нулю, но из-за наличия тяги мы получаем орбиту, отличную от 1, которая обеспечивает начальное приближение для изменения орбитального периода ${{t}_{f}}$ на следующем шаге.

3. На основе обиты 2 при $\varepsilon = 1,$ проводится процесс перемещения по параметру, чтобы постепенно увеличивать (или уменьшать) орбитальный период ${{t}_{f}}$ для искусственной гало-орбиты. Для изменения ${{t}_{f}}$ двигатель должен включаться, поэтому коэффициент регулирования u постепенно начинает увеличиваться. Для одной и той же максимальной величины тяги ${{T}_{{\max }}},$ предельные значения до которых может увеличиваться или уменьшаться орбитальный период (обозначается как $t_{f}^{ + }$ и $t_{f}^{ - }$), соответствуют коэффициенту регулирования $u \equiv 1.$

4. После получения серии орбит оптимальных по критерию минимальной энергии для заданной ${{T}_{{\max }}}$ и диапазона орбитальных периодов от $t_{f}^{ - }$ до $t_{f}^{ + }$ на 3 шаге гомотопический параметр $\varepsilon $ уменьшается от 1 до 0 для получения семейства искусственных гало-орбит происходящих от исходной гало-орбиты оптимальных с точки зрения минимума расхода рабочего тела.

5. Затем возвращаемся к шагу 2, увеличиваем максимальную величину тяги ${{T}_{{\max }}}$ до другого уровня T2 и пересчитываем новое семейство искусственных орбит в соответствии с процедурами 2, 3 и 4.

В целом шаг 2 увеличивает амплитуду тяги с нулевой стоимостью; шаг 3 позволяет получить искусственную гало-орбиту с заданным периодом; 4 шаг – это процесс оптимизации гомотопического процесса, то есть переход от задачи оптимизации энергии к задаче оптимизации расхода рабочего тела. Проиллюстрируем методику генерирования искусственной гало-орбиты на примере трансформации устойчивой опорной гало-орбиты относительно L2. Параметры орбиты представлены в табл. 4. Исходной точкой расположения КА принята точка P, соответствующая максимальному отклонению Max|x|, так как именно эта точка удобна для выведения КА на орбиту. Кроме того, при выключенном двигателе данная орбита остается вблизи области устойчивых орбит.

Таблица 4.  

Параметры выбранной орбиты

Параметры Значение
Период T0 9.96 дней
Max|x| 34 368 км
$\left| {Az} \right|$ 77 751 км
φr 0

На рис. 9 представлена информация о нескольких искусственных орбитах, которые сгенерированы из гало-орбиты, описанной в табл. 4 при максимальной тяге ${{T}_{{\max }}} = 0.1$ Н, включая фигуры орбит, динамику изменения периода, коэффициента регулирования u и единичного вектора направления тяги α, а также мгновенные положения точки L2. Тонкой красной линией обозначен диапазон устойчивой классической гало-орбиты.

Рис. 9.

Формирование искусственных гало-орбит при ${{T}_{{\max }}}$ = 0.1 Н: (а) период 10.51 дней, потребление топлива 4.64 кг; (б) период 10.46 дней, потребление топлива 3.32 кг; (в) период 9.96 дней, потребление топлива 0 кг; (г) период 9.83 дней, потребление топлива 0.60 кг; (д) период 9.49 дней, потребление топлива 4.18 кг.

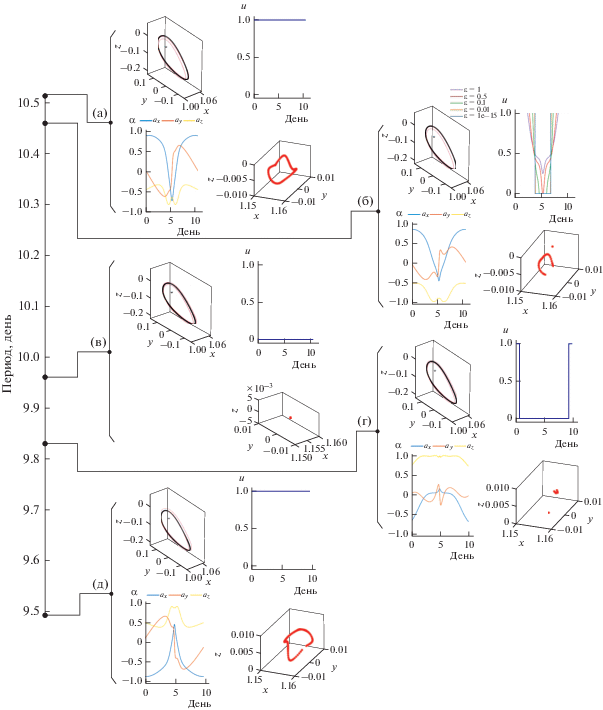
Орбитальный период изменяется от 9.49 до 10.51 дней, при этом форма орбиты существенно не изменяется. Процесс гомотопии показан на рис. 9б. По мере того, как параметр гомотопии ε уменьшается с 1 до 0, задача управления постепенно переходит от минимальной энергии к минимальному расходу топлива, создается ступенчатый профиль включения-выключения двигателя. Только при исходном орбитальном периоде ${{t}_{f}} = {{T}_{0}}$ не требуется включение двигателя, при увеличении или уменьшении периода требуется включать двигатель малой тяги для поддержания орбиты. Пределом, которого может достичь орбитальный период искусственных орбит является момент, при котором двигатель достигает полной нагрузки в течение всего полета КА, т.е. $u \equiv 1,$ как показано на рис. 9а и 9д. В остальных случаях u изменяется от 0 до 1.

С изменением величины тяги, можно получить все семейства искусственных гало-орбит, происходящих с этой гало-орбиты, которые изображены на рис. 10. Для одного и того же периода меньшая тяга требует меньшего расхода топлива, но большая тяга обеспечивает более широкий диапазон изменения орбитального периода. Стратегия генерации орбит может значительно изменять период, сохраняя при этом исходную форму гало-орбиты неизменной, что обеспечивает большую осуществимость миссии по сравнению со сценарием постоянной тяги.

Рис. 10.

Зависимость между расходами топлива и периодами семейства искусственных гало-орбит.

Для КА массой 1500 кг, тяга двигателя составляет от 0.02 до 0.2 Н, а расход топлива за один орбитальный период составляет менее 0.6% от общей массы, поэтому расчет показывает, что орбитальное управление и стратегия генерация орбиты осуществима.

Теперь обсудим изменение периода, когда исходная точка P находится в произвольном положении на орбите. Обозначим ${{\tau }} = {t \mathord{\left/ {\vphantom {t {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}$ – отношение времени полета КА от Max|x| до точки P по классической опорной гало-орбите $t$ к исходному орбитальному периоду T0. На рис. 11 показано изменение искусственных орбитальных периодов по параметру ${{\tau }}$ при различных уровнях тяги ${{T}_{{\max }}}.$ Пунктирная линия представляет период T0 классической гало-орбиты, выше находятся орбиты с искусственно увеличенным периодом, а ниже – с уменьшенным. Видно, что чем больше тяга, тем больше диапазон изменения периода и больше влияние ${{\tau }}$ на орбитальный период. Для ${{T}_{{\max }}}$ = 0.2 Н изменение диапазона периода составляет всего 0.2 дня, а при ${{T}_{{\max }}}$ = 0.02 Н меньше чем 0.02 дня.

Рис. 11.

Влияние положения отсчетной точки на верхнюю и нижнюю границы периода искусственных гало-орбит.

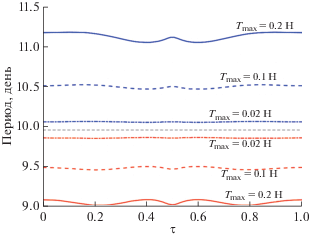
Мы также проанализировали случай, при котором ${{T}_{{\max }}}$ продолжает увеличиваться выше значения 0.2 Н. Хотя это имеет небольшое практическое значение из-за ограничений технологии современных электроракетных двигателей, но поведение динамики системы трех тел в этом случае можно исследовать. При изменении ${{T}_{{\max }}}$ от 0.2 до 1 Н кривая зависимости расхода топлива от орбитального периода представлена на рис. 12. Можно видеть, что в случае большей тяги, орбиты, полученные путем уменьшения орбитального периода ${{t}_{f}},$ аналогичны предыдущему анализу при использовании меньшей тяги (рис. 10). Существенные изменения происходят при ${{T}_{{\max }}} = 0.8$ и $1.0\,{\text{Н}}{\text{.}}$ Рассмотрим орбиту сформированную за счет работы двигателя с максимальной тягой ${{T}_{{\max }}}$ = 0.8 Н (рис. 12). Проводится метод продолжения по параметру для увеличения орбитального периода, а метод коллокации используется для решения задачи оптимального управления для каждого заданного периода. В отличие от сценария при меньшей тяге, надежный метод коллокации может найти набор сходящихся решений, даже если период увеличивается до большого значения. Построим график зависимости расхода рабочего тела от требуемого орбитального периода, как показано на рис. 12 и отметим две точки перегиба A и B.

Рис. 12.

Зависимость между расходом топлива и периодом семейства искусственных гало-орбит при изменении ${{T}_{{\max }}}$ от 0.2 до 1 Н.

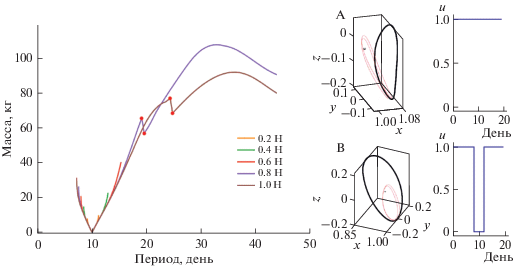
После отображения орбит, соответствующих точкам разрыва A и B, обнаруживаем, что орбита в точке A по-прежнему принадлежит искусственной гало-орбите, происходящей от исходной гало-орбиты, и двигатель все время работает с полной нагрузкой, $u \equiv 1.$ Однако орбита в точке B уже выходит из окрестности точки L2 в системе Земля–Луна, и КА вращается непосредственно вокруг Луны. Начиная с точки B постепенно уменьшаем ${{t}_{f}},$ т.е. перемещаемся по кривой зависимости масса-период в обратном направлении до точки C. Таким образом получаем другое семейство искусственных периодических орбит, как нарисовано красной пунктирной линией на рис. 13а. Этот тип орбиты исходит из точки C (или D) в зависимости от орбитального периода на орбите искусственных гало-орбит и постепенно превращается в орбиту вокруг точки L2 (рис. 13б).

Рис. 13.

(а) Два семейства искусственных орбит получены при ${{T}_{{\max }}}$ = 0.8 Н; (б) эволюция бифуркаций решений орбит.

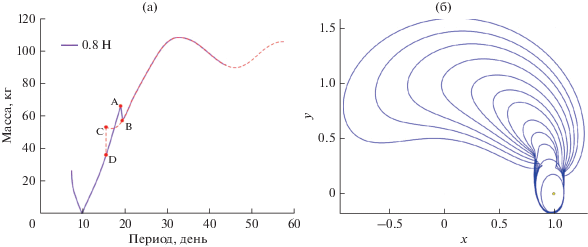
Итак, мы опознали бифуркацию решений: когда тяга ${{T}_{{\max }}}$ повышается до определенной степени, с увеличением орбитального периода ${{t}_{f}}$ искусственная орбита из классической гало-орбиты в коллинеарной точке постепенно превращается в искусственную орбиту вокруг треугольной точки либрации. Бифуркация решений для искусственных гало-орбит может являться темой последующих исследований, которые помогут глубже понять динамику естественных и искусственных систем трех тел.

ЗАКЛЮЧЕНИЕ

В данной статье анализируется возможность использования ускорения от двигательной установки малой тяги для формирования искусственных гало-орбит, формы и периоды которых отличаются от классических. Создание искусственных гало-орбит предназначено для обеспечения альтернативных рабочих орбит для будущих лунных миссий, например, если необходимая рабочая гало-орбита занята другими спутниками, или в случае необходимости выполнения орбитальной фазовой модуляции на той же гало-орбите.

При использовании постоянного ускорения фигуры и периоды сгенерированных искусственных гало-орбит изменяются одновременно. Кроме того, смещается область существования устойчивых орбит. Но применение такого управления на практике непросто. При использовании переменного ускорения учитывается расход рабочего тела и регулирование двигателей. При этом удается получить орбиты с практически неизменной формой, но с возможностью изменения орбитального периода, что обеспечивает большие возможности для будущих лунных миссий, а также позволяют осуществить фазовую модуляцию орбиты.

Например, для случая постоянной тяги из табл. 2 можно сделать вывод, что тяга 0.2 Н может изменить только периоды семейства гало-орбит вокруг точки L2 с 5.96–14.82 дней до 5.93–15.60 дней, и каждому значению ускорения соответствует один из периодов обращения. При управлении орбитой с переменной тягой под действием тяги 0.2 Н диапазон изменения периодов обращения значительно расширяется. Для исходной гало-орбиты с периодом обращения 9.96 дней период может быть изменен от 9.09 до 11.17 дней.

Выбранные в данной работе тяга двигателя, удельный импульс и расход топлива соответствуют современной технологии электроракетных двигателей, поэтому стратегия создания искусственных гало-орбит, предложенная в этой статье, является осуществимым и экономичным решением.

Список литературы

  1. Аксенов С.А., Бобер С.А. Управление движением космического аппарата на гало-орбите при наличии ограничений на направления корректирующих маневров. Некоторые аспекты современных проблем механики и информатики. М.: ИКИ РАН, 2018.

  2. Ильин И.С., Сазонов В.В., Тучин А.Г. Траектории перелета с низкой околоземной орбиты на многообразие ограниченных орбит в окрестности точки либрации L_2 системы Солнце–Земля. Препринты ИПМ им. М.В. Келдыша РАН. 2012. № 66.

  3. Шайхутдинов А.Р., Костенко В.И. Перспективы использования гало-орбиты в окрестности точки либрации L2 системы Солнце–Земля для наземно-космического радиоинтерферометра Миллиметрон // Космич. исслед. 2020. Т. 58. № 5. С. 434–442.

  4. Fain M.K., Starinova O.L. Ballistic optimization of the L1–L2 and L2–L1 low thrust transfers in the Earth-Moon system // 7th International Conference on Recent Advances in Space Technologies (RAST). IEEE, 2015.

  5. Farquhar R.W., Kamel A.A. Quasi-periodic orbits about the translunar libration point // Celestial mechanics. 1973. V. 7. № 4. P. 458–473.

  6. Richardson D.L. Analytic construction of periodic orbits about the collinear points // Celestial mechanics. 1980. V. 22. № 3. P. 241–253.

  7. Celletti A., Pucacco G., Stella D. Lissajous and Halo orbits in the restricted three-body problem // J. Nonlinear Science. 2015. V. 25. № 2. P. 343–370.

  8. Широбоков М.Г., Трофимов С.П. Перелеты с малой тягой на окололунные орбиты с гало-орбит вокруг лунных точек либрации L1 и L2 // Космич. исслед. 2020. Т. 58. № 3. С. 223–234.

  9. Biggs J.D., McInnes C., Waters T. New periodic orbits in the solar sail restricted three-body problem // 2nd Conference on Nonlinear Science and Complexity, 2008.

  10. Huang J., Biggs J.D., Cui N. Families of halo orbits in the elliptic restricted three-body problem for a solar sail with reflectivity control devices // Advances in Space Research. 2020. V. 65. № 3. P. 1070–1082.

  11. Lukyanov L.G. Stability of Coplanar libration points in the restricted photogravitational three-body problem // Soviet Astronomy. 1987. V. 31. № 6. P. 677–681.

  12. Куницын А.Л., Турешбаев А.Т. О компланарных точках либрации фотогравитационной задачи трех тел // Письма в Астрон. журн. 1983. Т. 9. № 7. С. 432–435.

  13. Chidambararaj P., Sharma R.K. Halo orbits around Sun-Earth L1 in photogravitational restricted three-body problem with oblateness of smaller primary // International J. Astronomy and Astrophysics. 2016. V. 6. № 3. P. 293–311.

  14. Pathak N., Thomas V.O., Abouelmagd E.I. The perturbed photogravitational restricted three-body problem: Analysis of resonant periodic orbits // Discrete & Continuous Dynamical Systems-S. 2019. V. 12. № 4–5. P. 849–875.

  15. Красильников П.С. Кривые Хилла и точки либрации в ограниченной круговой задаче трех тел с малым ускорением // Нелинейная динамика. 2017. Т. 13. № 4. С. 543–556.

  16. Baig S., McInnes C.R. Artificial halo orbits for low-thrust propulsion spacecraft // Celestial Mechanics and Dynamical Astronomy. 2009. V. 104. № 4. P. 321–335.

  17. Curtis H.D. Orbital mechanics for engineering students. Oxford: Butterworth-Heinemann, 2013.

  18. Иванюхин А.В., Петухов В.Г. Низкоэнергетические квазиоптимальные траектории с малой тягой к точкам либрации и гало-орбитам // Космич. исслед. 2020. Т. 58. № 2. С. 165–176.

  19. Ferrari F., Lavagna M. Periodic motion around libration points in the Elliptic Restricted Three-Body Problem // Nonlinear Dynamics. 2018. V. 93. № 2. P. 453–462.

  20. Trofimov S., Shirobokov M., Tselousova A. et al. Transfers from near-rectilinear halo orbits to low-perilune orbits and the Moon’s surface // Acta Astronautica. 2020. V. 167. P. 260–271.

  21. Koon W.S., Lo M.W., Marsden J.E. et al. Dynamical systems, the three-body problem and space mission design. Equadiff 99. 2000. V. 99. P. 1167–1181.

  22. Аксенов С.А., Бобер С.А. Расчет и исследование ограниченных орбит вокруг точки либрации L2 системы Солнце–Земля // Космич. исслед. 2018. Т. 56. № 2. С. 160–167.

  23. Howell K.C. Three-dimensional, periodic,‘halo’orbits // Celestial mechanics. 1984. V. 32. № 1. P. 53–71.

  24. Thurman R., Worfolk P.A. The geometry of halo orbits in the circular restricted three-body problem. University of Minnesota: Geometry Center Research Report GCG95, 1996.

  25. Grebow D.J., Ozimek M.T., Howell K.C. et al. Multibody orbit architectures for lunar south pole // J. Spacecraft and Rockets. 2008. V. 45. № 2. P. 344–358.

  26. Cielaszyk D., Wie B. New approach to halo orbit determination and control // J. guidance, control, and dynamics. 1996. V. 19. № 2. P. 266–273.

  27. Boudad K.K., Howell K.C., Davis D.C. Dynamics of synodic resonant near rectilinear halo orbits in the bicircular four-body problem // Advances in Space Research. 2020. V. 66. № 9. P. 2194–2214.

  28. Петухов В.Г. Метод продолжения для оптимизации межпланетных траекторий с малой тягой // Космич. исслед. 2012. Т. 50. № 3. С. 258–258.

  29. Петухов В.Г., Чжоу Ж. Расчет возмущенной импульсной траектории перелета между околоземной и окололунной орбитами методом продолжения по параметру // Вестник Московского авиационного института. 2019. Т. 26. № 2. С. 155–165.

  30. Mingotti G., Topputo F., Bernelli-Zazzera F. Combined Optimal Low-Thrust and Stable-Manifold Trajectories to the Earth-Moon Halo Orbits. AIP Conference Proceedings // American Institute of Physics, 2007. V. 886. № 1. P. 100–112.

  31. Pritchett R., Howell K., Grebow D. Low-thrust transfer design based on collocation techniques: applications in the restricted three-body problem // Astrodynamics Specialists Conference, 2017.

  32. Shampine L.F., Kierzenka J., Reichelt M.W. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c // Tutorial notes. 2000. P. 1–27.

  33. Higham D.J., Higham N.J. MATLAB guide. Society for Industrial and Applied Mathematics, 2016.

  34. Zhang C., Topputo F., Bernelli-Zazzera F. et al. Low-thrust minimum-fuel optimization in the circular restricted three-body problem // J. Guidance, Control, and Dynamics. 2015. V. 38. № 8. P. 1501–1510.

  35. Saghamanesh M., Baoyin H. A robust homotopic approach for continuous variable low-thrust trajectory optimization // Advances in Space Research. 2018. V. 62. № 11. P. 3095–3113.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал