Космические исследования, 2022, T. 60, № 2, стр. 134-150
Периодическая аппроксимация вращательного движения спутника Фотон-12
Д. М. Буланов 1, В. В. Сазонов 2, *
1 Московский государственный университет им. М.В. Ломоносова
Москва, Россия
2 Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
* E-mail: sazonov@keldysh.ru
Поступила в редакцию 11.07.2021
После доработки 18.08.2021
Принята к публикации 25.08.2021
- EDN: HXEELG
- DOI: 10.31857/S0023420622020017
Аннотация
Описаны результаты повторной обработки магнитных измерений, выполненных на спутнике Фотон-12 (находился на орбите 9.IX–24.IX.1999). Обработка проводилась для реконструкции неуправляемого вращательного движения этого спутника. При повторной обработке использовалась упрощенная математическая модель вращательного движения. Фактическая орбита спутника (высота апогея 380 км, высота перигея 220 км) заменена круговой орбитой, упрощено выражение для действующего на спутник аэродинамического момента. Лежащая в основе новой модели система дифференциальных уравнений автономна и оказалась достаточно точной для реконструкции движения спутника по магнитным измерениям в случае, когда угловая скорость спутника была не очень мала и постепенно возрастала. В последней трети полета, когда движение спутника практически установилось и имело достаточно большую угловую скорость, эту систему можно свести к обобщенно-консервативной системе. Такое сведение делает более определенным набор ее решений, подходящих для приближенного описания реального движения спутника. На некоторых отрезках движения, объединение которых охватывает примерно 3 сут, для этой цели удалось использовать периодические решения, продолженные из периодических решений Ляпунова.
ВВЕДЕНИЕ
Данная статья является продолжением работ [1, 2]. В [1] проведена повторная обработка магнитных измерений, выполненных в 1999 г. на спутнике Фотон-12. Первоначальная обработка была сделана вскоре после полета [3] с использованием детальной модели вращательного движения этого спутника. Модель, принятая в [1], проще модели [3], но сравнима с ней по точности при реконструкции движения с не очень малой угловой скоростью. Модель [1] позволила реконструировать эволюцию фактического движения Фотон-а-12 с возрастающей угловой скоростью. Ниже используется еще более простая модель, в которой реальная орбита спутника (высота апогея 380 км, высота перигея 220 км), заменена круговой орбитой. Эта замена позволила описать вращательное движение спутника автономными дифференциальными уравнениями, которые в случае установившегося движения с достаточно большой угловой скоростью (результат указанной выше эволюции) можно свести к обобщенно-консервативной системе. Такое сведение позволило приближенно, но достаточно точно описать реальное движение спутника на отрезках времени до 3.5 ч периодическими решениями, продолженными из периодических решений Ляпунова. Подходящие для этой цели периодические решения были изучены в [2]. Там же отмечалось их сходство с фактически вращательным движением Фотон-12. Однако такое сходство не было исследовано детально. Ниже такое исследование проводится.
УРАВНЕНИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ СПУТНИКА
Спутник считаем осесимметричным твердым телом, центр масс которого движется по неизменной круговой орбите. Для записи уравнений движения спутника введем четыре правых декартовых системы координат.
Система $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ образована главными центральными осями инерции спутника. Точка $O$ – центр масс спутника, ось $O{{x}_{1}}$ – ось материальной симметрии спутника. Эта ось близка к продольной оси спутника и направлена от спускаемого аппарата к приборному отсеку. Момент инерции спутника относительно оси $O{{x}_{1}}$ обозначим ${{I}_{1}},$ равные моменты инерции относительно осей $O{{x}_{2}}$ и $O{{x}_{3}}$ обозначим ${{I}_{2}}.$
Вспомогательная система координат $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ служит для записи уравнений вращательного движения спутника. Ось $O{{y}_{1}}$ совпадает с осью $O{{x}_{1}};$ оси $O{{x}_{2}},$ $O{{x}_{3}}$ получаются из осей $O{{y}_{2}},$ $O{{y}_{3}}$ поворотом системы $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ на угол $\chi $ вокруг оси $O{{y}_{1}}.$ Кинематическая связь между системами $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ и $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ задается условием, что проекция абсолютной угловой скорости второй из них на ось $O{{y}_{1}}$ равна нулю. Проекции этой угловой скорости на оси $O{{y}_{2}},$ $O{{y}_{3}}$ обозначим ${{w}_{2}},$ ${{w}_{3}}.$ Пусть абсолютная угловая скорость спутника ${\mathbf{\omega }}$ имеет в системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ компоненты $({{\omega }_{1}},{{\omega }_{2}},{{\omega }_{3}}).$ Тогда $\dot {\chi } = {{\omega }_{1}}$ и
(1)
$\begin{gathered} {{\omega }_{2}} = {{w}_{2}}\cos \chi + {{w}_{3}}\sin \chi ,\,\, \\ {{\omega }_{3}} = - {{w}_{2}}\sin \chi + {{w}_{3}}\cos \chi . \\ \end{gathered} $В приборной системе координат $O{{z}_{1}}{{z}_{2}}{{z}_{3}}$ интерпретируются данные измерений бортовых магнитометров. Эту систему можно перевести в систему $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ двумя последовательными поворотами. Первый поворот выполняется на угол ${{\alpha }_{c}}$ вокруг оси $O{{z}_{2}},$ второй поворот – на угол ${{\beta }_{c}}$ – выполняется вокруг оси $O{{z}_{3}},$ получившийся после первого поворота. В общем случае, чтобы задать положение одной системы координат относительно другой, необходимы три угла. В данном случае можно было бы ввести еще угол поворота приборной системы вокруг ее оси $O{{z}_{1}},$ получившейся после первых двух поворотов. Однако поскольку направление одной из осей $O{{x}_{2}},$ $O{{x}_{3}}$ можно выбирать произвольно, третий угол удобно принять равным нулю, фиксировав тем самым положение системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ относительно системы $O{{z}_{1}}{{z}_{2}}{{z}_{3}}.$ Матрицу перехода между этими системами координат обозначим $\left\| {{{b}_{{ij}}}} \right\|_{{i,j = 1}}^{3},$ где ${{b}_{{ij}}}$ – косинус угла между осями $O{{z}_{i}}$ и $O{{x}_{j}}.$ Элементы этой матрицы выражаются через углы ${{\alpha }_{c}}$ и ${{\beta }_{c}}$ по формулам
Система уравнений вращательного движения спутника образована динамическими уравнениями Эйлера для угловых скоростей ${{w}_{2}},$ ${{w}_{3}}$ и кинематическими уравнениями Пуассона для первой и третьей строк матриц $\left\| {{{a}_{{ij}}}} \right\|.$ В уравнениях Эйлера учитываются гравитационный и восстанавливающий аэродинамический моменты, а также постоянный момент вдоль оси $O{{x}_{1}}.$ При вычислении аэродинамического момента атмосфера считается неподвижной в абсолютном пространстве, ее плотность вдоль орбиты постоянна, внешняя оболочка спутника принимается сферой с центром на оси $O{{x}_{1}}.$ При сделанных допущениях аэродинамический момент характеризуется одним скалярным параметром. Система уравнений вращательного движения имеет вид [4, 5]
(2)
$\begin{gathered} {{{\dot {w}}}_{2}} + \lambda {{\omega }_{1}}{{w}_{3}} = - 3\omega _{0}^{2}(1 - \lambda ){{a}_{{31}}}{{a}_{{23}}} + p{{a}_{{13}}}, \\ {{{\dot {w}}}_{3}} - \lambda {{\omega }_{1}}{{w}_{2}} = 3\omega _{0}^{2}(1 - \lambda ){{a}_{{31}}}{{a}_{{32}}} - p{{a}_{{12}}}, \\ {{{\dot {a}}}_{{11}}} + {{w}_{2}}{{a}_{{13}}} - {{w}_{3}}{{a}_{{12}}} = - {{\omega }_{0}}{{a}_{{31}}}, \\ {{{\dot {a}}}_{{12}}} + {{w}_{3}}{{a}_{{11}}} = - {{\omega }_{0}}{{a}_{{32}}},\,\,\,\,{{{\dot {a}}}_{{13}}} - {{w}_{2}}{{a}_{{11}}} = - {{\omega }_{0}}{{a}_{{33}}}, \\ {{{\dot {a}}}_{{31}}} + {{w}_{2}}{{a}_{{33}}} - {{w}_{3}}{{a}_{{32}}} = {{\omega }_{0}}{{a}_{{11}}}, \\ {{{\dot {a}}}_{{32}}} + {{w}_{3}}{{a}_{{31}}} = {{\omega }_{0}}{{a}_{{12}}},\,\,\,\,{{{\dot {a}}}_{{31}}} - {{w}_{2}}{{a}_{{31}}} = {{\omega }_{0}}{{a}_{{13}}}, \\ {{\omega }_{1}} = \Omega + \varepsilon (t - {{t}_{0}}),\,\,\,\,\lambda = \frac{{{{I}_{1}}}}{{{{I}_{2}}}}. \\ \end{gathered} $При численном интегрировании уравнений (2) единицей измерения времени служит 103 c, единицы измерения других величин: $[{{\omega }_{i}}] = [{{w}_{i}}] = {{10}^{{ - 3}}}\,\,{{{\text{c}}}^{{ - 1}}},$ $[\varepsilon ] = [p] = {{10}^{{ - 6}}}\,\,{{{\text{c}}}^{{ - 2}}}.$ Переменные ${{a}_{{1i}}}$ и ${{a}_{{3i}}}$ зависимы, они связаны условиями ортогональности матрицы $\left\| {{{a}_{{ij}}}} \right\|.$ По этой причине начальные условия ${{a}_{{1i}}}({{t}_{0}})$ и ${{a}_{{3i}}}({{t}_{0}})$ выражаются через углы $\psi ,$ $\theta $ и $\delta .$ Элементы второй строки матрицы $\left\| {{{a}_{{ij}}}} \right\|$ вычисляются как векторное произведение ее третьей и первой строк. Формулы (1) и соотношение $\chi = \Omega (t - {{t}_{0}}) + {{\varepsilon {{{(t - {{t}_{0}})}}^{2}}} \mathord{\left/ {\vphantom {{\varepsilon {{{(t - {{t}_{0}})}}^{2}}} 2}} \right. \kern-0em} 2}$ позволяют найти функции ${{\omega }_{2}}(t),$ ${{\omega }_{3}}(t)$ и движение системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}},$ решая уравнения (2).
Параметр $\lambda $ известен: $\lambda \approx 0.24.$ Тем не менее, он и параметры $p$ и $\varepsilon $ определяются из обработки данных измерений наряду с неизвестными начальными условиями движения спутника, т.е. служат параметрами согласования.
Уравнения (2) получены из аналогичных уравнений вращательного движения [1] переходом к круговой орбите и использованием орбитальной системы координат в качестве системы, относительно которой рассматривается движение спутника. Для компенсации всех сделанных упрощений реконструировались движения спутника, в которых компонента угловой скорости ${{\omega }_{1}}$ достаточно велика. Обработка измерений с помощью уравнений (2) выполнялась по схеме [1] и дала близкие результаты.
РЕКОНСТРУКЦИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ СПУТНИКА ПО МАГНИТНЫМ ИЗМЕРЕНИЯМ
На борту Фотона-12 находилась аппаратура “Мираж” с несколькими трехкомпонентными магнитометрами. Поскольку движение спутника было неуправляемым, данные измерений этой аппаратуры и уравнения (2) можно использовать для определения фактического вращательного движения спутника по обычным статистическим методикам. Методика, использованная ниже, состоит в следующем [1, 4]. По измерениям, выполненным на некотором отрезке времени ${{t}_{0}} \leqslant t \leqslant {{t}_{0}} + T,$ строились функции ${{\hat {h}}_{i}}(t),$ которые задавали на этом отрезке компоненты вектора местной напряженности магнитного поля в системе координат $O{{z}_{1}}{{z}_{2}}{{z}_{3}}.$ Среднеквадратичные ошибки аппроксимации не превышали 200$\gamma $ ($1\gamma = {{10}^{{ - 5}}}$ Э). Затем вычислялись псевдоизмерения $h_{i}^{{(n)}} = {{\hat {h}}_{i}}({{t}_{n}}),$ ${{t}_{n}} = {{t}_{0}} + {{nT} \mathord{\left/ {\vphantom {{nT} N}} \right. \kern-0em} N},$ где $n = 0,1,2,...N.$ Обычно было $T = 100{\kern 1pt} - {\kern 1pt} 300$ мин, ${T \mathord{\left/ {\vphantom {T N}} \right. \kern-0em} N} \approx 1$ мин. Псевдоизмерения служили исходной информацией для отыскания решений уравнений (2), описывающих фактическое движение спутника.
В соответствии с методом наименьших квадратов реконструкцией фактического движения спутника считалось решение уравнений (2), доставляющее минимум функционалу
(3)
$\begin{gathered} \Phi = \sum\limits_{i = 1}^3 {\left\{ {\sum\limits_{n = 0}^N {{{{\left[ {h_{i}^{{(n)}} - {{h}_{i}}({{t}_{n}})} \right]}}^{2}} - (N + 1)\Delta _{i}^{2}} } \right\}} , \\ {{\Delta }_{i}} = \frac{1}{{N + 1}}\sum\limits_{n = 0}^N {\left[ {h_{i}^{{(n)}} - {{h}_{i}}({{t}_{n}})} \right]} ,\,\,\,\,{{h}_{i}}(t) = \sum\limits_{j = 1}^3 {{{b}_{{ij}}}h_{j}^{^\circ }(t)} . \\ \end{gathered} $Чтобы использовать уравнения (2) для вычисления функционала (3), необходимо задать связь системы $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ с гринвичской системой координат, в которой задана реальная орбита спутника и вычисляется напряженность магнитного поля Земли. С этой целью фактическая орбита спутника на отрезке ${{t}_{0}} \leqslant t \leqslant {{t}_{0}} + T$ аппроксимировалась круговой орбитой. Аппроксимация строилась методом наименьших квадратом по достаточно точным значениям реального фазового вектора центра масс спутника, заданным на равномерной сетке с шагом 3 мин. Круговая орбита задавалась 5-ю элементами: радиусом, средним движением (орбитальной частотой ${{\omega }_{0}}$), начальным значением аргумента широты, долготой восходящего узла и наклонением. Вдоль круговой орбиты вычислялись компоненты напряженности МПЗ в системе координат $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ на моменты ${{t}_{n}}.$ Эти компоненты использовались при многократном вычислении функционала (3) в процессе его минимизации. С помощью решения уравнений (2) они пересчитывались в систему $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ и затем в систему $O{{x}_{1}}{{x}_{2}}{{x}_{3}}.$ В качестве ${{t}_{0}}$ в уравнениях (2) всегда использовалась начальная точка обрабатываемого отрезка данных.
Оценку приемлемости сделанного перехода к круговой орбите, а также оценку ожидаемой точности аппроксимации псевдоизмерений экстремалью функционала (3) дает минимизация функции
При $T = 210$ мин для большинства отрезков псевдоизмерений среднеквадратичное отклонение ${{\sigma }_{ * }} = \sqrt {{{{{\Psi }_{{\min }}}} \mathord{\left/ {\vphantom {{{{\Psi }_{{\min }}}} {(N - 3)}}} \right. \kern-0em} {(N - 3)}}} $ лежит в пределах 1600–2000γ. При расчете ${{\Psi }_{{\min }}}$ с использованием реальной орбиты ${{\sigma }_{ * }}$ меньше и лежит в пределах 1400–1600γ. Два примера минимизации функции $\Psi $ приведены на рис. 1. В верхней части рисунка сравниваются модули вектора напряженности МПЗ, рассчитанные по скорректированным псевдоизмерениям и по модели IGRF. Расчет по псевдоизмерениям представлен маркерами, расчет по модели IGRF – сплошными линиями. Графики в нижней части рисунка характеризуют отклонения псевдоизмерений от модели. Эти графики – ломаные, вершины которых отвечают ошибкам аппроксимации. В подписи к рисунку указаны значения ${{\sigma }_{ * }}$; рядом с ними в скобках указаны значения ${{\sigma }_{ * }}$, полученные с использованием реального орбитального движения. В функционал (3) подставлялись псевдоизмерения, масштаб которых был скорректирован множителем $\kappa .$ Значения этого множителя уточнялись для каждого обрабатываемого отрезка данных.
Рис. 1.
Сравнение модулей измеренной и расчетной напряженности МПЗ; (а) момент времени ${{t}_{0}} = 0{\text{1:39:31}}$ UTC 13.IX.1999, ${{\sigma }_{ * }} = 1561(1374)\gamma ;$ (б) момент времени ${{t}_{0}} = {\text{18:50:05}}$ UTC 18.IX.1999, ${{\sigma }_{ * }} = 2059(1649)\gamma .$

Функционал (3) минимизировался по 11 величинам: начальным условиям решения системы (2) $\psi ({{t}_{0}}),$ $\theta ({{t}_{0}}),$ $\delta ({{t}_{0}}),$ $\Omega ,$ ${{w}_{2}}({{t}_{0}}),$ ${{w}_{3}}({{t}_{0}})$ и параметрам $\lambda ,$ $p,$ $\varepsilon ,$ ${{\alpha }_{c}},$ ${{\beta }_{c}}.$ Заключительный этап минимизации выполнялся методом Гаусса–Ньютона. Точность аппроксимации псевдоизмерений и разброс в оцениваемых величинах характеризовались соответствующими стандартными отклонениями. Стандартные отклонения рассчитывались в предположении, что ошибки в псевдоизмерениях $h_{i}^{{(n)}}$ некоррелированы и имеют одинаковые дисперсии, средние значения ошибок в псевдоизмерениях с одинаковым нижним индексом $i$ одинаковы (величины ${{\Delta }_{i}}$ в (3) – оценки этих средних значений). Стандартные отклонения вычислялись так. Пусть ${{\Phi }_{{\min }}}$ – значение функционала (3) в точке минимума, $C$ – матрица системы нормальных уравнений метода Гаусса–Ньютона в этой точке (матрица $2C$ приблизительно равна матрице квадратичной формы ${{d}^{2}}\Phi $ в точке минимума $\Phi $). Тогда дисперсия ошибок в псевдоизмерениях оценивается величиной $\sigma _{H}^{2} = {{{{\Phi }_{{\min }}}} \mathord{\left/ {\vphantom {{{{\Phi }_{{\min }}}} {(3N - 11)}}} \right. \kern-0em} {(3N - 11)}}.$ Стандартные отклонения оцениваемых величин равны квадратным корням из соответствующих диагональных элементов матрицы $\sigma _{H}^{2}{{C}^{{ - 1}}}.$ Эти стандартные обозначим ${{\sigma }_{\psi }},$ ${{\sigma }_{\theta }},$ ${{\sigma }_{\delta }},$ ${{\sigma }_{\Omega }},$ ${{\sigma }_{{w2}}},$ ${{\sigma }_{{w3}}},$ ${{\sigma }_{\lambda }},$ ${{\sigma }_{p}},$ ${{\sigma }_{\varepsilon }},$ ${{\sigma }_{{\alpha c}}},$ ${{\sigma }_{{\beta c}}}.$
Движение спутника Фотон-12 реконструировано на 25 временных интервалах [5]. Некоторые результаты реконструкции, относящиеся к интервалам 10–25 приведены в табл. 1, реконструкции движения на интервалах 14 и 17 представлены на рис. 2–4. В подписях к рисункам и в таблице использовано Всемирное координированное время (UTC). В табл. 1 приведены начальные точки интервалов ${{t}_{0}}$ и их фактическая длина T. Номинальная длина $T = 210$ мин выбрана таким образом, чтобы получаемые значения ${{\sigma }_{H}}$ не более чем в 2 раза превышали указанные выше типичные значения ${{\sigma }_{ * }}.$ Иными словами, чтобы принятая модель движения была достаточно адекватна. Поскольку принятая модель является упрощенной, с ее помощью реконструировались движения спутника с заметной угловой скоростью, которые возникли через несколько (~2) суток после начала неуправляемого движения. Табл. 1 содержит данные по интервалам, на которых угловая скорость достаточно большая.
Таблица 1.
Результаты обработки измерений МПЗ на спутнике Фотон-12
| № инт. | Дата 09.1999 |
${{t}_{0}}$ UTC |
$T$, мин |
${{\sigma }_{H}}$, $\gamma $ |
${{\bar {\omega }}_{1}}$, град/с |
$\delta {{\omega }_{1}}$, град/с |
${{\bar {\omega }}_{ \bot }}$, град/с |
$\delta {{\omega }_{ \bot }}$, град/с |
|---|---|---|---|---|---|---|---|---|
| 10 | 15 | 13:18:34 | 210 | 2835 | 0.8169 | 0.0039 | 0.1611 | 0.0069 |
| 11 | 15 | 23:40:47 | 210 | 2308 | 0.8526 | 0.0007 | 0.1437 | 0.0090 |
| 12 | 16 | 11:40:41 | 210 | 2296 | 0.8746 | 0.0050 | 0.1439 | 0.0079 |
| 13 | 16 | 16:59:44 | 210 | 2409 | 0.8894 | 0.0042 | 0.1439 | 0.0068 |
| 14 | 17 | 19:05:14 | 210 | 2043 | 0.9380 | 0.0009 | 0.1577 | 0.0055 |
| 15 | 18 | 18:33:07 | 210 | 2181 | 0.9696 | 0.0005 | 0.1788 | 0.0054 |
| 16 | 18 | 21:54:51 | 210 | 2192 | 0.9867 | 0.0040 | 0.1658 | 0.0052 |
| 17 | 19 | 08:54:51 | 210 | 1924 | 1.0099 | 0.0014 | 0.1083 | 0.0044 |
| 18 | 19 | 21:55:05 | 197 | 1810 | 1.0165 | 0.0008 | 0.0962 | 0.0056 |
| 19 | 20 | 07:55:22 | 206 | 2248 | 1.0280 | 0.0005 | 0.1472 | 0.0064 |
| 20 | 20 | 19:56:17 | 210 | 3260 | 1.0361 | 0.0010 | 0.1487 | 0.0057 |
| 21 | 21 | 05:50:08 | 210 | 2261 | 1.0428 | 0.0011 | 0.1295 | 0.0082 |
| 22 | 21 | 21:13:34 | 210 | 2639 | 1.0394 | 0.0060 | 0.1423 | 0.0096 |
| 23 | 22 | 07:55: 02 | 210 | 2694 | 1.0498 | 0.0034 | 0.1313 | 0.0068 |
| 24 | 22 | 22:54:54 | 210 | 2376 | 1.0452 | 0.0014 | 0.1376 | 0.0067 |
| 25 | 23 | 02:53:52 | 275 | 3119 | 1.0276 | 0.0022 | 0.1646 | 0.0079 |
Рис. 2.
Аппроксимация магнитных измерений; (а) на интервале 14, ${{\sigma }_{H}} = 2043\gamma ;$ (б) на интервале 17, ${{\sigma }_{H}} = 1924\gamma .$

Рис. 3.
Компоненты угловой скорости ${{w}_{2}},{{w}_{3}};$ (а) на интервале 14, $0.9364 \leqslant {{\omega }_{1}} \leqslant \;0.9395$ град/с; (б) на интервале 17, $1.0074 \leqslant {{\omega }_{1}} \leqslant \;1.0124$ град/с.

Рис. 2 иллюстрирует типичное качество аппроксимации псевдоизмерений. Здесь сплошными линиями изображены графики функций ${{h}_{i}}(t)$ при ${{t}_{0}} \leqslant t \leqslant {{t}_{0}} + T,$ маркеры указывают точки $\left( {{{t}_{n}},h_{i}^{{(n)}} - {{\Delta }_{i}}} \right),$ $n = 0,1,2,...,N.$ Количественно аппроксимация псевдоизмерений характеризуется стандартными отклонениями ${{\sigma }_{H}},$ значения которых приведены в табл. 1 и в подписи к рисунку. Значения ${{\sigma }_{H}}$ в табл. 1 несколько выше, чем в [1]. Тем не менее, достигнутая точность достаточна для целей данной работы.
На рис. 3 помещены графики компонент угловой скорости ${{w}_{2}}$ и ${{w}_{3}}.$ Компонента угловой скорости ${{\omega }_{1}}$ в движении на рис. 3а монотонно убывает, а в движении на рис. 3б монотонно возрастает. Пределы изменения этой переменной указаны в подписи к рисунку.
По мере увеличения компоненты ${{\omega }_{1}}$ движение спутника становилось все больше похоже на регулярную прецессию Эйлера осесимметричного твердого тела. Формирование регулярной прецессии с медленно возрастающей угловой скоростью ${{\omega }_{1}}$ и мало меняющимся значением ${{\omega }_{ \bot }} = \sqrt {w_{2}^{2} + w_{3}^{2}} $ завершилось после нескольких суток полета.
Точная регулярная прецессия Эйлера может иметь место лишь в случае, когда спутник осесимметричен и главный момент приложенных к нему внешних сил равен нулю. Тогда величины ${{\omega }_{1}}$ и $\omega {}_{ \bot }$ остаются неизменными во время движения. Для используемой модели первое условие выполнено, а второе – нет. По этой причине можно говорить лишь о движениях, близких к регулярной прецессии. Такие движения удобно характеризовать величинами
На рис. 4 приведены графики зависимости от времени углов $\psi $ и $\theta ,$ задающих положение оси $O{{x}_{1}}$ относительно координат $O{{X}_{1}}{{X}_{2}}{{X}_{3}}.$ Эти углы рассчитывались с использованием формул
Дополнительную информацию о движении спутника дает рис. 5. Здесь для двух рассмотренных выше реконструкций приведены графики угла $\alpha $ между осью $O{{x}_{1}}$ и вектором кинетического момента спутника в его движении относительно центра масс и угла $\rho $ между этим вектором и осью $O{{X}_{2}}.$ В регулярной прецессии Эйлера $\alpha = {\text{const}}{\text{.}}$ В примерах на рис. 5 этот угол меняется в достаточно узких пределах вблизи значений ${{\alpha }_{ * }} = {\text{arctg(}}{{{{{\bar {\omega }}}_{ \bot }}} \mathord{\left/ {\vphantom {{{{{\bar {\omega }}}_{ \bot }}} {\lambda {{{\bar {\omega }}}_{1}}}}} \right. \kern-0em} {\lambda {{{\bar {\omega }}}_{1}}}}{\text{),}}$ указанных в подписи к рисунку. Вектор кинетического момента колеблется вблизи оси $O{{X}_{2}}$ (см. графики угла $\rho $), угловая скорость которой менее 5 град/сут. Движения такого типа имели место 15–19.IX, в частности, на интервалах 10 и 14–18. Оценки параметров $p,$ $\lambda ,$ $\varepsilon ,$ ${{\alpha }_{c}},$ ${{\beta }_{c}}$ и их стандартные отклонения для этих интервалов приведены в табл. 2. Здесь углы выражены в радианах, величины $p$ и $\varepsilon $ – в единицах ${{10}^{{ - 6}}}\,{{{\text{c}}}^{{ - 2}}}.$ Данные этой таблицы характерны для всех интервалов 1–25 [5]. Стандартные отклонения начальных условий реконструкций на интервалах 1–25, выраженные в радианах и 0.001 с–1, лежат в диапазонах [5]: ${{\sigma }_{\delta }} = 0.01{\kern 1pt} - {\kern 1pt} 0.025,$ ${{\sigma }_{{\theta ,\psi }}} = 0.01{\kern 1pt} - {\kern 1pt} 0.02,$ ${{\sigma }_{\Omega }} = 0.01{\kern 1pt} - {\kern 1pt} 0.025,$ ${{\sigma }_{{w2,w3}}} = 0.02{\kern 1pt} - {\kern 1pt} 0.08.$ Приведенные примеры демонстрируют менее точную, чем в [1, 3], аппроксимацию псевдоизмерений. Значения ${{\sigma }_{H}}$ в табл. 1 несколько выше, чем в [1, 3]. Тем не менее, реконструкции данной работы передают все особенности вращательного движения спутника.
Рис. 5.
Угол нутации спутника $\alpha $ и угол $\rho $ между вектором кинетического момента спутника относительно центра масс и осью $O{{X}_{2}};$ (а) на интервале 14, ${{\alpha }_{ * }} = 35.4^\circ ;$ (б) на интервале 17, ${{\alpha }_{ * }} = 24.3^\circ .$
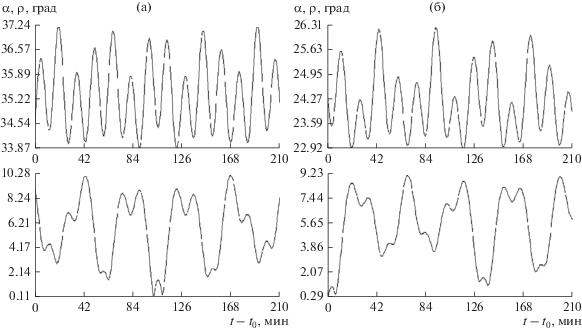
Таблица 2.
Оценки и стандартные отклонения параметров уравнений движения
| № инт. | $p$ | ${{\sigma }_{p}}$ | $\lambda $ | ${{\sigma }_{\lambda }}$ | $\varepsilon $ | ${{\sigma }_{\varepsilon }}$ | ${{\alpha }_{c}}$ | ${{\sigma }_{{\alpha c}}}$ | ${{\beta }_{c}}$ | ${{\sigma }_{{\beta c}}}$ |
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | –0.0187 | 0.041 | 0.2323 | 0.0013 | 0.0185 | 0.0011 | $ - 0.0120$ | 0.0065 | $ - 0.0665$ | 0.0065 |
| 14 | –0.0300 | 0.033 | 0.2362 | 0.0013 | –0.0044 | 0.00069 | $ - 0.0344$ | 0.0045 | $ - 0.0563$ | 0.0045 |
| 15 | –0.0802 | 0.043 | 0.2302 | 0.00085 | 0.0023 | 0.00079 | $ - 0.0149$ | 0.0047 | $ - 0.0638$ | 0.0047 |
| 16 | –0.0846 | 0.046 | 0.2395 | 0.00075 | 0.0194 | 0.00072 | $ - 0.0296$ | 0.0049 | $ - 0.0560$ | 0.0049 |
| 17 | 0.0216 | 0.029 | 0.2403 | 0.00059 | 0.0070 | 0.00071 | $ - 0.0461$ | 0.0053 | $ - 0.0591$ | 0.0053 |
| 18 | –0.2518 | 0.029 | 0.2379 | 0.00051 | 0.0041 | 0.00070 | $ - 0.0531$ | 0.0044 | $ - 0.0651$ | 0.0044 |
Интервалы 10 и 14–18 представляют особый интерес для дальнейшего, поскольку движения на них допускают приемлемую аппроксимацию периодическими движениями обобщенно-консервативной механической системы.
ОБОБЩЕННО-КОНСЕРВАТИВНАЯ МОДЕЛЬ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ СПУТНИКА
Как видно из табл. 1, значения ${{\bar {\omega }}_{1}}$ со временем стабилизировались. По-видимому, возрастал не учитываемый в уравнениях (2) момент сопротивления, пропорциональный ${{\omega }_{1}}$ [1]. На интервалах из той части табл. 1, где значения $\varepsilon $ малы, для реконструкции движения спутника можно использовать решения уравнений (2) при $\varepsilon = 0.$ Графики, иллюстрирующие такую реконструкцию на интервалах 10 и 14–18, приведены в [5]. Они очень похожи на графики, полученные с помощью исходной системы (2), но имеют увеличенные значения ${{\sigma }_{H}}.$ Эти значения на указанных интервалах приведены в табл. 3 вместе с оценками величин $\Omega ,$ $p,$ $\lambda ,$ ${{\alpha }_{c}},$ ${{\beta }_{c}}$ и их стандартными отклонениями. В этой таблице $[\Omega ] = 0.001\,\,{{{\text{c}}}^{{ - 1}}},$ $[p] = {{10}^{{ - 6}}}\,\,{{{\text{c}}}^{{ - 2}}}.$ Сравнение данных в табл. 2 и 3 позволяет понять, что дало сделанное огрубление модели. Найденные при новой обработке значения $\Omega $ весьма близки соответствующим значениям ${{\bar {\omega }}_{1}}$ из табл. 1.
Таблица 3.
Оценки и стандартные отклонения параметров уравнений движения при $\varepsilon = 0$
| № инт. | ${{\sigma }_{H}}$, $\gamma $ | $\Omega $ | ${{\sigma }_{\Omega }}$ | $p$ | ${{\sigma }_{p}}$ | $\lambda $ | ${{\sigma }_{\lambda }}$ | ${{\alpha }_{c}}$ | ${{\sigma }_{{\alpha c}}}$ | ${{\beta }_{c}}$ | ${{\sigma }_{{\beta c}}}$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 3393 | 14.199 | 0.027 | –0.1388 | 0.049 | 0.2281 | 0.0015 | $ - 0.0114$ | 0.0078 | $ - 0.0667$ | 0.0078 |
| 14 | 2107 | 16.372 | 0.026 | –0.0372 | 0.033 | 0.2362 | 0.0014 | $ - 0.0345$ | 0.0047 | $ - 0.0565$ | 0.0047 |
| 15 | 2193 | 16.920 | 0.017 | –0.0802 | 0.043 | 0.2302 | 0.00085 | $ - 0.0149$ | 0.0047 | $ - 0.0638$ | 0.0047 |
| 16 | 3228 | 17.253 | 0.022 | 0.0969 | 0.066 | 0.2415 | 0.0010 | $ - 0.0302$ | 0.0072 | $ - 0.0552$ | 0.0072 |
| 17 | 2063 | 17.622 | 0.014 | –0.0159 | 0.031 | 0.2398 | 0.00064 | $ - 0.0451$ | 0.0057 | $ - 0.0597$ | 0.0056 |
| 18 | 1862 | 17.739 | 0.011 | –0.2323 | 0.030 | 0.2379 | 0.00052 | $ - 0.0532$ | 0.0045 | $ - 0.0651$ | 0.0045 |
Ниже в этом разделе полагаем в (2) $\varepsilon = 0,$ ${{\omega }_{1}} = \Omega $ и считаем $\Omega $ параметром. Уравнения (2) дополним уравнениями Пуассона для компонент орта оси $O{{X}_{2}}$ в системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}{\text{:}}$
(4)
$\begin{gathered} a_{{11}}^{2} + a_{{21}}^{2} + a_{{31}}^{2} = 1,\,\,\,\,{{a}_{{31}}}\left[ {3\omega _{0}^{2}(1 - \lambda ){{a}_{{11}}} + p} \right] = 0, \\ {{\omega }_{0}}({{\omega }_{0}}{{a}_{{21}}} - \lambda \Omega )\left( {1 - a_{{21}}^{2}} \right) + \\ + \,\,{{a}_{{21}}}\left[ {3\omega _{0}^{2}(1 - \lambda )a_{{31}}^{2} - p{{a}_{{11}}}} \right] = 0, \\ \end{gathered} $(5)
$\begin{gathered} {{{\dot {a}}}_{{22}}} + {{\omega }_{0}}{{a}_{{21}}}{{a}_{{23}}} = 0,\,\,\,\,{{{\dot {a}}}_{{23}}} - {{\omega }_{0}}{{a}_{{21}}}{{a}_{{22}}} = 0, \\ {{a}_{{12}}} = \frac{{{{a}_{{31}}}{{a}_{{23}}} - {{a}_{{11}}}{{a}_{{21}}}{{a}_{{22}}}}}{{1 - a_{{21}}^{2}}},\,\,\,\,{{a}_{{13}}} = - \frac{{{{a}_{{31}}}{{a}_{{22}}} + {{a}_{{11}}}{{a}_{{21}}}{{a}_{{23}}}}}{{1 - a_{{21}}^{2}}}, \\ {{a}_{{32}}} = - \frac{{{{a}_{{11}}}{{a}_{{23}}} + {{a}_{{31}}}{{a}_{{21}}}{{a}_{{22}}}}}{{1 - a_{{21}}^{2}}},\,\,\,\,{{a}_{{33}}} = \frac{{{{a}_{{11}}}{{a}_{{22}}} - {{a}_{{31}}}{{a}_{{21}}}{{a}_{{23}}}}}{{1 - a_{{21}}^{2}}}. \\ \end{gathered} $Для описания движений спутника, в которых ось Ox1 отклоняется от оси $O{{X}_{2}}$ менее чем на 90°, положение системы Ox1x2x3 относительно системы OX1X2X3 удобно задавать введенными выше углами $\psi ,$ $\theta $ и третьим углом $\varphi ,$ поворот на который вокруг оси $O{{x}_{1}}$ завершает преобразование системы OX1X2X3 в систему Ox1x2x3. Преобразование OX1X2X3 → Ox1x2x3 можно представить в виде суперпозиции преобразований OX1X2X3 → Oy1y2y3 и Oy1y2y3 → Ox1x2x3. Первое преобразование задается углами $\psi ,$ $\theta $ и $\delta ,$ второе преобразование – углом $\chi .$ Повороты на углы $\delta $ и $\chi $ выполняются вокруг оси $O{{x}_{1}} = O{{y}_{1}}$ в одном направлении, поэтому $\varphi = \delta + \chi .$
Если интересоваться только движением оси симметрии спутника $O{{x}_{1}},$ то удобно использовать углы $\psi ,$ $\theta $ и комбинации угловых скоростей
ПЕРИОДИЧЕСКИЕ ДВИЖЕНИЯ ОСИ СИММЕТРИИ СПУТНИКА
Для переменных $\psi ,$ $\theta ,$ ${{\Omega }_{2}},$ ${{\Omega }_{3}}$ справедливы уравнения [2]
(6)
$\begin{gathered} \dot {\theta } = {{\Omega }_{2}} - {{\omega }_{0}}\cos \psi ,\,\,\,\,\dot {\psi } = \frac{{{{\Omega }_{3}}}}{{\cos \theta }} - {{\omega }_{0}}{\text{tg}}\theta \sin \psi , \\ {{{\dot {\Omega }}}_{2}} = - \left( {\lambda \Omega + {{\Omega }_{3}}{\text{tg}}\theta - {{\omega }_{0}}\frac{{\sin \psi }}{{\cos \theta }}} \right){{\Omega }_{3}} + 3\omega _{0}^{2}(1 - \lambda ) \times \\ \times \,\,\sin \theta \cos \theta + p\cos \psi \sin \theta , \\ {{{\dot {\Omega }}}_{3}} = \left( {\lambda \Omega + {{\Omega }_{3}}{\text{tg}}\theta - {{\omega }_{0}}\frac{{\sin \psi }}{{\cos \theta }}} \right){{\Omega }_{2}} + p\sin \psi . \\ \end{gathered} $Система (6) инвариантна относительно преобразования переменных $t \to - t,$ $\theta \to - \theta ,$ ${{\Omega }_{3}} \to - {{\Omega }_{3}},$ поэтому можно искать ее решения, в которых переменные $\theta $ и ${{\Omega }_{3}}$ – нечетные, а переменные $\psi $ и ${{\Omega }_{2}}$ – четные функции времени. Периодические решения с такими свойствами называются симметричными. Симметричные периодические решения с периодом $T$ определяются краевыми условиями
(7)
$\theta (0) = {{\Omega }_{3}}(0) = \theta \left( {\frac{T}{2}} \right) = {{\Omega }_{3}}\left( {\frac{T}{2}} \right) = 0.$Для аппроксимации использовались короткопериодические решения. Параметры системы (6) $p,$ $\lambda ,$ $\Omega $ для каждого аппроксимируемого интервала определялись в результате обработки магнитных измерений (табл. 3). Значение периода $T$ находились в результате спектрального анализа решений системы (2a), аппроксимирующих магнитные измерения на исследуемом интервале. Переменные системы (2a) в этом решении указанным выше способом пересчитывались в функции θ(t), $\psi (t),$ ${{\Omega }_{2}}(t),$ ${{\Omega }_{3}}(t),$ и для каждой из этих функций определялся пробный период. Опишем определение пробного периода на примере функции θ(t). Эта функция (как и остальные из приведенного набора) вычислялась на равномерной временной сетке $\left\{ {t_{m}^{'}} \right\}_{{m = 0}}^{M},$ $t_{m}^{'} = {{t}_{0}} + mh,$ $h = 20$ с, $(M - 1)h < T \leqslant Mh.$ Строилась ее аппроксимация выражением
где ${{a}_{0}},$ $a,$ $b$ и $f$ – параметры. Значения параметров искались методом наименьших квадратов посредством минимизации выраженияНа интервалах 10 и 14–18 функции ${{\Psi }_{1}}(f)$ для переменных θ(t), $\psi (t),$ ${{\Omega }_{2}}(t),$ ${{\Omega }_{3}}(t)$ имели только один значимый минимум, причем значения $\min {{\Psi }_{1}}$ отличались от значений этих функций вне малой окрестности точки ${{f}_{{\min }}}$ (они близки $\max {{\Psi }_{1}}$) в 10 и более раз [5].
Пробные периоды, найденные по функциям θ(t), $\psi (t),$ ${{\Omega }_{2}}(t)$ и ${{\Omega }_{3}}(t),$ совпадали достаточно точно. Так как в движениях на интервалах 10 и 14–18 наиболее интенсивно изменялись переменные ${{\Omega }_{2}}$ и ${{\Omega }_{3}},$ пробный период определялся по периодограммам функций ${{\Omega }_{2}}(t)$ и ${{\Omega }_{3}}(t).$ Для них значения ${{f}_{{\min }}}$ попадали в одни и те же узлы сетки с шагом $2 \cdot {{10}^{{ - 7}}}$ Гц. Найденное значение пробного периода использовалось для построения аппроксимирующего решения краевой задачи (6), (7). Эта задача решалась методом пристрелки (см. [2]). Начальным приближением неизвестных начальных условий $\psi (0)$ и ${{\Omega }_{2}}(0)$ служили амплитуды соответствующих выражений (8) при $f = {{f}_{{\min }}}.$ Можно также использовать значения переменных $\psi $ и ${{\Omega }_{2}}$ в аппроксимируем решении в точке ${{t}_{ * }},$ определяемой соотношением $\theta ({{t}_{ * }}) \approx 0.$
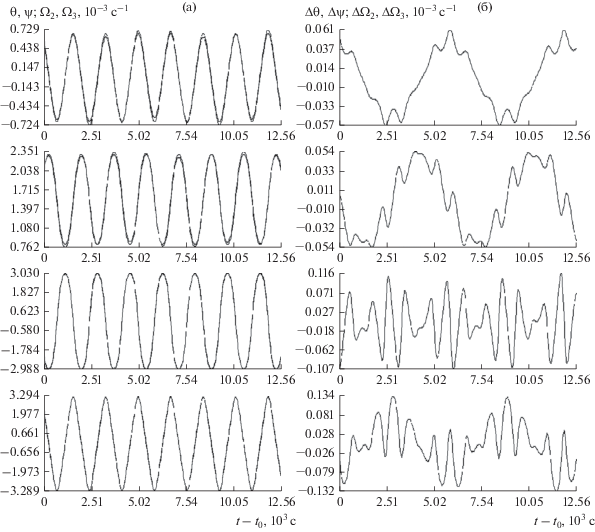
Примеры построенных периодических решений приведены на рис. 7, 8 и в табл. 4. В таблице указаны параметры решений задачи (6), (7): $T{\text{/}}2,$ $\psi (0)$ и ${{\Omega }_{2}}(0)$, а также орбитальная частота ${{\omega }_{0}}$ на данном интервале и коэффициент $a$ в характеристическом уравнении ${{(\rho - 1)}^{2}}({{\rho }^{2}} - 2a\rho + 1) = 0,$ определяющем мультипликаторы периодического решения. Здесь единица измерения времени – 1000 с, единицы измерения угловой скорости – 0.001 c–1. Как видим, все найденные периодические решения орбитально устойчивы в первом приближении. На рисунках приведены графики переменных θ(t), $\psi (t),$ ${{\Omega }_{2}}(t)$ и ${{\Omega }_{3}}(t)$ в периодических решениях на отрезке $0 \leqslant t \leqslant 2T$ и проекции орта оси $O{{x}_{1}}$ и орта кинетического момента спутника на плоскость $O{{X}_{1}}{{X}_{3}}.$ Проекция орта кинетического момента лежит внутри проекции орта оси $O{{x}_{1}}.$
Рис. 7.
Периодические решения, используемые для аппроксимации движения спутника; (а) на интервале 14, (б) на интервале 17.

Рис. 8.
Проекции годографов ортов оси $O{{x}_{1}}$ (внешние кривые) и кинетического момента вращательного движения (внутренние кривые) на плоскость $O{{X}_{1}}{{X}_{3}};$ (а) на интервале 14, (б) на интервале 17.
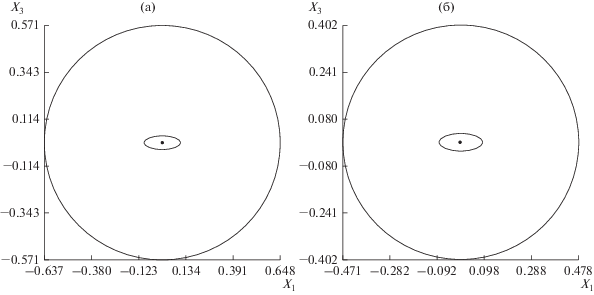
Таблица 4.
Параметры периодических решений
| № инт. | ${{\omega }_{0}}$ | T/2 | $\psi (0)$ | ${{\Omega }_{2}}(0)$ | $a$ | $\tau $ |
|---|---|---|---|---|---|---|
| 10 | 1.15738 | 1.05241 | 0.70850 | 2.76801 | $ - {\text{0}}{\text{.61081}}$ | 0.7478 |
| 14 | 1.15362 | 0.92799 | 0.86721 | 2.64021 | $ - 0.{\text{26236}}$ | 0.7746 |
| 15 | 1.15883 | 0.86088 | 0.80933 | 3.02129 | $ - 0.{\text{21134}}$ | 1.1359 |
| 16 | 1.15688 | 0.84976 | 0.92197 | 2.72420 | $ - 0.{\text{11559}}$ | 1.1784 |
| 17 | 1.15787 | 0.97637 | 1.07276 | 1.83328 | $ - 0.0{\text{7819}}$ | 0.2050 |
| 18 | 1.15976 | 1.00929 | 1.06703 | 1.68321 | $ - 0.0{\text{4319}}$ | 1.6910 |
Сопоставление движений, найденных обработкой магнитных измерений, и периодических решений выполнялось по следующей схеме. Переменные θ(t), $\psi (t),$ ${{\Omega }_{2}}(t)$ и ${{\Omega }_{3}}(t)$ в периодическом решении аппроксимировались дискретными рядами Фурье [7]. Четные функции разлагались в ряд по косинусам, нечетные – в ряд по синусам. В каждом аппроксимирующем выражении использовалось 200 гармоник. Построенные ряды обозначим, $\tilde {\theta }(t),$ $\tilde {\psi }(t),$ ${{\tilde {\Omega }}_{2}}(t)$ и ${{\tilde {\Omega }}_{3}}(t).$ Составлялось выражение
В полете Фотона-12 реализовалась редкая ситуация, когда реальные достаточно сложные вращательные движения спутника удалось аппроксимировать периодическими решениями уравнений движения обобщенно-консервативной механической системы. Этот факт служит очередным оправданием использования упрощенных математических моделей в задачах механики космического полета.
Список литературы
Буланов Д.М., Сазонов В.В. Исследование эволюции вращательного движения спутника Фотон-12. Препринты ИПМ им. М.В. Келдыша. 2020. № 53. https://keldysh.ru/papers/2020/prep2020_53.pdf
Нейштадт И.А., Сазонов В.В. Периодические колебания оси симметрии спутника под действием гравитационного и аэродинамического моментов // Известия Академии наук. Механика твердого тела. 2003. № 4. С. 20–35.
Абрашкин В.И., Балакин В.Л., Белоконов И.В. и др. Неуправляемое вращательное движение спутника Фотон-12 и квазистатические микроускорения на его борту // Космич. исслед. 2003. Т. 41. № 1. С. 45–56.
Буланов Д.М., Сазонов В.В. Исследование эволюции вращательного движения спутника Фотон М-2 // Космич. исслед. 2020. Т. 58. № 4. С. 291–304.
Буланов Д.М., Сазонов В.В. Периодическая аппроксимация вращательного движения спутника Фотон-12. Препринты ИПМ им. М.В. Келдыша. 2020. № 90. https://keldysh.ru/papers/2020/prep2020_ 90.pdf
Белецкий В.В. Движение спутника относительно центра масс в гравитационном поле. М.: Издательство МГУ, 1975.
Ланцош К. Практические методы прикладного анализа. М.: Физматгиз, 1960.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования