Космические исследования, 2022, T. 60, № 3, стр. 218-226

Определение параметров модели гравитационного поля астероида с помощью группы малых аппаратов

М. Ю. Воронина^1, *, М. Г. Широбоков¹

¹ Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия

Поступила в редакцию 06.09.2021
После доработки 15.10.2021
Принята к публикации 24.11.2021

EDN: KPDPJT
DOI: 10.31857/S0023420622030104

Аннотация

В работе предлагается методика определения параметров гравитационного поля астероида с помощью группы аппаратов. Гравитационное поле астероида описывается моделью сферических гармоник и характеризуется коэффициентами Стокса и гравитационным параметром тела. Группа аппаратов состоит из материнского и дочерних космических аппаратов. Траекторными измерениями являются расстояние и радиальная скорость между материнским и каждым дочерним аппаратом. Предложенная методика апробируется на примерах уже изученных астероидов Эрос и Итокава. Исследуется точность определения параметров гравитационного поля в зависимости от ошибок траекторных измерений. Исследуется возможность улучшения точности расчета параметров гравитационного поля с помощью увеличения числа дочерних аппаратов в группе.

1. ВВЕДЕНИЕ

В последние десятилетия растет интерес к исследованию астероидов. Было совершено множество космических миссий, среди которых можно выделить миссии с выходом на орбиту (миссии Dawn [1], NEAR Shoemaker) [2], мягкой посадкой (NEAR Shoemaker) и забором грунта астероида (миссии Hayabusa [3], Hayabusa-2 [4], OSIRIS-Rex [5]). В рамках миссии OSIRIS-Rex успешно выполнен забор грунта с астероида Бенну в октябре 2020 г. Интерес к исследованию астероидов обусловлен тем, что они могут служить ключом к получению важной информации о раннем строении Солнечной системы и Вселенной в целом, содержат в себе полезные ископаемые и являются потенциально опасными объектами.

Астероиды различаются по форме и размеру между собой. Некоторые из них имеют форму близкую к сферически симметричной (например, астероид Веста), форма других сильно вытянута (например, Эрос, Итокава). Размеры астероидов варьируются от нескольких метров до нескольких сотен километров. Разнообразие формы и размеров астероидов приводит к разнообразию динамики орбитального движения вокруг них. Построение точной модели гравитационного поля астероида является важнейшей задачей при проектировании и проведении космических миссий по их исследованию.

В настоящий момент существует множество моделей гравитационного поля тел различной формы, в частности модель сферических и эллиптических гармоник [6], полиэдральная модель тела с постоянной плотностью [7], модель точечной массы [8]. Каждая из моделей обладает рядом преимуществ и недостатков. Например, модель сферических гармоник имеет простой вид и не требует больших вычислительных мощностей в сравнении с полиэдральной моделью, но она плохо отражает гравитационное поле вблизи к поверхности тела. Напротив, полиэдральная модель и модель точечной массы определяют гравитационное поле тела вблизи поверхности тела с высокой точностью, но требуют большой вычислительной мощности по сравнению с моделью сферических гармоник.

Исходными данными для построения модели гравитационного поля тела могут быть измерения положения и скорости КА на орбите вокруг тела, относительные положения и радиальные скорости между несколькими КА, визуальные наблюдения поверхности тела и др. Существует множество методик определения параметров гравитационного поля. Например, исследовать поле можно с помощью интеграла энергии [9]. На практике широко применяется метод определения параметров поля с помощью решения задачи минимизации специально выбранной целевой функции. Оптимизируемыми переменными целевой функции являются параметры модели гравитационного поля, а сама функция представляет собой невязку траекторных измерений и аналогичных измерений, полученных в уточняемой модели гравитационного поля. Данный метод был введен У. Каулой для исследования гравитационного поля Земли [10].

Эффективность методов определения гравитационного поля тела существенно зависит от точности траекторных измерений. Отметим, что в миссиях GRACE [11] и GRAIL [12] проблема точности траекторных измерений решалась с использованием межспутниковой навигации. Это позволило исключить нежелательные возмущения и получить траекторные измерения с недостижимой ранее точностью. В статье [13] было произведено теоретическое исследование гравитационного поля Земли группой двух и четырех КА. Исследование показало, что применение группы четырех КА позволяет определять параметры поля точнее, чем при использовании группы двух аппаратов. Итак, приведенные выше исследования показали, что межспутниковая навигация гораздо точнее, чем навигация через связь с Землей или оптические наблюдения. Применение групп двух и более аппаратов к задачам исследования гравитационного поля удаленных космических тел может существенно улучшить точность определяемых характеристик.

Целью данной работы является исследование методики определения гравитационного поля астероида группой двух и более аппаратов. Группа состоит из материнского и дочерних аппаратов. Траекторными измерениями являются расстояние и радиальная скорость между материнским и дочерними КА. В работе исследована зависимость точности определения параметров гравитационного поля от ошибок траекторных измерений. Кроме того, исследована возможность уточнить определяемые параметры с помощью увеличения числа аппаратов в группе. Предложенная в данной работе методика рассматривается на примерах исследования гравитационного поля астероидов Эрос и Итокава, чьи гравитационные поля были изучены в миссиях NEAR Shoemaker [14] и Hayabusa [15] соответственно.

2. ПОСТАНОВКА ЗАДАЧИ

Группа аппаратов движется вокруг астероида. Группа состоит из материнского аппарата и дочерних аппаратов. В процессе движения управление аппаратами не рассматривается, поскольку считается, что оно отсутствует на этапе первоначального исследования астероида. Траекторными измерениями являются расстояние и радиальная скорость, которые формируются с помощью межспутниковой навигации между материнским и каждым из дочерних КА. Считается, что тело астероида не влияет на межспутниковую связь. Аппараты движутся в поле силы гравитационного притяжения астероида, Солнца и планет Солнечной системы, а также силы давления солнечного излучения. Гравитационное поле астероида определяется моделью сферических гармоник.

Определим динамику движения аппаратов. Для расчета точного положения массивных тел Солнечной системы используется эфемеридная модель движения DE430 [16]. В ней основной системой координат является Международная небесная система координат (МНСК). В МНСК введем постоянно ориентированную в пространстве систему координат (СК), связанную с астероидом. Начало СК лежит в центре масс астероида, а оси направленны вдоль главных осей инерции. Такую СК будем считать кёниговой поскольку движение аппаратов рассматривается в течении короткого, относительно периода орбиты астероида, интервала времени. Ориентация кёниговой системы координат (КСК) относительно МНСК задается с помощью значений углов прямого восхождения и склонения полюса астероида.

Поскольку в работе исследуется методика, то для упрощения расчетов примем несколько допущений. Во-первых, угловая скорость вращения астероида считается постоянной по направлению и значению. Тогда положение КА относительно поверхности астероида определяется с помощью матрицы поворота. Во-вторых, направление вектора нормали к поверхности аппарата всегда совпадает с направлением на Солнце. Влияние тени от астероида на освещенность поверхности КА не учитывается. Аппараты имеют форму параллелепипеда.

Уравнения движения аппарата в ИСК с учетом гравитационного притяжения N тел Солнечной системы и силы светового давления имеют вид:

(1)

$\left\{ \begin{gathered} {\mathbf{\dot {r}}} = {\mathbf{v}} \hfill \\ {\mathbf{\dot {v}}} = {{\nabla }_{{xyz}}}U - \sum\limits_{i = 1}^N {{{{{\mu }}}_{i}}\left( {\frac{{{\mathbf{r}} - {{{\mathbf{r}}}_{i}}}}{{{{{\left| {{\mathbf{r}} - {{{\mathbf{r}}}_{i}}} \right|}}^{3}}}} + \frac{{{{{\mathbf{r}}}_{i}}}}{{{{{\left| {{{{\mathbf{r}}}_{i}}} \right|}}^{3}}}}} \right) + {{{\mathbf{a}}}_{{SRP}}}} \hfill \\ \end{gathered} \right.,$

где $\left[ {{\mathbf{r}};{\mathbf{v}}} \right]$ – фазовый вектор аппарата, $U$ – силовая функция гравитационного поля астероида, ${{{{\mu }}}_{i}}$ – гравитационный параметр i-го тела Солнечной системы, ${{{\mathbf{r}}}_{i}}$ – его радиус-вектор, ${{{\mathbf{a}}}_{{SRP}}}$ – ускорение за счет силы давления солнечного излучения.

В общем виде силовая функция гравитационного поля астероида в точке имеет вид:

(2)

$\begin{gathered} U\left( {r,{{\theta }},{{\varphi }}} \right) = \frac{{{\mu }}}{r}\sum\limits_{n = 0}^\infty {\sum\limits_{m = 0}^n {{{{\left( {\frac{{R{\text{*}}}}{r}} \right)}}^{n}}{{P}_{{nm}}}\left( {\sin {{\theta }}} \right)} } \times \\ \times \,\,\left[ {{{C}_{{nm}}}\cos \left( {m{{\varphi }}} \right) + {{S}_{{nm}}}\sin \left( {m{{\varphi }}} \right)} \right], \\ \end{gathered} $

где $\left( {r,{{\theta }},{{\varphi }}} \right)$ – положение точки в сферической системе координат, ${{\mu }}$ – гравитационный параметр астероида, $R{\text{*}}$ – радиус аппроксимирующей сферы, ${{P}_{{nm}}}\left( {\sin {{\theta }}} \right)$ – присоединенная функция Лежандра порядка n и степени m, а ${{C}_{{nm}}}$ и ${{S}_{{nm}}}$ – коэффициентами перед гармониками гравитационного поля (коэффициенты Стокса).

Уравнение ускорения за счет силы давления солнечного излучения выражается формулой:

(3)

${{{\mathbf{a}}}_{{SRP}}} = - \frac{{{{S}_{0}}}}{c}{{\left( {\frac{{AU}}{{\left| {{{{\mathbf{r}}}_{{{\text{sun}}}}}} \right|}}} \right)}^{2}} \cdot {{S}_{M}} \cdot {{{\mathbf{\hat {r}}}}_{s}}\left[ {\frac{1}{3}{{\alpha }}\left( {2 + {{\mu }}} \right) - 1} \right],$

где ${{S}_{0}} = 1361$ Вт/м² – солнечная постоянная, $AU = 149~597~870.7$ км – астрономическая единица, $c = {\text{2}}{\text{.99792458}} \cdot {\text{1}}{{{\text{0}}}^{5}}$ км/с – скорость света, $\left| {{{{\mathbf{r}}}_{{{\text{sun}}}}}} \right|$ – расстояния от аппарата до Солнца, ${{S}_{M}}$ – отношения площади к массе КА, ${{{\mathbf{\hat {r}}}}_{s}}$ – вектор направления от аппаратная Солнце, ${{\alpha }},{{\mu }}$ – коэффициенты отражения и зеркальности соответственно [17].

Через заданные интервалы времени рассчитывается расстояние и радиальная скорость между материнским и каждым дочерним аппаратом по формулам:

(4)

$\begin{gathered} {{{{\rho }}}_{{ij}}} = \sqrt {{{{\left( {{{{\mathbf{r}}}_{{ij}}} - {\mathbf{r}}_{j}^{{chief}}} \right)}}^{T}}\left( {{{{\mathbf{r}}}_{{ij}}} - {\mathbf{r}}_{j}^{{chief}}} \right)} , \\ {{{{{\dot {\rho }}}}}_{{ij}}} = \frac{1}{{{{{{\rho }}}_{{ij}}}}}{{\left( {{{{\mathbf{v}}}_{{ij}}} - {\mathbf{v}}_{j}^{{chief}}} \right)}^{T}}\left( {{{{\mathbf{r}}}_{{ij}}} - {\mathbf{r}}_{j}^{{chief}}} \right), \\ \end{gathered} $

где ${{{{\rho }}}_{{ij}}}$ и ${{{{\dot {\rho }}}}_{{ij}}}$ – расстояние и радиальная скорость между i-м дочерним аппаратом в j-ый момент времени, $\left[ {{{{\mathbf{r}}}_{i}};{{{\mathbf{v}}}_{i}}} \right]$ – фазовый вектор i-го дочернего аппарата, $\left[ {{{{\mathbf{r}}}^{{chief}}};{{{\mathbf{v}}}^{{chief}}}} \right]$ – фазовый вектор материнского КА. Значения ${{{{\rho }}}_{{ij}}}$ и ${{{{\dot {\rho }}}}_{{ij}}}$ образуют множество траекторных измерений $D = \left\{ {{{{{\rho }}}_{{ij}}},{{{{{\dot {\rho }}}}}_{{ij}}}} \right\}.$

Задача определения гравитационного поля астероида сводится к задаче определения коэффициентов Стокса и гравитационного параметра тела по данным траекторных измерений. Для этого ставится оптимизационная задача

(5)

$J\left( {\mathbf{p}} \right) \to \min ,$

где ${\mathbf{p}} = \left[ {{{C}_{{nm}}};{{S}_{{nm}}};{{\mu }}} \right].$ Целевая функция $J\left( {\mathbf{p}} \right)$ зависит от данных измерений $\left\{ {{{\rho }}_{{ij}}^{{dat}},{{\dot {\rho }}}_{{ij}}^{{dat}}} \right\},$ моделируемых измерений $\left\{ {{{{{\rho }}}_{{ij}}}\left( {\mathbf{p}} \right),{{{{{\dot {\rho }}}}}_{{ij}}}\left( {\mathbf{p}} \right)} \right\}$ и имеет вид:

(6)

$\begin{gathered} J\left( {\mathbf{p}} \right) = \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^{{{N}_{t}}} {{{{\left( {{{{{\rho }}}_{{ij}}}\left( {\mathbf{p}} \right) - {{\rho }}_{{ij}}^{{dat}}} \right)}}^{2}}} } + \\ + \,\,\sum\limits_{i = 1}^k {\sum\limits_{j = 1}^{{{N}_{t}}} {{{{\left( {{{{{{\dot {\rho }}}}}_{{ij}}}\left( {\mathbf{p}} \right) - {{\dot {\rho }}}_{{ij}}^{{dat}}} \right)}}^{2}}} } , \\ \end{gathered} $

где i – номер дочернего аппарата, j – номер измерения, k – количество дочерних КА, ${{N}_{t}}$ – количество измерений на орбите.

Итак, мы определили модель движения аппаратов и сформулировали оптимизационную задачу, решая которую возможно оценить параметры модели гравитационного поля астероида. Существует несколько важных аспектов, влияющих на работу и эффективность предлагаемого метода:

1. инициализация начального фазового вектора аппаратов, момента времени и числа аппаратов в группе,

2. моделирование ошибок траекторных измерений,

Эти аспекты задачи рассматриваются в следующем разделе.

3. АСПЕКТЫ ЗАДАЧИ

3.1. Инициализация начального фазового вектора аппаратов, момента времени и числа аппаратов в группе

Начальный фазовый вектор материнского аппарата выбирается так, что орбита имеет характеристики, представленные в табл. 1. В ней R – радиус орбиты, i – наклонение орбиты, T_orbit – период орбитального движения. Начальный фазовый вектор дочерних аппаратов рассчитывается как случайное независимое отклонение от начального фазового вектора материнского аппарата $\left[ {{\mathbf{r}}_{0}^{{chief}};{\mathbf{v}}_{0}^{{chief}}} \right] = {\mathbf{x}}_{0}^{{chief}}$ подчиненное нормальному закону распределения $N\left( {{\mathbf{x}}_{0}^{{chief}},{{\sigma }}_{{deputy,0}}^{2}} \right).$ Значения среднеквадратичного отклонения ${{\sigma }}_{{deputy,0}}^{2}$ по положению составляют 5% от расстояния R и 10% от модуля вектора начальной скорости. Аппараты движутся вокруг астероида в течение времени T. ${{S}_{{M,chief}}}$ и ${{S}_{M}}$ являются значениями отношения площади к массе материнского и дочерних КА соответственно.

Таблица 1.

Параметры орбит и аппаратов

Параметр	Эрос	Итокава
R, км	50	1.5
i, град	85	85
T_orbit, ч	29.2	66
T, ч	29.2	33
${{S}_{{M,chief}}}$, м²/кг	10^–1	10^–2
${{S}_{M}}$, м²/кг	10^–5	10^–5

Начальный момент времени движения аппарата для обоих астероидов соответствует 1.I.2020.

При формировании данных траекторных измерений и при расчете параметров гравитационного поля используются одинаковые начальные фазовые векторы дочерних аппаратов, а начальный фазовый вектор материнского аппарата отличается на величину ошибки навигации, которая приводится в следующем подразделе.

3.2. Моделирование ошибок траекторных измерений

Ошибки измерений моделируются как независимые случайные отклонения от истинных значений переменных и подчиненные нормальному закону распределения с нулевым средним и некоторой дисперсией $N\left( {0,{{{{\sigma }}}^{2}}} \right).$ При этом к каждому значению расстояния и радиальной скорости между аппаратами добавляется ошибка $N\left( {0,{{{{\sigma }}}^{2}}\left( {{{\rho }},{{\dot {\rho }}}} \right)} \right)$ и получается множество траекторных измерений $\left\{ {{{\rho }}_{{ij}}^{{dat}},{{\dot {\rho }}}_{{ij}}^{{dat}}} \right\}.$ Для исследования точности расчета параметров гравитационного поля при различных значениях ошибок траекторных измерений среднеквадратичное отклонение определим как некоторое число, умноженное на коэффициент ${{K}_{1}}.$ Тогда значения среднеквадратичных отклонений равны:

${{\sigma }}\left( {{\rho }} \right) = 3 \cdot {{10}^{{ - 3}}}{{K}_{1}}\,\,{\text{км,}}\,\,\,\,{{\sigma }}\left( {{{\dot {\rho }}}} \right) = 0.05{{K}_{1}}\,\,{\text{мм/с,}}$

где ${{K}_{1}}$ принимает значения от ${{10}^{{ - 4}}}$ до ${{10}^{3}}.$

4. МЕТОД РЕШЕНИЯ ОПТИМИЗАЦИОННОЙ ЗАДАЧИ

Поставленная в разделе 2 оптимизационная задача (5) решается в среде MATLAB методом Левенберга–Марквардта [20] функцией “lsqnonlin”. Функция “lsqnonlin” создана для решения нелинейных задач, целевая функция которых представлена в виде суммы квадратов невязок. Для работы с “lsqnonlin” требуется записать целевую функцию в виде вектора, размер которой должен превышать или быть равным числу переменных в задаче оптимизации. Также функция “lsqnonlin” требует задание ограничений на значения переменных целевой функции.

Реализованный в функции “lsqnonlin” метод Левенберга–Марквардта требует задания градиента целевой функции. Обозначим первый и второй члены целевой функции ${{J}_{{1,\,ij}}}$ и ${{J}_{{2,\,ij}}}$ соответственно

(7)

$J\left( {\mathbf{p}} \right) = \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^{{{N}_{t}}} {{{{\left( {{{J}_{{1,ij}}}\left( {\mathbf{p}} \right)} \right)}}^{2}}} } + \sum\limits_{i = 1}^k {\sum\limits_{j = 1}^{{{N}_{t}}} {{{{\left( {{{J}_{{2,ij}}}\left( {\mathbf{p}} \right)} \right)}}^{2}}} } ,$

где

(8)

${{J}_{{1,ij}}}\left( {\mathbf{p}} \right) = {{{{\rho }}}_{{ij}}}\left( {\mathbf{p}} \right) - {{\rho }}_{{ij}}^{{dat}},\,\,\,\,{{J}_{{2,ij}}}\left( {\mathbf{p}} \right) = {{{{\dot {\rho }}}}_{{ij}}}\left( {\mathbf{p}} \right) - {{\dot {\rho }}}_{{ij}}^{{dat}}.$

Распишем матрицу первых производных:

(9)

$\begin{gathered} \frac{{\partial {{J}_{{1,ij}}}}}{{\partial {\mathbf{p}}}} = \frac{{\partial {{J}_{{1,ij}}}}}{{\partial {\mathbf{r}}_{j}^{{chief}}}}\left[ {\frac{{\partial {\mathbf{r}}_{j}^{{chief}}}}{{\partial {\mathbf{p}}}} - \frac{{\partial {{{\mathbf{r}}}_{{ij}}}}}{{\partial {\mathbf{p}}}}} \right], \\ \frac{{\partial {{J}_{{2,ij}}}}}{{\partial {\mathbf{p}}}} = \frac{{\partial {{J}_{{2,ij}}}}}{{\partial {\mathbf{r}}_{j}^{{chief}}}}\left[ {\frac{{\partial {\mathbf{r}}_{j}^{{chief}}}}{{\partial {\mathbf{p}}}} - \frac{{\partial {{{\mathbf{r}}}_{{ij}}}}}{{\partial {\mathbf{p}}}}} \right] + \frac{{\partial {{J}_{{2,ij}}}}}{{\partial {\mathbf{v}}_{j}^{{chief}}}}\left[ {\frac{{\partial {\mathbf{v}}_{j}^{{chief}}}}{{\partial {\mathbf{p}}}} - \frac{{\partial {{{\mathbf{v}}}_{{ij}}}}}{{\partial {\mathbf{p}}}}} \right], \\ \end{gathered} $

где ${{\partial {{J}_{{1,ij}}}} \mathord{\left/ {\vphantom {{\partial {{J}_{{1,ij}}}} {\partial {{{\mathbf{r}}}^{{chief}}}}}} \right. \kern-0em} {\partial {{{\mathbf{r}}}^{{chief}}}}},$ ${{\partial {{J}_{{2,ij}}}} \mathord{\left/ {\vphantom {{\partial {{J}_{{2,ij}}}} {\partial {{{\mathbf{r}}}^{{chief}}}}}} \right. \kern-0em} {\partial {{{\mathbf{r}}}^{{chief}}}}},$ ${{\partial {{J}_{{2,ij}}}} \mathord{\left/ {\vphantom {{\partial {{J}_{{2,ij}}}} {\partial {{{\mathbf{v}}}^{{chief}}}}}} \right. \kern-0em} {\partial {{{\mathbf{v}}}^{{chief}}}}}$ выражаются следующим образом:

(10)

$\begin{gathered} \frac{{\partial {{J}_{{1,ij}}}}}{{\partial {\mathbf{r}}_{j}^{{chief}}}} = \frac{{{{{\left( {{\mathbf{r}}_{j}^{{chief}} - {{{\mathbf{r}}}_{{ij}}}} \right)}}^{T}}}}{{{\rho }}},\,\,\,\,\frac{{\partial {{J}_{{2,ij}}}}}{{\partial {\mathbf{r}}_{j}^{{chief}}}} = \frac{{{{{\left( {{\mathbf{v}}_{j}^{{chief}} - {{{\mathbf{v}}}_{{ij}}}} \right)}}^{T}}}}{{{{{{\rho }}}^{2}}}} - \\ - \,\,\frac{{{{{\left( {{\mathbf{v}}_{j}^{{chief}} - {{{\mathbf{v}}}_{{ij}}}} \right)}}^{T}}\left( {{\mathbf{r}}_{j}^{{chief}} - {{{\mathbf{r}}}_{{ij}}}} \right){{{\left( {{\mathbf{r}}_{j}^{{chief}} - {{{\mathbf{r}}}_{{ij}}}} \right)}}^{T}}}}{{{{{{\rho }}}^{3}}}}, \\ \frac{{\partial {{J}_{{2,ij}}}}}{{\partial {\mathbf{v}}_{j}^{{chief}}}} = \frac{{{{{\left( {{\mathbf{r}}_{j}^{{chief}} - {{{\mathbf{r}}}_{{ij}}}} \right)}}^{T}}}}{{{\rho }}}. \\ \end{gathered} $

Производные ${{\partial {\mathbf{r}}_{j}^{{chief}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{j}^{{chief}}} {\partial {\mathbf{p}}}}} \right. \kern-0em} {\partial {\mathbf{p}}}},$ ${{\partial {{{\mathbf{r}}}_{{ij}}}} \mathord{\left/ {\vphantom {{\partial {{{\mathbf{r}}}_{{ij}}}} {\partial {\mathbf{p}}}}} \right. \kern-0em} {\partial {\mathbf{p}}}},$ ${{\partial {\mathbf{v}}_{j}^{{chief}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{v}}_{j}^{{chief}}} {\partial {\mathbf{p}}}}} \right. \kern-0em} {\partial {\mathbf{p}}}},$ ${{\partial {{{\mathbf{v}}}_{{ij}}}} \mathord{\left/ {\vphantom {{\partial {{{\mathbf{v}}}_{{ij}}}} {\partial {\mathbf{p}}}}} \right. \kern-0em} {\partial {\mathbf{p}}}}$ определяются из решения уравнений в вариациях:

(11)

$\left\{ \begin{gathered} \frac{d}{{dt}}\left( {\frac{{\partial {\mathbf{x}}}}{{\partial {\mathbf{p}}}}} \right) = \frac{{\partial {\mathbf{f}}}}{{\partial {\mathbf{x}}}}\left( {\frac{{\partial {\mathbf{x}}}}{{\partial {\mathbf{p}}}}} \right) + \frac{{\partial {\mathbf{f}}}}{{\partial {\mathbf{p}}}} \hfill \\ {\mathbf{x}}\left( {{{t}_{0}}} \right) = {{{\mathbf{O}}}_{{6 \times s}}}, \hfill \\ \end{gathered} \right.$

где

(12)

$\begin{gathered} {\mathbf{x}} = \left[ {{\mathbf{r}};{\mathbf{v}}} \right], \\ {\mathbf{f}} = \left[ {{\mathbf{v}};{{\nabla }_{{xyz}}}\operatorname{U} \,\, - \sum\limits_{i = 1}^N {{{{{\mu }}}_{i}}\left( {\frac{{{\mathbf{r}} - {{{\mathbf{r}}}_{i}}}}{{{{{\left| {{\mathbf{r}} - {{{\mathbf{r}}}_{i}}} \right|}}^{3}}}} + \frac{{{{{\mathbf{r}}}_{i}}}}{{{{{\left| {{{{\mathbf{r}}}_{i}}} \right|}}^{3}}}}} \right) + {{{\mathbf{a}}}_{{SRP}}}} } \right], \\ \end{gathered} $

${{{\mathbf{O}}}_{{6 \times s}}}$ – матрица нулей, s – число переменных целевой функции.

5. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Начальное приближение для метода оптимизации представляет собой вектор, состоящий из нулей (начальное приближение коэффициентов Стокса) и ${{{{\mu }}}_{0}}$ (начальное приближение значения гравитационного параметра):

(13)

${{{\mathbf{p}}}_{0}} = \left[ {{{{\mathbf{O}}}_{{(s - 1) \times 1}}};{{{{\mu }}}_{0}}} \right],$

где оптимизационная процедура сходится при ${{{{\mu }}}_{{0,{\text{Eros}}}}} = 0.3{{{{\mu }}}_{{{\text{Eros}}}}} - 1.4{{{{\mu }}}_{{{\text{Eros}}}}}$ для Эроса и ${{{{\mu }}}_{{{\text{Itokawa}},0}}} = $ $ = 0.1{{{{\mu }}}_{{{\text{Itokawa}}}}} - 2{{{{\mu }}}_{{{\text{Itokawa}}}}}$ для Итокавы, ${{{{\mu }}}_{{{\text{Eros}}}}}$ и ${{{{\mu }}}_{{{\text{Itokawa}}}}}$ известны из публикаций [14, 15].

Из [14] и [15] можно видеть, что значения параметров гравитационного поля имеют разный порядок по величине. Для удобства интерпретации результатов всюду в данной работе точность расчета переменных целевой функции определяется модулем относительной погрешности измерений ${{\delta }}{\mathbf{p}},$ выраженный в процентах, которая представляет собой вектор размерности s, j-й компонент которого вычисляется по формуле:

(14)

${{\delta }}{{p}_{j}} = \frac{{\left| {{{p}_{{dat,j}}} - {{p}_{j}}} \right|}}{{{{p}_{{dat,j}}}}} \cdot 100\% ,$

где ${{p}_{{dat,j}}}$ – параметр гравитационного поля [14, 15], ${{p}_{j}}$ – параметр в определяемом поле.

Далее в работе нас будут интересовать значения ${{K}_{1}} \geqslant 1,$ поскольку подобная точность измерений физически воспроизводима. Все расчеты параметров гравитационного поля астероидов проводился для группы $k = 5$ дочерних аппаратов. Расчет повторялся 50 раз. На графиках представлены средние значения величин.

5.1. Результаты расчета коэффициентов Стокса

В данном разделе результатом расчета коэффициентов Стокса является максимальное значение относительной погрешности ${{\delta }}{\mathbf{p}}$ для порядка разложения силовой функции $n = 2,3,4.$

Результаты расчетов для астероида Эрос представлены на рис. 1, 2 и 3 . Из рис. 1 видно, что при увеличении значений среднеквадратического отклонения относительная ошибка расчета резко возрастает. Например, для ${{K}_{1}} = 10$ процент ошибки варьируется от $10\% $ (для $n = 2$) до ${{10}^{5}}\% $ (для $n = 4$). Для понимания влияния ошибки в расчетах коэффициентов Стокса на динамику аппарата вокруг астероида рассмотрим рис. 2 и 3. На рис. 2 представлена зависимость абсолютного суммарного отклонения орбиты КА в исследуемом и рассчитываемом гравитационных полях в течении ${{T}_{{{\text{orbit}}}}}$ (50 точек на орбите) и $10{{T}_{{{\text{orbit}}}}}$ (500 точек на орбите). Данная зависимость рассчитывалась для одного аппарата на круговой орбите с $R = 50\,\,{\text{км}}{\text{.}}$ Из графика видно, что при ${{K}_{1}} = 10$ суммарное отклонение орбиты в течении ${{T}_{{{\text{orbit}}}}}$ равно 1 км, а для $10{{T}_{{{\text{orbit}}}}}$ равно 100 км. Соответствующие орбиты представлены на рис. 3. Видно, что орбиты близки друг к другу.

Рис. 1.

Зависимость относительной ошибки расчета коэффициентов Стокса с n = 2, 3, 4 от ошибок траекторных измерений для астероида Эрос.

Рис. 2.

Зависимость абсолютного суммарного отклонение между орбитами одного аппарата с $R = 50$ км в исследуемом и рассчитываемом гравитационных полях в течении ${{T}_{{{\text{orbit}}}}}$ и $10{{T}_{{{\text{orbit}}}}}$ для астероида Эрос.

Рис. 3.

Орбиты аппарата в исследуемом (красная линия) и рассчитываемом (черная линия) гравитационных полях астероида Эрос. Размер орбиты $R = 50$ км, время полета $10{{T}_{{{\text{orbit}}}}} = 292$ ч.

Результаты расчетов для астероида Итокава представлены на рис. 4, 5 и 6 . Аналогично с предыдущим случаем относительная ошибка расчета резко возрастает при увеличении значений среднеквадратических отклонений. Однако, в отличие от исследования астероида Эрос, значения относительной ошибки расчета гораздо выше. Зависимость суммарного отклонения орбит с $R = 1.5\,\,{\text{км}}$ в двух гравитационных полях от значений среднеквадратического отклонения представлена на рис. 5. Из графика видно, что при ${{K}_{1}} = 1$ суммарное отклонение в течении ${{T}_{{{\text{orbit}}}}}$ равно 0.8 км, $10{{T}_{{{\text{orbit}}}}}$ – 12 км. Соответствующие орбиты в исследуемом и рассчитываемом при ${{K}_{1}} = 1$ гравитационных полях представлен на рис. 6. Видно, что орбиты смещены друг относительно друга. Следовательно, в случае астероида Итокава данный метод более чувствителен к ошибкам измерения.

Рис. 4.

Зависимость относительной ошибки расчета коэффициентов Стокса с n = 2, 3, 4 от ошибок траекторных измерений для астероида Итокава.

Рис. 5.

Зависимость абсолютного суммарного отклонения между орбитами одного аппарата с $R = 1.5$ км в исследуемом и рассчитываемом гравитационных полях в течение ${{T}_{{{\text{orbit}}}}}$ и $10{{T}_{{{\text{orbit}}}}}$ для астероида Итокава.

Рис. 6.

Орбиты аппарата в исследуемом (красная линия) и рассчитываемом (черная линия) гравитационных полях астероида Эрос. Размер орбиты $R = 1.5$ км, время полета $10{{T}_{{{\text{orbit}}}}} = 660$ ч.

5.2. Результаты расчета гравитационного параметра

Рассмотрим влияния ошибок измерения и навигации аппаратов на определение гравитационного параметра астероидов (рис. 7). Из графика видно, что для всех представленных значений среднеквадратического отклонения ошибка расчета гравитационного параметра не превосходит 10%.

Рис. 7.

Зависимость относительной погрешности расчета гравитационного параметра астероидов от ошибок траекторных измерений для астероидов Эрос и Итокава.

5.3. Результаты расчета коэффициентов Стокса от числа аппаратов в группе

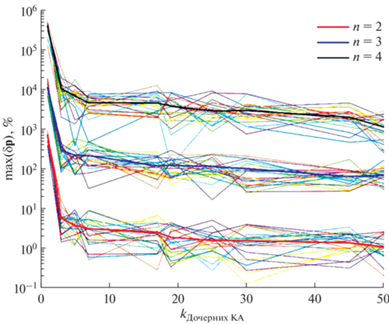
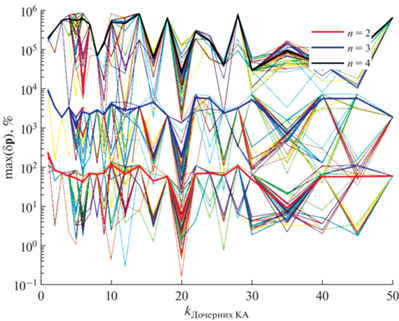
Зависимость точности определяемых коэффициентов Стокса от числа дочерних аппаратов для астероидов Эрос и Итокава представлены на рис. 8 и 9 соответственно. При исследовании астероида Эрос среднеквадратические отклонения ошибки траекторных измерений равны ${{\sigma }}\left( {{\rho }} \right) = 3 \cdot {{10}^{{ - 3}}}$ км и ${{\sigma }}\left( {{{\dot {\rho }}}} \right) = 0.05$ мм/с. Из рис. 8 следует, что точность расчетов резко улучшается при увеличении числа аппаратов до 5. Последующее увеличение числа аппаратов в группе на точность расчетов сильно не влияет. Для астероида Итокава расчеты проводились при следующих значениях среднеквадратических отклонений: ${{\sigma }}\left( {{\rho }} \right) = 3 \cdot {{10}^{{ - 6}}}$ км и ${{\sigma }}\left( {{{\dot {\rho }}}} \right) = 5 \cdot {{10}^{{ - 5}}}$ мм/с. Зависимость точности расчета от числа аппаратов в группе для астероида Итокава представлена на рис. 9. Из графика видно, что характер зависимости сильно отличается от рис. 8 и резкого улучшения результата расчета не наблюдается. Однако при 20 дочерних аппаратов степень относительной погрешности расчета ${{\delta }}{\mathbf{p}}$ снижается на порядок.

Рис. 8.

Зависимость степени относительной погрешности расчета коэффициентов Стокса от числа аппаратов при ${{\sigma }}\left( {{\rho }} \right) = 3 \cdot {{10}^{{ - 3}}}$ км и ${{\sigma }}\left( {{{\dot {\rho }}}} \right) = 0.05$ мм/с для астероида Эрос.

Рис. 9.

Зависимость степени относительной погрешности расчета коэффициентов Стокса от числа аппаратов при ${{\sigma }}\left( {{\rho }} \right) = 3 \cdot {{10}^{{ - 6}}}$ км и ${{\sigma }}\left( {{{\dot {\rho }}}} \right) = 5 \cdot {{10}^{{ - 5}}}$ мм/с для астероида Итокава.

ЗАКЛЮЧЕНИЕ

Продемонстрирована и изучена методика определения гравитационного поля тела с помощью группы аппаратов. Было показано, что гравитационный параметр рассчитывается с ошибкой менее 10% при всех предложенных значениях среднеквадратического отклонения. В случае расчета значений коэффициентов Стокса оказалось, что метод сильно чувствителен к ошибкам измерений. При увеличении значений среднеквадратических отклонений процент относительной ошибки расчета резко возрастает. Для демонстрации влияния неточности расчета на динамику аппарата вокруг астероида была рассмотрена зависимость абсолютного суммарного отклонения орбиты аппарата в исследуемом и рассчитываемом гравитационных полях. Было выявлено, что для астероида Эрос при значениях ${{\sigma }}\left( {{\rho }} \right) \geqslant 3$ м и ${{\sigma }}\left( {{{\dot {\rho }}}} \right) \geqslant 5 \cdot {{10}^{{ - 5}}}$ м/с ошибки расчета слабо влияют на динамику аппарата. Однако, в случае астероида Итокава подобных значений подобрать не удалось. Кроме того, на примере астероида Эрос было показано влияние числа аппаратов в группе на точность расчета параметров гравитационного поля.

Так же была обнаружена высокая чувствительность метода к ошибкам начального вектора состояния аппаратов в группе.

Применение группы аппаратов к задачам исследования гравитационного поля массивного тела обладает рядом преимуществ. Главное преимущество группового полета заключается в высокой точности межспутниковой навигации. Кроме того, большое число аппаратов позволяет относительно быстро, за период (для Эроса) или половины периода (для Итокавы) орбитального движения аппаратов, набрать необходимый (для расчета) объем траекторных измерений. Однако метод последующего расчета должен обладать устойчивостью как к ошибкам траекторных измерений, так и к ошибкам начального фазового вектора аппаратов. Разработка подобного метода требует дальнейшего исследования.

Работа поддержана грантом Российского научного фонда (проект № 19-11-00256).

Список литературы

Russell C.T., Raymond C.A. The Dawn Mission to Vesta and Ceres. N.Y.: Springer, 2011.
Bell J. Jacqueline Mitton Asteroid Rendezvous: NEAR Shoemaker’s Adventures at Eros. Cambridge: Cambridge University Press, 2002.
Michel P., DeMeo F.E., Bottke W.F. Asteroids IV. Arizona: University of Arizona Press, 2015.
Tsuda Yu., Yoshikawa M., Abe M., Minamino H. et al. System design of the Hayabusa 2 – Asteroid sample return mission to 1999 JU3 // Acta Astronautica. 2013. V. 91. P. 356–362.
Beckman M. et al. Trajectory and Mission Design for the Origins Spectral Interpretation Resource Identification Security Regolith Explorer (OSIRIS-REx) Asteroid Sample Return Mission // Proceedings of the 2013 IAA Planetary Defense Conference. 2013. P. 1–13.
Дубошин Г.Н. Небесная механика. Основные задачи и методы. М.: Наука, 1968.
Werner R.A., Scheeres D.J. Mutual potential of homogenous polyhedra // Celestial Mechanics and Dynamical Astronomy. 2005. V. 91. P. 337–349.
Ananda M.P. Lunar gravity: A mass point model // Geophysical Research. 1977. V. 82. P. 3049–3064.
Visser P.N.A.M., Sneeuw N., Gerlach C. Energy integral method for gravity field determination from satellite orbit coordinates // J. Geodesy. 2003. V. 77. P. 207–216.
Каула У. Спутниковая геодезия. М.: Мир, 1970.
Tapley B.D., Bettadpur S., Watkins M. et al. The gravity recovery and climate experiment: Mission overview and early results // Geophysical Research Letters. 2004. V. 31. № 9. P. 1–4.
Roncoli R., Fujii K. Mission Design Overview for the Gravity Recovery and Interior Laboratory (GRAIL) Mission // AIAA Guidance, Navigation, and Control Conference. Toronto. 2010. V. 83. P. 1–22.
Wiese D.N., Folkner W.M., Nerem R.S. Alternative mission architectures for a gravity recovery satellite mission // J. Geodesy. 2009. V. 83. P. 569–581.
Miller J.K., Konopliv A.S., Antreasian P.G. et al. Determination of Shape, Gravity, and Rotational State of Asteroid 433 Eros // Icarus. 2002. V. 155. P. 3–17.
Scheeres D.J., Gaskell R. et al. The actual dynamical environment about Itokawa // Astrodynamics Specialist Conference and Exhibit. Colorado. 2006. P. 1–22.
JPL Planetary and Lunar Ephemerides. URL: https:// ssd.jpl.nasa.gov/horizons.cgi#top (дата обращения: 18.02.2021).
Yelnikov R.V., Mashtakov Y.V., Ovchinnikov M.Yu. et al. Orbital and Angular Motion Construction for Low Thrust Interplanetary Flight // Cosmic Research. 2016. V. 54. № 6. P. 483–490.
JPL Small-Body Database Browser. URL: https://s sd.jpl.nasa.gov/sbdb.cgi?sstr=2000433 (дата обращения: 18.02.2021).
JPL Small-Body Database Browser. URL: https:// ssd.jpl.nasa.gov/sbdb.cgi?sstr=2025143 (дата обращения: 18.02.2021).
Moré J.J. The Levenberg-Marquardt Algorithm: Implementation and Theory // Numerical Analysis. Lecture Notes in Mathematics. 1977. V. 630. P. 105–116.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал