Космические исследования, 2022, T. 60, № 5, стр. 413-425

ВВЕДЕНИЕ

С тросовыми группировками космических аппаратов (ТГКА) связаны новые нетрадиционные технологии создания в космосе протяженных и в тоже время легких конструкций, которые могут иметь много полезных применений, например, многоточечные, включая распределенные в плоскости и в пространстве, измерения гравитационного и магнитного полей Земли, ее ионосферы; космическая интерферометрия; распределенные системы наблюдения и сканирования земной поверхности с базой в несколько километров; транспортные операции в космосе, создание искусственной тяжести при межпланетных полетах и т.д. В связи с этим во многих странах мира в последнее время появляется большое количество проектов ТГКА различной геометрической конфигурации. Наиболее простая и естественная геометрическая структура – это линейная ТГКА, когда КА, связанные тросами, образуют прямолинейную цепь [1–5]. Такая конструкция обычно располагается вдоль местной вертикали в режиме гравитационной стабилизации, что обеспечивает ее устойчивость в течение достаточно длительного времени. Более сложные геометрические конфигурации ТГКА можно условно разделить на плоские и пространственные. Тросовые группировки КА, отличные от линейных, обычно стабилизированы вращением вокруг центра масс всей системы с некоторой заданной угловой скоростью. В этом случае натяжение тросов в системе связано с действием центробежных сил инерции. Центры масс КА, входящих в состав плоских тросовых группировок, в идеальном (или номинальном) случае совершают движение в одной плоскости. Обычно это орбитальная плоскость движения центра масс всей системы, хотя иногда рассматривают вращающиеся ТГКА в плоскости перпендикулярной орбитальной плоскости [6]. К плоским ТГКА можно отнести конфигурации типа “кольца” [1, 7–14] и лучевые структуры или “созвездия” с центральным КА [15–20], которые могут быть как открытые, так и замкнутые. Последние конфигурации получили название “ступица – спицы” (hub-spoke formation). Среди пространственных ТГКА следует отметить пирамидальные структуры, например, пирамида (четыре спутника) [22 ] или двойная пирамида (пять спутников) [1, 23]. Перечисленные работы, связанные с динамикой и управлением движением ТГКА, составляют лишь небольшую часть того множества работ, которые появились в последние десятилетия в этом научном направлении. Несмотря на большое количество работ, связанных с ТГКА, вопросы динамики и управления движением таких систем еще недостаточно проработаны. Это в основном связанно с этапом формирования (или развертывания) ТГКА, с совершенствованием методов управления и с уточнением математических моделей движения ТГКА как систем с распределенными параметрами, включая учет движения КА относительно своих центров масс (или относительно направлений тросов).

В настоящей работе рассматривается динамика и разработка метода управления движением ТГКА лучевой структуры (разомкнутая система), состоящей из базового центрального КА (далее просто КА) и трех микроспутников (далее просто спутников), на этапе ее формирования. После развертывания системы центры масс спутников в номинальном случае образуют правильный треугольник, и вся системы вращается вокруг общего центра масс в плоскости орбиты с некоторой заданной угловой скоростью. В исходном состоянии КА и спутники жестко связаны друг с другом в виде правильного треугольника и вращаются в плоскости орбиты (возможны ошибки в направлении вектора угловой скорости) с некоторой угловой скоростью, которая выбирается в процессе решения задачи. В данной работе КА представляет собой твердое тело, а спутники, масса которых существенно меньше массы центрального КА, сначала рассматриваются как материальные точки, а потом в более полной модели как твердые тела конечных размеров. В момент разделения на основании законов сохранения импульса и момента импульса вычисляются скорости центров масс КА и спутников и их компоненты угловых скоростей. Управление процессом формирования ТГКА является комбинированным: используются двигатели малой тяги, расположенные на спутниках, и механизмы выпуска тросов – на КА. Двигатели малой тяги работают в релейном режиме, причем силы тяги постоянны, постоянны и их направления, определенные относительно направления тросов (или относительно направлений “точки крепления тросов к центральному КА – спутник”, если тросы не натянуты). В случае, когда спутники рассматриваются как твердые тела, векторы сил тяги сохраняют свою ориентацию в связанных со спутниками системах координат. Имеются два активных участка для сил тяги и один средний – пассивный. Первый участок начинается сразу после разделения КА. Назначения этого участка компенсировать падение угловой скорости вращения системы из-за увеличения ее момента инерции при увеличении длины тросов. На втором (пассивном) участке с помощью механизмов выпуска тросов, которые работают только на торможение, регулируется сила натяжения тросов так, чтобы при достижении заданных длин тросов их скорость выпуска была равна нулю. После окончания выпуска тросов реактивные двигатели включаются вновь для доведения угловой скорости вращения системы до заданной величины. Описанная здесь номинальная программа формирования ТГКА имеет много параметров: тяга и направление реактивных сил, продолжительных характерных участков, начальная угловая скорость всей системы до разделения, относительные скорости разделения КА и др. Для упрощения решения многопараметрической задачи приведения системы в заданное состояние с помощью уравнений Лагранжа производится построение упрощенной модели плоского движения ТГКА, в которой предполагается полная симметрия движения системы в процессе развертывания. Полученное движение принимается за номинальное, а отклонения от этого движения определяются действующими возмущениями. На пассивном участке формирования системы механизмы выпуска троса реализуют управление с обратной связью, используя отклонения по длине троса и его скорости. Аналогичное регулирование применялось в реальном тросовом эксперименте YES2 [24]. Действие возмущений учитывается при моделировании пространственного движения системы с использованием более полных уравнений, записанных в геоцентрической системе координат и учитывающих движения КА и спутников относительно своих центров масс, растяжимость тросов, ошибки в начальных условиях движения, и при разделении КА и спутников, инерционность механизмов выпуска тросов и т.д. Приводятся характерные примеры численного моделирования процесса формирования ТГКА с учетом действующих возмущений.

ПОСТАНОВКА ЗАДАЧИ

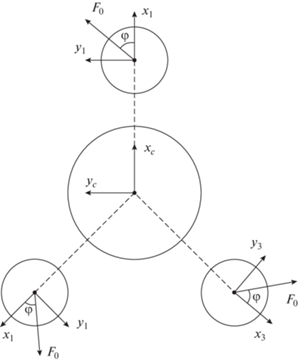
В исходном состоянии при отсутствии возмущений (номинальный случай) КА и спутники представляют собой твердое тело симметричной треугольной конфигурации (рис. 1), которое вращается в плоскости орбиты с угловой скоростью ${{{{\omega }}}_{0}}$, причем направление вращения совпадает с направлением угловой скорости перемещения центра масс системы по околоземной орбите. Начальная орбита центра масс составного спутника круговая. В начальный момент происходит отделение спутников от КА с некоторыми относительными скоростями ${{V}_{r}}$. На спутниках расположены двигатели малой тяги, причем они сориентированы так, что векторы тяг составляют постоянный угол $\varphi $ со связанными осями спутников ${{x}_{k}}\,\left( {k = 1,2,3} \right)$ (рис. 1), причем плоскости ${{с}_{k}}{{x}_{k}}{{y}_{k}}\,$ в номинальном случае совпадают с орбитальной плоскостью. Если спутники рассматриваются как материальные точки (на предварительном этапе анализа движения системы), то это угол между направлениями векторов тяг и тросов. На КА имеются механизмы управления, которые реализуют управление c обратной связью по длине и скорости троса в соответствии в предварительно построенной с помощью упрощенной модели движения системы номинальной программы выпуска тросов [24]. Используя описанные органы управления процессом формирования ТГКА (двигатели малой тяги и механизмы выпуска тросов) необходимо перевести систему в заданное состояние, которое характеризуется заданными длинами тросов ${{l}_{{end}}}$ $\left( {{{{\dot {l}}}_{{end}}} \approx 0} \right)$ и некоторой угловой скоростью вращения системы в орбитальной плоскости ${{{{\omega }}}_{{end}}}$, сохраняя ее правильную треугольную конфигурацию. В процессе решения сформулированной задачи рассматриваются два варианта: 1) управление угловым движением для центрального КА отсутствует; 2) имеется возможность коррекции угловой скорости КА для ее согласования с угловыми скоростями вращения тросов.

УПРОЩЕННАЯ МОДЕЛЬ ДВИЖЕНИЯ ТГКА

Для предварительного параметрического анализа движения системы при ее формировании, для построения номинальной программы выпуска тросов и для выбора закона изменения тяг двигателей рассматривается построение модели движения ТГКА относительно центра масс с помощью уравнений Лагранжа. При этом принимаются следующие основные допущения: 1) симметрия системы при ее формировании сохраняется; 2) движение системы вокруг центра масс не зависит от движения ее центра масс по орбите и при определении кинетической энергии системы не учитывается; 3) влияние гравитационных сил на движение системы относительно центра масс не учитывается; 4) рассматривается плоское движение системы (в орбитальной плоскости); 5) тросы нерастяжимы и невесомы; 6) спутники – материальные точки.

Уравнения Лагранжа записываются в традиционной форме

где $q = {{\left( {l,{{\theta }},{{{{\theta }}}_{t}}} \right)}^{T}}$ – вектор обобщенных координат (рис. 2), $\dot {q}$ – соответствующий вектор обобщенных скоростей, ${{T}_{c}}$ – кинетическая энергия системы, $Q = {{\left( {{{Q}_{l}},{{Q}_{{{\theta }}}},{{Q}_{{{{\theta }}\,t}}}} \right)}^{T}}$ – вектор обобщенных сил.

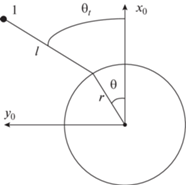
Координаты спутников как материальных точек в орбитальной системе координат $O{{x}_{o}}{{y}_{o}}$ (рис. 2), связанной с центром масс системы, определяются из следующих выражений

где ${{{{\theta }}}_{{ok}}} = {{\theta }} + 2\left( {k - 1} \right)\pi {\kern 1pt} /{\kern 1pt} 3\,\,\left( {k = 1,2,3} \right)$, $r$ – радиус центрального КА, который имеет форму, близкую к сфере.

В этом случае кинетическая энергия системы равна

где $J$ – момент инерции КА относительно своего центра масс, который в симметричном случае совпадает с центром масс всей системы; $m$ – масса спутников.

Подставляя выражения (2)–(4) в (1) и проводя дифференцирование, получим

где $q = {{\left( {\ddot {l},{{\ddot {\theta }}},{{{{{\ddot {\theta }}}}}_{t}}} \right)}^{T}},$

Силы и моменты, определяющие выражения для обобщенных сил, следующие: 1) малые тяги двигателей ${{F}_{0}}$, составляющие угол ${{\varphi }}$ с направления тросов и приложенные к каждому спутнику; 2) сила торможения троса в механизмах управления ${{F}_{с}}$; 3) момент ${{M}_{{{\theta }}}}$ системы стабилизации углового движения КА. Как было сказано выше, здесь рассматривается два варианта, когда ${{M}_{{{\theta }}}} = 0$ и ${{M}_{{{\theta }}}} \ne 0$. В последнем случае осуществляется дополнительная стабилизация движения КА для согласования его угловой скорости с угловыми скоростями тросов.

Составляющие обобщенных сил, зависящие от векторов тяг ${{F}_{k}}$, определяются через скалярные произведения

где вектор ${{r}_{k}}$ имеет компоненты (2)–(3), ${{Q}^{{\left( F \right)}}} = {{\left( {Q_{l}^{{\left( F \right)}},Q_{{{\theta }}}^{{\left( F \right)}},Q_{{{{\theta }}t}}^{{\left( F \right)}}} \right)}^{T}}$.

К составляющим (6) добавляются компоненты

которые определяются стандартным способом через возможные элементарные перемещения. Суммируя (6) и (7), получим

Таким образом, система уравнений (5) совместно с выражениями (8) описывает движение ТГКА с точностью до задания векторов тяги ${{F}_{k}}$, сил торможения в механизмах выпуска тросов ${{F}_{с}}$ и момента ${{M}_{{{\theta }}}}$ системы стабилизации движения КА. Кроме параметров и сил от которых зависят правые части уравнений (4) необходимо задать начальные и конечные условия движения ТГКА: $l\left( 0 \right) = {{l}_{0}},{{\theta }}\left( 0 \right) = {{{{\theta }}}_{t}}\left( 0 \right) = 0,\,\,\dot {l}\left( 0 \right) = {{V}_{r}},$ ${{\dot {\theta }}}\left( 0 \right) = {{{{\dot {\theta }}}}_{t}}\left( 0 \right)$ = = ω₀ и $l\left( {{{t}_{{end}}}} \right) = {{l}_{{end}}}$, $\dot {l}\left( {{{t}_{{end}}}} \right) = 0$, ${{\dot {\theta }}}\left( {{{t}_{{end}}}} \right) = {{{{\dot {\theta }}}}_{t}}\left( {{{t}_{{end}}}} \right)$ = = ω_end.

НОМИНАЛЬНАЯ ПРОГРАММА РАЗВЕРТЫВАНИЯ ТГКА

Номинальная программа формирования вращающейся ТГКА включает в себя несколько характерных участков. На первом начальном участке сразу после разделения КА и спутников с относительными скоростями ${{V}_{r}}$ естественно увеличивается момент инерции всей системы относительно своего центра масс. Поэтому свободное или неуправляемое движение ТГКА на этом участке приводит (закон сохранения момента импульса), во-первых, к уменьшению угловой скорости системы практически до нуля, а во-вторых, к ослаблению или провисанию тросов, что недопустимо. В связи с этим для компенсации этого эффекта с помощью реактивных двигателей малой тяги, расположенных на спутниках, создается положительный момент, который поддерживает угловую скорость системы на приемлемом уровне. Назначение второго участка – это обеспечение выполнения конечных условий для выпуска троса $l\left( {{{t}_{{end}}}} \right) = {{l}_{{end}}}$, $\dot {l}\left( {{{t}_{{end}}}} \right) = 0$. На этом участке двигатели малой тяги выключаются и происходит торможение троса с помощью механизмов, расположенных на КА. После выполнения конечных условий движения для тросов двигатели малой тяги включаются снова для доведения угловой скорости вращения ТГКА до заданной величины.

Таким образом, релейная программа работы двигателей малой тяги имеет вид

где ${{t}_{k}}\,\,\left( {k = 1,2,3} \right)$ – моменты времени, определяющие характерные участки процесса формирования ТГКА. Здесь момент времени ${{t}_{{end}}}$ определяется из условия достижения заданной угловой скорости вращения системы ${{{{\omega }}}_{{end}}}$.

Силы торможения тросов в механизмах управления их выпуском задаются следующим образом

где ${{F}_{{in}}} = m\left( {l + r} \right){{\left( {{{\dot {\theta }}} + {{{{{\dot {\theta }}}}}_{t}}} \right)}^{2}}{\text{/}}4$ – приближенное значение центробежной силы инерции, натягивающей тросы; ${{k}_{v}}$ – коэффициент, определяющий интенсивность торможение троса.

Для согласования угловых скоростей КА и тросов вводится момент

где ${{k}_{\theta }} < 0$ – коэффициент обратной связи. Момент (11) приложен к центральному КА и здесь он вводится формально для обеспечения идеального развертывания системы в номинальном случае, чтобы в любой момент времени обеспечить симметричную конфигурацию системы.

Номинальная программа развертывания ТГКА зависит от многих параметров, входящих в выражения (9)–(11). Эти параметры должны быть выбраны так, чтобы выполнялись очевидные ограничения на некоторые характеристики движения системы: 1) конечные условия для выпуска троса $l\left( {{{t}_{{end}}}} \right) = {{l}_{{end}}}$, $\dot {l}\left( {{{t}_{{end}}}} \right) = 0$; 2) сила торможения в механизме управления ${{F}_{c}} \geqslant {{F}_{{\min }}} > 0$; 3) скорость выпуска троса $\dot {l} \geqslant 0$; 4) обеспечение заданной угловой скорости вращения системы ${{\dot {\theta }}}\left( {{{t}_{{end}}}} \right) = {{{{\dot {\theta }}}}_{t}}\left( {{{t}_{{end}}}} \right) = {{{{\omega }}}_{{end}}}$. Здесь ${{F}_{{\min }}}$ – минимальное значение силы торможения, которую могут обеспечить механизмы управления выпуском троса. Так как трос невесом, то сила натяжения троса равна силе торможения ${{F}_{c}}$. Из множества параметров, от которых зависит номинальная программа, выделяются основные (или наиболее значимые), выбором которых можно обеспечить выполнение приведенных выше условий и ограничений. Это следующие параметры: угол ${{\varphi }}$, определяющий направление реактивных сил ${{F}_{k}}\,\left( {k = 1,2,3} \right)$ (величину сил будем считать заданной); время окончания первого активного характерного участка движения системы ${{t}_{1}}$; коэффициент ${{k}_{v}}$, определяющий силу торможения тросов; относительная скорость разделения КА и спутников ${{V}_{r}}$; начальная угловая скорость вращения системы до разделения системы ${{{{\omega }}}_{0}}$. Выбор параметров осуществляется последовательно по участкам и ключевыми являются первые два участка, на которых задаются параметры ${{\varphi }},{{t}_{1}},{{k}_{v}},{{V}_{r}},{{{{\omega }}}_{0}}$ так, чтобы выполнялись граничные условия $l\left( {{{t}_{{end}}}} \right) = {{l}_{{end}}}$, $\dot {l}\left( {{{t}_{{end}}}} \right) = 0$ и приведенные выше ограничения. Как показал опыт решения рассматриваемой параметрической задачи, выбор параметров не представляет затруднений. Кроме того, имеется избыточное количество параметров, поэтому решение параметрической задачи не единственно.

В табл. 1 приводятся исходные данные, принятые при построении номинальной программы управления развертыванием ТГКА, и пример выбора ее параметров, обеспечивающих правильную треугольную конфигурацию системы при длине тросов 1 км, где $\tau = {{{{\omega }}}_{0}}t$ – безразмерное время.

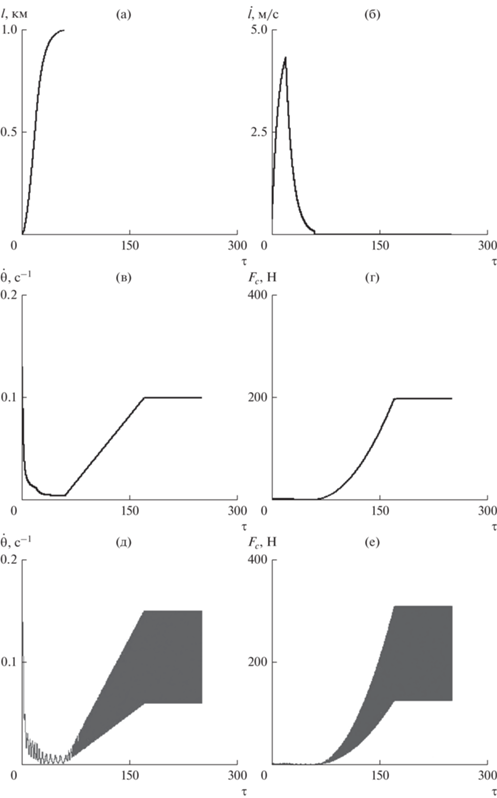
Изменение характеристик номинального движения ТГКА при ее формировании приводится на рис. 3, где также показан вариант рис. 3д–3е отсутствия управления ориентацией центрального КА $\left( {{{k}_{{{\theta }}}} = 0} \right)$. В последнем случае угловая скорость центрального КА ${{\dot {\theta }}}$ совершает колебания относительно угловой скорости тросов ${{{{\dot {\theta }}}}_{t}}$ (рис. 3в). Соответственно силы натяжения троса (рис. 3е) колеблются относительно значений, которые определены для ${{k}_{{{\theta }}}} \ne 0$ (рис. 3г).

УРАВНЕНИЯ ДВИЖЕНИЯ ЦЕНТРОВ МАСС КА И СПУТНИКОВ

Уравнения движения центров масс центрального КА и спутников в более полной модели движения системы записываются в геоцентрической системе координат $OXYZ$, где плоскость $OXY$ совпадает с плоскостью экватора, а ось $OX$ направлена в точку весеннего равноденствия

где ${{T}_{{ck}}} = - {{T}_{{kc}}}$ – силы натяжения тросов, ${{R}_{c}}$,${{R}_{k}}$ – радиус-векторы центров масс КА и спутников, ${{F}_{k}}$ – реактивные силы малой тяги, ${{G}_{с}} = {{ - {{\mu }}{{m}_{c}}{{R}_{с}}} \mathord{\left/ {\vphantom {{ - {{\mu }}{{m}_{c}}{{R}_{с}}} {R_{с}^{3}}}} \right. \kern-0em} {R_{с}^{3}}}$, ${{G}_{k}} = {{ - {{\mu }}m{{R}_{k}}} \mathord{\left/ {\vphantom {{ - {{\mu }}m{{R}_{k}}} {R_{k}^{3}}}} \right. \kern-0em} {R_{k}^{3}}}$ – гравитационные силы, ${{\mu }}$ – гравитационная постоянная.

Силы натяжения тросов соответствуют односторонней механической связи между КА и спутниками

где $\Delta {{r}_{k}}\,\left( {\,k = 1,2,3} \right)$ – радиусы-векторы, соединяющие точки крепления тросов; ${{L}_{k}}$ – нерастянутые длины тросов, $C = ES$, $E$ – модуль упругости Юнга, $S$ – площадь поперечного сечения тросов.

Векторы $\Delta {{r}_{k}}\,\left( {\,k = 1,2,3} \right)$ определяются выражениями

где векторы ${{r}_{k}},\,{{r}_{{ck}}}$ – определяют положение точек крепления тросов к КА и к спутникам относительно их центров масс. На рис. 4 в качестве примера показано, как определяется вектор $\Delta {{r}_{1}}$.

Векторы тяг двигателей ${{F}_{k}}\,\,\,\,\left( {k = 1,2,3} \right)$ составляют постоянные углы ${{{{\varphi }}}_{k}} = {{\varphi }}\,\,\,\,$(рис. 1) с осями ${{с}_{k}}{{x}_{k}}$ связанных систем координат спутников (лежат в плоскостях ${{с}_{k}}{{x}_{k}}{{y}_{k}}$). При отсутствии возмущений (номинальный случай) плоскости ${{с}_{k}}{{x}_{k}}{{y}_{k}}$ совпадают с плоскостью вращения всей системы относительно своего центра масс.

Процесс выпуска троса моделируется с помощью динамических уравнений [25, 26]

где коэффициент ${{m}_{{in}}}$ учитывает инерционность механизмов управления (тросы считаются невесомыми), ${{U}_{k}}$ – управляющие силы.

Силы торможения в механизмах управления определяются с использованием принципа обратной связи

где номинальные значения ${{l}_{k}},{{\dot {l}}_{k}}$ определяются интегрирования системы уравнений (5), ${{K}_{l}},{{K}_{v}}$ – коэффициенты обратной связи. Такой принцип управления выпуском троса использовался ранее при проведении реального тросового эксперимента на орбите YES2 [24]. Предполагается, что механизмы выпуска троса осуществляют только торможение троса, поэтому если ${{\dot {L}}_{k}} \leqslant 0$ или ${{T}_{{kc}}} \leqslant 0$, то выпуск троса прекращается ${{\dot {L}}_{k}} = {{\ddot {L}}_{k}} = 0$.

УРАВНЕНИЯ ДВИЖЕНИЯ ОТНОСИТЕЛЬНО ЦЕНТРОВ МАСС КА И СПУТНИКОВ

Динамические уравнения Эйлера для КА и спутников записываются в традиционной форме

где ${{\omega }_{c}},\,{{\omega }_{k}}$ и ${{J}_{c}},\,{{J}_{k}}$ – векторы угловых скоростей и тензоры инерции КА и $k$-ого спутника, ${{M}_{с}},\,{{M}_{k}}$ – векторы моментов, действующих на КА и спутники. Так как предполагается, что эллипсоиды инерции КА и спутников близки к сфере и рассматривается движение ТГКА на высоких орбитах, то гравитационные и аэродинамические моменты не учитываются. Tензоры инерции ${{J}_{c}},\,{{J}_{k}}$ здесь определяются в главных связанных системах координат.

Кинематические уравнения используются в форме уравнений Эйлера–Пуассона

где ${{e}_{{xk}}},\,{{e}_{{yk}}},\,{{e}_{{zk}}}\,\left( {\,k = 1,2,3} \right)$ – орты главных связанных систем координат. Аналогично записываются кинематические уравнения для КА.

Моменты ${{M}_{с}},{{M}_{k}}$ в главных связанных системах координат определяются следующим образом

где ${{M}_{{Fk}}}$ – моменты от сил тяги ${{F}_{k}}\,\left( {\,k = 1,2,3} \right)$, если линии их действия не проходят через центры масс спутников; ${{M}_{\theta }}$ – управляющий момент, приложенный к КА для согласования угловых скоростей вращения КА и тросов. Момент ${{M}_{{{\theta }}}}$ определяется по формуле (10) и его вектор перпендикулярен плоскости связанной с КА системы координат ${{c}_{c}}{{x}_{c}}{{y}_{c}}$ (рис. 1). В номинальном случае плоскость ${{c}_{c}}{{x}_{c}}{{y}_{c}}$ совпадает с плоскостью вращения системы до ее разделения с угловой скоростью ${{\omega }_{o}}$.

Проекции единичных векторов ${{e}_{{xk}}},\,{{e}_{{yk}}},\,{{e}_{{zk}}}$ на оси неподвижной системы координат $OXYZ$ являются компонентами матриц $OXYZ$ перехода от системы координат $OXYZ$ к связанным системам координат каждого спутника (аналогично для КА)

При интегрировании уравнений (18) должны с заданной погрешностью выполняться условия ортогональности векторов ${{e}_{{xk}}},{{e}_{{yk}}},{{e}_{{zk}}}$ и $\left| {{{e}_{{xk}}}} \right| = \left| {{{e}_{{yk}}}} \right| = \left| {{{e}_{{zk}}}} \right| = 1$${{e}_{{xk}}},{{e}_{{yk}}},{{e}_{{zk}}}$. Для этого используется алгоритм коррекции, основанный на минимизации корректирующих добавок при изменении значений компонент векторов ${{e}_{{xk}}},{{e}_{{yk}}},{{e}_{{zk}}}$ [27].

Для контроля колебаний спутников относительно тросов и колебаний тросов относительно направлений векторов ${{r}_{{ck}}}$ (рис. 4) осуществляется вычисление углов (рис. 4)

В общем случае при наличии возмущений амплитуды колебаний пространственных углов (21) должны быть ограничены относительно своих невозмущенных значений $\,{{\alpha }_{k}} = {{\alpha }_{{ck}}} = 0$.

Система уравнений (12), (17), (18) описывает пространственное движение ТГКА с учетом растяжимости тросов (они считаются невесомыми), работы механизмов выпуска тросов и движения спутников и КА относительно своих центров масс, и может быть проинтегрирована при соответствующем задании начальных условий (начальная задача). При интегрировании системы (12), (17), (18) в основном используются матричные вычисления.

ПРОЦЕСС РАЗДЕЛЕНИЯ КА И СПУТНИКОВ

Для задания начальных условий движения ТГКА, для учета возникающих при этом возмущений необходимо рассмотреть процесс разделения КА и спутников. Векторы скоростей центров масс, угловых скоростей КА и спутников определяются в соответствии с теоремами механики. Пусть ${{V}_{{rk}}}\,\,\left( {k = 1,2,3} \right)$ относительные скорости отделения спутников от КА. Используя закон сохранения импульса, определим скорости центра масс КА и спутников ${{V}_{c}}$, ${{V}_{k}}$ после их разделения

где ${{V}_{s}}$ – вектор скорости центра масс системы до разделения, ${{m}_{s}} = {{m}_{c}} + 3m$ – масса всей системы.

Используя теорему об изменении кинетического момента твердого тела при ударном взаимодействии, получаем

где $\Delta {{K}_{c}}$, $\Delta {{K}_{k}}$ – приращение моментов импульса КА и спутников, ${{S}_{k}} = m\left( {{{V}_{k}} - {{V}_{s}}} \right) = - S_{k}^{'}$ – и-мпульсы, действующие на k‑ый спутник при его отделении.

Используя приращения моментов импульса (23), определяются изменение угловых скоростей КА и спутников после их разделения:

В номинальном случае линии действия импульсов ${{S}_{k}}$ проходят через центры масс КА и спутников, поэтому $\Delta {{K}_{k}} = \,\,\Delta {{K}_{c}} = 0$, и их угловые скорости равны угловой скорости системы до отделения спутников ${{\omega }_{0}}$. В противоположном случае, когда $\Delta {{K}_{k}} \ne 0,\,\,\Delta {{K}_{c}} \ne 0$, имеют место возмущения при разделении КА и спутников, и их угловые скорости изменяются.

ВОЗМУЩЕННОЕ ДВИЖЕНИЕ ТГКА

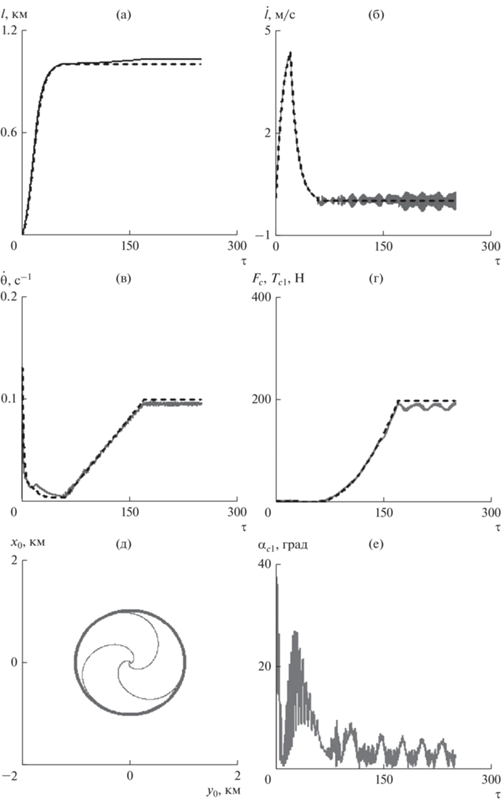
В табл. 2 показаны исходные данные, принятые для численного моделирования движения тросовой группировки по математической модели (12), (17), (18). Табл. 2 дополняет данные, представленные в табл. 1. Коэффициенты обратной связи ${{K}_{l}},\,\,{{{\text{K}}}_{v}}$ были выбраны в соответствии с работой [26], где рассматривалось движение тросовой системы, состоящей из двух КА, однако масса малого КА, характеристики троса и механизма управления его выпуском были такими же как в данной работе. Эллипсоиды инерции КА и спутников в невозмущенном случае – сферы. При численном анализе движения ТГКА с использованием модели (12), (17), (18) сначала анализировался случай, который был наиболее близок к номинальному движению системы, то есть спутники рассматривались как материальные точки. Другие характерные особенности системы (12), (17), (18) учитывались: растяжимость троса, работа механизмов выпуска тросов, пространственный характер движения системы, возмущения при разделении КА и спутников, статическая и динамическая асимметрия КА как твердого тела. На рис. 5 показано изменение характеристик движения ТГКА в этом случае, где рассматривались следующие возмущения: вектор ${{\omega }_{0}}$ не перпендикулярен орбитальной плоскости и имеет составляющие ${{{{\omega }}}_{{x0}}} = 0.05\,\,{{{\text{c}}}^{{ - 1}}}$, ${{{{\omega }}}_{{y0}}} = - 0.05\,\,{{{\text{c}}}^{{ - 1}}}$, ${{{{\omega }}}_{{z0}}} = 0.1\,\,{{{\text{c}}}^{{ - 1}}}$ в связанной с КА системе координат (пространственное движение), центр масс КА смещен относительно связанной оси ${{c}_{c}}{{x}_{c}}$ на $0.1r$(статическая асимметрия КА), учитывается динамическая асимметрия вида ${{\left( {{{J}_{{zc}}} - {{J}_{{yc}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{J}_{{zc}}} - {{J}_{{yc}}}} \right)} {{{J}_{{xc}}}}}} \right. \kern-0em} {{{J}_{{xc}}}}} = 0.1$. Наличие статической и динамической асимметрии КА приводит к изменению угловых скоростей КА после отделения спутников в соответствии с (24). Характерные зависимости для этого случая приведены на рис. 5, где на рис. 5a–5г штриховой линией показаны характеристики номинального движения, сплошной линией – возмущенное движение. На рис. 5д представлены траектории спутников относительно центра масс всей системы $\left( {0,0} \right)$, на рис. 5е – колебания угла ${{{{\alpha }}}_{{c1}}}$ (рис. 4), которые ограничены и после развертывания ТГКА амплитуда этих колебаний почти постоянна. Аналогично изменяется углы ${{{{\alpha }}}_{{c2}}},\,\,{{{{\alpha }}}_{{c3}}}$, которые соответствуют другим тросам.

Если рассматривать спутники как твердые тела, то реализация движения ТГКА, близкого к номинальному, усложняется. Как показали результаты моделирования движения ТГКА с использованием всех уравнений системы (12), (17), (18), угловое движение спутников относительно направлений тросов оказывается неустойчивым. Это в свою очередь ведет к тому, что ориентация реактивных двигателей относительно направлений троса нарушается (заданный угол $\varphi $ не реализуется) и формирование системы заданной конфигурации не происходит. Для устранения рассматриваемой неустойчивости движения ТГКА можно использовать простой вариант управления угловым движением спутников, когда стабилизация их колебаний относительно направлений тросов осуществляется по показаниям датчиков угловых скоростей (ДУС) с помощью использования стандартных малых реактивных двигателей системы ориентации и стабилизации движения КА. Проектирование системы управления спутников и соответствующие конструктивные решения выходят за рамки представленной статьи. Принципиально управляющие моменты системы стабилизации движения спутников в этом случае можно задать в виде

где ${{K}_{{{\omega }}}} < 0$ – коэффициент обратной связи, ${{{{\omega }}}_{{xk,yk,zk}}}$ – угловые скорости, определенные в связанных осях спутников.

После введения стабилизации угловых скоростей спутников (${{K}_{{{\omega }}}} = - 0.1\,\,{\text{кг}}\,\,{{{\text{м}}}^{{\text{2}}}}{\text{/с}}$) формирование заданной конфигурации ТГКА осуществляется успешно, и результаты мало отличаются от случая, когда спутники рассматривались как материальные точки. Результаты моделирования движения ТГКА для этого случая с использованием уравнений (12), (17), (18) показаны на рис. 6. Графики для длин тросов и их скоростей на рис. 6 не приводятся, так как они практически не отличаются от зависимостей, представленных на рис. 5.

Из рис. 6в и рис. 6г следует ограниченность колебаний КА и спутников как твердых тел относительно направлений тросов, причем углы, определяющие ориентацию спутников относительно тросов, вследствие введения стабилизации вида (25) стремятся к нулю (для примера на рис. 6г показан угол ${{\alpha }_{1}}$, соответствующий первому спутнику). На рис. 6д и рис. 6е показано, как изменяются управляющие моменты, приложенные к КА и первому спутнику, и обеспечивающие успешное формирование ТГКА заданной конфигурации. Если при моделировании движения системы отказаться от стабилизации движения КА $\left( {{{M}_{{{\theta }}}} = 0} \right)$, то это накладывает очень жесткие ограничения на величину возмущений. Если в плоском случае развертывание ТГКА оказывается успешным (угловая скорость вращения КА ${{\dot {\theta }}}$ совершает ограниченные колебания относительно угловых скоростей вращения тросов ${{{{\dot {\theta }}}}_{t}}$), то в пространственном случае (для данных, соответствующих рис. 6) процесс формирования ТГКА оказывается неустойчивым.

ЗАКЛЮЧЕНИЕ

В работе предлагается метод формирования ТГКА в виде треугольного созвездия, основанный на использовании комбинированного управления, при котором часть управляющих функций возложено на центральный КА, а другая часть – на концевые спутники. Для построения законов управления используются две модели. Первая простая модель движения системы в плоском случае, построенная с помощью уравнений Лагранжа в предположении полной геометрической симметрии ТГКА в каждый момент времени. Эта модель позволяет построить номинальную программу развертывания системы. Вторая модель, построенная с помощью общих теорем механики, учитывает растяжимость тросов (односторонняя механическая связь), работу систем стабилизации КА и спутников, их движения относительно своих центров масс и других возмущений. Эта модель служит для проверки реализуемости построенной номинальной программы развертывания ТГКА. Очевидно, что такой подход к построению управлений для формирования ТГКА в виде симметричных вращающихся созвездий может быть использован для ТГКА с более сложной структурой, например, с четырьмя или пятью спутниками.

Исследование выполнено при финансовой поддержке РФФИ и ГФЕН Китая в рамках совместного научного проекта № 21-51-53002.