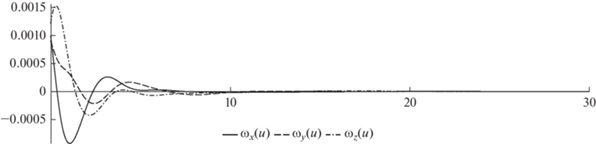Космические исследования, 2022, T. 60, № 5, стр. 404-412

Электродинамическое управление с распределенным запаздыванием для стабилизации ИСЗ на экваториальной орбите

А. Ю. Александров^1, *, А. А. Тихонов^1, **

¹ Санкт-Петербургский государственный университет
Санкт-Петербург, Россия

^* E-mail: a.u.aleksandrov@spbu.ru
^** E-mail: a.tikhonov@spbu.ru

Поступила в редакцию 03.11.2021
После доработки 19.01.2022
Принята к публикации 11.03.2022

EDN: GPFQMV
DOI: 10.31857/S002342062204001X

Аннотация

Рассматривается ИСЗ с электродинамической системой стабилизации. Для решения задачи о трехосной стабилизации ИСЗ в произвольном положении в орбитальной системе координат ставится вопрос о возможности создания системы электродинамического управления угловым движением ИСЗ по типу PID-регулятора, отличающегося от классического PID-регулятора тем, что восстанавливающая компонента управляющего момента содержит распределенное запаздывание. Доказана теорема об асимптотической устойчивости стабилизируемого положения равновесия ИСЗ, подтверждающая возможность создания указанной системы электродинамического управления. Эффективность предложенной системы управления и целесообразность ее применения для сглаживания переходных процессов подтверждается численным моделированием.

1. ВВЕДЕНИЕ

Электродинамическое взаимодействие искусственного спутника Земли (ИСЗ) с магнитным полем Земли оказывает существенное влияние на динамику вращательного движения спутника относительно его центра масс и может использоваться при построении систем управления ориентацией ИСЗ. Основанные на указанном взаимодействии магнитные системы управления (МСУ), их преимущества, особенности, недостатки, а также различные варианты применения, описаны, например, в работах [1–8]. Метод стабилизации ИСЗ, основанный на использовании момента лоренцевых сил (ЛСУ), предложенный в работе [9], получил развитие в работах [10–13], а также в недавних работах авторов данной статьи. Интерес к этому способу управления основан, в частности, на том, что создание управляющего лоренцева момента, значительно превышающего по величине гравитационный и другие возмущающие моменты, не вызывает технических трудностей [9].

Электродинамический метод стабилизации ИСЗ [14] использует одновременно момент магнитного взаимодействия и лоренцев момент и благодаря этому снимает проблему недостатка управления, свойственную как МСУ, так и ЛСУ по-отдельности. В работе [14] сформулирован механизм синтеза восстанавливающих и демпфирующих компонент управляющих моментов. В дальнейшем электродинамическая система управления угловым движением ИСЗ получила развитие в [15–18], а также в работах авторов данной статьи, направленных на решение ряда задач стабилизации различных режимов вращательного движения ИСЗ относительно центра масс.

В вышеупомянутых работах [14–17] построение электродинамической системы управления, адаптированной для решения той или иной задачи управления, опирается на использование восстанавливающих моментов, пропорциональных первым степеням норм разностей между программными и текущими значениями векторов, связанных с ИСЗ, а также – на использование демпфирующих моментов, пропорциональных первой степени относительной угловой скорости ИСЗ в базовой системе координат. Условия асимптотической устойчивости программного режима движения выводятся на базе прямого метода Ляпунова.

Однако, в некоторых задачах динамики вращательного движения ИСЗ принципиально важным является не только выполнение условий асимптотической устойчивости программного режима движения, но и определенная гладкость переходных процессов. Например, при стабилизации больших космических конструкций или ИСЗ с высокоточными чувствительными приборами, для которых вибрации, вызванные работой системы управления, являются нежелательными. Известный в задачах управления способ сглаживания переходных процессов, основанный на увеличении демпфирующих компонент управляющих моментов, может оказаться сложным для реализации в условиях космического пространства. По этой причине в задачах динамики ИСЗ часто используется другой, более подходящий способ сглаживания, основанный на использовании PID-регуляторов [19, 20]. Недостаток этого способа становится заметным в процессе управления по мере приближения к программному режиму движения и является следствием того, что интегральная компонента в управляющем моменте продолжает учитывать предысторию поведения системы управления в то время, когда эта предыстория уже не играет роли. В результате в системе управления появляется постоянно действующее возмущение, препятствующее точной стабилизации или точному наведению ИСЗ.

Для преодоления этого недостатка предлагается использовать управление с распределенным запаздыванием. Сравнение такой модификации PID-регулятора со стандартным PID-регулятором, а также с PD-регулятором, дано в работе [21] для линейного дифференциального уравнения с постоянными коэффициентами. В ней же отмечаются значительные трудности аналитического анализа и обоснования эффективности данного метода управления.

Тем не менее, в работе [22] разработан аналитический подход к анализу устойчивости в задаче об управлении вращательным движением твердого тела с использованием PID-регулятора с распределенным запаздыванием. Исследование основано на развитии прямого метода Ляпунова и метода декомпозиции на дифференциальные системы с распределенным запаздыванием. В результате получены сформулированные в конструктивном виде и представленные в простой форме достаточные условия асимптотической устойчивости равновесного положения твердого тела. Компьютерное моделирование подтвердило не только ожидаемый эффект сглаживания переходных процессов, но и существенное сокращение времени сходимости.

В данной работе рассматривается задача трехосной электродинамической стабилизации в орбитальной системе координат для ИСЗ, движущегося по круговой экваториальной орбите. Ранее такая задача рассматривалась в [16] для случая стабилизации ИСЗ в прямом положении равновесия. Цель данной работы заключается в развитии исследования, выполненного в [16], путем решения более общей задачи о стабилизации ИСЗ в произвольном положении в орбитальной системе координат, причем на базе нового подхода, учитывающего преимущества управления с распределенным запаздыванием, выявленные в [22]. Возникает вопрос о возможности создания электродинамической системы управления по типу PID-регулятора, в котором восстанавливающие компоненты лоренцева момента и момента магнитного взаимодействия содержат распределенное запаздывание. В данной работе дается положительный ответ на этот вопрос. Анализируется эффективность предложенного управления. В отличие от вышеупомянутой работы [22], опирающейся в аналитическом исследовании на метод декомпозиции, в данной статье используется оригинальная конструкция функционала Ляпунова–Красовского при исследовании устойчивости программного режима движения ИСЗ.

2. ЭЛЕКТРОДИНАМИЧЕСКОЕ УПРАВЛЕНИЕ

Рассматривается ИСЗ, центp масс котоpого движется по круговой экваториальной орбите радиуса $R.$ Пpедполагается, что ИСЗ снабжен управляемым электростатическим зарядом $Q = \int_V {\sigma dV} ,$ распределенным по некоторому объему $V$ с плотностью $\sigma $ и управляемым собственным магнитным моментом $I.$ В качестве базовой системы координат, в которой решается задача стабилизации ИСЗ, используется орбитальная система координат $C\xi \eta \zeta $ с началом в центре масс ИСЗ, ось $C\xi ({{\xi }_{0}})$ которой направлена по касательной к орбите в сторону движения, ось $C\eta ({{\eta }_{0}})$ – по нормали к плоскости орбиты, ось $C\zeta ({{\zeta }_{0}})$ – вдоль радиуса-вектора $R = \overleftarrow {{{O}_{{\text{З}}}}C} = R{{\zeta }_{0}}$ центра масс ИСЗ относительно центра Земли ${{O}_{{\text{З}}}}.$ Исследование проводится с учетом вращения орбитальной системы координат относительно инерциальной системы с угловой скоростью ${{\omega }_{0}}.$ С ИСЗ жестко связана система его главных центральных осей инерции $Cxyz$ (орты $i,j,k$). Все системы координат, используемые в данной статье, являются правыми декартовыми прямоугольными. Ориентация осей $Cxyz$ относительно осей $C\xi \eta \zeta $ определяется матрицей ${\mathbf{A}}$ направляющих косинусов ${{\alpha }_{i}},$ ${{\beta }_{i}},$ ${{\gamma }_{i}}\,\,(i = 1,2,3).$ Орты ${{\xi }_{0}},{{\eta }_{0}},{{\zeta }_{0}}$ в орбитальной системе координат определяются равенствами

${{\xi }_{0}}{{ = (1,0,0)}^{{\rm T}}},\,\,\,\,{{\eta }_{0}}{{ = (0,1,0)}^{{\rm T}}},\,\,\,\,{{\zeta }_{0}}{{ = (0,0,1)}^{{\rm T}}}.$

Те же орты в системе координат $Cxyz$ обозначим через ${{s}_{1}},{{s}_{2}},{{s}_{3}}{\text{:}}$

$\begin{gathered} {{A}^{{\rm T}}}{{\xi }_{0}} = ({{\alpha }_{1}},{{\alpha }_{2}},{{\alpha }_{3}}{{)}^{{\rm T}}} = {{s}_{1}},\,\,\,\,{{A}^{{\rm T}}}{{\eta }_{0}} = ({{\beta }_{1}},{{\beta }_{2}},{{\beta }_{3}}{{)}^{{\rm T}}} = {{s}_{2}}, \\ {{A}^{{\rm T}}}{{\zeta }_{0}} = ({{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}}{{)}^{{\rm T}}} = {{s}_{3}}. \\ \end{gathered} $

В программной ориентации ИСЗ матрица $A$ принимает значение ${{A}_{0}}$ с элементами ${{\alpha }_{{i0}}},$ ${{\beta }_{{i0}}},$ ${{\gamma }_{{i0}}}$ $(i = 1,2,3).$ Следовательно, в программной ориентации ИСЗ орты ${{s}_{i}}$ принимают значения ${{r}_{i}}$ $(i = 1,2,3),$ определяемые следующим образом:

$\begin{gathered} A_{0}^{{\rm T}}{{\xi }_{0}}\, = {{({{\alpha }_{{10}}},{{\alpha }_{{20}}},{{\alpha }_{{30}}})}^{{\rm T}}}\, = {{r}_{1}},\,\,\,A_{0}^{{\rm T}}{{\eta }_{0}} = {{({{\beta }_{{10}}},{{\beta }_{{20}}},{{\beta }_{{30}}})}^{{\rm T}}}\, = {{r}_{2}}, \\ A_{0}^{{\rm T}}{{\zeta }_{0}} = ({{\gamma }_{{10}}},{{\gamma }_{{20}}},{{\gamma }_{{30}}}{{)}^{{\rm T}}} = {{r}_{3}}. \\ \end{gathered} $

Пусть $\omega {\kern 1pt} ' = \omega _{x}^{'}i + \omega _{y}^{'}j + \omega _{z}^{'}k$ – угловая скорость ИСЗ относительно орбитальной системы координат. Вращательное движение ИСЗ, в котором

(1)

$A = {{A}_{0}},\,\,\,\,\omega {\kern 1pt} ' = {\mathbf{0}}$

будем называть программным режимом вращательного движения ИСЗ относительно его центра масс. В терминах введенных выше ортов программный режим (1) определяется равенствами

(2)

${{{\mathbf{s}}}_{i}} = {{{\mathbf{r}}}_{i}},\,\,\,\,\omega {\kern 1pt} ' = 0,\,\,\,\,i = 1,2,3.$

Поскольку ИСЗ движется со скоростью ${{{\mathbf{v}}}_{C}}$ относительно геомагнитного поля с магнитной индукцией $B$ (векторы ${{{\mathbf{v}}}_{C}}$ и $B$ считаются заданными в орбитальной системе координат), то он подвергается воздействию лоренцева момента ${{{\mathbf{M}}}_{L}}$ и момента магнитного взаимодействия ${{{\mathbf{M}}}_{M}},$ соответственно имеющих вид

${{{\mathbf{M}}}_{L}} = {\mathbf{P}} \times {\mathbf{T}},\,\,\,\,{{{\mathbf{M}}}_{M}} = {\mathbf{I}} \times {{{\mathbf{A}}}^{{\rm T}}}{\mathbf{B}},$

где ${\mathbf{P}} = Q{{\rho }_{0}},$ ${{\rho }_{0}} = {{x}_{0}}{\mathbf{i}} + {{y}_{0}}{\mathbf{j}} + {{z}_{0}}{\mathbf{k}}{{Q}^{{ - 1}}}\int_V {\sigma \rho dV} $ – pадиус-вектоp центра заряда ИСЗ относительно его центра масс, ${\mathbf{T}} = {{{\mathbf{A}}}^{{\rm T}}}({{{\mathbf{v}}}_{C}} \times {\mathbf{B}}).$ Значение ${\mathbf{B}}$ в этих формулах совпадает со значением ${\mathbf{B}}$ в центре масс ИСЗ. Векторы ${\mathbf{P}}$ и ${\text{I}}$ считаются заданными в системе координат $Cxyz.$

В программном режиме вращательного движения векторы ${\mathbf{T}}$ и ${{{\mathbf{A}}}^{{\rm T}}}{\mathbf{B}}$ соответственно принимают значения ${{{\mathbf{T}}}_{0}} = {\mathbf{A}}_{0}^{{\rm T}}({{{\mathbf{v}}}_{C}} \times {\mathbf{B}})$ и ${{{\mathbf{B}}}_{0}} = {\mathbf{A}}_{0}^{{\rm T}}{\mathbf{B}}.$

Синтез электродинамического управления предполагает, что для реализации программного режима вращательного движения (1) должны быть подобраны такие законы изменения параметров ${\mathbf{P}}$ и ${\mathbf{I}},$ которые обеспечивают создание восстанавливающих, демпфирующих, а также, в общем случае, компенсирующих компонент управляющих моментов в окрестности данного программного движения.

Следуя [14], построим каждый из электродинамических параметров в виде суммы восстанавливающих, демпфирующих и компенсирующих компонент:

(3)

${\mathbf{P}} = {{{\mathbf{P}}}_{R}} + {{{\mathbf{P}}}_{D}} + {{{\mathbf{P}}}_{C}},\,\,\,\,{\mathbf{I}} = {{{\mathbf{I}}}_{R}} + {{{\mathbf{I}}}_{D}} + {{{\mathbf{I}}}_{C}}.$

Здесь ${{{\mathbf{P}}}_{R}} = Q{{k}_{L}}{{{\mathbf{T}}}_{0}}$ и ${{{\mathbf{I}}}_{R}} = {{k}_{M}}{{{\mathbf{B}}}_{0}}$ обеспечивают создание восстанавливающих компонент управляющих моментов ${{{\mathbf{M}}}_{L}}$ и ${{{\mathbf{M}}}_{M}},$ ${{{\mathbf{P}}}_{D}} = Q{{h}_{L}}\omega {\kern 1pt} '\,\, \times {\mathbf{T}}$ и ${{{\mathbf{I}}}_{D}} = {{h}_{M}}\omega {\kern 1pt} '\,\, \times ({{{\mathbf{A}}}^{{\rm T}}}{\mathbf{B}})$ – создание демпфирующих компонент управляющих моментов ${{{\mathbf{M}}}_{L}}$ и ${{{\mathbf{M}}}_{M}},$ а ${{{\mathbf{P}}}_{C}}$ и ${{{\mathbf{I}}}_{C}}$ – создание компенсирующих компонент ${{{\mathbf{M}}}_{{LC}}}$ и ${{{\mathbf{M}}}_{{MC}}}$ тех же управляющих моментов. Необходимость компенсирующих компонент в управляющих моментах возникает в тех случаях, когда программный режим движения не является решением системы дифференциальных уравнений движения в силу тех или иных возмущающих моментов. Компенсирующие компоненты строятся в зависимости от конкретных возмущающих моментов и будут рассмотрены в следующем разделе при построении математической модели задачи. Кроме того, добавим интегральные члены, построенные на основе восстанавливающих компонент. Тогда управляющие моменты примут вид

(4)

$\begin{gathered} {{{\mathbf{M}}}_{L}} = Q{{k}_{L}}{{{\mathbf{T}}}_{0}} \times {\mathbf{T}} + \\ + \,\,Qc{{k}_{L}}\int\limits_{t - \tau }^t {{{{\mathbf{T}}}_{0}} \times {\mathbf{T}}(u)du + Q{{h}_{L}}(\omega {\kern 1pt} '\,\, \times {\mathbf{T}}) \times {\mathbf{T}} + {{{\mathbf{M}}}_{{LC}}}} , \\ \end{gathered} $

(5)

$\begin{gathered} {{{\mathbf{M}}}_{M}} = {{k}_{M}}{{{\mathbf{B}}}_{0}} \times {{{\mathbf{A}}}^{{\rm T}}}{\mathbf{B}} + c{{k}_{M}}\int\limits_{t - \tau }^t {{{{\mathbf{B}}}_{0}} \times {{{\mathbf{A}}}^{{\rm T}}}{\mathbf{B}}(u)du} + \\ + \,\,{{h}_{M}}(\omega {\kern 1pt} '\,\, \times {{{\mathbf{A}}}^{{\rm T}}}{\mathbf{B}}) \times {{{\mathbf{A}}}^{{\rm T}}}{\mathbf{B}} + {{{\mathbf{M}}}_{{MC}}}, \\ \end{gathered} $

где параметры управления ${{k}_{L}},{{k}_{M}},{{h}_{L}},{{h}_{M}}$ могут быть скалярными функциями времени, $c$ и $\tau $ – постоянные параметры, причем $c \ne 0,$ $\tau \geqslant 0.$

3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

На данном этапе исследования, когда основное внимание направлено не столько на всестороннюю точность учета факторов, воздействующих на ИСЗ, сколько на анализ влияния распределенного запаздывания на процесс управляемого вращательного движения ИСЗ, в качестве модели геомагнитного поля возьмем простую модель “прямой магнитный диполь”. В этом случае магнитная индукция ${\mathbf{B}}$ постоянна во всех точках экваториальной орбиты и определяется по формуле ${\mathbf{B}} = {{B}_{\eta }}{\kern 1pt} {{\eta }_{0}} = - {{({{{{R}_{{\text{E}}}}} \mathord{\left/ {\vphantom {{{{R}_{{\text{E}}}}} R}} \right. \kern-0em} R})}^{3}}g_{1}^{0}{{\eta }_{0}},$ где ${{R}_{{\text{E}}}}$ – радиус Земли, $g_{1}^{0}$ – первый гауссов коэффициент. Для круговой экваториальной орбиты ${{{\mathbf{v}}}_{C}} = R({{\omega }_{0}} - {{\omega }_{{\text{E}}}}){{\xi }_{0}},$ где ${{\omega }_{{\text{E}}}}$ – угловая скорость суточного вращения Земли. Поэтому

$\begin{gathered} {{{\mathbf{v}}}_{C}} \times {\mathbf{B}} = {{v}_{{C\xi }}}{{B}_{\eta }}{{\zeta }_{0}},\,\,\,\,{\mathbf{T}} = {{v}_{{C\xi }}}{{B}_{\eta }}{{{\mathbf{s}}}_{3}},\,\,\,\,{{{\mathbf{T}}}_{0}} = {{v}_{{C\xi }}}{{B}_{\eta }}{{{\mathbf{r}}}_{3}}, \\ {\mathbf{B}} = {{B}_{\eta }}{{{\mathbf{s}}}_{2}},\,\,\,\,{{{\mathbf{B}}}_{0}} = {{B}_{\eta }}{{{\mathbf{r}}}_{2}}. \\ \end{gathered} $

Подставляя эти выражения в (4) и (5), получим

(6)

$\begin{gathered} {{{\mathbf{M}}}_{L}} = {{k}_{{L0}}}{{{\mathbf{r}}}_{3}} \times {{{\mathbf{s}}}_{3}} + c{{k}_{{L0}}}\int\limits_{t - \tau }^t {{{{\mathbf{r}}}_{3}}} \times {{{\mathbf{s}}}_{3}}(u)du - \\ - \,\,{{h}_{{L0}}}[\omega {\kern 1pt} '\, - {{{\mathbf{s}}}_{3}}({{{\mathbf{s}}}_{3}}\omega {\kern 1pt} ')] + {{{\mathbf{M}}}_{{LC}}}, \\ \end{gathered} $

(7)

$\begin{gathered} {{{\mathbf{M}}}_{M}} = {{k}_{{M0}}}{{{\mathbf{r}}}_{2}} \times {{{\mathbf{s}}}_{2}} + c{{k}_{{M0}}}\int\limits_{t - \tau }^t {{{{\mathbf{r}}}_{2}}} \times \\ \times \,\,{{{\mathbf{s}}}_{2}}(u)du - {{h}_{{M0}}}[\omega {\kern 1pt} '\, - {{{\mathbf{s}}}_{2}}({{{\mathbf{s}}}_{2}}\omega {\kern 1pt} ')] + {{{\mathbf{M}}}_{{MC}}}, \\ \end{gathered} $

где

$\begin{gathered} Q{{k}_{L}} = \frac{{{{k}_{{L0}}}}}{{{{{({{v}_{{C\xi }}}{{B}_{\eta }})}}^{2}}}},\,\,\,\,Q{{h}_{L}} = \frac{{{{h}_{{L0}}}}}{{{{{({{v}_{{C\xi }}}{{B}_{\eta }})}}^{2}}}}, \\ {{k}_{M}} = \frac{{{{k}_{{M0}}}}}{{B_{\eta }^{2}}},\,\,\,\,{{h}_{M}} = \frac{{{{h}_{{M0}}}}}{{B_{\eta }^{2}}}, \\ \end{gathered} $

а ${{k}_{{L0}}},$ ${{k}_{{M0}}},$ ${{h}_{{L0}}},$ ${{h}_{{M0}}}$ – положительные постоянные.

Вращательное движение ИСЗ описывается динамическими уравнениями Эйлера

(8)

$\frac{d}{{dt}}({\mathbf{J}}\omega ) + \omega \times ({\mathbf{J}}\omega ) = {{{\mathbf{M}}}_{G}} + {{{\mathbf{M}}}_{L}} + {{{\mathbf{M}}}_{M}},$

где ${\mathbf{J}} = {\text{diag}}(A,B,C)$ – тензор инерции ИСЗ в системе координат $Cxyz,$ $\omega = \omega {\kern 1pt} '\,\, + {{\omega }_{0}}$ = $\omega {\kern 1pt} '\,\, + {{\omega }_{0}}{{{\mathbf{s}}}_{2}}$ – угловая скорость ИСЗ, ${{{\mathbf{M}}}_{G}} = 3\omega _{0}^{2}{\kern 1pt} {{{\mathbf{s}}}_{3}} \times ({\mathbf{J}}{{{\mathbf{s}}}_{3}})$ – гравитационный момент [23], являющийся одним из наиболее значимых возмущающих моментов, особенно для ИСЗ с типичной конфигурацией и находящихся на орбитах средних высот. Заметим, что

$\begin{gathered} \omega \times ({\mathbf{J}}\omega ) = ({\kern 1pt} \omega {\kern 1pt} ' + {{\omega }_{0}}{{{\mathbf{s}}}_{2}}) \times ({\mathbf{J}}\omega {\kern 1pt} ') + \\ + \,\,{{\omega }_{0}}{\kern 1pt} \omega {\kern 1pt} ' \times ({\mathbf{J}}{{{\mathbf{s}}}_{2}}) + \omega _{0}^{2}{{{\mathbf{s}}}_{2}} \times ({\mathbf{J}}{{{\mathbf{s}}}_{2}}). \\ \end{gathered} $

Поскольку программный режим движения ИСЗ не является в общем случае прямым положением равновесия ИСЗ в орбитальной системе координат, то гравитационный момент не обращается в ноль в программном режиме движения ИСЗ. Также не обращается в ноль и выражение $\omega _{0}^{2}{\kern 1pt} {{{\mathbf{s}}}_{2}} \times ({\mathbf{J}}{{{\mathbf{s}}}_{2}})$ в левой части уравнений (8).

Для компенсации этих слагаемых, представленных в виде возмущающего момента

${{{\mathbf{M}}}_{d}} = \omega _{0}^{2}\left( {{{{\mathbf{s}}}_{3}} \times ({\mathbf{J}}{{{\mathbf{s}}}_{3}}) - {{{\mathbf{s}}}_{2}} \times ({\mathbf{J}}{{{\mathbf{s}}}_{2}})} \right),$

будем использовать подход, развитый в [24] и основанный на создании компенсирующих компонент электродинамических параметров в следующем виде:

$\begin{gathered} {{{\mathbf{P}}}_{C}} = \frac{{{{{\mathbf{M}}}_{d}} \cdot ({{{\mathbf{A}}}^{{\rm T}}}{\mathbf{B}})}}{{\left| {\mathbf{B}} \right|\left| {\mathbf{T}} \right|}}\left( {{{{\mathbf{V}}}^{{\rm T}}} \cdot {{{(0,0,1)}}^{{\rm T}}}} \right) \times {\mathbf{T}}, \\ {{{\mathbf{I}}}_{C}} = \frac{1}{{\left| {\mathbf{B}} \right|}}{{{\mathbf{V}}}^{{\rm T}}} \cdot {{\left( {0,\frac{{{{{\mathbf{M}}}_{d}} \cdot (({{{\mathbf{A}}}^{{\rm T}}}{\mathbf{B}}) \times {\mathbf{T}})}}{{\left| {\mathbf{B}} \right|\left| {\mathbf{T}} \right|}}, - \frac{{{{{\mathbf{M}}}_{d}} \cdot {\mathbf{T}}}}{{\left| {\mathbf{T}} \right|}}} \right)}^{{\rm T}}}. \\ \end{gathered} $

Здесь ${\mathbf{V}}$ – известная матрица:

${\mathbf{V}} = \left( {\begin{array}{*{20}{c}} {{{{{B}_{x}}} \mathord{\left/ {\vphantom {{{{B}_{x}}} {\left| B \right|}}} \right. \kern-0em} {\left| B \right|}}}&{{{{{B}_{y}}} \mathord{\left/ {\vphantom {{{{B}_{y}}} {\left| B \right|}}} \right. \kern-0em} {\left| B \right|}}}&{{{{{B}_{z}}} \mathord{\left/ {\vphantom {{{{B}_{z}}} {\left| B \right|}}} \right. \kern-0em} {\left| B \right|}}} \\ {{{{{T}_{x}}} \mathord{\left/ {\vphantom {{{{T}_{x}}} {\left| T \right|}}} \right. \kern-0em} {\left| T \right|}}}&{{{{{T}_{y}}} \mathord{\left/ {\vphantom {{{{T}_{y}}} {\left| T \right|}}} \right. \kern-0em} {\left| T \right|}}}&{{{{{T}_{z}}} \mathord{\left/ {\vphantom {{{{T}_{z}}} {\left| T \right|}}} \right. \kern-0em} {\left| T \right|}}} \\ {\frac{{{{B}_{y}}{{T}_{z}} - {{B}_{z}}{{T}_{y}}}}{{B\left| T \right|}}}&{\frac{{{{B}_{z}}{{T}_{x}} - {{B}_{x}}{{T}_{z}}}}{{\left| B \right|\left| T \right|}}}&{\frac{{{{B}_{x}}{{T}_{y}} - {{B}_{y}}{{T}_{x}}}}{{B\left| T \right|}}} \end{array}} \right).$

После подстановки ${{{\mathbf{P}}}_{C}}$ и ${{{\mathbf{I}}}_{C}}$ в управляющие моменты, получаем ${{{\mathbf{M}}}_{{LC}}} = {{{\mathbf{P}}}_{C}} \times {\mathbf{T}},$ ${{{\mathbf{M}}}_{{MC}}} = {{{\mathbf{I}}}_{C}} \times ({{{\mathbf{A}}}^{{\rm T}}}{\mathbf{B}}).$ Непосредственной проверкой легко убедиться в том, что ${{{\mathbf{M}}}_{{LC}}} + {{{\mathbf{M}}}_{{MC}}} + {{{\mathbf{M}}}_{d}} = {\mathbf{0}}.$

Поэтому, подставляя (6) и (7) в (8), получим следующую систему динамических дифференциальных уравнений:

(9)

$\begin{gathered} \frac{d}{{dt}}[{\mathbf{J}}(\omega {\kern 1pt} ' + {{\omega }_{0}}{{{\mathbf{s}}}_{2}})] + (\omega {\kern 1pt} ' + {{\omega }_{0}}{{{\mathbf{s}}}_{2}}) \times ({\mathbf{J}}\omega {\kern 1pt} ') + {{\omega }_{0}}\omega {\kern 1pt} ' \times ({\mathbf{J}}{{{\mathbf{s}}}_{2}}) = \\ = {{k}_{{L0}}}({{{\mathbf{r}}}_{3}} \times {{{\mathbf{s}}}_{3}}) + {{k}_{{M0}}}({{{\mathbf{r}}}_{2}} \times {{{\mathbf{s}}}_{2}}) + c{{k}_{{L0}}}\int\limits_{t - \tau }^t {{{{\mathbf{r}}}_{3}}} \times {{{\mathbf{s}}}_{3}}(u)du + \\ + \,\,c{{k}_{{M0}}}\int\limits_{t - \tau }^t {{{{\mathbf{r}}}_{2}}} \times {{{\mathbf{s}}}_{2}}(u)du - {{h}_{{L0}}}[\omega {\kern 1pt} ' - {{{\mathbf{s}}}_{3}}({{{\mathbf{s}}}_{3}}{\kern 1pt} \omega {\kern 1pt} ')] - \\ - \,\,{{h}_{{M0}}}[\omega {\kern 1pt} ' - {{{\mathbf{s}}}_{2}}({{{\mathbf{s}}}_{2}}\omega {\kern 1pt} ')]. \\ \end{gathered} $

Для замыкания дифференциальной системы будем рассматривать динамические уравнения (9) совместно с кинематическими уравнениями Пуассона

(10)

$\frac{{d{{{\mathbf{s}}}_{i}}}}{{dt}} + \omega {\kern 1pt} ' \times {{{\mathbf{s}}}_{i}} = 0\,\,(i = 1,2,3).$

Каждое решение ${{({{\omega }^{{'{\rm T}}}}(t),{\mathbf{s}}_{1}^{{\rm T}}(t),{\mathbf{s}}_{2}^{{\rm T}}(t),{\mathbf{s}}_{3}^{{\rm T}}(t))}^{{\rm T}}}$ системы (9), (10) при $t \geqslant {{t}_{0}}$ определяется начальным моментом времени ${{t}_{0}} \geqslant 0$ и начальной функцией $\phi (\theta ),$ где $\phi (\theta )$ принадлежит пространству $C([ - \tau ,0],{{\mathbb{R}}^{{12}}})$ непрерывных функций с равномерной нормой

${{\left\| \phi \right\|}_{\tau }} = \mathop {\max }\limits_{\theta \in [ - \tau ,0]} \left\| {\phi (\theta )} \right\|,$

а $\left\| \cdot \right\|$ – евклидова норма вектора.

Исследование процесса стабилизации ИСЗ в орбитальной системе координат в программной ориентации (2) будет проводиться на базе нелинейных дифференциальных уравнений (9), (10).

4. АНАЛИЗ УСТОЙЧИВОСТИ

Пусть ${{{\mathbf{I}}}_{3}}$ – ($3 \times 3$) – единичная матрица, ${{{\mathbf{r}}}_{i}} = ({{r}_{{i1}}},{{r}_{{i2}}},{{r}_{{i3}}}{{)}^{{\rm T}}}$ при $i = 2,3,$ Ψ(t) = k_L0r₃ × s₃(t) + $ + \,\,{{k}_{{M0}}}{{{\mathbf{r}}}_{2}} \times {{{\mathbf{s}}}_{2}}(t),$ ${{h}_{{L0}}} = h{{\bar {h}}_{L}},$ ${{h}_{{M0}}} = h{{\bar {h}}_{M}},$ где ${{\bar {h}}_{L}}$ и ${{\bar {h}}_{M}}$ – фиксированные положительные числа, а $h$ — положительный параметр.

Имеем

$\begin{gathered} {{\omega }_{0}}\frac{{d{{{\mathbf{s}}}_{2}}}}{{dt}}\, + \,{{\omega }_{0}}{{{\mathbf{s}}}_{2}} \times ({\mathbf{J}}{\kern 1pt} \omega {\kern 1pt} ') + {{\omega }_{0}}\omega {\kern 1pt} ' \times ({\mathbf{J}}{{{\mathbf{s}}}_{2}}) = \\ = - {{\omega }_{0}}\omega {\kern 1pt} ' \times {{{\mathbf{r}}}_{2}} + {\mathbf{G}}\omega {\kern 1pt} ' + {{\Xi }_{1}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})\omega {\kern 1pt} ', \\ {{h}_{{L0}}}[\omega {\kern 1pt} ' - {{{\mathbf{s}}}_{3}}({{{\mathbf{s}}}_{3}}\omega {\kern 1pt} ')] + {{h}_{{M0}}}[\omega {\kern 1pt} ' - {{{\mathbf{s}}}_{2}}({{{\mathbf{s}}}_{2}}\omega {\kern 1pt} ')] = \\ = h{\mathbf{D}}\omega {\kern 1pt} ' + {{\Xi }_{2}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})\omega {\kern 1pt} '. \\ \end{gathered} $

Здесь

$\begin{gathered} {\mathbf{G}} = {{\omega }_{0}}\left( {\begin{array}{*{20}{c}} 0&{(C - B){{r}_{{23}}}}&{(C - B){{r}_{{22}}}} \\ {(A - C){{r}_{{23}}}}&0&{(A - C){{r}_{{21}}}} \\ {(B - A){{r}_{{21}}}}&{(B - A){{r}_{{22}}}}&0 \end{array}} \right), \\ {\mathbf{D}} = {{{\bar {h}}}_{L}}\left( {{{{\mathbf{I}}}_{3}} - {{{\mathbf{r}}}_{3}}{\mathbf{r}}_{3}^{{\rm T}}} \right) + {{{\bar {h}}}_{M}}\left( {{{{\mathbf{I}}}_{3}} - {{{\mathbf{r}}}_{2}}{\mathbf{r}}_{2}^{{\rm T}}} \right), \\ \end{gathered} $

$\left\| {{{\Xi }_{j}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})} \right\| \to 0$ при $\left\| {{{{\mathbf{s}}}_{2}} - {{{\mathbf{r}}}_{2}}} \right\| + \left\| {{{{\mathbf{s}}}_{3}} - {{{\mathbf{r}}}_{3}}} \right\| \to 0,$ $j = 1,2.$ Конкретный вид матриц ${{\Xi }_{1}}$ и ${{\Xi }_{2}}$ несущественен, поскольку при стремлении к программной ориентации слагаемые, в которые они входят, имеют более высокий порядок малости по сравнению с остальными слагаемыми. Заметим, что матрица ${\mathbf{D}}$ является симметричной и положительно определенной.

Таким образом, уравнения Эйлера можно записать в виде

(11)

$\begin{gathered} {\mathbf{J}}{\kern 1pt} \dot {\omega }{\kern 1pt} ' = {{\omega }_{0}}\omega {\kern 1pt} ' \times {{{\mathbf{r}}}_{2}} - {\mathbf{G}}\omega {\kern 1pt} ' - {{\Xi }_{1}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})\omega {\kern 1pt} ' + \Psi (t) + \\ + \,\,c\int\limits_{t - \tau }^t \Psi (u)du - h{\mathbf{D}}\omega {\kern 1pt} ' - {{\Xi }_{2}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})\omega {\kern 1pt} '. \\ \end{gathered} $

Сначала, согласно подходу, разработанному в статьях [25–27], выберем функцию Ляпунова для системы (10), (11) в виде

$\begin{gathered} V = \frac{\mu }{2}{{\omega }^{{'{\rm T}}}}{\mathbf{J}}\omega {\kern 1pt} ' + \frac{1}{2}\left( {{{k}_{{M0}}}{{{\left\| {{{{\mathbf{r}}}_{2}} - {{{\mathbf{s}}}_{2}}} \right\|}}^{2}} + {{k}_{{L0}}}{{{\left\| {{{{\mathbf{r}}}_{3}} - {{{\mathbf{s}}}_{3}}} \right\|}}^{2}}} \right) - \\ - \,\,\frac{1}{h}{{\Psi }^{{\rm T}}}(t){{{\mathbf{D}}}^{{ - 1}}}{\mathbf{J}}\omega {\kern 1pt} ', \\ \end{gathered} $

где $\mu $ – вспомогательный положительный параметр. Получим

$\begin{gathered} \mu {{a}_{1}}{{\left\| {\omega {\kern 1pt} '} \right\|}^{2}} + \frac{1}{2}\left( {{{k}_{{M0}}}{{{\left\| {{{{\mathbf{r}}}_{2}} - {{{\mathbf{s}}}_{2}}} \right\|}}^{2}} + {{k}_{{L0}}}{{{\left\| {{{{\mathbf{r}}}_{3}} - {{{\mathbf{s}}}_{3}}} \right\|}}^{2}}} \right) - \\ - \,\,\frac{{{{a}_{3}}}}{h}\left\| {\omega {\kern 1pt} '} \right\|\left( {{{k}_{{M0}}}\left\| {{{{\mathbf{r}}}_{2}} - {{{\mathbf{s}}}_{2}}} \right\| + {{k}_{{L0}}}\left\| {{{{\mathbf{r}}}_{3}} - {{{\mathbf{s}}}_{3}}} \right\|} \right) \leqslant \\ \leqslant V \leqslant \mu {{a}_{2}}{{\left\| {\omega {\kern 1pt} '} \right\|}^{2}} + \frac{1}{2}\left( {{{k}_{{M0}}}{{{\left\| {{{{\mathbf{r}}}_{2}} - {{{\mathbf{s}}}_{2}}} \right\|}}^{2}} + {{k}_{{L0}}}{{{\left\| {{{{\mathbf{r}}}_{3}} - {{{\mathbf{s}}}_{3}}} \right\|}}^{2}}} \right) + \\ + \,\,\frac{{{{a}_{3}}}}{h}\left\| {\omega {\kern 1pt} '} \right\|\left( {{{k}_{{M0}}}\left\| {{{{\mathbf{r}}}_{2}} - {{{\mathbf{s}}}_{2}}} \right\| + {{k}_{{L0}}}\left\| {{{{\mathbf{r}}}_{3}} - {{{\mathbf{s}}}_{3}}} \right\|} \right), \\ \end{gathered} $

где

${{a}_{1}} = \frac{1}{2}\min \{ A,B,C\} ,\,\,{{a}_{2}} = \frac{1}{2}\max \{ A,B,C\} ,\,\,\,{{a}_{3}} = \left\| {{{{\mathbf{D}}}^{{ - 1}}}{\mathbf{J}}} \right\|.$

Используя критерий Сильвестра, нетрудно показать, что если

(12)

$\mu {{h}^{2}} > \frac{{a_{3}^{2}({{k}_{{M0}}} + {{k}_{{L0}}})}}{{2{{a}_{1}}}},$

то найдутся положительные числа ${{b}_{1}}$ и ${{b}_{2}}$ такие, что

$\begin{gathered} {{b}_{1}}\left( {{{{\left\| {\omega {\kern 1pt} '} \right\|}}^{2}} + {{{\left\| {{{{\mathbf{r}}}_{2}} - {{{\mathbf{s}}}_{2}}} \right\|}}^{2}} + {{{\left\| {{{{\mathbf{r}}}_{3}} - {{{\mathbf{s}}}_{3}}} \right\|}}^{2}}} \right) \leqslant V \leqslant \\ \leqslant {{b}_{2}}\left( {{{{\left\| {\omega {\kern 1pt} '} \right\|}}^{2}} + {{{\left\| {{{{\mathbf{r}}}_{2}} - {{{\mathbf{s}}}_{2}}} \right\|}}^{2}} + {{{\left\| {{{{\mathbf{r}}}_{3}} - {{{\mathbf{s}}}_{3}}} \right\|}}^{2}}} \right). \\ \end{gathered} $

Продифференцируем теперь функцию $V$ в силу системы (10), (11). Имеем

$\begin{gathered} \dot {V} = - \mu h{{\omega }^{{'{\rm T}}}}{\mathbf{D}}\omega {\kern 1pt} {\kern 1pt} '\,\, - \mu {{\omega }^{{'{\rm T}}}}{\mathbf{G}}\omega {\kern 1pt} {\kern 1pt} '\,\, - \mu {{\omega }^{{'{\rm T}}}}{{\Xi }_{1}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})\omega {\kern 1pt} ' + \\ + \,\,\mu {{\omega }^{{'{\rm T}}}}\Psi (t) + c\mu {{\omega }^{{'{\rm T}}}}\int\limits_{t - \tau }^t {\Psi (u)du} - \mu {{\omega }^{{'{\rm T}}}}{{\Xi }_{2}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})\omega {\kern 1pt} ' - \\ - \,\,\frac{1}{h}{{\omega }^{{\rm T}}}{\mathbf{J}}{{{\mathbf{D}}}^{{ - 1}}}\left( {{{k}_{{L0}}}{{{\mathbf{r}}}_{3}} \times ({{{\mathbf{s}}}_{3}} \times \omega {\kern 1pt} ') + {{k}_{{M0}}}{{{\mathbf{r}}}_{2}} \times ({{{\mathbf{s}}}_{2}} \times \omega {\kern 1pt} ')} \right) - \\ - \,\,\frac{1}{h}{{\Psi }^{{\rm T}}}(t){{{\mathbf{D}}}^{{ - 1}}}\left( {{{\omega }_{0}}\omega {\kern 1pt} ' \times {{{\mathbf{r}}}_{2}} - {\mathbf{G}}\omega {\kern 1pt} ' - {{\Xi }_{1}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})\omega {\kern 1pt} ' + _{{_{{_{{}}^{{}}}}^{{}}}}^{{^{{^{{^{{^{{}}}}}}}}}}} \right. \\ + \,\,\left. {\Psi (t) + c\int\limits_{t - \tau }^t \Psi (u)du - {{\Xi }_{2}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})\omega {\kern 1pt} '} \right) \leqslant \\ \leqslant - \left( {\mu h{{\lambda }_{1}} + \mu {{\lambda }_{2}} + \frac{{{{\lambda }_{3}}}}{h}} \right){{\left\| {\omega {\kern 1pt} '} \right\|}^{2}} + \left( {\mu + \frac{{{{a}_{4}}}}{h}} \right)\left\| {\omega {\kern 1pt} '} \right\|\left\| {\Psi (t)} \right\| + \\ + \,\,\left| c \right|\mu \left\| {\omega {\kern 1pt} '} \right\|\int\limits_{t - \tau }^t {\left\| {\Psi (u)} \right\|du} - \frac{1}{h}{{\Psi }^{{\rm T}}}(t){{{\mathbf{D}}}^{{ - 1}}}\Psi (t) - \\ - \,\,\frac{c}{h}{{\Psi }^{{\rm T}}}(t){{{\mathbf{D}}}^{{ - 1}}} \times \,\,\int\limits_{t - \tau }^t {\Psi (u)du} + \frac{1}{h}{{\omega }^{{'{\rm T}}}}{{\Xi }_{3}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})\omega {\kern 1pt} {\kern 1pt} ' - \\ - \,\,\mu {{\omega }^{{'{\rm T}}}}\left( {{{\Xi }_{1}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}}) + {{\Xi }_{2}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})} \right)\omega {\kern 1pt} ' + \\ + \,\,\frac{1}{h}{{\Psi }^{{\rm T}}}(t){{{\mathbf{D}}}^{{ - 1}}}\left( {{{\Xi }_{1}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}}) + {{\Xi }_{2}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})} \right)\omega {\kern 1pt} ', \\ \end{gathered} $

где $\left\| {{{\Xi }_{3}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})} \right\| \to 0$ при $\left\| {{{{\mathbf{s}}}_{2}} - {{{\mathbf{r}}}_{2}}} \right\| + \left\| {{{{\mathbf{s}}}_{3}} - {{{\mathbf{r}}}_{3}}} \right\| \to 0,$ ${{\lambda }_{1}}$ – наименьшее собственное число матрицы ${\mathbf{D}},$ ${{\lambda }_{2}}$ – наименьшее собственное число матрицы ${{({\mathbf{G}} + {{{\mathbf{G}}}^{{\rm T}}})} \mathord{\left/ {\vphantom {{({\mathbf{G}} + {{{\mathbf{G}}}^{{\rm T}}})} 2}} \right. \kern-0em} 2},$ ${{\lambda }_{3}}$ – наименьшее собственное число матрицы ${{({\mathbf{F}} + {{{\mathbf{F}}}^{{\rm T}}})} \mathord{\left/ {\vphantom {{({\mathbf{F}} + {{{\mathbf{F}}}^{{\rm T}}})} 2}} \right. \kern-0em} 2},$

$\begin{gathered} {\mathbf{F}} = {\mathbf{J}}{{{\mathbf{D}}}^{{ - 1}}}\left( {{{k}_{{L0}}}\left( {\begin{array}{*{20}{c}} {r_{{31}}^{2} - 1}&{{{r}_{{31}}}{{r}_{{32}}}}&{{{r}_{{31}}}{{r}_{{33}}}} \\ {{{r}_{{31}}}{{r}_{{32}}}}&{r_{{32}}^{2} - 1}&{{{r}_{{32}}}{{r}_{{33}}}} \\ {{{r}_{{31}}}{{r}_{{33}}}}&{{{r}_{{32}}}{{r}_{{33}}}}&{r_{{33}}^{2} - 1} \end{array}} \right) + } \right. \\ + \,\,\left. {{{k}_{{M0}}}\left( {\begin{array}{*{20}{c}} {r_{{21}}^{2} - 1}&{{{r}_{{21}}}{{r}_{{22}}}}&{{{r}_{{21}}}{{r}_{{23}}}} \\ {{{r}_{{21}}}{{r}_{{22}}}}&{r_{{22}}^{2} - 1}&{{{r}_{{22}}}{{r}_{{23}}}} \\ {{{r}_{{21}}}{{r}_{{23}}}}&{{{r}_{{22}}}{{r}_{{23}}}}&{r_{{23}}^{2} - 1} \end{array}} \right)} \right), \\ {{a}_{4}} = \left\| {{{{\mathbf{D}}}^{{ - 1}}}{\mathbf{G}}} \right\| + {{\omega }_{0}}\left\| {{{{\mathbf{D}}}^{{ - 1}}}\left( {\begin{array}{*{20}{c}} 0&{{{r}_{{23}}}}&{ - {{r}_{{22}}}} \\ { - {{r}_{{23}}}}&0&{{{r}_{{21}}}} \\ {{{r}_{{22}}}}&{ - {{r}_{{21}}}}&0 \end{array}} \right)} \right\|. \\ \end{gathered} $

Далее строим функционал Ляпунова–Красовского по формуле

$\tilde {V} = V + \frac{1}{h}\int\limits_{ - \tau }^0 {\int\limits_{t + u}^t {{{\Psi }^{{\rm T}}}(\theta ){\mathbf{W}}\Psi (\theta )d\theta du} } ,$

где ${\mathbf{W}}$ – постоянная, симметричная и положительно определенная матрица. Тогда

$\tilde {V} = \dot {V} + \frac{\tau }{h}{{\Psi }^{{\rm T}}}(t){\mathbf{W}}\Psi (t) - \frac{1}{h}\int\limits_{t - \tau }^t {{{\Psi }^{{\rm T}}}(u){\mathbf{W}}\Psi (u)du} .$

Рассмотрим выражение

$\begin{gathered} \chi (t) = {{\Psi }^{{\rm T}}}(t){{{\mathbf{D}}}^{{ - 1}}}\Psi (t) + c{{\Psi }^{{\rm T}}}(t){{{\mathbf{D}}}^{{ - 1}}}\int\limits_{t - \tau }^t {\Psi (u)du} - \\ - \,\,\tau {{\Psi }^{{\rm T}}}(t){\mathbf{W}}\Psi (t) + \int\limits_{t - \tau }^t {{{\Psi }^{{\rm T}}}(u){\mathbf{W}}\Psi (u)du} . \\ \end{gathered} $

С помощью замены ${\mathbf{z}}(t) = {{{\mathbf{D}}}^{{ - 1{\text{/}}2}}}\Psi (t)$ получаем

$\begin{gathered} \chi (t) = {{{\mathbf{z}}}^{{\rm T}}}(t){\mathbf{z}}(t) + c{{{\mathbf{z}}}^{{\rm T}}}(t)\int\limits_{t - \tau }^t {{\mathbf{z}}(u)du} - \tau {{{\mathbf{z}}}^{{\rm T}}}(t){\mathbf{Lz}}(t) + \\ + \,\,\int\limits_{t - \tau }^t {{{{\mathbf{z}}}^{{\rm T}}}(u){\mathbf{Lz}}(u)du} = \int\limits_{t - \tau }^t {{{{\left( {\begin{array}{*{20}{c}} {{\mathbf{z}}(t)} \\ {{\mathbf{z}}(u)} \end{array}} \right)}}^{{\rm T}}}} \Gamma \left( {\begin{array}{*{20}{c}} {{\mathbf{z}}(t)} \\ {{\mathbf{z}}(u)} \end{array}} \right){\kern 1pt} du, \\ \end{gathered} $

где ${\mathbf{L}} = {{{\mathbf{D}}}^{{1{\text{/}}2}}}{\mathbf{W}}{{{\mathbf{D}}}^{{1{\text{/}}2}}},$

$\Gamma = \left( {\begin{array}{*{20}{c}} {\frac{1}{\tau }{{{\mathbf{I}}}_{3}} - {\mathbf{L}}}&{\frac{c}{2}{{{\mathbf{I}}}_{3}}} \\ {\frac{c}{2}{{{\mathbf{I}}}_{3}}}&{\mathbf{L}} \end{array}} \right).$

С использованием результатов работ [28, 29] нетрудно показать, что для существования положительно определенной матрицы ${\mathbf{L}},$ при которой матрица $\Gamma $ положительно определена, необходимо и достаточно, чтобы выполнялось условие

(13)

$\tau \left| c \right| < 1.$

Кроме того (см. [28, 29]), если справедливо неравенство (13), то матрицу ${\mathbf{L}}$ можно выбрать в виде ${\mathbf{L}} = {{\left| c \right|{{{\mathbf{I}}}_{3}}} \mathord{\left/ {\vphantom {{\left| c \right|{{{\mathbf{I}}}_{3}}} 2}} \right. \kern-0em} 2}.$

Получим ${\mathbf{W}} = {{\left| c \right|{{{\mathbf{D}}}^{{ - 1}}}} \mathord{\left/ {\vphantom {{\left| c \right|{{{\mathbf{D}}}^{{ - 1}}}} 2}} \right. \kern-0em} 2},$

$\chi (t) \geqslant {{\lambda }_{4}}\tau {{\left\| {\Psi (t)} \right\|}^{2}} + {{\lambda }_{4}}\int\limits_{t - \tau }^t {{{{\left\| {\Psi (u)} \right\|}}^{2}}du} ,$

где

${{\lambda }_{4}} = \frac{{\left| c \right|}}{{2{{\lambda }_{5}}}}\left( {\frac{1}{{\left| c \right|\tau }} - \sqrt {{{{\left( {\frac{1}{{\left| c \right|\tau }} - 1} \right)}}^{2}} + 1} } \right),$

а ${{\lambda }_{5}}$ – наибольшее собственное число матрицы ${\mathbf{D}}.$

Следовательно, справедливо неравенство

$\begin{gathered} \dot {\tilde {V}} \leqslant - \left( {\mu h{{\lambda }_{1}} + \mu {{\lambda }_{2}} + \frac{{{{\lambda }_{3}}}}{h}} \right){{\left\| {\omega {\kern 1pt} '} \right\|}^{2}} - \frac{1}{h}{{\lambda }_{4}}\tau {{\left\| {\Psi (t)} \right\|}^{2}} - \\ - \,\,\frac{1}{h}{{\lambda }_{4}}\int\limits_{t - \tau }^t {{{{\left\| {\Psi (u)} \right\|}}^{2}}du} + \left( {\mu + \frac{{{{a}_{4}}}}{h}} \right)\left\| {\omega {\kern 1pt} '} \right\|\left\| {\Psi (t)} \right\| + \\ + \,\,\left| c \right|\mu \sqrt \tau \left\| {\omega {\kern 1pt} '} \right\|{{\left( {\int\limits_{t - \tau }^t {{{{\left\| {\Psi (u)} \right\|}}^{2}}{\kern 1pt} du} } \right)}^{{\frac{1}{2}}}} + \frac{1}{h}{{\omega }^{{'{\rm T}}}}{{\Xi }_{3}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})\omega {\kern 1pt} {\kern 1pt} ' - \\ - \,\,\mu {{\omega }^{{'{\rm T}}}}\left( {{{\Xi }_{1}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}}) + {{\Xi }_{2}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})} \right)\omega {\kern 1pt} ' + \\ + \,\,\frac{1}{h}{{\Psi }^{{\rm T}}}(t){{{\mathbf{D}}}^{{ - 1}}}\left( {{{\Xi }_{1}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}}) + {{\Xi }_{2}}({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}})} \right)\omega {\kern 1pt} {\kern 1pt} '. \\ \end{gathered} $

Снова применяя критерий Сильвестра, получаем, что если

(14)

$4{{\lambda }_{4}}\tau \left( {\mu {{\lambda }_{1}} + \frac{\mu }{h}{{\lambda }_{2}} + \frac{{{{\lambda }_{3}}}}{{{{h}^{2}}}}} \right) > {{\left( {\mu + \frac{{{{a}_{4}}}}{h}} \right)}^{2}} + {{c}^{2}}{{\mu }^{2}}{{\tau }^{2}},$

то положительные числа ${{b}_{3}}$ и $\delta $ можно выбрать так, чтобы имела место оценка

$\dot {\tilde {V}} \leqslant - {{b}_{3}}\left( {{{{\left\| {\omega {\kern 1pt} '} \right\|}}^{2}} + {{{\left\| {\Psi (t)} \right\|}}^{2}} + \int\limits_{t - \tau }^t {{{{\left\| {\Psi (u)} \right\|}}^{2}}du} } \right)$

при $\left\| {{{{\mathbf{s}}}_{2}} - {{{\mathbf{r}}}_{2}}} \right\| + \left\| {{{{\mathbf{s}}}_{3}} - {{{\mathbf{r}}}_{3}}} \right\| < \delta .$

Значит (см. [30]), при выполнении условий (12)–(14) положение равновесия (2) асимптотически устойчиво.

С помощью замены переменной $\varepsilon = \mu h$ неравенства (12) и (14) можно привести к виду

$h > \frac{{a_{3}^{2}({{k}_{{M0}}} + {{k}_{{L0}}})}}{{2{{a}_{1}}\varepsilon }},\,\,\,\,h > f(\varepsilon ),$

где

$\begin{gathered} f(\varepsilon ) = \frac{1}{{4{{\lambda }_{1}}{{\lambda }_{4}}\tau }} \times \\ \times \,\,\left( {\left( {1 + {{c}^{2}}{{\tau }^{2}}} \right)\varepsilon + \left( {a_{4}^{2} - 4{{\lambda }_{3}}{{\lambda }_{4}}\tau } \right)\frac{1}{\varepsilon } + 2{{a}_{4}} - 4{{\lambda }_{2}}{{\lambda }_{4}}\tau } \right). \\ \end{gathered} $

Таким образом, справедлива следующая теорема.

Теорема. Если

$h > \mathop {\min }\limits_{\varepsilon > 0} \max \left\{ {\frac{{a_{3}^{2}({{k}_{{M0}}} + {{k}_{{L0}}})}}{{2{{a}_{1}}\varepsilon }};f(\varepsilon )} \right\}$

и выполнено неравенство (13), то положение равновесия (2) системы (9), (10) асимптотически устойчиво.

При практическом использовании доказанной теоремы задаются значения конструктивных параметров и коэффициентов при восстанавливающих компонентах управляющих моментов и по ним находится область допустимых значений коэффициентов при диссипативных составляющих управляющих моментов.

5. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Рассмотрим для примера ИСЗ, движущийся по круговой экваториальной орбите с высотой $630$ км над поверхностью Земли. В этом случае ${{\omega }_{0}} = 1.1 \cdot {{10}^{{ - 3}}}$ с^–1. Пусть главные центральные моменты инерции ИСЗ принимают значения $A = 1500$ кг м², $B = 1050$ кг м², $C = 1200$ кг м². Постоянные множители, входящие в коэффициенты управляющих моментов (6) и (7), соответственно равны ${{k}_{{L0}}} = 2.5 \cdot {{10}^{{ - 3}}}$ Н м, ${{k}_{{M0}}} = 2 \cdot {{10}^{{ - 3}}}$ Н м, ${{h}_{{L0}}} = 0.1$ Н м с, ${{h}_{{M0}}} = 0.5$ Н м с.

Пусть программная ориентация ИСЗ (2) в орбитальной системе координат определяется следующими значениями “самолетных” углов (в радианах): $\varphi = 0.3$ (угол крена), $\theta = 0.2$ (угол тангажа), $\psi = 0.1$ (угол рыскания). Начальная ориентация ИСЗ определяется углами $\varphi (t) = 0.5,$ $\theta (t) = - 0.5,$ $\psi (t) = 0.5$ при $t \in [ - \tau ,0].$ Начальные значения проекций угловой скорости ИСЗ $\omega $ выбраны следующими: ${{\omega }_{x}}(t) = 0.5{{\omega }_{0}},$ ${{\omega }_{y}}(t) = 1.5{{\omega }_{0}},$ ${{\omega }_{z}}(t) = 0.5{{\omega }_{0}}$ при $t \in [ - \tau ,0].$

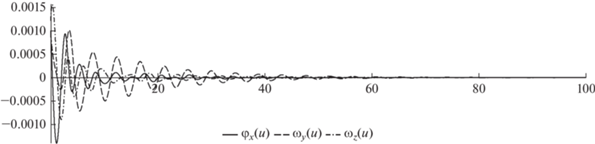
Вначале расчеты были выполнены для случая $\tau = 0,$ соответствующего управлению без интегрального члена. Процесс стабилизации ИСЗ показан на рис. 1 и рис. 2. По оси абсцисс откладывается аргумент широты — угол $u = {{\omega }_{0}}t.$

Рис. 1.

Самолетные углы ($\tau = 0$).

Рис. 2.

Проекции относительной угловой скорости ($\tau = 0$).

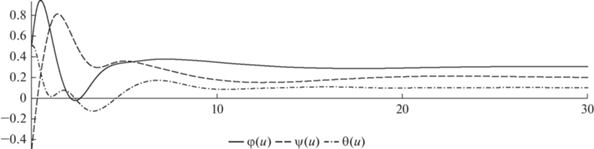
Затем аналогичные расчеты при тех же параметрах и тех же начальных условиях были выполнены для управления с распределенным запаздыванием. С целью выполнения неравенства (13) были взяты значения $c = 1$ и $\tau = 0.7.$ Процесс стабилизации ИСЗ в этом случае происходит в соответствии с рис. 3 и рис. 4.

Рис. 3.

Самолетные углы ($\tau = 0.7$).

Рис. 4.

Проекции относительной угловой скорости ($\tau = 0.7$).

Сравнение рис. 1 и рис. 3, а также рис. 2 и рис. 4 свидетельствует о том, что при наличии распределенного запаздывания в управлении: 1) переходные процессы становятся намного более гладкими; 2) угловая стабилизация ИСЗ происходит в несколько раз быстрее.

ЗАКЛЮЧЕНИЕ

Электродинамический метод управления угловой ориентацией ИСЗ [14], опирающийся на взаимно дополняющие свойства лоренцева момента и момента магнитного взаимодействия, может использоваться для решения широкого круга задач динамики управляемого движения ИСЗ. К числу публикаций, отражающих это направление исследований, относятся, например, [15–17]. В частности, представляет практический интерес задача об электродинамической стабилизации ИСЗ в орбитальной системе координат. Для этой задачи, рассмотренной в [16], были получены аналитически в явном виде достаточные условия асимптотической устойчивости стабилизируемого прямого положения равновесия ИСЗ. При этом было показано, что для обеспечения выполнения данных условий не требуется накладывать никаких условий на параметры ${{h}_{{L0}}}$ и ${{h}_{{M0}}},$ кроме их положительности.

В данной работе рассмотрена более общая задача, как по постановке, так и по методу управления: стабилизируемое положение ИСЗ в орбитальной системе координат может быть произвольным, а управление содержит члены с распределенным запаздыванием. Показано, что электродинамическое управление, построенное таким образом по типу PID-регулятора, позволяет не только существенно уменьшить нежелательные колебания ИСЗ в процессе стабилизации, но и значительно (в разы) сократить время установления программного режима движения.

Доказанная в данной работе теорема об асимптотической устойчивости произвольного углового положения ИСЗ в орбитальной системе координат (программного режима движения) позволила получить конструктивные условия асимптотической устойчивости программного режима движения. Интересно заметить, что эти условия (в противоположность работе [16]) накладывают ограничения лишь на параметры ${{h}_{{L0}}}$ и ${{h}_{{M0}}},$ но не накладывают никаких ограничений на параметры ${{k}_{{L0}}}$ и ${{k}_{{M0}}},$ кроме их положительности.

Предложенная в работе методика построения функционала Ляпунова–Красовского может быть использована для распространения полученных результатов на более общие случаи, приводящие к более сложным дифференциальным уравнениям с почти периодическим коэффициентами (неэкваториальные и некеплеровы орбиты, недипольные модели геомагнитного поля и др.).

Раздел 4 (Анализ устойчивости) выполнен при поддержке Министерства науки и высшего образования Российской Федерации (соглашение № 075-15-2021-573).

Список литературы

Коваленко А.П. Магнитные системы управления космическими летательными аппаратами. М.: Машиностроение, 1975.
Алпатов А.П., Драновский В.И., Салтыков Ю.Д., Хорошилов В.С. Динамика космических аппаратов с магнитными системами управления. М.: Машиностроение, 1978.
Silani E., Lovera M. Magnetic spacecraft attitude control: A survey and some new results // Control Engineering Practice. 2005. V. 13. № 3. P. 357–371. https://doi.org/10.1016/j.conengprac.2003.12.017
Овчинников М.Ю., Пеньков В.И., Ролдугин Д.С., Иванов Д.С. Магнитные системы ориентации малых спутников. М.: ИПМ им. М.В. Келдыша, 2016.
Ivanov D.S., Ovchinnikov M.Y., Penkov V.I. et al. Advanced numerical study of the three-axis magnetic attitude control and determination with uncertainties // Acta Astronautica. 2017. V. 132. P. 103–110. https://doi.org/10.1016/j.actaastro.2016.11.045
Игнатов А.И., Сазонов В.В. Стабилизация режима солнечной ориентации искусственного спутника Земли электромагнитной системой управления // Космич. исслед. 2018. Т. 56. № 5. C. 375–383. https://doi.org/10.31857/S002342060002224-4
Sofyali A., Jafarov E.M., Wisniewski R. Robust and global attitude stabilization of magnetically actuated spacecraft through sliding mode // Aerospace Science and Technology. 2018. V. 76. P. 91–104. https://doi.org/10.1016/j.ast.2018.01.022
Морозов В.М., Каленова В.И. Управление спутником при помощи магнитных моментов: управляемость и алгоритмы стабилизации // Космич. исслед. 2020. Т. 58. № 3. С. 199–207.https://doi.org/10.31857/S0023420620030048
Тихонов А.А. Метод полупассивной стабилизации космического аппарата в геомагнитном поле // Космич. исслед. 2003. Т. 41. № 1. С. 69–79.
Abdel-Aziz Y.A., Shoaib M. Numerical analysis of the attitude stability of a charged spacecraft in the Pitch-Roll-Yaw directions // Int. J. Aeronaut. Space Sci. 2014. V. 15. P. 82–90.
Giri D.K., Sinha M. Magneto-coulombic attitude control of Earth-pointing satellites // J. Guid. Control. Dyn. 2014. V. 37. № 6. P. 1946–1960. https://doi.org/10.2514/ 1.G000030
Giri D.K., Sinha M., Kumar K.D. Fault-tolerant attitude control of magneto-Coulombic satellites // Acta Astronaut. 2015. V. 116. P. 254–270. https://doi.org/10.1016/ j.actaastro.2015.06.020
Giri D.K., Sinha M. Three-axis attitude control of Earth-pointing isoinertial magneto-Coulombic satellites // International J. Dynamics and Control. 2017. V. 5. № 3. P. 644–652. https://doi.org/10.1007/s40435-015-0206-x
Антипов К.А., Тихонов А.А. Параметрическое управление в задаче о стабилизации космического аппарата в магнитном поле Земли // Автоматика и телемеханика. 2007. № 8. С. 44–56.
Тихонов А.А., Спасич Д.Т., Антипов К.А., Саблина М.В. Оптимизация электродинамического метода стабилизации ИСЗ // Автоматика и телемеханика. 2011. № 9. P. 112–121. https://doi.org/10.1134/S0005117911090116
Александров А.Ю., Тихонов А.А. Электродинамическая стабилизация ИСЗ на экваториальной орбите // Космич. исслед. 2012. Т. 50. № 4. С. 335–340.
Aleksandrov A.Yu., Aleksandrova E.B., Tikhonov A.A. Stabilization of a programmed rotation mode for a satellite with electrodynamic attitude control system // Advances in Space Research. 2018. V. 62. № 1. P. 142–151. https://doi.org/10.1016/j.asr.2018.04.006
Каленова В.И., Морозов В.М. Стабилизация положения относительного равновесия спутника при помощи магнитных и лоренцевых моментов // Космич. исслед. 2021. Т. 59. № 5. С. 393–407. https://doi.org/10.31857/S0023420621050058
Moradi M. Self-tuning PID controller to three-axis stabilization of a satellite with unknown parameters // International J. Non-Linear Mechanics. 2013. V. 49. P. 50–56. https://doi.org/10.1016/j.ijnonlinmec.2012.09.002
Li Y., Zhaowei S., Dong Y. Time Efficient Robust PID Plus Controller for Satellite Attitude Stabilization Control Considering Angular Velocity and Control Torque Constraint // J. Aerospace Engineering. 2017. V. 30. № 5. P. 04017030. https://doi.org/10.1061/(ASCE)AS.1943-5525.0000743
Formal’sky A.M. On a Modification of the PID Controller // Dynamics and Control. 1997. V. 7. № 3. P. 269–277. https://doi.org/10.1023/A:1008202618580
Aleksandrov A.Y., Tikhonov A.A. On the attitude stabilization of a rigid body under control with distributed delay // Mechanics Based Design of Structures and Machines. 2021. https://doi.org/10.1080/15397734.2021.1891935
Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, 1965.
Tikhonov A.A., Antipov K.A., Korytnikov D.G., Nikitin D.Yu. Electrodynamical compensation of disturbing torque and attitude stabilization of a satellite in J2 perturbed orbit // Acta Astronautica. 2017. V. 141. P. 219–227. https://doi.org/10.1016/j.actaastro.2017.10.009
Aleksandrov A.Yu., Kosov A.A. Asymptotic stability of equilibrium positions of mechanical systems with a nonstationary leading parameter // J. Computer and Systems Sciences Intern. 2008. V. 47. № 3. P. 332–345. https://doi.org/10.1134/S1064230708030027
Aleksandrov A.Yu., Kosov A.A., Chen Y. Stability and stabilization of mechanical systems with switching // Automation and Remote Control. 2011. V. 72. № 6. P. 1143–1154. https://doi.org/10.1134/S0005117911060026
Aleksandrov A.Y., Tikhonov A.A. Attitude stabilization of a rigid body under the action of a vanishing control torque // Nonlinear Dynamics. 2018. V. 93. № 2. P. 285–293. https://doi.org/10.1007/s11071-018-4191-4
Aleksandrov A.Y., Mason O. Diagonal Riccati stability and applications // Linear Algebra Appl. 2016. V. 492. P. 38–51.
Aleksandrov A.Y., Mason O. Diagonal stability of a class of discrete-time positive switched systems with delay // IET Control Theory and Applications. 2018. V. 12. № 6. P. 812–818.
Kharitonov V.L. Time-Delay Systems. Lyapunov Functionals and Matrices. Basel. Birkhauser, 2013.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал