Космические исследования, 2023, T. 61, № 2, стр. 116-123

ВВЕДЕНИЕ

Турбулентное электромагнитное поле в солнечном ветре является нестационарным, в нем могут появляться различные структуры, такие как токовые слои, вихри, жгуты, плазмоиды. Из-за наличия подобных локальных особенностей, поле неоднородно и имеет мультифрактальный перемежаемый характер [1–4]. Ранее уже разрабатывались модели турбулентного поля с перемежаемостью, например, в работах [5–7] моделирование производилось добавлением в однородное турбулентное поле, моделируемое при помощи суперпозиции фурье-гармоник, локальных структур – плазмоидов. Также были работы по исследованию ферми-ускорения между локальными структурами [8, 9]. Однако в указанных работах не учитывалось, что перемежаемое турбулентное поле в солнечном ветре имеет широкий мультифрактальный спектр. Мы предлагаем модель турбулентного поля с перемежаемостью, в которой можно легко варьировать ширину мультифрактального спектра. Свойство мультифрактальности заключается в локально нерегулярном поведении турбулентности, т.е. показатели Херста в разных точках могут различаться, поэтому для описания мультифрактальных процессов недостаточно одного параметра Херста. В связи с этим используют локальные экспоненты Херста или экспоненты Гельдера h(x₀), которые описывают поведение турбулентного поля в точке x₀ [10]. Также удобным инструментом для описания мультифрактальной турбулентности представляется функция мультифрактального спектра f(h), которая описывает спектр экспонент Гельдера [10–13].

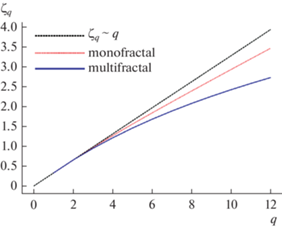
В нашей модели турбулентное поле моделируется при помощи суперпозиции вейвлетов, равномерно распределенных по всей вычислительной области. Вейвлеты позволяют довольно гибко управлять амплитудой полученного поля в любой точке пространства и потому хорошо подходят для описания процессов с различными локальными особенностями. Благодаря специальному распределению амплитудных коэффициентов вейвлетов мы добиваемся того, что в моделируемом нами турбулентном поле появляется целый континуум показателей Гельдера, т.е. широкий мультифрактальный спектр f(h), ширину которого легко варьировать. Полученное мультифрактальное поле также будет перемежаемым, ведь, как известно, для Колмогоровской неперемежаемой турбулентности характерна линейная зависимость показателей структурных функций ζ_q от степени q, а при наличии перемежаемости будут наблюдаться отклонения кривой ζ_q(q) от прямой ζ_q ~ q. Чем сильнее отклонение, тем больше будет уровень перемежаемости [11]. Для мультифрактальной турбулентности, зависимость показателей структурных функций ζ_q от степени q является нелинейной и имеет следующий вид: ${{\zeta }_{q}}(q) = \mathop {\inf }\limits_h \left( {qh - f(h)} \right).$ Таким образом, варьируя ширину мультифрактального спектра, мы можем управлять уровнем перемежаемости полученного поля. Разработанная модель является довольно гибкой, и пригодна к моделированию различных турбулентных систем. В частности, для моделирования турбулентного электромагнитного поля в хвосте магнитосферы во время суббурь.

1.1. ЧИСЛЕННАЯ МОДЕЛЬ

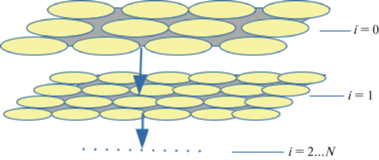
Для моделирования двумерного турбулентного электромагнитного поля сначала при помощи суперпозиции вейвлетов зададим компоненту магнитного поля B_z, затем при помощи уравнений Максвелла найдем электрическое поле. Распределение вейвлетов в вычислительной области происходит следующим образом: вейвлеты самого крупного масштаба равномерно распределяются по всей вычислительной области, затем берутся вейвлеты поменьше и тоже равномерно распределяются по вычислительной области. Число вейвлетов выбирается так, чтобы каждый масштабный класс вейвлетов полностью покрывал всю вычислительную область. На рис. 1 схематично изображено распределение вейвлетов по вычислительной области. Все они движутся в одном направлении и с одинаковой скоростью V = = V_x + V_y.

В качестве базового вейвлета выбран Гауссов вейвлет:

где ${\text{d}}{{r}_{{i,j}}}(t) = \sqrt {{{{\left( {x - {{x}_{{i,j}}}(t)} \right)}}^{2}} + {{{\left( {y - {{y}_{{i,j}}}(t)} \right)}}^{2}}} ,$ ${{x}_{{i,j}}}(t)$ = = $x_{{i,j}}^{0} + {{V}_{x}}t$ и ${{y}_{{i,j}}}(t) = y_{{i,j}}^{0}\left( t \right) + {{V}_{y}}t$ – координаты соответствующего вейвлета в зависимости от времени; $x_{{i,j}}^{0}$ и $y_{{i,j}}^{0}$ – начальные координаты вейвлетов; V_x и V_y – их скорости по осям x и y соответственно; a_i – параметр, характеризующий размер; индекс i характеризует класс вейвлетов с одинаковыми размерами; a_i, c_i – амплитудный коэффициент для каждого масштабного класса вейвлетов; ${{r}_{{i,j}}} \in [ - 1;1]$ – случайный коэффициент. Итоговое поле получается путем суперпозиции вейвлетов:

Для того чтобы полученное таким образом поле было самоподобным, соотношение между размерами вейвлетов из соседних классов должно быть независимым от i. Для этого введем некоторое значение l, характеризующее соотношение размеров между соседними классами вейвлетов: ${{{{a}_{{i + 1}}}} \mathord{\left/ {\vphantom {{{{a}_{{i + 1}}}} {{{a}_{i}}}}} \right. \kern-0em} {{{a}_{i}}}} = l.$ Пусть N_i – количество вейвлетов i-го класса, а D – размерность пространства, в котором моделируется поле. Введем понятие площади ${{S}_{i}}~\sim ~{{N}_{i}}a_{i}^{D},$ занимаемой i-м классом вейвлетов. Тогда в силу самоподобия отношение между площадями, занимаемыми соседними классами ${{{{S}_{{i + 1}}}} \mathord{\left/ {\vphantom {{{{S}_{{i + 1}}}} {{{S}_{i}}}}} \right. \kern-0em} {{{S}_{i}}}}$ должно иметь степенную зависимость от l: ${{{{S}_{{i + 1}}}} \mathord{\left/ {\vphantom {{{{S}_{{i + 1}}}} {{{S}_{i}}}}} \right. \kern-0em} {{{S}_{i}}}} = {{l}^{\beta }}$ (β – варьируемый степенной показатель). Соотношение между амплитудными коэффициентами соседних классов вейвлетов ${{{{c}_{{i + 1}}}} \mathord{\left/ {\vphantom {{{{c}_{{i + 1}}}} {{{c}_{i}}}}} \right. \kern-0em} {{{c}_{i}}}}$ так же должно иметь степенную зависимость от l. Определим степенной показатель λ как ${{{{c}_{{i + 1}}}} \mathord{\left/ {\vphantom {{{{c}_{{i + 1}}}} {{{c}_{i}}}}} \right. \kern-0em} {{{c}_{i}}}} = {{l}^{\lambda }}.$

Рассчитаем спектр энергии поля, моделируемого таким способом. Фурье-спектр одного вейвлета:

Спектр моделируемого турбулентного поля можно найти путем суперпозиции спектров отдельных вейвлетов:

После некоторых преобразований, получаем спектр энергии полученного поля:

где S – площадь нашей вычислительной области [15].

1.2. ПЕРЕМЕЖАЕМОСТЬ И МУЛЬТИФРАКТАЛЬНОСТЬ

Для того чтобы полученное поле было мультифрактальным, разобьем вычислительную область по следующей схеме: для класса самых крупных вейвлетов, вычислительная область разбивается на четыре одинаковых квадратных ячейки. Вейвлеты из каждой ячейки умножаются на свой весовой коэффициент p₁ – p₄, тем самым мы получим, что суммарный вклад в энергию поля от разных частей класса вейвлетов будет не одинаковым. Для класса вейвлетов размером вдвое меньше первоначального, каждая исходная ячейка разбивается еще на четыре квадратных ячейки, в каждой из которых весовой коэффициент исходной ячейки снова умножается на один из четырех весовых коэффициентов. На рис. 2 изображено разбиение вычислительной области с распределением весовых коэффициентов: слева – для класса самых крупных вейвлетов, справа – для класса вейвлетов, размером вдвое меньше. Для класса вейвлетов с еще вдвое меньшим размером вейвлета – снова разбиваем каждую ячейку на четыре части и т.д. При таком разбиении, показатели Гёльдера будут распределены в интервале величин h_min и h_max, значения которых зависят от выбора весовых коэффициентов p_k.

Найдем значения h_min и h_max. Учитывая, что амплитудные коэффициенты N-го класса вейвлетов будет относиться к амплитудным коэффициентам самого крупного класса вейвлетов как ${{{{c}_{N}}} \mathord{\left/ {\vphantom {{{{c}_{N}}} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}} = {{l}^{{\lambda N}}},$ рассчитаем обобщенную статистическую сумму:

где ${{n}_{k}} = {{{{p}_{k}}} \mathord{\left/ {\vphantom {{{{p}_{k}}} 4}} \right. \kern-0em} 4},$ k = 1, …, 4. Из обобщенной статистической суммы можно найти скейлинговую экспоненту τ(q): $Z(q,N) = a_{N}^{{\tau (q)}},$ откуда $\tau (q) = \mathop {\lim }\limits_{{{a}_{N}} \to 0} \frac{{\ln Z(q,N)}}{{\ln {{a}_{N}}}}.$ Получив выражение для скейлинговой экспоненты, можно найти значения h_min и h_max:

Функция мультифрактального спектра, представляющая собой спектр фрактальных размерностей однородных подмножеств L_h, на которые разбито исходное множество L, равна $f(h) = q\left( {{{{\text{d}}\tau } \mathord{\left/ {\vphantom {{{\text{d}}\tau } {{\text{d}}q}}} \right. \kern-0em} {{\text{d}}q}}} \right) - \tau .$ Данная функция выпуклая и может быть аппроксимирована параболой:

где ${{D}_{0}} = \lambda + {{\tau (q)} \mathord{\left/ {\vphantom {{\tau (q)} {(q - 1)}}} \right. \kern-0em} {(q - 1)}};$ ${{h}_{0}} = {{\left. {\frac{{{\text{d}}\tau }}{{{\text{d}}q}}} \right|}_{{q = 0}}}$ [12, 16]. На рис. 3 изображена полученная функция мультифрактального спектра. Подобный колоколообразный спектр характерен для большинства турбулентных мультифрактальных полей [17].

Покажем, что полученное поле будет перемежаемым. Как известно, показатели структурной функции ζ_q, для мультифрактального турбулентного поля рассчитываются следующим образом: ${{\zeta }_{q}}(q) = \mathop {\inf }\limits_h \left( {qh - f(h)} \right)$ [11]. Изменением весовых коэффициентов p₁, p₂, p₃, p₄ можно варьировать ширину спектра f(h). Варьируя его ширину, мы можем изменять степень отклонения ζ_q(q) от прямой ζ_q(q) ~ q, и тем самым регулировать уровень перемежаемости моделируемого электромагнитного поля.

1.3. ГРАНИЧНЫЕ УСЛОВИЯ

Как уже было сказано выше, вейвлеты распределены равномерно по всей вычислительной области. При этом если вейвлеты будут двигаться и выходить за пределы области, то возникнут проблемы, поскольку вместо вейвлетов, вышедших за границу области, необходимо так ввести новые, чтобы в моделируемом поле не образовывалось резких скачков и неоднородностей, не свойственных турбулентному полю в хвосте магнитосферы. Один из способов сделать это – моделировать поле на небольшом участке за границей вычислительной области. Вклад вейвлета в поле при увеличении расстояния от его центра r падает довольно быстро и на расстоянии r ~ 2.5a, где a – параметр, характеризующий размер вейвлета, его вклад в поле упадет в 10¹⁰ раз и будет несущественным, сравнимым с компьютерной ошибкой.

Координаты вейвлетов, в зависимости от времени задаются следующим образом:

где $v$ – скорость вейвлета; $x_{{ij}}^{0}$ и $y_{{ij}}^{0}$ – начальные координаты конкретного вейвлета; L – линейный размер вычислительной области; borderLen – размер области, за пределами вычислительной области, в которой мы продолжаем моделировать вейвлеты, fmod(A, B) – функция, возвращающая остаток от деления A на B. Таким образом, получается, что вейвлеты, которые выходят за пределы моделируемой области, сразу появляются с противоположной стороны.

2.1. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Положим далее, что $l = {{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},$ т.е. размер вейвлетов будет уменьшаться вдвое через каждые четыре класса вейвлетов, а значит, и разбиение каждой квадратной ячейки на более мелкие будет также происходить через каждые четыре класса вейвлетов. Также положим β = 0, таким образом, каждый класс вейвлетов занимает одинаковую площадь в пространстве; D = 2 – размерность пространства, в котором мы моделируем электромагнитное поле; λ = 1/3 – показательный коэффициент для соотношений между амплитудами соседних классов вейвлетов.

При таком выборе параметров энергетический спектр полученного магнитного поля W(k) ~ k^–5/3 [15], что соответствует колмогоровскому спектру, наблюдаемому в турбулентном поле в хвосте магнитосферы Земли [18]. Размер вычислительной области l = 2 · 10⁵ км. Магнитное поле задается как суперпозиция вейвлетов:

Скорость всех вейвлетов одинакова и равна 500 км/с. Электрическое поле можно найти при помощи уравнений Максвелла. Число вейвлетов для самого большого класса N = 14 × 14, их размеры для самого большого класса a₀ = 2.5 · 10⁴ км. Количество классов вейвлетов n = 24. При этом их размеры для самого маленького класса вейвлетов будут равны ${{a}_{n}} = {{a}_{0}}{{l}^{N}} = {{a}_{0}}{{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)}^{{\left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right) \times ~24}}} = 0.4 \cdot {{10}^{3}}\;{\text{км}}.$ Таким образом, частоты моделируемого поля соответствуют частотам турбулентного поля в хвосте магнитосферы, где наблюдаутся колмогоровский спектр [19–21].

Для моделирования мультифрактального поля выберем следующие значения весовых коэффициентов: p₁ = 1.4, p₂ = 0.48, p₃ = 1.6, p₄ = 0.72. При таком выборе значения показателей Гёльдера, центрированные на единицу, лежат в пределах от 0.45 до 1.4, что близко к наблюдаемым значениям ширины мультифрактального спектра для многих регистрируемых сигналов [22]. На рис. 4 показана функция мультифрактального спектра для выбранных весовых коэффициентов. На рис. 5а приведено сечение магнитного поля плоскостью XY для монофрактального поля, где p₁ = p₂ = p₃ = = p₄ = 1, и для мультифрактального поля рис. 5б с указанными ранее весовыми коэффициентами. Видно, что полученное нами мультифрактальное поле менее однородно и склонно к образованию локализированных структур.

Вычислим структурную функцию для магнитного поля для различных степенных показателей q:

и найдем показатели структурной функции ζ_q из выражения ${{S}_{q}}\sim ~{{\delta }^{{{{\zeta }_{q}}}}}.$ На рис. 6 изображена зависимость ζ_q(q) для монофрактального и мультифрактального случаев. Видно, что для мультифрактального случая отклонение зависимости показатели структурной функции ζ_q от степени q довольно сильно отличается от линейной, из чего можно сделать вывод, что полученное мультифрактальное поле является перемежаемым.

2.2. УСКОРЕНИЕ ЧАСТИЦ

На первом этапе исследования модели рассмотрим нерелятивистское ускорение частиц в полученном турбулентном поле для мультифрактального и монофрактального режимов и проведем сравнение между ними. Для этого введем 2000 протонов в вычислительную область со случайными начальными координатами. Начальные скорости частиц распределены по Гауссу с пиковым значением скорости 120 км/с. На границе используются периодические граничные условия. На рис. 7а изображено распределение частиц по энергиям после 15 мин ускорения в турбулентном поле. Видно, что для мультифрактального случая отдельные частицы набрали чуть большую энергию по сравнению с монофрактальной турбулентностью. Мы также рассчитали изменение средней энергии введенных частиц. На рис. 7б показан график средней энергии ансамбля частиц в зависимости от времени. Как видно, средняя энергия частиц для мультифрактального и монофрактального случаев практически одинакова. Подобный характер ускорения можно объяснить следующим образом: когда пространственные или временные масштабы турбулентности близки к гирорадиусам частиц ${{r}_{g}}\sim {{{{v}_{{particle}}}} \mathord{\left/ {\vphantom {{{{v}_{{particle}}}} {{{B}_{z}}}}} \right. \kern-0em} {{{B}_{z}}}},$ эти частицы будут ускоряться. Как только частицы набирают столько энергии, что их гирорадиус начинает превышать размер системы или самую длинную существующую длину волны, ускорение становится неэффективным, и процесс почти насыщается.

ЗАКЛЮЧЕНИЕ

В настоящей работе построена двумерная модель турбулентного мультифрактального электромагнитного поля. Модель позволяет гибко управлять наклоном энергетического спектра, а также шириной мультифрактального спектра и уровнем перемежаемости, которая в турбулентных полях достаточно тесно связана с мультифрактальностью. Тем самым разработанная модель применима ко многим типам турбулентных полей, в частности к турбулентному полю в хвосте магнитосферы Земли и других планет. При помощи данной модели исследовано ускорение частиц в мультифрактальном и монофрактальном турбулентном поле. Показано, что при ускорении в мультифрактальном турбулентном поле максимальная энергия, которую способны набрать отдельные частицы немного больше, по сравнению с монофрактальной турбулентностью.