Космические исследования, 2023, T. 61, № 2, стр. 103-115

ВВЕДЕНИЕ

Проблема исследования волновых процессов, наблюдающихся в околоземном космическом пространстве, – крайне актуальная задача, имеющая фундаментальное значение и обширное прикладное применение. Не смотря на полученные к настоящему времени результаты [1–3], не достигнуто понимания, например, высокочастотных волновых процессов, происходящих в ионосфере Земли. Стандартный подход к изучению волн в околоземном космическом пространстве с помощью космических аппаратов и наземных станций связан с исследованием спектров колебаний наблюдаемого параметра космической среды, чаще всего электронной концентрации в плазме. Однако для изучения волновых процессов, как правило, не достаточно знания только частотных спектров наблюдаемых колебаний. Для анализа именно волновых процессов необходимо иметь возможность получать данные о пространственно-временных спектрах процессов, которые содержат сведения о преимущественном направлении распространения волн и распределении энергии по волновым числам. Наиболее эффективным методом оценивания пространственно-временных спектров волновых процессов является метод пространственных измерительных решеток [4–12]. С точки зрения применения этого метода в задачах изучения волновых процессов в космической среде наиболее подходящими его реализациями могут служить измерительные решетки из набора датчиков, размещенных на космических аппретах, как орбитальных, так и межпланетных. Под измерительной решеткой в этом случае понимается набор датчиков, расположенных на некотором удалении друг от друга, измеряющих один и тот же параметр среды синхронно.

Ключевым свойством рассматриваемых далее измерительных решеток представляется их перемещение в пространстве и, возможно, изменение геометрического расположения их элементов друг относительно друга. Такие решетки далее будут называться динамическими. Статические измерительные решетки, отдельные датчики которых не меняют своего положения друг относительно друга и относительно выбранной лабораторной системы отсчета, широко используются для оценивания параметров волновых процессов в различных прикладных задачах. Например, такие измерительные решетки используются для оценивания параметров метеорологических волновых процессов [10, 11]. Другой областью приложения таких измерительных решеток могут служить задачи, связанные с измерениями волн по сериям изображений каких-либо астрономических объектов. Например, в работе [12] такой способ использовался для оценивания параметров распространения волн в атмосфере Солнца и построения их дисперсионных соотношений.

Именно динамические измерительные решетки представляют особый интерес в задачах, связанных с исследованием волновых процессов в космической среде, в том числе и в околоземном космическом пространстве. Примером могут служить группировки спутников, например GOES (англ. Geostationary Operational Environmental Satellite) или NOAA (англ. National Oceanic and Atmospheric Administration), которые проводят измерения целого набора параметров магнитосферы Земли, включая потоки заряженных частиц, например электронов и протонов, а также параметров магнитного поля Земли. Другим примером могут служить спутниковые кластеры, например, MMS (англ. Magnitospheric Multiscale Mission), Cluster II, Swarm, или кластеры наноспутников. Но при обработке данных, поступающих от таких группировок или кластеров, практически никогда не используют процедуры спектральных методов оценивания параметров волн, опираясь в основном на градиентные измерения параметров космической среды. Основной причиной этого стало нарушение условий стационарности в широком смысле регистрируемых сигналов от датчиков, что обусловлено различиями в движении отдельных элементов решетки друг относительно друга.

В работах [13, 14] была разработана общая процедура оценивания пространственно-временных спектров на основе динамических измерительных решеток в предположении стационарности в широком смысле волнового поля в среде по отношению к лабораторной системе отсчета. Однако такие процедуры требуют больших объемов вычислений и специфических наборов рядов наблюдений, что ограничивает их применение на практике. Тем не менее, в некоторых ситуациях, когда движение датчиков происходит по простым законам, например, в форме вращения решетки относительно некоторой общей оси, можно построить процедуру оценивания параметров волновых процессов, опираясь на стандартную процедуру спектрального анализа для статических измерительных решеток, дополняя ее простой корректировкой спектральной плотности.

В данной работе предложен подход и метод оценивания параметров волновых процессов с помощью перемещающихся в пространстве датчиков, но периодически занимающих в пространстве набор стандартных положений, в которых и проводится измерение параметра среды. В этом случае совместная обработка цифровых рядов, получаемых во время синхронных измерений, позволяет определить направление распространения волн, их длину и частоту. Основа процедуры – оценивание спектральной матрицы цифровых рядов, представляющих последовательность измерений отдельных датчиков решетки. Оценка спектральной матрицы на данной частоте позволяет при высокой когерентности сигналов оценить сдвиг фаз между колебаниями изучаемого параметра для любой пары датчиков и на основе этого построить оценку волнового вектора сигнала на данной частоте.

1. ЦИКЛИЧЕСКИЙ ОТБОР ДАННЫХ

Предположим, что в качестве источника данных о стационарном в широком смысле волновом процессе в пространстве используются измерения, полученные от набора датчиков, движущихся по окружностям вокруг общей оси вращения. Примером могут служить спутники, находящиеся на одной и той же неизменяющейся со временем круговой орбите вокруг некоторого небесного тела. Обозначим через T – период обращения датчиков вокруг оси вращения. Предположим, что каждый из датчиков проводит измерения одного и того же параметра космической среды X синхронно со всеми остальными космическими аппаратами с фиксированной дискретностью Δt. В результате в качестве набора данных мы будем получать совокупность цифровых рядов X_a(i), где a – номер датчика, a = 1, …, M; i – дискретный отсчет времени, соответствующий моменту t_i = t₀ + + iΔt, 0, …, N измерения параметра среды, отсчитываемому от некоторого начального момента времени t₀. Число N обозначает длину ряда измерения данных.

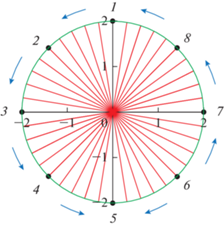
В силу того, что спутники движутся по окружностям, их расположение относительно некоторой лабораторной системы отсчета постоянно меняется. Следовательно, такой набор датчиков невозможно использовать в качестве статической измерительной решетки, если не применять специальный отбор данных. Простейший способ подходящего для этого отбора данных связан с ситуацией, когда датчики расположены симметрично на одной и той же окружности. Предположим, что спутники располагаются на окружности так, что в некоторый момент времени t₀ они занимают положения на окружности, соответствующие углам:

Такой вариант расположения датчиков представлен на рис. 1. Очевидно, что спустя время ΔT_M = T/M, где T – период обращения спутников по орбите, датчики будут занимать то же самое положение, что и в момент времени t₀ с единственным отличием, что датчик с номером a будет в момент времени t_M = t₀ + ΔT_M находиться в положении, который занимал датчик a + 1 в момент t₀ и т.д. Поэтому измерение, полученное датчиком a в момент времени t_M можно использовать как измерение датчика a + 1 в момент времени t₀. Другими словами, фиксированное положение измерительной решетки для всех моментов времени t_I = t₀ + KIΔt будет оставаться статичным. Здесь K – число шагов дискретности измерений, необходимых для перемещения спутников к новому положению в статической решетке: T_M = KΔt.

Отбор данных, соответствующий такой процедуре превращения решетки в статическую (при круговом движении датчиков по часовой стрелке и нумерацией их против часовой стрелки), должен определяться следующими соотношениями:

Здесь i mod M – остаток от деления i на M; [N/K] – целая часть деления числа N на K. Можно видеть, что дискретность по времени рядов Y_a(i) теперь будет равна не Δt, а KΔt. В силу этого для исключения элайзинга (просачивания высокочастотных составляющих из новой подсеточной области в область оцениваемых частот) следует проводить сглаживание рядов с окном порядка K. Такую процедуру желательно проводить до проведения процедуры отбора данных.

В результате процедуры отбора получаем набор рядов, который представляет собой последовательность измерений строго в фиксированных узлах статической решетки, но имеющих временные задержки между измерениями в отдельных узлах. В результате мы можем для построения оценок спектральной плотности стационарного в широком смысле процесса относительно инерциальной системы отсчета использовать обычную теорию спектрального анализа, дополняя ее процедурой фазовой коррекции спектральной матрицы. Измерительные решетки, построенные по такому принципу, будем называть циркулярными.

2. НЕСИММЕТРИЧНЫЕ КОНФИГУРАЦИИ РЕШЕТОК

Рассмотрим теперь отдельно случай, когда датчики располагаются на окружности несимметрично или неравномерно. В этом случае датчики занимают одно и то же положение только спустя строго фиксированный интервал времени полного периода обращения T. Формально такая возможность повторяет рассмотренный в предыдущем разделе случай с той разницей, что дискретность вновь сформированных рядов будет равна периоду обращения T. Измерительные решетки такого типа будем называть неравномерными циркулярными решетками.

Решетки, построенные по принципу неравномерной циркулярной решетки, можно усложнить, увеличивая число ее элементов за счет положения датчиков в другие моменты времени, не совпадающие с t_i = t₀ + iT. Предположим, что, как и в предыдущем разделе, выполняется правило, состоящее в том, что время дискретности Δt измерений датчиков параметров среды связано с периодом T следующим образом:

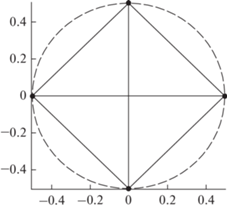
где K – целое число. Обозначим через T₁ интервал времени, равный K₁Δt, такой, что 1 ≤ K₁ ≤ K. Согласно исходным предположениям, после начала отсчета времени t₀M датчики вернутся в свое начальное положение через любой промежуток времени, кратный T. Спустя время T₁ от начала отсчета датчики займут некоторое новое положение. Предположим, что в этом новом положении ни один из спутников не занимает положения спутников в начальный момент времени. Если теперь рассматривать движение спутников, отсчитывая время от нового начального момента T₀ + + T₁, то спутники через время, кратное T, будут занимать это же положение. Таким образом, датчики решетки в этом новом положении также можно рассматривать в качестве рядов от статической измерительной решетки, имеющих фиксированную задержку относительно первоначального положения решетки. Поскольку время задержки фиксировано, мы можем рассматривать совокупность из 2M цифровых рядов от одних и тех же M датчиков как данные от статической решетки с 2M датчиками. Отличием процедуры вычисления спектральной плотности от такой решетки по сравнению с обычной статической решеткой, является необходимость учета сдвига фаз по времени, что не представляет особого труда для всех основных методов оценивания пространственно-временной спектральной плотности. Измерительные решетки такого типа будем называть дополненными циркулярными решетками. Пример такой решетки приведен на рис. 2.

Очевидно, что такая процедура построения циркулярной решетки за счет включения в нее цифровых рядов от датчиков в других положениях M датчиков может продолжаться до тех пор, пока все допустимые положения не будут исчерпаны из всего набора положений, определяемого дискретностью измерений Δt и числом датчиков M. Для этого необходимо лишь указать положения спутников для некоторого набора временных интервалов T₁, T₂, …, T_n, имеющих вид: T_i = K_iΔt, где K_i — целые числа, удовлетворяющие условию: 1 ≤ K₁ < K₂ < … < K_n < K. В результате мы будем иметь решетку из nM узлов. В этом случае для построения оценивания спектральной плотности необходимо учитывать фиксированный сдвиг фаз для каждой группы из M спутников. Более того, формально можно рассматривать такие положения M спутников, в которых некоторые из них в моменты времени T_i занимают положение спутников из другой группы. Для формирования решетки в этом случае достаточно исключить совпадающие положения, поскольку в них дискретность измерений будет отличаться от периода обращения T. В этом случае общее число элементов сформированной решетки будет меньше, чем nM.

Таким образом, единственным недостатком неравномерной циркулярной решетки становится неизменная дискретность измерений в ее узлах, равная периоду ее обращения вокруг своей оси, которую невозможно уменьшить или увеличить произвольно. С другой стороны такой подход дает возможность превращать в измерительную решетку даже один датчик, например, орбитальный спутник, что невозможно сделать для истинно неподвижной решетки. Для этого необходимо повторить все построения, описанные в данном разделе в отношении одного датчика, вращающегося вокруг некоторого центра. Примером может служить датчик, расположенный на борту вращающегося вокруг своей оси космического аппарата, находящегося на орбите Земли. Действительно, в случае M = 1 мы можем использовать все доступные из K измерений, проводимых датчиками спутника за один период T обращения вокруг орбиты (T = kΔt), для образования циркулярной решетки. Поскольку при таком периодическом движении временные промежутки между отдельными измерениями фиксированы, можно их использовать для вычисления фиксированного сдвига фаз на любой заданной частоте, что позволяет использовать стандартные методы оценивания спектральной плотности для статической решетки.

Отметим, что обобщением равномерных и неравномерных циркулярных решеток представляются решетки произвольной формы, не обязательно расположенные на круговой орбите, смещение узлов которых происходит также произвольно, но с единственным условием возвращения элементов решетки в исходное базовое положение через заданный интервал времени T, который будет определять шаг дискретности измерений по времени.

3. ПОСТРОЕНИЕ ОЦЕНКИ ПРОСТРАНСТВЕННО-ВРЕМЕННОГО СПЕКТРА

Изложенные в предыдущих разделах идеи использования данных от датчиков, движущихся по круговым траекториям, в качестве данных от циркулярных измерительных решеток требуют определенной модификации алгоритмов оценивания пространственно-временной спектральной плотности и проверки этих алгоритмов с помощью тестов. Стандартными алгоритмами оценивания пространственно-временной спектральной плотности S(k, f) по данным от статической антенной решетки выступают два основных алгоритма. Это алгоритм, который часто называют алгоритмом Бартлетта, и метод максимального правдоподобия [4–6]. Оба метода исходят из предположения, что на данной частоте из диапазона 0 ≤ f ≤ f_N имеется оценка элементов S_ab(f) спектральной матрицы S(f). Здесь f_N = 1/(2Δt) — частота Найквиста, определяющаяся временной дискретностью цифровых рядов наблюдений, а индексы a и b – номера узлов измерительной решетки. Спектральная матрица для стационарного в широком смысле дискретного по времени векторного процесса X(i) с компонентами X_a(i) может быть представлена в следующей форме:

где R_ab(m) – компоненты ковариационной матрицы R(m) процесса X(i).

Оценка Бартлетта S(k, f) строится как формальное фурье-преобразование спектральной матрицы S_ab(f) по координатам узлов измерительной решетки:

где k = (k_x, k_y, k_z) – волновой вектор, определенный в декартовой системе координат отсчета, связанной с неподвижными узлами измерительной решетки. Этот метод имеет меньшее разрешение по сравнению с методом максимального правдоподобия в определении направления распространения падающей на решетку волны, однако обладает большей устойчивостью к шуму в узлах решетки [4–6].

Другим подходом к оцениванию пространственно-временного спектра представляется метод максимального правдоподобия [4–9], который эквивалентен методу максимальной энтропии [10, 11], при условии достоверности оценки спектральной матрицы. Метод максимальной энтропии при условии, что исследуемый процесс представляет собой стационарный в широком смысле нормальный процесс, сводится к построению оценки S(k, f), доставляющей максимум функционалу:

Здесь f, k_x, k_y, k_z – нормированные частота и компоненты волнового вектора, изменяющиеся в диапазоне [–1/2, 1/2]. Предполагается, что точно известна спектральная матрица процесса на частоте f. Последнее условие эквивалентно соотношению: Таким образом, согласно методу множителей Лагранжа, решение задачи сводится к поиску максимума функционала: Здесь Λ_ab(f) – множители Лагранжа. В результате приходим к оценке следующего вида:

Как доказывается в исследованиях [10, 11], такая оценка эквивалентна оценке максимального правдоподобия [4–6]:

Именно этой оценкой будем пользоваться в дальнейшем. При этом предполагается, что сама оценка спектральной матрицы строится на основе метода максимальной энтропии [4–11].

4. МОДИФИКАЦИЯ ОЦЕНКИ C УЧЕТОМ ВРЕМЕННЫХ СДВИГОВ МЕЖДУ РЯДАМИ

Построим теперь модификацию оценки пространственно-временного спектра с использованием данных от одного или нескольких спутников, находящихся на круговой орбите. Для простоты изложения будем предполагать, что исследуемые волны распространяются в плоскости орбиты. Это означает, что пространственно-временной спектр S(k, f) зависит от волнового вектора k = (k_x, k_y) с компонентами относительно декартовой системы координат в плоскости орбиты. Начнем со случая движения одного спутника. Для использования оценки пространственно-временного спектра на основе данных, поступаемых от одного спутника, необходимо учесть, что ряды измерений, относящихся к узлам статической решетки, смещены друг относительно друга на фиксированный интервал времени. Предположим, что за период обращения спутник проходит M положений в плоскости орбиты с координатами:

где R – радиус орбиты. Как уже обсуждалось, в этих точках датчики спутника проводят измерения с периодом T, однако сами измерения смещены относительно элемента с номером k = 0 по времени, соответственно, на интервалы времени:

Следовательно, при формулировании способа оценивания спектральной матрицы необходимо учитывать этот временной сдвиг.

Рассмотрим с формальной точки зрения изменения в форме спектральной матрицы, вычисленной на основе рядов, измеренных с некоторым временным сдвигом τ. Пусть имеются два ряда измерений одной и той же величины X₁(t) и Y₂(t) = X₂(t + τ), проведенные в моменты времени t и t + τ. В этом случае фурье-образы этих процессов имеют такой вид:

Простым преобразованием подынтегрального выражения для второго ряда находим:

Исходя из того, что кросспектральная функция S₁₂(f) (недиагональный элемент спектральной матрицы) процессов X₁(t) и X₂(t) может быть вычислена формально с помощью усреднения по ансамблю следующим образом: ${{S}_{{12}}}(f) = $ $ = \left\langle {\widehat {{{X}_{1}}}(f)\widehat {{{X}_{2}}}(f)} \right\rangle ,$ находим:

Поскольку нас интересуют измерения, отнесенные к фиксированному моменту времени t, то кросспектральная функция, описывающая такие изменения, есть S₁₂(f), а кросспектральная функция $S_{{12}}^{'}(f)$ отражает данные, поступающие в реальности от датчиков в моменты времени, смещенные по времени на величину τ. В результате находим:

Исходя из этих общих рассуждений, находим, что спектральная матрица антенной решетки $S_{{ab}}^{'}(f),$ сформированная с помощью измерений одного датчика в нескольких положениях круговой орбиты, связана со спектральной матрицей S_ab(f) волнового процесса в фиксированный момент времени следующим образом:

Вводя стандартные определения автоспектров: S_a(f) = S_aa(f), когерентности q_ab между узлами a и b: ${{q}_{{ab}}} = {{\left| {{{S}_{{ab}}}(f)} \right|} \mathord{\left/ {\vphantom {{\left| {{{S}_{{ab}}}(f)} \right|} {\sqrt {{{S}_{{aa}}}(f){{S}_{{bb}}}(f)} }}} \right. \kern-0em} {\sqrt {{{S}_{{aa}}}(f){{S}_{{bb}}}(f)} }},$ и сдвига фаз: ${{\varphi }_{{ab}}} = \arg \left( {{{S}_{{ab}}}(f)} \right)$ так, что ${{S}_{{ab}}}(f)$ = = ${{q}_{{ab}}}(f)\exp \left( {i{{\varphi }_{{ab}}}(f)} \right),$ находим, что в силу преобразования (6) изменяются лишь сдвиги фаз в матрице S_ab(f) по отношению к матрице $S_{{ab}}^{'}(f):$

Таким образом, алгоритм корректировки спектральной матрицы сводится к соотношению (6), что легко реализуется на практике.

В случае неравномерной решетки фазовая коррекция спектральной матрицы будет осуществляться в соответствии со следующими более общими правилами. Обозначим через τ_a, a = = 1, …, M временную задержку между измерениями датчиков в положении a по отношению к фиксированному времени в течение периода обращения решетки вокруг своей оси. Будем считать, что τ_a выражена в долях периода обращения T. Тогда аналогом соотношения (6) станет соотношение:

Эти соотношения применимы для любых типов неравномерных циркулярных решеток.

5. ТЕСТ ДЛЯ ОДНОЭЛЕМЕНТНОЙ ЦИРКУЛЯРНОЙ РЕШЕТКИ

В качестве тестового примера рассматривалась на первом этапе циркулярная решетка с одним датчиком, движущимся по окружности радиуса R = 0.5 (в относительных единицах), и проводящим измерения в трех и четырех равноотстоящих друг от друга точках. Положение точек, в которых производились измерения, определяется соотношениями (4). Они изображены на рис. 3.

Программа, реализующая оценивание спектральной матрицы, а затем и пространственно-временного спектра, была написана на языке Python. Для демонстрации эффекта фазовой корректировки были сгенерированы тестовые ряды, соответствующие падению на решетку двух плоских волн на нормированных частотах f₁ = 0.15 и f₂ = 0.25. Волна с частотой f₁ имела проекции нормированного волнового вектора на оси координат k_x = –0.15, k_y = 0.25, а волна с частотой f₂ – проекции волнового вектора: k_x = 0.12, k_y = 0.2. Амплитуды волн были одинаковыми и равными единице. В узлах решетки генерировался независимый случайный нормальный белый шум со стандартным отклонением σ = 0.025. Оценка спектральной матрицы строилась с помощью метода максимальной энтропии, а оценка спектральной плотности пространственного спектра на заданной частоте – с помощью метода максимального правдоподобия. Результаты оценивания компонентов спектральной матрицы представлены на рис. 4.

Результаты оценивания спектральной плотности пространственного спектра на частотах, соответствующих спектральным пикам, представлены на рис. 5 для четырехпозиционной решетки. На рис. 5а, б приведены оценки спектральной плотности без фазовой коррекции. Черными точками указано истинное положение спектрального пика, соответствующее сгенерированному ряду. Максимум оценки спектральной плотности отмечен как перекрестие белых пунктирных линий, в квадратных скобках указаны координаты положения максимума. На рис. 5в, г представлены оценки спектральной плотности с фазовой коррекцией. Из рисунков видно, что в случае коррекции положение максимумов практически не отличается от истинных. Выбор в тесте сравнительно небольшого стандартного отклонения для шума был сделан намеренно для демонстрации самого эффекта фазовой коррекции спектральной плотности.

6. ТЕСТ ДЛЯ НЕРЕГУЛЯРНОЙ ЦИРКУЛЯРНОЙ РЕШЕТКИ

Для возможности сравнения работы алгоритмов оценивания тест для неравномерной циркулярной решетки проводится для тех же параметров волнового поля, что и для равномерной. Число позиций решетки выбрано равным четырем, но в качестве дополнительного узла выбрано неподвижное положение датчика в центре циркулярной решетки. В качестве позиций неравномерной решетки выбраны положения, соответствующие задержкам: τ₁ = 0, τ₂ = 0.2, τ₃ = 0.6, τ₄ = 0.75, τ₅ = 0 относительно первого элемента. Пятый узел в центре циркулярной решетки в силу его неподвижности имеет задержку равную нулю. Здесь указаны задержки в долях шага дискретизации рядов по времени, который равен периоду обращения циркулярной решетки. Положение узлов измерительной решетки, соответствующее задержкам, приведено на рис. 6.

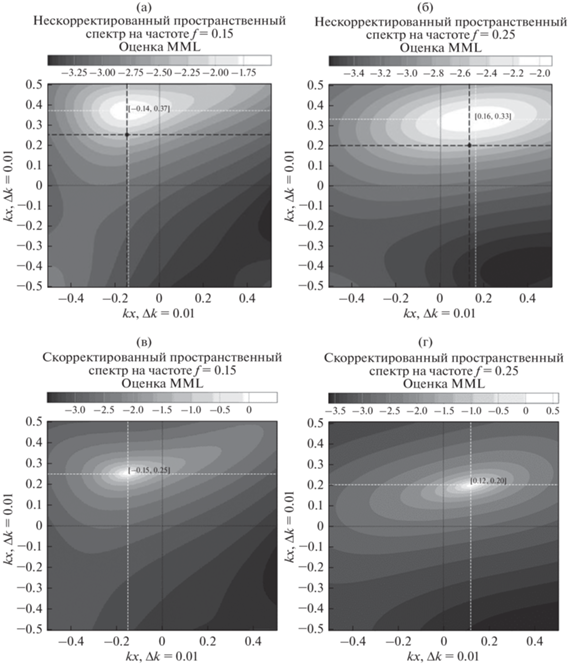
На рис. 7 приведены нескорректированные и скорректированные оценки пространственного спектра в соответствии с (7).

Из приведенных изображений видно, что и для пятиэлементной неравномерной решетки фазовая коррекция спектральной матрицы является эффективной процедурой получения несмещенной оценки спектральной матрицы. После коррекции положение пика в точности совпадает с истинной величиной волнового вектора, но, кроме этого, ширина пика существенным образом сужается. Это говорит о том, что разрешающая способность метода фазовой коррекции остается такой же, как и в случае оценивания волновых векторов на основе статической решетки. Таким образом, можно констатировать, что неравномерность распределения узлов не влияет на точность фазовой коррекции спектральной матрицы циркулярной решетки.

7. ПРИМЕНЕНИЕ ЦИРКУЛЯРНЫХ РЕШЕТОК

Развитый метод построения спектральных оценок волн на основе циркулярных решеток может применяться в целом ряде реальных систем. Однако для своей реализации он требует выполнения ряда условий. Примером может служить задача оценивания параметров волновых возмущений, генерируемых Солнцем, с помощью циркулярной решетки, сформированной из позиций геостационарных спутников GOES. Действительно, с формальной точки зрения датчики на спутниках GOES могут быть использованы в качестве элементов циркулярной решетки с шагом дискретизации по времени, равным одним суткам. За период, равный суткам, спутники GOES делают полный оборот по орбите вокруг Земли и восстанавливают свое пространственное положение относительно нее. Поэтому даже один из спутников GOES в нескольких положениях на орбите можно рассматривать в качестве несимметричной циркулярной одноэлементной решетки. Однако положение этих спутников по отношению к Солнцу в гелиоцентрической системе координат не восстанавливается через сутки из-за орбитального движения Земли вокруг Солнца и наклонения плоскости экватора Земли, в которой движутся геостационарные спутники, и плоскостью эклиптики. В результате направление волн, генерируемых в космической среде Солнцем, будут непрерывно менять свое направление по отношению к циркулярной решетке, сформированной из позиций спутников GOES. Последнее делает практически бесполезным получаемые от такой циркулярной решетки данные о волновых возмущениях, приходящих от Солнца. С другой стороны, использование циркулярной решетки из позиций геостационарных спутников могло бы быть полезным в высокочастотной области с периодами значительно меньше суточного. В этой области частот представляют интерес волновые возмущения магнитосферы, связанные с самой Землей. Для реализации процедур спектральной обработки в области частот с периодом дискретности порядка одного часа с помощью геостационарных спутников необходимо размещать на геостационарной орбите с равномерным шагом не менее 24 спутников. В этом случае через каждый час геостационарные спутники будут восстанавливать исходное положение решетки. Однако решение такой задачи представляется достаточно сложной и затратной задачей.

В плане исследования волновых возмущений от Солнца гораздо лучшими с точки зрения статичности циркулярной решетки оказываются данные, получаемые от полярных спутников, находящихся на солнечно-синхронных орбитах. В качестве таких группировок спутников, данные от которых имеются в открытом доступе, выступают спутники серии NOAA. Поворот плоскости орбиты солнечно-синхронных спутников вместе с орбитальным движением Земли вокруг Солнца решает проблему изменения положения позиций спутников относительно Солнца в полярной системе координат в плоскости эклиптики с началом координат на Солнце. Однако проблема при реализации таких процедур оценивания заключается в том, что высота орбиты таких спутников над поверхностью Земли не превышает 1000 км, что значительно меньше радиуса самой Земли. Близость орбиты к поверхности Земли будет приводить к существенным искажениям волнового поля возмущений космической среды, вызванных процессами на Солнце. Однако циркулярные одноэлементные решетки, связанные с каждым отдельным спутником на круговой орбите, могут быть использованы для анализа волнового поля самой магнитосферы Земли. В этом отношении полезным является то, что характерная дискретность времени такой циркулярной решетки будет порядка 1.5 ч, что позволяет исследовать диапазон частот с периодами значительно меньше суток. Наличие множества малогабаритных спутников на одной и той же круговой орбите с равномерным их распределением по орбите может позволить исследовать еще более высокочастотный диапазон с периодами меньше часа. Такая задача представляется вполне реализуемой с помощью вывода на орбиту наноспутников.

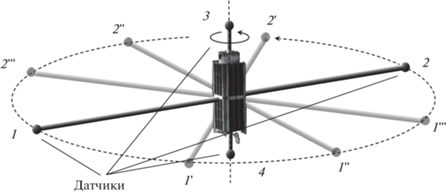
Еще одной областью применения циркулярных решеток могут служить исследования локального волнового поля вблизи каждого отдельного космического аппарата. Примером подходящей для этого схемы может служить вращающийся вокруг своей оси космический аппарат, снабженный несколькими симметрично расположенными на нем датчиками параметров космической среды. При собственном вращении космического аппарата с периодом T вокруг своей оси датчики будут восстанавливать свое положение через время ΔT = T/M, где M — число датчиков. Пример такого космического аппарата приведен на рис. 8, на котором представлен вариант космического аппарата с двумя вращающимися датчиками (датчики 1 и 2) и двумя датчиками на оси вращения (датчики 3 и 4). Цифрами со штрихами показаны дополнительные позиции циркулярной решетки.

С помощью таких космических аппаратов можно измерять параметры волновых процессов вблизи их траектории на частотах с периодами порядка периода собственного вращения спутника. Если период собственного вращения спутника будет намного меньше, чем период орбитального движения такого аппарата, то на каждом относительно коротком по времени и прямолинейном в пространстве отрезке пути можно получать данные спектрального анализа, корректируя частоты волн с помощью формулы Доплера.

Таким образом, при создании космических аппаратов, реализующих циркулярные измерительные решетки, следует опираться на следующие выводы.

Период вращения спутника вокруг своей оси T определяет дискретность цифровых рядов по времени. Согласно теореме Котельникова, диапазон [0, f_N], доступный для оценивания спектральной плотности волнового поля, определяется частотой Найквиста f_N. Для решеток с полностью несимметричным расположением позиций частота Найквиста определяется соотношением: f_N = = (2T)^–1. В случае же полностью симметричного расположения позиций решетки с N датчиками частота Найквиста будет такой: f_N = N(2T)^–1, т.е. верхняя граница диапазона может быть существенно увеличена. Следует также отметить, что диапазон, доступный для оценивания, ограничен также и снизу погрешностями в определении временных интервалов на борту КА и чувствительностью датчиков, поскольку они определяют погрешность в измерении сдвига фаз между элементами решетки.

Доступный для надежного определения спектральной плотности диапазон волновых чисел определяется апертурой решетки:

где r_ij – расстояние между всеми парами элементов решетки, ${{r}_{{ij}}} = \sqrt {{{{({{x}_{i}} - {{x}_{j}})}}^{2}} + {{{({{y}_{i}} - y)}}^{2}} + {{{({{z}_{i}} - {{z}_{j}})}}^{2}}} $. Апертура определяет минимальную длину волны, для которой согласно теореме Котельникова еще доступна оценка спектральной плотности:

Следует отметить, что диаграмма направленности измерительных решеток не является в общем случае круговой или сферической. Поэтому для некоторых направлений прихода волн минимальная длина волны может быть несколько меньшей по сравнению с равенством (8). Для циркулярных решеток апертура в основном определяется расстоянием положения датчиков от оси вращения КА.

При реализации процедур измерения волновых процессов в космической среде с помощью КА следует также учитывать, что сам аппарат при движении вносит в среду возмущения, которые могут искажать структуру волнового поля. Этот фактор может изменять доступные для оценивания спектральной плотности диапазоны частот и длин волн, а также диаграмму направленности циркулярной решетки.

ЗАКЛЮЧЕНИЕ

Из приведенного анализа построения спектральных оценок волнового поля с помощью циркулярных измерительных решеток следует, что динамические решетки такого типа позволяют с достаточной степенью точности получать несмещенные оценки пространственно-временных спектров. Процедура построения таких оценок гораздо проще, чем аналогичные процедуры построения оценок пространственно-временных спектров с помощью динамических решеток с произвольным движением их узлов относительно неподвижной системы отсчета [13, 14].

Приведенный анализ показывает, что циркулярные решетки могут быть использованы для исследования волновых полей в околоземном космическом пространстве с помощью глобальных спутниковых систем, таких как GOES или NOAA. Однако в этом случае необходимо модифицировать системы, например, увеличить число элементов таких систем как GOES с целью уменьшить шаг дискретизации по времени, что позволило бы уменьшить ошибки от изменения структуры циркулярной решетки по отношению к изучаемому волновому полю. Поэтому на данном этапе наиболее перспективным направлением использования циркулярных решеток могут быть малые космических аппараты, в том числе наноспутники. Такие аппараты могут дать новую полезную информацию о волновом поле космической среды, окружающей аппарат, как на орбите, так и на межпланетных траекториях.

Исследование выполнено при финансовой поддержке РФФИ и БРФФИ в рамках научного проекта № 20-58-00018, частично в рамках проекта РФФИ № 20-02-00280, а также в рамках проекта № 0777-2020-0018, финансируемого из средств государственного задания победителям конкурса научных лабораторий образовательных организаций высшего образования, подведомственных Минобрнауки России в части использования циркулярных измерительных решеток при проведении космических экспериментов.