Космические исследования, 2023, T. 61, № 2, стр. 134-142

Устойчивость стабилизации космического аппарата в направлении Солнца магнитными исполнительными органами на солнечно-синхронной орбите

Д. С. Ролдугин^*

Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия

Поступила в редакцию 31.10.2022
После доработки 02.11.2022
Принята к публикации 02.11.2022

EDN: LUEJWA
DOI: 10.31857/S002342062260026X

Аннотация

Рассматривается угловое движение космического аппарата с магнитными катушками на солнечно-синхронной орбите. Аппарат поддерживает ориентацию одной из осей в направлении Солнца для заряда аккумуляторных батарей, вращаясь вокруг этого направления. Приводится интуитивный алгоритм стабилизации, задающий требуемые направление и скорость вращения. С помощью эволюционных уравнений исследуется устойчивость как требуемого режима движения, так и других нежелательных положений равновесия. Получены условия на моменты инерции аппарата и параметры управления, при которых достигается требуемая ориентация. Приведены примеры численного моделирования движения, демонстрирующие стабилизацию в различных положениях с учетом действия возмущающих факторов.

ВВЕДЕНИЕ

Обеспечение стабилизации на Солнце – важный служебный режим, предусмотренный на многих искусственных спутниках Земли. Требования по точности ориентации при этом невелики. Достаточно поддерживать ориентацию нормали к поверхности солнечных панелей относительно Солнца с точностью в несколько градусов. Для этого можно использовать магнитные исполнительные элементы, обычно обеспечивающие заметно худшую точность ориентации по сравнению с маховиками. Это позволяет снизить энергопотребление системы, сохранить ресурс маховиков, избежать их насыщения. Серьезным недостатком магнитной системы ориентации считается невозможность создания механического момента вдоль вектора геомагнитной индукции. Хотя в целом система управляема [1, 2], практическое преодоление этого ограничения представляет определенную проблему. Однако в случае одноосной ориентации на Солнце можно использовать стабилизацию вращением [3], примененную совместно с магнитной системой с запуска аппарата Tiros-II в 1960 г. В этом случае собственные динамические свойства аппарата дополняют возможности системы управления.

Так, три основных режима управления – поддержание скорости вращения, гашение нутационных колебаний и переориентация оси симметрии [4, 5] – требуют создания моментов, доступных магнитной системе ориентации. При этом управление зачастую задают независимо по разным каналам [6–8]. Не требующий разделения режимов управления подход основан на вычислении разницы текущего и требуемого кинетических моментов аппарата [9], что может быть использовано при отказе части магнитных катушек [10]. Отдельно стоит отметить специальные алгоритмы, учитывающие специфику получаемой с датчиков ориентации информации. Так, в работе [11] показания солнечного датчика и магнитометра используются для стабилизации аппарата на солнечно-синхронной орбите. В публикации [12] используется разница токосъема солнечных панелей, а в статье [13] – направление на Солнце. Его производная, вычисляемая по двум последовательным измерениям, используется в алгоритме Sdot [14–16]. В работе [17] применяется модификация алгоритма Bdot.

В настоящей работе исследуется алгоритм стабилизации, примененный на аппарате Prisma и основанный на текущих данных о требуемом направлении и скорости аппарата [18]. Для исследования динамики аппарата используются эволюционные переменные [19, 20]. Для усредненных уравнений движения исследуется устойчивость возникающих положений равновесия на солнечно-синхронной орбите. При этом оказалось, что стабилизация оси минимального момента инерции возможна только при правильном выборе параметров управления и заданном соотношении между максимальным и минимальным моментами инерции. Показано, что существуют также устойчивые косые положения, когда аппарат вращается вокруг заданной оси, но эта ось вращается вокруг направления на Солнце вместо того, чтобы совпадать с ним. Для выявленных режимов движения приведены примеры численного моделирования динамики аппарата с учетом различных возмущающих факторов.

УРАВНЕНИЯ ДВИЖЕНИЯ

Рассмотрим движение осесимметричного аппарата в режиме поддержания скорости вращения и стабилизации оси вращения в требуемом направлении, пренебрегая действием на него каких-либо моментов помимо управляющего.

Эволюционные уравнения

Введем систему координат $O{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$, связанную с центром Земли, третья ось которой направлена на Солнце. Эту систему будем считать инерциальной на интервалах времени в несколько часов. Относительно этой системы описывается ориентация КА при проведении исследования его движения. Поскольку интерес представляет лишь одноосная ориентация аппарата, направление первой и второй осей этой системы может быть выбрано произвольным образом.

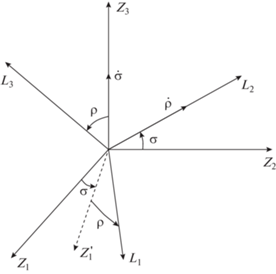
Для описания динамики спутника используем эволюционные переменные. Эти переменные разделяются на две группы. Первая группа включает модуль вектора кинетического момента $L$ и углы его ориентации относительно системы $OZ$$\rho $ и $\sigma $. С вектором кинетического момента связана система координат $O{{L}_{1}}{{L}_{2}}{{L}_{3}}$, третья ось которой совпадает с направлением вектора момента. Чтобы определить две другие оси, произведем поворот вокруг оси $O{{Z}_{3}}$ на угол $\sigma $, а затем поворот вокруг оси $O{{L}_{2}}$ на угол $\rho $ (рис. 1).

Рис. 1.

Ориентация кинетического момента в инерциальном пространстве.

Вторая группа переменных описывает ориентацию системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, заданной главными центральными осями аппарата, относительно $OL$. Для этого используются углы Эйлера $\psi $, $\theta $, $\varphi $ (последовательность поворотов 3-1-3).

Матрицы перехода между системами координат $OL$ → $OZ$ и $Ox$ → $OL$ имеют, соответственно, вид

(1)

${\mathbf{Q}} = \left( {\begin{array}{*{20}{c}} {\cos \rho \cos \sigma }&{ - \sin \sigma }&{\sin \rho \cos \sigma } \\ {\cos \rho \sin \sigma }&{\cos \sigma }&{\sin \rho \sin \sigma } \\ { - \sin \rho }&0&{\cos \rho } \end{array}} \right),$

(2)

${\mathbf{A}} = \left( {\begin{array}{*{20}{c}} {\cos \varphi \cos \psi - \cos \theta \sin \varphi \sin \psi }&{ - \sin \varphi \cos \psi - \cos \theta \cos \varphi \sin \psi }&{\sin \theta \sin \psi } \\ {\cos \varphi \sin \psi + \cos \theta \sin \varphi \cos \psi }&{ - \sin \varphi \sin \psi + \cos \theta \cos \varphi \cos \psi }&{ - \sin \theta \cos \psi } \\ {\sin \theta \sin \varphi }&{\sin \theta \cos \varphi }&{\cos \theta } \end{array}} \right)$

Будем считать спутник осесимметричным с тензором инерции ${\mathbf{J}} = {\text{diag}}(A,A,C)$. Эволюционные уравнения движения имеют вид [21]

(3)

$\left. \begin{gathered} \frac{{dL}}{{dt}} = {{M}_{{3L}}},\quad \frac{{d\rho }}{{dt}} = \frac{1}{L}{{M}_{{1L}}},\quad \frac{{d\sigma }}{{dt}} = \frac{1}{{L\sin \rho }}{{M}_{{2L}}}, \\ \frac{{d\theta }}{{dt}} = \frac{1}{L}\left( {{{M}_{{2L}}}\cos \psi - {{M}_{{1L}}}\sin \psi } \right), \\ \frac{{d\varphi }}{{dt}} = L\cos \theta \left( {\frac{1}{C} - \frac{1}{A}} \right) + \\ + \,\,\frac{1}{{L\sin \theta }}\left( {{{M}_{{1L}}}\cos \psi + {{M}_{{2L}}}\sin \psi } \right), \\ \frac{{d\psi }}{{dt}} = \frac{L}{A} - \frac{1}{L}{{M}_{{1L}}}\cos \psi \operatorname{ctg} \theta - \\ - \,\,\frac{1}{L}{{M}_{{2L}}}\left( {\operatorname{ctg} \rho + \sin \psi \operatorname{ctg} \theta } \right), \\ \end{gathered} \right\}$

где компоненты момента ${{M}_{{kL}}}$ записаны в системе $OL$. Отметим, что в этих уравнениях особый интерес представляют три переменные. Это величина вектора кинетического момента, показывающая скорость закрутки аппарата, угол между вектором кинетического момента (ось $O{{L}_{3}}$) и направлением на Солнце (ось $O{{Z}_{3}}$) $\rho $, и угол между вектором кинетического момента и третьей осью спутника $\theta $ (будем считать, что именно вокруг этой оси необходимо поддерживать вращение). Чтобы уяснить поведение этих трех переменных, применим метод усреднения, исключив из уравнений несущественные для описания основной динамики аппарата переменные [22].

Построение алгоритма одноосной стабилизации

Механический момент со стороны системы управления, действующий на аппарат, имеет вид

${\mathbf{M}} = {\mathbf{m}} \times {\mathbf{B}},$

что требует задания конкретных выражений для управляющего дипольного момента ${\mathbf{m}}$ и вектора геомагнитной индукции ${\mathbf{B}}$.

Рассмотрим управление, предложенное в публикации [18] для миссии Prisma. Управление основано на рассогласовании угловой скорости аппарата с требуемым значением. Заданная величина скорости складывается из двух компонент,

${{{\mathbf{\omega }}}_{{ref}}} = {{\omega }_{0}}\left( {\mu {{{\mathbf{S}}}_{x}} + {{{\mathbf{e}}}_{3}}} \right).$

Первое слагаемое означает, что вектор угловой скорости должен совпадать с направлением на Солнце ${{{\mathbf{S}}}_{x}}$, заданным в связанной системе координат. Второе слагаемое указывает, что вращение при этом также должно происходить вокруг оси ${{{\mathbf{e}}}_{3}}$, которую считаем перпендикулярной плоскости солнечных панелей.

Коэффициент $\mu $ – параметр управления, показывающим относительный вклад обеих компонент. Параметр ${{\omega }_{0}}$ задает целевую скорость закрутки. Отметим, что можно ожидать выход скорости на значение ${{\omega }_{0}}\left( {1 + \mu } \right)$. Магнитное управление, которое обеспечивает заданный режим движения, имеет вид

(4)

${\mathbf{m}} = k\left( {{\mathbf{\omega }} - {{{\mathbf{\omega }}}_{{ref}}}} \right) \times {\mathbf{b}},$

где ${\mathbf{b}}$ – единичный (или близкий к единичному) вектор геомагнитной индукции, $k$– коэффициент усиления.

Моделирование геомагнитного поля

Введем систему $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$, первая ось которой направлена в восходящий узел орбиты, третья ось совпадает с осью вращения Земли. Считая орбиту круговой и пренебрегая прецессией оси вращения Земли, эту систему будем считать инерциальной. В этой системе будет проводиться численное моделирование движения аппарата с учетом различных возмущающих факторов.

Далее вводим систему $O{{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$, полученную поворотом на угол $\Theta $ вокруг оси $O{{X}_{2}}$. Этот угол задается выражением

${\text{tg}}\Theta = \frac{{3\sin 2i}}{{2\left( {1 - 3{{{\sin }}^{2}}i + \sqrt {1 + 3{{{\sin }}^{2}}i} } \right)}},$

где $i$ – наклонение орбиты. Эта система координат используется для записи вектора геомагнитной индукции в осредненной модели. А именно, предполагая, что вектор индукции вращается равномерно по круговому конусу с углом полураствора $\Theta $, в системе $O{{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$ имеем компактное выражение [23, 24]

(5)

${{{\mathbf{B}}}_{Y}} = {{B}_{0}}\left( {\begin{array}{*{20}{c}} {\sin \Theta \sin 2u} \\ {\sin \Theta \cos 2u} \\ {\cos \Theta } \end{array}} \right),$

где $u = {{\omega }_{{{\text{орб}}}}}t + u(0)$– аргумент широты, ${{\omega }_{{{\text{орб}}}}}$ – постоянная орбитальная скорость, ${{B}_{0}}$ – величина вектора индукции. Эта простая модель поля будет применена при анализе динамики аппарата, тогда как в численном моделировании будет использоваться модель IGRF [25].

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ В ЭВОЛЮЦИОННЫХ УРАВНЕНИЯХ

Для применения метода усреднения необходимо разделить переменные на быстрые и медленные. В отсутствие управляющего момента кинетический момент в инерциальном пространстве сохраняется, что выражается в постоянстве его величины и углов ориентации в уравнениях (3). Также остается постоянным угол нутации $\theta $. Аппарат совершает регулярную прецессию, в которой быстро изменяются углы $\varphi $ и $\psi $. При воздействии на систему управления постоянные в невозмущенном движении переменные начинают изменяться. Если величина управления достаточно мала, эти переменные можно считать медленными и уравнения (3) можно усреднить по быстрым переменным и времени.

Для формализации понятия медленного изменения уравнения движения должны быть записаны в безразмерном виде. Для этого в качестве меры времени в уравнениях (3) используем период обращения по орбите и, соответственно, вместо времени – аргумент широты, кинетический момент относим к его невозмущенному значению $L = {{L}_{0}}l$, и вводим малый параметр, характеризующий величину изменения кинетического момента за один виток по орбите $\varepsilon = {{k{{B}_{0}}} \mathord{\left/ {\vphantom {{k{{B}_{0}}} {{{\omega }_{0}}C}}} \right. \kern-0em} {{{\omega }_{0}}C}}$. Безразмерные уравнения запишем в виде

(6)

$\left. \begin{gathered} \frac{{dl}}{{du}} = \varepsilon l{{{\bar {M}}}_{{3L}}},\quad \frac{{d\rho }}{{du}} = \varepsilon {{{\bar {M}}}_{{1L}}},\quad \frac{{d\sigma }}{{du}} = \frac{\varepsilon }{{\sin \rho }}{{{\bar {M}}}_{{2L}}}, \\ \frac{{d\varphi }}{{du}} = {{\eta }_{1}}l\cos \theta + \frac{\varepsilon }{{\sin \theta }}\left( {{{{\bar {M}}}_{{1L}}}\cos \psi + {{{\bar {M}}}_{{2L}}}\sin \psi } \right), \\ \frac{{d\psi }}{{du}} = {{\eta }_{2}}l - \varepsilon {{{\bar {M}}}_{{1L}}}\cos \psi \operatorname{ctg} \theta - \\ - \,\,\varepsilon {{{\bar {M}}}_{{2L}}}\left( {\operatorname{ctg} \rho + \sin \psi \operatorname{ctg} \theta } \right), \\ \frac{{d\theta }}{{du}} = \varepsilon \left( {{{{\bar {M}}}_{{2L}}}\cos \psi - {{{\bar {M}}}_{{1L}}}\sin \psi } \right), \\ \end{gathered} \right\},$

где ${{\eta }_{1}} = \frac{{{{L}_{0}}}}{{{{\omega }_{{{\text{орб}}}}}}}\left( {\frac{1}{C} - \frac{1}{A}} \right)$, ${{\eta }_{2}} = \frac{{{{L}_{0}}}}{{A{{\omega }_{{{\text{орб}}}}}}}$, компоненты безразмерного момента обозначены ${{\bar {M}}_{{kL}}}$. Параметры ${{\eta }_{k}}$ являются большими по сравнению с $\varepsilon $.

Для усреднения необходимо записать непосредственное выражение для управляющего момента, которое задается в связанной с аппаратом системе координат

${{{\mathbf{M}}}_{x}} = k{{B}_{0}}\left\{ {\left( {{{{\mathbf{\omega }}}_{x}} - \mu {{\omega }_{0}}{{{\mathbf{S}}}_{x}} - {{\omega }_{0}}{{{\mathbf{e}}}_{3}}} \right) \times {{{\mathbf{b}}}_{x}}} \right\} \times {{{\mathbf{b}}}_{x}}.$

Безразмерный вектор индукции вводится как ${\mathbf{B}} = {{B}_{0}}{\mathbf{b}}$, и в случае использования осредненной модели поля вектор ${\mathbf{b}}$ является единичным. В уравнениях (6) необходимо задать момент в системе координат, связанной с вектором кинетического момента. Используя матрицы направляющих косинусов (1) и (2), момент запишем как

(7)

$\begin{gathered} {{{\mathbf{M}}}_{L}} = \frac{{k{{B}_{0}}L}}{C}\left\{ {\left[ {\frac{C}{L}{{{\mathbf{\omega }}}_{L}} - \mu \frac{{{{L}_{{ref}}}}}{L}{{{\mathbf{Q}}}^{T}}\left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right)} \right.} \right. - \\ - \,\,\left. {\left. {\frac{{{{L}_{{ref}}}}}{L}{\mathbf{A}}\left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right)} \right] \times {{{\mathbf{Q}}}^{T}}{{{\mathbf{b}}}_{Z}}} \right\} \times {{{\mathbf{Q}}}^{T}}{{{\mathbf{b}}}_{Z}}, \\ \end{gathered} $

где ${{L}_{{ref}}} = C{{\omega }_{0}}$. Для того чтобы определить выражение угловой скорости в системе $OL$, будем опираться на ее связь с кинетическим моментом ${\mathbf{J}}{{{\mathbf{\omega }}}_{x}} = {{{\mathbf{L}}}_{x}}$. Кинетический момент при этом задан в системе $OL$, ${{{\mathbf{L}}}_{L}} = \left( {0,0,L} \right)$. Записывая его в системе $Ox$ с помощью матрицы ${\mathbf{A}}$, и далее переходя в систему $OL$, имеем

(8)

${{{\mathbf{\omega }}}_{L}} = \frac{L}{C}\left( {\begin{array}{*{20}{c}} {\frac{C}{A}{{a}_{{11}}}{{a}_{{31}}} + \frac{C}{A}{{a}_{{12}}}{{a}_{{32}}} + {{a}_{{13}}}{{a}_{{33}}}} \\ {\frac{C}{A}{{a}_{{21}}}{{a}_{{31}}} + \frac{C}{A}{{a}_{{22}}}{{a}_{{32}}} + {{a}_{{23}}}{{a}_{{33}}}} \\ {\frac{C}{A}{{a}_{{31}}}{{a}_{{31}}} + \frac{C}{A}{{a}_{{32}}}{{a}_{{32}}} + {{a}_{{33}}}{{a}_{{33}}}} \end{array}} \right).$

Далее для определения эволюционных уравнений, показывающих изменение вектора кинетического момента и угла нутации, необходимо выражения (7), (8) усреднить по быстрым переменным $\varphi $, $\psi $, $u$. Вид выражения для вектора индукции ${{{\mathbf{b}}}_{Z}}$ пока не определен. Этот вектор задан в системе $OY$, тогда как движение вектора кинетического момента описывается в системе $OZ$. Не проводя пока усреднение по времени и обозначая ${{b}_{k}}$ компоненты единичного вектора геомагнитной индукции в системе $OL$, получаем после усреднения по $\psi $

(9)

$\left. \begin{gathered} \frac{1}{{\varepsilon l}}\dot {l} = - \left( {b_{1}^{2} + b_{2}^{2}} \right)\left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right) + \\ + \,\,\mu \frac{{{{l}_{{ref}}}}}{l}\left\{ {{{b}_{1}}{{b}_{3}}\sin \rho + \left( {b_{1}^{2} + b_{2}^{2}} \right)\cos \rho } \right\} + \\ + \,\,\frac{{{{l}_{{ref}}}}}{l}\left( {b_{1}^{2} + b_{2}^{2}} \right)\cos \theta , \\ \frac{1}{\varepsilon }\dot {\rho } = {{b}_{1}}{{b}_{3}}\left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right) - \\ - \,\,\mu \frac{{{{l}_{{ref}}}}}{l}\left\{ {{{b}_{1}}{{b}_{3}}\cos \rho + \left( {b_{2}^{2} + b_{3}^{2}} \right)\sin \rho } \right\} - \\ - \,\,\frac{{{{l}_{{ref}}}}}{l}{{b}_{1}}{{b}_{3}}\cos \theta , \\ \frac{1}{\varepsilon }\sin \rho \dot {\sigma } = {{b}_{2}}{{b}_{3}}\left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right) + \\ + \,\,\mu \frac{{{{l}_{{ref}}}}}{l}\left\{ {{{b}_{1}}{{b}_{2}}\sin \rho - {{b}_{2}}{{b}_{3}}\cos \rho } \right\} - \frac{{{{l}_{{ref}}}}}{l}{{b}_{2}}{{b}_{3}}\cos \theta . \\ \end{gathered} \right\}$

Отметим, что для усредненных переменных сохраняются обозначения, ${{l}_{{ref}}} = {{{{L}_{{ref}}}} \mathord{\left/ {\vphantom {{{{L}_{{ref}}}} {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}$ задает целевую величину вектора кинетического момента.

Движение на орбите, близкой к солнечно-синхронной

Дальнейший анализ требует конкретных выражений для компонент вектора индукции. Для этого нужно определить матрицу перехода от системы $OY$ к системе $OZ$. Напомним, что в системе $OZ$ третья ось направлена на Солнце, тогда как две другие выбираются произвольным образом. Система $OY$, напротив, задана единственным образом. Чтобы получить переход между $OY$ и $OZ$, зададим ориентацию вектора направления на Солнце в системе $OY$. Для этого можно применить тот же подход, как и при определении ориентации вектора кинетического момента в инерциальном пространстве и введении системы $OL$. А именно, задавая ориентацию направления на Солнце в системе $OY$ углами ${{\rho }^{S}}$ и ${{\sigma }^{S}}$ так, как показано на рис. 1, матрицу перехода ${{{\mathbf{Q}}}^{S}}$ между системами $OY$ и $OZ$ зададим так же, как в выражении (1).

При определении компонент вектора индукции в системе $OZ$ возникают громоздкие выражения ${{b}_{{kZ}}} = \sum\nolimits_{n = 1}^3 {q_{{nk}}^{S}{{b}_{{nY}}}} $, содержащие постоянные элементы матрицы ${{{\mathbf{Q}}}^{S}}$, выраженные через постоянные углы ${{\rho }^{S}}$, ${{\sigma }^{S}}$. Чтобы получить компактные выражения, пригодные для анализа, сделаем следующее упрощение. Рассмотрим движение аппарата на солнечно-синхронной орбите, практически перпендикулярной направлению на Солнце. Чтобы дополнительно упростить выражения, будем считать, что в выражении (5) $\sin \Theta \approx 1,$ $\cos \Theta \approx 0$, так как $\Theta \approx i \approx 90^\circ $. Основным упрощающим фактором становится практически полное совпадение систем $OY$ и $OZ$. Действительно, третья ось системы $OZ$ направлена на Солнце, что для рассматриваемой конфигурации орбиты означает, что эта ось практически перпендикулярна к плоскости орбиты. Вместе с тем, третья ось $OY$ перпендикулярна плоскости орбиты, если $\Theta = i = 90^\circ $, и практически перпендикулярна для солнечно-синхронной орбиты.

Окончательно, считая, что системы $OY$ и $OZ$ совпадают (пренебрегая различием в направлении осей на уровне десятка градусов), и принимая $\sin \Theta \approx 1$, $\cos \Theta \approx 0$, для вектора индукции в системе $OZ$ получаем простое выражение ${{{\mathbf{b}}}_{Z}} = \left( {\sin 2u,\;\cos 2u,\;0} \right)$. Тогда, используя переход ${{{\mathbf{b}}}_{L}} = {{{\mathbf{Q}}}^{T}}{{{\mathbf{b}}}_{Z}}$ и усредняя уравнения (9) по аргументу широты, получаем

(10)

$\left. \begin{gathered} \frac{1}{{\varepsilon l}}\dot {l} = - \frac{1}{2}\left( {1 + {{{\cos }}^{2}}\rho } \right)\left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right) + \\ + \,\,\mu \frac{{{{l}_{{ref}}}}}{l}\cos \rho + \frac{1}{2}\frac{{{{l}_{{ref}}}}}{l}\left( {1 + {{{\cos }}^{2}}\rho } \right)\cos \theta , \\ \frac{1}{\varepsilon }\dot {\rho } = \left\{ {\frac{1}{2}\cos \rho \left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right) - } \right. \\ - \left. {\,\,\mu \frac{{{{l}_{{ref}}}}}{l} - \frac{1}{2}\frac{{{{l}_{{ref}}}}}{l}\cos \rho \cos \theta } \right\}\sin \rho , \\ \frac{1}{\varepsilon }\dot {\theta } = \frac{1}{2}\left( {\frac{{A - C}}{A}\cos \theta - \frac{{{{l}_{{ref}}}}}{l}} \right)\left( {1 + \frac{1}{2}{{{\sin }}^{2}}\rho } \right)\sin \theta . \\ \end{gathered} \right\}$

Исследование устойчивости

Исследуем устойчивость полученной системы, чтобы выяснить, как ориентируется аппарат. Из второго и третьего уравнений видно, что положениям равновесия соответствуют $\sin \rho = 0$ и $\sin \theta = 0$, а также некоторые “косые” конфигурации. В зависимости от того, чему равны углы $\rho $ и $\theta $, аппарат выходит на разную скорость закрутки согласно первому уравнению в уравнениях (10). Рассмотрим все положения равновесия отдельно.

1. $\theta = 0$, $\rho = 0$ (требуемый режим движения).

Это положение равновесия представляет основной интерес, так как именно оно соответствует выходу аппарата на требуемый режим вращения вокруг направления на Солнце. Из первого уравнения (10) в положении равновесия имеем

$\frac{1}{{\varepsilon l}}\dot {l} = - 1 + \mu \frac{{{{l}_{{ref}}}}}{l} + \frac{{{{l}_{{ref}}}}}{l},$

откуда заключаем, что аппарат выходит на вращение с кинетическим моментом $l = \left( {1 + \mu } \right){{l}_{{ref}}}$. Далее, используя эту величину и линеаризуя два оставшихся уравнения в выражении (10), получаем:

$\frac{1}{\varepsilon }\dot {\rho } = - \frac{1}{2} \cdot \frac{\mu }{{1 + \mu }}\rho ,\,\,\,\,\frac{1}{\varepsilon }\dot {\theta } = - \frac{1}{2}\left( {\frac{{C - A}}{A} + \frac{1}{{\mu + 1}}} \right)\theta .$

Отметим, что при $C > A$ положение равновесия устойчиво. То есть, если требуется поддерживать вращение вокруг оси максимального момента инерции, заданный режим движения устойчив. Если же необходимо поддерживать вращение вокруг оси с меньшим моментом инерции, такое движение будет устойчиво, если

$\frac{{C - A}}{A} + \frac{1}{{\mu + 1}} > 0,$

откуда:

(11)

$C > A\frac{\mu }{{1 + \mu }}.$

Так, при $\mu = 1$ имеем $C > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}A$, при $\mu = 2$ имеем $C > {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}A$. При необходимости вращения вокруг оси минимального момента инерции его отличие от максимального не должно быть слишком велико. Причем чем меньше параметр $\mu $, тем большее отличие является допустимым.

2. Рассмотрим положение равновесия $\theta = 0$, $\rho = \pi $ (ось ${{{\mathbf{e}}}_{3}}$ развернута от Солнца).

Из первого уравнения (10) получаем, что аппарат выходит на вращение со скоростью $l = \left( {1 - \mu } \right){{l}_{{ref}}}$, откуда заключаем, что положение равновесия может быть устойчиво только при $\mu < 1$. Линеаризуя второе уравнение (10), получаем

$\frac{1}{\varepsilon }\dot {\rho } = \frac{1}{2}\frac{\mu }{{1 - \mu }}\rho ,$

что с учетом $\mu < 1$ указывает на неустойчивость равновесия.

3. Положение равновесия $\theta = \pi $, $\rho = 0$ (также ось ${{{\mathbf{e}}}_{3}}$ развернута от Солнца).

Аппарат выходит на вращение $l = \left( { - 1 + \mu } \right){{l}_{{ref}}}$, откуда $\mu > 1$. Линеаризация дает:

$\frac{1}{\varepsilon }\dot {\rho } = - \frac{1}{2}\frac{\mu }{{ - 1 + \mu }}\rho ,\,\,\,\,\frac{1}{\varepsilon }\dot {\theta } = - \frac{1}{2}\left( {\frac{{C - A}}{A} - \frac{1}{{\mu - 1}}} \right)\theta .$

Из второго уравнения следует, что положение равновесия устойчиво, если

$C > A\frac{\mu }{{ - 1 + \mu }}.$

Так, при $\mu = 2$ имеем $C > 2A$, что, однако, невозможно в силу свойств тензора инерции осесимметричного спутника. При $\mu = 3$ имеем $C > 1.5A$. Фактически, аппарат должен иметь весьма специфическую форму.

Подводя итог рассмотрению трех положений равновесия, можно заключить, что желательно принять параметр $\mu $ в диапазоне 1–2, чтобы избежать устойчивости в случае 3, а также реализовывать вращение вокруг оси максимального момента инерции. Если же необходимо поддерживать вращение вокруг оси минимального момента инерции, его отличие от максимального не должно быть слишком существенным.

4. Рассмотрим теперь косые положения равновесия, получаемые из третьего уравнения (10)

(12)

$\frac{{A - C}}{A}\cos \theta - \frac{{{{l}_{{ref}}}}}{l} = 0$.

Аналогичные положения возможны и для $\rho $ согласно второму уравнению в выражении (10). Как оказалось, для их существования необходимо $\mu = 0$. Фактически, учитывая анализ случаев 1–3, можно заключить, что кинетический момент аппарата всегда оказывается направленным на Солнце, то есть $\rho = 0$. Относительно оси симметрии этого сказать нельзя. Возможна как ориентация КА в обратном направлении, так и движение в косых положениях.

Подставим выражение (12) в первое уравнение выражения (10), в котором примем $\rho = 0,$ и приравняем к нулю, что будет означать выход на некоторое вращение (равновесие по переменной $l$),

$ - \left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right)\frac{A}{{A - C}}\frac{1}{{\cos \theta }} + \mu + \cos \theta = 0,$

откуда получаем

$\begin{gathered} - \left( {\frac{A}{{A - C}}{{{\cos }}^{2}}\theta + \frac{C}{{A - C}}{{{\sin }}^{2}}\theta } \right) + \\ + \,\,\mu \cos \theta + \frac{{A - C}}{{A - C}}{{\cos }^{2}}\theta = 0 \\ \end{gathered} $

и для положения равновесия имеем выражение

(13)

$\cos \theta = \frac{1}{\mu }\frac{C}{{A - C}}.$

Для кинетического момента получаем $l = {{\mu A{{l}_{{ref}}}} \mathord{\left/ {\vphantom {{\mu A{{l}_{{ref}}}} C}} \right. \kern-0em} C}$. В отличие от случаев 1 и 3, кинетический момент не направлен по оси ${{{\mathbf{e}}}_{3}}$. Проекция кинетического момента на эту ось, задающая скорость вращения,

(14)

${{l}_{3}} = {{\mu A{{l}_{{ref}}}\cos \theta } \mathord{\left/ {\vphantom {{\mu A{{l}_{{ref}}}\cos \theta } C}} \right. \kern-0em} C} = \frac{A}{{A - C}}{{l}_{{ref}}}.$

Далее, чтобы такое положение равновесия существовало, необходимо

(15)

$ - 1 < \frac{1}{\mu }\frac{C}{{A - C}} < 1.$

Полагая, что $C > A$, отсюда получаем

$C > \frac{\mu }{{\mu + 1}}A\,\,{\text{и}}\,\,C > \frac{\mu }{{\mu - 1}}A.$

Эти неравенства не выполняются при $\mu \in \left[ {1,2} \right]$ в силу свойств тензора инерции. Таким образом, можно снова заключить, что параметр $\mu $ следует брать в этом диапазоне, дабы исключить опасность попадания в косое положение равновесия.

Если же $C < A$, то из (15) получаем

(16)

$A > \frac{{\mu - 1}}{\mu }C\,\,{\text{и }}A > \frac{{\mu + 1}}{\mu }C.$

Так, при $\mu = 1$ имеем $A > 2C$, при $\mu = 2$ имеем $A > 1.5C$. Покажем устойчивость положения равновесия (13) при выполнении условий (16), чтобы убедиться, что аппарат выходит на косое положение. Линеаризуя третье уравнение выражений (10) около положения ${{\theta }_{0}}$, $\theta = {{\theta }_{0}} + \alpha $, получаем

$\begin{gathered} \frac{1}{\varepsilon }\dot {\theta } = \frac{1}{2}\left( {\lambda \left\{ {\cos {{\theta }_{0}} - \sin {{\theta }_{0}}\alpha } \right\} - \frac{1}{\mu }\frac{C}{A}} \right) \times \\ \times \,\,\left\{ {\sin {{\theta }_{0}} + \cos {{\theta }_{0}}\alpha } \right\}, \\ \end{gathered} $

где $\lambda = \frac{{A - C}}{A} = \frac{1}{{\cos {{\theta }_{0}}}}\frac{1}{\mu }\frac{C}{A}$. Подставляя это выражение, получаем

$\frac{1}{\varepsilon }\dot {\theta } = - \frac{1}{2}\frac{1}{\mu }\frac{C}{A}\cos {{\theta }_{0}}{\text{t}}{{{\text{g}}}^{2}}{{\theta }_{0}}\alpha .$

Положение равновесия устойчиво, если $\cos {{\theta }_{0}} > 0$, т.е. $\frac{1}{\mu }\frac{C}{{A - C}} > 0$, что выполняется для рассматриваемого случая $A > \frac{{\mu + 1}}{\mu }C$ согласно выражению (16).

Сравнивая условия (16) и (11), можно обнаружить, что они по сути задают границу, когда при необходимости вращения вокруг оси минимального момента инерции аппарат выходит на требуемое вращение, а когда – выходит на движение в косом положении.

В целом можно заключить, что если минимальный момент инерции существенно меньше максимального, стабилизировать его в нужном положении не удастся.

Подводя итог исследованию, приведем условия успешной работы управления:

• параметр $\mu $ следует брать в диапазоне от 1 до 2;

• желательно осуществлять закрутку вокруг оси максимального момента инерции;

• при вращении вокруг оси минимального момента инерции необходимо выполнить условие $C > A\frac{\mu }{{1 + \mu }}$. В частности, оно выполняется при $C > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}A$ и $\mu \in \left[ {1,2} \right]$.

Если же при $\mu = 1$ выполняется $C < {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}A$, аппарат выходит на косое положение.

МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ КОСМИЧЕСКОГО АППАРАТА

Проведем численное моделирование движения аппарата под воздействием различных возмущающих факторов, не учтенных при исследовании устойчивости. Примем следующие параметры аппарата и его орбиты:

– Наклонение орбиты 97°, высота 550 км, эксцентриситет 0.01, долгота восходящего узла 90°;

– Направление на Солнце в системе $OY$ задано углами ${{\rho }^{S}}$ и ${{\sigma }^{S}}$, равными 80° и 10°. Таким образом, направление на Солнце близко к оси $O{{Y}_{1}}$. К ней же близка нормаль к плоскости орбиты.

– Коэффициент усиления k = 600 Н м с Тл^–1, целевая скорость закрутки ω₀ = 0.5 град/с.

– Вычисление аэродинамического момента (сумма моментов, действующих на стороны аппарата, обращенные к набегающему потоку):

• спутник — параллелепипед со сторонами 30 см;

• центр масс смещен относительно центра давления на 2, 3 и 4 см вдоль осей связанной системы;

• плотность атмосферы 1.8 · 10^–13 кг/м³ (средняя солнечная активность).

– Остаточный дипольный момент 2 · 10^–2 А м^–2, имеющий постоянную и нормально распределенную компоненты.

– Точность определения направления на солнце 1°, угловой скорости – 10^–4 с^–1 (постоянное смещение и нормально распределенный шум).

– Помимо гравитационного и аэродинамического, действует момент неизвестной природы, примерно вдвое меньший, чем гравитационный.

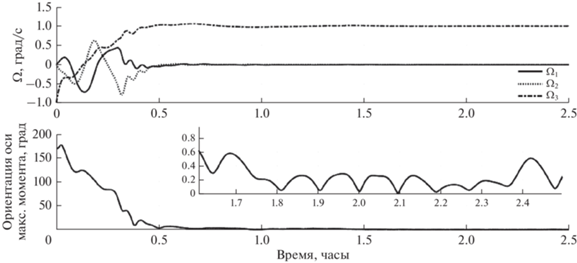
На рис. 2 приведен пример моделирования для аппарата с тензором инерции 1.0, 0.8, 1.3 кг м², параметр $\mu $ равен единице. Таким образом, вращение происходит вокруг оси максимального момента, что при $\mu = 1$ обеспечивает устойчивость требуемого режима движения.

Рис. 2.

Стабилизация в требуемом положении.

На рис. 2 ${{\Omega }_{k}}$ – компоненты угловой скорости аппарата в системе $Ox$. Пример выхода аппарата на стабилизацию в обратном направлении приведен на рис. 3. Тензор инерции 1.0, 0.8, 1.6 кг м², параметр $\mu $ равен 3. Таким образом, выполняются условия случая 2 ($C > 1.5A$ при $\mu = 3$).

Рис. 3.

Стабилизация в обратном положении.

Отметим, что начальные данные выбраны таким образом, что аппарат изначально близок к стабилизации в обратном направлении. Такие же начальные данные можно видеть и на рис. 2, где, однако, аппарат стабилизировался в требуемом направлении.

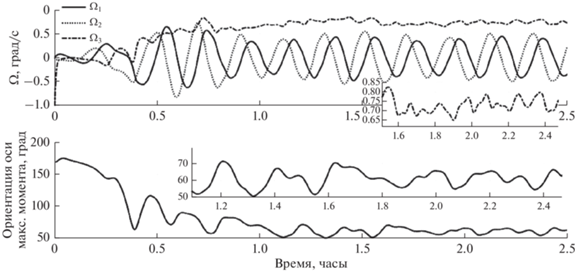
Наконец, на рис. 4 приведен пример стабилизации в косом положении с тензором инерции 1.0, 0.8, 0.3 кг м², параметр $\mu $ равен 1.

Рис. 4.

Стабилизация в косом положении.

Аппарат должен выйти на вращение с углом $\theta \approx 60^\circ $ согласно (13) и скоростью вращения около 0.75 град/с согласно (14). При этом в силу отличия моментов инерции $A$ и $B$ в выражениях (13) и (14) принята средняя величина 0.9 кг м² для $A$.

ЗАКЛЮЧЕНИЕ

Рассмотрено угловое движение аппарата в режиме одноосной стабилизации в направлении Солнца с помощью электромагнитной системы ориентации. Использован алгоритм управления, основанный на информации о текущей и требуемой ориентации одной из осей спутника и вектора его кинетического момента. Показано, что существует опасность стабилизации аппарата в противоположном направлении и косых положениях. Получены условия на параметры управления и моменты инерции аппарата, при которых достигается требуемая ориентация, в том числе при необходимости вращения вокруг оси минимального момента инерции.

Исследование выполнено за счет гранта Российского научного фонда № 22-71-10009 (https:// rscf.ru/project/22-71-10009/).

Список литературы

Морозов В.М., Каленова В.И. Управление спутником при помощи магнитных моментов: управляемость и алгоритмы стабилизации // Косм. исслед. 2020. Т. 58. № 3. С. 199–207. (Cosmic Research. 2020. Т. 58. № 3. С. 158–166.)
Bhat S.P. Controllability of nonlinear time-varying systems: applications to spacecraft attitude control using magnetic actuation // IEEE Trans. Automat. Contr. 2005. V. 50(11). P. 1725–1735.
Артюхин Ю.П., Каргу Л.И., Симаев В.Л. Системы управления космических аппаратов, стабилизированных вращением. М.: Наука, 1979.
Shigehara M. Geomagnetic attitude control of an axisymmetric spinning satellite // J. Spacecr. Rockets. 1972. V. 9(6). P. 391–398.
Овчинников М.Ю., Ролдугин Д.С., Пеньков В.И. Исследование связки трех алгоритмов магнитного управления угловой скоростью и ориентацией спутника, стабилизируемого вращением // Косм. исслед. 2012. Т. 50. № 4. С. 326–334.
Thomson W.T. Spin stabilization of attitude against gravity torque // J. Astronaut. Sci. 1962. V. 9(1). Paper AAS 9-1-31-3.
Alfriend K.T. Magnetic attitude control system for dual-spin satellites // AIAA J. 1975. V. 13(6). P. 817–822.
Wheeler P.C. Spinning Spacecraft Attitude Control via the Environmental Magnetic Field // J. Spacecr. Rockets. 1967. V. 4(12). P. 1631–1637.
Avanzini G., de Angelis E.L., Giulietti F. Spin-axis pointing of a magnetically actuated spacecraft // Acta Astronaut. 2014. V. 94. № 1. P. 493–501.
de Ruiter A. A fault-tolerant magnetic spin stabilizing controller for the JC2Sat-FF mission // Acta Astronaut. 2011. V. 68(1–2). P. 160–171.
You H., Jan Y. Sun Pointing Attitude Control with Magnetic Torquers Only // Intern. Astronautical Congress. 2006. Paper IAC-06-C1.2.01.
Kim J., Worrall K. Sun tracking controller for UKube-1 using magnetic torquer only // IFAC Proc. 2013. V. 46(19). P. 541–546.
Игнатов А.И., Сазонов В.В. Стабилизация режима солнечной ориентации искусственного спутника Земли электромагнитной системой управления // Косм. исслед. 2018. Т. 56. № 5. С. 375–383. (Cosmic Research. 2018. Т. 56. № 5. С. 388–399.)
Karpenko S.O., Ovchinnikov M.Y., Roldugin D.S., Tkachev S.S. One-axis attitude of arbitrary satellite using magnetorquers only // Cosmic Research. 2013. V. 51. № 6. P. 478–484.
Roldugin D.S., Tkachev S.S., Ovchinnikov M.Y. Satellite Angular Motion under the Action of SDOT Magnetic One Axis Sun Acquisition Algorithm // Cosmic Research. 2021. V. 59. № 6. P. 529–536.
Roldugin D., Tkachev S., Ovchinnikov M. Asymptotic Motion of a Satellite under the Action of Sdot Magnetic Attitude Control // Aerospace. 2022. V. 9(11). Paper 639.
Cubas J., Farrahi A., Pindado S. Magnetic Attitude Control for Satellites in Polar or Sun-Synchronous Orbits // J. Guid. Control. Dyn. 2015. V. 38(10). P. 1947–1958.
Chasset C., Berge S., Bodin P., Jakobsson B. 3-axis magnetic control with multiple attitude profile capabilities in the PRISMA mission // 57th Intern. Astronautical Congress. 2006. Paper IAC-06-C1.2.3.
Белецкий В.В. Эволюция вращения динамически-симметричного спутника // Косм. исслед. 1963. Т. 1. № 3. С. 339–385.
Черноусько Ф.Л. О движении спутника относительно центра масс под действием гравитационных моментов // Прикладные математика и механика. 1963. Т. 27. № 3. С. 473–483.
Белецкий В.В. Движение спутника относительно центра масс в гравитационном поле. М.: Изд-во Московского ун-та, 1975.
Арнольд В.И., Нейштадт А.И., Козлов В.В. Динамические системы-3 / ред. Арнольд В.И. М.: ВИНИТИ, 1985.
Белецкий В.В., Новогребельский А.Б. Существование устойчивых относительных равновесий искусственного спутника в модельном магнитном поле // Астрон. журн. 1973. Т. 50. № 2. С. 327–335.
Белецкий В.В., Хентов А.А. Вращательное движение намагниченного спутника. М.: Наука, 1985.
Alken P., Thébault E., Beggan C.D. et al. International Geomagnetic Reference Field: the thirteenth generation // Earth, Planets and Space. 2021. V. 73(1). Art. No. 49.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал