Космические исследования, 2023, T. 61, № 2, стр. 143-156
Реализация режима солнечной ориентации космического аппарата с помощью системы двигателей-маховиков
А. И. Игнатов 1, *, Г. А. Иванов 1, Е. С. Коломиец 1, Е. В. Мартыненкова 1
1 Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия
* E-mail: general_z@mail.ru
Поступила в редакцию 06.04.2022
После доработки 15.04.2022
Принята к публикации 15.06.2022
- EDN: LUGGZP
- DOI: 10.31857/S0023420622700017
Аннотация
Исследован режим поддержания солнечной ориентации космического аппарата –гиростата на низкой околоземной орбите в течение длительного времени. Аппарат по форме близок к цилиндру с двумя неподвижными панелями солнечных батарей. Панели расположены вдоль продольной оси цилиндра, симметрично относительно нее. В режиме солнечной ориентации нормаль к плоскости солнечных батарей аппарата неизменно направлена на Солнце, продольная ось совершает колебания относительно плоскости орбиты. Для реализации указанного режима движения космического аппарата используется система четырех двигателей-маховиков, оси вращения которых направлены параллельно боковым ребрам четырехугольной пирамиды. Положение боковых ребер пирамиды относительно жестко связанной с аппаратом системы координат задается двумя углами, которые являются параметрами системы двигателей-маховиков. Рассматривается закон управления гиростатическим моментом, при котором обеспечивается затухание возмущенного движения космического аппарата в окрестности положения его солнечной ориентации и ограничивается накопление собственного кинетического момента двигателей-маховиков за счет управления углом поворота аппарата вокруг нормали к светочувствительной стороне солнечных батарей. В работе показано, что c помощью определенного выбора параметров системы двигателей-маховиков возможно реализовать режим солнечной ориентации без проведения разгрузок гиростатического момента в течение всего времени полета. Приведены результаты численного моделирования полной системы уравнений движения космического аппарата в режиме его солнечной ориентации с учетом воздействия гравитационного и аэродинамического моментов, подтверждающие правильность выбранных значений параметров.
ВВЕДЕНИЕ
Режим солнечной ориентации часто используется в процессе эксплуатации космических аппаратов (КА), поскольку обеспечивает максимальный приток электроэнергии на борт. В работе исследуется поддержание режима солнечной ориентации КА на низкой околоземной орбите с помощью гиросистемы в течение длительного времени. Специфика рассматриваемого КА состоит в том, что на нем расположены неподвижные панели солнечных батарей, поэтому для наиболее их эффективного использования необходимо поддерживать непрерывную ориентацию вектора нормали к светочувствительной стороне панелей батарей на Солнце. При использовании гиросистемы одним из основных требований к режиму ориентации КА является малая скорость накопления собственного кинетического момента гиросистемы (гиростатического момента), для увеличения интервалов времени между проведением разгрузок. Накопление гиростатического момента происходит за счет воздействия на КА гравитационного и аэродинамического моментов. В настоящей работе рассматривается закон управления гиростатическим моментом КА, при котором обеспечивается затухание возмущенного движения КА в окрестности положения его солнечной ориентации и ограничивается накопление гиростатического момента за счет управления углом поворота КА вокруг нормали к светочувствительной стороне солнечных батарей [1–3].
УРАВНЕНИЯ ДВИЖЕНИЯ КОСМИЧЕСКОГО АППАРАТА
КА считаем гиростатом, для описания его движения будем использовать три правых декартовых системы координат.
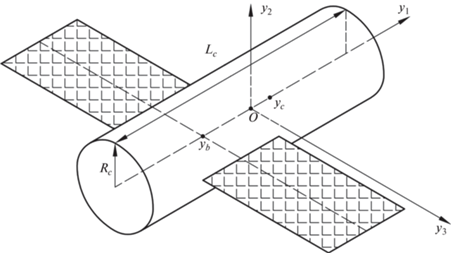
• Oy1y2y3 — связанная система координат, образованная главными центральными осями инерции КА. Полагаем, что КА имеет форму прямого кругового цилиндра (рис. 1) радиуса Rc и высоты Lc с двумя прикрепленными к нему одинаковыми прямоугольными пластинами – солнечными батареями суммарной площади Sb. Ось цилиндра совпадает с осью Oy1. Солнечные батареи расположены в плоскости Oy1y3 симметрично относительно оси Oy1, стороны батарей параллельны осям и Oy3, ось Oy2 перпендикулярна плоскости солнечных батарей. Светочувствительная сторона солнечных батарей обращена к полупространству y2 > 0. Координаты геометрических центров цилиндра и пластин солнечных батарей обозначим (yc, 0, 0) и (yb, 0, 0) соответственно, базисные орты этой системы – e1, e2, e3. Ниже, если не оговорено особо, компоненты векторов и координаты точек относятся к системе Oy1y2y3.
• OEY1Y2Y3 – гринвичская система координат. Ее начало находится в центре Земли, плоскость OEY1Y2 совпадает с плоскостью экватора, ось OEY1 пересекает гринвичский меридиан, ось OEY3 направлена к Северному полюсу.
• OEZ1Z2Z3 – квазиинерциальная система координат. Ось OEZ2 параллельна вектору кинетического момента орбитального движения КА, ось OEZ3 лежит в плоскости экватора и направлена в восходящий узел оскулирующей орбиты КА. Базис этой системы образован ортами E1, E2, E3.
Матрицу перехода от системы OEZ1Z2Z3 к системе OEY1Y2Y3 обозначим $C = \left\| {{{c}_{{ij}}}} \right\|_{{i,j = 1}}^{3},$ где cij – косинус угла между осями OEYi и OEZj. Элементы этой матрицы выражаются через координаты и компоненты скорости центра масс КА в гринвичской системе координат. Матрицы перехода от системы Oy1y2y3 к гринвичской системе координат и системе OEZ1Z2Z3 обозначим соответственно $B = \left\| {{{b}_{{ij}}}} \right\|_{{i,j = 1}}^{3}$ и $A = \left\| {{{a}_{{ij}}}} \right\|_{{i,j = 1}}^{3}.$ Здесь bij и aij – косинусы углов, которые образует ось Oyj с осями OEY1 и OEZ1. Справедливы соотношения aij = Ei × ej, B = = CA.
Положение системы Oy1y2y3 относительно системы OEZ1Z2Z3 будем также задавать углами ψ, θ и φ, которые введем следующим образом. Если точку OE перенести в точку O, то систему OEZ1Z2Z3 можно перевести в систему Oy1y2y3 тремя последовательными поворотами: 1) на угол ψ вокруг оси OEZ2, 2) на угол π/2 – θ вокруг новой оси OEZ1, 3) на угол φ + π вокруг новой оси OEZ2, совпадающей с осью Oy2. Элементы матрицы A выражаются через эти углы с помощью следующих формул:
Уравнения движения КА состоят из двух подсистем. Одна подсистема описывает движение центра масс КА в гринвичской системе координат с учетом нецентральности гравитационного поля Земли и сопротивления атмосферы. Другая подсистема описывает движение КА относительно центра масс (вращательное движение).
В векторном виде подсистему уравнений движения центра масс КА можно представить, как в работе [4]:
Подсистема уравнений вращательного движения КА имеет вид:
(1)
$\left. \begin{gathered} \frac{{{{\tilde {d}}}{\mathbf{K}}}}{{{\text{d}}t}} + {\mathbf{\omega }} \times {\mathbf{K}} = {{{\mathbf{M}}}_{g}} + {{{\mathbf{M}}}_{a}}, \\ {\mathbf{K}} = \hat {I}{\kern 1pt} {\mathbf{\omega }} + {\mathbf{H}},\quad \frac{{{{\tilde {d}}}{\mathbf{H}}}}{{{\text{d}}t}} + {\mathbf{\omega }} \times {\mathbf{H}} = - {{{\mathbf{M}}}_{c}}, \\ \frac{{{{\tilde {d}}}{{{\mathbf{b}}}_{1}}}}{{{\text{d}}t}} + {\mathbf{\omega }} \times {{{\mathbf{b}}}_{1}} = {{\omega }_{E}}{{{\mathbf{b}}}_{2}},\quad \frac{{{{\tilde {d}}}{{{\mathbf{b}}}_{2}}}}{{{\text{d}}t}} + {\mathbf{\omega }} \times {{{\mathbf{b}}}_{2}} = - {{\omega }_{E}}{{{\mathbf{b}}}_{1}}. \\ \end{gathered} \right\}$Гравитационный момент задается формулой [5]:
Формула аэродинамического момента имеет вид
Чтобы замкнуть подсистему уравнений вращательного движения, надо добавить к уравнениям (1) выражение для Mc. Оно приведено ниже.
В расчетах использовались следующие параметры описанной модели. Параметры КА: m = = 6440 кг, I1 = 2600 кг м2, I2 = 11100 кг м2, I3 = = 10 900 кг м2, Rc = 1.3 м, Lc = 5.0 м, Sb = 33 м2, c = = 0.005 м2/кг, yb = –1 м, yc = 0.3 м. Параметры модели атмосферы: F10.7 = F81 = 150, Ap = 12.
Начальные условия движения центра масс КА задавались в восходящем узле орбиты в момент времени 07.13.07 UTC 21.XII.2013. При этом элементы орбиты составляли: высота в апогее 575.2 км, высота в перигее 546.8 км, наклонение 64.87°, аргумент широты перигея –124.65°, долгота восходящего узла в гринвичской системе координат 209.70°. На отрезке времени моделирования движения КА максимальное значение угла ϑ между ортом направления “Земля–Солнце” и плоскостью орбиты КА достигало 88°.
Начальные условия уравнений (1) задавались в тот же момент времени, что и начальные условия орбитального движения КА. Этот момент служил началом отсчета времени – точкой t = 0.
РЕЖИМ СОЛНЕЧНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА
Сначала рассмотрим режим трехосной солнечной ориентации КА, в котором ось Oy2 неизменно направлена на Солнце, ось Oy1 лежит в плоскости орбиты, абсолютная угловая скорость КА мала. Пусть s – орт направления “Земля–Солнце”. Орт ${\mathbf{n}} = ({{{\mathbf{s}} \times {{{\mathbf{E}}}_{2}})} \mathord{\left/ {\vphantom {{{\mathbf{s}} \times {{{\mathbf{E}}}_{2}})} {\left| {{\mathbf{s}} \times {{{\mathbf{E}}}_{2}}} \right|}}} \right. \kern-0em} {\left| {{\mathbf{s}} \times {{{\mathbf{E}}}_{2}}} \right|}}$ лежит в плоскости орбиты КА и ортогонален орту s. Изменение ортов s и n в системе Oy1y2y3 описывается уравнениями
Закон управления гиросистемой Mc = Mc(ω, s, n), обеспечивающий затухание возмущенного движения КА в окрестности положения ω = 0, e1 = n, e2 = s с требуемой скоростью, имеет вид [2]:
Рассмотрим возможность использования закона управления, позволяющего не только обеспечить затухание возмущенного движения КА в окрестности положения e2 = s с требуемой скоростью, но и дополнительно ограничить рост накапливаемого кинетического момента гиросистемы. Чтобы не нарушать режим солнечной ориентации КА накопление кинетического момента гиросистемы будем контролировать только за счет управления углом поворота КА вокруг орта e2 = s. Закон управления гиросистемой, обеспечивающий поддержание режима солнечной ориентации с заданными выше условиями, имеет вид [2]:
(2)
$\left. \begin{gathered} {{{\mathbf{M}}}_{c}} = {{\xi }^{2}}\hat {I}({{{\mathbf{e}}}_{2}} \times {\mathbf{s}} + {{{\mathbf{e}}}_{1}} \times {\mathbf{n}}) - \\ - \,\,2\xi \hat {I}\hat {W}{\mathbf{\omega }} - \hat {I}(\chi {{\omega }_{2}} + f){{{\mathbf{e}}}_{2}}, \\ f = - \frac{{3{{\mu }_{E}}}}{{{{r}^{5}}}}\left[ { - ({{\kappa }_{3}} - {{\kappa }_{1}}){{r}_{1}}{{r}_{2}}K_{1}^{{}}} \right. + \\ \left. { + \,\,{{\kappa }_{2}}\left( {r_{1}^{2} - r_{3}^{2}} \right){{K}_{2}} + ({{\kappa }_{3}} - {{\kappa }_{1}}){{r}_{2}}{{r}_{3}}{{K}_{3}}} \right], \\ \end{gathered} \right\}$Покажем, что выбранный закон изменения управляющего момента (2) действительно обеспечивает солнечную ориентацию КА и при этом ограничивает накопление кинетического момента гиросистемы. С этой целью вычислим решение системы (1), (2) приняв χ = 2ξ, ξ = 0.01 с–1, κ1 = = κ2 =1 (Нмс)–1, κ3 = 3 (Нмс)–1.
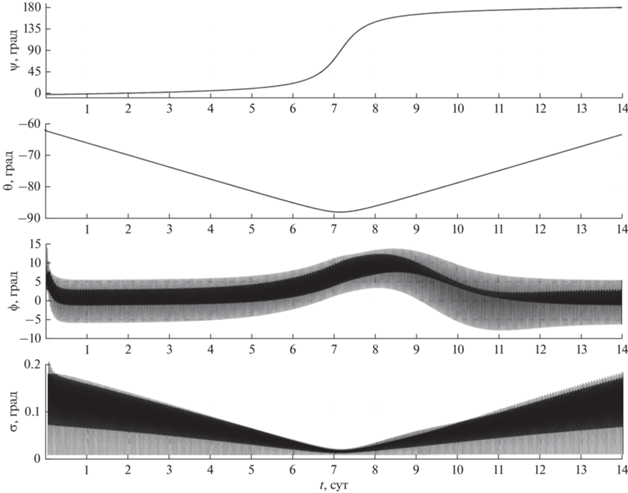
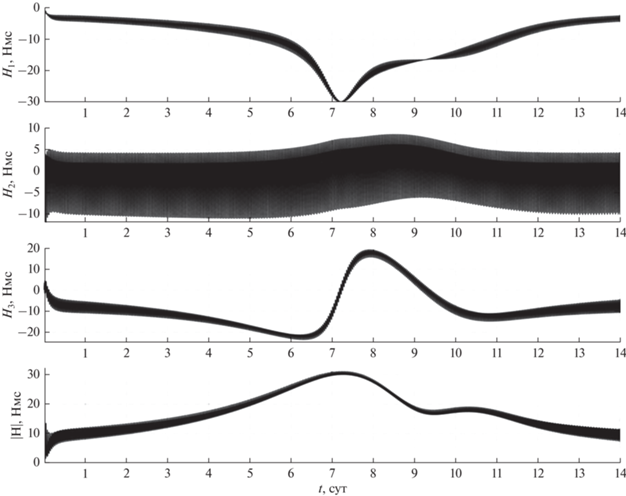
Компоненты орта s в гринвичской системе координат рассчитывались по приближенным формулам [6]. Начальные условия системы (1), (2) в момент времени t = 0 задавались следующим образом. КА в гринвичской системе координат занимает положение e1 = n, e2 = s. Гиростатический момент H(0) = 0, начальные значения компонент угловой скорости ωi, задавались с учетом ошибок в их реализации: ω1(0) = ω2(0) = ω3(0) = 0.01 град/с. Результаты расчетов движения КА, полученные в рамках принятой модели, приведены на рис. 2, 3. Эти результаты представлены графиками зависимости от времени углов ψ, θ и φ, угла σ = arcos(s × e2) (θ = ϑ при σ = 0). На рисунках также представлены графики компонент гиростатического момента КА Hi (i = 1, 2, 3) и модуля вектора гиростатического момента $\left| {\mathbf{H}} \right|.$
Все графики на рис. 2, 3 построены на интервале времени 14 сут. Переходной процесс (процесс гашения возмущенного движения КА), обусловленный ошибками в задании начальной угловой скорости, длится менее 20 мин и из-за масштаба на рисунках не виден. Результаты моделирования показывают, что использование закона управления (2) обеспечивает солнечную ориентацию КА и затухание его возмущенного движения в окрестности положения e2 = s. Ошибка солнечной ориентации иллюстрируется графиком угла σ(t) (см. рис. 2). Как видно из приведенного графика, ошибка ориентации достаточно мала. Амплитуды установившихся колебаний компонент абсолютной угловой скорости ωi ограничены значениями:
На рис. 3 видны установившиеся колебания величин Hi (i = 1, 2, 3) с доминирующей частотой 2ω0 (ω0 – среднее движение центра масс КА, для рассматриваемой в данной работе орбиты ω0 ≈ ≈ 1.1 · 10–3 с–1), которые вызваны воздействием гравитационного момента [3]. На рис. 3 видно, что из-за использования закона управления (2) постоянного возрастания (накопления) величины кинетического момента гиросистемы не происходит, значение $\left| {\mathbf{H}} \right|$ остается ограниченным на всем интервале времени моделирования. Однако когда Солнце относительно плоскости орбиты поднимается достаточно высоко (ϑ > 70°), значения $\left| {\mathbf{H}} \right|$ начинают возрастать, достигая своего максимума $\left| {\mathbf{H}} \right| \approx 31\;{\text{Нмс}}$ при ϑ ≈ 88°. Это связано с тем, что по мере увеличения угла θ изменение угла φ поворота КА вокруг оси Oy2 уже не может остановить накопление $\left| {\mathbf{H}} \right|$ за счет воздействия гравитационного момента. В дальнейшем, при уменьшении θ уменьшается и кинетический момент гиросистемы до значений $\left| {\mathbf{H}} \right| < 12\;{\text{Нмс}}{\text{.}}$ Таким образом, результаты моделирования показали, что, используя закон управления (2), можно реализовать режим солнечной ориентации КА без постоянного накопления абсолютного значения кинетического момента гиросистемы $\left| {\mathbf{H}} \right|.$ В работах [1–3] также показано, что в случаях, когда угол ϑ < 70° величина $\left| {\mathbf{H}} \right|$ не превышает значения 12 Нмс за счет использования закона управления (2). Можно утверждать, что на рис. 3 представлен один из самых неблагоприятных случаев с точки зрения накопления гиростатического момента гиросистемы, когда величина $\left| {\mathbf{H}} \right|$ достигает наибольшего значения для всех возможных положений Солнца относительно рассматриваемой орбиты КА. В настоящей работе конкретные параметры гиросистемы КА подбираются для случая, при котором реализуется максимальное накопление значения $\left| {\mathbf{H}} \right|.$
СОБСТВЕННЫЙ КИНЕТИЧЕСКИЙ МОМЕНТ СИСТЕМЫ ДВИГАТЕЛЕЙ-МАХОВИКОВ
Динамические требования к системе управления КА, включающей в свой состав гиросистему, во многом определяются множеством требуемых значений кинетического момента HT. Множество HT является областью изменения в связанной с КА системе координат вектора суммарного кинетического момента, создаваемого гиросистемой. Изменение этого вектора в указанной области в соответствии с реализуемыми в системе законами должно обеспечивать требуемое управление параметрами вращательного движения КА. Естественно, что множество HT должно содержаться внутри множества максимальных значений кинетического момента HC, реализуемых гиросистемой.
Таким образом, для всех вариантов построения гиросистемы должно быть обеспечено выполнение условия:
При этом можно утверждать, что величина суммарного кинетического момента, создаваемого гиросистемой, будет достаточной для обеспечения требуемой угловой скорости вращения КА [7].
В настоящей работе в качестве гиросистемы предназначенной для создания управляющих моментов рассматривается система четырех двигателей-маховиков (ДМ) [7]. Область вариации возможных значений суммарного кинетического момента HC, создаваемого системой ДМ, зависит от схемы их расположения относительно связанной с КА системы координат и максимального значения кинетического момента, реализуемого каждым из ДМ. Суммарный кинетический момент системы ДМ выражается формулой
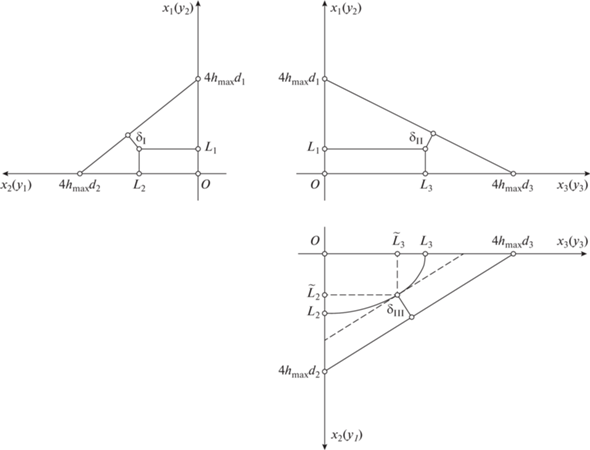
где hk – алгебраическое значение кинетического момента ДМ с номером k (k = 1, …, 4); gk – орт оси вращения ДМ с номером k.Введем связанную с системой ДМ правую декартову систему координат Ox1x2x3, в которой вектор H представлен своими компонентами Hi (i = 1, 2, 3). Рассмотрим область P4 пространства R3(H1, H2, H3), заполняемую концами векторов (4) (начала векторов помещены в точку O). Здесь и далее считаем, что система состоит из одинаковых ДМ. В этом случае –hmax ≤ hk ≤ hmax, где hmax — абсолютная величина предельного значения кинетического момента отдельного ДМ. В данном случае принято значение hmax = 18 Нмс. Оси вращения ДМ расположены параллельно боковым ребрам четырехугольной пирамиды. Высота пирамиды параллельна оси Ox1, линии пересечения граней пирамиды с плоскостью Ox2x3 параллельны или перпендикулярны осям Ox2, Ox3 (рис. 4).
Орты gk, k = 1, …, 4, в системе Ox1x2x3 имеют компоненты
(5)
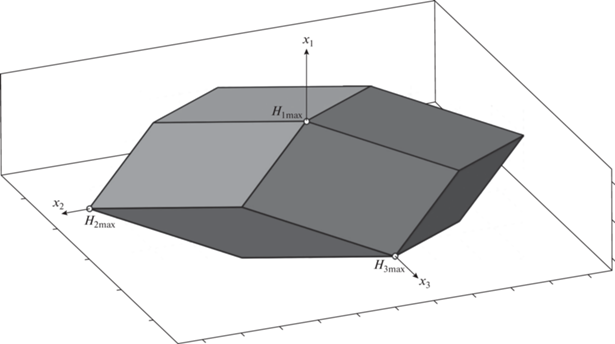
$\begin{gathered} {{H}_{1}} = ({{h}_{1}} - {{h}_{2}} + {{h}_{3}} - {{h}_{4}}){{d}_{1}}, \\ {{H}_{2}} = ( - {{h}_{1}} + {{h}_{2}} + {{h}_{3}} - {{h}_{4}}){{d}_{2}}, \\ {{H}_{3}} = ({{h}_{1}} + {{h}_{2}} - {{h}_{3}} - {{h}_{4}}){{d}_{3}}. \\ \end{gathered} $Область пространства, заполняемая концами векторов H, представляет собой выпуклый многогранник P4 (рис. 5).
Все необходимые при построении P4 соотношения для координат вершин, а также параметризация граней приведены в исследовании [7]. На рис. 5 обозначены вершины многогранника P4 в которых реализуются значения Hi max – максимальные абсолютные значения кинетического момента, создаваемые системой ДМ по каждой из осей Oxi, i = 1, 2, 3. Для системы четырех ДМ, расположенных по схеме “четырехугольная пирамида”, значения Hi max определяются соотношениями (5):
РАСПОЛОЖЕНИЕ ДВИГАТЕЛЕЙ-МАХОВИКОВ НА КОСМИЧЕСКОМ АППАРАТЕ
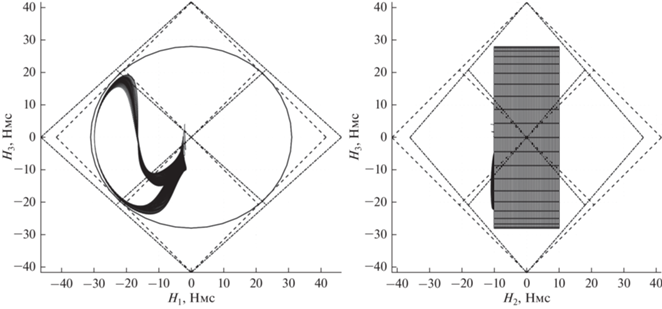
Множество HT в данном случае задается множеством значений гиростатического момента H системы ДМ реализуемого в процессе поддержания режима солнечной ориентации КА (рис. 3). На рис. 6 представлен годограф вектора H (кривые линии черного цвета), а также показана аппроксимация области его вариации частью прямого эллиптического цилиндра.
Проверить выполнение условия (3) можно сравнением области вариации HT и многогранника P4, для чего их необходимо построить в одной системе координат и в едином масштабе. Как видно из рис. 3, максимальное значение $\left| {{{H}_{2}}} \right|$ примерно в 2.5 раза меньше чем максимальное значение $\left| {{{H}_{3}}} \right|$ и примерно в три раза меньше, чем максимальное значение $\left| {{{H}_{1}}} \right|.$ Исходя из этих соотношений между размерами области вариации вектора H, наиболее рационально будет расположить систему ДМ таким образом, чтобы вершина “пирамиды” лежала на оси Oy2. Совместим начала систем координат Ox1x2x3 и Oy1y2y3 в центре масс КА (начало системы Ox1x2x3 можно поместить в любое место, важно лишь угловое положение осей Oxi относительно осей Oyi) и расположим ось Ox1 вдоль оси Oy2, а ось Ox3 вдоль оси Oy3. Зная hmax, для построения многогранника P4 остается только выбрать значения α и β параметров системы ДМ. При выборе значений параметров α и β можно использовать разные критерии, из которых самый очевидный – это максимальный объем многогранника P4. Рассмотрим все возможные расстояния от каждой из граней P4 до точки O. Эти расстояния по сути представляют собой абсолютные значения кинетического момента, реализуемого системой ДМ в направлении, перпендикулярном соответствующей грани. Для схемы ДМ “четырехугольная пирамида” все грани многогранника P4 можно условно разделить на три группы в зависимости от их удаленности от его геометрического центра. Соответствующие значения HI, HII, HIII кинетического момента, реализуемого системой ДМ в направлении от точки O по нормали к какой-либо грани, принадлежащей своей группе, можно вычислить по одной из следующих формул:
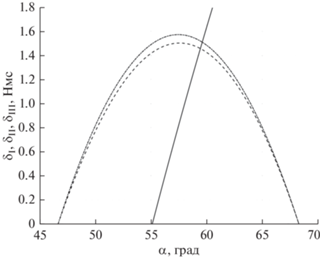
Наименьшее из значений HI, HII, HIII соответствует максимальному радиусу сферы, полностью вписанной в многогранник P4. На рис. 7 представлены три поверхности: ${{\tilde {H}}_{{\text{I}}}}(\alpha ,\beta ) = {{{{H}_{{\text{I}}}}} \mathord{\left/ {\vphantom {{{{H}_{{\text{I}}}}} {{{h}_{{\max }}}}}} \right. \kern-0em} {{{h}_{{\max }}}}}$ (показана темно-серым цветом), ${{\tilde {H}}_{{{\text{II}}}}}(\alpha ,\beta ) = {{{{H}_{{{\text{II}}}}}} \mathord{\left/ {\vphantom {{{{H}_{{{\text{II}}}}}} {{{h}_{{\max }}}}}} \right. \kern-0em} {{{h}_{{\max }}}}}$ (показана светло-серым цветом) и ${{\tilde {H}}_{{{\text{III}}}}}(\alpha ,\beta ) = {{{{H}_{{{\text{III}}}}}} \mathord{\left/ {\vphantom {{{{H}_{{{\text{III}}}}}} {{{h}_{{\max }}}}}} \right. \kern-0em} {{{h}_{{\max }}}}}$ (показана белым цветом). Поверхности имеют одну точку пересечения, соответствующую значениям углов $\alpha = {\text{arctg}}(\sqrt 2 ) \approx 54.7^\circ $ и β = 45°, при которых максимальный радиус сферы, полностью вписанной в многогранник P4, а также объем P4 будут иметь наибольшее значение, равное ${{H}_{{\text{I}}}} = {{H}_{{{\text{II}}}}} = {{H}_{{{\text{III}}}}} = {{4{{h}_{{\max }}}} \mathord{\left/ {\vphantom {{4{{h}_{{\max }}}} {\sqrt 6 }}} \right. \kern-0em} {\sqrt 6 }}.$
Рис. 7.
Поверхности ${{\tilde {H}}_{{\text{I}}}}(\alpha ,\beta ),$ ${{\tilde {H}}_{{{\text{II}}}}}(\alpha ,\beta ),$ ${{\tilde {H}}_{{{\text{III}}}}}(\alpha ,\beta ).$

Еще один из способов выбрать значения углов α и β – это разместить аппроксимирующий цилиндр, изображенный на рис. 6, внутри многогранника P4 таким образом, чтобы кратчайшие расстояния δI, δII, δIII от поверхности цилиндра до каждой из трех групп граней, образующих P4, были равны между собой. На рис. 8 схематично показано взаимное расположение проекций цилиндра и граней многогранника на координатные плоскости систем Ox1x2x3 и Oy1y2y3. Значения δI, δII, δIII вычисляются по формулам:
Рис. 8.
Проекции цилиндра и граней многогранника P4 на координатные плоскости систем Ox1x2x3 и Oy1y2y3.
При выполнении условий
На рис. 10 показано взаимное расположение проекций годографа H, аппроксимирующего цилиндра и двух вариантов многогранника P4. Штрихпунктирными линиями показаны проекции многогранника при значении углов α = 60°, β = 48°, пунктирными линиями — при значении углов α = 54.7° и β = 45°. На рис. 10 видно, что в случае, когда значения углов α = 60°, β = 48°, грани многогранника P4 располагаются на большем расстоянии от поверхности цилиндра чем в случае α = 54.7° и β = 45°.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РЕЖИМА СОЛНЕЧНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА
Выбрав значения углов α и β, проверим возможность системы ДМ реализовать рассматриваемый режим солнечной ориентации КА, т.е. на всем рассматриваемом интервале времени движения КА должно выполняться условие $\left| {{{h}_{k}}} \right| < {{h}_{{\max }}},$ k = 1, …, 4. Для этого подсистему уравнений вращательного движения КА (1), (2) необходимо дополнить уравнениями, описывающими изменение собственного кинетического момента каждого из ДМ системы. Матрицу перехода от Ox1x2x3 к Oy1y2y3 обозначим U,
Запишем орты gk, k = 1, …, 4, осей вращения маховиков в виде матрицы $D = \left\| {{{{\mathbf{g}}}_{1}},\; \ldots ,\;{{{\mathbf{g}}}_{n}}} \right\|,$ тогда выражение (4) можно представить как
где D – прямоугольная матрица размерности 3 × × 4, G = (h1, h2, h3, h4)T. Соотношение (6) нельзя единственным образом разрешить относительно величин hk, k = 1, …, 4. Чтобы достичь единственности, потребуем, чтобы решение системы (6) относительно hk имело минимальную евклидову нормуТогда
где D+ = DT(DDT)–1 – матрица, псевдообратная для матрицы D [8]. Матрица D+ существует при условии, что в системе есть любые три ДМ, у которых орты gk, k = 1, …, 4, осей вращения линейно независимы. Для схемы ДМ “четырехугольная пирамида” (см. рис. 4) матрицы D и D+ можно представить в виде:На рис. 11 показаны графики зависимости от времени собственных кинетических моментов hk, k = 1, …, 4, каждого из ДМ, полученные в результате численного моделирования движения КА в рамках модели, приведенной выше, с учетом соотношений (6), (7), при значениях углов α = 60°, β = 48°. Как и на рис. 2, 3, графики на рис. 11 построены на интервалах времени 14 сут. Переходной процесс (процесс гашения возмущенного движения КА), обусловленный ошибками в задании начальной угловой скорости, длится менее 20 мин и из-за масштаба на рисунках не виден. Из рис. 11 видно, что на интервале времени с 6-х по 8-е сутки полета КА величины hk, k = 1, …, 4, превышают максимально допустимое значение hmax = 18 Нмс, что вызвано наличием колебаний составляющих вектора гиростатического момента КА (см. рис. 3). Ограничить колебания величин hk, k = 1, …, 4, можно использовав другое условие достижения единственности решение системы (6) относительно hk.
МЕТОД МИНИМАЛЬНОЙ НОРМЫ l∞
Еще одним из способов достижения единственности решения системы (6) относительно hk, k = 1, …, 4, является требование минимума нормы
Применение метода минимальной нормы l∞ позволяет системе ДМ наиболее эффективно использовать весь возможный объем области HC создаваемого кинетического момента. В общем случае указанный метод представлен в виде некоторых алгоритмов поиска решения, примеры реализации которых приведены в работах [9–11]. Однако в случае, когда гиросистема состоит из четырех ДМ, оси вращения которых расположены параллельно боковым ребрам симметричной пирамиды (см. рис. 4) решение системы (6) с помощью метода минимальной нормы l∞ можно представить в виде [10]:
(8)
$\begin{gathered} {\mathbf{G}} = {{D}^{ + }}{{U}^{T}}{\mathbf{H}} + {{h}_{0}}{\mathbf{\tilde {G}}}, \\ {{h}_{0}} = - \frac{{\min ({{D}^{ + }}{{U}^{T}}{\mathbf{H}}) + \max ({{D}^{ + }}{{U}^{T}}{\mathbf{H}})}}{2}. \\ \end{gathered} $На рис. 12 показаны графики, аналогичные приведенным на рис. 11, полученные в результате численного моделирования движения КА с учетом соотношений (6), (8). Графики на рис. 15 также построены на интервалах времени 14 сут при значениях углов α = 60°, β = 48°. Приведенные результаты моделирования показали, что использование метода минимальной нормы l∞ при решении системы (6) позволяет выполнить условие $\left| {{{h}_{k}}} \right| < {{h}_{{\max }}},$ k = 1, …, 4, в процессе реализации рассматриваемого режима солнечной ориентации КА на всем интервале времени моделирования.
ЗАКЛЮЧЕНИЕ
В работе показано, что c помощью системы двигателей-маховиков, расположенных по схеме “четырехугольная пирамида”, можно реализовать режим солнечной ориентации космического аппарата без проведения разгрузок кинетического момента. Предложенный в работе способ сравнения областей требуемого и реализуемого кинетического момента позволяет выбрать необходимые значения геометрических параметров схемы расположения двигателей-маховиков. Приведены результаты численного моделирования системы уравнений движения космического аппарата, подтверждающие правильность выбранных значений геометрических параметров, обеспечивающих реализацию режима солнечной ориентации космического аппарата.
Полученные в работе результаты могут быть использованы при предварительном проектировании систем управления ориентацией космического аппарата, использующих в качестве исполнительных органов двигатели-маховики.
Список литературы
Игнатов А.И., Сазонов В.В. Оценка низкочастотных микроускорений на борту ИСЗ в режиме одноосной солнечной ориентации // Космич. исслед. 2013. Т. 51. № 5. С. 380–388. https://doi.org/10.7868/S0023420613050051 (Cosmic Research. 2013. Т. 51. № 5. С. 342–349.)
Игнатов А.И. Стабилизация режима солнечной ориентации искусственного спутника Земли без накопления кинетического момента гиросистемы // Изв. РАН. Теория и системы управления. 2020. № 3. С. 164–176. https://doi.org/10.31857/S0002338820030063
Игнатов А.И. Оценка низкочастотных микроускорений на борту искусственного спутника Земли в режиме солнечной ориентации // Космич. исслед. 2022. Т. 60. № 1. С. 43–56. https://doi.org/10.31857/S0023420622010046 (Cosmic Research. 2022. Т. 60. № 1. С. 38–50.)
Бажинов И.К., Гаврилов В.П., Ястребов В.Д. и др. Навигационное обеспечение полета орбитального комплекса “Салют-6” – “Союз” – “Прогресс”. М.: Наука, 1985.
Белецкий В.В. Движение искусственного КА относительно центра масс. М.: Наука, 1965.
Меес Ж. Астрономические формулы для калькуляторов. М.: Мир, 1988.
Игнатов А.И. Выбор геометрических параметров расположения системы двигателей-маховиков при управлении вращательным движением космического аппарата // Изв. РАН. Теория и системы управления. 2022. № 1. С. 124–144. https://doi.org/10.31857/S0002338822010061
Гантмахер Ф.Р. Теория матриц. Москва, Наука. Главная редакция физ.-мат. литературы, 1988.
Markley F.L., Reynolds R.G., Liu F.X. Maximum torque and momentum envelopes for reaction-wheel arrays // J. Guidance, Control, and Dynamics. 2010. V. 33. № 5. P. 1606–1614. https://doi.org/10.2514/1.47235
Yoon H., Seo H.H., Choi H.-T. Optimal uses of reaction wheels in the pyramid configuration using a new minimum infinity-norm solution // Aerospace Science and Technology. 2014. V. 39. P. 109–119. https://doi.org/10.1016/j.ast.2014.09.002
Yoon H., Seo H.H., Park Y.-W., Choi H.-T. A New Minimum Infinity-Norm Solution: with Application to Capacity Analysis of Spacecraft Reaction Wheels // American Control Conf. (ACC). 2015. P. 1241–1245.
Стренг Г. Линейная алгебра и ее применения. М.: Мир, 1980.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования