Кристаллография, 2019, T. 64, № 6, стр. 845-849

ВВЕДЕНИЕ

Граф Кэли некоторой группы представляет собой граф, каждая вершина которого соответствует одному из элементов группы, а каждое ребро есть порождающий элемент с таким направлением, чтобы элемент в начале ребра, умноженный на него, равнялся элементу в конце ребра [1]. Если порождающий элемент обратен самому себе, то стрелки на ребре направлены в обе стороны и в этом случае их можно не изображать. Графы Кэли конечных групп конечны, графы Кэли бесконечных групп бесконечны. Порождающими элементами, или генераторами, называют такие элементы группы, что все остальные ее элементы можно представить в виде произведения генераторов и обратных к ним элементов [2].

Набором генераторов группы называется такое ее подмножество, что наименьшая подгруппа, содержащая этот набор, совпадает с исходной группой. Минимальным набором генераторов группы называется такой набор генераторов, которой не содержит никакого другого набора генераторов данной группы [3]. Как следует из определения, минимальные наборы генераторов одной и той же группы могут иметь разную мощность, что создает проблему нахождения минимальных порождающих наборов минимальной мощности. Назовем такие наборы существенно минимальными, а их мощность – рангом группы.

Поиск ранга групп представляет собой довольно сложную задачу, так как существует огромное множество различных пересекающихся классов групп, а принадлежность группы к тому или иному классу иногда кардинально влияет на ранг. Для кристаллографических групп частично удалось упростить эту задачу [4], связав ранг с порядком p-группы голономий и первым числом Бетти кристаллографической группы, однако полученная оценка имеет три параметра, что не сильно упрощает задачу.

Для трехмерных кристаллографических (федоровских) групп автору удалось найти границы допустимых значений ранга группы, исходя из более простых посылок. Как известно, федоровская группа есть расширение группы трансляций при помощи кристаллического класса [5]. Трехмерная группа трансляций является свободной абелевой группой с тремя генераторами, в то время как любая точечная группа имеет два или три генератора [5]. При расширении группы трансляций может возникнуть эффект уменьшения ранга вследствие появления новых элементов, являющихся порождающими для самих трансляций. Так, у группы P2₁2₁2₁ всего два генератора в существенно минимальном наборе (два поворота со сдвигом вокруг ближайших скрещивающихся осей). Тем не менее наименьшее число генераторов федоровской группы не может быть меньше двух, так как если бы порождающий элемент был единственным, он бы порождал циклическую точечную группу или одномерную группу трансляций, но никак не федоровскую группу. С другой стороны, таких элементов не может быть больше шести, т.е. наибольшей возможной суммы числа генераторов группы трансляций и кристаллического класса [6, 7].

В томе “А” Международных таблиц по кристаллографии [8] содержится информация о наборе порождающих элементов для каждой федоровской группы (раздел Generators selected). Ранее в программной среде Mathematica был разработан алгоритм, позволяющий минимизировать набор генераторов из Международных таблиц [9]. Оказалось, что у многих федоровских групп исходный набор не содержит ни одного существенно минимального набора. Более того, попытка минимизировать набор всех элементов, используемых для построения общей орбиты федоровской группы (раздел Symmetry operations), тоже далеко не всегда приводит к существенно минимальному набору. Одним из ярких примеров является группа P6₃ второго ранга, у которой существенно минимальный набор генераторов должен содержать поворот третьего порядка и поворот со сдвигом второго порядка вокруг ближайших друг к другу осей, расстояние между которыми равно $\frac{{a\sqrt 3 }}{6}$. Однако все повороты из раздела Symmetry operations у этой группы проходят через начало координат, и минимизация этого набора приводит к трем генераторам, а не к двум.

МИНИМАЛЬНЫЕ СЕТИ

Далее используем определения, предложенные в первой кристаллографической статье о минимальных сетях [10]. Слово “сеть” зачастую используется в литературе без четкого определения, однако ее можно определить как простой трехсвязный граф. Граф называется трехсвязным, если удаление из него менее чем трех вершин (вместе с исходящими из них ребрами) никогда не приведет к несвязному графу. По общему правилу сеть отождествляют с ее вложением, обладающим наивысшей трансляционной симметрией (наименьшим числом занятых вершинами орбит группы трансляций), в евклидово пространство. Сеть называется p-периодической, если она может быть вложена в евклидово пространство некоторой размерности так, чтобы у этого вложения были трансляции по p независимым направлениям, и если даже в пространствах с еще большей размерностью не существует ее вложений с трансляциями более чем по p независимым направлениям.

Минимальной сетью называется сеть, у которой удаление хотя бы одной системы трансляционно эквивалентных ребер (решетки ребер) приведет к несвязному графу. Важные свойства минимальных сетей были выведены с помощью анализа их фактор-графа [11]. Под фактор-графом сети понимают ее отображение на конечный граф, при котором каждая решетка вершин отображается на одну вершину, а каждая решетка ребер – на одно ребро конечного графа. Любой конечный граф, в частности фактор-граф сети, характеризуется цикломатическим числом – наибольшим числом ребер, которое можно удалить из графа, чтобы он остался связным. В [10] доказана теорема о том, что конечный граф Q является фактор-графом p-периодической минимальной сети тогда и только тогда, когда: 1) Q – связный граф; 2) наименьшая степень вершин у Q равна трем; 3) цикломатическое число Q равно p. Как следствие этой теоремы в [10] были перечислены все 2-, 3- и 4-периодические минимальные сети (общим числом 3, 15 и 111 соответственно). Позже Эон [12] повторно доказал рассмотренную теорему другим способом. Используем эту теорему для исследования свойств графов Кэли кристаллографических групп, построенных на минимальном наборе генераторов. Назовем такие графы Кэли минимальными.

Теорема 1. Всякий минимальный граф Кэли кристаллографической группы $G_{p}^{p}$ (p > 1) гомеоморфен некоторой минимальной сети.

Доказательство. В минимальном графе Кэли кристаллографической группы все вершины имеют одинаковую степень. Эта степень должна быть больше двух, потому что в противном случае граф представляет собой либо цикл, либо бесконечную цепь, что противоречит условию p > 1. Фактор-граф исходного графа тем более имеет степень вершин больше двух. Кроме того, он является связным, поэтому, согласно рассмотренной выше теореме, этот фактор-граф отвечает некоторой q-периодической минимальной сети, где q – его цикломатическое число. Теорема доказана.

Теорема 2. Минимальная сеть, гомеоморфная минимальному графу Кэли кристаллографической группы $G_{p}^{p}$ (p > 1), как минимум p-периодична.

Доказательство. Предположим обратное: пусть существует минимальный граф Кэли группы $G_{p}^{p}$, гомеоморфный q-периодической минимальной сети, у которой q < p. Поскольку минимальная сеть имеет наивысшую трансляционную симметрию из возможных, то все минимальные графы Кэли имели бы трансляции менее чем по p независимым направлениям. Одновременно с этим любой граф Кэли (в том числе минимальный) гомеоморфен точкам общей орбиты группы $G_{p}^{p}$, соединенным между собой ребрами, каждое из которых отвечает некоторому генератору группы. Очевидно, что такой граф имеет p независимых трансляций, так как даже если их нет в исходном наборе генераторов, они оказываются порождены. Это противоречит сделанному предположению.

Теорема 3. Всякому графу Кэли кристаллографической группы $G_{p}^{p}$ (p > 1) гомеоморфна хотя бы одна p-периодическая минимальная сеть, планарная в (p + 1)-мерном евклидовом пространстве.

Доказательство. Если у всех q-периодических минимальных графов Кэли данной группы q > p, то все они в (p + 1)-мерном пространстве не планарны (не укладываются на p-мерной плоскости без пересечения ребер). Рассмотрим минимальный граф Кэли, вершины которого расположены в точках общей орбиты группы $G_{p}^{p}$. Удаление хотя бы одной решетки ребер из него всегда приведет к несвязному графу независимо от исходной конфигурации ребер. Следовательно, общая орбита данной группы более чем p-мерна, но при этом p-периодична, что противоречит классу группы $G_{p}^{p}$ (верхний индекс должен быть больше). Поэтому найдется по крайней мере один планарный q-периодический граф Кэли, но с учетом Теоремы 2 это возможно только при q = p.

Ниже рассмотрим минимальные графы Кэли плоских и федоровских групп и укажем среди них минимально периодические, и притом планарные, минимальные сети. Напомним, что в данном случае они должны иметь вершины одинаковой степени.

ПЛОСКИЕ ГРУППЫ

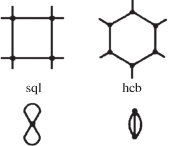
Из трех существующих 2-периодических минимальных сетей [10] все имеют вершины одинаковой степени, но планарны только две (рис. 1): квадратная сетка sql и “пчелиные соты” hcb (здесь и далее для обозначения сеток используются символы О’Киффа [13]).

Рис. 1.

Планарные минимальные 2-периодические сети и их фактор-графы.

Плоские группы $G_{p}^{p}$ имеют от двух до четырех генераторов в минимальном наборе [14]. Закрытым операциям симметрии второго порядка ($\overline 1 $, 2, m) в графе Кэли соответствуют ненаправленные ребра, а всем остальным операциям – направленные, однако эти направления не имеют значения при анализе минимальной сети с точностью до гомеоморфизма.

Если у группы четыре генератора в минимальном наборе (p2mm), ее минимальному графу Кэли может быть гомеоморфна только sql, поскольку в hcb вершины всего лишь 3-координированы. Группа с тремя генераторами теоретически может иметь графы, гомеоморфные как sql, так и hcb. Во втором случае все генераторы должны быть второго порядка, иначе степень вершин в графе будет недостаточно мала. Группа с двумя генераторами тоже может иметь графы, гомеоморфные обеим сетям. Если это сеть sql, то оба генератора обязаны быть более чем второго порядка, иначе степень вершин будет недостаточно велика.

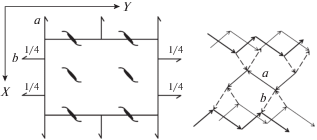
Приведем пример. Группа p2 имеет три генератора в минимальном наборе (рис. 2), однако они могут быть выбраны по-разному. Если взять три поворота второго порядка, попарно ближайшие друг другу вдоль соответствующих направлений, то группа задается ими так: {a, b, c| a² = b² = c² = = abcabc = e}, что приводит к графу Кэли, гомеоморфному hcb (рис. 2 справа вверху). Обе трансляции в этом случае порождены: T_X = ca; T_Y = cb. Если берется одна из трансляций и два ближайших друг к другу поворота по другой трансляции, например {a, T_Y, c| a² = c² = aT_YaT_Y = cT_YcT_Y = e}, то получается граф Кэли, гомеоморфный sql (рис. 2 слева внизу). Трансляция T_X порождена так же, как в предыдущем случае. Однако две трансляции, взятые одновременно вместе с одним из поворотов, например {T_X, T_Y, c| c² = cT_XcT_X = cT_YcT_Y = = T_XT_Y$T_{X}^{{ - 1}}T_{Y}^{{ - 1}}$ = e}, порождают уже не 2-периодический, а 4-периодический граф Кэли (рис. 2 справа внизу), так как цикломатическое число его фактор-графа равно четырем.

Рис. 2.

График группы p2 и ее минимальные графы Кэли на разных минимальных наборах генераторов.

ФЕДОРОВСКИЕ ГРУППЫ

Из 15 существующих 3-периодических минимальных сетей ранее были выделены семь, имеющие пересечения (collisions) в барицентрических координатах [15]. На практике это означает непланарность сети в 4-мерном евклидовом пространстве. Остальные восемь сетей планарны, однако одинаковая степень вершин только у пяти из них (рис. 3).

Рис. 3.

Планарные минимальные 3-периодические сети с вершинами одинаковой степени и их фактор-графы.

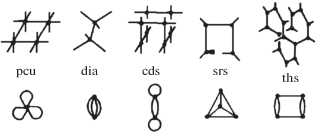
Среди пространственных групп есть единственная группа с шестью генераторами в минимальном наборе (Pmmm). Ее минимальному графу Кэли может быть гомеоморфна только pcu, поскольку другие сети имеют меньшую степень вершин. Группы, имеющие два генератора в минимальном наборе (таких групп 38, но с учетом энантиоморфных пар 34), не могут иметь степень вершин больше четырех, поэтому их минимальные графы Кэли могут быть гомеоморфны, наоборот, любой из перечисленных сетей, кроме pcu. На рис. 4 представлен фрагмент минимального графа Кэли группы P2₁2₁2₁, гомеоморфный dia. В качестве генераторов выбираются два взаимно перпендикулярных поворота со сдвигом вокруг ближайших друг к другу осей: {a, b| ba²b^–1a² = = ab²a^–1b² = e}.

Рис. 4.

График группы P2₁2₁2₁ и ее минимальный граф Кэли.

Единственными сетями с 3-координированными вершинами являются ths/srs. Минимальный граф Кэли группы, заданной двумя генераторами, может быть гомеоморфен ей лишь в том случае, если только один из генераторов представляет собой закрытую операцию симметрии второго порядка ($\overline 1 $, 2 или m). Однако при этом непросто сгенерировать все три некомпланарные трансляции, потому что другой генератор порождает только одну трансляцию. В сочетании с осью второго порядка 2 или плоскостью m он может породить сразу две дополнительные трансляции при соблюдении условий: его сдвиг не перпендикулярен элементу симметрии второго порядка; его поворот сдвинут относительно элемента симметрии второго порядка. Так что два генератора в минимальном наборе не исключают минимальный граф Кэли топологии ths/srs, но на них налагается много ограничений. Три генератора также не исключают эту сеть, но они все должны быть закрытыми операциями симметрии второго порядка, причем их сочетание должно порождать сдвиги сразу в трех некомпланарных направлениях. Группы более чем c тремя генераторами в минимальном наборе исключают сеть ths/srs.

Группы с пятью генераторами в минимальном наборе (таких групп 12) не сочетаются ни с какими минимальными сетями, кроме pcu, причем только один из генераторов обязан быть закрытой операцией симметрии второго порядка. Со всеми минимальными сетями (рис. 3) формально сочетаются лишь группы третьего ранга. Группы второго и четвертого ранга, как было показано выше, не сочетаются с одной из сетей (pcu и ths/srs соответственно). Группы пятого и шестого ранга сочетаются лишь с pcu. Распределение федоровских групп по рангам более подробно изложено в [16].

ЗАКЛЮЧЕНИЕ

Всякому графу Кэли кристаллографической группы $G_{p}^{p}$ (p > 1), построенному на минимальном наборе порождающих элементов, гомеоморфна хотя бы одна p-периодическая минимальная сеть. Такие сети перечислены в литературе для p = 2, 3 и 4. Указанный гомеоморфизм может быть полезен при интерпретации p-мерных кристаллических структур, в которых нет определенного местоположения химических связей между структурными единицами. К структурам такого типа относятся молекулярные органические кристаллы: трехмерный каркас в них обеспечивается наиболее сильными межмолекулярными контактами [17], которые даже у близких структур могут отвечать разным симметрическим операциям федоровской группы. Поскольку именно расположение молекул формирует группу (а не наоборот), а энергия их взаимодействия является переменной величиной, с физической точки зрения минимальный набор генераторов группы можно трактовать как нечеткий [14]. Однако такому нечеткому набору соответствует весьма ограниченный круг минимальных сетей межмолекулярных взаимодействий.