Кристаллография, 2019, T. 64, № 6, стр. 850-856

ВВЕДЕНИЕ

Одним из ярчайших открытий в кристаллографии второй половины XX в. является открытие квазикристаллов [1], т.е. класса соединений, обладающих точечным дифракционным спектром, но запрещенной для классических кристаллов симметрией пятого и более высоких порядков. Другими словами, квазикристаллы представляют собой структуры, в которых расположение атомов не является периодическим, но обладает дальним порядком. Естественным образом возникла задача построения математических моделей квазикристаллических структур, в качестве которых выступили квазипериодические точечные множества, разбиения и графы. Представляет интерес вопрос о поиске свойств, характеризующих наличие дальнего порядка в структуре, помимо точечного дифракционного спектра.

В качестве одного из таких свойств выступает форма роста в модели послойного роста, впервые введенной в качестве чисто геометрической модели процесса кристаллообразования [2]. Данная модель основана на последовательном присоединении координационных окружений к выбранной затравке. Форма послойного роста характеризует предельную форму n-го координационного окружения, получаемого в результате такого последовательного присоединения.

Известно [3–5], что предельными формами роста периодических структур являются выпуклые центрально-симметричные многогранники. Полное описание таких многогранников дано в [6]. С другой стороны, в [7] показано, что в случае некоторых графов с элементами случайности форма роста является комбинацией линейных и нелинейных (гипотетически эллиптических) участков.

Для ряда двумерных квазипериодических структур получены экспериментальные либо теоретические данные о многоугольной форме роста [8–15]. В частности, соответствующие результаты были получены для наиболее важных с точки зрения кристаллографии математических моделей, обладающих симметрией пятого порядка: разбиения Пенроуза [13, 15] и его графа вершин [14]. Однако общая задача о форме роста квазипериодических структур остается нерешенной.

В настоящее время известны квазикристаллы, обладающие симметрией восьмого порядка. В 1987 г. в пленках быстро охлажденных сплавов V–Ni–Si и Cr–Ni–Si были открыты двумерные квазикристаллы [16], характеризующиеся симметрией восьмого порядка. Удобным кристаллическим аппроксимантом октагональной квазикристаллической фазы оказалась кристаллическая структура β-Mn, имеющая кубическую симметрию (пр. гр. P4₁32). Так, в [17, 18] обнаружены двумерные квазикристаллические фазы Mn₄Si, сосуществующие с кристаллической фазой β-Mn, а в [19, 20] исследован процесс перехода из октагонального квазикристалла в кристалл со структурой типа β-Mn в сплаве Cr–Ni–Si. В [21] была предложена модель атомной квазикристаллической структуры октагональной фазы, особенностью которой является наличие локальных винтовых осей 8₃ и которая может быть получена в результате небольших локальных искажений кристаллической структуры β-Mn. Исследована возможность получения двумерных октагональных структур методом среза и проекции из четырехмерной кубической решетки [22], а также трехмерных октагональных квазикристаллических структур из шестимерного пространства [23]. Наконец, в [24] структура с локальной октагональной симметрией получена в результате малых геометрических искажений кристаллической структуры β-Mn, сохраняющих ее кристаллографическую симметрию.

Наиболее естественной математической моделью октагональных квазикристаллов, особенно двумерных, является квазипериодическое разбиение Амманна–Бинкера. Это разбиение можно также рассматривать как квазипериодический граф, если обращать внимание не на фигуры разбиения, а на вершины и соединяющие их ребра. Данный граф будем называть графом Амманна–Бинкера.

Целью настоящей работы было экспериментальное и теоретическое исследование послойного роста графа Амманна–Бинкера.

ГРАФ АММАННА–БИНКЕРА

Известно множество различных подходов к построению разбиения Амманна–Бинкера и соответствующего графа: локальные правила [25, 26], метод проекции и среза [27, 28], использование покрытий [29] и так далее.

В настоящей работе применим вариант метода среза и проекции, взятый из [30]. В рамках этого подхода множество вершин графа Амманна–Бинкера представляется в виде модельного множества ${{\Lambda }_{W}} = \{ {{\pi }_{1}}({\mathbf{x}}):{\mathbf{x}} \in L,\;{{\pi }_{2}}({\mathbf{x}}) \in W\} $, где L – целочисленная четырехмерная решетка ${{{\mathbf{Z}}}^{4}}$, точки которой имеют координаты (h, j, k, l), где h, j, k, l пробегают все возможные целые числа, π₁ и π₂ – проекции решетки L на комплексную плоскость C, задаваемые уравнениями ${{\pi }_{1}}((h,j,k,l))$ = $h + j\zeta + k{{\zeta }^{2}} + l{{\zeta }^{3}}$ и ${{\pi }_{2}}((h,j,k,l))$ = $h + j{{\zeta }^{3}} + k{{\zeta }^{6}} + l\zeta $ соответственно. Здесь $\zeta = \exp \left( {\frac{{\pi i}}{4}} \right)$ – комплексный корень восьмой степени из единицы. Образы четырехмерного пространства ${{{\mathbf{R}}}^{4}}$ под действием отображений π₁ и π₂ обычно называют физическим и фазовым пространством (пространством параметров) соответственно. Множество W, называемое окном, представляет собой правильный восьмиугольник со стороной, длина которой равна единице, с центром в начале координат, ориентированный таким образом, что одно из его ребер параллельно действительной оси. Для построения ребер графа Аммана–Бинкера используется следующее правило: две вершины соединены ребром тогда и только тогда, когда расстояние между ними равно единице. На рис. 1 приведены фрагмент графа Амманна–Бинкера и изображение соответствующего окна W.

Замечание 1. Данная конструкция множества вершин графа Амманна–Бинкера является частным случаем более общей конструкции циклотомических модельных множеств [31], связанных с корнями из единицы произвольной степени. Однако для большинства циклотомических модельных множеств неизвестно, образуют ли они разбиения. Кроме того, для некоторых циклотомических модельных множеств с симметрией порядка 10 или 12 разбиения известны, однако правила построения ребер существенно более сложные, чем в случае графа Аммана–Бинкера. Сама конструкция циклотомических модельных множеств является частным случаем более общей конструкции совокупных модельных множеств [31], для которой, впрочем, процесс поиска разбиений представляет еще более сложную задачу.

Замечание 2. В случае графа Амманна–Бинкера не существует точек четырехмерной решетки ${{{\mathbf{Z}}}^{4}}$, π₂-проекции которых лежат на границе окна W. Поэтому в отличие, например, от аналогичной конструкции построения вершин разбиения Пенроуза вопрос о том, какая часть границы принадлежит окну, не является актуальным.

МОДЕЛЬ ПОСЛОЙНОГО РОСТА

В основе модели послойного роста лежит изучение последовательности координационных сфер $e{{q}_{n}}(x)$ произвольной вершины $x$ некоторого графа. Данную последовательность можно определить индуктивно: координационная сфера $e{{q}_{0}}(x)$ представляет собой саму вершину x; координационная сфера $e{{q}_{{n + 1}}}(x)$ определяется как множество вершин графа, соседних с вершинами из координационной сферы $e{{q}_{n}}(x)$ и не входящих в координационные сферы $e{{q}_{k}}(x)$ с $0 \leqslant k \leqslant n$.

Координационную сферу $e{{q}_{n}}(x)$ можно также определить с помощью равенства $e{{q}_{n}}(x) = \{ y \in $ $ \in \;G:d(x,y) = n\} $. Здесь d(x, y) – естественная метрика на графе G, определяемая как число ребер в кратчайшей цепи графа, соединяющей вершины x и y.

Если существует предел

то он называется формой послойного роста графа. Известно, что если форма роста существует, то она не зависит от выбора начальной вершины x.

ФОРМА РОСТА ГРАФА АММАННА–БИНКЕРА

С точки зрения компьютерного эксперимента удобнее строить не координационные сферы $e{{q}_{n}}(x)$, а координационные окружения $E{{q}_{n}}(x)$, определяемые равенством

Другими словами,

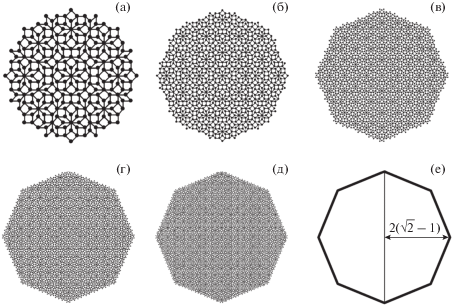
На основе приведенного выше описания графа Амманна–Бинкера разработана компьютерная программа для построения его координационных окружений. На рис. 2 представлены нормированные координационные окружения $\frac{{E{{q}_{n}}(0)}}{n}$ графа вершин разбиения Амманна–Бинкера для n = 10, 20, 30, 40, 50 (рис. 2а–2д) и форма послойного роста γ этого графа (рис. 2е). Проведенные компьютерные эксперименты позволяют предположить, что предельная форма роста графа Амманна–Бинкера представляет собой правильный восьмиугольник.

Дальнейшая цель состоит в доказательстве следующей теоремы.

Теорема 1. Форма послойного роста γ графа Амманна–Бинкера существует и представляет собой правильный восьмиугольник, вершины которого имеют координаты $R\exp \left( {\frac{{k\pi i}}{4}} \right)$, $0 \leqslant k \leqslant 7$, $R = 2(\sqrt 2 - 1)$.

Доказано, что форма роста, если она существует, не зависит от начальной затравки послойного роста [4], поэтому данную теорему достаточно доказать для случая x = 0. Кроме того, из общей теории послойного роста вытекает, что форма послойного роста сохраняет поворотную симметрию графа. Поэтому рассматриваемую теорему достаточно доказать для сектора, ограниченного действительной осью и лучом в направлении $\exp \left( {\frac{{\pi i}}{4}} \right)$. Доказательство теорем о форме послойного роста обычно разбивается на две независимые части: доказательство верхней и нижней границы.

НИЖНЯЯ ГРАНИЦА ПОСЛОЙНОГО РОСТА

Известно, что для доказательства нижней границы достаточно построить цепи длиной n, ведущие в точки, расположенные в окрестности размера o(n) множества nγ. Запись o(n) означает, что отношение размера окрестности к размеру множества nγ стремится к нулю с ростом n.

В качестве первого этапа необходимо построить цепи, ведущие в вершины восьмиугольника nγ. В силу сказанного выше достаточно построить цепь ${{\Gamma }_{0}}$, ведущую в вершину графа, ближайшую к точке Rn, расположенной на действительной оси.

Для построения данной цепи потребуется понятие кластера, введенное в [32]. Кластер Cl задается конечным множеством векторов ${{V}^{ + }}$. Будем говорить, что вершина x графа Амманна–Бинкера является отмеченной точкой кластера типа Cl, если для любого вектора ${v} \in {{V}^{ + }}$ точка $x + {v}$ является вершиной графа Амманна–Бинкера. Обычно также предполагается, что $0 \in {{V}^{ + }}$.

Определим отображение из физического пространства в фазовое по правилу $x{\kern 1pt} * = {{\pi }_{2}}(\pi _{1}^{{ - 1}}(x))$. Введенную величину $x{\text{*}}$ будем называть параметром вершины x. В [32] была доказана формула, позволяющая найти множество параметров отмеченных точек всех кластеров, соответствующих множеству векторов ${{V}^{ + }}$. Данная формула имеет вид

Цепь Γ₀, фрагмент которой представлен на рис. 3а, состоит из кластеров двух видов, соответствующие множества параметров которых изображены на рис. 3б.

Рассматриваемые кластеры определяют цепи графа, которые будем обозначать Γ_0,1 и Γ_0,2 соответственно. Длина цепи Γ_0,1 равна единице, ей соответствует сдвиг вдоль действительной оси на вектор длиной ${{s}_{1}} = 1$. Длина цепи Γ_0,2 равна двум, и ей соответствует сдвиг вдоль действительной оси на вектор длиной ${{s}_{1}} = \zeta + {{\zeta }^{7}} = \sqrt 2 $. В фазовом пространстве $s_{1}^{*} = 1$ и $s_{2}^{*} = - \sqrt 2 $. Отсюда вытекает, что если начать движение в точке ноль, то конец цепи Γ_0,k (k = 1, 2) будет началом другой цепи такого же вида. Таким образом, построение цепи ${{\Gamma }_{0}}$ корректно определено.

Средняя скорость движения вдоль построенной цепи $\bar {R} = \bar {s}{\text{/}}\bar {n}$ будет определяться как отношение среднего сдвига $\bar {s} = \nu ({{\Gamma }_{{0,1}}}){{s}_{1}} + \nu ({{\Gamma }_{{0,2}}}){{s}_{2}}$ к средней длине цепей Γ_0,k$\bar {n} = \nu ({{\Gamma }_{{0,1}}})\left| {{{\Gamma }_{{0,1}}}} \right| + \nu ({{\Gamma }_{{0,2}}})\left| {{{\Gamma }_{{0,2}}}} \right|$, где $\nu ({{\Gamma }_{{0,k}}})$ – частота появления кластера Γ_0,k в строящейся цепи, а |Γ_0,k| – длина цепи Γ_0,k.

Движение вдоль цепи Γ₀ на множестве параметров описывается соотношением

Можно показать, что данное отображение изоморфно отображению $t \to \{ t + \sqrt 2 \} $ (фигурные скобки обозначают дробную часть числа). В силу иррациональности $\sqrt 2 $ орбита этого отображения равномерно распределена на отрезке [0;1]. Отсюда получаем, что $\nu ({{\Gamma }_{{0,k}}}) = \frac{{\left| {{{I}_{k}}} \right|}}{{\left| {{{I}_{1}}} \right| + \left| {{{I}_{2}}} \right|}}$. Дальнейшее вычисление дает $\bar {R} = 2(\sqrt 2 - 1)$, т.е. цепь Γ₀ действительно дает требуемую скорость роста.

Отметим, что из рис. 3б вытекает, что цепи типа Γ₀ можно строить не только из начала координат, но и из множества вершин, которое определяется условием $\left| {\operatorname{Im} x*} \right| < \sin \frac{\pi }{8}$. В частности, существует постоянная C такая, что на расстоянии не более C от произвольной вершины графа найдется вершина графа, из которой можно построить цепь типа Γ₀.

В случае произвольной вершины $x$ графа Амманна–Бинкера цепь из нуля в $x$ ищется в виде: $0 \to {{\Gamma }_{0}} \to z \to z{\text{'}} \to {{\Gamma }_{1}} \to x{\text{'}} \to x$. Цепь Γ₁ строится аналогично Γ₀, но с поворотом на угол $\left( {\frac{\pi }{4}} \right)$, а длины цепей $z \to z{\text{'}}$ и $x{\text{'}} \to x$ не превосходят C. Непосредственное вычисление показывает, что данные цепи обеспечивают требуемую скорость роста, что и доказывает нижнюю границу.

Замечание 3. Используя более тонкие теоретико-числовые результаты, позволяющие оценивать отклонение числа точек вида $\{ m\sqrt 2 \} $, $1 \leqslant m \leqslant n$, попавших в заданный интервал, от ожидаемого значения, можно показать, что полосу шириной o(n) в конструкции нижней границы можно заменить полосой, ширина которой ограничена константой, не зависящей от n.

ВЕРХНЯЯ ГРАНИЦА

Общая идея доказательства верхних оценок формы роста квазипериодических графов G, множество вершин которых является модельным множеством, основана на их вложении в периодические графы более высокой размерности.

Пусть Ĝ – периодический граф, удовлетворяющий двум условиям: если x – вершина графа G, то $\pi _{1}^{{ - 1}}(x)$ – вершина графа Ĝ; если x и y – две вершины графа G, соединенные ребром, то вершины $\pi _{1}^{{ - 1}}(x)$ и $\pi _{1}^{{ - 1}}(y)$ графа Ĝ также соединены ребром.

Поскольку граф Ĝ периодический, для него существует предельная форма роста, представляющая собой эффективно вычисляемый выпуклый центрально-симметричный многогранник $\widehat {Pol}$. Справедлива следующая теорема [14].

Теорема 2. Пусть гиперплоскость P задается уравнением π₂(х) = 0. Тогда для формы послойного роста графа G имеет место включение

Замечание 4. Формально, в [14] аналог теоремы 2 сформулирован и доказан в частном случае графа вершин разбиения Пенроуза. Однако внимательный анализ показывает, что рассуждение из [14] без каких-либо изменений переносится на случай произвольного графа, множество вершин которого является модельным множеством.

В случае графа Амманна–Бинкера в качестве графа Ĝ рассматривается четырехмерный периодический граф, множество вершин которого есть четырехмерная целочисленная решетка ${{{\mathbf{Z}}}^{4}}$, а вершины x и y соединены ребром тогда и только тогда, когда ${\mathbf{x}} - {\mathbf{y}} \in \{ \pm {{{\mathbf{e}}}_{k}}\} $, $1 \leqslant k \leqslant 4$, где у вектора ${{{\mathbf{e}}}_{k}}$ k-я координата равна единице, а остальные три координаты равны нулю.

Многогранник роста $\widehat {Pol}$ представляет собой правильный четырехмерный многогранник, “натянутый” на векторы $\{ \pm {{{\mathbf{e}}}_{k}}\} $. Данный многогранник характеризуется символом Шлефли {3, 3, 4} и имеет восемь вершин, 24 ребра, 32 двумерные грани (правильные треугольники) и 16 трехмерных граней, представляющих собой правильные тетраэдры. Непосредственное применение теоремы 2 дает верхнюю границу, требуемую в теореме 1. Интересно также отметить, что многогранник $\widehat {Pol}$ определяется системой корней, связанной с диаграммой Коксетера–Дынкина ${{B}_{4}}$. Проекция решетки корней, соответствующей данной диаграмме, на плоскость Коксетера также может быть использована при определении множества вершин разбиения Амманна–Бинкера [30]. На рис. 4 приведена π₁-проекция многогранника $\widehat {Pol}$. Его сечение $P \cap \widehat {Pol}$, совпадающее с формой роста γ(G), изображено пунктирной линией.

Замечание 5. Используя доказанный в [3] факт, что для произвольного периодического графа n-я координационная сфера лежит в полосе, ширина которой ограничена не зависящей от n константой, вокруг многогранника роста, увеличенного в n раз, можно показать, что в графе G точки из $e{{q}_{n}}(0)$ не могут заходить за пределы множества $n \times {{\pi }_{1}}(P \cap \widehat {Pol})$ на расстояние больше некоторой константы, не зависящей от n.

Объединяя результаты замечаний 3 и 5, теорему 1 можно переписать в более “сильной” форме.

Теорема 3. Существует постоянная C, не зависящая от n такая, что все вершины координационной сферы $e{{q}_{n}}(0)$ графа Амманна–Бинкера лежат в C-окрестности многоугольника nγ.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Граф Амманна–Бинкера – еще один пример графа, множество вершин которого является модельным множеством, для которого получены теоретические данные о многоугольной форме роста. Другими примерами являются граф вершин разбиения Пенроуза [14] и двойственный ему граф [13, 15], а также граф, двойственный разбиению Рози [9, 10] (в последнем случае получены лишь частичные теоретические результаты). Рассмотрение данных примеров позволяет выдвинуть следующую гипотезу.

Гипотеза 1. Пусть G – граф, множество вершин которого есть модельное множество с окном W, причем степени всех вершин графа ограничены константой, не зависящей от выбора вершины. Пусть также существует разбиение окна $W = \bigcup {{{W}_{k}}} $ на конечное число непересекающихся множеств W_k, причем если параметры двух вершин x и y графа G принадлежат одному множеству W_k, то первые координационные окружения этих вершин трансляционно эквивалентны, т.е. $e{{q}_{1}}(y) = e{{q}_{1}}(x) + y - x$. Тогда граф G имеет предельную форму роста в виде выпуклого центрально симметричного многогранника.

В настоящее время мы очень далеки от доказательства данной гипотезы. Существующие доказательства нижней границы, в первую очередь, требуют построения цепей, ведущих в вершины многогранника роста. Такое построение в каждом конкретном случае является чисто технической задачей, требующей, однако, априорного знания вершин формы роста, получаемых из эксперимента. Нет никакой хорошей гипотезы, позволяющей без проведения эксперимента получить координаты вершин в общем случае.

Сама цепь, ведущая в вершину, имеет достаточно простую структуру. Она состоит из участков конечного числа типов, а движение вдоль нее кодируется в пространстве параметров перекладыванием отрезков. Во всех известных примерах число перекладываемых отрезков не превосходит трех. Неясно, насколько этот факт является общим. Во всех известных примерах имелось целое семейство параллельных друг другу цепей, возможно, различной структуры, но дающих одинаковую скорость движения вдоль них. Простого объяснения данного факта, а также понимания его общности в настоящее время нет. Кроме того, хотелось бы иметь простой способ нахождения структуры цепи, зная лишь ее направление. По всей видимости, ответы на эти вопросы требуют детального изучения одномерных сечений модельных множеств.

В случае верхней границы достаточно легко строить графы, удовлетворяющие условиям теоремы 2. Однако неясно, всегда ли существует граф Ĝ, для которого выполняется равенство $\gamma (G) = {{\pi }_{1}}(P \cap \widehat {Pol})$. В частности, такой граф неизвестен для задачи о послойном росте графа, двойственного разбиению Рози.

Структура модельного множества зависит от двух факторов: проекций π₁ и π₂, а также формы и размеров окна W. Однако роль каждого из этих факторов остается неясной. Представляет интерес экспериментальное исследование этой зависимости. Простейший вопрос в данной области: как будет изменяться форма роста при растяжении или сжатии окна?

Также представляет интерес вопрос о форме роста квазипериодических структур, которые не формируются методом среза и проекции. Наиболее интересным объектом исследования здесь представляются самоподобные разбиения, получаемые при помощи преобразований инфляции и дефляции. В частности, представляет интерес задача о форме роста разбиения, известного как “pinwheel tiling” [33]. Это самоподобное разбиение интересно тем, что в нем каждая фигура имеет бесконечное число различных ориентаций.

ВЫВОДЫ

Проведенное исследование позволило получить следующие результаты. Экспериментально обнаружено и теоретически доказано, что граф Амманна–Бинкера имеет предельную форму роста в виде правильного восьмиугольника с вершинами $R\exp \left( {\frac{{k\pi i}}{4}} \right)$, $0 \leqslant k \leqslant 7$, $R = 2(\sqrt 2 - 1)$. Показано, что n-я координационная сфера графа Амманна–Бинкера лежит в C-окрестности данного многоугольника, растянутого в n раз, причем ширина C этой окрестности не зависит от n. Cформулирована общая гипотеза о росте графов, совокупность вершин которых является модельным множеством, и сформулирован ряд нерешенных задач, связанных с этой гипотезой.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (гранты № 17-02-00835 и 17-42-330787).