1. На главную
  2. Электронные версии
  3. Кристаллография
  4. T. 67, № 1, 2022

Кристаллография, 2022, T. 67, № 1, стр. 90-102

Изучение спин-волновой динамики аморфных ферромагнетиков и гелимагнетиков со взаимодействием Дзялошинского–Мория

С. В. Григорьев 1, 2, *, Е. В. Алтынбаев 1, 3, К. А. Пшеничный 1, 2, 3

1 Петербургский институт ядерной физики НИЦ “Курчатовский институт”
Гатчина, Санкт-Петербург, Россия

2 Санкт-Петербургский государственный университет
Санкт-Петербург, Россия

3 Институт физики высоких давлений им. Л.Ф. Верещагина РАН
Троицк, Москва, Россия

* E-mail: grigoryev_sv@pnpi.nrcki.ru

Поступила в редакцию 17.06.2020
После доработки 17.06.2020
Принята к публикации 29.07.2020

Полный текст (PDF)

Аннотация

Метод “косой” динамики, разработанный для изучения спиновых волн в ферромагнетиках, предложен и реализован в Ленинградском институте ядерной физики в середине 1980-х годов в Гатчине. Метод основан на анализе лево-правой асимметрии в магнитном рассеянии поляризованных нейтронов, возникающей в случае, когда направление намагниченности в образце наклонено по отношению к волновому вектору падающего пучка. Рассеяние нейтронов на спиновых волнах сконцентрировано внутри конуса, ограниченного критическим углом – углом отсечки, который равен отношению массы магнона к массе нейтрона. Измеряя это отношение, находят массу магнона и константу жесткости спиновых волн в ферромагнитном материале. Эксперименты по измерению жесткости спиновых волн в гелимагнетиках со взаимодействием Дзялошинского–Мория методом малоуглового рассеяния поляризованных нейтронов показали наличие квадратичного закона дисперсии, смещенного в направлении поля на величину волнового вектора спирали: ${{{{\epsilon}}}_{q}} = A{{({\mathbf{q}} - {\mathbf{k}})}^{2}} - g{{{{\mu }}}_{{\text{B}}}}(H - {{H}_{{C2}}})$. Измерена величина жесткости спиновых волн в зависимости от температуры для бинарных и квазибинарных соединений: MnSi, ${\text{M}}{{{\text{n}}}_{{1--x}}}$FexSi, FeGe, ${\text{M}}{{{\text{n}}}_{{1--x}}}$FexGe, ${\text{F}}{{{\text{e}}}_{{1--x}}}$CoxSi, Cu2OSeO3.

ОГЛАВЛЕНИЕ

Введение

1. Малоугловое рассеяние поляризованных нейтронов на спиновых волнах в ферромагнетиках

1.1. Кинематика рассеяния: как измерить массу магнона

1.2. Поляризованные нейтроны и киральность спиновых волн

1.3. Методика измерения и обработки полученных данных

1.4. Жесткость спиновых волн в ферромагнитных аморфных материалах и поликристаллических сплавах

2. Малоугловое рассеяние нейтронов на спиновых волнах в геликоидальных магнетиках со взаимодействием Дзялошинского–Мория

2.1. Влияние ДМ-взаимодействия на кинематику рассеяния нейтронов

2.2. Методика измерения и обработки полученных данных

2.3. Жесткость спиновых волн в гелимагнетиках и проверка теории Бака–Йенсена

Заключение

ВВЕДЕНИЕ

Измерение фононных и магнонных спектров с использованием трехосных и времяпролетных спектрометров нейтронов стало рутинной работой нейтронных центров. За последнее время появилось несколько книг, посвященных методам нейтронной спектроскопии и исследованиям возбуждений в кристаллах с использованием этих методов [1–4].

Менее известен способ измерения основной константы спиновой динамики ферромагнетиков, жесткости спиновых волн, предложенный и реализованный в Ленинградском институте ядерной физики в середине 1980-х годов [5–7]. Измерения константы спин-волновой жесткости A (коэффициента в дисперсионном соотношении для ферромагнетиков $E = A{{q}^{2}}$) проводились методом малоуглового рассеяния поляризованных нейтронов (МУРН). Метод основан на анализе лево-правой асимметрии в магнитном рассеянии поляризованных нейтронов, возникающей в случае, когда направление намагниченности в образце наклонено по отношению к волновому вектору падающего пучка.

Известно, что в случае квадратичной дисперсии спин-волновое рассеяние нейтронов сконцентрировано в узком конусе с максимальным углом ${{\theta }_{C}}$, который зависит от магнитного поля и однозначно связан с жесткостью спиновых волн $A$ [8, 9].

Поскольку в экспериментах методом МУРН использовалась наклонная (по отношению к оси падающего пучка) геометрия магнитного поля, то он был назван методом наклонной геометрии. Метод успешно применялся для исследования спиновых волн в аморфных ферромагнетиках [6, 7] и поликристаллических инварных сплавах: железо-никелевом Fe65Ni35 [10, 11] и железо-платиновом Fe75Pt25 [12], а также в образце монокристалла Ni–Mn–Ga [12, 13].

Интересное развитие эта методика недавно получила при измерении жескости спиновых волн в геликоидальных магнетиках со взаимодействием Дзялошинского–Мория (ДМ). Как показано в [14], даже в полностью поляризованном состоянии присутствие ДМ-взаимодействия приводит к киральности спиновых волн и асимметричному сдвигу кривой дисперсии в направлении магнитного поля на величину, равную волновому вектору спирали: ${{{{\epsilon}}}_{k}} = A{{({\mathbf{k}} - {{{\mathbf{k}}}_{S}})}^{2}}$ – $g{{{{\mu }}}_{{\text{B}}}}(H - {{H}_{{C2}}})$, где ${{{\mathbf{k}}}_{S}}$ – волновой вектор спиновой спирали, а ${{H}_{{C2}}}$ – критическое поле перехода из геликоидального состояния в ферромагнитное, поляризованное магнитным полем.

В таких системах магноны, распространяющиеся параллельно и антипараллельно внешнему магнитному полю, имеют различный характер. Это явление названо магнитохиральной невзаимностью распространяющихся магнонов, причем знак их невзаимности зависит от киральности магнитной системы [15, 16]. Именно благодаря высокому импульсному разрешению метода МУРН удалось экспериментально показать необычный вид дисперсионного соотношения и измерить величину и температурную зависимость жесткости спиновых волн для целого ряда соединений: MnSi [14], Mnx${\text{F}}{{{\text{e}}}_{{1--x}}}$Si [17], Fex${\text{C}}{{{\text{o}}}_{{1--x}}}$Si [18, 19], Cu2OSeO3 [20].

В настоящей работе кратко изложим теоретические основы метода и представим обзор экспериментальных результатов, полученных с его помощью.

1. МАЛОУГЛОВОЕ РАССЕЯНИЕ ПОЛЯРИЗОВАННЫХ НЕЙТРОНОВ НА СПИНОВЫХ ВОЛНАХ В ФЕРРОМАГНЕТИКАХ

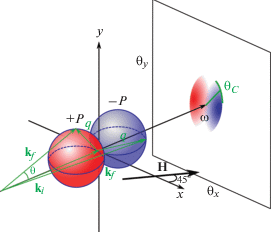
Рассмотрим задачу неупругого рассеяния нейтрона с импульсом ${{{\mathbf{k}}}_{i}}$, рассеянного на спиновой волне, подчиняющейся закону дисперсии ${{E}_{q}}$. После рассеяния нейтрон изменит как направление, так и величину импульса ${{{\mathbf{k}}}_{f}}$. Однако характеристики нейтрона после рассеяния не могут быть произвольными, они жестко связаны с дисперсией спиновых волн исследуемой системы, поскольку совокупные энергия и импульс двух сталкивающихся частиц (нейтрона и магнона) должны сохраняться. В пределе МУР, когда модуль вектора рассеяния равен $\left| {\mathbf{q}} \right| = \left| {{{{\mathbf{k}}}_{i}} - {{{\mathbf{k}}}_{f}}} \right| \ll \left| {{{{\mathbf{k}}}_{i}}} \right|,\left| {{{{\mathbf{k}}}_{f}}} \right|$, компоненты переданного импульса нейтрона можно представить в виде [5, 11]:

(1)
$\left\{ \begin{gathered} {{q}_{x}} = {{k}_{i}}{{\theta }_{x}}, \hfill \\ {{q}_{y}} = {{k}_{i}}{{\theta }_{y}}, \hfill \\ {{q}_{z}} = {{k}_{i}}\hbar \omega {\text{/}}2{{E}_{n}}, \hfill \\ \end{gathered} \right.$
где ${{E}_{n}}$ – энергия падающего нейтрона. В этой системе уравнений x- и y-компоненты вектора q описывают упругое рассеяние, а z-компонента – неупругое.

В случае рассеяния нейтронов на спиновых волнах в ферромагнетике дисперсионное соотношение имеет вид

(2)
${{E}_{q}} = A{{q}^{2}},$
где A – жесткость спиновых волн ферромагнетика, а q и Eq – импульс и энергия спиновой волны. Для простоты пренебрежем пока щелью, наводимой магнитным полем. Учитывая закон сохранения импульса и подставляя разложенные компоненты вектора переданного импульса q из выражения (1) в дисперсионное соотношение (2), получим
(3)
${{E}_{q}} = Ak_{i}^{2}\left\{ {{{\theta }^{2}} + {{{\left( {\frac{{\hbar \omega }}{{2{{E}_{n}}}}} \right)}}^{2}}} \right\},$
где ${{\theta }^{2}} = \theta _{x}^{2} + \theta _{y}^{2}$. Принимая во внимание закон сохранения энергии для поглощения и возбуждения магнонами нейтронов $\omega - {{E}_{q}} = 0$ и $\omega + {{E}_{q}} = 0$ и делая замену $\tilde {\omega } = \hbar \omega {\text{/}}2{{E}_{n}}$, из (3) получим уравнения:
(4)
$\begin{gathered} Ak_{i}^{2}{{{\tilde {\omega }}}^{2}} - 2{{E}_{n}}\tilde {\omega } + Ak_{i}^{2}\theta _{0}^{2} = 0, \hfill \\ Ak_{i}^{2}{{{\tilde {\omega }}}^{2}} + 2{{E}_{n}}\tilde {\omega } + Ak_{i}^{2}\theta _{0}^{2} = 0, \hfill \\ \end{gathered} $
корни которых можно представить в виде:

${{\tilde {\omega }}_{1}} = - \frac{{{{E}_{n}}}}{{Ak_{i}^{2}}} - \sqrt {\frac{{E_{n}^{2}}}{{{{A}^{2}}k_{i}^{4}}} - {{\theta }^{2}}} ,$
(5)
$\begin{gathered} {{{\tilde {\omega }}}_{2}} = - \frac{{{{E}_{n}}}}{{Ak_{i}^{2}}} + \sqrt {\frac{{E_{n}^{2}}}{{{{A}^{2}}k_{i}^{4}}} - {{\theta }^{2}}} , \\ {{{\tilde {\omega }}}_{3}} = \frac{{{{E}_{n}}}}{{Ak_{i}^{2}}} - \sqrt {\frac{{E_{n}^{2}}}{{{{A}^{2}}k_{i}^{4}}} - {{\theta }^{2}}} , \\ \end{gathered} $
${{\tilde {\omega }}_{4}} = \frac{{{{E}_{n}}}}{{Ak_{i}^{2}}} + \sqrt {\frac{{E_{n}^{2}}}{{{{A}^{2}}k_{i}^{4}}} - {{\theta }^{2}}} .$

1.1. Кинематика рассеяния: как измерить массу магнона

Уравнения (4) можно представить в виде канонических уравнений двух сфер:

(6)
$\begin{gathered} {{(\tilde {\omega } - \theta {}_{0})}^{2}} + {{\theta }^{2}} = \theta _{0}^{2}, \hfill \\ {{(\tilde {\omega } + \theta {}_{0})}^{2}} + {{\theta }^{2}} = \theta _{0}^{2}, \hfill \\ \end{gathered} $
где ${{\theta }_{0}} = \frac{{{{m}_{m}}}}{{{{m}_{n}}}}$, ${{m}_{m}} = \frac{{{{\hbar }^{2}}}}{{2A}}$ – эффективная масса магнона, а ${{m}_{n}}$ – масса нейтрона. Уравнения (6) удобно представить графически (рис. 1) в пространстве переданных импульсов и энергий нейтрона $({{k}_{i}}\theta ,\tilde {\omega })$ в виде двух сфер с радиусом ${{\theta }_{0}}$, сдвинутых на величину ${{\theta }_{0}}$ вдоль оси $\tilde {\omega }$ в положительном и отрицательном направлениях [9].

Рис. 1.

Кинематическая схема рассеяния поляризованных нейтронов на спиновых волнах в ферромагнетике.

1.2. Поляризованные нейтроны и киральность спиновых волн

Поскольку метод МУРН является интегральным по энергии $\omega $, то для получения поляризационно-зависящей части интенсивности рассеяния необходимо взять интеграл следующего вида [5, 11]:

(7)
$\Delta I = 2{{k}_{{\text{B}}}}T\int {\frac{{({\mathbf{\hat {q}\hat {m}}})}}{{{\omega }}}} [{{\delta }}({{\omega }} - {{E}_{q}}) + {{\delta }}({{\omega }} + {{E}_{q}})]{\kern 1pt} d{{\omega ,}}$
где $({\mathbf{\hat {q}\hat {m}}})$ – геометрический фактор рассеяния нейтронов, а ${\mathbf{\hat {m}}}$ – единичный вектор, направленный вдоль намагниченности образца. Далее согласно [11] для поляризации нейтронов, направленной под углом $\alpha $ к падающему пучку нейтронов, можно получить аналитическое выражение для зависящего от поляризации сечения рассеяния нейтронов:
(8)
$\Delta I = \sin (2{{\alpha }})\frac{{2{{k}_{{\text{B}}}}T}}{{{{E}_{n}}}}\frac{{{{{{\theta }}}_{x}}\left| {{{{{\theta }}}_{0}}} \right|}}{{{{\theta }}_{0}^{2}\sqrt {{{\theta }}_{0}^{2} - {{{{\theta }}}^{2}}} }}.$
Без потери общности рассмотрения можно учесть влияние магнитного поля на дисперсию спиновых волн: ${{E}_{q}} = A{{q}^{2}} + g{{{{\mu }}}_{{\text{B}}}}H$. В этом случае критический угол зависит от магнитного поля: ${{\theta }}_{C}^{2} = {{\theta }}_{0}^{2} - {{{{\theta }}}_{0}}\frac{{g{{{{\mu }}}_{{\text{B}}}}H}}{{{{E}_{n}}}}$.

Изображенная на рис. 1 кинематическая схема рассеяния поясняет суть происходящего. При интегрировании по энергии сферы следует спроецировать на плоскость $({{\theta }_{x}},{{\theta }_{y}})$ с учетом геометрического фактора $({\mathbf{\hat {q}\hat {m}}})$ (7). На рис. 2 показаны результирующие двумерные карты поляризационно-зависящей части рассеяния нейтронов, полученные из выражения (8) для трех значений приложенного магнитного поля: B = 10, 50 и 100 мТл, где $B = {{\mu }_{0}}H$, а на рис. 3 представлены зависимости интенсивности (8) от угла рассеяния ${{\theta }_{x}}$ для магнитных полей B = 10, 250 и 500 мТл.

Рис. 2.

Двумерная карта поляризационно-зависящей части рассеяния поляризованных нейтронов с длиной волны ${{\lambda }} = 5.1$ Å на магнонах в ферромагнетике при А = 100 мэВ Å2 в магнитном поле B, равном 10 (а), 50 (б) и 100 мТл (в).

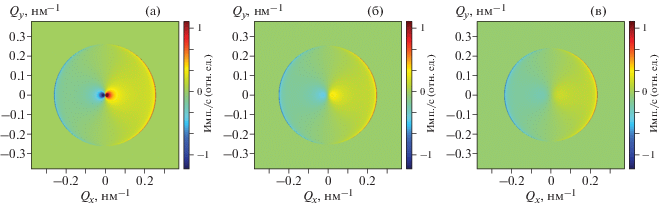
Рис. 3.

Зависимость разности интенсивности рассеяния поляризованных нейтронов на магнонах в ферромагнетике от угла рассеяния при различных приложенных магнитных полях: ${{\theta }_{C}} = 20$ мрад при 10 мТл, ${{\theta }_{C}} = 15$ мрад при 250 мТл и ${{{{\theta }}}_{C}} = 6.8$ мрад при 500 мТл.

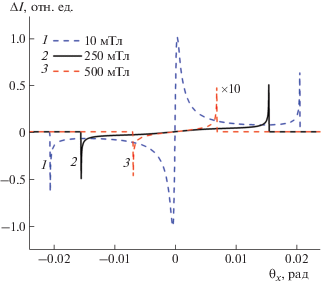
Из рис. 2 видно, что картина рассеяния представляет собой круг с четко очерченной границей при $\theta = {{\theta }_{C}}$, а из рис. 3 – что угол отсечки ${{\theta }_{C}}$ плавно уменьшается с ростом поля так, что его квадрат $\theta _{C}^{2}$ линейно зависит от поля. Рассеяние исчезает при ${{\theta }_{C}} = 0$, т.е. при напряженности поля $g{{{{\mu }}}_{{\text{B}}}}H = {{E}_{n}}{{{{\theta }}}_{0}}$. В малых полях наблюдается особенность в области малых углов $\theta $. Эта особенность подавляется с ростом поля как $1{\text{/}}{{{{\theta }}}^{2}} + g{{{{\mu }}}_{{\text{B}}}}\frac{H}{{{{E}_{n}}}}$. Отметим, что влияние магнитного поля на картину рассеяния сводится к быстрому (как $1{\text{/}}{{H}^{2}}$) спаданию интенсивности рассеяния при малых углах рассеяния $\theta $, в то время как угол отсечки ${{\theta }_{C}}$ медленно уменьшается с ростом поля пропорционально $\sqrt {{{{{\theta }}}_{{\text{0}}}} - g{{{{\mu }}}_{{\text{B}}}}H{\text{/}}{{E}_{n}}} $.

1.3. Методика измерения и обработки полученных данных

Методика измерения спин-волновой жесткости ферромагнетиков заключается в использовании поляризационно-зависимой части (киральный канал) рассеяния поляризованных нейтронов для выделения исключительно рассеяния на спиновых волнах в ферромагнетике, вычитая при этом фон как от ядерного рассеяния, так и от падающего нейтронного пучка. Для измерения необходимо подготовить образец таким образом, чтобы количества измеряемого материала хватало для получения достаточной интенсивности для набора статистически разрешимого сигнала [22]. Интенсивность $I({{{\mathbf{P}}}_{0}},{\mathbf{Q}})$ измеряется в зависимости от угла рассеяния с поляризацией падающих нейтронов по или против направления поля при разных значениях поля и разных температурах. Таким образом получают набор “карт интенсивности”, из которых методом азимутального усреднения левой и правой частей карты и последующей аппроксимации ступенчатой функцией находят значение угла отсечки ${{\theta }_{C}}$. Имея набор зависимостей ${{\theta }_{C}}(H,T)$, можно получить значение спин-волновой жесткости для каждой измеренной температуры.

1.4. Жесткость спиновых волн в ферромагнитных аморфных материалах и поликристаллических сплавах

При помощи метода, основанного на эффекте асимметрии МУРН, в 1986 г. впервые была измерена спин-волновая жесткость в аморфных ферромагнитных материалах Fe50Ni22Cr10P18 и Fe48Ni34P18 в критической области вблизи температуры Кюри [5]. В эксперименте использовались образцы размером 1 × 10 × 50 мм3, приготовленные из отрезков ленты толщиной 30 мкм. Измерения проводились на пучке поляризованных нейтронов “Вектор” на реакторе ВВР-М с длиной волны λ = = 8.8 Å. В результате была получена температурная зависимость спин-волновой жесткости, из которой был экспериментально определен критический индекс спин-волновой жесткости x. Для соединения Fe50Ni22Cr10P18 он составил x = = 0.36 ± 0.025, а для Fe48Ni34P18 получили x = = 0.31 ± 0.02.

В [6] при помощи МУРН с высокой точностью была исследована спин-волновая динамика в аморфном соединении Fe50Ni22Cr10P18. В качестве образца использовалась стопка из 40 лент длиной 50 мм, шириной 10 мм и толщиной 30 мкм. Эксперимент проводили на установке малоуглового рассеяния нейтронов SANS-2 на реакторе FRG-1 в Гестахте (Германия), использовались поляризованные нейтроны с длинной волны 5.25 и 9.6 Å. Рассеяние нейтронов измерялось при комнатной температуре, которая заметно меньше критической температуры Кюри ТС = 335 К. Магнитное поле прикладывалось вдоль лент в диапазоне $30 \leqslant {{\mu }_{0}}H \leqslant 300$ мТл под углом к падающему пучку в 45°. Из анализа данных получили набор параметров, характеризующих спиновые волны, т.е. жесткость, затухание и напряженность внутреннего поля. Показано сильное влияние диполь-дипольного взаимодействия на поведение спиновых волн при малых импульсах.

В [10, 11] представлены результаты измерения спин-волновой жесткости в классическом инварном сплаве Fe65Ni35. Эксперимент МУРН проводился на установке SANS-2 на реакторе FRG-1 в Гестахте (Германия). Поляризация составляла P0 = 0.9 при длине волны λ = 5.6 Å. Сплав Fe65Ni35 изучали в широком температурном интервале ниже критической температуры TC = 485 К в диапазоне магнитного поля 0.05–0.25 Тл. Показано, что спин-волновое рассеяние сконцентрировано в узком конусе внутри критического угла ${{\theta }_{C}}$, который зависит от магнитного поля как ${{\theta }}_{C}^{2}(H) = {{\theta }}_{0}^{2} - {{{{\theta }}}_{0}}g{{{{\mu }}}_{{\text{B}}}}H{\text{/}}{{E}_{n}}$, где ${{\theta }_{0}}$ – значение угла отсечки в нулевом поле. В окрестности критического угла ${{\theta }_{C}}$ теоретически предсказываемый резкий обрыв интенсивности размыт спин-волновым затуханием. Постоянная жесткости спиновой волны была получена сравнением антисимметричного вклада в рассеяние с модельной функцией. Величина спин-волновой жесткости A уменьшается с ростом температуры. Установлено [11], что температурная зависимость хорошо аппроксимируется выражением $A = {{A}_{0}}{{\left| \tau \right|}^{x}}$, где τ = 1 – T/TC > 0.1, $x = 0.48 \pm 0.01$ и ${{A}_{0}} = 137 \pm 3$ мэВ Å2. Полученное значение x близко к предсказаниям теории среднего поля x = 0.5. Удивительным является тот факт, что спиновую жесткость можно шкалировать на критическую температуру не только в критической области, но и во всем температурном диапазоне ниже ${{T}_{C}}$. Это может быть связано с близостью магнитной системы инварных сплавов к магнитному переходу порядок–беспорядок по концентрации x. Действительно, критическая температура перехода парамагнетик–ферромагнетик ${{T}_{C}}$ инварных сплавов FexNi1 ‒ x стремительно падает с ростом концентрации Fe от TC = 600 К при x = 0.6 до TC = 0 при $x \approx 0.75$. Причиной нестабильности ферромагнитной структуры, возможно, следует признать конкуренцию взаимодействий ферромагнитного обменного взаимодействия между атомами никеля и между атомами никеля и железа; антиферромагнитного или неколлинеарного (типа ДМ) обменного взаимодействия, появляющегося с ростом числа связей между атомами железа. Такого вида переходы часто наблюдаются в сплавах переходных металлов.

В [12] представлены результаты измерения спин-волновой жесткости другого инварного сплава состава Fe75Pt25. Образец представлял собой “таблетку” диаметром 12 мм и толщиной 1 мм. Состав был гомогенизирован в течение 100 ч при температуре 1100°C. После быстрого охлаждения образец отжигался при 600°C в течение 100 ч. Степень порядка, оцененная из величины критической температуры (TC = 400 К), достигала 70%. Эксперимент МУРН также проводился на дифрактометре SANS-2 реактора FRG-1 в Гестахте (Германия). Поляризация падающего пучка составляла ${{P}_{0}} = 0.95$ при длине волны λ = 0.58 нм. Спиновую динамику сплава изучали в диапазоне температур от 300 до 400 К. Магнитное поле величиной от 1 до 230 мТл прикладывали под углом 45° к падающему пучку. В результате была получена зависимость спин-волновой жесткости от температуры A(T), которая уменьшается от 54 до 25 мэВ Å2 с ростом температуры от 300 до 400 К.

В [13, 21] исследованы мезоскопическая структура и магнитная динамика в сплаве Гейслера Ni49.1Mn29.4Ga21.5 методом МУРН в диапазоне температур от 15 до 400 К. Образцы характеризуются температурами фазового перехода ферромагнитной фазы TC = 347 К и мартенситного перехода при ${{T}_{m}} = 306$ К. Эксперименты МУРН проводились на установке ВЕКТОР (реактор ВВР-М, Гатчина) на длине волны ${{\lambda }} = 9.2$ Å (Δλ/λ = 0.25). В результате были получены следующие выводы: все наблюдаемые структурные фазовые переходы идут через мезоскопические негомогенные фазы; структурные изменения в сплавах, включая изменения модуляции решетки, сопровождаются изменениями в спиновой динамике.

Методами МУРН и трехосной спектроскопии установлено, что в аустенитной фазе константа спин-волновой жесткости составила $A = 97 \pm 2$ мэВ Å2, а величина магнонной энергетической щели равна $\Delta {{E}_{g}} = 0.067 \pm 0.02$ мэВ. В тетрагональной фазе, которая была измерена при температуре 220 и 170 К, значения константы спин-волновой жесткости и магнонной щели не показали существенной разницы по сравнению со значениями, полученными в аустенитной фазе. Однако в тетрагональной мартенситной фазе константа спин-волновой жесткости показывает существенное отличие и составляет $A = 149 \pm 3$ мэВ Å2, а значение магнонной щели выросло в 4 раза: $\Delta {{E}_{g}} = 0.24 \pm 0.02$ мэВ. Более того, измерения спин-волновой динамики в низкотемпературной мартенситной фазе показывают значения константы спин-волновой жесткости $A = 197 \pm 7$ мэВ Å2 и $\Delta {{E}_{g}} = 0.19 \pm 0.03$ мэВ.

В [22] представлено измерение константы спин-волновой жесткости в аморфных ферромагнитных микропроводах. Микропровод представляет собой аморфную жилу соединения Fe77.55Si7.5B15 в стеклянной оболочке [23, 24]. Диаметр жилы 10 мкм, а диаметр всего провода вместе со стеклянной оболочкой 21 мкм. Магнитные микропровода с положительной магнитострикцией имеют доменную структуру типа Ландау–Лифшица, которая состоит в основном из одного большого домена с намагниченностью, ориентированной в осевом направлении. Перемагничивание происходит скачком Баркгаузена, т.е. быстрым распространением вдоль оси микропровода доменной границы, находящейся между большим аксиальным и кольцевым доменами. Петля гистерезиса в таком случае имеет прямоугольный вид с коэрцитивной силой, равной 159.15 А/м, а сами микропровода обладают свойством магнитной бистабильности. При перемагничивании микропровода доменная стенка движется по проводу с определенной скоростью, которая заметно меняется в зависимости от температуры прикладываемого магнитного поля [23–25].

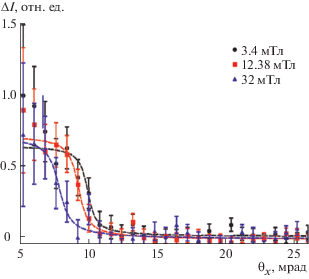
Эксперимент МУРН проводили на установке SANS-1 в центре Майер–Лейбница (Мюнхен, Германия). Использовали пучок поляризованных нейтронов с длиной волны ${{\lambda }} = 0.6$ нм. В качестве образца использовали набор из 100 микропроводов длиной 10 мм соединения Fe77.55Si7.5B15. Набор микропроводов длинной осью располагали под углом 35° к падающему пучку нейтронов и параллельно нанонитям. Зависимость интенсивности рассеяния от угла рассеяния $\theta $ представлена на рис. 4 для разных значений магнитного поля ${{{{\mu }}}_{0}}H = 3.4$, ${{{{\mu }}}_{0}}H = 12.38$ и ${{{{\mu }}}_{0}}H = 32.0$ мТл при температуре 300 К. Угол отсечки ${{\theta }_{C}}(H)$ получали из экспериментальной зависимости I от ${{\theta }_{x}}$, аппроксимируя полученные данные следующей функцией: $1{\text{/}}2 - (1{\text{/}}\pi )\arctan (2[\theta - {{\theta }_{C}}]{\text{/}}\delta )$. Положение угла отсечки ${{\theta }_{C}}$ определяется как среднее положение на обрыве arctan-функции, а размытие обрыва $\delta $ определяется разрешением установки.

Рис. 4.

Зависимость интенсивности малоуглового рассеяния поляризованных нейтронов $\Delta I$от угла ${{\theta }_{x}}$.

Квадрат угла отсечки $\theta _{C}^{2}$ изображен на рис. 5 в зависимости от приложенного магнитного поля при температуре 300 К. В соответствии с квадратичной моделью дисперсии в ферромагнетиках $\theta _{C}^{2}$ линейно зависит от магнитного поля:

(9)
${{\theta }}_{C}^{2}(H) = {{\theta }}_{0}^{2} - {{{{\theta }}}_{0}}(g{{{{\mu }}}_{{\text{B}}}}H + \Delta {{E}_{g}}){\text{/}}2{{E}_{n}}.$
Рис. 5.

Зависимость квадрата угла отсечки $\theta _{C}^{2}$ от напряженности приложенного магнитного поля.

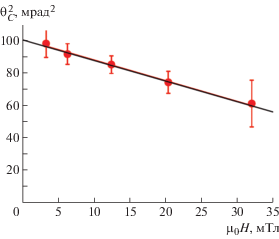
В выражении (9) была введена добавка $\Delta {{E}_{g}}$, обусловленная тем, что в ином случае два параметра линейной аппроксимации в (9) приводят к различным значениям величины ${{\theta }_{0}}$. Для того чтобы избежать противоречия, вводится ненулевое значение энергетической щели $\Delta {{E}_{g}}$ [22]. Аппроксимируя экспериментальную зависимость этим выражением, можно с высокой точностью определить значение параметра ${{\theta }_{0}} = 25(1)$ мрад и $\Delta {{E}_{g}} = 0.048$ мэВ. Величина спин-волновой жесткости при комнатной температуре равна $A = 82(3)$ мэВ Å2.

2. МАЛОУГЛОВОЕ РАССЕЯНИЕ НЕЙТРОНОВ НА СПИНОВЫХ ВОЛНАХ В ГЕЛИКОИДАЛЬНЫХ МАГНЕТИКАХ СО ВЗАИМОДЕЙСТВИЕМ ДЗЯЛОШИНСКОГО–МОРИЯ

Метод измерения спин-волновой жесткости при помощи МУРН [5–7] был успешно применен при измерениях спин-волновой константы в геликоидальных магнетиках с ДМ-взаимодействием, формирующихся в кубических кристаллах без центра инверсии (пр. гр. P213) [14]. Конкуренция между ферромагнитным обменным взаимодействием J и антисимметричным ДМ-взаимодействием D приводит к появлению геликоидальной магнитной структуры в соединениях этого типа. Внешнее магнитное поле HC2 требуется для перехода структуры с волновым вектором ${{{\mathbf{k}}}_{S}} = {\mathbf{D}}{\text{/}}J$ в полностью поляризованное коллинеарное состояние (ферромагнитное состояние). Несмотря на коллинеарное состояние магнитных моментов, присутствие ДМ-взаимодействия приводит к асимметрии закона дисперсии спиновых волн. В этом случае закон дисперсии может быть записан следующим образом [26]:

(10)
${{E}_{q}} = A{{({\mathbf{q}} - {\mathbf{k}})}^{2}} - g{{{{\mu }}}_{{\text{B}}}}(H - {{H}_{{C2}}}),$
где A – жесткость спиновых волн. Отметим, что ферромагнитное состояние гелимагнетиков оказывается единственным примером системы с возбуждениями, которые описываются асимметричным законом дисперсии.

Метод МУРН успешно применен к наиболее известному представителю геликомагнетиков с ДМ-взаимодействием – MnSi, чтобы подтвердить основные закономерности геликомагнонного спектра в ферромагнитном состоянии [14].

Было показано, что из-за асимметричности закона дисперсии сечение рассеяния содержит поляризационно-зависящую часть. Следовательно, рассеяние на спиновых волнах в ферромагнитном состоянии геликомагнетиков может быть экспериментально выделено путем вычитания измеренных интенсивностей рассеяния нейтронов для различной поляризации падающего нейтронного пучка. Неупругое рассеяние нейтронов на магнонах появляется в узком конусе вокруг брэгговского пика при углах рассеяния меньше, чем ${{\theta }_{0}} = {{\hbar }^{2}}{\text{/}}2A{{m}_{n}}$, где ${{m}_{n}}$ – масса нейтрона. Значение жесткости спиновых волн и ее температурные зависимости установлены в результате аппроксимации экпериментальных данных и анализа параметров этой аппроксимации [14]. Выводы [14] подтверждены методом трехосной спектрометрии нейтронов [27].

Как было показано позднее, метод применим и для поликристаллов. В [28] методом МУР неполяризованных нейтронов успешно изучена спиновая динамика поликристаллического образца FeGe в диапазоне температур 200–278 К.

Таким образом, была продемонстрирована возможность с помощью МУРН измерять динамику спиновых волн в поликристаллических образцах гелимагнетиков с ДМ-взаимодействием в полностью поляризованном состоянии с приемлемой статистикой за приемлемое время. Метод позволяет измерять спин-волновую жесткость в широком интервале температур и, прежде всего, открывает совершенно новые возможности в исследовании таких соединений, которые могут быть синтезированы только в виде порошка или поликристалла [28, 29]. Для описания этих экспериментальных результатов была разработана аналитическая модель, основанная на дисперсии гелимагнонов (10).

2.1. Влияние ДМ-взаимодействия на кинематику рассеяния нейтронов

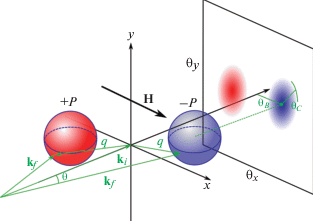
ДМ-взаимодействие, приводящее к виду дисперсионного соотношения (10), заметно меняет кинематику рассеяния нейтронов. Подставляя компоненты вектора рассеяния (1) в дисперсионное выражение для геликоидального магнетика с ДМ-взаимодействием (10) при условии, что прикладываемое поле H направлено вдоль оси ${{\theta }_{x}}$, получим два квадратных уравнения:

(11)
$\begin{gathered} Ak_{i}^{2}{{\tilde {\omega }}} - 2{{E}_{n}}{{\tilde {\omega }}} + A\{ k_{i}^{2}{{{{\theta }}}^{2}} - 2{{k}_{i}}{{k}_{S}}{{{{\theta }}}_{x}} + k_{S}^{2}\} + \\ \, + g{{{{\mu }}}_{{\text{B}}}}(H - {{H}_{{C2}}}) = 0, \\ Ak_{i}^{2}{{\tilde {\omega }}} + 2{{E}_{n}}{{\tilde {\omega }}} + A\{ k_{i}^{2}{{{{\theta }}}^{2}} + 2{{k}_{i}}{{k}_{S}}{{{{\theta }}}_{x}} + k_{S}^{2}\} + \\ \, + g{{{{\mu }}}_{{\text{B}}}}(H - {{H}_{{C2}}}) = 0, \\ \end{gathered} $
которые можно свести к каноническим уравнениям двух сфер:
(12)
$\begin{gathered} {{(\tilde {\omega } - \theta {}_{0})}^{2}} + {{({{\theta }_{x}} - {{\theta }_{S}})}^{2}} + \theta _{y}^{2} = \theta _{C}^{2}, \\ {{(\tilde {\omega } + \theta {}_{0})}^{2}} + {{({{\theta }_{x}} + {{\theta }_{S}})}^{2}} + \theta _{y}^{2} = \theta _{C}^{2}, \\ \end{gathered} $
где ${{\theta }}_{C}^{2} = {{\theta }}_{0}^{2} - {{{{\theta }}}_{0}}g{{{{\mu }}}_{{\text{B}}}}(H - {{H}_{{C2}}}){\text{/}}2{{E}_{n}}$. Центры этих сфер сдвинуты вдоль оси $\tilde {\omega }$ на величину $ \pm {{\theta }_{0}}$, однако в отличие от ферромагнетика центры сфер также сдвинуты на величину $ \pm {{\theta }_{S}}$ вдоль оси ${{\theta }_{x}}$, а радиус сфер равен ${{\theta }_{C}}$.

На рис. 6 изображена кинематическая схема рассеяния поляризованных нейтронов в случае геликоидального магнетика, намагниченного полем H > HC2. Иллюстрация показывает, что вектор рассеяния подчиняется законам сохранения импульса и энергии в соответствии с уравнениями (12), т.е. конец вектора kf пробегает по поверхностям сфер. При этом при одной поляризации рассеяние будет происходить только на одной сфере, при изменении поляризации падающих нейтронов рассеяние будет происходить на другой сфере. Интеграл (7) учитывает разницу интенсивностей при различной поляризации, и поляризационно-зависящее сечение МУРН на спиновых волнах в случае гелимагнетика примет вид

(13)
${{\Delta }}I = 2{{k}_{{\text{B}}}}T\int {\frac{1}{{{\omega }}}} \frac{{{{\theta }}_{x}^{2}}}{{{{{{\theta }}}^{2}} + {{\tilde {\omega }}}}}[{{\delta }}({{\omega }} - {{E}_{q}}) + {{\delta }}({{\omega }} + {{E}_{q}})],$
где было учтено, что вектор приложенного магнитного поля H направлен вдоль оси x, а геометрический фактор принимает вид

(14)
${{({\mathbf{\hat {q}\hat {m}}})}^{2}} = \frac{{\theta _{x}^{2}}}{{{{\theta }^{2}} + {{{\tilde {\omega }}}^{2}}}}.$
Рис. 6.

Кинематическая схема рассеяния поляризованных нейтронов на геликоидальном магнетике, намагниченном в поле H > HC2.

2.2. Методика измерения и обработки полученных данных

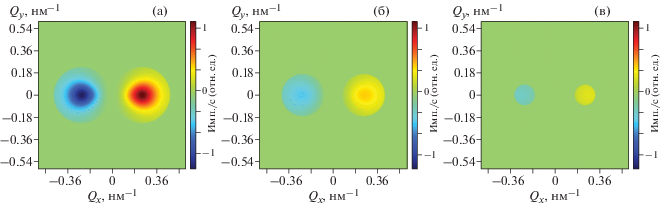
Методика измерения заключается в том, чтобы получить карты интегрального неупругого МУРН для разных значений магнитного поля и разных температур, что позволит определить зависимость спин-волновой жесткости от температуры. Для получения неупругого рассеяния необходимо перевести геликоидальный магнетик в состояние индуцированной ферромагнитной фазы. Для того чтобы избавиться от упругого рассеяния, прикладывается поле $H > {{H}_{{C2}}}$. В методе МУРН интенсивность рассеяния интегрируется по энергии, поэтому сферы рассеяния проецируются на плоскость $({{\theta }_{x}},{{\theta }_{y}})$, а детектируемая интенсивность представляет собой два круга, как показано на рис. 7. В случае эксперимента с поляризованными нейтронами законами сохранения энергии разрешено рассеяние только в одну из сфер в зависимости от направления поляризации нейтронов и знака ДМ-константы системы. В случае рассеяния неполяризованных нейтронов наблюдаются два круга интенсивности. Радиус этих кругов представляет собой величину ${{\theta }_{C}}$, которую можно получить путем аппроксимации азимутального интегрирования карт МУР возле центра круга. Здесь также нужно учитывать, что круги сдвинуты по оси x на величину ${{k}_{S}}$, которую можно определить из расстояния между упругими пиками при $H < {{H}_{{C2}}}$.

Рис. 7.

Двумерные карты поляризационно-зависящей части рассеяния поляризованных нейтронов на магнонах в гелимагнетике в случае, когда ${{\theta }_{0}} \leqslant {{\theta }_{S}}$, $H > {{H}_{{C2}}}$ для A = 100 мэВ Å2, ${{\theta }_{S}} = 28$ мрад, для трех значений приложенного магнитного поля ${{\mu }_{0}}(H - {{H}_{{C2}}})$ = 100 (a), 300 (б) и 500 мТл (в) при длине волны нейтронов ${{\lambda }} = 5.1$ Å.

2.3. Жесткость спиновых волн в гелимагнетиках и проверка теории Бака–Йенсена

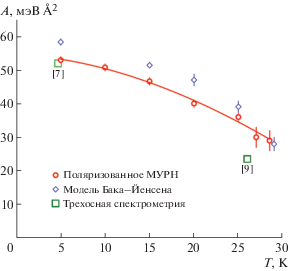
Справедливость дисперсионного выражения (10) проверена на монокристалле соединения MnSi в [14], где была разработана методика изучения при помощи МУРН спин-волновой динамики геликоидальных магнетиков с ДМ-взаимодействием в полностью поляризованном (ферромагнитном) состоянии. Экспериментально показано, что дисперсия спиновых волн в геликоидальных магнетиках с ДМ-взаимодействием имеет анизотропный вид. Продемонстрировано, что малоугловое неупругое рассеяние нейтронов представляет собой два круга с ограниченными радиусами и центрированными по передаче импульсами в соответствии с волновым вектором магнитной спирали kS, ориентированных вдоль приложенного вектора напряженности магнитного поля H. Радиус этих кругов напрямую связан с константой спин-волновой жесткости А. Константа A для MnSi геликоидального магнетика уменьшается в 2 раза с изменением температуры T от 0 К до критической температуры фазового перехода в парамагнитное состояние ${{T}_{C}} = 29$ К (рис. 8). Для сравнения на рис. 8 представлены экспериментальные значения жесткости, полученные методом трехосной спектрометрии [30, 31].

Рис. 8.

Температурная зависимость константы спин-волновой жесткости, полученная при помощи МУРН (круги) [15] в сравнении с моделью Бака–Йенсена (ромбы) и результатами, полученными при помощи трехосного спектрометра (квадраты) [30, 31].

Теоретическая оценка величины спин-волновой жесткости может быть получена из модели Бака–Йенсена [32, 33] с использованием соотношения, связывающего критическое магнитное поле HC2 и разность энергий между поляризованным (ферромагнитным) и спиральным состояниями магнитной системы: $g{{{{\mu }}}_{{\text{B}}}}{{H}_{{C2}}} = Ak_{S}^{2}$, учитывая, что величина волнового вектора спирали удовлетворяет соотношению ${{k}_{S}} = SD{\text{/}}A$, где S – упорядоченный спин системы, а D – константа Дзялошинского. Решая эти два уравнения с двумя неизвестными (A, D), из экспериментальных значений (kS, S, HC2) получим величины параметров A, D, которые определяют энергетический ландшафт магнитной системы.

Температурная зависимость жесткости, рассчитанная по этой модели, показана на рис. 8. Как величина жесткости, так и тенденция к небольшому снижению с температурой одинаковы для расчетных и измеренных значений, за исключением небольшого расхождения в области низких температур. Согласно [14] рассчитанные значения жесткости могут быть завышенными, так как приведенное выше выражение должно быть скорректировано на кубическую анизотропию [34]. Тем не менее было продемонстрировано, что выражение, связывающее HC2 и kS, можно использовать для оценки жесткости спиновых волн во всем диапазоне температур от нуля до критической температуры TC.

В [17] использовали МУРН для измерения жесткости спиновой волны гелимагнетиков с ДМ-взаимодействием в соединениях ${\text{M}}{{{\text{n}}}_{{1--x}}}$FexSi с x = 0.03, 0.06, 0.09 0.10. Известно, что эти соединения не только магнитно упорядочиваются в спиновую спираль ниже TC, но и демонстрируют режим сильных геликоидальных флуктуаций выше температуры упорядочения TC в широком диапазоне вплоть до TDM [35]. Критические температуры TC и TDM уменьшаются с x и стремятся к 0 при x = 0.11 и x = 0.17 соответственно. Установлено, что жесткость спиновых волн A слабо изменяется с температурой для каждого отдельного соединения, легированного железом (рис. 9). С другой стороны, жесткость A заметно уменьшается с ростом x, буквально повторяя зависимость TDM(x), и отклоняется от зависимости ${{T}_{C}}(x)$. Связь между спин-волновой жесткостью A и критическими температурами TC и TDM для различных соединений ${\text{M}}{{{\text{n}}}_{{1--x}}}$FexSi показана на рис. 10. Как видно из рисунка, спин-волновая жесткость меняется линейно с увеличением TDM, но не TC. Это обусловлено тем, что образование дальнего порядка, связанного с TC, не тривиально определяется изотропным обменом A, но дестабилизируется другим механизмом.

Рис. 9.

Температурная зависимость константы спин-волновой жесткости A(T) в соединениях ${\text{M}}{{{\text{n}}}_{{1--x}}}$FexSi с x = 0.03, 0.06, 0.09 и 0.10.

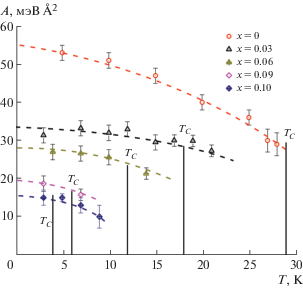
Рис. 10.

Константа спин-волновой жесткости в соединениях ${\text{M}}{{{\text{n}}}_{{1--x}}}$FexSi в зависимости от критической температуры перехода в парамагнитное состояние TС и от критической температуры флуктуаций геликоидальной фазы TDM [18].

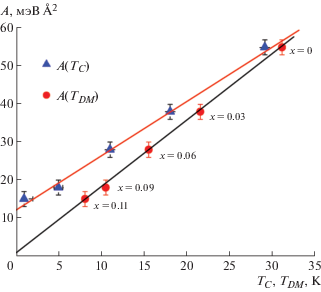
Полученные данные демонстрируют, что величина критической температуры TC не определяется только ферромагнитным взаимодействием, но заметно зависит от ДМ-взаимодействия, что говорит о его значительной роли как дестабилизирующего фактора магнитного порядка в этих соединениях. Роль ДМ-взаимодействия возрастает с уменьшением обменного взаимодействия A. Возможно, при константе спин-волновой жесткости, меньшей 10 мэВ Å2, ДМ-взаимодействие способно полностью разрушить дальний магнитный порядок и привести к ближнему магнитному порядку, что в результате и приводит к флуктуациям ориентации вектора магнитной спирали kS.

Как показано в [19], соединения ${\text{F}}{{{\text{e}}}_{{1--x}}}$CoxSi, характеризующиеся геликоидальной структурой ниже критической температуры TC в диапазоне концентраций $x \in \left[ {0.05;0.8} \right]$, также демонстрируют необычные магнитные свойства. Зависимость критической температуры TC от концентрации кобальта x имеет асимметричнную колоколообразную форму с максимумом при $x \approx 0.4$. Напротив, оценка величины жесткости спиновых волн с использованием модели Бака–Йенсена из макроскопических параметров показывает линейную зависимость жесткости A от концентрации в диапазоне x от 0.1 до 0.6 [36].

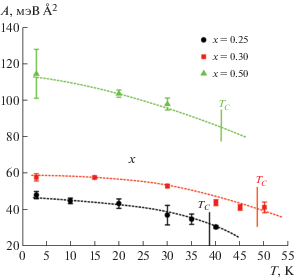
Прямое экспериментальное измерение жесткости с помощью МУРН в соединениях ${\text{F}}{{{\text{e}}}_{{1--x}}}$CoxSi с концентрациями x = 0.25, 0.3 и 0.5 показало, что спин-волновая жесткость A слабо зависит от температуры (рис. 11) и смягчения спектра с ростом температуры не происходит. По-видимому, такое температурное поведение спин-волновой жесткости характерно для гелимагнетиков с ДМ-взаимодействием, поскольку оно также наблюдалось для образца MnSi [14]. Более того, можно заключить, что разрушение дальнего магнитного порядка (спиновой спирали) в этих системах является результатом конкуренции ферромагнитного обменного взаимодействия и ДМ-взаимодействия, а температурный фазовый переход в них следует признать переходом первого рода.

Рис. 11.

Температурная зависимость константы спин-волновой жесткости для соединений ${\text{F}}{{{\text{e}}}_{{1--x}}}$CoxSi с x = 0.25, 0.3 и 0.5 [20].

Зависимость константы спин-волновой жесткости A от концентрации x для соединений ${\text{F}}{{{\text{e}}}_{{1--x}}}$CoxSi изображена на рис. 12. Несмотря на то что экспериментально при помощи МУРН было получено всего три точки, они очень хорошо ложатся на линейную зависимость с нулем в точке x = 0.05. Это концентрация, при которой система становится магнитоупорядоченной. Спин-волновая жесткость хорошо коррелирует с критической температурой TC в диапазоне концентраций $x \in [0.05{\kern 1pt} - {\kern 1pt} 0.4]$. Эта корреляция неудивительна, она также наблюдалась для соединений ${\text{M}}{{{\text{n}}}_{{1--x}}}$FexSi.

Рис. 12.

Зависимость константы спин-волновой жесткости A от концентрации x в соединениях ${\text{F}}{{{\text{e}}}_{{1--x}}}$CoxSi: кругами обозначены результаты, полученные в ходе МУРН, квадратами – оценка при помощи модели Бака–Йенсена, треугольниками – зависимость спин-волновой жесткости от критической температуры TC [20].

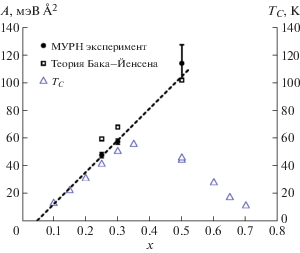
Отметим, что жесткость спиновых волн A повторяет x-зависимость критической температуры TC в области больших концентраций Fe и сильно отклоняется от нее в соединениях, обогащенных Co. Тем не менее полученные значения жесткости A демонстрируют количественную применимость модели Бака–Йенсена по крайней мере для соединений ${\text{F}}{{{\text{e}}}_{{1--x}}}$CoxSi для x = 0.25, 0.30 и 0.50.

В [20] методом МУРН исследовали спиновую динамику соединения Cu2OSeO3 с пр. гр. P213, которая имеет киральную кристаллографическую структуру и, как следствие этого, возникшее ДМ-взаимодействие приводит к появлению геликоидальной ферримагнитной структуры [37]. Магнитная фазовая диаграмма этого соеденения схожа с фазовой диаграммой классического MnSi. При этом Cu2OSeO3 является магнитным изолятором, обладает сегнетоэлектрическими свойствами и, кроме того, является ферримагнетиком. Нет сомнений в том, что сложная магнитная фазовая диаграмма Cu2OSeO3 требует для ее понимания детального знания всех параметров взаимодействия спинового гамильтониана. Недавно было предложено несколько микроскопических теоретических моделей для описания спиновой системы Cu2OSeO3 [38–42]. Эти модели включают в рассмотрение пять интегралов магнитного обмена и пять анизотропных ДМ-связей между соседними $S = 1{\text{/}}2$ спинами атомов меди. Полный набор спиновых возбуждений в Cu2OSeO3 получен в широких диапазонах переданных энергий и импульсов с использованием неупругого рассеяния нейтронов [43], а параметры взаимодействия получены из аппроксимации полученного спектра спиновых возбуждений. Практически все наблюдаемые особенности могут быть превосходно описаны теоретическими моделями взаимодействия тетраэдров меди Cu4 с двумя параметрами сильного взаимодействия: $J_{S}^{{AF}} = 145$, $J_{S}^{{AF}} = - 170$ K (в тетраэдрах) и тремя параметрами слабого взаимодействия $J_{w}^{{AF}} = 27$, $J_{w}^{{AF}} = - 50$ и $J_{{O..O}}^{{AF}} = 45$ K (между тетраэдрами) [43]. Однако относительно низкое инструментальное разрешение измерений, позволявшее разрешить низкоэнергетическую моду с ферромагнитной дисперсией ${{{{\epsilon}}}_{q}} = A{{q}^{2}}$, не может разрешить влияние на спектр ДМ-взаимодействия. Тем не менее эту модель можно рассматривать как основу для более сложных теорий низких энергий, способных объяснить сложную магнитную фазовую диаграмму Cu2OSeO3, включая гелимагнитный порядок и А-фазу со скирмионнной решеткой.

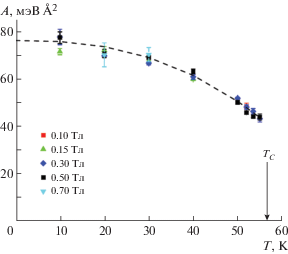
В [20] была измерена зависимость константы спин-волновой жесткости A от температуры T в монокристалле Cu2OSeO3 и установлено, что данная величина слабо зависит от температуры (рис. 13). Жесткость спиновых волн равна $76 \pm 1$ мэВ Å2 при низких температурах и уменьшается с температурой до $39 \pm 3$ мэВ Å2 при TC. Отметим, что температурная зависимость жесткости A в этом геликоидальном ферримагнетике Cu2OSeO3 схожа с температурным поведением жесткости спиновых волн как в архетипическом гелимагнетике MnSi [15], так и архетипическом ферримагнетике Fe3O4 [44, 45]. Согласно [46] именно флуктуации спина между подрешетками определяют величину жесткости спиновых волн A при T = 0 и влияют на ее температурную зависимость, тогда как флуктуации спина внутри подрешетки не вносят существенного вклада.

Рис. 13.

Температурная зависимость константы спин-волновой жесткости для нескольких значений магнитного поля [21].

ЗАКЛЮЧЕНИЕ

Представлен краткий обзор работ с использованием метода малоуглового рассеяния поляризованных нейтронов, разработанного для измерения жескости спиновых волн в аморфных и поликристаллических ферромагнетиках. Метод был апробирован на серии амофных ферромагнетиков как в низкотемпературной области, так и вблизи критических температур. Измерения жесткости спиновых волн в широком температурном диапазоне классического инварного сплава Fe65Ni35 показали, что температурная зависимость жесткости описывается единым скейлинговым выражением $A = {{A}_{0}}{{\left| \tau \right|}^{x}}$, где $x = 0.48 \pm 0.01$ и ${{A}_{0}} = 137 \pm 3$ мэВ Å2. Полученное значение x = 0.5 близко к предсказаниям теории среднего поля. Другой особенностью метода является возможность измерения энергетической щели в спектре спиновых волн, которая была продемонстрирована в аморфных ферромагнитных микропроводах соединения Fe77.55Si7.5B15 при Т = 300 К.

Метод измерения жесткости спиновых волн апробирован для гелимагнетиков на классическом монокристалле MnSi и поликристаллическом образце FeGe. Продемонстрировано явление магнитохиральной невзаимности распространяющихся магнонов для нецентросимметричных гелимагнетиков MnSi, ${\text{M}}{{{\text{n}}}_{{1--x}}}$FexSi, ${\text{F}}{{{\text{e}}}_{{1--x}}}$CoxSi, Cu2OSeO3. Методом МУРН показана справедливость квадратичного закона дисперсии, смещенного в направлении поля на величину волнового вектора спирали: ${{{{\epsilon}}}_{q}} = A{{({\mathbf{q}} - {\mathbf{k}})}^{2}} - g{{{{\mu }}}_{{\text{B}}}}(H - {{H}_{{C2}}})$. Экспериментально определены константы обменных взаимодействий, формирующих магнитную структуру исследованных соединений, в зависимости от температуры для бинарных и квазибинарных соединений MnSi, ${\text{M}}{{{\text{n}}}_{{1--x}}}$FexSi, FeGe, ${\text{M}}{{{\text{n}}}_{{1--x}}}$FexGe, ${\text{F}}{{{\text{e}}}_{{1--x}}}$CoxSi, а также для геликоидального ферримагнетика Cu2OSeO3.

Работа выполнена при поддержке Российского научного фонда (грант № 17-12-01050).

Список литературы

  1. Dorner B. // Coherent Inelastic Neutron Scattering in Lattice Dynamics. Springer, 1982. P. 106.

  2. Izyumov Yu.A., Chernoplekov N.A. // Neutron Spectroscopy, Springer, 1994. P. 373.

  3. Mitchell P.C.H., Parker S.F., Ramirez-Cuesta A.J. // Vibrational Spectroscopy With Neutrons: With Applications in Chemistry, Biology, Materials Science and Catalysis (Neutron Techniques and Applications), World Scientific Publishing, 2005. C. 668.

  4. Fishman R.S., Fernandez-Baca J.A., Rõõm T. // Spin-Wave Theory and its Applications to Neutron Scattering and THz Spectroscopy, Morgan & Claypool Publishers, 2018. P. 225. https://doi.org/10.1088/978-1-64327-114-9

  5. Окороков А.И., Рунов В.В., Топерверг Б.П. и др. // Письма в ЖЭТФ. 1986. Т. 43. С. 390.

  6. Deriglazov V., Okorokov A., Runov V. et al. // Physica B. 1992. V. 181–182. P. 262. https://doi.org/10.1016/0921-4526(92)90728-B

  7. Toperverg B.P., Deriglazov V.V., Mikhailova V.E. // Physica B. 1993. V. 183. P. 326.

  8. Малеев С.В. // Усп. физ. наук. 2002. Т. 172. С. 617.

  9. Пшеничный К.А., Алтынбаев Е.В., Григорьев С.В. // Поверхность. Рентген., синхротр. и нейтр. исследования. 2018. № 5. С. 18.

  10. Grigoriev S.V., Maleyev S.V., Deriglazov V.V. et al. // Appl. Phys. A. 2002. V. 74. P. 719.

  11. Григорьев С.В., Алтынбаев Е.В., Eckerlebe H., Окороков А.И. // Поверхность. Рентген., синхротр. и нейтр. исследования. 2014. № 10. С. 71.

  12. Metelev S.V., Grigoriev S.V., Maleyev S.V. et al. // Physica B. 2004. V. 350. № 1–3. Suppl. 1. P. E319.

  13. Рунов В.В., Черненков Ю.П., Рунова М.К. // ЖЭТФ. 2006. Т. 129. С. 117.

  14. Grigoriev S.V., Sukhanov A.S., Altynbaev E.V. et al. // Phys. Rev. B. 2015. V. 92. P. 220415(R).

  15. Iguchi Y., Uemura S., Ueno K., Onose Y. // Phys. Rev. B. 2015. V. 92. P. 184419.

  16. Seki S., Okamura Y., Kondou K. et al. // Phys. Rev. B. 2016. V. 93. P. 235131.

  17. Grigoriev S.V., Altynbaev E.V., Siegfried S.-A. et al. // Phys. Rev. B. 2018. V. 97. P. 024409.

  18. Григорьев С.В., Пшеничный К.А., Алтынбаев Е.В. и др. // Письма в ЖЭТФ. 2018. Т. 107. Вып. 10. С. 673.

  19. Grigoriev S.V., Pschenichnyi K.A., Altynbaev E.V. et al. // Phys. Rev. B. 2019. V. 100. P. 094409.

  20. Grigoriev S.V., Pschenichnyi K.A., Altynbaev E.V. et al. // Phys. Rev. B. 2019. V. 99. P. 054427.

  21. Runov V., Stuhr U. // J. Magn. Magn. Mater. 2011. V. 323. P. 244.

  22. Григорьев С.В., Пшеничный К.А., Барабан И.А. и др. // Письма в ЖЭТФ. 2019. Т. 110. № 12. С. 799.

  23. Zhukova V., Blanco J.M., Corte-Leon P. et al. // Acta Mater. 2018. V. 155. P. 279.

  24. Baraban I., Leble S., Panina L.V., Rodionova V. // J. Magn. Magn. Mater. 2019. V. 477. P. 415.

  25. Varga R., Zhukov A., Usov N. et al. // J. Magn. Magn. Mater. 2007. V. 316. P. 337.

  26. Kataoka M. // J. Phys. Soc. Jpn. 1987. V. 56. № 10. P. 3635.

  27. Sato T.J., Okuyama D., Hong T. et al. // Phys. Rev. B. 2016. V. 84. P. 144420.

  28. Siegfried S.-A., Sukhanov A.S., Altynbaev E.V. et al. // Phys. Rev. B. 2017. V. 95. P. 134415.

  29. Grigoriev S.V., Altynbaev E.V., Siegfried S.-A. et al. // J. Magn. Magn. Mater. 2018. V. 459. P. 159.

  30. Ishikawa Y., Shirane G., Tarvin J.A., Kohgi M. // Phys. Rev. B. 1977. V. 16. P. 4956.

  31. Semadeni F., Boni P., Endoh Y. et al. // Physica B. 1999. V. 267–268. P. 248.

  32. Nakanishia O., Yanase A., Hasegawa A., Kataoka M. // Solid State Commun. 1980. V. 35. P. 995.

  33. Bak P., Jensen M.H. // J. Phys. C. 1980. V. 13. P. L881.

  34. Grigoriev S.V., Sukhanov A.S., Maleyev S.V. // Phys. Rev. B. 2015. V. 91. P. 224429.

  35. Grigoriev S.V., Moskvin E.V., Dyadkin V.A. et al. // Phys. Rev. B. 2011. V. 83. P. 224411.

  36. Grigoriev S.V., Maleyev S.V., Dyadkin V.A. et al. // Phys. Rev. B. 2007. V. 76 P. 092407.

  37. Dyadkin V., Prša K., Grigoriev S.V. et al. // Phys. Rev. B. 2014. V. 89. P. 140409(R).

  38. Yang J.H., Li Z.L., Lu X.Z. et al. // Phys. Rev. Lett. 2012. V. 109. P. 107203.

  39. Romhanyi J., van den Brink J., Rousochatzakis I. // Phys. Rev. B. 2014. V. 90. P. 140404 (R).

  40. Janson O., Rousochatzakis I., Tsirlin A. et al. // Nat. Commun. 2014. V. 5. P. 5376.

  41. Ozerov M., Romhányi J., Belesi M. et al. // Phys. Rev. Lett. 2014. V. 113. P. 157205.

  42. Chizhikov V.A., Dmitrienko V.E. // J. Magn. Magn. Mater. 2015. V. 382. P. 142.

  43. Portnichenko P.Y., Romhaґnyi J., Onykiienko Y.A. et al. // Nature Commun. 2016. V. 7. P. 10725.

  44. Brockhouse B.N. // Phys. Rev. 1957. V. 106. P. 859.

  45. Watanabe H., Brockhouse B.N. // Phys. Lett. 1962. V. 1. P. 189.

  46. Srivastava C.M., Aiyar R. // J. Phys. C. 1987. V. 20. P. 1119.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Кристаллография

Архивы выпусков Информация о журнале Отправить рукопись в журнал