Кристаллография, 2022, T. 67, № 2, стр. 185-193

ВВЕДЕНИЕ

Оптические интерферометры уже более двух столетий используются в различных измерениях, имеющих как практический, так и научный характер [1]. В настоящее время существуют интерферометры разных типов, но наибольшую известность получил первый интерферометр с двумя щелями, известный как интерферометр Юнга. При дифракции на щели с шириной d монохроматическое излучение с длиной волны λ приобретает угловую расходимость с шириной α = λ/d, даже если на щель падает плоская волна. При дифракции на двух щелях пучки от них начинают пересекаться на расстоянии z₀ = x₀/α вдоль оптической оси, где x₀ – расстояние между щелями в поперечном направлении. Если через щели проходит когерентное излучение, то фазовые соотношения в разных пучках согласованы и при сложении двух полей возникают интерференционные полосы с периодом p = λz₁/x₀, где z₁ > z₀ – расстояние от щелей до детектора.

Для рентгеновских лучей развитие такой интерферометрии долгое время сдерживалось отсутствием когерентных источников, т.е. достаточно малой длиной когерентности и недостаточной яркостью излучения. Ситуация изменилась в середине 90-х годов прошлого столетия с появлением источников синхротронного излучения (СИ) третьего поколения, первым из которых стал источник в г. Гренобле (Франция). В настоящее время опубликовано много работ по рентгеновской интерферометрии разного типа. Отметим работы [2–7], в которых тестировались наиболее интересные интерферометры на основе составных преломляющих линз [8].

Вместе с тем в оптике рентгеновских лучей существует возможность принципиально новой интерферометрии на основе дифракции рентгеновских лучей в монокристаллах [9]. В двухщелевом интерферометре необходимо, чтобы пучки имели достаточно высокую угловую расходимость и пересекались на возможно близком расстоянии. Для рентгеновских лучей в стандартном интерферометре Юнга это сложно сделать из-за очень малой длины волны λ.

С другой стороны, известно, что при двухволновой дифракции в монокристалле пучок, ограниченный узкой щелью, засвечивает так называемый треугольник Бормана с углом 2θ_B, где θ_B – угол Брэгга, который может принимать любое значение от 0° до 90°. Этот факт впервые был обнаружен экспериментально в [10] и теоретически объяснен в [11, 12]. При этом пучки от двух щелей могут интерферировать в кристалле с толщиной меньше миллиметра, создавая периодические полосы с большой и малой интенсивностью.

Дифракционная интерферометрия от двух щелей, т.е. аналог интерферометра Юнга, но в монокристалле, была исследована теоретически в [13]. В этой работе была получена аналитическая формула для периода интерференционных полос p = = 2Λ t  tg²(θ_B)/x₀, где x₀ – расстояние между щелями, Λ = λcos(θ_B)/|χ_h| – длина экстинкции, χ_h – параметр дифракции, t – толщина кристалла. Параметры p и x₀ измеряются в направлении, параллельном поверхности кристалла.

Хотя такая постановка эксперимента вполне заслуживает внимания, все же нельзя не отметить ее недостатки. Во-первых, любой эксперимент с двумя щелями использует очень малую часть падающего пучка и поэтому имеет малую светосилу. Во-вторых, данная схема спектрально неустойчива, если расстояние Z между щелями и детектором не является слишком малым. То есть она требует очень высокой монохроматичности излучения. Заметим также, что перед двумя щелями все равно нужно ставить еще одну щель, размер которой меньше длины когерентности. Доля когерентного излучения на современных источниках СИ, хоть и возрастает, но часто только за счет уменьшения угловой расходимости пучка. А такой пучок не пройдет через две щели. Его все равно надо расширять. Если пучок широкий, то у него, как правило, длина когерентности невелика, и щель необходима для выделения когерентного излучения.

Интересно, что можно сделать аналог такого интерферометра, в котором две щели отсутствуют. Достаточно одной щели либо для расширения пучка, либо для выделения когерентной части излучения. Дело в том, что, во-первых, дифракция в кристалле сразу создает два пучка (прямой и отраженный) и, во-вторых, есть эффект дифракционной фокусировки. Эффект был предсказан теоретически в [14, 15] и сразу же обнаружен экспериментально в [16–18]. Позднее в [19, 20] этот эффект исследовался в случае дифракции на двух последовательных кристаллах, разделенных большим расстоянием. Как было показано в первой работе [14] и в ряде последующих [21–24], для заданной толщины кристалла t сферическая волна от вторичного источника с малыми поперечными размерами фокусируется на определенном расстоянии между источником и детектором Z = = tF_B/|χ_h|, где F_B = $\sin {{\theta }_{{\text{B}}}}\sin (2{{\theta }_{{\text{B}}}})$, как в прямом, так и в отраженном пучках.

Фокусировка происходит при достаточно большой толщине t₁ кристалла, когда дополнительно есть эффект Бормана, состоящий в том, что для части излучения коэффициент поглощения уменьшается во много раз и только эта часть излучения способна пройти через кристалл, причем как в прямом, так и в отраженном направлениях. Именно эта часть и фокусируется. При этом фокусировка в обоих пучках происходит идентично, а волновые функции имеют одинаковую фазу. На выходе из кристалла два почти одинаковых пучка с очень малой поперечной шириной двигаются каждый в своем направлении и разделяются в пространстве на расстояние 2t_gsin(θ_B) в направлении, перпендикулярном каждому из пучков, где t_g – толщина слоя воздуха.

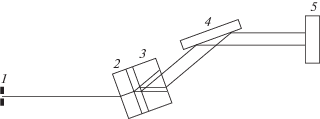
Если на их пути поставить второй кристалл с толщиной t₂, то каждый из них снова будет дифрагировать, засвечивая в кристалле область в виде треугольника Бормана, а при пересечении этих областей возникнет интерференция. Единственное отличие от экспериментальной схемы с двумя щелями, рассматривавшейся в [13], состоит в том, что прямой пучок будет дифрагировать на векторе обратной решетки h, как и в первом кристалле, а отраженный пучок будет дифрагировать на векторе –h. Описанную ситуацию иллюстрирует рис. 1. На нем кристалл 2 фокусирует пучки, а в кристалле 3 они интерферируют. Кристалл 4 нужен только для того, чтобы вернуть отраженный пучок в первоначальное направление, что важно при работе на источниках СИ.

Одним из преимуществ такой схемы является возможность эффекта полихроматической фокусировки для отраженного пучка, описание которого можно найти в [25]. Такая фокусировка реализуется при равных расстояниях от интерферометра до источника и детектора. Соответственно, имеет место спектральная устойчивость интерференционной картины, т.е. эффект интерференции можно наблюдать при весьма скромной монохроматизации СИ. Эффект полихроматической фокусировки иллюстрирует рис. 2. Пусть расходящийся пучок из точки 1 падает на кристалл 2 для дифракции по Лауэ. Для заданной длины волны λ кристалл ориентирован таким образом, что угол Брэгга θ_B соответствует горизонтальному лучу. Это средний луч на рис. 2. Он отражается на угол 2θ_B и, попадая на кристалл 3, вторично отражается в первоначальном направлении.

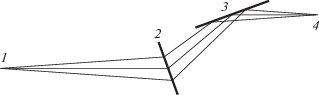
При уменьшении длины волны угол Брэгга тоже уменьшается. При этом условие дифракции выполнится для нижнего луча на рис. 2 в другом месте кристалла. После отражения в кристалле 3 этот луч становится верхним и в точке 4 он попадает в то же место на детекторе, что и первый (горизонтальный) луч. То же самое происходит при увеличении длины волны. То есть весь диапазон длин волн, который способен отразить кристалл 3, попадет в детектор в одно и то же место. По этой причине интерференционные полосы будут четко видны и ухудшения контраста не произойдет.

Другим преимуществом является то, что в таком интерферометре расщепление пучков в пространстве происходит после их дифракционной фокусировки, которая не приводит к потере интенсивности, т.е. такая схема имеет большую светосилу. Описанная выше схема также заслуживает внимания. Она предложена впервые в данной работе.

Однако, как показал более глубокий анализ, совсем не обязательно фокусировать пучки на конце первого кристалла. Главными элементами нового интерферометра является разделение пучков в пространстве, т.е. воздушный слой между первым и вторым кристаллами, а также эффект Бормана, т.е. выделение только одного поля из двух, которое слабо поглощается. Можно рассмотреть и другие схемы, причем интерференция происходит при любом расстоянии Z между вторичным источником (например, щелью) и детектором. Если это расстояние стремится к нулю, точнее достаточно мало, то наиболее четкая интерференция имеет место при равенстве толщин первого и второго кристаллов.

В данной работе представлены основы теории и метод численного расчета интерференционной картины в описанном выше интерферометре при любом соотношении между расстоянием Z, толщинами кристаллов и толщиной воздушного слоя; результаты расчетов для конкретных значений параметров; получены аналитические формулы для периода осцилляций и ширины пучков.

ОСНОВЫ ТЕОРИИ И МЕТОД ЧИСЛЕННОГО РАСЧЕТА

В [11, 14] показано, что дифракцию рентгеновских лучей в кристаллах удобнее всего вычислять методом преобразования Фурье. В общем виде этот метод состоит в следующем. Сначала проводится расчет волновой функции (ВФ) рентгеновского излучения на детекторе при отсутствии кристаллов, т.е. в реальном пространстве и в плоскости дифракции (x, z). При этом ось z направлена вдоль пучка (от источника к детектору), а ось x – в перпендикулярном направлении – поперек пучка. Расстояние между вторичным источником и детектором равно Z.

Затем такая ВФ на детекторе $E_{0}^{{(0)}}$(x) представляется в виде интеграла по плоским волнам, т.е. вычисляется преобразование Фурье $E_{0}^{{(0)}}$(q). Так как при дифракции в кристалле возникает отраженная (дифрагированная) волна, то удобно учесть это в самом начале и ввести вектор ВФ из двух компонент $E_{0}^{{(0)}}$(q) и $E_{1}^{{(0)}}$(q). При этом первоначально $E_{1}^{{(0)}}$(q) = 0. Решение задачи о дифракции плоской волны в кристалле с толщиной t₁, имеющем форму пластины, давно получено и описано в учебниках (например, [26–28]).

Это решение можно представить в виде умножения матрицы M_ik(q_,t₁) на вектор E_k(q), где индексы i и k имеют два значения 0 и 1. Таким образом, решение на детекторе $E_{i}^{{(1)}}$(q) при наличии на пути пучка одного кристалла с толщиной t₁ можно представить в виде

Здесь и далее по дважды повторяющимся индексам подразумевается суммирование.

Если на пути пучка расположены несколько кристаллов, которые плотно прижаты один к другому, то необходимо дополнительно выполнить умножение для второго кристалла с толщиной t₂:

и так далее для каждого следующего кристалла. Вместо кристалла на пути пучка может находиться слой аморфного вещества или просто воздух. Они тоже описываются матрицей M_ik(q_,t) специального вида. Но при этом для справедливости такого подхода предполагается, что суммарная толщина всего такого комплекса не слишком велика. Для кристаллов это очевидно, так как они поглощают. Для слоев воздуха это следует из структуры используемой матрицы, так как при ее выводе предполагается справедливость геометрической оптики.

После того, как выполнены умножения на все слои, делается обратное преобразование Фурье и получается результат снова в прямом пространстве, т.е. на детекторе в плоскости дифракции, но с учетом системы кристаллов. Из описанного выше метода расчета сразу становится ясно, что система кристаллов может находиться в любом положении между вторичным источником и детектором, так как результат от этого не зависит, если используется симметричное отражение. То есть наблюдаемая картина интерференции зависит только от суммарного расстояния Z. Кристаллы никак не влияют на это расстояние.

В данной работе применим общий метод к схеме эксперимента, показанной на рис. 1. Вторичным источником излучения является узкая щель с шириной d, на которую падает плоская волна. Щель может иметь резкие или сглаженные края, все это легко учитывается в расчете. Между щелью и детектором ничего, кроме кристаллов, нет. Дифракция излучения на щели с резкими краями вычисляется аналитически. Но для общности рассмотрим численный метод. Он удобен для решения рассмотренной выше задачи учета кристаллов.

Пусть щель в прямом пространстве описывается ВФ ψ(x). Вычислим преобразование Фурье ψ(q) и тогда фурье-образ ВФ на детекторе можно записать в виде

где введен нормировочный множитель C₁, а есть фурье-образ пропагатора Френеля. При такой постановке задачи сразу получаем $E_{0}^{{(0)}}$(q), в то время как для вычисления $E_{0}^{{(0)}}$(x) нужно делать обратное преобразование Фурье. Однако в этом нет необходимости, если интересует дифракция рентгеновского излучения в кристаллах. Можем сразу выполнить умножения, показанные в формулах (1) и (2).

Ниже представлены формулы для расчета матрицы M_ik(q_,t) в случае симметричной дифракции по Лауэ:

где Здесь параметр g по определению имеет положительную мнимую часть, χ₀, χ_h, χ_–h – параметры дифракции, представляющие собой компоненты Фурье поляризуемости кристалла на векторах обратной решетки 0, h, –h соответственно, θ_B – угол Брэгга, K = 2π/λ, параметр q₀ = Kθ₀ описывает возможное отклонение в угловом положении кристалла от угла Брэгга.

Отметим, что матрица дифракции M_ik(q, t), определенная формулами (5)–(11), показывает угловую зависимость интенсивности при дифракции плоских волн в кристалле в таком виде, что на хвостах кривых, т.е. при |q| ≫ X кривые стремятся к константе либо к нулю плавно. Это удобно при показе функций на графике. Однако при вычислении преобразования Фурье область дифракции (треугольник Бормана) получается слева от начала координат, а само начало координат соответствует прохождению луча от точечного источника вдоль направления падающей волны. И это как раз неудобно.

Более удобная картина получается, когда треугольник Бормана симметрично расположен слева и справа от начала координат. То есть надо сдвинуть начало координат на оси x таким образом, чтобы оно соответствовало середине треугольника Бормана. Дополнительный сдвиг на расстояние x_s = –Zθ₀ необходимо выполнить для конечного расстояния Z, чтобы скорректировать изменение брэгговского направления при угловом смещении кристалла. Правильный выбор центра пучка особенно важен для толстого кристалла, потому что в этом случае из-за эффекта Бормана через кристалл проходит только часть пучка, соответствующая середине треугольника Бормана. Сдвиг начала координат в программе выполняется умножением подынтегральной функции перед выполнением преобразования Фурье на множитель

Представленная на рис. 1 схема эксперимента все же должна удовлетворять некоторым дополнительным требованиям. Дело в том, что наиболее интересная картина интерференции появляется в отраженном пучке и при соблюдении условия полихроматической фокусировки, когда расстояния до и после интерферометра равны. При этом расстояние между интерферометром и детектором не может быть малым, если использовать эффект дифракционной фокусировки для относительно толстого кристалла. Как следствие этих условий, отраженный пучок на детекторе может сильно отклониться в поперечном направлении от оптической оси. Поскольку на источниках СИ мало места в поперечном направлении, такие отклонения пучка необходимо исправлять дополнительным отражением на такой же угол в обратном направлении. Как показано на рис. 1, для этой цели нужно использовать отражение по Брэггу от толстого кристалла, так как отражение по Лауэ нарушит условие полихроматической фокусировки, а отражение по Брэггу это условие не нарушает (рис. 2).

Как показывают расчеты, дополнительное симметричное отражение по Брэггу от кристалла 4 на рис. 1 почти не портит интерференционную картину при правильном угловом положении кристалла. Амплитуда симметричного отражения по Брэггу для толстого кристалла с центром инверсии тоже хорошо известна. Приведем ее для справки о том, какая формула использовалась в расчете

Здесь по определению мнимая часть параметра a больше нуля. Поэтому при больших значениях |q| получаем, что a примерно равно –σ и M_B(q) стремится к нулю. Кроме того, q₁ = Kφ, φ – угол возможного отклонения кристалла из точного положения дифракции.

Как известно [26–28], при отражении по Брэггу центр угловой области отражения смещен на величину –Re(χ₀)/sin(2θ_B), если кристалл выставлен строго под углом Брэгга. Это смещение можно компенсировать дополнительным поворотом кристалла. В формулах (13), (14) считается, что такая компенсация уже сделана, а условие q₁ = 0 соответствует такому положению кристалла, когда центр угловой области отражения находится в точке q = 0. Именно в таком положении кристалл-отражатель минимально портит интерференционную картину.

Формулы (1)–(14) были использованы для написания компьютерной программы, вычисляющей распределение интенсивности в пространстве перед детектором при дифракции на двух кристаллах с толщинами t₁ и t₂, которые разделены слоем воздуха с толщиной t_g, и возможном дополнительном отражении отраженного пучка в направление прямого пучка. При этом параметры дифракции вычислялись с помощью онлайн программы [29].

Компьютерная программа написана на языке ACL [30]. Интегралы Фурье вычислялись с помощью процедуры быстрого преобразования Фурье (FFT, [31]), встроенной в язык ACL. Код этой процедуры на языке Фортран известен с середины прошлого века как часть библиотеки NAG [32]. В расчетах использовалось число точек N = = 16 384. Шаг d_x сетки точек задается, а шаг d_q = = Kd_θ = 2π/(Nd_x) и размер расчетной области Nd_q в обратном пространстве должны быть достаточно большими, чтобы подынтегральная функция равнялась нулю на концах области.

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО РАСЧЕТА И ИХ ОБСУЖДЕНИЕ

Разработанная программа позволяет выполнить расчеты как угловой зависимости интенсивности при дифракции плоских волн, так и различные схемы дифракции сферической волны. Можно легко проверить очевидный результат, что если толщина слоя воздуха t_g = 0, а первый и второй кристаллы имеют одинаковую структуру и атомный состав, то результат расчета для двух кристаллов совпадает с результатом расчета для одного кристалла суммарной толщины 2t = t₁ + t₂.

В данной работе представлены результаты расчета для двух случаев. Первый соответствует дифракционной фокусировке в первом кристалле. Он имеет аналогию с интерферометром Баляна [13]. В этом случае толщина первого кристалла t₁ соответствует фокусировке излучения в плоскости детектора при отсутствии второго кристалла. На некотором расстоянии после выхода из второго кристалла пучки расходятся в пространстве и каждую из волн нужно рассматривать независимо. Легко понять, что в прямом пучке интерферируют дважды прошедшая и дважды отраженная волны, а в отраженном пучке – сначала прошедшая, потом отраженная и сначала отраженная, потом прошедшая волны.

Соответственно, получаем асимметричную картину в прямом пучке и симметричную картину в отраженном пучке. На рис. 3 показан результат расчета интерференционной картины в отраженном пучке при изменении толщины второго кристалла и без отражения третьим кристаллом для следующих значений параметров: размер щели d = 5 мкм, расстояние Z = 5 м, кристалл Ge, отражение 220, энергия фотонов 25 кэв (λ = = 0.0496 нм), толщина первого кристалла t₁ = 0.4 мм, толщина слоя воздуха t_g = 0.25 мм. Показан интервал толщин второго кристалла t₃ от 0.55 мм до 1.15 мм. Предполагается, что СИ поляризовано в плоскости, перпендикулярной плоскости дифракции. При указанных значениях параметров θ_B = 7.12°.

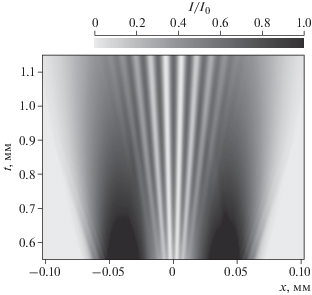
Так как поглощение в кристалле приводит к уменьшению интенсивности с ростом его толщины, то для увеличения контраста все значения относительной интенсивности выше заданного значения I₀ были заменены на I₀, что эффективно соответствует выходу за динамический диапазон измерения детектором. На рис. 3 значение I₀ выбрано как половина максимального значения, которое появляется при самой малой толщине кристалла. При этом I₀ = 0.023, если за единицу принять интенсивность на детекторе без кристаллов.

На рисунке можно видеть два типа интерференционных полос. Первые находятся по краям треугольников Бормана для каждого из пучков при малых значениях толщины второго кристалла t₂. Они имеют переменный период и соответствуют интерференции слабо и сильно затухающих волновых полей при дифракции сферической волны и малом расстоянии от источника до кристалла. Эти полосы были изучены в работах 1961 г. [11, 12]. С ростом толщины кристалла эти полосы пропадают из-за поглощения сильно затухающего волнового поля.

Второй тип полос находится в центре картины при больших значениях t₂. В этой области интерферируют слабопоглощающие волновые поля от разных источников. По этой причине они не исчезают в центре картины даже при больших толщинах второго кристалла. Это и есть интерференция, аналогичная той, которая наблюдается в эксперименте Юнга. Но два источника были созданы в воздушном промежутке благодаря тому, что кристалл добавляет к проходящей волне отраженную волну. Период этих полос пропорционален толщине кристалла и соответствует формуле, полученной в [13] и приведенной во введении.

Расчет с учетом кристалла-отражателя, установленного в точном положении отражения, почти никак не меняет интерференционные полосы при больших толщинах. Наблюдается только очень слабый, на малые доли периода, сдвиг полос вправо. С другой стороны, полосы по краям треугольников Бормана сильно размазываются. Причина в том, что кристалл-отражатель все-таки ограничивает угловой диапазон излучения, что приводит к ослаблению высокочастотных изменений на картине распределения интенсивности.

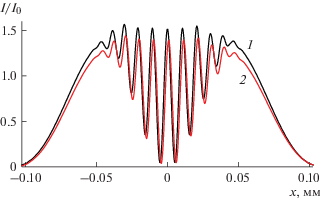
Описанную ситуацию иллюстрирует рис. 4, на котором показано распределение интенсивности при толщине второго кристалла 1 мм. При этом черная кривая получена при расчете без учета кристалла-отражателя и полностью соответствует сечению рис. 3. Кривая 2 получена с учетом кристалла-отражателя. Видно, что интенсивность слегка уменьшается из-за неполного отражения третьим кристаллом. Кроме того, в целом интерференционные полосы немного смещаются вправо. Это смещение никакой роли не играет, важно, что период полос сохраняется.

Интересно, что если выводить кристалл-отражатель из точного положения отражения, то интенсивность отраженного пучка резко уменьшается, а контраст портится. Поэтому необходима хорошая юстировка кристалла. Однако угловая ширина области отражения вполне достаточна для воспроизведения практически всей картины интерференции.

Второй случай соответствует малому расстоянию Z от вторичного источника до кристалла, конкретно, 0.1 м. На таком расстоянии эффект дифракционной фокусировки отсутствует полностью. Преимущество такой схемы в том, что не требуется очень толстых кристаллов и поэтому потери на поглощение уменьшаются. Дело в том, что для уменьшения периода осцилляций необходимо увеличивать толщину воздушного слоя. С другой стороны, желательно получить пучки с максимально большой шириной, чтобы они пересекались. В описанной выше схеме все происходит во втором кристалле, а первый кристалл, наоборот, сжимает пучки.

В схеме с минимальным расстоянием оба кристалла расширяют пучки, поэтому пересечение пучков происходит при меньших толщинах второго кристалла. В следующем разделе показано, что в такой схеме максимально хорошая интерференция получается при равенстве толщин первого и второго кристаллов, когда t₂ = t₁. На рис. 5 показаны кривые относительной интенсивности в прямом пучке (1) и отраженном пучке (2) при следующих значениях параметров: Z = 0.1 м, t₂ = t₁ = = 0.5 мм, t_g = 0.2 мм. Значение I₀ равно 0.0001 части от интенсивности на детекторе без кристаллов. Такое малое значение определяется тем, что эффект Бормана имеет место в очень ограниченной области углов, которая соответствует большому расстоянию.

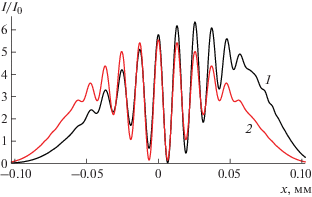
Из рисунка видно, что при относительно малой толщине кристаллов можно получить девять интерференционных полос, контраст которых быстро уменьшается при движении от центра к краям области пересечения пучков. Период полос описывается формулой, представленной во введении, если заменить толщину кристалла на сумму толщин двух кристаллов. Вывод этой формулы из расчетных формул дан в следующем разделе. Заметим, что в [13] был дан другой вывод. Кроме периода важным параметром является ширина пересекающихся пучков, формула для оценки которой также приведена в следующем разделе.

АНАЛИТИКА. ПЕРИОД ПОЛОС И ШИРИНА ПУЧКОВ

Рассмотрим наиболее простой и интересный случай, а именно, щель очень малых размеров и очень малое расстояние, а также t₁ = t₂ = t. При этом фурье-образы ВФ после щели и пропагатора Френеля можно считать равными единице и достаточно рассмотреть только кристаллы. Угловая зависимость ВФ отраженного пучка ψ₁(q) складывается из двух членов, которые имеют вид M₁₀M₀₀ и M₁₁M₁₀, если нет воздушного слоя. Если есть воздушный слой с толщиной t_g, то каждый из двух членов получает свой дополнительный фазовый множитель. В результате имеем

где x_g = t_gsin(θ_B). Mатричные элементы M_ik(q, t) рассчитываются по формулам (5)–(11).

Заметим, что по определению параметр G имеет отрицательную реальную часть. Параметр A также имеет отрицательную реальную часть. Пусть толщина t настолько велика, что реализуется эффект Бормана. В этом случае функция E_p будет намного меньше функции E_m и ее можно считать равной нулю. Тогда формулу (15) можно переписать в виде

Волновая функция в реальном пространстве равна интегралу Фурье от этого выражения: В интеграле с учетом (8) имеем два члена. Рассмотрим первый из них ψ₁₁(x). В нем в подынтегральной функции самым быстро меняющимся множителем является экспонента. Она быстро осциллирует, поэтому интеграл можно оценить методом стационарной фазы.

Суть метода состоит в том, что основной вклад в интеграл (18) дает область вблизи точки q₀, где фаза φ(q) экспоненты является почти постоянной, т.е. производная от фазы равна нулю. Далее делаются следующие приближения: множитель перед экспонентой заменяется константой, равной значению в этой точке, а в самой фазе φ(q) в окрестности этой точки учитывается только нулевой и второй члены степенного ряда по q, так как первый член равен нулю:

Здесь φ"(q₀) означает вторую производную от φ(q) в точке q₀.

Интеграл от такой функции вычисляется аналитически и равен

Из представленных выше формул следует, что фаза равна Здесь учтено, что Re(A(q)) приводит к сдвигу всей картины как целого в нежелательном направлении. В численном расчете она полагалась равной нулю, чтобы получить симметричную зависимость относительно начала координат. Поэтому она опущена и в данном расчете. С другой стороны, Знак зависит от того, как определять знак Re(X). Он выбран из условия, что Re(X) > 0.

Так как работаем в условиях эффекта Бормана, то нельзя сильно отклоняться от точки q = 0, иначе поглощение быстро растет. Предположим, что q₀ ≪ q_a . Тогда вместо (21) приближенно имеем

Из уравнения φ'(q) = 0 получаем решение Интересен член в фазе функции ψ₁₁(x), который меняет знак при изменении знака x_g. Кроме того, обычно t_g ≪ 2t и в центральной части интерференционной картины r ² ≈ 1.

С учетом указанных приближений сумму двух вкладов в ВФ отраженного пучка в центре можно записать в виде

Модуль этой функции осциллирует с периодом 2p, а интенсивность, т.е. квадрат модуля, осциллирует с периодом p, где Здесь учли (10), (22), а ось x, как и в расчетных формулах, перпендикулярна направлению пучков. При отходе от центра к краям интерференционной картины r² уменьшается, и контраст становится не полным, а потом совсем исчезает. Легко понять из приведенного вывода, что если толщины двух кристаллов не равны, то надо использовать среднее значение t = (t₁ + t₂)/2.

Другим важным параметром является ширина пучка в пространстве в условиях эффекта Бормана. При малых значениях толщины кристалла, когда поглощение не имеет значения, узкий пучок засвечивает треугольник Бормана с шириной основания 2 t sin(θ_B) в направлении, перпендикулярном направлению пучка. Однако поглощение приводит к тому, что ширина пучка становится меньше. При очень больших толщинах кристаллов профиль интенсивности в условиях эффекта Бормана имеет гауссовый вид с полушириной

Вывод этой формулы в общем случае несимметричной дифракции дан в [14], а в (28) представлен частный случай симметричной дифракции и сигма-поляризации. Здесь, как и выше, t = (t₁ + t₂)/2. Параметр χ_ih представляет собой фурье-компоненту мнимой части поляризуемости кристалла.

На самом деле интерферируют ВФ двух пучков, и нас интересует полуширина кривой модуля ВФ. Она будет в 2^1/2 = 1.414 раза шире. Заметим, что формула (28) дает правильное значение, совпадающее с численным расчетом, только при толщинах кристаллов больше 5 мм для параметров, рассматриваемых в данной статье. При меньших толщинах она дает завышенные значения. Например, для толщины 1 мм она дает значение в 1.4 раза больше по сравнению с численным расчетом.

ЗАКЛЮЧЕНИЕ

Дифракция рентгеновского излучения в кристалле в условиях эффекта Бормана создает два пучка с примерно одинаковыми свойствами. Воздушный зазор между двумя блоками кристалла разделяет пучки в пространстве, а пересечение пучков во втором блоке приводит к их интерференции. Наиболее интересные ситуации возникают в двух случаях: при реализации дифракционной фокусировки пучков в первом блоке; на нулевом расстоянии между вторичным источником (щелью) и блоком из двух кристаллов.

Разработан метод расчета такой интерференции, представлены результаты численного моделирования, а также дан вывод аналитических формул для периода осцилляций интенсивности излучения и ширины пучков. Интерферометр обладает спектральной устойчивостью и позволяет получать прецизионные значения как параметров дифракции, так и коэффициентов преломления любых материалов, которые можно поставить на пути пучков в воздушном зазоре.

Период осцилляций пропорционален толщине той части суммы толщин блоков кристалла, которая находится после толщины фокусировки. В первом случае это толщина второго блока, во втором случае – суммарная толщина двух блоков.