Кристаллография, 2022, T. 67, № 2, стр. 310-317

ВВЕДЕНИЕ

Исследования механических свойств кристаллических материалов, таких как пластичность или внутреннее трение, дали старт изучению динамики протяженных квазиодномерных объектов – дислокаций и краудионов [1]. Затем первоначальные идеи и методы были распространены на широкий класс других объектов: доменные границы, джозефсоновские контакты, биологические макромолекулы и поверхности кристаллов. В последнее время в связи со стремлением к миниатюризации устройств микроэлектроники повышенное внимание исследователей привлекают свойства наноразмерных систем типа проволок и им подобных [2, 3]. Интересны приложения нанопроволок в качестве однофотонных детекторов и другие, относящиеся к низкотемпературной области, в которой существенно проявление квантовых эффектов [3]. Признание потенциальных достоинств квантовых компьютеров вызвало поиск реализаций кубитов, некоторые из которых основаны на сверхпроводящих наносистемах [3, 4]. Изучение квантовых механизмов распада метастабильных состояний тем более насущно ввиду появления таких сугубо квантовых приложений наносистем, как хранение информации для квантовых компьютеров, квантовая телепортация, распределение квантовых ключей и др. [2, 5].

Возможности различных приложений нанопроволок связаны со стабильностью их состояний в барьерных структурах по отношению к флуктуациям. Достаточно сильными флуктуациями, ограничивающими время жизни состояния, являются так называемые проскальзывания фазы между положениями в соседних минимумах потенциального рельефа. В сверхпроводящих нанопроволоках проскальзывание фазы – это топологическая флуктуация, переносящая параметр порядка между различными токонесущими состояниями [6]. Вследствие этих флуктуаций низкоразмерные сверхпроводники приобретают электрическое сопротивление [6, 7]. Хорошо известно, что при высоких температурах проскальзывание фазы в квазиодномерных наносистемах происходит посредством термоактивационного преодоления барьера, разделяющего состояния в различных минимумах потенциального рельефа, как это впервые было рассмотрено в 1967 г. [7, 8]. Однако при понижении температуры нередко наблюдаются заметные отклонения от термоактивационных закономерностей аррениусовского типа. Это объясняется тем, что при вымораживании тепловых флуктуаций существенную конкуренцию могут составлять механизмы квантового туннелирования.

Квантовое проскальзывание фазы является примером так называемого макроскопического квантового туннелирования, изучение которого было инициировано работами [9–11] и др. Поскольку в проскальзывании фазы участвует много атомов, для его описания необходимо рассматривать динамику системы с большим числом степеней свободы. Это представляет определенные сложности, и во многих случаях такое описание до настоящего времени отсутствует. При термоактивируемом преодолении барьера ситуация значительно проще, так как кинетика перехода определяется законом Аррениуса, в главном экспоненциальном приближении характеризуемым энергией активации, отвечающей статической высоте барьера. Динамика при этом играет второстепенную роль, сказываясь на предэкспоненциальном множителе. В квантовом случае уже экспоненциальный фактор в квазиклассическом приближении определяется величиной действия, вычисляемого вдоль траектории туннельного перехода сквозь барьер [12–14]. Расчет такой траектории для многомерной системы часто представляет сложную динамическую задачу.

Во множестве представлений экспериментальных данных по низкотемпературной кинетике протяженных систем температурная граница смены режимов T_tr от классического термоактивационного к квантовому находится приравниванием вероятности классического термоактивационного перескока через барьер W_cl0exp(–E_M/kT) к вероятности квантового туннелирования сквозь барьер W_qexp(–S₀/$\hbar $). Здесь E_M – высота барьера, T – температура, k – постоянная Больцмана, S₀ – действие вдоль траектории подбарьерного перехода из основного состояния, $\hbar $ – постоянная Планка. В пренебрежении разницей малосущественных предэкспоненциальных множителей W_cl0 и W_q это сводится к T_tr ≈ $\hbar $E_M/kS₀. При T > T_tr применяется термоактивационная аррениусовская температурная зависимость W_cl0exp(‒E_M/kT), при T < T_tr используется атермическое выражение W_qexp(–S₀/$\hbar $). Тем самым предполагается, что смена режима происходит скачком. Естественно, такой никак не обоснованный подход нельзя считать достаточно удовлетворительным. Дальнейшее наглядно проиллюстрирует отличие получаемых в его рамках закономерностей от результатов последовательного расчета.

В настоящей работе изучено температурное поведение скорости распада метастабильного состояния в низкотемпературной области T < T_tr. Расчет проведен последовательно от задания потенциального рельефа до вычисления зависимости частоты процессов проскальзывания фазы от температуры и внешней нагрузки. Для этого применен эффективный метод коллективных координат, включающий в себя две степени свободы. Основы такого подхода, показавшего, несмотря на свою упрощенность, по крайней мере качественную пригодность, были заложены в [15–17].

РЕДУКЦИЯ МНОГОМЕРНОГО ЭНЕРГЕТИЧЕСКОГО РЕЛЬЕФА К ДВУМЕРНОМУ

Стартовой точкой расчета является задание функционала энергии, зависящего от конфигурации системы. Используется модель упругой струны, находящейся в потенциальном рельефе типа “стиральной доски”, ранее применявшаяся для описания динамики дислокаций в кристаллическом рельефе, а затем и для других систем [11, 18]. Энергия струны в плоском потенциале U₀(y) под действием внешней силы f описывается выражением

Здесь y(x) – конфигурация струны, x – координата вдоль долин потенциала U₀(y), имеющего несколько минимумов, отвечающих метастабильным состояниям системы, κ – жесткость струны. В качестве U₀(y) рассматривается гармонический потенциал синус-Гордона [19]: Здесь h – период потенциала, U_m – высота барьеров. При наличии внешней движущей силы f возникает неэквивалентность минимумов U₀(y), определяемых выражением (2), в результате состояния системы в минимумах становятся метастабильными и имеют конечное время жизни. Распад метастабильных состояний происходит вследствие флуктуаций через локально неоднородные конфигурации струны. Время распада определяется высотой барьеров в конфигурационном пространстве, рассчитываемых с помощью выражения (1). Часто это выражение записывают в терминах фазы φ = 2πy/h, а смещение в соседний эквивалентный минимум потенциального рельефа на 2π называют проскальзыванием фазы.

Будем измерять y в единицах h, а x в d₀ = = h(κ/U_m)^1/2. Энергия струны с потенциалом (2) примет вид

где переменные безразмерны: $E \to E{\text{/}}h\sqrt {\kappa {{U}_{m}}} $, f → → fh/U_m. Пусть струна первоначально находится в минимуме потенциала U₀(y) – fy, отвечающего y₀ = $\frac{1}{{2{{\pi }}}}$arcsin(f/π). Будем далее отсчитывать y(x) от y₀ и проведем перенормировку потенциала U₀(y) – ‒ fy так, чтобы минимуму отвечала нулевая энергия U(y) → U(y) = U₀(y) – fy – U₀(y₀) + fy₀ = $\frac{1}{2}${[1 – ‒ (f/π)²]^1/2[1 – cos(2πy)] + $\frac{f}{{2{{\pi }}}}$sin(2πy)} – fy, здесь y отсчитывается от 0.

Главной задачей является описание процесса образования зародыша нового состояния, соответствующего наиболее легкому пути преодоления барьера. К отысканию этого пути подходим вариационным образом, используя для описания конфигураций струны пробную функцию, зависящую от двух параметров d и x₀:

Здесь и далее e = exp(x₀/d), e_s = e + 1/e. Выбранная пробная функция (4) позволяет описывать широкий спектр промежуточных состояний от малых подбарьерных флуктуаций до вполне сформировавшихся зародышей за барьером.

Подставим пробную функцию (4) в функционал энергии (3) для получения двумерного потенциального рельефа E(x₀, d). Изменяя масштаб переменной интегрирования и заменяя переменную x₀ на e, представим E(e, d) в виде

Здесь I₁, I₂, I₂₂ и I₃ – функции одной переменной e, для некоторых из которых можно получить аналитические выражения, а остальные должны находиться численно:

Двумерный потенциальный рельеф на рис. 1 показан линиями постоянного уровня энергии и линией дна долины, ведущей к точке перевала в рельефе.

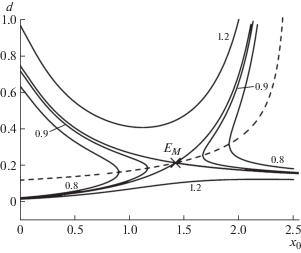
При изменении координат вдоль долины встречается максимум энергии E_M. С точки зрения двумерного рельефа этой точке отвечает перевал или “седло” с понижением энергии при удалении от нее вдоль одной координаты и ростом по другой. Отметим, что E_M играет роль энергии активации при термофлуктуационном образовании зародыша нового состояния системы. Для наглядного представления об эффективности используемого метода коллективных координат на рис. 2 проведено сравнение получаемой зависимости энергии E_M от движущей силы f с зависимостью, рассчитанной численно при полном многомерном подходе. Здесь используется отмеченный выше факт, что исследование статической высоты барьера в потенциальном рельефе, в данном случае даваемым выражением (1), является сравнительно простой задачей поиска экстремума функционала (1), имеющей известное решение при любом числе измерений.

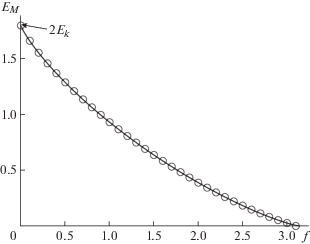
Зависимость энергии активации от движущей силы может быть удовлетворительно аппроксимирована простой функцией

При f → 0 E_M переходит в значение, приближающееся к энергии пары кинк–антикинк уравнения синус-Гордона. Выражение (10) позволяет описывать классическую термоактивируемую кинетику преодоления барьера в зависимости от температуры и движущей силы с помощью закона Аррениуса Вероятность термоактивируемого распада состояния системы резко убывает с понижением температуры. Однако предел этому убыванию полагают квантовые эффекты, создающие конкурирующий канал ухода из метастабильного состояния посредством квантово-механического туннелирования.

ТУННЕЛЬНЫЙ МЕХАНИЗМ РАСПАДА МЕТАСТАБИЛЬНОГО СОСТОЯНИЯ ПРОТЯЖЕННОЙ СИСТЕМЫ

В квазиклассическом приближении с экспоненциальной точностью вероятность квантово-механического туннельного преодоления барьера дается выражением [12–14]:

где S – действие, вычисляемое вдоль траектории подбарьерного перехода. Для его расчета к потенциальной энергии струны (1) следует добавить кинетическую энергию Здесь ρ – плотность массы на единицу длины системы.

Подставим в (13) пробную функцию (4), считая x₀ и d зависящими от времени. Переходя к безразмерным переменным с использованием в качестве масштаба времени h(ρ/U_m)^1/2, получим кинетическую энергию в виде

где

Эвклидов лагранжиан (с перевернутым потенциалом) L = T_k + E(e, d) дает возможность стандартным способом рассчитать действие S = $\int {Ldt} $ решением системы двух уравнений Эйлера–Лагранжа. В общем случае при произвольном соотношении эффективных скоростей на квазиклассических траекториях и характерной скорости “звука” (κ/ρ)^1/2 движение аналогично релятивистской динамике. Однако расчет температурной зависимости вероятности перехода в окрестности температуры подключения туннельного канала можно проводить в используемом ниже нерелятивистском приближении. Основанием для этого служит то обстоятельство, что вблизи верхушки барьера эффективные скорости движения по траектории невелики, так как энергия предактивации делает барьер мелким.

Движению по различным координатам ввиду анизотропии задачи соответствуют различные массы, и уравнения Эйлера–Лагранжа имеют вид

Система двух уравнений второго порядка (18), (19) позволяет сравнительно просто рассчитывать траектории подбарьерных переходов. Начальное значение e₀ берется как параметр, начальное d₀ вычисляется на линии уровня, отвечающей заданной энергии E, представляющей границу классически разрешенной области. Методом “пристрелки” находится траектория, достигающая границы классически разрешенной области по другую сторону барьера. Для этой траектории вычисляется действие S(E), минимальное значение которого отвечает касанию линии уровня за барьером в точке поворота e_turn и возвращению в начальную точку e₀. Пример такой траектории изображен на рис. 3. Вследствие анизотропии масс в выражении для кинетической энергии траектория проходит в потенциальном ландшафте несимметричным образом, минуя точку перевала.

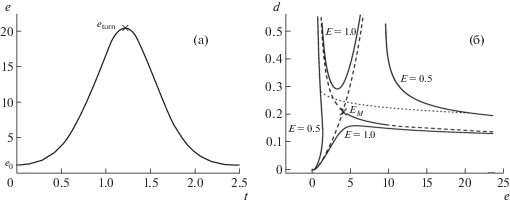
АКТИВАЦИОННО-ТУННЕЛЬНЫЙ РЕЖИМ

При ненулевой температуре в преодоление барьера дают вклад и квантовые, и тепловые флуктуации. Возможен промежуточный комбинированный процесс: туннелирование не из основного, а из термически возбужденного состояния системы. Вероятность такого комбинированного процесса в основном определяется некоторой оптимальной энергией, предваряющей туннелирование. Температурой перехода является та, при которой энергия предактивации сравнивается с высотой барьера E_M и выше которой процесс имеет характер классической термоактивации.

Высота барьера для туннелирования с предварительной активацией понижается, и действие является убывающей функцией энергии предактивации S(E). Вероятность перехода равна произведению вероятности активации на энергию E, даваемую больцмановским фактором exp(–E/kT), и вероятности туннельного перехода в пониженном на E барьере, что составляет W_q = W_q0exp{‒E/kT) – ‒ S(E)/$\hbar $}. Оптимальная энергия предактивации соответствует максимуму показателя экспоненты по E и находится из уравнения

Решением уравнения (20) определяется зависимость оптимальной энергии предактивации от температуры E(T). Подставляя это решение в рассчитанное с помощью уравнений Эйлера–Лагранжа действие S(E), выражаем температурную зависимость вероятности перехода в виде где S(T) = $\hbar $E(T)/kT + S(E(T)). Смена классической температурной зависимости на активационно-туннельную для двух значений движущей силы f показана на рис. 4, где видно, как квантовые эффекты замедляют убывание вероятности флуктуаций при понижении температуры. Однако они не приводят к полной атермичности, как это иногда предполагают. Пунктирные линии изображают такой гипотетический резкий переход между классической и квантовой температурными зависимостями, в то время как в действительности при T = T_tr происходит гладкое смыкание квантовой и классической вероятностей преодоления барьера, как это диктуется известным поведением по типу фазового перехода второго рода [20, 21].

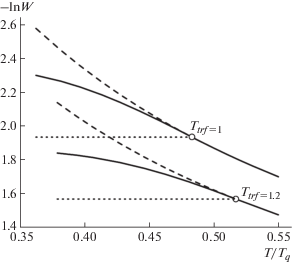
Практическое использование температурно-зависимого действия S(T) упрощается применением аппроксимирующих выражений. Так, для интервала значений движущей силы 0.5 < f < 2.8 полное действие S(T) может быть удовлетворительно аппроксимировано функцией

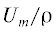где S₀ = h²(κρ)^1/2, T_q = $\frac{\hbar }{{kh}}$()^1/2,

ВЫВОДЫ

Заметные отклонения низкотемпературной кинетики проскальзывания фазы от термоактивационной закономерности неоднократно наблюдались для нанопроволок из различных материалов [22–31]. Ввиду тенденции этих отклонений к атермичности их естественно связывали с наиболее фундаментальной причиной – вступлением в игру квантовых механизмов. Это дает основание применить для их описания развиваемую в настоящей работе теорию. Результаты проведенного расчета могут быть проиллюстрированы экспериментальными данными [25] по измерению распределений токов переключения Mo₇₉Ge₂₁-нанопроволок из сверхпроводящего в нормальное состояние, как это показано на рис. 5. Процедура извлечения частоты переходов из функций распределений довольно сложная, поэтому сравнение с теорией может быть только полуколичественным. Потенциальная энергия нанопроволоки аналогично ситуации с контактом Джозефсона выражается через разность фаз волновых функций на концах образца, которая определена с точностью до 2π. Это определяет периодическую составляющую потенциальной энергии системы. Роль движущей силы, снижающей высоту барьера для проскальзывания фазы, может играть магнитное поле или создающий магнитное поле протекающий нормальный ток I.

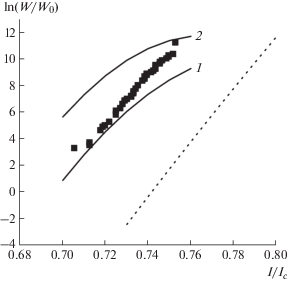
При относительно высокой температуре экспериментальные данные хорошо аппроксимируются законом Аррениуса с энергией активации E = E₀E_M(I) при значении характерной энергии E₀ ≈ 10^–3 эВ. Однако в низкотемпературной области T < 1.2 К экспериментальные данные не могут быть описаны термоактивационной зависимостью, и расхождение составляет несколько порядков величины. Предполагается, что повышение частоты флуктуаций связано с включением канала квантового туннелирования. На рис. 5 показано качественное сравнение активационно-туннельной W_q и термоактивационной W_cl вероятностей проскальзывания фазы в MoGe-нанопроволоке с поперечным сечением 74.2 нм² и длиной 110 нм при температуре T = 0.7 К по данным [25]. Несмотря на упрощенность и погрешность используемой модели, из этих данных можно приблизительно оценить величину квазиклассического параметра S₀/$\hbar $ как находящегося в пределах 160 < S₀/$\hbar $ < 200. Большая величина этого параметра оправдывает использование в настоящей работе квазиклассического метода расчета. Поскольку активационно-туннельная вероятность преодоления барьера, как видно из рисунка, заметно превышает классическую активационную, можно сделать вывод, что при температуре T = 0.7 К канал квантового туннелирования вносит значительный вклад в частоту проскальзывания фазы в данной нанопроволоке.

Итак, в работе изучен переход с понижением температуры от классического термоактивационного механизма движения протяженной системы через потенциальные барьеры к движению с участием квантово-механического туннелирования. Перечислим основные полученные результаты:

– с использованием метода коллективных координат проведена редукция многомерного потенциального рельефа протяженной наносистемы к двумерному, что позволяет существенно упростить расчеты кинетики флуктуационных явлений типа распада метастабильных состояний в барьерных структурах и проскальзывания фазы;

– с целью объяснения наблюдаемых в низкотемпературных экспериментах атермических отклонений от термоактивационной кинетики преодоления барьеров построена модель квантово-механического туннелирования в редуцированном двумерном потенциальном рельефе;

– в рамках квазиклассического подхода получены уравнения динамики подбарьерных переходов, позволяющие находить вероятности квантово-механического туннельного преодоления барьеров, и проведен ряд расчетов с использованием этих уравнений;

– рассчитана температурная зависимость активационно-туннельной динамики протяженной наносистемы в широком интервале нагрузок, позволяющая объяснить наблюдаемые экспериментально отклонения от закона Аррениуса при понижении температуры наиболее универсальным, а именно квантовым механизмом.