Кристаллография, 2022, T. 67, № 3, стр. 462-466

ВВЕДЕНИЕ

За последнее время существенно увеличилась вычислительная мощность компьютерной техники как специализированного, так и персонального назначения. Возросли объемы компьютерной памяти и скорость выполнения прикладных программ, что позволило практически каждому исследователю решать вычислительные задачи различной направленности. Результатом этих процессов применительно к области оптимизационных задач явилась возможность использовать так называемые “жадные” алгоритмы – алгоритмы, заключающиеся в принятии локально оптимальных решений на каждом этапе своего исполнения. Такие алгоритмы оказываются весьма требовательными к вычислительным ресурсам компьютерной техники [1]. Одним из них является простой метод прямого поиска или поиск перебором. Этот алгоритм и его модификации известны также как метод поиска на равномерной сетке или метод заполнения пространства (space filling) [2]. Метод имеет полиноминальную вычислительную сложность относительно определяемых параметров, но при этом является методом безусловной оптимизации, не требует вычисления каких-либо производных, крайне прост в реализации и всегда приводит к нахождению глобального минимума (максимума) задачи с наперед заданной точностью. Найденный экстремум является истинно глобальным по определению. Реализованный в работе метод оптимизации является частью аналитического комплекса BARD (Basic Analisys of Reflectometry Data) [3] и далее будет называться методом прямого поиска – Direct Search (DS-метод).

ОСНОВНЫЕ ПОЛОЖЕНИЯ

Дадим формальное определение метода. Без потери общности рассмотрим задачу нахождения минимума функции одной переменной F(x) на отрезке [a, b]: F(x) → min {x ∈ [a, b]}. Это простейшая задача оптимизации с ограничениями типа неравенства. Функция F(x) может иметь аналитическое выражение либо быть представленной в виде таблицы значений (например, экспериментально измеряемая величина). Зададим число N – число значений (отсчетов) и разобьем отрезок [a, b] на (N – 1) равных интервалов точками деления x_i с шагом разбиения Δx, равным

Вычислив значения F(x) в точках x_i, путем их сравнения найдем точку x_m такую, что F(x_m) = = min(F(x_i)) для всех i = 1…N. При этом погрешность определения точки минимума x_m функции F(x) определяется шагом разбиения Δx и уменьшается с увеличением числа точек разбиения N, Δx → 0 при N →∞ (1).

Картина и сущность алгоритма остаются практически такими же простыми при переходе к многомерной задаче. Здесь поиск вектора значений ${\mathbf{X}}_{{\min }}^{P}$, минимизирующих функцию Φ^P(X) в P-мерном гиперкубе [A, B]^P, сводится к мультипликативному исполнению P циклов вычислений значений Φ^P. Отметим, что в этом случае можно ввести “многомерную точность” метода – вектор значений (ΔX)^P, определяющий шаг разбиения области поиска каждого параметра аналогично (1):

При этом появляется возможность независимо контролировать точность определения каждого отдельного параметра задачи, разделяя их на важные и второстепенные.

Тестирование и оценка эффективности любого метода глобальной оптимизации – крайне сложная задача вычислительной математики. В настоящее время не выработано единого точного формального алгоритма такой оценки. Главным звеном в процедуре тестирования метода является выбор тестовой функции, которая должна адекватно описывать исследуемое явление или процесс либо должна быть нацелена на проверку особенных свойств самого метода. Здесь не будем вдаваться в подробности тестирования, а только отметим, что оно успешно прошло на ряде самых распространенных тестовых функций: функций Розенброка, Растригина, Пауэла и др. [4].

РЕЗУЛЬТАТЫ

DS-метод использован при решении обратной задачи рефлектометрии, представляющей собой поиск профиля электронной плотности слоистой пленки [5]. Для проверки работоспособности метода и достоверности получаемых на его основе результатов были рассмотрены модельные пленки. Предполагалось, что пленка нанесена на подложку и представлена в виде стопки слоев различной плотности и протяженности. Каждый слой характеризуется набором из четырех параметров: толщиной слоя d, поправками к показателям преломления и поглощения (δ, β), связанными с электронной плотностью вещества, и параметром шероховатости (размытия) слоя σ. Далее параметр δ для простоты будем называть электронной плотностью.

На рис. 1 приведены профиль электронной плотности δ двухслойной пленки (а) и кривая интенсивности зеркального рассеяния от нее (б), рассчитанная для заданного набора слоев с использованием рекуррентного метода Паррата [5]. Пленка нанесена на кремниевую подложку с δ₁ = = 7.6 × 10^–6 и шероховатостью σ_s = 2.0 Å и состоит из двух слоев, каждый из которых определяется тремя параметрами: толщиной (d₁ = 46, d₂ = 12 Å), электронной плотностью (δ₁ = 2.5 × 10^–5, δ₂ = 3.0 × × 10^–6) и шероховатостью (σ₁ = 3.0, σ₂ = 2.6 Å) (поглощение здесь не учитывали). Используя кривую интенсивности рассеяния, рассчитанную для заданных параметров с учетом 3%-ного гауссовского шума, в качестве “экспериментальной”, было проведено восстановление профиля электронной плотности. Определение шести параметров пленки осуществлено с помощью однократного применения DS-метода с заданной точностью в 1% для каждого из параметров (2). Модельная “экспериментальная” кривая показана на рис. 1б точками, результирующая восстановленная рефлектограмма представлена сплошной линией. Попадание восстановленной кривой интенсивности рассеяния в коридор ошибок зашумленной кривой (рис. 1б) и совпадение с кривой, рассчитанной для данного профиля без учета шума, демонстрируют полное соответствие результатов, вычисленных DS-методом, с “экспериментом”.

Для сравнения в качестве конкурирующего оппонента методу DS выступал другой метод глобальной оптимизации – метод симуляции отжига Simulation Annealing (SA-метод) [2]. Отметим, что даже в таком простейшем случае двухслойной модели SA-метод не всегда приводил к нахождению точного глобального минимума. Это можно объяснить сложным топологическим видом функционала задачи, который представляет собой многоэкстремальную поверхность в P-мерном пространстве параметров. Таким образом, использование традиционных методов оптимизации часто требует дополнительной обработки как входных, так и выходных и даже промежуточных данных, например сглаживания целевого функционала [6]. DS-метод в этом случае является истинно “прямым” и не требует привлечения дополнительных процедур обработки.

Приведем результаты применения DS-метода для анализа реальных экспериментальных данных ряда отдельных прикладных задач.

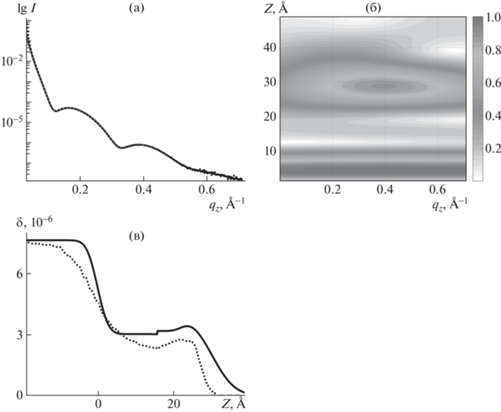
Для апробации метода использованы экспериментальные кривые зеркального отражения рентгеновского излучения с длиной волны λ = 1.5405 Å от монослоя порфирин-фуллереновых диад ZnDHD6ee толщиной 28.0 Å, нанесенного на кремниевую подложку [7]. Пленки из одинаково ориентированных в слое диад имеют большой практический интерес с точки зрения применения их для создания солнечных батарей благодаря возможности создания тонкопленочных донорно-акцепторных систем, способных генерировать направленный фотоиндуцированный перенос электрона в пленках. Исследования структурной организации приготовленных таким образом пленок, проведенные ранее методами стоячих рентгеновских волн (рентгеновской флуоресценции) и рефлектометрии [8], подтвердили факт формирования в них мономолекулярных структур с однородной ориентацией диад на поверхности твердой подложки, что повлияло на выбор результатов данного рефлектометрического эксперимента в качестве тестовых данных для применения предложенного метода. На рис. 2 приведены результаты рефлектометрических измерений монослоя порфирин-фуллереновых диад, заимствованные из [8]. При помощи вейвлет-преобразования исходной рефлектометрической кривой (рис. 2а) была предварительно определена общая толщина пленки. На вейвлетограмме, вычисленной для этой кривой (рис. 2б), общая толщина соответствует координате наиболее интенсивной полосы Z = 29 Å (разрешение такого расчета составило ∼4.0 Å). Далее был проведен анализ этих рефлектометрических кривых с использованием DS-метода в рамках ступенчатой модели электронного профиля пленки. Восстановление профиля плотности с использованием трехслойных моделей и оценка толщины пленки показали хорошее совпадение с результатами [8] (рис. 2в).

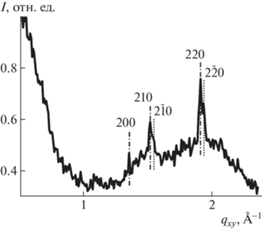
DS-метод использован также для определения структурных параметров молекулярного ленгмюровского слоя порфиразина магния (MgPz) на водной субфазе по данным дифракции скользящего падения (GIXD) (рис. 3) [9]. На кривой GIXD при q_z = 0 выявлено три узких дифракционных пика с координатами $q_{{xy}}^{{{\text{exp}}}}$ = 1.36, 1.52–1.55, 1.91–1.94 Å^–1, характеризующими отражение лучей от семейства параллельных плоскостей с соответствующими межплоскостными расстояниями. Это указывает на формирование в слабоупорядоченных слоях агрегатов, образующих кристаллические решетки с параметрами a, b, c и углами α, β, γ элементарных ячеек. Для исследования этих слоев можно применить используемые в кристаллографии методы дифракционного анализа. В частности, задавая параметры кристаллической решетки определенной симметрии, можно получить межплоскостные расстояния и сравнить их с экспериментальными значениями.

Факт, что в эксперименте рефлексы наблюдаются только в экваториальной плоскости, указывает на то, что отражающими являются плоскости, нормальные к поверхности субфазы (α = β = = 90°). Поэтому достаточно ограничиться поиском параметров a, b и γ элементарной ячейки, описываемой моделью параллелепипеда с размерами сторон в пределах 9 ≤ a = b ≤ 11 Å и стороной c, направленной по нормали к плоскости слоя.

Поиск структурных параметров предложенной модели осуществляли DS-методом путем минимизации невязок между экспериментальными и расчетными координатами дифракционных рефлексов с вычислением индексов Миллера соответствующих основных рефлексов [10]. Отметим, что применение оптимизационного DS-метода в определении индексов Миллера наиболее эффективно из-за ограниченности диапазона принимаемых ими значений и дискретности величин – они принадлежат целочисленному диапазону [–4 : 4].

В процессе оптимизации параметров был найден наилучший вариант упаковки, представляющий собой слегка деформированную квадратную ячейку, лежащую на поверхности воды и имеющую псевдотетрагональную симметрию: a = b = = 9.25 Å, γ = 89.0°. Для окончательного подтверждения полученного решения требуется дополнительная проверка реализуемости предложенной структурной упаковки с привлечением сведений о химическом составе анализируемого молекулярного слоя, что не является задачей данной работы.

ЗАКЛЮЧЕНИЕ

Приведенные примеры анализа реальных экспериментальных данных показывают достоверность и надежность метода прямого поиска в решении различных исследовательских задач на нахождение экстремума. Особенно эффективным метод становится в случае небольшого количества варьируемых параметров (порядка десяти) и ограниченности их диапазона изменений. При этом имеется возможность независимого контроля точности определения этих параметров. Таким образом, исследователи получают эффективный и простой в реализации универсальный метод математической оптимизации, применимый практически для всех задач нахождения оптимального решения.

Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию ФНИЦ “Кристаллография и фотоника” РАН.