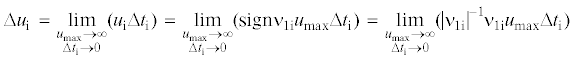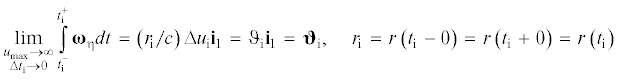Известия РАН. Механика твердого тела, 2019, № 1, стр. 3-22
ИМПУЛЬСНАЯ ОПТИМАЛЬНАЯ ПЕРЕОРИЕНТАЦИЯ ОРБИТЫ КОСМИЧЕСКОГО АППАРАТА ПОСРЕДСТВОМ РЕАКТИВНОЙ ТЯГИ, ОРТОГОНАЛЬНОЙ ПЛОСКОСТИ ОСКУЛИРУЮЩЕЙ ОРБИТЫ. II
Я. Г. Сапунков a, Ю. Н. Челноков a, b, *
a Институт проблем точной механики и управления РАН
Саратов, Россия
b Саратовский государственный университет им. Н.Г. Чернышевского
Саратов, Россия
* E-mail: chelnokovyun@gmail.com
Поступила в редакцию 09.02.2016
После доработки 09.02.2016
Принята к публикации 16.11.2016
Аннотация
Излагаются в строгой нелинейной постановке новая теория и новый алгоритм численного решения задачи оптимальной переориентации орбиты космического аппарата (КА) посредством импульсной (большой) реактивной тяги, ортогональной плоскости оскулирующей орбиты, для нефиксированного числа импульсов реактивной тяги. В качестве управления используется вектор реактивного ускорения от тяги двигателя. Минимизируется комбинированный функционал, равный взвешенной сумме времени переориентации и импульса реактивного ускорения (характеристической скорости) за время переориентации орбиты КА (частный случай этого функционала – случай минимизации характеристической скорости). Для построения теории используется изложенное в первой части статьи решение задачи оптимальной переориентации орбиты КА в непрерывной постановке (с использованием ограниченной (малой) реактивной тяги).
Показано, что задача оптимальной импульсной переориентации орбиты КА в случае, когда оптимальное управление состоит из двух импульсов реактивного ускорения, сообщаемых КА в начальный и конечный моменты времени движения, решается аналитически. Приведены примеры численного решения задачи оптимальной импульсной переориентации орбиты КА, иллюстрирующие возможности предлагаемого метода.
1. Введение. В настоящей (второй) части статьи рассматривается в нелинейной постановке задача оптимальной переориентации орбиты космического аппарата с помощью импульсной (большой) реактивной тяги, ортогональной плоскости оскулирующей орбиты КА, и с использованием кватернионного дифференциального уравнения ориентации орбитальной системы координат. При таком управлении орбита КА поворачивается в пространстве как неизменяемая (недеформируемая) фигура. Частным случаем этой задачи является хорошо известная и имеющая большое практическое значение задача коррекции угловых элементов орбиты КА, когда изменения угловых элементов орбиты в процессе управления имеют малые значения. В качестве управления используется вектор реактивного ускорения центра масс КА, ортогональный плоскости оскулирующей орбиты КА. Использование управления, ортогонального плоскости оскулирующей орбиты КА, позволяет корректировать элементы орбиты КА, сохраняя форму и размеры орбиты КА неизменными. Это ценное свойство изучаемого процесса переориентации орбиты КА является полезным как при решении задачи коррекции угловых элементов орбиты КА, так и других задач механики космического полета, например, при управлении конфигурацией группировки спутников.
Задача оптимальной импульсной переориентации орбиты КА исследуется в общем случае, когда изменения угловых элементов орбиты в процессе управления могут принимать любые конечные значения и когда осуществляется управление не только ориентацией плоскости орбиты КА, но и поворотом орбиты в ее плоскости. Минимизируется комбинированный функционал, равный взвешенной сумме времени переориентации и импульса реактивного ускорения центра масс КА (характеристической скорости) за время переориентации орбиты КА (частный случай этого функционала – случай минимизации характеристической скорости).
В ранее опубликованных наших работах (обзор этих работ приведен в первой части статьи [1]) задача оптимальной переориентации орбиты КА посредством реактивного ускорения центра масс КА, ортогонального плоскости оскулирующей орбиты, рассматривалась в различных постановках с использованием различных кватернионных моделей орбитального движения и различных критериев качества. Причем рассматривалось решение задачи лишь с использованием двигателя малой тяги (в непрерывной постановке).
На практике [2] также рассматривается управление плоскостью орбиты КА (долготой восходящего узла Ωu или (и) наклоном орбиты I) импульсного типа с помощью вектора реактивного ускорения, ортогонального плоскости оскулирующей орбиты КА. При этом время работы реактивного двигателя считается малым, так что изменением радиуса-вектора r центра масс КА за время маневра пренебрегается. Схемы маневров такого типа описаны в [2], где приводятся векторные диаграммы маневров для малых углов поворота плоскости орбиты КА. Отмечается, что если маневр импульсного типа выполнить в восходящем узле орбиты, то будет получено изменение ΔI наклонения орбиты величиной ΔI = θ = (r/c)$\int\limits_0^{\Delta t} {udt} $, при этом долгота восходящего узла Ωu не изменится (здесь r – модуль радиуса-вектора центра масс КА, с – постоянная площадей (модуль вектора с = r × v момента скорости v центра масс КА), u – алгебраическая величина реактивного ускорения, перпендикулярного плоскости оскулирующей орбиты КА). Такое же изменение плоскости орбиты можно выполнить маневром (другого знака) и на нисходящем узле орбиты; с точки зрения минимизации затрат энергии, маневр следует выполнять на максимальном радиусе. Если маневр выполнить на расстоянии ωπ + φ от восходящего узла (ωπ – угловое расстояние перицентра от узла, φ – истинная аномалия), то он изменит и наклонение орбиты, и долготу ее восходящего узла. При ωπ + φ = 90° происходит изменение (в первом приближении) долготы восходящего узла: ΔΩu = θ/sinI. Двумя последовательными маневрами можно получить заданные коррекции наклонения (ΔI = θ1) и долготы восходящего узла орбиты (ΔΩu = θ2/sin I). Для нахождения зависимостей в [2] используют теоремы сферической тригонометрии. При этом вопросы оптимизации маневров (в строгой линейной или нелинейной постановке) не затрагиваются.
Основная цель настоящей работы – решение задачи оптимальной переориентации орбиты КА с использованием двигателя большой тяги (в импульсной постановке) и с использованием кватернионного дифференциального уравнения ориентации орбитальной системы координат. При решении этой задачи нами в соответствии с известной методологией решения задач оптимальных импульсных перелетов КА [3] используются соответствующие предельные переходы в кватернионных уравнениях и соотношениях, полученных с помощью принципа максимума Понтрягина в задаче оптимальной переориентации орбиты КА с использованием ограниченной (малой) тяги и приведенных в первой части статьи [1]. Отметим, что исследованию задачи оптимальной переориентации орбиты КА с использованием двигателя малой тяги (в непрерывной постановке) и с использованием кватернионного дифференциального уравнения ориентации орбитальной системы координат также посвящены работы [4–7].
В настоящей (второй) части статьи излагаются в строгой нелинейной постановке: новая теория и новый алгоритм решения задачи оптимальной переориентации орбиты КА посредством импульсного реактивного ускорения, ортогонального плоскости оскулирующей орбиты, для нефиксированного числа импульсов тяги.
Построенная теория содержит формулы, лежащие в основе оптимальной импульсной переориентации орбиты КА: формулу, связывающую величину импульса реактивного ускорения с углом поворота орбиты КА вокруг радиуса-вектора центра масс КА; формулы для приращений на активном участке траектории кватерниона и вектора конечного поворота орбитальной системы координат, приращений кватернионной сопряженной переменной и скалярной сопряженной (по отношению к истинной аномалии) переменной, а также формулы для приращений переменных, описывающих процесс (линию) переключения управления, и формулу, описывающую дополнительное условие для внутреннего импульса реактивного ускорения.
Предложенный алгоритм численного решения задачи оптимальной импульсной переориентации орбиты КА справедлив для нефиксированного числа импульсов реактивного ускорения и позволяет определять оптимальные моменты включения реактивного двигателя, оптимальные величины импульсов реактивного ускорения и их оптимальное число.
Во второй части статьи также показано, что задача оптимальной импульсной переориентации орбиты КА в случае, когда оптимальное управление состоит из двух импульсов реактивного ускорения, сообщаемых КА в начальный и конечный моменты времени движения, решается аналитически. Приведены примеры численного решения задачи оптимальной импульсной переориентации орбиты КА, иллюстрирующие возможности предлагаемого метода.
2. Решение задачи оптимальной переориентации орбиты КА посредством импульсного реактивного ускорения, ортогонального плоскости оскулирующей орбиты. Решение задачи оптимальной переориентации орбиты КА (и коррекции угловых элементов орбиты) с помощью импульсного реактивного ускорения центра масс КА, ортогонального плоскости оскулирующей орбиты, построим с помощью предельных переходов в уравнениях и соотношениях, полученных для активных участков траектории КА в задаче оптимальной переориентации орбиты КА с использованием ограниченной (малой) тяги и приведенных в 3–5 разделах первой части статьи [1]. При этом предполагается, что максимальное значение реактивного ускорения u неограниченно увеличивается (umax → ∞), а длительность Δti каждого из активных участков движения КА неограниченно уменьшается (Δti → 0).
В те моменты времени ti, когда в соответствии с законом оптимального управления (4.7) [1] выполняется равенство
(2.1)
${\text{|}}{{\nu }_{{\text{1}}}}\left( {{{t}_{{\text{i}}}}} \right){\text{|}} = {\text{2}}{{\alpha }_{{\text{2}}}}c{\text{/}}r\left( {{{t}_{{\text{i}}}}} \right) = {\text{2}}{{\alpha }_{{\text{2}}}}\left( {c{\text{/}}p} \right)({\text{1}} + e{\text{cos}}{{\varphi }_{{\text{i}}}})$Равенство (2.1) определяет собой моменты включения двигателя большой тяги. В нем ν1 – переменная, являющаяся комбинацией фазовых и сопряженных переменных и характеризующая знак (направление) вектора реактивного ускорения; p и e – параметр и эксцентриситет орбиты; с, по-прежнему, – постоянная площадей; φi – значение истинной аномалии φ, характеризующей положение центра масс КА на орбите, в момент времени ti; α2 > 0 – постоянный коэффициент в комбинированном функционале качества (3.4) [1], характеризующий долю затрат характеристической скорости на процесс переориентации орбиты КА.
Во все остальные моменты времени, соответствующие движению КА на пассивных участках траектории, двигатель большой тяги выключен, орбита КА остается неподвижной в инерциальном пространстве и выполняется неравенство
(2.2)
${\text{|}}{{\nu }_{{\text{1}}}}{\text{|}} < {\text{2}}{{\alpha }_{{\text{2}}}}c{\text{/}}r = {\text{2}}{{\alpha }_{{\text{2}}}}\left( {c{\text{/}}p} \right)({\text{1}} + e{\text{cos}}\varphi )$2.1. Активный участок траектории КА. Пусть $t_{i}^{ - }$ и $t_{i}^{ + }$ – начало и конец i-го активного участка траектории КА, а Δti – длительность активного участка: Δti = $t_{i}^{ + }$ – $t_{i}^{ - }$. Пусть теперь длительность активного участка Δti = $t_{i}^{ + }$ – $t_{i}^{ - }$ → 0, так что $t_{i}^{ - }$ → ti – 0, $t_{i}^{ + }$ → ti + 0, где ti ∈ [$t_{i}^{ - }$, $t_{i}^{ + }$] – некоторый фиксированный момент времени. Тогда предел произведения величины реактивного ускорения u с учетом его знака в момент времени ti (т.е. предел величины ui = signν1iumax) на длительность активного участка Δti при условии, что umax → ∞, Δti → 0, будем называть импульсом реактивного ускорения и обозначать Δui:
Знак импульса реактивного ускорения Δui будет совпадать со знаком переменной ν1.
Функционал, определяющий качество процесса импульсной переориентации орбиты КА и принимающий минимальное значение для оптимального процесса, имеет в соответствии с (3.4) [1] вид
На активном участке импульсного управления полагается, что КА не меняет своего положения на орбите и что действующее на него управление u сохраняет свое значение постоянным. Поэтому на этом участке
(2.4)
$r = {\text{const}},\quad \varphi = {\text{const}},\quad u = {\text{sign}}{{\nu }_{{\text{1}}}}{{u}_{{{\text{max}}}}} = {\text{const}}$Поэтому кватернионное дифференциальное уравнение ориентации орбитальной системы координат (2.9) [1] и его решение на активном участке траектории принимают соответственно вид (2.5) и (2.6):
(2.5)
${\text{2}}d{\mathbf{\lambda }}{\text{/}}dt = {\mathbf{\lambda }} \circ {{{\mathbf{\omega }}}_{\eta }} = (r{\text{/}}c)u{\mathbf{\lambda }} \circ {{{\mathbf{i}}}_{{\text{1}}}}$(2.6)
${\mathbf{\lambda }}(t) = {\mathbf{\lambda }}({{t}_{0}}) \circ [{\text{cos}}((1{\text{/}}2)\omega (t - {{t}_{0}})) + {{\omega }^{{ - {\text{1}}}}}{{{\mathbf{\omega }}}_{\eta }}{\text{sin}}((1{\text{/}}2)\omega (t - {{t}_{0}}))]$(2.7)
${{{\mathbf{\omega }}}_{\eta }} = (r{\text{/}}c)u{{{\mathbf{i}}}_{{\text{1}}}},\quad \omega = {\text{|}}{\mathbf{\omega }}{\text{|}} = (r{\text{/}}c){\text{|}}u{\text{|}} = (r{\text{/}}c){{u}_{{{\text{max}}}}}$Решение (2.6) с учетом соотношений (2.7) и (2.4) принимает вид
(2.8)
${\mathbf{\lambda }}(t) = {\mathbf{\lambda }}({{t}_{0}}) \circ [{\text{cos}}((1{\text{/}}2)\omega (t - {{t}_{0}})) + {{{\mathbf{i}}}_{{\text{1}}}}({\text{sign}}{{\nu }_{{\text{1}}}}{\text{sin}}((1{\text{/}}2)\omega (t - {{t}_{0}}))],\quad \omega = (r{\text{/}}c){{u}_{{{\text{max}}}}}$Таким образом, на i-ом активном участке траектории КА после сообщения импульса реактивного ускорения длительностью Δti кватернион λ ориентации орбитальной системы координат в соответствии с (2.8) будет определяться соотношением
(2.9)
${\mathbf{\lambda }}(t_{{\text{i}}}^{ + }) = {\mathbf{\lambda }}(t_{{\text{i}}}^{ - }) \circ [{\text{cos}}((1{\text{/}}2){{\omega }_{{\text{i}}}}\Delta {{t}_{{\text{i}}}}) + {{{\mathbf{i}}}_{{\text{1}}}}({\text{sign}}{{\nu }_{{\text{1}}}}_{{\text{i}}}{\text{sin}}((1{\text{/}}2){{\omega }_{{\text{i}}}}\Delta {{t}_{{\text{i}}}}))],\quad {{\omega }_{{\text{i}}}} = ({{r}_{{\text{i}}}}{\text{/}}c){{u}_{{{\text{max}}}}}$Совершая в (2.9) предельный переход (полагая, что umax → ∞, Δti → 0) и учитывая обозначение (2.3) для импульса реактивного ускорения, получим окончательное выражение для кватерниона ориентации орбитальной системы координат в конце i-го активного участка:
(2.10)
${\mathbf{\lambda }}\left( {{{t}_{{\text{i}}}} + 0} \right) = {\mathbf{\lambda }}\left( {{{t}_{{\text{i}}}} - 0} \right) \circ [{\text{cos}}((1{\text{/}}2){{\vartheta }_{{\text{i}}}}) + {{{\mathbf{i}}}_{{\text{1}}}}{\text{sin}}((1{\text{/}}2){{\vartheta }_{{\text{i}}}})],\quad {{\vartheta }_{{\text{i}}}} = {{r}_{{\text{i}}}}{{c}^{{ - {\text{1}}}}}\Delta {{u}_{{\text{i}}}}$Приращение Δλi кватерниона ориентации орбитальной системы координат под действием импульса реактивного ускорения центра масс КА на i-м активном участке траектории КА в соответствии с (2.10) имеет вид
(2.11)
$\Delta {{{\mathbf{\lambda }}}_{{\text{i}}}} = \tilde {\lambda }\left( {{{t}_{{\text{i}}}} - 0} \right) \circ \lambda \left( {{{t}_{{\text{i}}}} + 0} \right) = {\text{cos}}((1{\text{/}}2){{\vartheta }_{{\text{i}}}}) + {{{\mathbf{i}}}_{{\text{1}}}}{\text{sin}}(1{\text{/}}2){{\vartheta }_{{\text{i}}}}),\quad {{\vartheta }_{{\text{i}}}} = {{r}_{{\text{i}}}}{{c}^{{ - {\text{1}}}}}\Delta {{u}_{{\text{i}}}}$Отметим, что здесь под приращением Δλi кватерниона λ (или, далее, μ) понимается его приращение в мультипликативном смысле, вытекающим из кватернионной формулы сложения двух конечных поворотов (2.10). Кватернион Δλi характеризует конечный поворот орбиты КА из ее углового положения, которое она занимает в момент времени ti – 0, в угловое положение, которое она принимает в момент времени ti + 0. Отметим также, что формула для угла ϑi поворота орбиты КА согласуется с формулами, приведенными в [2].
Рассмотрим другой подход к нахождению приращения Δλi кватерниона ориентации орбитальной системы координат, полученного под действием импульса реактивного ускорения на i-м активном участке траектории, с использованием теоремы о среднем. Вектор абсолютной угловой скорости орбитальной системы координат определяется кватернионным соотношением
(2.12)
${{{\mathbf{\omega }}}_{\eta }} = {{\omega }_{{\text{1}}}}{{{\mathbf{i}}}_{{\text{1}}}} + {{\omega }_{{\text{3}}}}{{{\mathbf{i}}}_{{\text{3}}}} = \left( {r{\text{/}}c} \right)u{{{\mathbf{i}}}_{{\text{1}}}} + (c{\text{/}}{{r}^{{\text{2}}}}){{{\mathbf{i}}}_{{\text{3}}}}$Интегрируя соотношение (2.12) на интервале времени Δti = $t_{{\text{i}}}^{ + }$ – $t_{{\text{i}}}^{ - }$ (с учетом того, что управление u на этом интервале является постоянной величиной) и используя теорему о среднем, получим
(2.13)
$\begin{gathered} \int\limits_{t_{{\text{i}}}^{ - }}^{t_{{\text{i}}}^{ + }} {{{\omega }_{\eta }}dt} = \left( {\int\limits_{t_{{\text{i}}}^{ - }}^{t_{{\text{i}}}^{ + }} {\left( {r{\text{/}}c} \right)udt} } \right){{{\mathbf{i}}}_{{\text{1}}}} + \left( {\int\limits_{t_{{\text{i}}}^{ - }}^{t_{{\text{i}}}^{ + }} {\left( {c{\text{/}}{{r}^{{\text{2}}}}} \right)dt} } \right){{{\mathbf{i}}}_{{\text{3}}}} = \\ = (({{r}_{a}}{\text{/}}c)({\text{sign}}{{\nu }_{{{\text{1i}}}}}{{u}_{{{\text{max}}}}})\Delta {{t}_{{\text{i}}}}){{{\mathbf{i}}}_{{\text{1}}}} + ((c{\text{/}}{{r}_{a}}^{{\text{2}}})\Delta {{t}_{{\text{i}}}}){{{\mathbf{i}}}_{{\text{3}}}} \\ \end{gathered} $Переходя в (2.13) к пределу в предположении, что umax → ∞, Δti → 0, получим, учитывая (2.3),
где ϑi и ϑi – угол и вектор конечного поворота орбитальной системы координат КА на i-м активном участке траектории КА в инерциальной системе координат (эти величины равны углу и вектору конечного поворота орбиты КА на i-м активном участке траектории).Отметим, что вектор абсолютной угловой скорости ω и вектор конечного поворота ϑ орбитальной системы координат на i-м активном участке траектории КА имеют одинаковое направление: они направлены вдоль радиуса-вектора ri = r(ti) центра масс КА, не изменяющегося на этом участке ни по модулю, ни по направлению.
Таким образом, в соответствии с (2.14) приращение Δλi кватерниона поворота орбитальной системы координат на i-м активном участке траектории КА будет иметь вид (2.11).
Перейдем к нахождению приращений на i-м активном участке переменных ν1, ν2, ν3, описывающих линию переключения управления [1]. Эти переменные являются компонентами кватерниона
(2.15)
$\nu = {{\nu }_{0}} + {{\nu }_{{\text{1}}}}{{{\mathbf{i}}}_{{\text{1}}}} + {{\nu }_{{\text{2}}}}{{{\mathbf{i}}}_{{\text{2}}}} + {{\nu }_{{\text{3}}}}{{{\mathbf{i}}}_{{\text{3}}}} = \tilde {\lambda } \circ \mu $(2.16)
$\begin{gathered} d{{\nu }_{{\text{1}}}}{\text{/}}dt = (c{\text{/}}{{r}^{{\text{2}}}}){{\nu }_{{\text{2}}}} \\ d{{\nu }_{{\text{2}}}}{\text{/}}dt = - (c{\text{/}}{{r}^{{\text{2}}}}){{\nu }_{{\text{1}}}} + (r{\text{/}}c){{\nu }_{{\text{3}}}}u,\quad d{{\nu }_{{\text{3}}}}{\text{/}}dt = - (r{\text{/}}c){{\nu }_{{\text{2}}}}u \\ \end{gathered} $Дифференциальное уравнение (4.3) [1] для сопряженной кватернионной переменной μ имеет такой же вид, что и дифференциальное уравнение (2.9) [1] для фазовой кватернионной переменной λ. Поэтому значения μ(ti – 0) и μ(ti + 0) кватерниона μ в начальный ti – 0 (перед сообщением импульса) и конечный ti + 0 (после сообщения импульса) моменты времени i-го активного участка будут связаны соотношением, аналогичным (2.10):
(2.17)
$\begin{gathered} {\mathbf{\mu }}\left( {{{t}_{{\text{i}}}} + 0} \right) = {\mathbf{\mu }}\left( {{{t}_{{\text{i}}}} - 0} \right) \circ \Delta {{{\mathbf{\mu }}}_{{\text{i}}}} = {\mathbf{\mu }}\left( {{{t}_{{\text{i}}}} - 0} \right) \circ [{\text{cos}}((1{\text{/}}2){{\vartheta }_{{\text{i}}}}) + {{{\mathbf{i}}}_{{\text{1}}}}{\text{sin}}((1{\text{/}}2){{\vartheta }_{{\text{i}}}})] \\ {{\vartheta }_{{\text{i}}}} = {{r}_{{\text{i}}}}{{c}^{{ - {\text{1}}}}}\Delta {{u}_{{\text{i}}}},\quad {{r}_{{\text{i}}}} = r\left( {{{t}_{{\text{i}}}} - 0} \right) = r\left( {{{t}_{{\text{i}}}} + 0} \right) = r\left( {{{t}_{{\text{i}}}}} \right) \\ \end{gathered} $При этом приращение Δμi ненормированного кватерниона μ поворота сопряженной системы координат на i-м активном участке траектории КА будет совпадать с приращением Δλi нормированного кватерниона λ поворота орбитальной системы координат:
(2.18)
$\Delta {{{\mathbf{\mu }}}_{{\text{i}}}} = {{{\mathbf{\mu }}}^{{ - {\text{1}}}}}\left( {{{t}_{{\text{i}}}} - 0} \right) \circ {\mathbf{\mu }}\left( {{{t}_{{\text{i}}}} + 0} \right) = \Delta {{{\mathbf{\lambda }}}_{{\text{i}}}} = {\text{cos}}((1{\text{/}}2){{\vartheta }_{{\text{i}}}}) + {{{\mathbf{i}}}_{{\text{1}}}}{\text{sin}}((1{\text{/}}2){{\vartheta }_{{\text{i}}}}),\quad {{\vartheta }_{{\text{i}}}} = {{r}_{{\text{i}}}}{{c}^{{ - {\text{1}}}}}\Delta {{u}_{{\text{i}}}}$Подставляя соотношения (2.10) и (2.17) в (2.15), получим формулу
(2.19)
$\begin{gathered} {\mathbf{\nu }}({{t}_{{\text{i}}}} + 0) = \tilde {\lambda }({{t}_{{\text{i}}}} + 0) \circ {\mathbf{\mu }}({{t}_{{\text{i}}}} + 0) = \Delta {{{\tilde {\lambda }}}_{{\text{i}}}} \circ ({{t}_{{\text{i}}}} - 0) \circ {\mathbf{\mu }}({{t}_{{\text{i}}}} - 0) \circ \Delta {{{\mathbf{\mu }}}_{{\text{i}}}} = \\ = \Delta {{{\tilde {\lambda }}}_{{\text{i}}}} \circ {\mathbf{\nu }}({{t}_{{\text{i}}}} - 0) \circ \Delta {{{\mathbf{\mu }}}_{{\text{i}}}} = \Delta {{{\tilde {\lambda }}}_{{\text{i}}}} \circ {\mathbf{\nu }}({{t}_{{\text{i}}}} - 0) \circ \Delta {{{\mathbf{\lambda }}}_{{\text{i}}}} \\ \end{gathered} $Подставляя соотношения (2.11), (2.18) в формулу (2.19) и переходя к скалярной записи, получим связи компонент νj(ti – 0) и νj(ti + 0) кватерниона ν в начальный ti – 0 (перед сообщением импульса) и конечный ti + 0 (после сообщения импульса) моменты времени i-го активного участка траектории:
(2.20)
$\begin{gathered} {{\nu }_{0}}({{t}_{{\text{i}}}} + 0) = {{\nu }_{0}}({{t}_{{\text{i}}}} - 0) = {{\nu }_{0}}({{t}_{{\text{i}}}}),\quad {{\nu }_{{\text{1}}}}({{t}_{{\text{i}}}} + 0) = {{\nu }_{{\text{1}}}}({{t}_{{\text{i}}}} - 0) = {{\nu }_{{\text{1}}}}({{t}_{{\text{i}}}}) \\ {{\nu }_{{\text{2}}}}\left( {{{t}_{{\text{i}}}} + 0} \right) = {{\nu }_{{\text{2}}}}\left( {{{t}_{{\text{i}}}} - 0} \right){\text{cos}}{{\vartheta }_{{\text{i}}}} + {{\nu }_{{\text{3}}}}\left( {{{t}_{{\text{i}}}} - 0} \right){\text{sin}}{{\vartheta }_{{\text{i}}}} \\ {{\nu }_{{\text{3}}}}\left( {{{t}_{{\text{i}}}} + 0} \right) = - {{\nu }_{{\text{2}}}}\left( {{{t}_{{\text{i}}}} - 0} \right){\text{sin}}{{\vartheta }_{{\text{i}}}} + {{\nu }_{{\text{3}}}}\left( {{{t}_{{\text{i}}}} - 0} \right){\text{cos}}{{\vartheta }_{{\text{i}}}} \\ {{\vartheta }_{{\text{i}}}} = {{r}_{{\text{i}}}}{{c}^{{ - {\text{1}}}}}\Delta {{u}_{{\text{i}}}},\quad {{r}_{{\text{i}}}} = r\left( {{{t}_{{\text{i}}}} - 0} \right) = r\left( {{{t}_{{\text{i}}}} + 0} \right) = r\left( {{{t}_{{\text{i}}}}} \right) \\ \end{gathered} $Из соотношений (2.20) видно, что значения переменных ν0 и ν1 не меняются на активном участке.
Истинная аномалия φ, характеризующая положение КА на орбите, на i-м активном участке траектории не изменяется, поэтому
Найдем приращение на i-м активном участке траектории переменной χ, сопряженной по отношению к истинной аномалии φ. Из первого интеграла (5.4) [1], существующего для оптимального управления, найдем
Подставляя это выражение в дифференциальное уравнение (4.4) [1] для переменной χ, получим
(2.21)
$d\chi {\text{/}}dt = e{\text{sin}}\varphi {{({\text{1}} + e{\text{cos}}\varphi )}^{{ - {\text{1}}}}}[{\text{2}}({{\alpha }_{{\text{1}}}} + {{\alpha }_{{\text{2}}}}{\text{|}}{{u}^{{{\text{opt}}}}}{\text{|}}) - (3{\text{/}}2)(r{\text{/}}c){{\nu }_{{\text{1}}}}{{u}^{{{\text{opt}}}}}]$Интегрируя левую и правую части уравнения (2.21) на интервале времени Δti = $t_{{\text{i}}}^{ + } - t_{{\text{i}}}^{ - }$ с учетом того, что на этом интервале оптимальное управление uopt = signν1umax, получим
Используя теорему о среднем, из этого соотношения найдем:
(2.22)
$\begin{gathered} \chi (t_{{\text{i}}}^{ + }) - \chi (t_{{\text{i}}}^{ - }) = {\text{2}}e{\text{sin}}{{\varphi }_{a}}{{({\text{1}} + e{\text{cos}}{{\varphi }_{a}})}^{{ - {\text{1}}}}}\left( {{{\alpha }_{{\text{1}}}} + {{\alpha }_{{\text{2}}}}{{u}_{{{\text{max}}}}}} \right)\Delta {{t}_{{\text{i}}}} - \\ - \;(3{\text{/}}2)ep{{c}^{{ - {\text{1}}}}}{\text{sin}}{{\varphi }_{a}}{{({\text{1}} + e{\text{cos}}{{\varphi }_{a}})}^{{ - {\text{2}}}}}{{\nu }_{{{\text{1}}a}}}({\text{sign}}{{\nu }_{{{\text{1i}}}}}{{u}_{{{\text{max}}}}})\Delta {{t}_{{\text{i}}}}, \\ \end{gathered} $Переходя в (2.22) к пределу в предположении, что umax → ∞, Δti → 0, получим, учитывая (2.3), связи значений χ(ti – 0) и χ(ti + 0) сопряженной переменной χ в начальный ti – 0 (перед сообщением импульса) и конечный ti + 0 (после сообщения импульса) моменты времени i-го активного участка:
(2.23)
$\begin{gathered} \chi \left( {{{t}_{{\text{i}}}} + 0} \right) = \chi \left( {{{t}_{{\text{i}}}} - 0} \right) + e{\text{sin}}{{\varphi }_{{\text{i}}}}{{({\text{1}} + e{\text{cos}}{{\varphi }_{{\text{i}}}})}^{{ - {\text{1}}}}}[{\text{sign}}{{\nu }_{{{\text{1i}}}}}{\text{2}}{{\alpha }_{{\text{2}}}} - \\ - \,\,\,(3{\text{/}}2)p{{c}^{{ - {\text{1}}}}}{{({\text{1}} + e{\text{cos}}{{\varphi }_{{\text{i}}}})}^{{ - {\text{1}}}}}{{\nu }_{{{\text{1i}}}}}]\Delta {{u}_{{\text{i}}}} \\ \end{gathered} $Формулу (2.23) можно переписать в другом виде:
(2.24)
$\begin{gathered} \chi \left( {{{t}_{{\text{i}}}} + 0} \right) = \chi \left( {{{t}_{{\text{i}}}} - 0} \right) + e{\text{sin}}{{\varphi }_{{\text{i}}}}{{({\text{1}} + e{\text{cos}}{{\varphi }_{{\text{i}}}})}^{{ - {\text{1}}}}} \\ \, \times [{\text{2}}{{\alpha }_{{\text{2}}}} - ({\text{3/2)}}p{{c}^{{ - {\text{1}}}}}{{({\text{1}} + e{\text{cos}}{{\varphi }_{{\text{i}}}})}^{{ - {\text{1}}}}}{\text{|}}{{\nu }_{{{\text{1i}}}}}{\text{|}}]({\text{sign}}{{\nu }_{{{\text{1i}}}}}\Delta {{u}_{{\text{i}}}}) \\ \end{gathered} $Учитывая, что в соответствии с (2.1) |ν1i| = 2α2(c/p)(1 + ecosφi), из (2.24) получаем окончательно следующую связь значений χ(ti – 0) и χ(ti + 0) сопряженной переменной χ в начальный ti – 0 и конечный ti + 0 моменты времени i-го активного участка траектории:
(2.25)
$\chi \left( {{{t}_{{\text{i}}}} + 0} \right) = \chi \left( {{{t}_{{\text{i}}}} - 0} \right) - {{\alpha }_{{\text{2}}}}e{\text{sin}}{{\varphi }_{{\text{i}}}}{{({\text{1}} + e{\text{cos}}{{\varphi }_{{\text{i}}}})}^{{ - {\text{1}}}}}{\text{|}}\Delta {{u}_{{\text{i}}}}{\text{|}}$Для круговой орбиты e = 0, поэтому $\chi (t_{{\text{i}}}^{ + }) = \chi (t_{{\text{i}}}^{ - })$.
Соотношение (2.25) можно записать в другом виде. Из (2.1) имеем
Подставляя это выражение в (2.25), получим
(2.26)
$\chi \left( {{{t}_{{\text{i}}}} + 0} \right) = \chi \left( {{{t}_{{\text{i}}}} - 0} \right) - (1{\text{/}}2)e{{p}^{{ - {\text{1}}}}}{{c}^{{ - {\text{1}}}}}{{r}_{{\text{i}}}}^{{\text{2}}}{\text{sin}}{{\varphi }_{{\text{i}}}}{{\nu }_{{{\text{1i}}}}}\Delta {{u}_{{\text{i}}}},\quad {{r}_{{\text{i}}}} = p{\text{/}}({\text{1}} + e{\text{cos}}{{\varphi }_{{\text{i}}}})$Отметим, что эта формула может быть получена другим путем. Запишем уравнение (4.4) [1] для переменной χ в таком виде:
Интегрируя левую и правую части этого уравнения на интервале времени $\Delta {{t}_{{\text{i}}}} = t_{{\text{i}}}^{ + } - t_{{\text{i}}}^{ - }$ с учетом того, что на этом интервале оптимальное управление uopt = = signν1umax, используя теорему о среднем и переходя в полученном уравнении к пределу в предположении, что umax → ∞, Δti → 0, получим, учитывая конечность переменных ν3 и χ, формулу (2.26).
Сопряженная переменная χ на пассивном участке траектории КА в соответствии с (5.16) [1] удовлетворяет соотношению
(2.27)
${{\nu }_{{\text{3}}}} + {\text{2}}\chi = {\text{2}}{{\alpha }_{{\text{1}}}}{{r}^{{\text{2}}}}{\text{/}}c$Поэтому, если момент сообщения импульса реактивного ускорения не совпадает с начальным t0 = 0 или конечным t1 моментом времени, т.е. является внутренним моментом времени сообщения импульса, то согласно (2.27) в эти моменты времени (точнее, в начальный ti – 0 и конечный ti + 0 моменты времени сообщения такого импульса) переменные ν3 и χ должны удовлетворять соотношению
Отсюда следует следующее соотношение для приращений этих переменных для внутреннего импульса:
Подставляя в предпоследнее равенство соотношения для ν3(ti + 0) и χ(ti + 0) из (2.20) и (2.24), получим дополнительное условие для внутреннего импульса в следующем виде:
(2.28)
$({\text{1}} - {\text{cos}}{{\vartheta }_{{\text{i}}}}){{\nu }_{{\text{3}}}}\left( {{{t}_{{\text{i}}}} - 0} \right) + {\text{sin}}{{\vartheta }_{{\text{i}}}}{{\nu }_{{\text{2}}}}\left( {{{t}_{{\text{i}}}} - 0} \right) + {\text{2}}{{\alpha }_{{\text{2}}}}e{\text{sin}}{{\varphi }_{{\text{i}}}}{{({\text{1}} + e{\text{cos}}{{\varphi }_{{\text{i}}}})}^{{ - {\text{1}}}}}{\text{|}}\Delta {{u}_{{\text{i}}}}{\text{|}} = 0$Таким образом, с использованием предельных переходов в дифференциальных уравнениях и соотношениях, полученных в задаче оптимальной переориентации орбиты КА с использованием кватернионного дифференциального уравнения ориентации орбитальной системы координат в нелинейной непрерывной постановке (с использованием ограниченной (малой) тяги) и приведенных в первой части статьи [1], получены соотношения, лежащие в основе импульсной оптимальной переориентации орбиты КА: формула (вторая из формул (2.11)), связывающая импульс реактивного ускорения Δui на i-м активном участке траектории с углом ϑi поворота орбиты КА вокруг радиуса-вектора центра масс КА, формула (первая из формул (2.11)) для приращения Δλi на этом участке траектории кватерниона λ ориентации орбитальной системы координат, формулы (2.18) и (2.25) (или (2.26)) для приращений Δμi и Δχi = χ(ti + 0) – ‒ χ(ti – 0) кватернионной μ и скалярной χ сопряженных переменных, а также формулы (2.20), связывающие значения переменных ν1, ν2, ν3, описывающих процесс переключения управления, в начальный ti – 0 (перед сообщением импульса) и конечный ti + 0 (после сообщения импульса) моменты времени i-го активного участка траектории. Получено, кроме того, дополнительное условие (2.28) для внутреннего импульса реактивной тяги.
2.2. Пассивный участок траектории КА. Пусть $t_{{\text{k}}}^{ - }{\text{ и }}t_{{\text{k}}}^{ + }$ – начало и конец k-го пассивного участка траектории КА, а Δtk – длительность пассивного участка: Δtk = $t_{{\text{k}}}^{ - }{\text{ }} - t_{{\text{k}}}^{ + }$. Тогда кватернион ориентации орбитальной системы координат λ и переменные ν1, ν2, ν3, описывающие линию переключения управления, будут на этом участке изменяться в соответствии с зависимостями, имеющими вид [1]:
(2.29)
$\begin{gathered} \lambda \left( t \right) = \lambda (t_{{\text{k}}}^{ - }) \circ [{\text{cos}}((1{\text{/}}2)(\varphi \left( t \right) - \varphi _{{\text{k}}}^{ - })) + {\text{sin}}((1{\text{/}}2)(\varphi \left( t \right) - \varphi _{{\text{k}}}^{ - })){{{\mathbf{i}}}_{{\text{3}}}}] \\ {{\nu }_{{\text{1}}}}\left( t \right) = {{\nu }_{{\text{1}}}}(t_{{\text{k}}}^{ - }){\text{cos}}(\varphi \left( t \right) - \varphi _{{\text{k}}}^{ - }) + {{\nu }_{{\text{2}}}}(t_{{\text{k}}}^{ - }){\text{sin}}(\varphi \left( t \right) - \varphi _{{\text{k}}}^{ - }) \\ {{\nu }_{{\text{2}}}}\left( t \right) = d{{\nu }_{{\text{1}}}}{\text{/}}d\varphi = - {{\nu }_{{\text{1}}}}(t_{{\text{k}}}^{ - }){\text{sin}}(\varphi \left( t \right) - \varphi _{{\text{k}}}^{ - }) + {{\nu }_{{\text{2}}}}(t_{{\text{k}}}^{ - }){\text{cos}}(\varphi \left( t \right) - \varphi _{{\text{k}}}^{ - }) \\ {{\nu }_{{\text{3}}}}\left( t \right) = {{\nu }_{{\text{3}}}}(t_{{\text{k}}}^{ - }) = {\text{const}} \\ t \in [t_{{\text{k}}}^{ - },{{t}_{{\text{k}}}}^{ + }],\quad \varphi \; \in \;[\varphi _{{\text{k}}}^{ - },\varphi _{{\text{k}}}^{ + }],\quad \varphi _{{\text{k}}}^{ - } = \varphi (t_{{\text{k}}}^{ - }),\quad \varphi _{{\text{k}}}^{ + } = \varphi (t_{{\text{k}}}^{ - }) \\ \end{gathered} $Здесь, по-прежнему, φ – истинная аномалия, определяемая в результате интегрирования дифференциального уравнения
(2.30)
$d\varphi {\text{/}}dt = c{\text{/}}{{r}^{{\text{2}}}},\quad r = p{\text{/}}({\text{1}} + e{\text{cos}}\varphi ),\quad c = {\text{const}}$Момент времени $t_{{\text{k}}}^{ + }$, соответствующий окончанию k-го пассивного участка, и отвечающее ему значение истинной аномалии $\varphi _{{\text{k}}}^{ + }$ = φ($t_{{\text{k}}}^{ + }$) находятся в результате интегрирования уравнения (2.30) до момента времени, при котором выполняется условие
На пассивном участке траектории функция Гамильтона–Понтрягина имеет в соответствии с (5.16) [1] следующий вид:
а сопряженная переменная χ находится в соответствии с (5.17) [1] по формуле:(2.31)
$\chi (t) = {{\alpha }_{{\text{1}}}}{{p}^{{\text{2}}}}{{c}^{{ - {\text{1}}}}}{{({\text{1}} + e{\text{cos}}\varphi (t))}^{{ - {\text{2}}}}} - (1{\text{/}}2){{\nu }_{{\text{3}}}}(t_{{\text{k}}}^{ - }),t\; \in \;[t_{{\text{k}}}^{ - },t_{{\text{k}}}^{ + }]$Приведенные конечные соотношения описывают изменение фазовых и сопряженных переменных на пассивном участке движения КА (кватернионная сопряженная переменная μ описывается соотношением, аналогичным соотношению для кватернионной фазовой переменной λ).
3. Алгоритм решения задачи оптимальной переориентации орбиты КА посредством импульсного реактивного ускорения. 3.1. Краевые условия задачи. В начальный t0 = 0 и конечный t1 моменты времени заданы начальные Ωu(0), I(0), ωπ(0) и конечные Ωu(t1), I(t1), ωπ(t1) значения угловых оскулирующих элементов орбиты (долготы восходящего узла Ωu, наклона орбиты I и углового расстояния перицентра от узла ωπ), характеризующие начальную и конечную ориентации орбиты КА. Также задано начальное значение φ0 = φ(0) истинной аномалии φ, характеризующее начальное положение КА на орбите.
По этим заданным значениям с помощью формул (2.4) [1]:
Начальные значения компонент кватерниона λ могут быть также найдены непосредственно по формулам (2.8) [1]:
через начальные значения угловых оскулирующих элементов орбиты Ωu, I, ωπ и истинной аномалии φ.При импульсном управлении последний участок должен быть активным. Поэтому конечный момент времени t = t1 должен совпадать с моментом сообщения последнего импульса реактивного ускорения (напомним, что длительностью активных участков при импульсном решении задач оптимального управления пренебрегается). Следовательно, в конечный момент времени должны выполняться векторное краевое условие (3.5) [1] (или скалярные краевые условия (3.6) ((3.7))) [1], второе из условий трансверсальности (4.9) [1] и условие (2.1), которое должно выполняться при включении импульсного двигателя:
(3.1)
${\text{vect}}[\tilde {\lambda }\left( {{{t}_{{\text{1}}}}} \right) \circ \Lambda \left( {{{t}_{{\text{1}}}}} \right) \circ ({\text{cos}}({{\varphi }_{{\text{1}}}}{\text{/2}}) + {{{\mathbf{i}}}_{{\text{3}}}}{\text{sin}}({{\varphi }_{{\text{1}}}}{\text{/2}}))] = 0$(3.2)
${\text{2}}\chi \left( {{{t}_{{\text{1}}}}} \right) + {{\nu }_{{\text{3}}}}\left( {{{t}_{{\text{1}}}}} \right) = 0$(3.3)
${\text{|}}{{\nu }_{{\text{1}}}}\left( {{{t}_{{\text{1}}}}} \right){\text{|}} = {\text{2}}{{\alpha }_{{\text{2}}}}c{\text{/}}r({{\varphi }_{{\text{1}}}}) = {\text{2}}{{\alpha }_{{\text{2}}}}\left( {c{\text{/}}p} \right)({\text{1}} + e{\text{cos}}{{\varphi }_{{\text{1}}}})$Пусть $t_{{\text{f}}}^{ - }\;{\text{и }}\;{\text{ }}t_{{\text{f}}}^{ + }$ – начало и конец последнего активного участка траектории КА. Длительность этого участка Δtf = $t_{{\text{f}}}^{ + }$ – $t_{{\text{f}}}^{ - }$ → 0, так что tf– → tf – 0, $t_{{\text{f}}}^{ + }$ → tf + 0 = t1, где tf ∈ $[t_{{\text{f}}}^{ - },t_{{\text{f}}}^{ + }]$ – некоторый фиксированный момент времени.
В конечный момент времени (в конце последнего активного участка) сопряженная переменная χ в соответствии с (2.26) принимает значение
где Δuf – величина последнего импульса реактивного ускорения, χ(tf – 0) – значение переменной χ в начальный tf – 0 момент времени последнего активного участка, равное значению этой переменной в конечный момент времени последнего пассивного участка траектории, которое в соответствии с (2.31) находится по формулеЗдесь ν3(tf – 0) – значение переменной ν3 в конце последнего пассивного участка траектории.
Используя последние соотношения и соотношение
вытекающее из (3.2), получим(3.4)
${{\nu }_{{\text{3}}}}({{t}_{{\text{f}}}} + 0) - {{\nu }_{{\text{3}}}}({{t}_{{\text{f}}}} - 0) = {{c}^{{ - {\text{1}}}}}{{(p{\text{/}}({\text{1}} + e{\text{cos}}{{\varphi }_{{\text{1}}}}))}^{{\text{2}}}}(e{{p}^{{ - {\text{1}}}}}{\text{sin}}{{\varphi }_{{\text{1}}}}{{\nu }_{{\text{1}}}}({{t}_{{\text{1}}}})\Delta {{u}_{{\text{f}}}} - {\text{2}}{{\alpha }_{{\text{1}}}})$Таким образом, в конечный момент времени должны выполняться условия (3.1), (3.3), (3.4) (пять скалярных условий, так как векторное условие (3.1) эквивалентно трем скалярным условиям (3.6) или (3.7) [1]).
Если начальный момент времени t0 = 0 совпадает с моментом сообщения первого импульса реактивной тяги, то при φ(0) = φ0 должно выполняться условие
(3.5)
${\text{|}}{{\nu }_{{\text{1}}}}\left( {{{t}_{0}}} \right){\text{|}} = {\text{2}}{{\alpha }_{{\text{2}}}}c{\text{/}}r({{\varphi }_{0}}) = {\text{2}}{{\alpha }_{{\text{2}}}}\left( {c{\text{/}}p} \right)({\text{1}} + e{\text{cos}}{{\varphi }_{0}})$Таким образом, если оптимальное управление переориентацией орбиты КА осуществляется с помощью двух импульсов реактивного ускорения, которые сообщаются КА в начальный и конечный моменты времени, то соотношения (3.1) (или (3.7) [1]), (3.3)–(3.5) дают шесть уравнений для определения шести неизвестных: начального (первого) импульса реактивного ускорения Δu1, конечного (второго) импульса ускорения Δu2, значения φ1 истинной аномалии в конечный момент времени t1 и трех начальных значений ν10, ν20, ν30 переменных ν1, ν2, ν3, описывающих линию переключения управления.
Если оптимальное управление переориентацией орбиты КА осуществляется с помощью одного импульса реактивного ускорения, который сообщается КА в конечный момент времени, то соотношения (3.1) (или (3.7) [1]), (3.3), (3.4) дают пять уравнений для определения пяти неизвестных Δu2, φ1, ν10, ν20, ν30.
Если оптимальное управление переориентацией орбиты КА включает внутренние импульсы реактивного ускорения, которые сообщаются КА во внутренние моменты времени tm ∈ [t0, t1], то каждый такой внутренний импульс порождает две новые неизвестные Δum, φm и два новых уравнения, имеющих вид (3.1) и (2.28), для их нахождения.
Отметим, что при решении задачи вместо четырех сопряженных переменных μj (компонент сопряженной кватернионной переменной μ) нами используются три переменные ν1, ν2, ν3. Эти переменные, определяемые соотношениями (5.6) [1] и удовлетворяющие соотношению (5.9) [1], являются композициями фазовых λj и сопряженных μj переменных и описывают собой дифференциальную линию переключения управления (они удовлетворяют замкнутой системе дифференциальных уравнений (2.16).
Отметим также, что в случае двухимпульсной оптимальной переориентации орбиты КА, когда импульсы реактивного ускорения сообщаются КА в начальный и конечный моменты времени, углы ϑ1 и ϑ2 поворотов орбиты, получаемые в результате сообщения КА первого и второго импульсов реактивного ускорения, и значение истинной аномалии φ1 = φ(t1) в конце переориентации орбиты могут быть найдены из отдельной замкнутой системы четырех скалярных нелинейных алгебраических уравнений, имеющих в кватернионной записи следующий вид:
(3.6)
$\begin{gathered} \Lambda \left( 0 \right) \circ [{\text{cos}}({{\varphi }_{0}}{\text{/2}}) + {{{\mathbf{i}}}_{{\text{3}}}}{\text{sin}}({{\varphi }_{0}}{\text{/2}})\left] {\; \circ \;} \right[{\text{cos}}((1{\text{/}}2){{\vartheta }_{{\text{1}}}}) + {{{\mathbf{i}}}_{{\text{1}}}}{\text{sin}}((1{\text{/}}2){{\vartheta }_{{\text{1}}}})] \circ \\ \circ \;[{\text{cos}}(({{\varphi }_{{\text{1}}}} - {{\varphi }_{0}}){\text{/2}}) + {{{\mathbf{i}}}_{{\text{3}}}}{\text{sin}}(({{\varphi }_{{\text{1}}}} - {{\varphi }_{0}}){\text{/2}})\left] {\; \circ \;} \right[{\text{cos}}((1{\text{/}}2){{\vartheta }_{{\text{2}}}}) + {{{\mathbf{i}}}_{{\text{1}}}}{\text{sin}}((1{\text{/}}2){{\vartheta }_{{\text{2}}}})] = \\ = \Lambda ({{t}_{{\text{1}}}}) \circ [{\text{cos}}({{\varphi }_{{\text{1}}}}{\text{/2}}) + {{{\mathbf{i}}}_{{\text{3}}}}{\text{sin}}({{\varphi }_{{\text{1}}}}{\text{/2}})] \\ \end{gathered} $Из этих четырех уравнений может быть выделена система трех независимых алгебраических уравнений для нахождения трех указанных величин (они образуют векторную часть приведенного кватернионного уравнения). После этого импульсы реактивного ускорения Δu1 и Δu2 находятся из соотношений
(3.7)
$\Delta {{u}_{{\text{1}}}} = \left( {c{\text{/}}p} \right)({\text{1}} + e{\text{cos}}{{\varphi }_{0}}){{\vartheta }_{{\text{1}}}},\quad \Delta {{u}_{{\text{2}}}} = \left( {c{\text{/}}p} \right)({\text{1}} + e{\text{cos}}{{\varphi }_{{\text{1}}}}){{\vartheta }_{{\text{2}}}}$Можно показать, что начальные значения ν10, ν20, ν30 переменных ν1, ν2, ν3, описывающих линию переключения управления, могут быть найдены в этом случае из соотношений
(3.8)
$\begin{gathered} {{\nu }_{{{\text{1}}0}}} = {\text{sign}}\Delta {{u}_{{\text{1}}}}{\text{2}}{{\alpha }_{{\text{2}}}}\left( {c{\text{/}}p} \right)({\text{1}} + e{\text{cos}}{{\varphi }_{0}}) \\ {{\nu }_{{{\text{2}}0}}} = {{\nu }_{{\text{2}}}}\left( {{{t}_{0}} + 0} \right){\text{cos}}{{\vartheta }_{{\text{1}}}} - {{\nu }_{{\text{3}}}}\left( {{{t}_{0}} + 0} \right){\text{sin}}{{\vartheta }_{{\text{1}}}} \\ {{\nu }_{{{\text{3}}0}}} = {{\nu }_{{\text{2}}}}\left( {{{t}_{0}} + 0} \right){\text{sin}}{{\vartheta }_{{\text{1}}}} + {{\nu }_{{\text{3}}}}\left( {{{t}_{0}} + 0} \right){\text{cos}}{{\vartheta }_{{\text{1}}}} \\ \end{gathered} $Таким образом, в случае двухимпульсной оптимальной переориентации орбиты КА, когда импульсы реактивного ускорения сообщаются КА в начальный и конечный моменты времени, решение задачи сводится к решению выше указанной системы трех скалярных нелинейных алгебраических уравнений.
Более того, можно показать, что в этом случае значения ϑ1 и ϑ2 углов оптимальных импульсных поворотов орбиты и значение истинной аномалии φ1 = φ(t1) в конце процесса переориентации могут быть найдены в явном виде аналитически, так как вышеприведенная алгебраическая система уравнений решается аналитически. Таким образом, двухимпульсная задача оптимальной переориентации орбиты КА, когда импульсы реактивного ускорения сообщаются КА в начальный и конечный моменты времени, решается в строгой нелинейной постановке аналитически.
Приведем общий алгоритм решения задачи оптимальной импульсной переориентации орбиты КА в случае нефиксированного числа импульсов реактивного ускорения.
3.2. Алгоритм для активного участка траектории. На i-м активном участке траектории КА вычисляются следующие величины:
1) Угол ϑi поворота орбиты КА вокруг радиуса–вектора центра масс КА при сообщении космическому аппарату i-го импульса реактивного ускорения Δui:
где φi = φ(ti – 0) = φ(ti + 0) = φ(ti) – значение истинной аномалии в начале i-го активного участка.2) Кватернион λ(ti + 0) ориентации орбитальной системы координат в конце i-го активного участка траектории:
где λ(ti – 0) – значение кватерниона ориентации орбитальной системы координат в начале i-го активного участка.3) Значения ν1(ti + 0), ν2(ti + 0), ν3(ti + 0) переменных ν1, ν2, ν3, описывающих линию переключения управления, в конце i-го активного участка:
где ν1(ti – 0), ν2(ti – 0), ν3(ti – 0) – значения переменных ν1, ν2, ν3 в начале i-го активного участка.Для внутреннего i-го импульса реактивного ускорения, сообщаемого КА во внутренние моменты времени, принадлежащие интервалу времени [t0, t1], для нахождения двух новых появляющихся неизвестных Δui, φi (внутреннего импульса реактивного ускорения и соответствующего ему значения истинной аномалии) используются дополнительные соотношения
3.3. Алгоритм для пассивного участка траектории. На k-м пассивном участке траектории КА вычисляются следующие величины:
1) Кватернион λ(t) ориентации орбитальной системы координат в текущий момент времени t ∈ [$t_{{\text{k}}}^{ - },t_{{\text{k}}}^{ + }$]:
2) Значения ν1(t), ν2(t), ν3(t) переменных ν1, ν2, ν3, описывающих линию переключения управления, в текущий момент времени t ∈ [$t_{{\text{k}}}^{ - }$, $t_{{\text{k}}}^{ + }$]:
Значение φ(t) истинной аномалии в текущий момент времени t ∈ [$t_{{\text{k}}}^{ - }$, $t_{{\text{k}}}^{ + }$] определяется в результате интегрирования дифференциального уравнения
(3.9)
$d\varphi {\text{/}}dt = c{{p}^{{ - {\text{2}}}}}{{({\text{1}} + e{\text{cos}}\varphi )}^{{\text{2}}}}$Момент времени $t_{{\text{k}}}^{ + }$, соответствующий окончанию k-го пассивного участка, и отвечающее ему значение истинной аномалии $\varphi _{{\text{k}}}^{ + }$ = φ($t_{{\text{k}}}^{ + }$) находятся в результате интегрирования уравнения (3.9) до момента времени, при котором выполняется условие
4. Примеры численного решения задачи импульсной оптимальной переориентации орбиты КА. Для численного решения задачи уравнения и соотношения краевой задачи оптимизации были записаны в безразмерной форме (заметим, что переменные λj и Λj (параметры Эйлера) и коэффициент функционала α1 являются безразмерными). Безразмерные переменные rb, tb, функционал оптимизации Jb, коэффициент функционала $\alpha _{2}^{b}$, управление ub и импульс реактивного ускорения Δub связаны с соответствующими размерными величинами соотношениями
4.1. Задача двухимпульсной переориентации орбиты КА, когда импульсы реактивного ускорения сообщаются КА в начальный и конечный моменты времени, решалась с использованием соотношений (3.6)–(3.8) для следующих параметров задачи: весовые множители функционала минимизации α1 = 0.25, $\alpha _{2}^{b}$ = 1.0; эксцентриситет орбиты e = 0.1. Отметим, что для выбранного режима управления весовые множители не влияют на величины импульсов и на длительность пассивного этапа полета КА, а влияют на величину функционала качества процесса управления и на сопряженные переменные.
Вариант 1. Начальная и конечная ориентации орбиты КА задаются следующими значениями угловых оскулирующих элементов орбиты:
${{I}_{{in}}} = 4.0^\circ ,{{\Omega }_{{uin}}} = 29.0^\circ ,{{\omega }_{{\pi in}}} = 26.0^\circ $; ${{I}_{{fin}}} = 5.0^\circ ,\,\,{{\Omega }_{{ufin}}} = 30.0^\circ ,\,\,{{\omega }_{{\pi fin}}}$ = 25.0°; начальная истинная аномалия ${{\varphi }_{{in}}} = 30.0^\circ $, кватернион λ ориентации орбитальной системы координат КА имеет в начальный момент времени компоненты, равные λ0 = 0.736828, ${{\lambda }_{1}} = 0.033935,{{\lambda }_{2}} = - 0.008147,{{\lambda }_{3}} = 0.675179$.
В результате численного решения задачи получено следующее:
1) Первый импульс реактивного ускорения $\Delta u_{1}^{b}$ = 0.008486 сообщается КА в начальный момент времени t = 0.0; первый угол поворота орбиты ϑ1 = 0.4475°; кватернион λ ориентации орбитальной системы координат КА после сообщения ему первого импульса тяги имеет компоненты, равные
2) На пассивном участке ориентация орбиты КА определяется следующими значениями угловых оскулирующих элементов орбиты:

Длительность пассивного полета Δtb = 1.7690, при этом истинная аномалия КА изменяется в пределах: $30.0^\circ \leqslant \varphi \leqslant 133.2501^\circ $.
3) Кватернион λ ориентации орбитальной системы координат КА перед сообщением второго импульса реактивной тяги имеет компоненты, равные ${{\lambda }_{0}} = - 0.071996$, λ1 = 0.018533, λ2 = –0.032280, λ3 = 0.996710.
4) Второй (конечный) импульс реактивного ускорения $\Delta u_{2}^{b}$ = – 0.013022 сообщается КА при tb = 1.7690; второй угол поворота орбиты ϑ2 = –0.8010°; кватернион λ ориентации орбитальной системы координат КА после сообщения второго импульса ускорения имеет компоненты, равные
5) Безразмерное время движения КА tb = 1.7690; истинная аномалия φ, характеризующая конечное положение КА на орбите, равна 133.2501°.
6) Значение функционала минимизации Jb = 0.463746, сумма модулей импульсов равна 0.021508.
7) При численном решении задачи были вычислены координаты νk вектора ν в начальный момент времени (перед сообщением первого импульса) и в конечный момент времени (перед сообщением второго импульса), проверено выполнение условия отсутствия тяги (2.2) на пассивном этапе управления.
Вариант 2. Начальная и конечная ориентации орбиты КА задаются следующими значениями угловых оскулирующих элементов орбиты:
${{I}_{{{\text{in}}}}} = 15.0^\circ ,\,\,{{\Omega }_{{u{\text{in}}}}} = 30.0^\circ ,\,\,{{\omega }_{{\pi {\text{in}}}}} = 60.0^\circ $; ${{I}_{{{\text{fin}}}}} = 5.0^\circ ,\,\,{{\Omega }_{{u{\text{fin}}}}} = 40.0^\circ ,\,\,{{\omega }_{{\pi {\text{fin}}}}} = 50.0^\circ $; начальная истинная аномалия ${{\varphi }_{{{\text{in}}}}} = 30.0^\circ $, кватернион λ ориентации орбитальной системы координат КА имеет в начальный момент времени компоненты, равные
В результате численного решения задачи получено следующее:
1) Первый импульс реактивного ускорения $\Delta u_{1}^{b}$ = –0.024467 сообщается КА в начальный момент времени t = 0.0; первый угол поворота орбиты ϑ1 = –1.2901°; кватернион λ ориентации орбитальной системы координат КА после сообщения ему первого импульса тяги имеет компоненты, равные ${{\lambda }_{0}} = 0.496964,$ ${{\lambda }_{1}} = 0.107451$, λ2 = = ‒0.074925, λ3 = 0.857827.
2) На пассивном участке ориентация орбиты КА определяется следующими значениями угловых оскулирующих элементов орбиты: ${{I}_{{{\text{pas}}}}} = 15.0541^\circ ,$ Ωupas = 25.0271°, ${{\omega }_{{\pi {\text{pas}}}}} = 64.8030^\circ .$
Длительность пассивного полета Δtb = 1.2792, при этом истинная аномалия КА изменяется в пределах: $30.0^\circ \leqslant \varphi \leqslant 107.9644^\circ $.
3) Кватернион λ ориентации орбитальной системы координат КА перед сообщением второго импульса реактивного ускорения имеет компоненты, равные λ0 = = $ - 0.153331,{{\lambda }_{1}} = 0.036392$, λ2 = –0.125838, λ3 = 0.979454.
4) Второй (конечный) импульс реактивного ускорения $\Delta u_{2}^{b}$ = 0.174280 сообщается КА при tb = 1.2792; второй угол поворота орбиты ϑ2 = 10.3033°; кватернион λ ориентации орбитальной системы координат КА после сообщения второго импульса тяги имеет компоненты, равные ${{\lambda }_{0}} = - 0.155979\,,$ ${{\lambda }_{1}} = 0.022477,$ ${{\lambda }_{2}} = - 0.037382$, λ3 = = 0.986797.
5) Безразмерное время движения КА tb = 1.2792; истинная аномалия φ, характеризующая конечное положение КА на орбите, равна 107.9644°.
6) Значение функционала минимизации Jb = 0.518558, сумма модулей импульсов равна 0.198747.
7) При численном решении задачи, как и в первом примере, были вычислены координаты νk вектора ν в начальный момент времени (перед сообщением первого импульса) и в конечный момент времени (перед сообщением второго импульса), проверено выполнение условия отсутствия тяги (2.2) на пассивном этапе управления.
4.2. С помощью программы, в которой реализован алгоритм оптимальной импульсной переориентации орбиты КА без условия на число импульсов (для нефиксированного числа импульсов), проведены расчеты для двух вариантов начальной и конечной ориентации орбиты КА для различных значений весовых множителей в функционале, определяющем качество процесса управления.
Вариант 1. Начальная и конечная ориентации орбиты КА задаются следующими значениями угловых оскулирующих элементов орбиты: Iin = 5.0°, Ωuin = 30.0°, ${{\omega }_{{\pi {\text{in}}}}} = 25.0^\circ $; ${{I}_{{{\text{fin}}}}} = 40.0^\circ ,{{\Omega }_{{u{\text{fin}}}}} = 345.0^\circ ,{{\omega }_{{\pi {\text{fin}}}}} = 65.0^\circ $; начальная истинная аномалия ${{\varphi }_{{{\text{in}}}}} = 30.0^\circ $, эксцентриситет орбиты е = 0.1. Компоненты кватерниона λ ориентации орбитальной системы координат в начальный момент времени t = 0 имеют следующие значения:
Оптимальный процесс управления состоит из двух пассивных этапов и двух импульсов реактивного ускорения. Первый этап пассивный на промежутке времени $0 \leqslant t < {{t}_{1}}$, в момент $t = {{t}_{1}}$ с помощью двигателя большой тяги, ортогональной плоскости оскулирующей орбиты, космическому аппарату сообщается первый импульс реактивного ускорения, под действием которого совершается первый поворот орбиты КА вокруг радиуса-вектора центра масс КА. Далее, на втором этапе, на промежутке времени ${{t}_{1}} < t < {{t}_{2}}$ КА движется по орбите пассивного полета, в момент $t = {{t}_{2}}$ ему сообщается второй импульс ускорения, поворачивающий орбиту КА в ее конечную заданную ориентацию.
Оптимальная импульсная переориентация орбиты КА для весовых множителей α1 = = 0.5, ${{\alpha }_{2}} = 1.0$ функционала минимизации.
1) Первый импульс ускорения сообщается КА в момент $t_{1}^{b}$ = 1.6030, когда истинная аномалия ${{\varphi }_{1}}$ = 125.5778°, а параметры Родрига–Гамильтона λj, характеризующие ориентацию орбитальной системы координат, имеют значения: ${{\lambda }_{0}} = - 0.008525,$ λ1 = = 0.021487, ${{\lambda }_{2}} = - 0.037960,$ ${{\lambda }_{3}} = 0.999012{\text{;}}$ величина импульса $\Delta u_{1}^{b}$ = –0.55806, угол поворота орбиты ϑ1 = –33.9700°; значения параметров λj после сообщения импульса: ${{\lambda }_{0}} = - 0.001876,$ λ1 = 0.023040, ${{\lambda }_{2}} = - 0.328138$, ${{\lambda }_{3}} = 0.944347$.
2) Ориентация орбиты пассивного полета (после первого поворота орбиты) определяется классическими угловыми элементами ${{I}_{{{\text{pas}}}}} = 38.4096^\circ ,$ Ωupas = 4.1302°, ${{\omega }_{{\pi {\text{pas}}}}} = 50.1197^\circ .$
Длительность второго пассивного этапа $\Delta t_{{2{\text{pas}}}}^{b}$ = 2.0024.
3) Второй импульс ускорения сообщается КА в момент $t_{2}^{b}$ = 3.6054, когда истинная аномалия ${{\varphi }_{2}}$ = 219.8639°, а значения параметров λj следующие: ${{\lambda }_{0}}$ = –0.691292, ${{\lambda }_{1}} = - 0.224032,$ ${{\lambda }_{2}} = - 0.240862,$ ${{\lambda }_{3}} = 0.643358$; величина импульса $\Delta u_{2}^{b}$ = 0.195950, угол поворота орбиты ϑ2 = 12.1605°.
После сообщения второго импульса ориентация орбиты совпала с заданной конечной ориентацией, а значения параметров λj приняли следующие значения: ${{\lambda }_{0}} = - 0.663674$, ${{\lambda }_{1}} = - 0.295995$, ${{\lambda }_{2}} = - 0.171362$, ${{\lambda }_{3}} = 0.665252$.
Сумма абсолютных величин сообщенных импульсов равна 0.754009, значение функционала равно 2.556722.
Оптимальная импульсная переориентация орбиты КА для весовых множителей ${{\alpha }_{1}} = 0.25\,,\,\,\,{{\alpha }_{2}} = 1.0$ функционала минимизации.
1) Первый импульс тяги сообщается КА в момент $t_{1}^{b}$ = 1.6739, когда истинная аномалия ${{\varphi }_{1}}$ = 129.5620°, а параметры Родрига–Гамильтона λj, характеризующие ориентацию орбитальной системы координат, имеют значения:
Величина импульса $\Delta u_{1}^{b}$ = –0.473565, угол поворота орбиты ϑ1 = –28.9790°; значения параметров λj после сообщения импульса: ${{\lambda }_{0}} = - 0.033421$, ${{\lambda }_{1}} = 0.029592$, ${{\lambda }_{2}} = - 0.287152$, ${{\lambda }_{3}} = 0.956844$.
2) Ориентация орбиты пассивного полета (после первого поворота орбиты) определяется классическими угловыми элементами ${{I}_{{{\text{pas}}}}} = 33.5570^\circ $, ${{\Omega }_{{u{\text{pas}}}}} = 7.8842^\circ $, ωπpas = 46.5547°.
Длительность второго пассивного этапа $\Delta t_{{2{\text{pas}}}}^{b}$ = 2.3138.
3) Второй импульс тяги сообщается КА в момент $t_{2}^{b}$ = 3.9878, когда истинная аномалия ${{\varphi }_{2}}$ = 239.1014°, а значения параметров λj следующие: ${{\lambda }_{0}} = - 0.800868$,
Величина импульса $\Delta u_{2}^{b}$ = 0.249115, угол поворота орбиты ϑ2 = 15.0459°.
После сообщения второго импульса ориентация орбиты совпала с заданной конечной ориентацией, а значения параметров λj приняли следующие значения: λ0 = –0.765501, λ1 = –0.320467, ${{\lambda }_{2}} = - 0.119495$, ${{\lambda }_{3}} = 0.545005$.
Сумма абсолютных величин сообщенных импульсов равна 0.722680, значение функционала равно 1.719623.
Оптимальная импульсная переориентации орбиты КА для весовых множителей α1 = 0.125, ${{\alpha }_{2}} = 1.0$ функционала минимизации.
1) Первый импульс тяги сообщается КА в момент $t_{1}^{b}$ = 1.7271, когда истинная аномалия ${{\varphi }_{1}}$ = 132.2264°, а параметры Родрига–Гамильтона λj, характеризующие ориентацию орбитальной системы координат, имеют значения:
Величина импульса $\Delta u_{1}^{b}$ = –0.0426010, угол поворота орбиты ϑ1 = –26.1672°; значения параметров λj после сообщения импульса: ${{\lambda }_{0}} = - 0.056938$, ${{\lambda }_{1}} = 0.033135$, ${{\lambda }_{2}} = - 0.263768$, ${{\lambda }_{3}} = 0.9623$.
2) Ориентация орбиты пассивного полета (после первого поворота орбиты) определяется классическими угловыми элементами ${{I}_{{{\text{pas}}}}} = 30.8339^\circ $, ${{\Omega }_{{u{\text{pas}}}}} = 10.5461^\circ $, ${{\omega }_{{\pi {\text{pas}}}}} = 43.9995^\circ $.
Длительность второго пассивного этапа $t_{{2{\text{pas}}}}^{b}$ = 2.4076.
3) Второй импульс ускорения сообщается КА в момент $t_{2}^{b}$ = 4.1347, когда истинная аномалия ${{\varphi }_{2}}$ = 246.8083°, а значения параметров λj следующие: ${{\lambda }_{0}} = - 0.840500$, ${{\lambda }_{1}} = - 0.204036$, ${{\lambda }_{2}} = - 0.170414$, ${{\lambda }_{3}} = 0.4721$.
Величина импульса $\Delta u_{2}^{b}$ = 0.289207, угол поворота орбиты ϑ2 = 17.2496°.
После сообщения второго импульса ориентация орбиты совпала с заданной конечной ориентацией, а значения параметров λj приняли следующие значения: ${{\lambda }_{0}} = - 0.800397$, ${{\lambda }_{1}} = - 0.327773$, $\,{{\lambda }_{2}} = - 0.097687$, ${{\lambda }_{3}} = 0.492328$.
Сумма абсолютных величин сообщенных импульсов равна 0.715217, значение функционала равно 1.232058.
Оптимальный импульсная переориентации орбиты КА для весовых множителей α1 = 0.0, ${{\alpha }_{2}} = 1.0$ функционала минимизации (минимизируется характеристическая скорость).
1) Первый импульс ускорения сообщается КА в момент $t_{1}^{b}$ = 1.7907, когда истинная аномалия ${{\varphi }_{1}}$ = 135.3789°, а параметры Родрига–Гамильтона λj, характеризующие ориентацию орбитальной системы координат, имеют значения: ${{\lambda }_{0}} = - 0.090364$, ${{\lambda }_{1}} = 0.018304$, ${{\lambda }_{2}} = - 0.039593$, ${{\lambda }_{3}} = 0.994953$.
Величина импульса $\Delta u_{1}^{b}$ = –0.381300, угол поворота орбиты ϑ1 = –23.5210°; значения параметров λj после сообщения импульса: ${{\lambda }_{0}} = - 0.084736$, ${{\lambda }_{1}} = 0.036337$, ${{\lambda }_{2}} = - 0.241555$, ${{\lambda }_{3}} = 0.96599$7.
2) Ориентация орбиты пассивного полета (после первого поворота орбиты) определяется классическими угловыми элементами ${{I}_{{{\text{pas}}}}} = 28.2777^\circ $, ${{\Omega }_{{u{\text{pas}}}}} = 13.5680^\circ $, ${{\omega }_{{\pi {\text{pas}}}}} = 41.0792^\circ $.
Длительность второго пассивного этапа $\Delta t_{{2{\text{pas}}}}^{b}$ = 2.450434.
3) Второй импульс ускорения сообщается КА в момент $t_{2}^{b}$ = 4.2411, когда истинная аномалия ${{\varphi }_{2}}$ = 252.5139°, а значения параметров λj следующие: ${{\lambda }_{0}} = - 0.868431$, ${{\lambda }_{1}} = - 0.187158$, ${{\lambda }_{2}} = - 0.156975$, ${{\lambda }_{3}} = 0.431460$.
Величина импульса $\Delta u_{2}^{b}$ = 0.331772, угол поворота орбиты ϑ2 = 19.5980°.
После сообщения второго импульса ориентация орбиты совпала с заданной конечной ориентацией, а значения параметров λj приняли следующие значения: ${{\lambda }_{0}} = - 0.823908$, ${{\lambda }_{1}} = - 0.332228$, ${{\lambda }_{2}} = - 0.081253$, ${{\lambda }_{3}} = 0.451882$.
Сумма абсолютных величин сообщенных импульсов равна 0.713073, значение функционала равно 0.713073.
В табл. 1 представлены моменты времени сообщения первого и второго импульсов реактивного ускорения, значения истинных аномалий КА в эти моменты и значения импульсов для различных значений весового множителя ${{\alpha }_{1}}$.
Таблица 1
| α1 | $t_{1}^{b}$ | $\varphi _{1}^{^\circ }$ | Δ$u_{1}^{b}$ | $t_{2}^{b}$ | $\varphi _{2}^{^\circ }$ | Δu2b |
|---|---|---|---|---|---|---|
| 0.5 | 1.6030 | 125.9778 | –0.558059 | 3.605426 | 219.8639 | 0.195950 |
| 0.25 | 1.6739 | 129.5620 | –0.473565 | 3.987771 | 239.1014 | 0.249115 |
| 0.125 | 1.7271 | 132.2264 | –0.426010 | 4.134727 | 246.8083 | 0.289207 |
| 0.0 | 1.7907 | 135.3789 | –0.381300 | 4.241088 | 252.5139 | 0.331772 |
В табл. 2 приведены углы поворотов орбит под действием первого и второго импульсов реактивного ускорения, угловые элементы орбиты пассивного полета между первым и вторым импульсом и значения функционала качества процесса управления для различных значений весового множителя ${{\alpha }_{1}}$.
Таблица 2
| α1 | $\vartheta _{1}^{^\circ }$ | $\vartheta _{2}^{^\circ }$ | $I_{{{\text{pas}}}}^{^\circ }$ | $\Omega _{{u{\text{pas}}}}^{^\circ }$ | $\omega _{{\pi {\text{pas}}}}^{^\circ }$ | Jb |
|---|---|---|---|---|---|---|
| 0.5 | –33.9701 | 12.1605 | 38.4096 | 4.1302 | 50.1197 | 2.556722 |
| 0.25 | –28.9790 | 15.0459 | 33.5570 | 7.8842 | 46.5547 | 1.719623 |
| 0.125 | –26.1672 | 17.2496 | 30.8339 | 10.5462 | 43.9995 | 1.232058 |
| 0.0 | –23.5210 | 19.5980 | 28.2777 | 13.5680 | 41.0792 | 0.713073 |
Вариант 2. Начальная и конечная ориентации орбиты КА задаются следующими значениями угловых оскулирующих элементов орбиты: Iin = 20.0°, ${{\Omega }_{{u{\text{in}}}}} = 30.0^\circ $, ωπin = 25.0°; ${{I}_{{{\text{fin}}}}} = 30.0^\circ ,\,\,{{\Omega }_{{u{\text{fin}}}}} = 345.0^\circ ,\;\,{{\omega }_{{\pi {\text{fin}}}}} = 65.0^\circ $; начальная истинная аномалия ${{\varphi }_{{{\text{in}}}}}$ = 30.0°, эксцентриситет орбиты е = 0.1. Компоненты кватерниона λ ориентации орбитальной системы координат в начальный момент времени t = 0 имеют следующие значения: ${{\lambda }_{0}} = 0.726076$, ${{\lambda }_{1}} = 0.169532$, ${{\lambda }_{2}} = - 0.037584$, ${{\lambda }_{3}}$ = 0.665326.
Оптимальный процесс управления состоит из двух пассивных этапов и двух импульсов реактивного ускорения. Первый этап пассивный на промежутке времени $0 \leqslant t < {{t}_{1}}$, в момент $t = {{t}_{1}}$ с помощью двигателя большой тяги, ортогональной плоскости оскулирующей орбиты, космическому аппарату сообщается первый импульс реактивного ускорения, под действием которого совершается первый поворот орбиты КА вокруг радиуса-вектора центра масс КА. Далее, на втором этапе, на промежутке времени ${{t}_{1}} < t < {{t}_{2}}$ КА движется по орбите пассивного полета, в момент $t = {{t}_{2}}$ ему сообщается второй импульс ускорения, поворачивающий орбиту КА в ее конечную заданную ориентацию.
В табл. 3 представлены моменты времени сообщения первого и второго импульсов реактивного ускорения, значения истинных аномалий КА в эти моменты и значения импульсов для различных значений весового множителя ${{\alpha }_{1}}$.
Таблица 3
| ${{\alpha }_{1}}$ | $t_{1}^{b}$ | $\varphi _{1}^{^\circ }$ | Δ$u_{1}^{b}$ | $t_{2}^{b}$ | $\varphi _{2}^{^\circ }$ | Δ$u_{2}^{b}$ |
|---|---|---|---|---|---|---|
| 0.5 | 1.008009 | 94.1847 | –0.314067 | 3.019755 | 191.9564 | 0.128770 |
| 0.25 | 1.120844 | 100.4874 | –0.248028 | 3.420030 | 210.8718 | 0.172574 |
| 0.125 | 1.198080 | 104.7225 | –0.218057 | 3.541757 | 216.7531 | 0.198242 |
| 0.0 | 1.276359 | 108.9480 | –0.195241 | 3.617849 | 220.4720 | 0.220003 |
В табл. 4 приведены углы поворотов орбит под действием первого и второго импульсов реактивного ускорения, угловые элементы орбиты пассивного полета между первым и вторым импульсом и значения функционала качества процесса управления для различных значений весового множителя ${{\alpha }_{1}}$.
Таблица 4
| ${{\alpha }_{1}}$ | $\vartheta _{1}^{^\circ }$ | $\vartheta _{2}^{^\circ }$ | $I_{{{\text{pas}}}}^{^\circ }$ | $\Omega _{{u{\text{pas}}}}^{^\circ }$ | $\omega _{{\pi {\text{pas}}}}^{^\circ }$ | Jb |
|---|---|---|---|---|---|---|
| 0.5 | –18.1270 | 8.1780 | 32.7365 | 359.8483 | 52.2991 | 1.952714 |
| 0.25 | –14.4744 | 10.8161 | 30.6566 | 6.4756 | 46.4079 | 1.275609 |
| 0.125 | –12.8196 | 12.3478 | 29.7993 | 9.9155 | 43.3163 | 0.859019 |
| 0.0 | –11.5619 | 13.6431 | 29.1849 | 12.7870 | 40.7218 | 0.415244 |
Из анализа табл. 1–4 видно, что с уменьшением весового множителя ${{\alpha }_{1}}$ функционала минимизации, характеризующего затраты времени на процесс оптимальной переориентации орбиты КА, при неизменном значении множителя ${{\alpha }_{2}}$, характеризующего затраты характеристической скорости, происходит увеличение длительностей первого и второго пассивных этапов, увеличение значений истинных аномалий, характеризующих положения КА на орбите в моменты сообщения импульсов. При этом абсолютные величины первых импульсов убывают, а величины вторых импульсов возрастают, суммы абсолютных величин импульсов и значения функционалов убывают, а длительности процесса управления возрастают.
Заключение. В статье в строгой нелинейной постановке построены теория и алгоритмы численного решения задачи оптимальной импульсной переориентации орбиты КА посредством большой реактивной тяги, ортогональной плоскости оскулирующей орбиты КА, с использованием кватернионного дифференциального уравнения ориентации орбитальной системы координат для нефиксированного числа импульсов реактивного ускорения центра масс КА (в качестве управления используется вектор реактивного ускорения от тяги двигателя). Минимизируется комбинированный функционал, равный взвешенной сумме времени переориентации и импульса реактивного ускорения (характеристической скорости) за время переориентации орбиты КА (частный случай этого функционала – случай минимизации характеристической скорости). Построенные алгоритмы позволяют при численном решении задачи определять оптимальные моменты включения реактивного двигателя, оптимальные величины импульсов реактивного ускорения и их оптимальное число. Приведены примеры численного решения задачи оптимальной импульсной переориентации орбиты КА, иллюстрирующие возможности предлагаемого метода.
Частным случаем рассматриваемой задачи является хорошо известная и имеющая большое практическое значение задача коррекции угловых элементов орбиты КА. Использование указанного управления позволяет изменять элементы орбиты КА, сохраняя форму и размеры оскулирующей орбиты КА неизменными. Это ценное свойство изученного процесса переориентации орбиты КА является полезным как при решении задачи коррекции угловых элементов орбиты КА, так и других задач механики космического полета, например, при управлении конфигурацией группировки спутников.
Список литературы
Сапунков Я.Г., Челноков Ю.Н. Импульсная оптимальная переориентация орбиты космического аппарата посредством реактивной тяги, ортогональной плоскости оскулирующей орбиты. I // Изв. РАН. МТТ. 2018. № 5. C. 70–89.
Griffin M., French J. Space Vehicle Design. AIAA Education Series, 2004. 665 p.
Ильин В.А., Кузмак Г.Е. Оптимальные перелеты космических аппаратов с двигателями большой тяги. M.: Наука, 1976. 741 с.
Челноков Ю.Н. Оптимальная переориентация орбиты космического аппарата посредством реактивной тяги, ортогональной плоскости орбиты // Математика. Механика: Сб. науч. тр. Саратов: Изд-во Сарат. ун-та, 2006. Вып. 8. С. 231–234.
Челноков Ю.Н. Оптимальная переориентация орбиты космического аппарата: Кватернионный подход к решению задачи // Проблемы и перспективы прецезионной механики и управления в машиностроении: Материалы междунар. конф. / ИПТМУ РАН. Саратов: Изд-во СГТУ. 2006. С. 54–60.
Челноков Ю.Н. Оптимальная переориентация орбиты космического аппарата посредством реактивной тяги, ортогональной плоскости орбиты // Прикладная математика и механика. 2012. Т. 76. Вып. 6. С. 897–914.
Панкратов И.А., Сапунков Я.Г., Челноков Ю.Н. Решение задачи оптимальной переориентации орбиты космического аппарата с использованием кватернионных уравнений ориентации орбитальной системы координат // Изв. Сарат. ун-та. Нов. сер. 2013. Т. 13. Сер. Математика. Механика. Информатика, Вып. 1. Ч. 1. С. 84–92.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела