Известия РАН. Механика твердого тела, 2019, № 1, стр. 23-49
МОДЕЛИРОВАНИЕ ЗАНОСА АППАРАТА С ПОВЕРНУТЫМИ ПЕРЕДНИМИ КОЛЕСАМИ
А. В. Влахова a, *, А. П. Новодерова a, **
a Московский государственный университет имени М.В. Ломоносова
Москва, Россия
* E-mail: vlakhova@mail.ru
** E-mail: an.novoderova@yandex.ru
Поступила в редакцию 26.02.2018
После доработки 26.03.2018
Принята к публикации 11.04.2018
Аннотация
Рассмотрена задача о заносе двухосного четырехколесного аппарата на горизонтальной однородной плоскости, возникающем при блокировке или пробуксовке колес одной из его осей. Колеса другой оси аппарата сохраняют или теряют сцепление с опорной плоскостью. Обсуждаются случаи, когда следование принятой в теории вождения автомобиля рекомендации “поворачивать руль (передние колеса) в сторону заноса задней оси” позволяет уменьшить угловую скорость аппарата скорее, чем при неповернутых или повернутых в другую сторону передних колесах.
1. Введение. Причины возникновения заноса разнообразны и перечислены во многих работах, однако открытых теоретических исследований поведения колесных аппаратов при его возникновении существенно меньше. По коммерческим причинам фирмы, занимающиеся конструированием аппаратов, не дают информации об алгоритмах работы систем, обеспечивающих безопасность их движения. Вместе с тем даже у ведущих фирм возникают проблемы с работоспособностью таких систем. В настоящей работе построены математические модели начальной стадии заноса двухосного четырехколесного аппарата (автомобиля, робота), возникающего при блокировке или пробуксовке колес одной из его осей, в ходе которого колеса другой оси сохраняют сцепление с опорной плоскостью или начинают скользить по ней.
Для адекватного описания заноса следует определить модель сил взаимодействия колес аппарата с опорной плоскостью, отвечающую рассматриваемой задаче. В теории движения аппаратов традиционно пренебрегают моментами трения верчения, которые возникают из-за вращения колес вокруг осей, ортогональных областям их контакта с опорными поверхностями. Однако такое пренебрежение приводит к некорректной по Адамару постановке задач [1, 2], в связи с чем необходимо проводить оценку влияния верчения на динамику системы.
Поскольку движение, при котором колеса не заблокированной или не пробуксовывающей оси сохраняют сцепление с опорной плоскостью, более вероятно для аппаратов с пневматическими деформируемыми колесами, в работе оно рассматривается в предположении их непроскальзывания, а контакт заблокированных или пробуксовывающих колес с опорной плоскостью – в рамках традиционной модели кулонова трения. Эти модели являются предельными для модели взаимодействия колес с опорной плоскостью [3–5], сформированной на основе щеточной (brush) и схожих моделей описания контактных сил и моментов [6, 7], которые учитывают наличие зон проскальзывания и сцепления в областях контакта. Подходы к обоснованию предположения об отсутствии верчения для таких систем изложены в [5, 7, 8]. В рассматриваемой работе пренебрежение верчением можно обосновать тем, что [1, 2, 4] на начальной стадии заноса аппарата поперечная и угловая скорости его корпуса принимают небольшие значения.
В случае, когда все колеса аппарата теряют сцепление с опорной плоскостью (начинают скользить), их контакт описывается как при помощи модели кулонова трения, так и модели поликомпонентного сухого трения. При изучении начальной стадии заноса аппарата первая модель иллюстрирует движение в пренебрежении размерами областей контакта колес с опорной плоскостью; вторая позволяет обсудить ограничения значений угловой скорости верчения и размеров областей контакта, при которых моменты трения верчения оказывают влияние на движение аппарата с достаточно жесткими колесами.
Математические модели динамики аппарата формируются с использованием методов фракционного анализа [4, 5] и теории сингулярных возмущений [9]. Возможность применения этих методов связана с тем, что на начальной стадии заноса малые поперечная и угловая скорости корпуса аппарата изменяются быстро по сравнению с его продольной скоростью, а также с малостью масс колес по сравнению с массой аппарата. После разделения быстрых и медленных движений аппарата в работе с использованием метода фазовой плоскости проводится аналитическое исследование влияния угла поворота передних колес и моделей сухого трения, описывающих контакт колес с опорной плоскостью, на занос аппарата. Работа, продолжающая исследования [4, 10–12], может быть использована при создании систем управления рулем (передними колесами) аппаратов, обеспечивающих прекращение заноса или минимизацию его отрицательных последствий.
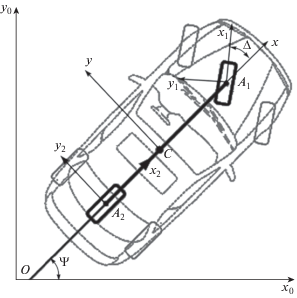
2. Постановка задачи и уравнения движения аппарата. Рассмотрим движение двухосного четырехколесного аппарата по горизонтальной однородной плоскости. В результате блокировки или пробуксовки колеса одной из осей аппарата теряют сцепление с опорной плоскостью (начинают скользить), что приводит к его заносу. Будем изучать начальную стадию этого процесса, возникающего после завершения блокировки или пробуксовки колес, когда поперечная и угловая скорости корпуса аппарата невелики. Для такого движения силы взаимодействия колес одной оси аппарата с опорной плоскостью различаются мало, и для описания его динамики может быть использована [4, 10–13] “велосипедная” модель, в рамках которой два передних (управляемых) колеса заменяют одним эквивалентным передним колесом, два задних – одним задним и пренебрегают боковыми наклонами корпуса (фиг. 1). Будем считать, что в случае, когда колесо аппарата не потеряло сцепление с опорной плоскостью, оно не проскальзывает относительно нее (при этом на обобщенные координаты и скорости системы накладываются соответствующие неголономные связи); колесо, потерявшее сцепление с опорной плоскостью, взаимодействует с ней посредством сухого трения. Составим уравнения движения исследуемой модели.
Свяжем с опорной плоскостью неподвижный трехгранник Ox0y0z0, с центрами масс C, A1 и A2 корпуса, первого – переднего и второго – заднего колес аппарата (последние далее считаются одинаковыми) – трехгранники Cxyz, A1x1y1z1 и A2x2y2z2. Оси Oz0, Cz, A1z1, A2z2 ориентированы по вертикали; оси Cx, A1x1, A2x2 лежат в плоскостях продольной симметрии корпуса и колес соответственно и направлены вперед по ходу движения (фиг. 1). Положение аппарата определяется декартовыми координатами X, Y точки C в системе координат Ox0y0z0, углом Ψ поворота его корпуса вокруг оси Cz, углами Θ1, Θ2 поворота переднего и заднего колес вокруг осей A1y1 и A2y2 их вращения и углом Δ поворота переднего колеса относительно корпуса вокруг оси A1z1. Как и в [4, 10–13], ограничимся случаем, когда масса колеса существенно меньше массы аппарата, и будем считать, что центр масс последнего находится в точке C.
Составим уравнения движения аппарата из уравнений изменения количества движения точки C в проекциях на оси трехгранника Cxyz, уравнений изменения его кинетического момента относительно точки C в проекциях на оси Cy и Cz, уравнений изменения кинетических моментов переднего и заднего колес относительно осей A1y1, A1z1 и A2y2, а также необходимых кинематических соотношений
(2.1)
${{I}_{z}}{{\dot {\Omega }}_{z}} = \left( {{{P}_{{x1}}}\sin \Delta + {{P}_{{y1}}}\cos \Delta } \right)A - {{P}_{{y2}}}B + {{M}_{z}} + {{M}_{{S1}}} + {{M}_{{S2}}}$Точкой обозначено дифференцирование по времени T; M – масса аппарата; Iz – его момент инерции относительно оси Cz; I = mρ2, Iz1 = m$\rho _{{z1}}^{2}$ – осевой момент инерции колес и момент инерции переднего колеса относительно оси A1z1; m, ρ, ρz1 – масса колеса и соответствующие радиусы инерции; R – радиус колес; A, B – продольные расстояния от точки C до осей A1y1, A2y2; H – высота точки C над опорной плоскостью Ox0y0; Fx, Fy, Mz – соответствующие проекции внешних возмущающих сил и моментов; Pxj, Pyj и Nj (j = 1, 2) – проекции касательной и нормальной составляющих контактных сил взаимодействия j-го колеса с опорной плоскостью на оси Ajxj, Ajyj и Ajzj; Lj – момент со стороны двигателя и тормозных колодок, приложенный к j-му колесу по направлению оси Ajyj; MSj – момент верчения в области контакта j-го колеса с опорной плоскостью; MΔ – момент рулевого привода, приложенный к переднему колесу по направлению оси A1z1; g – ускорение свободного падения. При выбранном направлении движения далее будем полагать Vx(0) > 0. Как и в работах [4, 10–13], механизм рулевого управления считается безынерционным и в силу условия
при записи уравнения изменения кинетического момента аппарата не учитываются проекции кинетических моментов его колес.Из третьего и четвертого уравнений (2.1) следуют выражения, связывающие нормальные реакции с касательными составляющими контактных сил
(2.3)
${{N}_{1}} = \frac{{MgB - ({{P}_{{x1}}}\cos \Delta - {{P}_{{y1}}}\sin \Delta + {{P}_{{x2}}})H}}{{A + B}},\quad {{N}_{2}} = Mg - {{N}_{1}}$Будем рассматривать значения
отвечающие движению аппарата без отрыва колес от опорной плоскости.Используя велосипедную модель, ограничимся случаем малости поперечной и угловой скоростей корпуса аппарата, а также углов поворота его передних колес относительно корпуса (вокруг вертикальных осей), и будем рассматривать следующие диапазоны изменения этих переменных
(2.5)
$\left| {{{V}_{y}}} \right|\sim \left| {{{\Omega }_{z}}} \right|(A + B) \lesssim {{V}_{x}}\left| \Delta \right|,\quad \left| \Delta \right| \ll 1$Для описания скольжения колес аппарата по опорной плоскости в настоящей работе используются две модели сухого трения: традиционная модель кулонова трения и модель поликомпонентного сухого трения В.Ф. Журавлева [2].
В рамках модели кулонова трения выражения для касательных составляющих контактных сил, действующих на j-е колесо аппарата, имеют вид [4, 10–12]
(2.6)
${{P}_{{xj}}} = - {{\kappa }_{{xj}}}{{N}_{j}}\frac{{{{U}_{{xj}}}}}{{\sqrt {U_{{xj}}^{2} + U_{{yj}}^{2}} }},\quad {{P}_{{yj}}} = - {{\kappa }_{{yj}}}{{N}_{j}}\frac{{{{U}_{{yj}}}}}{{\sqrt {U_{{xj}}^{2} + U_{{yj}}^{2}} }}$(2.7)
$\begin{gathered} {{U}_{{x1}}} = {{V}_{x}}\cos \Delta + ({{V}_{y}} + {{\Omega }_{z}}A)\sin \Delta - {{\Omega }_{1}}R \\ {{U}_{{y1}}} = - {{V}_{x}}\sin \Delta + ({{V}_{y}} + {{\Omega }_{z}}A)\cos \Delta \\ {{U}_{{x2}}} = {{V}_{x}} - {{\Omega }_{2}}R,\quad {{U}_{{y2}}} = {{V}_{y}} - {{\Omega }_{z}}B \\ \end{gathered} $Далее будем считать коэффициенты трения колес одинаковыми
В рамках модели поликомпонентного сухого трения касательные составляющие контактных сил и моменты верчения, как и в [13] вычисляются по формулам, построенным [2] для области контакта, которая представляет собой круг радиуса
в предположении равномерного распределения по нему нормальных давлений(2.10)
$\begin{gathered} {{P}_{{xj}}} = - \kappa {{N}_{j}}\frac{{{{U}_{{xj}}}}}{{\sqrt {U_{{xj}}^{2} + U_{{yj}}^{2}} + \beta \left| {{{\Omega }_{z}}} \right|r}},\quad {{P}_{{yj}}} = - \kappa {{N}_{j}}\frac{{{{U}_{{yj}}}}}{{\sqrt {U_{{xj}}^{2} + U_{{yj}}^{2}} + \beta \left| {{{\Omega }_{z}}} \right|r}} \\ {{M}_{{Sj}}} = - \gamma \kappa {{N}_{j}}\frac{{{{\Omega }_{z}}{{r}^{2}}}}{{\alpha \sqrt {U_{{xj}}^{2} + U_{{yj}}^{2}} + \left| {{{\Omega }_{z}}} \right|r}},\quad \alpha = \frac{8}{3},\quad \beta = 1,\quad \gamma = \frac{2}{3} \\ \end{gathered} $Выражения для Uxj и Uyj были введены при записи формул (2.7).
Блокировка j-го колеса происходит при подаче тормозного момента Lj < 0, по величине превосходящего максимальное значение момента продольной составляющей контактной силы, которое будем считать равным моменту силы кулонова трения скольжения: |Lj| > κNjR. При этом получим Ωj → 0. Выражения для продольных и поперечных составляющих Pxj, Pyj контактных сил, действующих на заблокированное колесо, будем вычислять из выражений (2.6), (2.10) при Ωj = 0. Для заблокированного колеса
и, соответственно, Pxj < 0.Пробуксовка j-го колеса возникает в результате подачи разгонного момента Lj > κNjR. Это приводит к быстрому разгону колеса с проскальзыванием, до угловой скорости пробуксовки $\Omega _{j}^{0}$ = const, определяемой характеристиками двигателя аппарата. Выражения для продольных и поперечных составляющих контактных сил, действующих на пробуксовывающее колесо, получаются из выражений (2.6), (2.10) при Ωj = $\Omega _{j}^{0}$. Здесь справедливы неравенства
и, соответственно, Pxj > 0.В рамках рассматриваемой постановки задачи колесо велосипедной модели аппарата, которое не потеряло сцепление с опорной плоскостью, предполагается непроскальзывающим. Из (2.7) следуют уравнения неголономных связей, запрещающих проскальзывание j-го колеса
Уравнения движения системы со связями имеют вид (2.1), (2.13), где выражения для реакций связей совпадают с выражениями для касательных составляющих Pxj, Pyj контактных сил на непроскальзывающем колесе. Такой подход, эквивалентный методу составления уравнений Лагранжа с множителями, может быть обоснован [4, 10, 14] путем проведения предельного перехода в свободной от связей (2.13) системе, где за счет предположения о малой деформируемости j-го колеса допускаются его малые смещения относительно опорной плоскости (увод), к бесконечным значениям жесткости колеса. С учетом (2.8) область применимости неголономной модели определяется неравенством
при выполнении которого вектор контактной силы на непроскальзывающем j-м колесе находится внутри конуса трения, построенного в его точке контакта с опорной плоскостью.Перейдем к построению моделей динамики аппарата. Для упрощения дальнейшего исследования, как и в [4, 10, 12], рассмотрим случай свободного движения не заблокированного (не пробуксовывающего) q-го колеса
пренебрежем внешними возмущающими силами и моментами и ограничимся случаем “закрепленного рулевого управления” [15](2.16)
${{F}_{x}} = 0,\quad {{F}_{y}} = {\text{ }}0,\quad {{M}_{z}} = {\text{ }}0,\quad \Delta = {\text{const}}$3. Движение аппарата при заносе одной из осей. 3.1. Занос аппарата с заблокированными передними колесами. Задние колеса не теряют сцепление с опорной плоскостью. Уравнения движения велосипедной модели аппарата с заблокированным передним (его контакт с опорной плоскостью описывается моделью кулонова трения) и непроскальзывающим задним колесом после пренебрежения в их правых частях малыми слагаемыми O(μ), μ = m/M, учета (2.13) и (2.15) для j, q = 2, а также (2.16) имеют вид
(3.1)
$\begin{gathered} \dot {X} = {{V}_{x}}\cos \Psi - {{\Omega }_{z}}B\sin \Psi ,\quad \dot {Y} = {{V}_{x}}\sin \Psi + {{\Omega }_{z}}B\cos \Psi \\ \dot {\Psi } = {{\Omega }_{z}},\quad \dot {\Delta } = {{\Omega }_{\Delta }} \\ \end{gathered} $Переменные Vy, Ω2 определяются из двух последних соотношений (2.7) и уравнений связей (2.13) для j = 2
(3.2)
${{V}_{y}} = {{\Omega }_{z}}B,\;\;\;\;{{\Omega }_{2}} = {{{{V}_{x}}} \mathord{\left/ {\vphantom {{{{V}_{x}}} R}} \right. \kern-0em} R}$Выражения для реакций связей (3.2) на том же уровне точности записываются в форме
(3.3)
${{P}_{{x2}}} = 0,\quad {{P}_{{y2}}} = \frac{{{{I}_{z}}}}{{{{I}_{z}} + M{{B}^{2}}}}\left( {\left( {{{P}_{{x1}}}\sin \Delta + {{P}_{{y1}}}\cos \Delta } \right)\frac{{(MAB - {{I}_{z}})}}{{{{I}_{z}}}} + M{{V}_{x}}{{\Omega }_{z}}} \right)$В силу условия (2.5) малости Vy, Ωz и Δ при анализе уравнений заноса аппарата будем пренебрегать членами второго и более высоких порядков малости по этим переменным.
Линеаризованные по Ωz и Δ динамические уравнения системы (3.1), которые описывают изменение продольной скорости центра масс аппарата и его вращение вокруг точки контакта заднего колеса, не потерявшего сцепление с опорной плоскостью имеют вид
(3.4)
$\begin{gathered} M{{{\dot {V}}}_{x}} = - \kappa {{N}_{1}},\quad ({{I}_{z}} + M{{B}^{2}}){{{\dot {\Omega }}}_{z}} = F({{V}_{x}},{{\Omega }_{z}}) \\ {{N}_{1}} = \frac{{MgB}}{{A + B - \kappa H}},\quad F({{V}_{x}},{{\Omega }_{z}}) = - \kappa {{N}_{1}}\frac{{{{\Omega }_{z}}{{{(A + B)}}^{2}}}}{{{{V}_{x}}}} - MB{{V}_{x}}{{\Omega }_{z}} \\ \end{gathered} $После линеаризации выражения для Ux1 из (3.1) условие (2.11) для j = 1 принимает форму
В соответствии с выражениями (2.3) и (3.4) для нормальных реакций справедливость условий (2.4) обеспечивается за счет неравенства
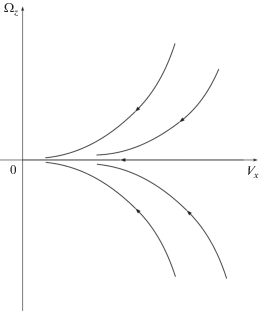
которое далее будем считать выполненным.Система (3.4), правые части которой не зависят от Δ, совпадает с аналогичной системой из [4, 10], составленной для случая Δ = 0, после линеаризации последней по переменной Ωz. Таким образом, на уровне точности системы (3.4) поворот заблокированных передних колес аппарата вокруг вертикальной оси не влияет на его занос. Фазовый портрет системы (3.4) показан на фиг. 2.
Поскольку второе уравнение системы (3.4) не изменяется при изменении знака Ωz, ее фазовые траектории на плоскости Vx, Ωz симметричны относительно оси Vx. Правая часть первого уравнения системы (3.4) постоянна и строго отрицательна, следовательно, продольная скорость Vx аппарата убывает в ходе равнозамедленного движения. На принятом уровне точности в силу условия (3.5) и неравенства (3.6) из второго уравнения (3.4) следует, что переменная |Ωz| монотонно убывает, то есть занос аппарата уменьшается; при Ωz = 0 касательные к фазовым траекториям горизонтальны: $d{{\Omega }_{z}}{\text{/}}d{{V}_{x}}$ = 0.
Обсудим область применимости построенного фазового портрета. В соответствии с неравенством (2.14) для j = 2, первым равенством (3.3) и неравенством (3.6) условие, ограничивающее область корректного использования системы (3.1), имеет вид
Пренебрегая во втором равенстве (3.3) членами второго и более высоких порядков малости по Ωz, Δ, получим выражение для подстановки в (3.7)
(3.8)
${{P}_{{y2}}} = \frac{{{{I}_{z}}}}{{{{I}_{z}} + M{{B}^{2}}}}\left( { - \kappa {{N}_{1}}\frac{{{{\Omega }_{z}}(A + B)}}{{{{V}_{x}}}}\frac{{(MAB - {{I}_{z}})}}{{{{I}_{z}}}} + M{{V}_{x}}{{\Omega }_{z}}} \right)$Выражения для N1 и N2 определяются из (3.4) и второго равенства (2.3).
Полученные выражения корректны при значениях переменных, удовлетворяющих ограничениям (2.5), (3.5).
Область, отвечающая выполнению условий (3.5), (3.7) и условия
которое дает оценку области (2.5), показана на фиг. 3. Здесь введено обозначениеВ силу постоянства нормальных реакций условие (3.7) не изменяется при изменении знака переменной Ωz, следовательно, эта область симметрична относительно оси Vx.
3.2. Занос аппарата с пробуксовывающими передними колесами. Задние колеса не теряют сцепление с опорной плоскостью. Уравнения движения велосипедной модели аппарата с пробуксовывающим передним колесом и задним колесом, не проскальзывающим относительно опорной плоскости, получаются по аналогии с тем, как это делалось в разделе 3.1. Как и ранее, связями служат равенства (3.2). Отличие этих уравнений от системы (3.1) состоит в выражениях для касательных составляющих Px1, Py1 контактной силы взаимодействия переднего колеса с опорной плоскостью. Это связано с тем, что выражение для Ux1 из (2.7) следует вычислять при ${{\Omega }_{1}} = \Omega _{1}^{0}$
Как и ранее при анализе системы (3.1) убывание переменной |Ωz| рассматривается как уменьшение заноса аппарата.
С учетом условия (2.12) для j = 1, которое на основании (3.10) имеет вид
аналоги уравнений (3.4) для рассматриваемого случая записываются в форме(3.12)
$\begin{gathered} M{{{\dot {V}}}_{x}} = \kappa {{N}_{1}},\quad ({{I}_{z}} + M{{B}^{2}}){{{\dot {\Omega }}}_{z}} = \tilde {F}({{V}_{x}},{{\Omega }_{z}},\Delta ) \\ {{N}_{1}} = \frac{{MgB}}{{A + B + \kappa H}} \\ \tilde {F}({{V}_{x}},{{\Omega }_{z}},\Delta ) = \kappa {{N}_{1}}\frac{{\Omega _{1}^{0}R\Delta - {{\Omega }_{z}}(A + B)}}{{\Omega _{1}^{0}R - {{V}_{x}}}}(A + B) - MB{{V}_{x}}{{\Omega }_{z}} \\ \end{gathered} $В соответствии с выражениями (2.3) и (3.12) для нормальных реакций в рассматриваемом случае условия (2.4) выполняются.
В отличие от системы (3.4), правая часть второго уравнения (3.12) зависит от переменной Δ. При Δ = 0 система (3.12) совпадает с аналогичной системой из [4, 10] после линеаризации последней по переменной Ωz.
Построим фазовый портрет системы (3.12) на плоскости Vx, Ωz. Поскольку правая часть первого уравнения постоянна и строго положительна, продольная скорость Vx аппарата возрастает, и он движется равноускоренно.
Рассмотрим уравнение $\tilde {F}({{V}_{x}},{{\Omega }_{z}},\Delta ) = 0$, которое задает кривую с горизонтальными касательными к фазовым траекториям. Разрешив его относительно переменной Ωz, получим
(3.13)
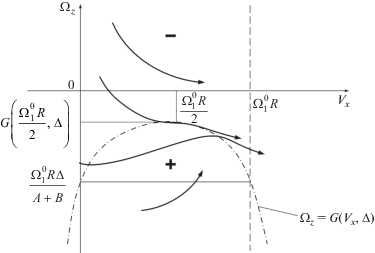
${{\Omega }_{z}} = G({{V}_{x}},\Delta ) = \frac{{\kappa {{N}_{1}}(A + B)\Omega _{1}^{0}R\Delta }}{{\kappa {{N}_{1}}{{{(A + B)}}^{2}} + MB{{V}_{x}}(\Omega _{1}^{0}R - {{V}_{x}})}}$Из второго уравнения (3.12) следует, что при положительных значениях функции $\tilde {F}({{V}_{x}},{{\Omega }_{z}},\Delta )$ угловая скорость Ωz корпуса аппарата возрастает, при отрицательных – убывает. Фазовый портрет системы (3.12) в случае Δ < 0 представлен на фиг. 4. График функции (3.13) показан штрихпунктирной кривой. Знаками “+” и “–“ отмечены разделяемые кривой (3.13) области фазовой плоскости, где функция $\tilde {F}({{V}_{x}},{{\Omega }_{z}},\Delta )$ имеет положительные и отрицательные знаки соответственно. В этих областях справедливы неравенства $d{{\Omega }_{z}}{\text{/}}d{{V}_{x}} > 0$ и $d{{\Omega }_{z}}{\text{/}}d{{V}_{x}} < 0$.
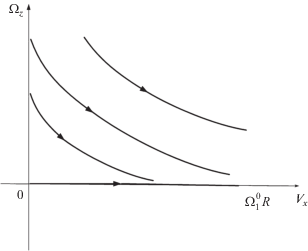
При Δ = 0 фазовый портрет системы (3.12) симметричен относительно оси Vx; переменная Vx возрастает, переменная |Ωz| убывает (фиг. 5). Для Δ ≠ 0 фазовый портрет системы (3.12) теряет свойство симметрии. В рассматриваемом случае Δ < 0 при начальных значениях переменной Ωz, заданных в области Ωz > 0, переменная Ωz, как и в случае Δ = 0, убывает, то есть занос аппарата уменьшается. Если начальные значения переменной Ωz выбраны в области Ωz < 0, то она остается отрицательной; если эти начальные значения находятся в области Ωz < G(Vx, Δ), где функция G(Vx, Δ) определена формулой (3.13), то переменная Ωz во все время движения не превышает $G({{\Omega _{1}^{0}R} \mathord{\left/ {\vphantom {{\Omega _{1}^{0}R} 2}} \right. \kern-0em} 2},\Delta )$.
Аналогично рассматривается случай Δ > 0. Поскольку второе уравнение системы (3.12) не изменяется при одновременном изменении знаков Δ и Ωz, соответствующий фазовый портрет системы (3.12) симметричен фазовому портрету на фиг. 4 относительно оси Vx.
Проведенное исследование показывает, что при выполнении условия
отвечающего “повороту руля (передних колес) в сторону заноса задней оси”, занос аппарата, как и в случае Δ = 0, уменьшается. Сравнить скорости уменьшения заноса в каждом из случаев можно путем сравнения значений $d{{\Omega }_{z}}{\text{/}}d{{V}_{x}}$ при Δ ≠ 0 и Δ = 0. Из уравнения фазовых траекторий системы (3.12) имеем(3.15)
$\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}} = {{\left. {\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}}} \right|}_{{\Delta = 0}}} + \frac{{M\Omega _{1}^{0}R(A + B)\Delta }}{{({{I}_{z}} + M{{B}^{2}})(\Omega _{1}^{0}R - {{V}_{x}})}}$Таким образом, в случае заноса аппарата с пробуксовывающими передними колесами при выполнении условия (3.14) занос аппарата уменьшается скорее, чем при неповернутых передних колесах. Рассогласование между скоростями убывания переменной |Ωz| определяется вторым слагаемым правой части равенства (3.15).
Анализ фазового портрета на фиг. 4 позволяет сформировать алгоритм эффективного подавления заноса аппарата с пробуксовывающими передними колесами. Следует повернуть их в сторону смещения задней оси аппарата (обеспечить выполнение условия (3.14)), и при достижении переменной Ωz близких к нулю или нулевых значений повернуть передние колеса в противоположную сторону и зафиксировать их вдоль корпуса, обеспечив выполнение условия Δ = 0. Для близких к нулю значений переменной |Ωz| это обеспечит дальнейшее уменьшение заноса аппарата, для Ωz = 0 получим Vy = 0, то есть занос аппарата прекратится. Если при изменении знака угловой скорости аппарата оставить угол поворота передних колес прежним, то занос аппарата начнет увеличиваться.
Условия, ограничивающие область корректного использования модели (3.12), имеют вид (2.5), (3.7), (3.11), где выражение для поперечной составляющей контактной силы на заднем колесе (аналог выражения (3.8)) записывается в форме
Выражения для N1 и N2 определяются из (3.12) и второго равенства (2.3).
Условиям (3.7), (3.9), (3.11) отвечает внутренняя часть области (3.9) слева от прямой ${{V}_{x}} = \Omega _{1}^{0}R$.
3.3. Занос аппарата с заблокированными задними колесами. Передние колеса не теряют сцепление с опорной плоскостью. Уравнения движения велосипедной модели аппарата с заблокированным задним и непроскальзывающим передним колесом после пренебрежения в их правых частях малыми слагаемыми O(μ) и учета (2.13), (2.15) для j, q = 1, а также (2.16) записываются по аналогии с (3.1)
(3.16)
$\begin{gathered} \dot {X} = {{V}_{x}}\cos \Psi - ({{V}_{x}}{\text{tg}}\Delta - {{\Omega }_{z}}A)\sin \Psi ,\quad \dot {Y} = {{V}_{x}}\sin \Psi + ({{V}_{x}}{\text{tg}}\Delta - {{\Omega }_{z}}A)\cos \Psi \\ \dot {\Psi } = {{\Omega }_{z}},\quad \dot {\Delta } = {{\Omega }_{\Delta }} \\ \end{gathered} $Переменные Vy, Ω1 определяются из первых двух соотношений (2.7) и уравнений связей (2.13) для j = 1
(3.17)
${{V}_{y}} = {{V}_{x}}{\text{tg}}\Delta - {{\Omega }_{z}}A,\quad {{\Omega }_{1}} = {{{{V}_{x}}} \mathord{\left/ {\vphantom {{{{V}_{x}}} {(R\cos \Delta )}}} \right. \kern-0em} {(R\cos \Delta )}}$(3.18)
$\begin{gathered} {{P}_{{x1}}} = 0 \\ {{P}_{{y1}}} = \frac{{{{I}_{z}}\cos \Delta }}{{{{I}_{z}} + M{{A}^{2}}{{{\cos }}^{2}}\Delta }}\left( {\frac{{(MAB - {{I}_{z}})}}{{{{I}_{z}}}}{{P}_{{y2}}} + ({{P}_{{x2}}} + M{{V}_{y}}{{\Omega }_{z}}{\text{)tg}}\Delta + M{{V}_{x}}{{\Omega }_{z}}} \right) \\ \end{gathered} $Из первого равенства (3.17) следует, что, в отличие от рассмотренных выше случаев заноса аппарата с заблокированными или пробуксовывающими передними колесами, при Δ ≠ 0 убывание переменной |Ωz| в общем случае не влечет за собой убывание переменной |Vy|. Поэтому занос аппарата следует изучать с учетом изменения обеих этих переменных.
После линеаризации динамических уравнений системы (3.16), которые описывают изменение продольной скорости центра масс аппарата и его вращение вокруг точки контакта переднего колеса, не потерявшего сцепление с опорной плоскостью, по Ωz и Δ, получим
(3.19)
$\begin{gathered} M{{{\dot {V}}}_{x}} = - \kappa {{N}_{2}},\quad ({{I}_{z}} + M{{A}^{2}}){{{\dot {\Omega }}}_{z}} = \Phi ({{V}_{x}},{{\Omega }_{z}},\Delta ) \\ {{N}_{2}} = \frac{{MgA}}{{A + B + \kappa H}},\quad \Phi ({{V}_{x}},{{\Omega }_{z}},\Delta ) = \kappa {{N}_{2}}\left( {B\Delta - \frac{{{{\Omega }_{z}}{{{(A + B)}}^{2}}}}{{{{V}_{x}}}}} \right) + MA{{V}_{x}}{{\Omega }_{z}} \\ \end{gathered} $С учетом выражения для Ux2 из (3.16) условие (2.11) для j = 2 имеет вид (3.5). В соответствии с выражениями (2.3) и (3.19) для нормальных реакций в рассматриваемом случае условия (2.4) выполняются.
При Δ = 0 система (3.19) совпадает с аналогичной системой из [4, 10] после ее линеаризации по переменной Ωz.
Построим фазовый портрет системы (3.19) на плоскости Vx, Ωz. Как и для случая блокировки переднего колеса, правая часть первого уравнения этой системы постоянна и строго отрицательна, что отвечает убыванию продольной скорости Vx аппарата в ходе равнозамедленного движения. Отсюда с учетом первого соотношения (3.17) следует, что в случае (3.14) убывание переменной |Ωz| вызывает убывание переменной |Vy|, то есть уменьшение заноса аппарата.
Разрешив уравнение $\Phi ({{V}_{x}},{{\Omega }_{z}},\Delta ) = 0$, определяющее кривую с горизонтальными касательными к фазовым траекториям, относительно переменной Ωz, получим
(3.20)
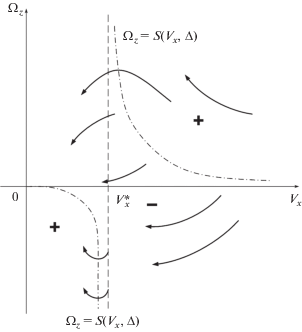
${{\Omega }_{z}} = S({{V}_{x}},\Delta ) = - \frac{{\kappa {{N}_{2}}B{{V}_{x}}\Delta }}{{MAV_{x}^{2} - \kappa {{N}_{2}}{{{(A + B)}}^{2}}}}$Фазовый портрет системы (3.19) в случае Δ < 0 представлен на фиг. 6. График функции (3.20) показан штрихпунктирной кривой, его асимптота
(3.21)
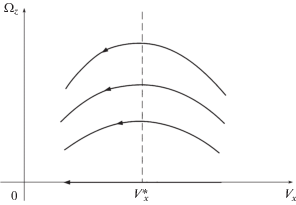
${{V}_{x}} = V_{x}^{ * } = (A + B)\sqrt {{{\kappa {{N}_{2}}} \mathord{\left/ {\vphantom {{\kappa {{N}_{2}}} {(MA)}}} \right. \kern-0em} {(MA)}}} $При Δ = 0 фазовый портрет системы (3.19) симметричен относительно оси Vx; переменная Vx монотонно убывает, переменная |Ωz| при ${\mkern 1mu} {{V}_{x}} > V_{x}^{ * }$ возрастает (здесь занос аппарата увеличивается), при ${\kern 1pt} {{V}_{x}} < V_{x}^{ * }$ – убывает (здесь в силу первого равенства (3.17) для Δ = 0 занос уменьшается) [4, 10] (фиг. 7). В рассматриваемом случае Δ < 0 фазовый портрет системы (3.19) теряет свойство симметрии. В области $0 < {{\Omega }_{z}} < S({{V}_{x}},\Delta )$, в отличие от случая Δ = 0, переменная Ωz убывает во все время движения (в силу (3.14) и первого равенства (3.17) при этом убывает и переменная |Vy|, то есть занос аппарата уменьшается); в остальных областях фазовой плоскости поведение переменной |Ωz| в зависимости от переменной Vx схоже со случаем Δ = 0, однако в случае (3.14) область убывания переменной |Ωz| превосходит свою область убывания при нарушении (3.14).
Из уравнения фазовых траекторий системы (3.19)
(3.22)
$\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}} = - \frac{M}{{{{I}_{z}} + M{{A}^{2}}}} \cdot \frac{{\Phi ({{V}_{x}},{{\Omega }_{z}},\Delta )}}{{\kappa {{N}_{2}}}}$Тем самым, в случае Δ < 0 при ${{V}_{x}} > V_{x}^{ * }$ возрастание переменной |Ωz| в области Ωz > 0 происходит медленнее, чем в области Ωz < 0; при ${{V}_{x}} < V_{x}^{ * }$ убывание переменной |Ωz| в области Ωz > 0 происходит быстрее, чем в области Ωz < 0.
Поскольку второе уравнение системы (3.19) не изменяется при одновременном изменении знаков Δ и Ωz, соответствующий фазовый портрет для случая Δ < 0 симметричен фазовому портрету на фиг. 6 относительно оси Vx.
Проведенное исследование показывает, что при Δ ≠ 0 для подавления заноса аппарата эффективнее обеспечивать выполнение условия (3.14). Сравним протекание заноса аппарата с повернутыми в соответствии с (3.14) и неповернутыми передними колесами. Из (3.22) имеем
(3.23)
$\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}} = {{\left. {\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}}} \right|}_{{\Delta = 0}}} - \frac{{MB\Delta }}{{{{I}_{z}} + M{{A}^{2}}}}$С учетом симметрии фазовых портретов системы (3.19) при Δ < 0 и Δ > 0 относительно оси Vx нетрудно показать, что при любых фиксированных значениях |Δ| = d, Vx = $\text{v}$ и |Ωz| = w
Таким образом, при выполнении условия (3.14) увеличение заноса аппарата с заблокированными задними колесами будет происходить менее интенсивно, а уменьшение – более интенсивно, чем при неповернутых передних колесах. Рассогласование между скоростями изменения переменной |Ωz| определяется вторым слагаемым правой части равенства (3.23), изменение переменной |Vy| может быть найдено из первой формулы (3.17). Нарушение условия (3.14) приводит к более опасному протеканию заноса аппарата.
Алгоритм эффективного подавления заноса аппарата в рассматриваемом случае схож с алгоритмом из раздела 3.2. Следует повернуть передние колеса в сторону смещения задней оси аппарата, и при достижении переменной Ωz близких к нулю или нулевых значений повернуть передние колеса в противоположную сторону и зафиксировать их вдоль корпуса, обеспечив выполнение условия Δ = 0. Это уменьшит значение поперечной скорости ${{V}_{y}} \approx {{V}_{x}}\Delta $ корпуса аппарата до близких к нулю значений, то есть обеспечит существенное уменьшение заноса; для значений Ωz = 0 получим Vy = 0, то есть занос аппарата прекратится. Если в момент прямолинейного положения передних колес аппарата переменная |Ωz| не достигла нулевых значений и снова начинает возрастать, нужно как можно скорее повторно повернуть передние колеса аппарата в сторону заноса его задней оси. Указанные циклы следует повторять вплоть до прекращения заноса аппарата.
В соответствии с неравенством (2.14) для j = 1 и первым выражением (3.18) условие, ограничивающее область корректного использования модели (3.16), построенной в предположении о непроскальзывании переднего колеса аппарата относительно опорной плоскости, имеет вид, аналогичный (3.7)
где выражение для поперечной составляющей контактной силы на переднем колесе после линеаризации второй формулы (3.18) по Ωz и Δ имеет видВыражения для N1 и N2 определяются из (3.19) и второго равенства (2.3).
Как и ранее, переменные и параметры должны удовлетворять ограничениям (2.5). Область, отвечающая выполнению условия (3.24) и неравенства (3.9), схожа с областью на фиг. 3.
3.4. Занос аппарата с пробуксовывающими задними колесами. Передние колеса не теряют сцепление с опорной плоскостью. Модель заноса велосипедной модели аппарата в рассматриваемом случае получается из (3.16) путем замены выражений Px2, Py2 выражениями, которые вычисляются для значений Ux2, отвечающих ${{\Omega }_{2}} = \Omega _{2}^{0}$
Связями, как и ранее, служат равенства (3.17).
С учетом условия (2.12) для j = 2, которое на основании (3.25) имеет вид
аналоги уравнений (3.19) записываются в форме(3.27)
$\begin{gathered} M{{{\dot {V}}}_{x}} = \kappa {{N}_{2}},\quad ({{I}_{z}} + M{{A}^{2}}){{{\dot {\Omega }}}_{z}} = \tilde {\Phi }({{V}_{x}},{{\Omega }_{z}},\Delta ) \\ {{N}_{2}} = \frac{{MgA}}{{A + B - \kappa H}} \\ \tilde {\Phi }({{V}_{x}},{{\Omega }_{z}},\Delta ) = \kappa {{N}_{2}}\left( {A\Delta + \frac{{{{V}_{x}}\Delta - {{\Omega }_{z}}(A + B)}}{{\Omega _{2}^{0}R - {{V}_{x}}}}(A + B)} \right) + MA{{V}_{x}}{{\Omega }_{z}} \\ \end{gathered} $Как и в разделе 3.1, выполнение условий (2.4) безотрывности движения колес аппарата обеспечивается за счет неравенства (3.6).
При Δ = 0 система (3.27) совпадает с аналогичной системой из [4, 10] после ее линеаризации по переменной Ωz.
Как и для случая пробуксовки переднего колеса, правая часть первого уравнения системы (3.27) постоянна и строго положительна, что отвечает возрастанию продольной скорости Vx аппарата в ходе равноускоренного движения. Тем самым здесь, в отличие от случая блокировки заднего колеса модели, при выполнении условия (3.14) убывание переменной |Ωz| не гарантирует убывание переменной |Vy|.
Разрешив уравнение $\tilde {\Phi }({{V}_{x}},{{\Omega }_{z}},\Delta ) = 0$, определяющее кривую с горизонтальными касательными к фазовым траекториям системы (3.27) на плоскости Vx, Ωz, относительно переменной Ωz, получим
(3.28)
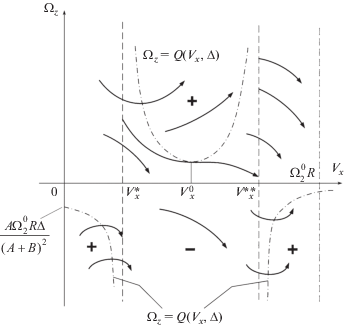
${{\Omega }_{z}} = Q({{V}_{x}},\Delta ) = \frac{{\kappa {{N}_{2}}\Delta (A\Omega _{2}^{0}R + {{V}_{x}}B)}}{{\kappa {{N}_{2}}{{{(A + B)}}^{2}} - MA{{V}_{x}}(\Omega _{2}^{0}R - {{V}_{x}})}}$Рассмотрим наиболее опасный случай заноса аппарата, отвечающий достаточно большим значениям угловой скорости $\Omega _{2}^{0}$ пробуксовки его заднего колеса, когда, как и в [4, 10], график функции (3.28) имеет вертикальные асимптоты
(3.29)
$\begin{gathered} {{V}_{x}} = V_{x}^{ * } = \frac{{MA\Omega _{2}^{0}R - \sqrt {{{{(MA\Omega _{2}^{0}R)}}^{2}} - 4MA\kappa {{N}_{2}}{{{(A + B)}}^{2}}} }}{{2MA}} \\ {{V}_{x}} = V_{x}^{{ * * }} = \frac{{MA\Omega _{2}^{0}R + \sqrt {{{{(MA\Omega _{2}^{0}R)}}^{2}} - 4MA\kappa {{N}_{2}}{{{(A + B)}}^{2}}} }}{{2MA}} \\ \end{gathered} $Фазовый портрет системы (3.27) для Δ < 0 представлен на фиг 8. График функции (3.28) показан штрихпунктирной кривой, его асимптоты (3.29) – пунктиром. Знаками “+” и “–” отмечены области между ветвями графика (3.28), где функция $\tilde {\Phi }({{V}_{x}},{{\Omega }_{z}},\Delta )$ имеет положительные и отрицательные знаки, что отвечает, соответственно, возрастанию и убыванию переменной Ωz и выполнению неравенств $d{{\Omega }_{z}}{\text{/}}d{{V}_{x}} > 0$ и $d{{\Omega }_{z}}{\text{/}}d{{V}_{x}} < 0$.
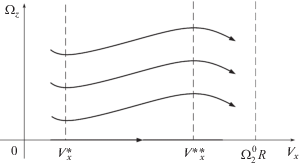
При Δ = 0 фазовый портрет системы (3.27) (фиг. 9) симметричен относительно оси Vx; в областях ${{V}_{x}} < V_{x}^{ * }$ и ${{V}_{x}} > V_{x}^{{ * * }}$ переменная |Ωz| убывает (в силу первого равенства (3.17) для Δ = 0 здесь занос уменьшается), в области $V_{x}^{ * } < {{V}_{x}} < V_{x}^{{ * * }}$ – возрастает, что говорит о развитии заноса аппарата. В рассматриваемом случае Δ < 0 фазовый портрет системы (3.27) теряет свойство симметрии. При значениях $0 < {{\Omega }_{z}} < Q({{V}_{x}},\Delta )$ переменная Ωz, в отличие от случая Δ = 0, убывает во все время движения аппарата; в остальных областях фазовой плоскости поведение переменной |Ωz| в зависимости от переменной Vx схоже со случаем Δ = 0. Как и для заноса аппарата с заблокированными задними колесами, при выполнении условия (3.14) область убывания переменной |Ωz| превосходит свою область убывания при нарушении этого условия.
Из уравнения фазовых траекторий системы (3.27)
(3.30)
$\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}} = \frac{M}{{{{I}_{z}} + M{{A}^{2}}}}\frac{{\tilde {\Phi }({{V}_{x}},{{\Omega }_{z}},\Delta )}}{{\kappa {{N}_{2}}}}$(3.31)
$\begin{gathered} {{\left. {\left| {\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}}} \right|} \right|}_{{\Delta = - d,\;V_{x}^{ * } < \text{v} < V_{x}^{{ * * }},\;{{\Omega }_{z}} = w}}} < {{\left. {\left| {\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}}} \right|} \right|}_{{\Delta = - d,\;V_{x}^{ * } < \text{v} < V_{x}^{{ * * }},\;{{\Omega }_{z}} = - w}}} \\ {{\left. {\left| {\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}}} \right|} \right|}_{{\Delta = - d,\;\text{v} < V_{x}^{ * },\;{{\Omega }_{z}} = w}}} > {{\left. {\left| {\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}}} \right|} \right|}_{{\Delta = - d,\;\text{v} < V_{x}^{ * },\;{{\Omega }_{z}} = - w}}} \\ {{\left. {\left| {\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}}} \right|} \right|}_{{\Delta = - d,\;\text{v} > V_{x}^{{ * * }},\;{{\Omega }_{z}} = w}}} > {{\left. {\left| {\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}}} \right|} \right|}_{{\Delta = - d,\;\text{v} > V_{x}^{{ * * }},\;{{\Omega }_{z}} = - w}}} \\ \end{gathered} $Тем самым, в случае Δ < 0 при $V_{x}^{ * } < {{V}_{x}} < V_{x}^{{ * * }}$ изменение переменной Ωz в области Ωz > 0 (в частности, возрастание ее величины при ${{\Omega }_{z}} > Q({{V}_{x}},\Delta )$) происходит медленнее, чем в области Ωz < 0; при ${{V}_{x}} < V_{x}^{ * }$ или ${{V}_{x}} > V_{x}^{{ * * }}$ изменение переменной Ωz в области Ωz > 0 происходит быстрее, чем в области Ωz < 0 (в частности, убывание |Ωz| при ${{\Omega }_{z}} < Q({{V}_{x}},\Delta )$).
Поскольку второе уравнение системы (3.27) не изменяется при одновременном изменении знаков Δ и Ωz, соответствующий фазовый портрет для случая Δ < 0 симметричен фазовому портрету на фиг. 9 относительно оси Vx.
Проведенное исследование показывает, что при Δ ≠ 0 для подавления заноса аппарата, как и ранее, эффективнее обеспечивать выполнение условия (3.14); нарушение этого условия приводит к более опасному протеканию заноса аппарата. Сравним протекание заноса аппарата с повернутыми и неповернутыми передними колесами. Из (3.30) имеем
(3.32)
$\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}} = {{\left. {\frac{{d{{\Omega }_{z}}}}{{d{{V}_{x}}}}} \right|}_{{\Delta = 0}}} + \frac{{M\Delta }}{{{{I}_{z}} + M{{A}^{2}}}}\left( {\frac{{A\Omega _{2}^{0}R + {{V}_{x}}B}}{{\Omega _{2}^{0}R - {{V}_{x}}}}} \right)$С учетом симметрии фазовых портретов системы (3.27) при Δ < 0 и Δ > 0 относительно оси Vx нетрудно показать, что при любых фиксированных значениях |Δ| = d, Vx = $\text{v}$ и |Ωz| = w
Таким образом, при выполнении условия (3.14) увеличение |Ωz| будет происходить менее интенсивно, а уменьшение – более интенсивно, чем при неповернутых передних колесах. Рассогласование между скоростями изменения переменной |Ωz| определяется вторым слагаемым правой части (3.32), изменение |Vy| может быть найдено из первой формулы (3.17).
Алгоритм эффективного подавления заноса аппарата с пробуксовывающими задними колесами, состоящий в повторении поворотов передних колес в сторону заноса задней оси вплоть до полного его прекращения, повторяет алгоритм из раздела 3.3.
Условие, ограничивающее область корректного использования рассматриваемой модели, имеет вид (3.24), где выражение для поперечной составляющей контактной силы на переднем колесе имеет вид
Выражения для N1 и N2 определяются из (3.27) и второго равенства (2.3). Переменные и параметры должны удовлетворять условиям (2.5). Область, отвечающая условиям (3.9), (3.24), (3.26), ограничена прямыми (3.9) и прямой ${{V}_{x}} = \Omega _{2}^{0}R$.
4. Движение аппарата при заносе обеих осей. 4.1. Приведение системы к сингулярно возмущенной форме. Уравнения движения велосипедной модели аппарата в случае, когда колеса обеих осей теряют сцепление с опорной плоскостью, в зависимости от используемой модели сухого трения, имеют вид (2.1), (2.6), (2.7) или (2.1), (2.7), (2.10). При выполнении условий (2.2), (2.5), (2.9) эти уравнения могут быть упрощены с применением асимптотических методов разделения движений [4, 5, 9]. Проведем нормализацию [4, 5] рассматриваемой системы, заменив переменные и время их безразмерными аналогами
(4.1)
$\begin{gathered} T = {{T}_{*}}t,\quad \Delta = {{\Delta }_{*}}\delta ,\quad {{V}_{x}} = {{V}_{{x*}}}{{\text{v}}_{x}},\quad {{V}_{y}} = {{V}_{{y*}}}{{\text{v}}_{y}},\quad {{\Omega }_{z}} = {{\Omega }_{{z*}}}{{\omega }_{z}} \\ {\mkern 1mu} {{\Omega }_{j}} = {{\Omega }_{{j*}}}{{\omega }_{j}},\quad {{N}_{j}} = {{N}_{{j*}}}{{n}_{j}},\quad {{P}_{{xj}}} = {{P}_{{xj*}}}{{p}_{{xj}}},\quad {{P}_{{yj}}} = {{P}_{{yj*}}}{{p}_{{yj}}} \\ {{M}_{{Sj}}} = {{M}_{{Sj*}}}{{m}_{{Sj}}},\quad {{U}_{{xj}}} = {{U}_{{xj*}}}{{u}_{{xj}}},\quad {{U}_{{yj}}} = {{U}_{{yj*}}}{{u}_{{yj}}} \\ {{V}_{{x*}}} = {{\Omega }_{{j*}}}R = {{U}_{{xj*}}} = \sqrt {g(A + B)} ,\quad {{V}_{{y*}}} = {{\Omega }_{{z*}}}(A + B) = {{U}_{{yj*}}} = {{V}_{{x*}}}{{\Delta }_{*}} \\ {{P}_{{xj*}}} = {{P}_{{yj*}}} = {{N}_{{j*}}} = Mg,\quad {{M}_{{Sj*}}} = {{Mg{{r}^{2}}} \mathord{\left/ {\vphantom {{Mg{{r}^{2}}} {(A + B)}}} \right. \kern-0em} {(A + B)}}\quad (j = 1,2) \\ \end{gathered} $Нижним индексом * обозначены характерные значения соответствующих постоянных и переменных величин для движения, определяемого условиями (2.2), (2.5), (2.9), в соответствии с которыми
(4.2)
${m \mathord{\left/ {\vphantom {m M}} \right. \kern-0em} M} = \mu \ll 1,\quad {{\Delta }_{ * }} = \varepsilon \ll 1,\quad {{\varepsilon }_{1}} = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R} \ll 1$Будем рассматривать μ, ε и ε1 в качестве малых параметров, ограничившись случаем
Соотношение между параметрами ε и ε1 будет обсуждаться позднее.
При выполнении первых двух условий (4.2) составляющие движения аппарата развиваются в сильно разнесенных временных масштабах. Их оценками служат величины ${{T}_{1}} = {{{{V}_{{{{x}_{*}}}}}} \mathord{\left/ {\vphantom {{{{V}_{{{{x}_{*}}}}}} g}} \right. \kern-0em} g}$ – постоянная времени изменения продольной (путевой) скорости корпуса аппарата Vx под действием сил порядка его веса; ${{T}_{2}} = {{\varepsilon {{V}_{{{{x}_{*}}}}}} \mathord{\left/ {\vphantom {{\varepsilon {{V}_{{{{x}_{*}}}}}} g}} \right. \kern-0em} g}$ – постоянная времени изменения поперечной и угловой скоростей корпуса аппарата Vy и Ωz; T3 = ${{\mu \rho _{z}^{2}{{V}_{{{{x}_{*}}}}}} \mathord{\left/ {\vphantom {{\mu \rho _{z}^{2}{{V}_{{{{x}_{*}}}}}} {({{R}^{2}}g)}}} \right. \kern-0em} {({{R}^{2}}g)}}$ – постоянная времени изменения угловых скоростей Ωq вращения не заблокированных и не пробуксовывающих колес вокруг оси Aqyq (фиг. 1). В соответствии с (4.3) справедливы неравенства
Рассматривая движение аппарата на характерных временах $T\sim {{T}_{2}}$, примем ${{T}_{*}} = {{T}_{2}}$. Нормализованным аналогом системы (2.1) (без третьего и четвертого уравнений) после линеаризации по ${{\text{v}}_{*}}$, ωz, Δ и учета (2.16) служит сингулярно возмущенная система [4, 5, 9]
(4.5)
$\begin{gathered} \text{v}_{x}^{'} = \varepsilon ({{p}_{{x1}}} - \varepsilon {{p}_{{y1}}}\delta + {{p}_{{x2}}}),\quad \text{v}_{y}^{'} = \varepsilon {{p}_{{x1}}}\delta + {{p}_{{y1}}} + {{p}_{{y2}}} - \varepsilon {{v}_{x}}{{\omega }_{z}} \\ i_{z}^{2}\omega _{z}^{'} = a(\varepsilon {{p}_{{x1}}}\delta + {{p}_{{y1}}}) - b{{p}_{{y2}}} + \varepsilon _{1}^{2}{{с }^{2}}({{m}_{{S1}}} + {{m}_{{S2}}}),\quad {{\mu }_{1}}{{i}^{2}}\omega _{q}^{'} = - {{p}_{{xq}}} \\ a = \frac{A}{{A + B}},\quad {\mkern 1mu} {\kern 1pt} b = \frac{B}{{A + B}},\quad h = \frac{H}{{A + B}},\quad c = \frac{R}{{A + B}} \\ i = \frac{\rho }{R},\quad {{i}_{z}} = \frac{{{{\rho }_{z}}}}{{A + B}},\quad {{\mu }_{1}} = \frac{\mu }{\varepsilon } \\ \end{gathered} $Выражения (2.3), (2.6), (2.7), (2.10) принимают вид
(4.6)
${{p}_{{xj}}} = - \kappa {{n}_{j}}\frac{{{{u}_{{xj}}}}}{{\sqrt {u_{{xj}}^{2} + {{{(\varepsilon {{u}_{{yj}}})}}^{2}}} }},\quad {{p}_{{yj}}} = - \kappa {{n}_{j}}\frac{{\varepsilon {{u}_{{yj}}}}}{{\sqrt {u_{{xj}}^{2} + {{{(\varepsilon {{u}_{{yj}}})}}^{2}}} }}\quad (j = 1,2)$(4.7)
$\begin{gathered} {{u}_{{xj}}} = {{\text{v}}_{x}} - {{\omega }_{j}},\quad {{u}_{{y1}}} = - {{\text{v}}_{x}}\delta + {{\text{v}}_{y}} + {{\omega }_{z}}a,\quad {{u}_{{y2}}} = {{\text{v}}_{y}} - {{\omega }_{z}}b \\ {{n}_{1}} = b - ({{p}_{{x1}}} - \varepsilon {{p}_{{y1}}}\delta + {{p}_{{x2}}})h,\quad {{n}_{2}} = 1 - {{n}_{1}} \\ \end{gathered} $(4.8)
${{m}_{{Sj}}} = - \gamma \kappa {{n}_{j}}\frac{{\varepsilon {{\omega }_{z}}}}{{\alpha \sqrt {u_{{xj}}^{2} + {{{(\varepsilon {{u}_{{yj}}})}}^{2}}} + \varepsilon {{\varepsilon }_{1}}c{\text{|}}{{\omega }_{z}}{\text{|}}}}\quad (j = 1,2)$Штрихом обозначены производные по безразмерному времени t.
Выражения для касательных составляющих контактных сил на заблокированном или пробуксовывающем l-м колесе получаются из соответствующих выражений (4.6)–(4.8) при значениях j = l и ${{\omega }_{l}} = 0$ или ${{\omega }_{l}} = \omega _{l}^{0} = \Omega _{l}^{0}R{\text{/}}{{V}_{{x*}}}$ соответственно.
В безразмерных переменных ограничения (2.5) принимают форму
(4.9)
$\left| {{{\text{v}}_{y}}} \right|\sim \left| {{{\omega }_{z}}} \right| \lesssim {{\text{v}}_{x}}\left| \delta \right|,\quad \left| \delta \right| \lesssim 1$4.2. Занос обеих осей аппарата с заблокированными или пробуксовывающими передними колесами. Колеса взаимодействуют с опорной плоскостью посредством кулонова трения. Положив в системе (4.5) для l = 1, q = 2 значения mS1, mS2 = 0, μ1 = 0 и считая параметр ε конечным, получим вырожденную систему уравнений
(4.10)
$\begin{gathered} \text{v}_{x}^{'} = \varepsilon ({{p}_{{x1}}} - \varepsilon {{p}_{{y1}}}\delta ),\quad \text{v}_{y}^{'} = \varepsilon {{p}_{{x1}}}\delta + {{p}_{{y1}}} + {{p}_{{y2}}} - \varepsilon {{v}_{x}}{{\omega }_{z}} \\ i_{z}^{2}\omega _{z}^{'} = a(\varepsilon {{p}_{{x1}}}\delta + {{p}_{{y1}}}) - b{{p}_{{y2}}},\quad {{p}_{{x2}}} = 0 \\ \end{gathered} $Составляющие контактных сил вычисляются из (4.6), (4.7). Последнее, конечное уравнение системы (4.10) имеет изолированный корень
отвечающий условию непроскальзывания заднего колеса велосипедной модели аппарата в направлении продольной оси A2x2 (фиг. 1).Для доказательства близости решений исходной и вырожденной систем воспользуемся теорией Тихонова–Васильевой [4, 5, 9]. Одним из основных условий, обеспечивающих притяжение траекторий исходной системы к многообразию, на котором развиваются медленные движения в силу вырожденной системы, служит затухание быстрых движений. Для его проверки требуется исследовать изолированность, асимптотическую устойчивость по первому приближению и область влияния точек покоя присоединенной системы, которая получается из (4.5)–(4.7) после замены времени $\tau = t{\text{/}}{{\mu }_{1}}$ и последующего приравнивания слагаемых порядка μ1 нулю. Присоединенная система, которая в данном случае сводится к одному скалярному уравнению, имеет вид
(4.12)
${{i}^{2}}\frac{{d{{\omega }_{2}}}}{{d\tau }} = \kappa {{n}_{2}}\frac{{{{\text{v}}_{x}} - {{\omega }_{2}}}}{{\sqrt {{{{({{\text{v}}_{x}} - {{\omega }_{2}})}}^{2}} + {{\varepsilon }^{2}}{{{({{\text{v}}_{y}} - {{\omega }_{z}}b)}}^{2}}} }}$Здесь медленные по сравнению с ω2 переменные ${{\text{v}}_{x}}$, ${{\text{v}}_{y}}$, ωz считаются постоянными. Проведя линеаризацию (4.12) около точки покоя (4.11), получим уравнение
(4.13)
${{i}^{2}}\frac{{d\Delta {{\omega }_{2}}}}{{d\tau }} = - \kappa {{n}_{2}}\frac{{\Delta {{\omega }_{2}}}}{{\varepsilon \left| {{{\text{v}}_{y}} - {{\omega }_{z}}b} \right|}},\quad \Delta {{\omega }_{2}} = {{\omega }_{2}} - {{\text{v}}_{x}}$В соответствии со вторым неравенством (2.4), которое в безразмерных переменных принимает вид n2 > 0, в случае ${{\text{v}}_{y}} \ne {{\omega }_{z}}b$ множитель при Δω2 отрицателен, то есть точка покоя асимптотически устойчива по первому приближению.
Выясним область влияния точки покоя (4.11), образованную совокупностью начальных значений ω2(0) переменной ω2, для которых соответствующие решения ω2(τ) уравнения (4.12) стремятся к точке покоя при $\tau \to \infty $. Скалярное уравнение (4.12) допускает качественное исследование методами [9]. Точке (4.11) на плоскости τ, ω2 отвечает горизонтальная прямая. При ω2(0) < ${{\text{v}}_{x}}$ правая часть уравнения (4.12) положительна, следовательно, решение ω2(τ), отвечающее этому начальному условию, возрастает, при ω2(0) > ${{\text{v}}_{x}}$ правая часть уравнения (4.12) отрицательна, то есть соответствующее решение ω2(τ) убывает. В силу теоремы существования и единственности кривая ω2(τ) не может пересечь прямую (4.11), следовательно, она асимптотически приближается к ней. Тем самым область влияния точки покоя (4.11) не ограничена.
В соответствии с теоремой Васильевой [4, 5, 9] рассогласование между решениями исходной системы (4.5)–(4.7) и соответствующей вырожденной системы (4.6), (4.7), (4.10) оценивается величиной $O({{\mu }_{1}})$ на конечном интервале времени $t\sim 1$, отвечающем интервалу $T\sim {{T}_{2}}$ размерного времени T. Для быстрой переменной ω2 эта оценка верна вне пограничного слоя ширины $O( - {{\mu }_{1}}\ln {{\mu }_{1}})$.
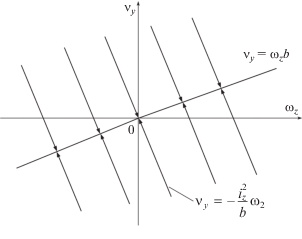
Рассмотрим систему (4.10). Согласно (4.6), (4.7), при выполнении равенства (4.11) нормализованное значение py2 поперечной составляющей контактной силы на заднем колесе велосипедной модели аппарата, имеющее порядок ε при ${{u}_{{x2}}} \ne 0$, делается величиной $O(1)$, то есть начинает существенно превосходить остальные слагаемые во втором и третьем уравнениях. Тем самым по завершении быстрого процесса, в ходе которого задние колеса аппарата обретают сцепление с опорной плоскостью в продольном направлении, переменные ${{\text{v}}_{y}}$ и ωz становятся быстрыми по сравнению с переменной ${{\text{v}}_{x}}$, и могут быть рассмотрены независимо от нее. Проведем приближенное исследование этих переменных при помощи метода фазовой плоскости.
Разделив второе уравнение системы (4.10) на третье, положив ε = 0 и учитывая (4.6), для случая ${{\text{v}}_{y}} \ne {{\omega }_{z}}b$ будем иметь
(4.14)
$\frac{{d{{\text{v}}_{y}}}}{{d{{\omega }_{z}}}} = \frac{{ - \kappa {{n}_{2}}{\text{sign}}({{\text{v}}_{y}} - {{\omega }_{z}}b)}}{{(b{\text{/}}i_{z}^{2})\kappa {{n}_{2}}{\text{sign}}({{\text{v}}_{y}} - {{\omega }_{z}}b)}} = - \frac{{i_{z}^{2}}}{b}$Согласно теореме Пуанкаре о малом параметре [4, 5], вытекающая из (4.14) зависимость
описывает связь между переменными ${{\text{v}}_{y}}$, ωz системы (4.10) с погрешностью $O(\varepsilon )$ на интервале времени $t\sim 1$. Постоянная C1 определяется начальными значениями этих переменных. Траектории (4.15) на фазовой плоскости ωz, ${{\text{v}}_{y}}$ и направления движения по ним, которые могут быть найдены из второго и третьего уравнений (4.10) в пренебрежении членами порядка ε, показаны на фиг. 10. Прямая, определяемая уравнением отвечает разрыву правой части первого равенства (4.14). Переход на эту прямую по прямым (4.15) происходит быстро, на временах $t\sim 1$ изменения переменных ${{\text{v}}_{y}}$, ωz. В соответствии с третьим выражением (4.7) уравнение (4.16) отвечает условию непроскальзывания заднего колеса велосипедной модели аппарата в поперечном направлении A2y2 к его плоскости (фиг. 1). Доопределить решение уравнения (4.14) на этой прямой можно при помощи методики исследования дифференциальных уравнений с разрывными правыми частями [16].Проведенный анализ показал, что в рамках рассматриваемой постановки задачи поворот передних колес не влияет на занос аппарата с заблокированными или пробуксовывающими передними колесами, в ходе которого колеса задней оси теряют сцепление с опорной плоскостью. При любых отвечающих (4.9) начальных условиях по переменным ${{\text{v}}_{y}}$, ωz, ω2 на временах $t\sim 1$ ($T\sim {{T}_{2}}$) аппарат входит в режим непроскальзывания задних колес (в продольном и поперечном направлениях). Дальнейшее движение аппарата развивается по рассмотренным в разделах 3.1, 3.2 сценариям заноса при блокировке или пробуксовке передних колес при непроскальзывающих задних колесах.
4.3. Занос обеих осей аппарата с заблокированными или пробуксовывающими задними колесами. Колеса взаимодействуют с опорной плоскостью посредством кулонова трения. Случаи блокировки или пробуксовки задних колес изучаются по аналогии с тем, как это делалось в разделе 4.2. Приближенной моделью системы (4.5)–(4.7) для l = 2, q = 1 служит система (4.10), последнее уравнение которой следует заменить уравнением
корень ${{\omega }_{1}} = {{\text{v}}_{x}}$ которого отвечает условию непроскальзывания переднего колеса велосипедной модели аппарата в направлении продольной оси A1x1 (фиг. 1).Зависимость между переменными ${{\text{v}}_{y}}$, ωz системы (4.10) приближенно описывается дифференциальным уравнением вида (4.14), решением которого служит аналог равенства (4.15)
(4.18)
${{\text{v}}_{y}} = \frac{{i_{z}^{2}}}{a}{{\omega }_{z}} + {{C}_{2}},\quad {{C}_{2}} = {\text{const}}$Уравнение
определяет прямую разрыва правой части этого дифференциального уравнения на плоскости ωz, ${{\text{v}}_{y}}$. Переход на эту прямую по прямым (4.18) происходит быстро, на временах $t\sim 1$ изменения переменных ${{\text{v}}_{y}}$, ωz. Медленная переменная ${{\text{v}}_{x}}$, изменяющаяся на временах $t\sim {1 \mathord{\left/ {\vphantom {1 \varepsilon }} \right. \kern-0em} \varepsilon }$, полагается постоянной, равной своему начальному значению.Как и в случае блокировки или пробуксовки передних колес, в силу рассматриваемой модели заноса обеих осей аппарата при любых начальных условиях по переменным ${{\text{v}}_{y}}$, ωz, ω1 на временах $t\sim 1$ ($T\sim {{T}_{2}}$) аппарат входит в режим непроскальзывания не заблокированных (не пробуксовывающих) колес (в продольном и поперечном направлениях), в данном случае – передних. Далее движение развивается по сценариям заноса с заблокированными или пробуксовывающими задними колесами при непроскальзывающих передних колесах из разделов 3.3, 3.4.
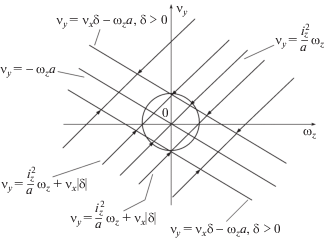
Обсудим, как поворот передних колес аппарата влияет на его занос. На фиг. 11 показана прямая (4.19) для δ = 0 и симметрично расположенные относительно нее прямые (4.19), которые отвечают одной и той же величине и разным знакам угла δ поворота переднего колеса велосипедной модели аппарата. При выборе любой из перечисленных прямых движение по фазовым траекториям (4.18) происходит по направлению к ней. Область применимости рассматриваемой модели движения аппарата, определяемая ограничениями (4.9) (она находится внутри и небольшой внешней окрестности круга на фиг. 11) практически полностью содержится в полосе
(4.20)
$\frac{{i_{z}^{2}}}{a}{{\omega }_{z}} - {{\text{v}}_{x}}\left| \delta \right| < {{\text{v}}_{y}} < \frac{{i_{z}^{2}}}{a}{{\omega }_{z}} + {{\text{v}}_{x}}\left| \delta \right|$4.4. Занос обеих осей аппарата с заблокированными или пробуксовывающими передними колесами. Колеса взаимодействуют с опорной плоскостью посредством модели поликомпонентного сухого трения. Положив в системе (4.5) для l = 1 и q = 2 параметр μ1 = 0 и считая параметр ε конечным, приходим к вырожденной системе уравнений, которая получается из (4.10) заменой третьего уравнения уравнением
(4.22)
$i_{z}^{2}\omega _{z}^{'} = a(\varepsilon \delta {{p}_{{x1}}} + {{p}_{{y1}}}) - b{{p}_{{y2}}} + \varepsilon _{1}^{2}{{c}^{2}}({{m}_{{S1}}} + {{m}_{{S2}}})$Составляющие контактных сил и моменты верчения задаются выражениями (4.7), (4.8).
Погрешность $O({{\mu }_{1}})$ вырожденной системы и равенства (4.11), справедливая на интервале времени $t\sim 1$ ($T\sim {{T}_{2}}$) вне пограничного слоя ширины $O( - {{\mu }_{1}}\ln {{\mu }_{1}})$, доказывается по аналогии с тем, как это делалось в разделе 4.2. Как и в разделах 4.2, 4.3 полученная система позволяет приближенно исследовать быстрые переменные ${{\text{v}}_{y}}$, ωz независимо от медленной переменной ${{\text{v}}_{x}}$ с использованием метода фазовой плоскости. Рассмотрим случай
Пренебрегая в вырожденной системе малым параметром ε и считая параметр ε1 конечным, получим систему уравнений
(4.24)
$\begin{gathered} {{\text{v}}_{x}} = {\text{const,}}\quad \text{v}_{y}^{'} = - \kappa {{n}_{2}}\frac{{{{\text{v}}_{y}} - {{\omega }_{z}}b}}{{\left| {{{\text{v}}_{y}} - {{\omega }_{z}}b} \right| + {{\varepsilon }_{1}}\beta \left| {{{\omega }_{z}}} \right|}} \\ i_{z}^{2}\omega _{z}^{'} = b\kappa {{n}_{2}}\frac{{{{\text{v}}_{y}} - {{\omega }_{z}}b}}{{\left| {{{\text{v}}_{y}} - {{\omega }_{z}}b} \right| + {{\varepsilon }_{1}}\beta \left| {{{\omega }_{z}}} \right|}} - \gamma \kappa {{n}_{2}}\frac{{\varepsilon _{1}^{2}{{c}^{2}}{{\omega }_{z}}}}{{\alpha \left| {{{\text{v}}_{y}} - {{\omega }_{z}}b} \right| + {{\varepsilon }_{1}}c\left| {{{\omega }_{z}}} \right|}} \\ \end{gathered} $Если в (4.24) принять ε1 = 0, то есть считать радиус областей контакта колес с опорной плоскостью пренебрежимо малым (r = 0), то зависимость между переменными ${{\text{v}}_{y}}$, ωz системы (4.24) находится из равенств (4.14), составленных для традиционной модели кулонова трения.
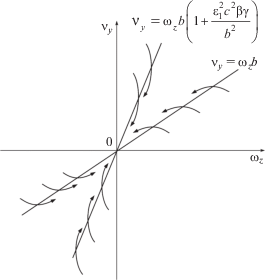
Рассмотрим случай ε1 ≠ 0, который соответствует конечному значению радиуса областей контакта колес с опорной плоскостью (r ≠ 0), и построим фазовый портрет системы (4.24). На прямой (4.16), где правая часть первого дифференциального уравнения системы (4.24) обращается в нуль, фазовые траектории имеют горизонтальные касательные. Уравнение кривой, на которой касательные к фазовым траекториям вертикальны, определяется путем приравнивания нулю правой части второго дифференциального уравнения системы (4.24). В пренебрежении членами $O(\varepsilon _{1}^{3})$ оно имеет вид
(4.25)
${{\text{v}}_{y}} = {{\omega }_{z}}b\left( {1 + \frac{{\varepsilon _{1}^{2}{{c}^{2}}\beta \gamma }}{{{{b}^{2}}}}} \right)$Анализ фазового портрета системы (4.24) на фиг. 12 показывает, что для модели поликомпонентного сухого трения результат остается тем же, что и для модели кулонова трения: угол поворота передних колес не влияет на занос обеих осей аппарата с заблокированными или пробуксовывающими передними колесами. Однако здесь для любых начальных условий по переменным ${{\text{v}}_{y}}$, ωz, отвечающих ограничениям (4.9), имеем ${{\text{v}}_{y}} \to 0$, ${{\omega }_{z}} \to 0$ при $t\sim 1$ ($T\sim {{T}_{2}}$), тогда из (4.7) получаем ${{u}_{{y2}}} \to 0$, то есть на временах $t\sim 1$ аппарат входит в режим непроскальзывания задних колес (в продольном и поперечном направлениях), и его занос полностью прекращается.
Таким образом, в рамках модели поликомпонентного сухого трения, учитывающей верчение в областях контакта колес с опорной плоскостью, занос аппарата уменьшается скорее, чем для модели кулонова трения, которая учитывает только возможность скольжения колес.
4.5. Занос обеих осей аппарата с заблокированными или пробуксовывающими задними колесами. Колеса взаимодействуют с опорной плоскостью посредством модели поликомпонентного сухого трения. Для случая блокировки (пробуксовки) задних колес аппарата аналог вырожденной для (4.5), (4.7), (4.8) по μ1 системы, отвечающей l = 2 и q = 1, получается из (4.10) заменой третьего и четвертого уравнений уравнениями (4.17) и (4.22). Как и в разделе 4.4, будем считать выполненным условие (4.23). Пренебрегая в полученной системе малым параметром ε и считая параметр ε1 конечным, приходим к аналогу системы (4.24)
(4.26)
${{\text{v}}_{x}} = {\text{const}},\quad \text{v}_{y}^{'} = - \kappa {{n}_{1}}\frac{{ - {{\text{v}}_{x}}\delta + {{\text{v}}_{y}} + {{\omega }_{z}}a}}{{\left| { - {{\text{v}}_{x}}\delta + {{\text{v}}_{y}} + {{\omega }_{z}}a} \right| + {{\varepsilon }_{1}}\beta \left| {{{\omega }_{z}}} \right|}}$При ε1 = 0 (r = 0) результат исследования системы (4.26) совпадает с результатом исследования вырожденной системы из раздела 4.3.
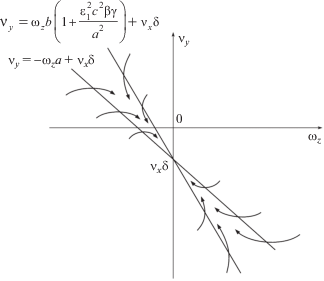
Рассмотрим случай ε1 ≠ 0 (r ≠ 0) и построим фазовый портрет системы (4.26) на плоскости ωz, ${{\text{v}}_{y}}$. На прямой (4.19), отвечающей условию непроскальзывания переднего колеса велосипедной модели в поперечном направлении A1y1, касательные к фазовым траекториям горизонтальны. Пренебрегая членами $O(\varepsilon _{1}^{3})$, получим уравнение кривой, на которой касательные к фазовым траекториям вертикальны
(4.27)
${{\text{v}}_{y}} = - {{\omega }_{z}}a\left( {1 + \frac{{\varepsilon _{1}^{2}{{c}^{2}}\beta \gamma }}{{{{a}^{2}}}}} \right) + {{\text{v}}_{x}}\delta $Фазовый портрет системы (4.26) для случая δ < 0 (Δ < 0) показан на фиг. 13. Фазовый портрет для δ > 0 (Δ > 0) получается из этого фазового портрета путем параллельного переноса прямых (4.19), (4.27) на $2{{\text{v}}_{x}}\left| \delta \right|$ вверх вдоль оси ${{\text{v}}_{y}}$. Анализ фазовых портретов показывает, что как в рамках модели поликомпонентного сухого трения, так и в рамках модели кулонова трения поворот передних колес влияет на занос обеих осей аппарата с заблокированными или пробуксовывающими задними колесами. Для любых отвечающих (4.9) начальных условий по переменным ${{\text{v}}_{y}}$, ωz имеем ${{\text{v}}_{y}} \to {{\text{v}}_{x}}\delta $, ${{\omega }_{z}} \to 0$, тогда из (4.7) вытекает ${{u}_{{y1}}} \to 0$. Тем самым на временах $t\sim 1$ ($T\sim {{T}_{2}}$) аппарат входит в режим непроскальзывания не заблокированных (не пробуксовывающих) колес (в продольном и поперечном направлениях), в данном случае – передних, и угловая скорость его корпуса будет полностью погашена. При δ = 0 занос аппарата на временах $t\sim 1$ полностью прекратится; в случае δ ≠ 0 его движение будет развиваться по сценарию заноса при блокировке или пробуксовке задних колес при непроскальзывающих передних колесах, начальная стадия которого сопровождается преимущественно смещением центра масс аппарата в поперечном направлении.
Как было показано в разделе 4.3, для модели кулонова трения в момент, когда задние колеса аппарата обретают сцепление с опорной плоскостью, угловая скорость корпуса в общем случае принимает ненулевые значения, следовательно, в рамках этой модели занос аппарата уменьшается медленнее, чем для модели поликомпонентного сухого трения.
Список литературы
Журавлев В.Ф. Динамика тяжелого однородного шара на шероховатой плоскости // Изв. РАН. МТТ. 2006. № 6. С. 3–9.
Андронов В.В., Журавлев В.Ф. Сухое трение в задачах механики. М.; Ижевск: Ин-т космич. исслед., НИЦ “Регулярная и хаотическая динамика”, 2010. 184 с.
Новожилов И.В., Кручинин П.А., Магомедов М.Х. Контактные силы взаимодействия колеса с опорной поверхностью // Сб. научно-методических статей. М.: Изд-во МГУ, 2000. Вып. 23. С. 86–95.
Влахова А.В. Математические модели движения колесных аппаратов. М.-Ижевск: АНО “Ижевский институт компьютерных исследований”, 2014. 148 с.
Новожилов И.В. Фракционный анализ. М.: Изд-во МГУ, 1995. 224 с.
Pacejka H.B. Tyre and vehicle dynamics. Warrendale, PA. Soc. Automotive Eng., 2005. 621 p.
Johnson K.L. Contact Mechanics. N.Y. ets.: Cambrige: Univ. Press, 1985 = Джонсон К. Механика контактного взаимодействия. М.: Мир, 1989. 510 с.
Кручинин П.А. Сухое трение в модели качения деформируемого колеса // Сб. научно-методических статей. М.: Изд-во МГУ, 2017. Вып. 30. С. 139–147.
Васильева А.Б., Бутузов В.Ф. Асимптотические методы в теории сингулярных возмущений. М.: Высшая школа, 1990. 208 с.
Влахова А.В., Новожилов И.В. О заносе колесного экипажа при “блокировке” и “пробуксовке” одного из колес // Фундамен. и прикл. математика. 2005. Т. 11. Вып. 7. С. 11–20.
Влахова А.В., Новожилов И.В., Смирнов И.А. Математическое моделирование заноса автомобиля // Вестн. Моск. ун-та. Сер. 1, Математика. Механика. 2007. № 6. С. 44–50.
Влахова А.В., Новодерова А.П. О влиянии моментов трения верчения на занос колесного аппарата // Фундамен. и прикл. математика. 2018. Т. 22. Вып. 2. С. 125–200.
Журавлев В.Ф., Климов Д.М., Плотников П.К. Новая модель шимми // Изв. РАН. МТТ. 2013. № 5. С. 13–23.
Влахова А.В. О реализации связей в задачах качения колесного аппарата // Изв. РАН. MТТ. 2013. № 3. С. 22–39.
Литвинов А.С. Управляемость и устойчивость автомобиля. М.: Машиностроение, 1971. 416 с.
Влахова А.В., Новожилов И.В. Разделение движений в системах с разрывными правыми частями // Проблемы механики. К 90-летию акад. А.Ю. Ишлинского. М.: Физматлит, 2003. С. 187–195.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела