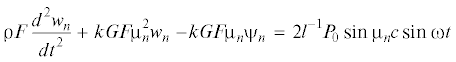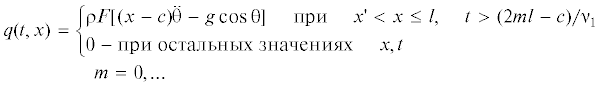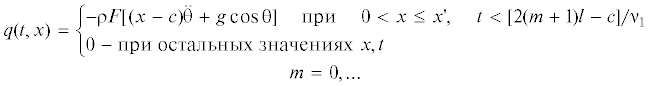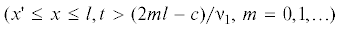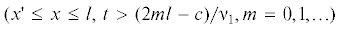Известия РАН. Механика твердого тела, 2019, № 1, стр. 141-153

Исследование вынужденных поперечных колебаний упругого шарнирно-опертого стержня с учетом вращательного движения

К. Ш. Мкртчян^*

Институт геофизики и инженерной сейсмологии им. А.Г. Назарова, НАН РА
Гюмри, Армения

Поступила в редакцию 22.06.2017
После доработки 29.01.2018
Принята к публикации 06.02.2018

DOI: 10.1134/S0572329919010070

Аннотация

Исследуются вынужденные поперечные колебания упругого шарнирно-опертого стержня под действием нормальной сосредоточенной периодической во времени силы. Задача решается методом, предложенным в [1] с использованием комбинированных условий, включающих динамическое воздействие на стержень и вращательное движение относительно фронта волны изгиба. В рамках линейной теории тонких прямолинейных нерастяжимых стержней, при помощи принципа Гамильтона–Остроградского получены уравнение движения и система уравнений поперечных колебаний упругого стержня. Решение поставленной задачи строится в виде ряда собственных форм колебаний. Получены два типа вынужденных поперечных колебаний и новые резонансные частоты. Численные результаты расчетов приведены в виде таблиц, графиков; дан анализ полученных результатов.

Ключевые слова: стержень, сечение, сила тяжести, поперечные колебания, собственные частоты, собственные формы

1. Введение. Вынужденные поперечные колебания упругого шарнирно-опертого стержня под действием нормально сосредоточенной периодической во времени силы представляет практический и теоретический интерес для приложений, например для мостовых работ. Важным фактором при исследовании поперечных колебаний упругого стержня является учет вращательного движения, поскольку под его воздействием в стержне возникают новые упругие колебания и дополнительные силы, обусловленные упругостью стержня. Основные достижения в этой области изложены в нашей недавней работе [1], где исследуется вынужденное поперечное колебание упругого стержня, когда одному концу придано перемещение, а другой свободен. Для решения была использована элементарная теория стержня. Однако, уравнение поперечных колебаний (1) в [1] негиперболическое, задачи о распространении волн носят совершенно иной характер. Существуют возмущения, которые распространяются мгновенно. На этот результат нужно смотреть как на дефект уравнения (1) в [1], пригодного лишь для достаточно длинных волн [2, c. 208]. Если волны короткие, то кроме инерции поступательного движения, следует учитывать инерцию вращения, а также влияние на прогиб не только нормальных напряжений, но также и касательных напряжений от перерезывающих сил. Учитывая эти факты, можно получить уточненное уравнение динамического изгиба, которое является гиперболическим и не допускает мгновенного распространения импульсов.

Цель данного исследования – сформулировать гораздо более общую задачу о вынужденных поперечных колебаниях упругого стержня с шарнирно-опертыми концами, описываемых при помощи модели Тимошенко, в котором учитываются вращательные движения.

Основное внимание уделено результатам теоретических исследований, относящихся к этой задаче. Основная задача, как и в работе [1], решается путем разделения ее на две задачи, в каждой из которых рассматриваются вынужденные поперечные колебания упругого шарнирно-опертого стержня, обусловленные различными частями комбинированного воздействия, включающие динамическое воздействие на стержень и вращательное движение относительно фронта волны изгиба. Приведены новые, более точные теоретические результаты для второй задачи, в которой исследованы вынужденные поперечные колебания упругого шарнирно-опертого стержня, обусловленные вращательным движением, что является основным результатом данного исследования.

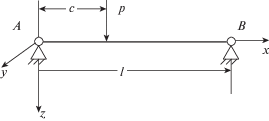
2. Математическая постановка задачи 1 и ее решение. Пусть упругий стержень с шарнирно-опертыми концами на расстоянии с от левой опоры подвергается действию нормально сосредоточенной периодической во времени силы. Эта сила вызывает в стержне динамическое напряженное состояние, возникают свободные и вынужденные колебания. Для общности поперечное сечение стержня примем произвольным, но постоянным вдоль ее оси. Предположим, что стержень однороден и работает на сдвиг и изгиб. В недеформированном состоянии нейтральная линия стержня прямолинейна и направлена горизонтально. Отнесем ее к декартовой системе координат x, y, z, в которой ось x направлена вдоль нейтральной линии недеформированного стержня, оси y и z вдоль осей симметрии поперечного сечения. Колебания стержня происходят в вертикальной плоскости xz геометрия которой представлена на фиг. 1. Ставится и решается следующая задача: требуется определить вынужденные поперечные колебания этого стержня, возникающие в результате приложения силы в виде

$P = {{P}_{0}}\delta (x - c)\sin \omega t$

Фиг. 1

Для рассматриваемой задачи вынужденные поперечные колебания стержня с учетом эффектов поперечного сдвига и инерции вращения описываются следующими уравнениями с граничными и начальными условиями [3]:

${{\rm E}}J\frac{{{{\partial }^{2}}\psi }}{{\partial {{x}^{2}}}} + kGF\left( {\frac{{\partial w}}{{\partial x}} - \psi } \right) = \rho J\frac{{{{\partial }^{2}}\psi }}{{\partial {{t}^{2}}}}$

$kGF\left( {\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} - \frac{{\partial {\psi }}}{{\partial x}}} \right) + {{P}_{0}}{\delta }\left( {x - c} \right)\sin {\omega }t = {\rho }F\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}{\;}$

$x = 0,l{\text{:}}\quad w = 0;\quad \partial \psi {\text{/}}\partial x = 0$

$t = 0{\text{:}}\,\,w = 0;\quad \partial w{\text{/}}\partial t = 0$

$\psi = 0;\quad \partial \psi {\text{/}}\partial t = 0$

где t – время; l – длина стержня; F – площадь поперечного сечения; J – момент инерции поперечного сечения; δ() – дельта-функция Дирака; P – силы, в некоторой точке x в момент времени t; ρ – плотность материала; Е, G-модули Юнга и сдвига, соответственно; k – безразмерный числовой коэффициент, зависящий от формы поперечного сечения стержня; w – перемещение центра изгиба сечения в направлении оси z (прогиб); ψ – угол поворота сечения вокруг центра изгиба; ω – круговая частота.

Граничные условия (2.2) будут удовлетворены, если решение системы (2.1) представить в вид

(2.4)

$w = \mathop \sum \limits_{n = 1}^\infty {{w}_{n}}(t)\sin {{{\mu }}_{n}}x$

(2.5)

$\psi = \mathop \sum \limits_{n = 1}^\infty {{\psi }_{n}}(t){\text{cos}}{{{\mu }}_{n}}x$

${{\mu }_{n}} = n\pi {\text{/}}l$

доставляя значения функций w и ψ из (2.4) и (2.5) в систему (2.1) получаем следующую систему обыкновенных дифференциальных уравнений относительно искомых функций w_n и ψ_n:

(2.6)

${\rho }J\frac{{{{d}^{2}}{{\psi }_{n}}}}{{d{{t}^{2}}}} + ({{\rm E}}J{\mu }_{n}^{2} + kGF){{\psi }_{n}} - kGF{{{\mu }}_{n}}{{w}_{n}} = 0$

Общее решение системы (2.6) при начальных условиях (2.3) имеет вид

(2.7)

${{w}_{n}}(t) = {{A}_{n}}\sin {{{\omega }}_{{n1}}}t + {{B}_{n}}\sin {{{\omega }}_{{n2}}}t + 2{{l}^{{ - 1}}}{{P}_{0}}{{H}_{n}}{{L}_{n}}\sin {{{\mu }}_{n}}c\sin {\omega }t\quad$

$\begin{gathered} {{{\psi }}_{n}}(t) = \left( {{{{\mu }}_{n}} - \frac{{{\;\rho \omega }_{{n1}}^{2}}}{{kG{{{\mu }}_{n}}}}} \right){{A}_{n}}\sin {{{\omega }}_{{n1}}}t + \left( {{{{\mu }}_{n}} - \frac{{{\;\rho \omega }_{{n2}}^{2}}}{{kG{{{\mu }}_{n}}}}} \right){{B}_{n}}\sin {{{\omega }}_{{n2}}}t + \\ + 2{{l}^{{ - 1}}}{{P}_{0}}{{\mu }_{n}}{{H}_{n}}\sin {{\mu }_{n}}c\sin \omega t \\ \end{gathered} $

${{A}_{n}} = \frac{{2{{P}_{0}}{\omega }{{{\text{H}}}_{n}}\sin {{{\mu }}_{n}}c[kG{\mu }_{n}^{2} - (kG{\mu }_{n}^{2} - {\rho \omega }_{{n2}}^{2}){{L}_{n}}]}}{{{\rho }l{{{\omega }}_{{n1}}}({\omega }_{{n1}}^{2} - {\omega }_{{n2}}^{2})}}$

${{B}_{n}} = - \frac{{2{{P}_{0}}{\omega }{{H}_{n}}\sin {{{\mu }}_{n}}c[kG{\mu }_{n}^{2} - (kG{\mu }_{n}^{2} - {\rho \omega }_{{n1}}^{2}){{L}_{n}}]}}{{{\rho }l{{{\omega }}_{{n2}}}({\omega }_{{n1}}^{2} - {\omega }_{{n2}}^{2})}}$

${{H}_{n}} = {{\left\{ {{{\rm E}}J{\mu }_{n}^{4} - \left[ {{\rho }F + \left( {{\rho }J + \frac{{{\rho {\rm E}}J}}{{kG}}} \right){\mu }_{n}^{2}} \right]{{{\omega }}^{2}} + \frac{{{{{\rho }}^{2}}J{{{\omega }}^{4}}}}{{kG}}} \right\}}^{{ - 1}}}\quad {{({{H}_{n}})}^{{ - 1}}} \ne 0$

${{L}_{n}} = 1 + \frac{{{{\rm E}}J{\mu }_{n}^{2}}}{{kGF}} - \frac{{{\rho }J{{{\omega }}^{2}}}}{{kGF}}$

ω_n1, ω_n2 – представляют частоту собственных колебаний рассматриваемого стержня, которые определяются из условия (H_n)^–1 = 0 и описываются выражением

(2.9)

${{{\omega }}_{{ni}}} = {{(2{\gamma })}^{{ - 1/2}}}{{({{{\lambda }}_{n}} + {{( - 1)}^{i}}{{({\lambda }_{n}^{2} - 4{\gamma }k_{n}^{2})}^{{1/2}}})}^{{1/2}}}$

${{\lambda }_{n}} = 1 + \left( {\frac{J}{F} + \frac{{{{\rm E}}J}}{{kGF}}} \right){\mu }_{n}^{2},\quad \quad\quad\quad{{k}_{n}} = \sqrt {\frac{{{{\rm E}}J}}{{{\rho }F}}} {\mu }_{n}^{2},\quad {\gamma } = \frac{{{\rho }J}}{{kGF}}$

Здесь и далее i = 1, 2; n – число полуволн, которые образует ось стержня при колебаниях. Формула (2.9) определяет два значения собственной частоты, отвечающих данному числу n полуволн.

Подставляя значения функций w_n(t), ψ_n(t) из (2.7), (2.8) в соответствующие формулы (2.4), (2.5), получаем, что вынужденные поперечные колебания рассматриваемого стержня определяются по закону

(2.10)

$w = \frac{{2{{P}_{0}}}}{l}\mathop \sum \limits_{n = 1}^\infty {{H}_{n}}{{L}_{n}}\sin {{{\mu }}_{n}}c\sin {\omega }t\sin {{{\mu }}_{n}}x$

(2.11)

$\psi = \frac{{2{{P}_{0}}}}{l}\mathop \sum \limits_{n = 1}^\infty {{{\mu }}_{n}}{{H}_{n}}\sin {{{\mu }}_{n}}c\sin {\omega }t\cos {{{\mu }}_{n}}x$

Состояние резонанса имеет место, когда частота возмущающей силы приближается к одной из собственных частот колебаний.

3. Описание задачи 2. Для описания задачи 2, кратко представим волновые процессы, происходящие в стержне. Система уравнений (2.1) – гиперболического типа и описывает распространение волн с дисперсией. Однако в рамках класса более коротких волн, согласно теореме предельности [4, с. 26] в стержне распространяются два типа волн (изгибного и сдвигового) со скоростями фронтов c₁ = $\sqrt {E{\text{/}}\rho } $, c₂ = $\sqrt {kG{\text{/}}\rho } $. Для длинных волн, перенос энергии в стержне характеризуется групповой скоростью. Групповая скорость для задачи (2.1)–(2.3) вычисляется по формуле

(3.1)

${{{\nu }}_{i}} = {{\left. {\frac{{\partial {{\omega }_{i}}}}{{\partial s}}} \right|}_{{s = {{\mu }_{n}}}}} = \frac{1}{{4{\gamma }{{{\omega }}_{{ni}}}}}\left[ {\frac{{\partial {{\lambda }_{n}}}}{{\partial {{{\mu }}_{n}}}} + {{{( - 1)}}^{i}}\frac{\partial }{{\partial {{{\mu }}_{n}}}}{{{({\lambda }_{n}^{2} - 4{\gamma }k_{n}^{2})}}^{{1/2}}}} \right]$

где ω_i = ω_i(s) – закон дисперсии волны изгиба. Этот закон можно получить с помощью формулы (2.9), заменив μ_n на s:

$\frac{\partial }{{\partial {{{\mu }}_{n}}}}{{({\lambda }_{n}^{2} - 4{\gamma }k_{n}^{2})}^{{1/2}}} = \frac{{{{\lambda }_{n}}\partial {{\lambda }_{n}}{\text{/}}\partial {{{\mu }}_{n}} - \quad4{\gamma }{{k}_{n}}\partial {{k}_{n}}{\text{/}}\partial {{{\mu }}_{n}}}}{{{{{({\lambda }_{n}^{2} - 4{\gamma }k_{n}^{2})}}^{{1/2}}}}}$

$\frac{{\partial {{\lambda }_{n}}}}{{\partial {{{\mu }}_{n}}}} = 2\left( {\frac{J}{F} + \frac{{{{\rm E}}J}}{{kGF}}} \right){{{\mu }}_{n}},\quad \frac{{\partial {{k}_{n}}}}{{\partial {{{\mu }}_{n}}}} = 2\sqrt {\frac{{{{\rm E}}J}}{{{\rho }F}}} {{{\mu }}_{n}}$

Движение в стержне будем исследовать в рамках линейной теории тонких прямолинейных нерастяжимых стержней, в соответствии с которой упругие смещения точек нейтральной линии стержня относительно их положения в недеформированном состоянии предполагаются малыми по сравнению с длиной стержня и перпендикулярными оси x. Движение в стержне можно разложить на два движения. Поступательное, определяемое движением полюса и вращательное движение вокруг оси, проходящей через полюс.

Для иллюстрации вращательного движения в стержне рассмотрим волны изгиба, образовавшиеся в результате приложения силы (фиг. 1) к сечению шарнирно-опертого стержня x = c в момент времени t = 0₊ и распространяющиеся по первоначально невозмущенному стержню. В прямом и обратном направлениях начнут распространяться волны изгиба. Закон распространения в прямом направлении переднего фронта волны изгиба вдоль стержня дается уравнением

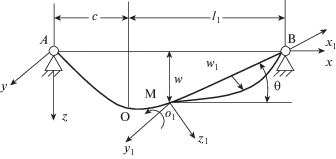
(3.2)

$\begin{gathered} x{\text{'}}(t) = \left\{ \begin{gathered} c + {{{\nu }}_{1}}t - 2ml\quad {\text{п р и }}\quad t > (2ml - c){\text{/}}{{{\nu }}_{1}} \hfill \\ 2(m + 1)l - {{{\nu }}_{1}}t - c\quad {\text{п р и }}\quad t < [2(m + 1)l - c]{\text{/}}{{{\nu }}_{1}} \hfill \\ \end{gathered} \right.{\;} \hfill \\ m\;{\text{ = }}\;{\text{0,}}\;{\text{1,}}\;... \hfill \\ \end{gathered} $

где ${{v}_{1}}$ – групповая скорость распространения волн изгиба вдоль стержня и определяется по формуле (3.1). Ввиду того что, волна изгиба (3.2) волна сильного разрыва, в этом случае на фронте волны изгиба (3.2) происходит скачкообразное изменение изгибающего момента M, угловой скорости $\dot {\psi }$ и т.д. Здесь и далее точкой обозначено дифференцирование по времени t. Функция ψ определяется из выражения (2.11). При этих условиях, кроме того, из условия непрерывности перемещения w и угла поворота элемента стержня ψ на фронте волны изгиба, можно представить форму возмущенной части стержня, в участке, от края В до точки приложения силы в момент времени t < l₁/ν₁, которое показано на фиг. 2 со следующими обозначениями: l₁ – длина рассматриваемого участка; o – точка приложения силы в выбранный момент времени; o₁ – точка в переднем фронте волны изгиба на нейтральной линии стержня; $o{{o}_{1}}$ – кривая, представляющая вид возмущенной части стержня; прямолинейный отрезок o₁. Β-вид невозмущенной части стержня; w(t, x') – прогиб поперечного сечения на фронте волны изгиба в момент времени относительно ее положения при недеформированном стержне (относительно оси x); x'(t) – измеряемое вдоль стержня расстояние от точки A до o₁. Для описания вращательного движения невозмущенной части стержня вводится подвижная система координат x₁, y₁, z₁ с началом отсчета в точке ${{o}_{{_{1}}}}$ на нейтральной линии стержня, неизменно связанная с фронтом волны изгиба, ось x₁ которой направим вдоль нейтральной линии невозмущенной части стержня, ось y₁ – параллельна оси y. Заметим, что в случае недеформированного состояния стержня оси системы координат x₁, x₂, z₁ параллельны соответствующим осям инерциальной системы x, y, z (фиг. 2). Система x₁, y₁, z₁ может перемещаться вдоль стержня со скоростью ν₁ вместе с фронтом волны изгиба, относительно инерциальной системы x, y, z.

Фиг. 2

Учитывая выше сказанное, легко убедиться, что момент изгиба на фронте волны изгиба превращается в момент вращения. Обозначим возникший момент вращения через M. Когда момент вращения $М $от приложения силы со скоростью ν₁ двигается до края стержня ${\text{B}}$, то невозмущенная часть стержня, при этом совершает вращательное движение вокруг оси y₁ в вертикальной плоскости xz, относительно фронта волны изгиба. Оно осуществляется моментом вращения M, формирующегося на фронте волны изгиба. При совершении вращательного движения в этой части стержня возникают новые упругие колебания w₁(t, x), ψ₁(t, x) и дополнительные силы, обусловленные упругостью стержня [5]. Обозначим обобщенный координат движения через θ(t), где θ – угол, который выражается углом поворота элемента стержня вокруг оси y₁ в точке o₁ (фиг. 2), чья зависимость от изменения точки o₁ вдоль стержня и времени t можно представить в виде

(3.3)

${\theta }(t) = \psi (t,x')$,

где точка o₁ движется вдоль стержня по закону (3.2).

4. Математическая постановка задачи 2 и основные уравнения. Рассмотрим в рамках уточненной теории Тимошенко вращательное движение невозмущенной части стержня, относительно фронта волны изгиба (фиг. 2). Вращательное движение происходит в вертикальной плоскости xz, вокруг оси ${{y}_{1}}$ и оно осуществляется вращательным моментом M(t), формирующимся на фронте волны изгиба. Ставится и решается следующая задача: требуется определить при этом вынужденные поперечные колебания w₁(t, x) и ψ₁(t, x), возникающие в результате вращательного движения невозмущенной части стержня, а также момент вращения M(t), обеспечивающего заданное движение этой части стержня.

Для решения поставленной задачи выведем уравнение движения и систему уравнений упругих поперечных колебаний невозмущенной части стержня. С этой целью в качестве обобщенной координаты движения примем θ(t), где θ определяется по формуле (3.3). Вектор упругих поперечных смещений точек невозмущенной части стержня в момент времени t, относительно оси x₁ обозначим через w₁(t, x). Радиус – вектор точек в участке x' < x ≤ l, t > (2ml – c)/ν₁ (m = 0, 1, …) стержня относительно точки o₁ обозначим

(4.1)

${\mathbf{R}}(t,x) = {{{\mathbf{R}}}_{{{{o}_{1}}}}}(t,x) + {{w}_{1}}(t,x)\quad$

где ${{{\mathbf{R}}}_{{{{o}_{1}}}}}$(t, x) – вектор недеформированного состояния стержня относительно точки ${{о }_{1}}$, причем |${{{\mathbf{R}}}_{{{{o}_{1}}}}}$| = x – c, x ≥ c (измеряемое вдоль стержня расстояние от точки А до ${{о }_{1}}$ равен c + ν₁t, а от точки А до произвольной точки $о '$ при t < l₁/ν_l равен x + ν_lt, следует, что вдоль стержня расстояние от точки ${{o}_{1}}$ до o' равен (x – c)).

Векторы ${{{\mathbf{R}}}_{{{{o}_{1}}}}}$ и w₁ имеют в инерциальной системе координат x, y, z следующие координатные представления:

${{{\mathbf{R}}}_{{{{o}_{1}}}}}(t,x) = \left\| \begin{gathered} (x - c)\cos {\theta } \\ 0 \\ - (x - c)\sin {\theta } \\ \end{gathered} \right\|,\quad \quad\quad\quad\quad\quad\quad{{{\mathbf{w}}}_{1}}(t,x) = \left\| \begin{gathered} {{w}_{1}}(t,x)\sin {\theta } \\ 0 \\ {{w}_{1}}(t,x)\cos {\theta } \\ \end{gathered} \right\|$

Кинетическая энергия движения стержня имеет вид

(4.3)

$K = \frac{1}{2}\mathop \smallint \limits_0^l [{\rho }J{{({{\dot {\psi }}_{1}})}^{2}} + {\rho }F{{[{\mathbf{\dot {R}}}]}^{2}}]dx$

В силу принятых выше предположений о нерастяжимости стержня и малости его поперечных упругих смещений и при исполненных в [5] предположениях относительно малости характерных величин движения, а также формулам (4.1)–(4.3) для кинетической энергии движения стержня, получим с точностью до величины порядок ε² (ε ≪ 1):

(4.4)

$K = \frac{1}{2}\mathop \smallint \limits_0^l \{ {\rho }J{{({{\dot {\psi }}_{1}})}^{2}} + {\rho }F[{{(x - c)}^{2}}{{{\dot {\theta }}}^{2}} + \dot {w}_{1}^{2}(t,x) - 2(x - c){\dot {\theta }}{{\dot {w}}_{1}}(t,x)]\} dx$

Потенциальная энергия стержня равна сумме потенциальных энергий упругих сил, возникающих при деформации стержня и силе тяжести

(4.5)

$\begin{gathered} {\Pi } = {\rho g}F\mathop \smallint \limits_0^l [ - (x - c)\sin {\theta } + {{w}_{1}}(t,x)\cos {\theta }]dx + \\ + \frac{1}{2}\int\limits_0^l {\left[ {EJ{{{\left( {\frac{{\partial {{\psi }_{1}}}}{{\partial x}}} \right)}}^{2}} + kGF{{{\left( {\frac{{\partial {{w}_{1}}}}{{\partial x}} - {{\psi }_{1}}} \right)}}^{2}}} \right]dx} \\ \end{gathered} $

Для получения уравнения движения и системы уравнений упругих поперечных колебаний стержня воспользуемся вариационным принципом механики Гамильтона–Остроградского:

(4.6)

$\int\limits_{{{t}_{1}}}^{{{t}_{2}}} {(\delta K - \delta \Pi + \delta A)dt = 0} $

где δK, δΠ – вариации кинетической и потенциальной энергии; δA = M(t)δt – элементарная работа вращающегося момента M(t) на виртуальных изменениях угла поворота θ.

Подставляя значения (4.4) и (4.5) в соотношение (4.6) и вычисляя вариации кинетической и потенциальной энергий с использованием принципа независимых вариаций, учитывая при этом, что вариации δθ, δw₁, в начальный t₁ и конечный t₂ моменты времени равны нулю, получим линейное интегро-дифференциальное уравнение движения

(4.7)

$\begin{gathered} {\rho }F\mathop \smallint \limits_0^l (x - c)[(x - c)\ddot {\theta } - {{{\ddot {w}}}_{1}}(t,x)]dx = M(t) + \\ + {\;\rho g}F\mathop \smallint \limits_0^l [(x - c)\cos {\theta } + {{w}_{1}}(t,x)\sin {\theta }]dx\quad \\ \end{gathered} $

и систему уравнений упругих поперечных колебаний упругого шарнирно-опертого стержня

(4.8)

$\begin{gathered} {{\rm E}}J\frac{{{{\partial }^{2}}{{{\psi }}_{1}}}}{{\partial {{x}^{2}}}} + kGF\left( {\frac{{\partial {{w}_{1}}}}{{\partial x}} - {{{\psi }}_{1}}} \right) = {\rho }J\frac{{{{\partial }^{2}}{{{\psi }}_{1}}}}{{\partial {{t}^{2}}}} \\ kGF\left( {\frac{{{{\partial }^{2}}{{w}_{1}}}}{{\partial {{x}^{2}}}} - \frac{{\partial {{{\psi }}_{1}}}}{{\partial x}}} \right) + q(t,x) = {\rho }F\frac{{{{\partial }^{2}}{{w}_{1}}}}{{\partial {{t}^{2}}}} \\ \end{gathered} $

с граничными и начальными условиями:

(4.9)

$x = 0,l{\text{:}}\quad {{w}_{1}} = 0,\quad \partial {{\psi }_{1}}{\text{/}}\partial x = 0$

(4.10)

$\begin{gathered} t = 0{\text{:}}\quad {{w}_{1}} = 0,\quad {{{\dot {w}}}_{1}} = 0 \hfill \\ {{\psi }_{1}} = 0,\quad {{{\dot {\psi }}}_{1}} = 0 \hfill \\ \end{gathered} $

где q(t, x) – дополнительные силы, которые возникли из вращательного движения стержня и чья зависимость от координаты x и времени t имеет вид

Если волна изгиба вдоль стержня распространяется в обратном направлении, то q(t, x) представляется в виде

С помощью (2.11), (3.3) в участке x' < x ≤ l, t > (2ml – c)/ν₁, (m = 0, 1, …) можно привести $\ddot {\theta }$(t) к следующему виду:

(4.11)

$\ddot {\theta } = \sum\limits_{n = 1}^\infty {{{{\ddot {\theta }}}_{n}}(t)} $

$\begin{gathered} {{{\ddot {\theta }}}_{n}}(t) = - {{P}_{0}}{{l}^{{ - 1}}}{{{\mu }}_{n}}{{{\rm H}}_{n}}\{ {{({{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })}^{2}}\sin [({{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })t + {{{\mu }}_{n}}{{{\alpha }}_{m}}] - \\ - {{({{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })}^{2}}\sin [({{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })t + {{{\mu }}_{n}}{{{\alpha }}_{m}}]\} \sin {{{\mu }}_{n}}c \\ \end{gathered} $

${{{\alpha }}_{m}} = c - 2ml,\quad m = 0,1,...$

После определения прогиба w₁(t, x) и угла поворота элемента стержня ψ₁(t, x) необходимый момент вращения M(t), обеспечивающий заданное движение в этой части стержня, вычисляется по формуле (4.7).

5. Решение задачи 2. Решение системы (4.8) (без учета собственного веса стержня) будем искать в такой форме, чтобы граничные условия (4.9) и начальные условия (4.10) удовлетворились полностью, а именно: будем полагать, что

${{w}_{1}} = \mathop \sum \limits_{n = 1}^\infty {{w}_{{1n}}}(t)\sin {{{\mu }}_{n}}x$

(5.1)

${{{\psi }}_{1}} = \mathop \sum \limits_{n = 1}^\infty {{{\psi }}_{{1n}}}(t)\cos {{{\mu }}_{n}}x$

Подставляя значения w₁ и ψ₁ из (5.1) в систему (4.8) получаем следующую систему обыкновенных дифференциальных уравнений относительно искомых функций w_1n, ψ_1n:

(5.2)

$\begin{gathered} {\rho }J\frac{{{{d}^{2}}{{\psi }_{{1n}}}}}{{d{{t}^{2}}}} + ({{\rm E}}J{\mu }_{n}^{2} + kGF){{\psi }_{{1n}}} - kGF{{{\mu }}_{n}}{{w}_{{1n}}} = 0 \\ {\rho }F\frac{{{{d}^{2}}{{w}_{{1n}}}}}{{d{{t}^{2}}}} + kGF{\mu }_{n}^{2}{{w}_{{1n}}} - \quad\;kGF{{{\mu }}_{n}}{{\psi }_{{1n}}} = {{q}_{n}}(t) \\ \end{gathered} $

${{q}_{n}}(t) = 2{{l}^{{ - 1}}}{\rho }F{{\ddot {\theta }}_{n}}{{D}_{n}}(x')$

${{D}_{n}}(x{\text{'}}) = \quad\left\{ \begin{gathered} \frac{1}{{{\mu }_{n}^{2}}}\{ {{{\beta }}_{n}} - [\sin {{{\mu }}_{n}}x' - {{{\mu }}_{n}}(x{\text{'}} - c)\cos {{{\mu }}_{n}}x']\} \quad {\text{п р и }}\quad t > (2ml - c){\text{/}}{{{\nu }}_{1}} \hfill \\ \frac{1}{{{\mu }_{n}^{2}}}\{ [\sin {{{\mu }}_{n}}x' - {{{\mu }}_{n}}(x{\text{'}} - c)\cos {{{\mu }}_{n}}x'] - c{{{\mu }}_{n}}\} \quad {\text{п р и }}\quad t < [2(m + 1)l - c]{\text{/}}{{{\nu }}_{1}} \hfill \\ \end{gathered} \right.$

${{{\beta }}_{n}} = \sin {{{\mu }}_{n}}l - {{{\mu }}_{n}}(l - c)\cos {{{\mu }}_{n}}l$

Построив решение системы (5.2) по методу вариаций постоянных при начальных условиях (4.10), заключаем, что упругие поперечные колебания стержней во времени движения определяются по закону:

(5.3)

${{w}_{1}} = \mathop \sum \limits_{n = 1}^\infty \left[ {\mathop \smallint \limits_0^t {{f}_{{1n}}}(\tau )\sin {{{\omega }}_{{n1}}}(t - \tau )d\tau + \mathop \smallint \limits_0^t {{f}_{{2n}}}(\tau )\sin {{{\omega }}_{{n2}}}(t - \tau )d\tau } \right]\sin {{{\mu }}_{n}}x$

$(x' \leqslant x \leqslant l,t > (2ml - c){\text{/}}{{{\nu }}_{1}},m = 0,1, \ldots )$

(5.4)

${{{\psi }}_{1}} = \mathop \sum \limits_{n = 1}^\infty \left[ {\mathop \smallint \limits_0^t {{{\text{g}}}_{{1n}}}(\tau )\sin {{{\omega }}_{{n1}}}(t - \tau )d\tau + \mathop \smallint \limits_0^t {{g}_{{2n}}}(\tau )\sin {{{\omega }}_{{n2}}}(t - \tau )d\tau } \right]\cos {{{\mu }}_{n}}x$

${{f}_{{1n}}}(t) = {{\ddot {\theta }}_{n}}(t){{D}_{n}}(x'){{{\text{P}}}_{{1n}}},\quad {{f}_{{2n}}}(t) = {{\ddot {\theta }}_{n}}(t){{D}_{n}}(x'){{{\text{P}}}_{{2n}}}$

${{{\text{P}}}_{{1n}}} = \frac{{2(kG{\mu }_{n}^{2} - {\rho \omega }_{{n2}}^{2})}}{{{\rho }l{{{\omega }}_{{n1}}}({\omega }_{{n1}}^{2} - {\omega }_{{n2}}^{2})}}{\text{,}}\quad {{{\text{P}}}_{{2n}}} = \frac{{2(kG{\mu }_{n}^{2} - {\rho \omega }_{{n1}}^{2})}}{{{\rho }l{{{\omega }}_{{n2}}}({\omega }_{{n1}}^{2} - {\omega }_{{n2}}^{2})}}$,

${{g}_{{1n}}}(t) = \left( {{{{\mu }}_{n}} - \frac{{{\;\rho \omega }_{{n1}}^{2}}}{{kG{{{\mu }}_{n}}}}} \right){{f}_{{1n}}}(t),\quad\quad {{g}_{{2n}}}(t) = \left( {{{{\mu }}_{n}} - \frac{{{\;\rho \omega }_{{n2}}^{2}}}{{kG{{{\mu }}_{n}}}}} \right){{f}_{{2n}}}(t)\quad$

Решения (5.3) и (5.4) после преобразований можно представить в виде вынужденных и свободных колебаний, вызванных возмущающими силами q(t, x). Опуская подробности, представим вынужденные поперечные колебания из общего решения (5.3), (5.4) в виде

(5.5)

${{w}_{1}} = {{P}_{0}}{{l}^{{ - 1}}}\mathop \sum \limits_{n = 1}^\infty {{H}_{n}}{\mu }_{n}^{{ - 1}}[ - {{P}_{{1n}}}{{u}_{n}}({{{\omega }}_{{n1}}},t) + {{P}_{{2n}}}{{u}_{n}}({{{\omega }}_{{n2}}},t)]\sin {{{\mu }}_{n}}c\sin {{{\mu }}_{n}}x$

(5.6)

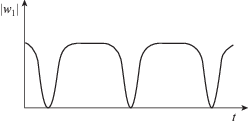
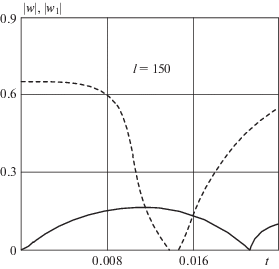
${{{\psi }}_{1}} = {{P}_{0}}{{l}^{{ - 1}}}\mathop \sum \limits_{n = 1}^\infty {{H}_{n}}{\mu }_{n}^{{ - 1}}[{\text{P}}_{{1n}}^{*}{{u}_{n}}({{{\omega }}_{{n1}}},t) + {\text{P}}_{{2n}}^{*}{{u}_{n}}({{{\omega }}_{{n2}}},t)]\sin {{{\mu }}_{n}}c\cos {{{\mu }}_{n}}x$

${\text{P}}_{{1n}}^{*} = - \left( {{{{\mu }}_{n}} - \frac{{{\;\rho \omega }_{{n1}}^{2}}}{{kG{{{\mu }}_{n}}}}} \right){{{\text{P}}}_{{1n}}},\quad {\text{P}}_{{2n}}^{*} = \left( {{{{\mu }}_{n}} - \frac{{{\;\rho \omega }_{{n2}}^{2}}}{{kG{{{\mu }}_{n}}}}} \right){{{\text{P}}}_{{2n}}}$

${{u}_{n}}({\lambda },t) = \frac{{{\lambda }{{{\beta }}_{n}}{{{({{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })}}^{2}}}}{{{{{\lambda }}^{2}} - {{{({{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })}}^{2}}}}\sin [({{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })t + {{{\mu }}_{n}}{{{\alpha }}_{m}}] - \frac{{{\lambda }{{{\beta }}_{n}}{{{({{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })}}^{2}}}}{{{{{\lambda }}^{2}} - {{{({{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })}}^{2}}}} \times $

$ \times \sin [({{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })t + {{{\mu }}_{n}}{{{\alpha }}_{m}}] + \quad\frac{{{\lambda }{{{\mu }}_{n}}({\mu }_{n}^{2}{\nu }_{1}^{{2\quad}} + {{{\omega }}^{2}})}}{{{{{\lambda }}^{2}} - {{{\omega }}^{2}}}}(x{\text{'}} - c)\sin {\omega }t - $

$ - \frac{{2{{{\mu }}_{n}}{{{\nu }}_{1}}{\omega \lambda }({{{\lambda }}^{2}} + {\mu }_{n}^{2}{\nu }_{1}^{{2\quad}})}}{{{{{({{{\lambda }}^{2}} - {{{\omega }}^{2}})}}^{2}}}}\cos {\omega }t + \frac{{{\lambda }{{{({{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })}}^{2}}}}{{2[{{{\lambda }}^{2}} - {{{(2{{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })}}^{2}}]}}\{ {{{\mu }}_{n}}(x{\text{'}} - c) \times $

$ \times \sin [(2{{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })t + 2{{{\mu }}_{n}}{{{\alpha }}_{m}}]\quad + \frac{{{{{\lambda }}^{2}} - (2{{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })(4{{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })}}{{{{{\lambda }}^{2}} - {{{(2{{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })}}^{2}}}} \times $

$ \times \cos [(2{{{\mu }}_{n}}{{{\nu }}_{1}} + {\omega })t + 2{{{\mu }}_{n}}{{{\alpha }}_{m}}]\} - \frac{{{\lambda }{{{({{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })}}^{2}}}}{{2[{{{\lambda }}^{2}} - {{{(2{{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })}}^{2}}]}}\{ {{{\mu }}_{n}}(x{\text{'}} - c) \times $

$ \times \sin [(2{{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })t + 2{{{\mu }}_{n}}{{{\alpha }}_{m}}] + \frac{{{{{\lambda }}^{2}} - (2{{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })(4{{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })}}{{{{{\lambda }}^{2}} - {{{(2{{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })}}^{2}}}} \times $

$ \times \cos [(2{{{\mu }}_{n}}{{{\nu }}_{1}} - {\omega })t + 2{{{\mu }}_{n}}{{{\alpha }}_{m}}]\} $

Вынужденные колебания в участке 0 ≤ x ≤ x', t < [2(m + 1)l – c]/ν₁, (m = 0, 1, …) упругого шарнирно-опертого стержня можно получить с помощью формул (5.5), (5.6), заменив c – 2ml, ν₁, β_n на 2(m + 1)l – c, –ν₁, cμ_n. Комбинируя задачу (2.1)–(2.3) с задачей (4.8)–(4.10), получаем, что выражения (5.5), (5.6) описывают вынужденные поперечные колебания упругого шарнирно-опертого стержня, вызванные возмущающими периодическими изменениями силы q(t, x). Физику данных колебаний можно объяснить следующим образом. Изменение этой силы в стержне имеет характер пульсации, которая возникает во всех точках стержня, во время движения в начальный момент перемещения изгибных возмущений вдоль стержня. В короткие промежутки времени, когда движение удаляется с данной точки, сила в этой точке резко падает до нуля и столь же быстро восстанавливает свое значение при отраженных от краев стержня изгибных возмущениях. Далее процесс повторяется. Эта сила вызывает в стержне интенсивное развитие прогиба w₁, со временем происходит падение этой силы и исчезает причина образования прогиба, после чего происходит восстановление этой силы. График, иллюстрирующий этот процесс, показан на фиг. 3. Величина |w₁| на фиг. 3 представляет абсолютное значение прогиба w₁.

Фиг. 3

Когда знаменатель n – х членов рядов (5.5), (5.6) становится равным нулю, частота возмущающей силы приближается к одному из значений

${{{\omega }}_{{ni}}},\quad {\omega }_{{ni}}^{\kappa } = \pm {{{\mu }}_{n}}{{{\nu }}_{1}} \pm {{{\omega }}_{{ni}}},\quad {\bar {\omega }}_{{ni}}^{\kappa } = \pm 2{{{\mu }}_{n}}{{{\nu }}_{1}} \pm {{{\omega }}_{{ni}}}\quad (\kappa = 1,2,3,4)$

которые определяются из условий

${{({{H}_{n}})}^{{ - 1}}} = 0,\quad {\omega }_{{ni}}^{2} - {{({{{\mu }}_{n}}{{{\nu }}_{1}} \pm {\omega })}^{2}} = 0,\quad {\omega }_{{ni}}^{2} - {{(2{{{\mu }}_{n}}{{{\nu }}_{1}} \pm {\omega })}^{2}} = 0$

В этом случае получаем состояние резонанса.

Сравнивая задачу (2.1)–(2.3) с задачей (4.8)–(4.10), получаем новые значения

(5.7)

${\omega }_{{ni}}^{\kappa } = \pm {{{\mu }}_{n}}{{{\nu }}_{1}} \pm {{{\omega }}_{{ni}}},\quad {\bar {\omega }}_{{ni}}^{\kappa } = \pm 2{{{\mu }}_{n}}{{{\nu }}_{1}} \pm {{{\omega }}_{{ni}}},\quad (\kappa = 1,2,3,4)$

для состояния резонанса.

Отметим, что полученные новые резонансные частоты (5.7) отличаются от частоты собственных колебаний ±μ_nν₁, ±2μ_nν₁ значениями, которые обратно пропорциональны длине стержня и возникли в результате распространения волны изгиба вдоль стержня.

Величины $\omega _{{ni}}^{\kappa }$, $\bar {\omega }_{{ni}}^{\kappa }$ пронумеруем так, чтобы выполнялись соотношения

${\omega }_{{ni}}^{3} = - {\omega }_{{ni}}^{2},\quad {\omega }_{{ni}}^{4} = - {\omega }_{{ni}}^{1},\quad {\bar {\omega }}_{{ni}}^{3} = - {\bar {\omega }}_{{ni}}^{2},\quad {\bar {\omega }}_{{ni}}^{4} = - {\bar {\omega }}_{{ni}}^{1}\quad\quad\quad$

6. Численные результаты. Для иллюстрации эффективности полученных результатов рассмотрим в качестве конкретного примера стальной стержень с квадратным поперечным сечением со следующими параметрами:

$F = 1\;{\text{с }}{{{\text{м }}}^{2}},\quad\quad k = 2{\text{/}}3,\quad {\omega } = 100\;{{{\text{c}}}^{{ - 1}}},\quad {\rho } = 7.85\;{\text{г /с }}{{{\text{м }}}^{3}},\quad c = 20\;{\text{с м }}$

${{P}_{0}} = 15.6 \times {{10}^{5}}\,\,{\text{д и н }},$ Е = 2.14 $ \times \,{{10}^{{12}}}\,\,{\text{д и н /с }}{{{\text{м }}}^{2}},\quad$ G = 8.19 $ \times \,{{10}^{{11}}}\,\,{\text{д и н /с }}{{{\text{м }}}^{2}}$.

Результаты расчетов приведены в следующих шести таблицах и на фиг. 4. В таблицах приведены значения, частоты собственных колебаний ω_ni и резонасные частоты ${\omega }_{{ni}}^{\kappa },{\bar {\omega }}_{{ni}}^{\kappa }$, (κ = 1, 2, 3, 4), вычисленные по формулам (2.9) и (5.7), для каждого из значений n = 1, …, 5, при разных значениях длины стержня.

Фиг. 4

Результаты вычислений, приведенные в этих таблицах, показывают, что во всех рассматриваемых случаях резонансные частоты отличаются от частоты собственных колебаний стержня. Это расхождение увеличивается с уменьшением длины стержня, причем, оно тем больше, чем больше n. На фиг. 4 показаны графики зависимостей |w| (сплошная линия) и |w₁| (штриховая линия) от времени $t$ в точке x = 80 см. Величины |w| и |w₁| представляют абсолютные значения величин вынужденных колебаний стержня, рассчитанных, соответственно, по формулам (2.10) и (5.5). В определенном диапазоне периодическими изменениями силы $q\left( {t,x} \right).$ Графики показывают, что абсолютное значение прогиба |w₁| выше, чем прогиба – |w|, причем с увеличением t значения |w|, |w₁| вначале возрастают, а затем убывают. Наибольшее абсолютное значение |w₁| в 3.5 раза больше |w|_.

7. Заключение. На основе вышеприведенных исследований можно сделать следующее заключение. Основные результаты данных исследований указывают на то, что вращательное движение в стержне является весьма существенным фактором и его следует учитывать при изучении изгибных колебаний упругого стержня при динамическом воздействии.

Общее решение (5.1) справедливо всегда, когда в зависимости от внешнего динамического воздействия в упругом стержне возникают волновые явления.

Предлагаемый метод является достаточно общим методом для решения широкого класса краевых задач, в частности он может быть применен для решения задач изгибных колебаний упругого стержня, при различных нагрузках и граничных условиях.

Таблица 1

i = 1	l = 50 см
n	ω_n1	$\omega _{{n1}}^{1}$= μ_nν₁ + ω_n1	$\omega _{{n1}}^{2}$= μ_nν₁ – ω_n1	$\bar {\omega }_{{n1}}^{1}$= 2μ_nν₁ + ω_n1	$\bar {\omega }_{{n1}}^{2}$= 2μ_nν₁ – ω_n1
1	539.3	1780.8	702.2	2967.8	1882.2
2	2370	7095	2355	11 820	7080
3	5311.4	15858.5	5235.6	26405.6	15782.7
4	9390.6	27937.1	9155.7	46483.6	27702.2
5	14571	43153.8	14011.8	71736.6	42594.6

Таблица 2

i = 1	l = 100 см
n	ω_n1	$\omega _{{n1}}^{1}$= μ_nν₁ + ω_n1	$\omega _{{n1}}^{2}$= μ_nν₁ – ω_n1	$\bar {\omega }_{{n1}}^{1}$= 2μ_nν₁ + ω_n1	$\bar {\omega }_{{n1}}^{2}$= 2μ_nν₁ – ω_n1
1	148.5	445.6	148.4	742.7	445.6
2	593.9	1780.8	592.9	2967.8	1779.9
3	1335	4000	1330.2	6665.5	3995.4
4	2370	7095	2354.8	11820	7079.8
5	3696	11052.9	3659.7	18409.2	11 016

Таблица 3

i = 1	l = 150 см
n	ω_n1	$\omega _{{n1}}^{1}$= μ_nν₁ + ω_n1	$\omega _{{n1}}^{2}$= μ_nν₁ – ω_n1	$\bar {\omega }_{{n1}}^{1}$= 2μ_nν₁ + ω_n1	$\bar {\omega }_{{n1}}^{2}$= 2μ_nν₁ – ω_n1
1	66	198.05	66.5	330.1	198.1
2	264	792	263.9	1320.1	791.9
3	593.9	1780	592.9	2967.8	1779.9
4	1055.2	3162.7	1052.2	5270.2	3159.7
5	1647.5	4935.15	1640.1	8222.8	4927.7

Таблица 4

i = 2	l = 50 см
n	ω_n2	$\omega _{{n2}}^{1}$= μ_nν₁ + ω_n2	$\omega _{{n2}}^{3}$= –μ_nν₁ + ω_n2	$\bar {\omega }_{{n2}}^{1}$= 2μ_nν₁ + ω_n2	$\bar {\omega }_{{n2}}^{3}$= –2μ_nν₁ + ω_n2
1	914 330	915 517	913 143	916 704	911 956
2	916 538	921 263	911 813	925 988	907 088
3	920 199	930 746	909 652	941 293	888 105
4	925 285	943 832	906 739	962 378	888 192
5	931 758	960 341	903 176	988 924	874 593

Таблица 5

i = 2	l = 100 см
n	ω_n2	$\omega _{{n2}}^{1}$ = μ_nν₁ + ω_n2	$\omega _{{n2}}^{3}$ = –μ_nν₁ + ω_n2	$\bar {\omega }_{{n2}}^{1}$ = 2μ_nν₁ + ω_n2	$\bar {\omega }_{{n2}}^{3}$ = –2μ_nν₁ + ω_n1
1	913 776	914 073	913 479	914 370	913 182
2	914 330	915 517	913 543	916 704	911 956
3	915 251	917 916	913 586	920 581	909 920
4	916 538	921 263	913 813	925 988	907 088
5	918 188	825 545	913 832	932 901	903 476

Таблица 6

i = 2	l = 150 см
n	ω_n2	$\omega _{{n2}}^{1}$ = μ_nν₁ + ω_n2	$\omega _{{n2}}^{3}$ = –μ_nν₁ + ω_n2	$\bar {\omega }_{{n2}}^{1}$ = 2μ_nν₁ + ω_n2	$\bar {\omega }_{{n2}}^{3}$ = –2μ_nν₁ + ω_n1
1	913 674	913 806	913 542	913 938	913 410
2	913 920	914 448	913 392	914 976	912 864
3	914 330	915 517	913 143	916 704	911 956
4	915 303	917 011	912 796	919 118	910 688
5	915 639	918 927	912 952	922 215	929 064

Список литературы

Мкртчян К.Ш. О двойственном характере поперечных колебаний упругого стержня // ПММ. 1999. Т. 63. Вып. 6. С. 1055–1058.
Работнов Ю.Н. Механика деформируемого твердого тела. М.: Наука, 1979. 744 с.
Тимошенко С.П. Колебания в инженерном деле. М.: Физматгиз, 1959. 439 с.
Григолюк Э.И., Селезов И.Т. Неклассические теории колебаний стержней, пластин и оболочек // Итоги науки и техники. Сер. Механика твердых деформир. тел. ВИНИТИ. 1973. Т. 5. 272 с.
Гукасян А.А., Саркисян С.В. О колебательном движении прямоугольной пластинки // Изв. АН Арм ССР. Механика. 1990. Т. 43. № 4. С. 13–23.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал