Известия РАН. Механика твердого тела, 2019, № 3, стр. 69-75

1. Постановка задачи. Рассмотрим задачу о движении эллипсоида вращения по горизонтальной плоскости с трением. Будем считать, что центр масс эллипсоида совпадает с его геометрическим центром, а ось вращения является осью динамической симметрии. Введем подвижную систему координат $C{{{\xi }}_{{\text{1}}}}{{{\xi }}_{{\text{2}}}}{{{\xi }}_{3}}$, оси которой совпадают с главными центральными осями инерции эллипсоида. Пусть $a$ и $c$ – экваториальный и осевой радиусы эллипсоида соответственно, и уравнение его поверхности имеет вид $f({\xi }) = ({\xi }_{1}^{2} + {\xi }_{2}^{2}){\text{/}}{{a}^{2}} + {\xi }_{3}^{2}{\text{/}}{{c}^{2}}$ = 0. Поскольку вектор восходящей вертикали γ определяется равенством

компоненты радиус-вектора r точки касания эллипсоида c опорной плоскостью имеют вид (здесь ${\rho } = {{(({{c}^{2}} - {{a}^{2}}){\gamma }_{3}^{2} + {{a}^{2}})}^{{1/2}}}$ – высота центра масс эллипсоида над плоскостью).

Теоремы об изменении количества движения и кинетического момента эллипсоида, условие постоянства вектора ${\kern 1pt} {\gamma }$ и условие безотрывности движения имеют соответственно вид

Здесь m – масса эллипсоида, ${\kern 1pt} {\mathbf{v}}{\kern 1pt} $ и ${\kern 1pt} {\mathbf{\omega }}{\kern 1pt} $ – векторы скорости центра масс и угловой скорости соответственно, ${\mathbf{J}} = {\text{diag}}(A,A,C)$ – центральный тензор инерции эллипсоида, $g$ – ускорение свободного падения, $N \geqslant 0$ – величина нормальной составляющей реакции опорной плоскости, ${\kern 1pt} {\mathbf{F}}{\kern 1pt} $ и ${\kern 1pt} {\mathbf{M}}{\kern 1pt} $ – сила и момент трения соответственно. При заданной модели трения

система (1.3)–(1.6) замкнута относительно переменных ${\kern 1pt} {\mathbf{v}}{\kern 1pt} $, ${\kern 1pt} {\mathbf{\omega }}{\kern 1pt} $, ${\kern 1pt} {\mathbf{\gamma }}{\kern 1pt} $ и $N$.

2. Абсолютно гладкая плоскость. Приведем результаты исследований динамики тела на абсолютно гладкой плоскости [1–3] в случае эллипсоида вращения.

При F = 0, M = 0 уравнения (1.3)–(1.6) допускают интеграл энергии $H = h = {\text{const}}$,

интегралы ${{{\omega }}_{3}} = {\omega } = {\text{const}}$ и $K = k = {\text{const}}$, выражающие постоянства проекций кинетического момента эллипсоида на ось симметрии и вертикаль соответственно, а также интеграл $U = u = {\text{const}}$, следующий из постоянства проекции скорости центра масс эллипсоида на опорную плоскость.

При $k = \pm C{\omega }$ система (1.3)–(1.6) имеет решения вида

соответствующие равномерным вращениям эллипсоида вокруг вертикально расположенной оси симметрии, равномерно движущейся вдоль плоскости.

При $k \ne \pm C{\omega }$ (${{{\gamma }}_{3}} \ne \pm 1$) указанные выше интегралы позволяют провести редукцию к одномерному движению и представить (2.1) в виде

где ${\theta }$ – угол нутации эллипсоида (${{{\gamma }}_{3}} = cos{\theta }$).

Движения эллипсоида с постоянным углом нутации ${\theta }$ соответствуют критическим точкам функции $V({\theta })$. В частности, при $k = 0$ и

в точках ${\theta } = \pm {\pi /}2$ достигается минимум $W({\theta })$, и соответствующие решения системы (1.3)–(1.6) устойчивы. Им соответствуют равномерные качения эллипсоида экваториальным сечением по прямой на плоскости.

Кроме того, при

где ${\varepsilon }$ – безразмерный малый параметр (${\varepsilon } \ll 1$), а ${{{\rho }}_{0}}$ – соответствующая углу нутации ${{{\theta }}_{0}}$ высота центра масс, область возможного движения приведенной системы (2.5) имеет ширину порядка ${\varepsilon }$, и соответствующее решение (1.3)–(1.6) можно представить в виде где ${\varphi }$ и ${\psi }$ – быстрая и медленные функции времени соответственно. Соответствующее (2.7) движение является псевдорегулярной прецессией эллипсоида вокруг центра масс, равномерно движущегося вдоль плоскости. Заметим, что решения (2.7) при ${\theta } = 0$ (${\theta } = {\pi }$) и ${\theta } = \pm {\pi /}2$ имеют вид (2.6) и (2.4) соответственно.

3. Плоскость с трением скольжения. Рассмотрим случай плоскости с трением скольжения (${\mathbf{M}} = 0$). Будем считать, что сила трения обращается в нуль только одновременно со скоростью проскальзывания. Тогда из рассмотренных выше движений реализуются те, на которых скорость точки контакта эллипсоида с опорной плоскостью равна нулю, т.е. решения вида (2.4) при $u = 0$ и решения (2.6) при $u = a{\omega }$.

Для исследования устойчивости указанных решений необходимо конкретизировать модель трения. Например, при классическом вязком трении ${\mathbf{F}} = - {\kappa }({\mathbf{v}} + [{\mathbf{\omega ,r}}])$ этот вопрос исследован в [4] для однородного эллипсоида. При произвольных моментах инерции A и C равномерные вращения (2.4) с неподвижным центром масс ($u = 0$) вытянутого вдоль оси симметрии эллипсоида (c > a) устойчивы при ${{{\omega }}^{2}} > {\omega }_{I}^{2}$, а для сжатого – при выполнении обратного неравенства. Равномерные качения (2.6) без проскальзывания ($u = a{\omega }$) вытянутого (сжатого) эллипсоида, параметры которого удовлетворяют неравенству $(c - a)(C - A) < 0$, устойчивы при ${{{\omega }}^{2}} > {\omega }_{{II}}^{2}$ (${{{\omega }}^{2}} < {\omega }_{{II}}^{2}$). Здесь

Из этих результатов в частности следует, что если вытянутый вдоль эллипсоид расположить на плоскости так, что ось его симметрии горизонтальна, и сообщить центру масс достаточно большую горизонтальную скорость, то в силу неустойчивости соответствующих качений ось симметрии не будет оставаться в горизонтальном положении. При этом она может занять вертикальное положение, соответствующее устойчивым решениям (2.4).

Для исследования указанных переходных процессов заметим, что проекция уравнения (1.4) на ось динамической симметрии эллипсоида имеет вид

и при достаточно малом трении ${{{\omega }}_{3}}$ является медленной переменной. Тогда приближенное уравнение, описывающее ее изменение, может быть получено заменой быстрых переменных периодическими решениями системы (1.3)–(1.6), соответствующими постоянству ${{{\omega }}_{3}}$ [5], [6], т.е. случаю абсолютно гладкой плоскости. Кроме того, K и U также являются медленными величинами в силу теоремы об изменении кинетического момента и теоремы о движении центра масс

Выберем в качестве указанного периодического решения (2.7), откинув слагаемые малого порядка. Тогда при классическом вязком трении из (3.1), (3.2), (3.3) получим

Здесь ${{u}_{1}}$, ${{u}_{2}}$ ($u_{1}^{2} + u_{2}^{2} = {{U}^{2}}$) и ${\psi }$ – неизвестные функции времени.

Считая малой скорость центра масс (${\text{|}}U{\text{|}} = a{{{\omega }}_{3}}$) из (3.4) получим

Уравнения (3.4) в совокупности с равенствами (2.7) приближенно описывают динамику эллипсоида на плоскости с вязким трением при малой скорости центра масс и начальных условиях, близких к (2.7). Заметим, что при выполнении неравенства ${\text{|}}U{\text{|}} > a{{{\omega }}_{3}}$ правая часть последнего равенства (3.4) отрицательна и величина проекции скорости центра масс на опорную плоскость убывает, причем при ${\text{|}}U{\text{|}} \gg a{{{\omega }}_{3}}$ по закону $U\, = \,U(0){\text{exp}}( - {\kappa }t{\text{/}}m)$.

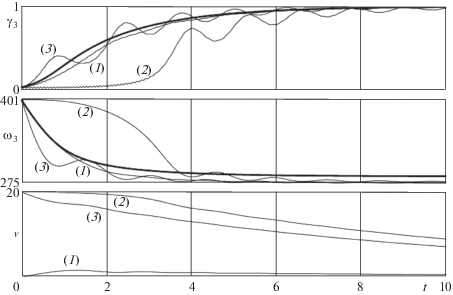
На фиг. 1 тонкими кривыми представлены результаты численного интегрирования точных уравнений движения (1.3)–(1.6) эллипсоида c параметрами $m = 1$ кг, $a = 0.05$ м, $c = 0.15$ м, на плоскости с коэффициентом вязкого трения ${\kappa } = 0.1$ кг/с при начальных условиях ${{{\omega }}_{1}}(0) = {{{\omega }}_{2}}(0) = 0$, ${{{\omega }}_{3}}(0) = 400$ c^–1, ${{{\gamma }}_{2}}(0) = 0$, ${{{\gamma }}_{3}}(0) = 0.05$ (величина ${{{\gamma }}_{1}}(0)$ определялась геометрическим интегралом), т.е. в начальный момент времени эллипсоид имеет достаточно большую угловую скорость, направленную вдоль его оси симметрии, и располагался на плоскости так, что эта ось почти горизонтальна. В экспериментах, обозначенных цифрами $(1)$, $(2)$ и $(3)$ принимались значения ${{v}_{2}}(0) = 0$, ${{v}_{2}}(0)$ = = 20 м/с и ${{v}_{2}}(0) = - 20$ м/с соответственно, и ${{v}_{1}}(0) = {{v}_{3}}(0) = 0$, т.е. в случае (1) начальная скорость центра масс отсутствует, а в случаях (2) и (3) – направлена вдоль плоскости, причем в случае (2) в начальный момент отсутствует проскальзывание в точке контакта с плоскостью.

Во всех трех экспериментах с течением времени косинус угла нутации эллипсоида увеличивается до единицы, угловая скорость уменьшается, но остается практически сонаправленной с осью симметрии (зависимости ${{{\omega }}_{1}}(t)$ и ${{{\omega }}_{2}}(t)$ мало отличаются от нуля и не приводятся на рисунке), скорость центра масс уменьшается до нуля в случаях (2), (3) и мало отличается от нуля в случае (1). Таким образом, финальным движением эллипсоида являются устойчивые вращения (2.4) (u = 0).

Жирной кривой на фиг. 1 представлены результаты интегрирования приближенных уравнений (3.5) при соответствующих начальных условиях. Они хорошо совпадают с результатами эксперимента без начальной скорости центра масс (1), с осредненными значениями соответствующих переменных при начальном движении без проскальзывания (2) и с их финальными значениями в случае (3). Разность финальных значений угловой скорости в интегрировании точных и приближенных уравнений объясняется потерями энергии на переходных процессах.

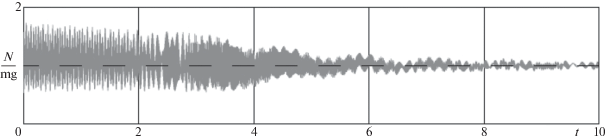
На фиг. 2 представлена зависимость отношения величины реакции опорной плоскости к весу эллипсоида в эксперименте (2). В остальных экспериментах соответствующие результаты аналогичны. Отрыва эллипсоида от плоскости не наблюдается.

4. Геометрическая интерпретация результатов. Заметим, что при любой скорости центра масс из (3.4) следует уравнение

интегрируя которое, получим

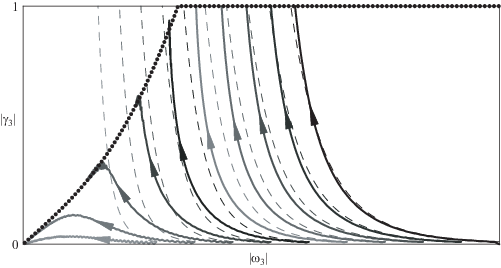
Таким образом при движениях эллипсоида с начальными условиями вида (2.7) при достаточно большой угловой скорости на плоскости параметров $({\text{|}}{{{\omega }}_{3}}{\text{|}},{\text{|}}{{{\gamma }}_{3}}{\text{|}})$ движение происходит в малой окрестности соответствующих кривых (4.1), заканчиваяcь на прямой ${\text{|}}{{{\gamma }}_{3}}{\text{|}} = 1$. Причем при малой скорости центра масс это движение монотонно.

На фиг. 3 пунктиром обозначены соответствующие равенствам (4.1) кривые, а сплошными кривыми – результаты соответствующих численных экспериментов без начальной скорости центра масс. При большой начальной угловой скорости эллипсоида указанные кривые практически совпадают. При ее уменьшении нарушается условие ${\varepsilon } \ll 1$ и наблюдается существенное различие результатов, а финальными движениями эллипсоида являются регулярные прецессии [4] или устойчивые качения (2.6).

5. Плоскость с поликомпонентным трением. При наличии трения верчения или качения (${\mathbf{M}} \ne 0$) система (1.3)–(1.6) имеет решения вида (2.6), (2.4), в которых следует положить $u = 0$, ${\omega } = {\omega }(t),$ где зависимость ${\omega }(t)$ определяется моделью трения. Уравнения (3.1), (3.2) в этом случае принимают вид

а уравнение (3.3) не меняется.

Заметим, что если мощность трения верчения и качения мала по сравнению с мощностью трения скольжения (например, в моделях трения [7], [8]), то порядок последних слагаемых правых частей (5.1) мал по сравнению с первым, и приближенные уравнения (3.4) также будут достаточно хорошо описывать соответствующие переходные процессы. Таким образом, движение на плоскости $({\text{|}}{{{\omega }}_{3}}{\text{|}},{\text{|}}{{{\gamma }}_{3}}{\text{|}})$ также будет происходить в окрестности кривых (4.1), с той только разницей, что по достижении прямой ${\text{|}}{{{\gamma }}_{3}}{\text{|}} = 1$ изображающая точка не остановится, а будет двигаться вдоль этой прямой влево, а при пересечении с соответствующей прецессиям кривой будет двигаться вдоль нее в сторону уменьшения ${\text{|}}{{{\gamma }}_{3}}{\text{|}}$ [9].

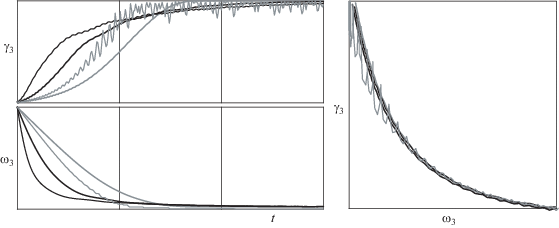
На фиг. 4 представлены численные результаты эксперимента с начальными условиями (1) в уже рассмотренном случае вязкого трения (жирная черная кривая), при классическом сухом трении (жирная серая кривая), поликомпонентном сухом трении [10] (тонкая серая кривая) и поликомпонентном вязком трении [8] (тонкая черная кривая), а также соответствующие кривые на плоскости $({\text{|}}{{{\omega }}_{3}}{\text{|}},{\text{|}}{{{\gamma }}_{3}}{\text{|}})$.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (16-01-00338, 18-01-00335, 19-01-00140) и Программы № 29 Президиума РАН.