Известия РАН. Механика твердого тела, 2019, № 3, стр. 76-85
Изгиб круглой пластины под действием давления газа
М. А. Ильгамов a, b, d, *, В. Е. Моисеева b, **
a Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
b Институт механики и машиностроения ФИЦ “Казанский научный центр РАН”
Казань, Республика Татарстан, Россия
c Башкирский государственный университет
Уфа, Республика Башкортостан, Россия
d Институт механики УФИЦ РАН
Уфа, Республика Башкортостан, Россия
* E-mail: ilgamov@anrb.ru
** E-mail: moiseeva@kfti.knc.ru
Поступила в редакцию 16.10.2017
После доработки 02.02.2018
Принята к публикации 06.02.2018
Аннотация
Изучено влияние среднего избыточного давления окружающей среды на линейный и нелинейный изгиб круглой пластины. Разные значения давления газов на обе поверхности пластины образуют поперечную распределенную нагрузку, состоящую из перепада давлений и взаимодействия среднего давления с кривизной срединной поверхности. При малом отношении среднего давления к модулю упругости материала и при большой относительной толщине влияние второй составляющей нагрузки на изгиб мало. При большом отношении среднего давления к модулю упругости и малой относительной толщине это влияние является значительным.
1. Введение. Анализу линейного и нелинейного изгиба круглых тонких пластин и мембран посвящена большая литература. То же самое относится к задаче устойчивости круглых пластин под действием радиально направленных сжимающих сил. Укажем, например, на работы [1–12]. В работах [13, 14] кроме упругой деформации пластин рассматривается упругопластический изгиб. В [13] исследован нелинейный изгиб круглых пластин, находящихся под действием давления и температуры, с позиций применения их в качестве предохранительных мембран, в [14] представлены результаты исследования нелинейного изгиба и устойчивости круглых пластин под действием давления нагретой или охлажденной сжимаемой рабочей среды.
Во всех этих работах принимается, что поперечная распределенная нагрузка q на тонкую пластину равна $q = \gamma h + {{p}_{2}} - {{p}_{1}}$, где γ – удельный вес материала, h – толщина, р1, р2 – избыточные давления газов на нижнюю и верхнюю поверхности пластины. В случае малой относительной толщины пластины и приложения давления только к одной из поверхностей или малом отношении среднего давления ${{p}_{m}} = {{({{p}_{1}} + {{p}_{2}})} \mathord{\left/ {\vphantom {{({{p}_{1}} + {{p}_{2}})} 2}} \right. \kern-0em} 2}$ к модулю упругости материала Е это значение q является достаточно точным.
Учет влияния разности площадей нижней и верхней поверхностей, среднего давления рm на цилиндрический изгиб удлиненной пластины приводит к выражению для распределенной поперечной нагрузки [15–17]
где функция прогиба w(x) зависит от приведенной жесткости D(1 + α). Здесь D – изгибная жесткость пластины, α – безразмерный параметр, который для шарнирно закрепленной пластины длиной L равенПри получении (1.1), (1.2) предполагается, что кромки пластины изолированы от действия давлений р1, р2.
Для конструкций типа железобетонных, корабельных при атмосферном давлении или односторонних невысоких давлениях параметр α равен нулю или весьма мал. Но для конструкций оборудования нефтехимии, энергетики, глубоководных аппаратов, аэрокосмической техники могут быть немалые значения α. Если $E = 2 \cdot {{10}^{6}}$ бар (сталь), ${{p}_{m}} = 20$ бар, $L{\text{/}}h = {{10}^{2}}$, то $\alpha = 0.1$. Приведенная жесткость повышается на 10%. В случае $E = 2 \cdot {{10}^{5}}$ бар (магниевый сплав) параметр α = 1. При этом приведенная жесткость равна 2D, прогиб меньше в два раза, чем в случае, когда не учитывается разность площадей верхней и нижней поверхностей пластины.
Если средами снизу и сверху пластины являются жидкости с удельными весами γ1 и γ2, то в выражении (1.1) появляется член (γ2 – γ1)w. Учет этого фактора приводит к задаче взаимодействия упругой и гидродинамической неустойчивостей [15]. Такая постановка усложняет анализ и здесь не рассматривается.
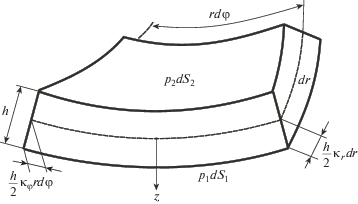
2. Постановка задачи. Рассматривается статический упругий изгиб круглой пластины диаметром 2с и толщиной h, на нижнюю и верхнюю поверхности которой действуют давления газов р0 + р1 и р0 + р2, где р0 – атмосферное давление, р1, р2 – избыточные давления. Давления р1 и р2 могут быть как положительными, так и отрицательными, причем отрицательные значения р1, р2 меньше, чем р0. Не учитывается влияние плотностей газов на поперечную нагрузку (γ1= γ2= 0). При изгибе пластины давления р1, р2 остаются неизменными. Кромка пластины изолирована от действия избыточного давления (действует только р0). До приложения давлений р1, р2 пластина под всесторонним давлением р0 находится в ненапряженном плоском состоянии. Направление оси z, нагрузки q и прогиба w(r) положительно вниз. Рассматривается осесимметричный изгиб.
На фиг. 1 представлен элемент пластины площадью dS = rdφdr срединной поверхности. В соответствии с гипотезами Кирхгоффа при деформации поперечное сечение остается плоским и перпендикулярным к срединной поверхности, толщина пластины не изменяется. При осесимметричном изгибе образующиеся кривизны вдоль радиуса κr и по углу κφ связаны с функцией прогиба w(r) формулами [10, с. 173]
(2.1)
${{\kappa }_{r}} = - \frac{{{{d}^{2}}w}}{{d{{r}^{2}}}},\quad {{\kappa }_{\varphi }} = - \frac{1}{r}\frac{{dw}}{{dr}}$При осесимметричном изгибе кривизна кручения равна нулю. Площади нижней и верхней поверхностей элемента равны
(2.2)
$\begin{gathered} d{{S}_{1}} = dr\left( {1 + \frac{h}{2}{{\kappa }_{r}}} \right)rd\varphi \left( {1 + \frac{h}{2}{{\kappa }_{\varphi }}} \right) \hfill \\ d{{S}_{2}} = dr\left( {1 - \frac{h}{2}{{\kappa }_{r}}} \right)rd\varphi \left( {1 - \frac{h}{2}{{\kappa }_{\varphi }}} \right) \hfill \\ \end{gathered} $Поперечная распределенная сила, действующая на площадь dS срединной поверхности, равна
Здесь собственный вес отнесен к срединной поверхности. Подставляя выражения (2.2), (2.1) в (2.3) и отбрасывая нелинейные члены, получаем
(2.4)
$\begin{gathered} q = {{p}_{e}} + {{p}_{m}}h{{\nabla }^{2}}w,\quad {{p}_{e}} = \gamma h + {{p}_{2}} - {{p}_{1}} \\ {{\nabla }^{2}} = \frac{1}{r}\frac{d}{{dr}}\left( {r\frac{d}{{dr}}} \right),\quad {{p}_{m}} = \frac{{{{p}_{1}} + {{p}_{2}}}}{2} \\ \end{gathered} $Система нелинейных уравнений осесимметричного изгиба в обозначениях [10, с. 178] имеет вид
(2.5)
$\begin{gathered} D\frac{{d({{\nabla }^{2}}w)}}{{dr}} - \frac{h}{r}\frac{{d\Phi }}{{dr}}\frac{{dw}}{{dr}} = \Psi ,\quad \frac{{d({{\nabla }^{2}}\Phi )}}{{dr}} + \frac{E}{{2r}}{{\left( {\frac{{dw}}{{dr}}} \right)}^{2}} = 0 \\ D = \frac{{E{{h}^{3}}}}{{12(1 - {{\nu }^{2}})}},\quad {{\sigma }_{r}} = \frac{{d\Phi }}{{rdr}},\quad {{\sigma }_{\varphi }} = \frac{{{{d}^{2}}\Phi }}{{d{{r}^{2}}}},\quad \Psi = \frac{1}{r}\int\limits_0^r {qrdr} \\ \end{gathered} $С учетом q из (2.4) выражению Ψ можно придать вид
(2.6)
$\Psi = \frac{{{{p}_{e}}r}}{2} + \frac{{{{p}_{m}}h}}{r}\int\limits_0^r {r{{\nabla }^{2}}wdr = } \frac{{{{p}_{e}}r}}{2} + {{p}_{m}}h\frac{{dw}}{{dr}}$В дальнейшем для функции прогиба w будут использованы условия шарнирного опирания пластины по контуру [10, с. 179]
(2.7)
$w = 0,\quad \frac{{{{d}^{2}}w}}{{d{{r}^{2}}}} + \frac{\nu }{r}\frac{{dw}}{{dr}} = 0\quad (r = c)$(2.8)
$w = 0,\quad {{dw} \mathord{\left/ {\vphantom {{dw} {dr}}} \right. \kern-0em} {dr}} = 0\quad (r = c)$Граничные условия для функции напряжения Φ в случае отсутствия смещения контура пластины по радиусу (и = 0) и свободного перемещения (σr = 0) соответственно имеют вид:
(2.9)
$\frac{{{{d}^{2}}\Phi }}{{d{{r}^{2}}}} - \frac{\nu }{r}\frac{{d\Phi }}{{dr}} = 0,\quad \frac{1}{r}\frac{{d\Phi }}{{dr}} = 0\quad (r = c)$Вопрос состоит о влиянии на изгиб пластины второго члена в (2.6), который появляется в результате учета разности площадей нижней и верхней поверхностей при определении поперечной распределенной силы. Для этого сначала рассмотрим линейную задачу.
3. Линейный изгиб. Из (2.5), (2.6) имеем уравнение
(3.1)
$\frac{{d({{\nabla }^{2}}w)}}{{dr}} - \frac{{{{p}_{m}}h}}{D}\frac{{dw}}{{dr}} = \frac{{{{p}_{e}}r}}{{2D}}$а) В случае защемления контура, принимая приближенное решение, удовлетворяющее условиям (2.8), в виде [10, с. 186]
и, интегрируя (3.1) по методу Бубнова–Галеркина, получаем следующее выражение для амплитуды относительного прогиба(3.3)
$\xi = \frac{f}{h} = \frac{{3(1 - {{\nu }^{2}})q{\text{*}}}}{{16(1 + \alpha )}},\quad q* = \frac{{{{p}_{e}}}}{E}{{\left( {\frac{c}{h}} \right)}^{4}}{\text{,}}\quad \alpha = \frac{{3(1 - {{\nu }^{2}}){{p}_{m}}{{c}^{2}}}}{{4E{{h}^{2}}}}$Таким образом, безразмерным параметром α определяется вклад второго члена в уравнении (3.1). При $E = 2 \cdot {{10}^{6}}$ бар (сталь), $\nu = 0.3$, $c{\text{/}}h = {{10}^{2}}$, ${{p}_{m}} = 2$ бар параметр $\alpha = 0.0068$. Если при тех значениях Е, ν принять $c{\text{/}}h = {{10}^{3}}$, ${{p}_{m}} = 20$ бар, то $\alpha = 6.8$. В первом случае среднее давление не играет никакой роли, классическая теория изгиба тонких пластин дает правильный результат. Во втором случае большее сопротивление изгибу оказывает среднее давление рm, чем модуль упругости Е (вернее, величина рmс2, чем Еh2). Это объясняется тем, что собственная изгибная жесткость пластины пропорциональна h3, а влияние среднего давления пропорционально h. Изогнутая под собственным весом γh пластина при ${{p}_{1}} = {{p}_{2}} = {{p}_{m}} = 20$ бар выпрямляется, при этом прогиб уменьшается почти в семь раз.
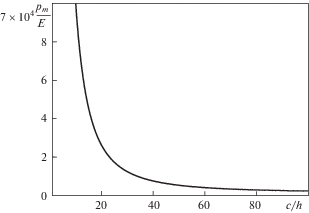
На фиг. 2 представлена кривая зависимости среднего давления от отношения радиуса к толщине пластины при значении параметра $\alpha = {{10}^{{ - 2}}}$ в (3.3), что означает однопроцентную поправку к значению амплитуды прогиба. Если при данных входных параметрах отображающая точка попадает в область ниже кривой, то влияния среднего давления на изгиб нет, выше кривой это влияние становится заметным.
При больших и близких значениях давлений р1 и р2, когда среднее давление рm также большое, а разность р2 – р1 мала, реализуется наибольшее влияние рm и параметра α на изгиб (для одинаковых значений Е, с, h). Наименьшее влияние их имеет место при одностороннем давлении. Пусть ${{p}_{1}} = 0$, ${{p}_{m}} = {{p}_{2}}{\text{/}}2$ и не учитывается собственный вес (γ = 0). Ограничим значение р2 применимостью линейного уравнения (3.1) и его решения (3.3). Полагая в (3.3) ξ ≤ 1, получаем
(3.4)
$\frac{{{{p}_{2}}}}{E} \leqslant \frac{{16(1 + \alpha )}}{{3(1 - {{\nu }^{2}})}}{{\left( {\frac{h}{c}} \right)}^{4}}$С учетом (3.4) и рm = р2/2 из (3.3) имеем наибольшее возможное значение параметра
Положив здесь α = 10 –2, получаем, что при с/h ≤ 14 отображающая точка на фиг. 2 находится выше кривой, а при с/h > 14 – ниже кривой (влияния среднего давления нет). Объясняется это тем, что с уменьшением относительной толщины изгибная жесткость и допустимое одностороннее давление быстро падают. При этом мало и отношение рm/Е.
Есть кажущееся противоречие между общим параметром α по (3.3), пропорциональным (с/h)2, и параметром α по (3.5), пропорциональным при ${{(c{\text{/}}h)}^{2}} \gg 2$ величине (h/с)2. В первом случае среднее давление рm может меняться в широких пределах при постоянном перепаде р2 – р1, во втором случае р1 = 0, поэтому рm жестко определяется давлением р2, величина которого ограничивается прогибом, не превышающим толщину пластины.
б) Условия шарнирного опирания (2.7) удовлетворяются при функции прогиба [10, с. 191]
(3.6)
$w = f\left( {1 - 2a\frac{{{{r}^{2}}}}{{{{c}^{2}}}} + ab\frac{{{{r}^{4}}}}{{{{c}^{4}}}}} \right),\quad a = \frac{{3 + \nu }}{{5 + \nu }},\quad b = \frac{{1 + \nu }}{{3 + \nu }}$Относительный прогиб равняется
(3.7)
$\xi = \frac{f}{h} = \frac{{3q{\text{*}}(1 - {{\nu }^{2}})}}{{16ab(1 + \alpha )}},\quad \alpha = \frac{{3(1 - {{\nu }^{2}}){{p}_{m}}{{c}^{2}}}}{{4E{{h}^{2}}\beta }},\quad \beta = \frac{{b(3 - 2b)}}{{6 - 8b + 3{{b}^{2}}}}$Таким образом, параметр α в случае шарнирного опирания равняется значению (3.3) для случая защемленного края пластины, деленному на коэффициент β, зависящий только от ν. Для ν = 0.3 коэффициент β = 0.26. Следовательно, по (3.7) параметр α почти в четыре раза больше, чем по (3.3). Влияние среднего давления на изгиб шарнирно закрепленной пластины в четыре раза больше, чем в случае защемления. Это объясняется тем, что согласно (2.4) поперечная сила q зависит также от кривизны, образующейся при изгибе. В случае шарнирного закрепления знак кривизны не меняется по всей площади, поэтому вклад последнего члена выражения q в решение является наибольшим. В случае защемления вблизи опоры и в центральной части пластины знаки кривизны разные. Согласно аппроксимации (3.2) точка перегиба находится на радиусе r ≈ 0.58 c.
Наибольшее значение одностороннего давления р2, дающее относительный прогиб ξ = 1, равно
(3.8)
$\frac{{{{p}_{2}}}}{E} = \frac{{16(1 + \alpha )}}{{3(1 - \nu )(5 + \nu )}}{{\left( {\frac{h}{c}} \right)}^{4}}$(3.9)
$\alpha = \frac{2}{{{{{\left( {c{\text{/}}h} \right)}}^{2}}(5 + \nu )\beta {\text{/}}2(1 + \nu ) - 2}}$Эти оценки показывают, что в случае шарнирного закрепления пластины среднее давление рm оказывает большее влияние на изгиб, чем при защемленном крае. Как указывалось выше, положительное среднее давление рm приводит к уменьшению прогиба. Отрицательное значение рm (вакуумирование) и соответственно отрицательное значение параметра α приводят к увеличению прогиба при одном и том же значении собственного веса и разности избыточных давлений р2 – р1.
Как видно из (3.3) и (3.7), эти решения справедливы только при α > –1. Значение α = –1 можно считать критическим, когда линейное решение неограниченно возрастает. Соответствующие критические значения среднего избыточного давления по (3.3) и (3.7) равны
(3.10)
$p_{m}^{*} = - \frac{{4E{{h}^{2}}}}{{3(1 - {{\nu }^{2}}){{c}^{2}}}},\quad p_{m}^{*} = - \frac{{4E{{h}^{2}}\beta }}{{3(1 - {{\nu }^{2}}){{c}^{2}}}}$Представляет интерес выяснить, могут ли реальные значения входных параметров Е, h, с дать значения $p_{m}^{*} > - {{p}_{0}} = - 1$ бар. Принятый выше первый вариант числовых данных ($E = 2 \cdot {{10}^{6}}$ бар, $\nu = 0.3$, $c{\text{/}}h = {{10}^{2}}$) приводит к большим значениям критического среднего избыточного давления в обоих случаях закрепления. Они лишены физического смысла. При втором варианте числовых данных ($E = 2 \cdot {{10}^{6}}$ бар, $\nu = 0.3$, $c{\text{/}}h = {{10}^{3}}$) из (3.10) получаем соответственно $p_{m}^{*} = - 2.93$ бар, $p_{m}^{*} = - 0.76$ бар. При принятых данных критическое значение среднего давления для защемленной пластины лишено физического смысла, в то время как для случая шарнирного закрепления представляется вполне приемлемым. Естественно, приведенное линейное решение справедливо только при прогибах, меньших толщины пластины.
4. Нелинейный изгиб. Принимаем те же аппроксимирующие функции для прогиба w, что в линейном решении.
а) В случае защемленного края, подставив функции (3.2) во второе уравнение (2.5), получаем следующее ограниченное при r = 0 выражение [10, с. 187]
(4.1)
$\frac{{d\Phi }}{{dr}} = - \frac{{E{{f}^{2}}{{r}^{3}}}}{{{{c}^{4}}}}\left( {1 - \frac{{2{{r}^{2}}}}{{3{{c}^{2}}}} + \frac{{{{r}^{4}}}}{{6{{c}^{4}}}}} \right) + \frac{{Cr}}{2}$В том случае, когда край пластины свободно смещается по радиусу, из второго условия (2.9) следует С = Еf 2/c2. Подставим в первое уравнение (2.5) и в (2.6) выражения
После интегрирования по методу Бубнова–Галеркина получаем уравнение
где q* и α представлены в (3.3).В нелинейном решении влияние среднего давления может быть значительным даже в случае одностороннего давления. Принимая по-прежнему ν = 0.3, γ = 0, р1 = 0, рm = = р2/2, представим (4.2) в виде
(4.3)
$0.857{{\xi }^{3}} + 5.862(1 + \alpha )\xi = q*,\quad q* = \frac{{{{p}_{2}}}}{E}{{\left( {\frac{c}{h}} \right)}^{4}},\quad \alpha \approx \frac{{{{p}_{2}}}}{{3E}}{{\left( {\frac{c}{h}} \right)}^{2}}$Наибольшие возможные значения р2/Е и α определим, например, из условия ξ = 4. Тогда из (4.3) следует
(4.4)
$\frac{{{{p}_{2}}}}{E} \approx {{\left( {\frac{h}{c}} \right)}^{4}}\left( {54.8 + 23.4(1 + \alpha )} \right),\quad \alpha \approx \frac{{26.07}}{{{{{(c{\text{/}}h)}}^{2}} - 7.8}}$По (4.4) заключаем, что при с/h ≥ 51 (принято α = 10–2) нет влияния среднего давления на изгиб, в то время как, например при с/h = 4, имеется сильное влияние (α ≈ 3.2). При этом по линейной теории (3.5) α ≈ 0.14. Таким образом, при нелинейном изгибе под односторонним давлением влияние среднего давления больше, чем при линейном изгибе.
Рассмотрим пример изгиба, когда при одном и том же перепаде давлений р2 – р1 (или q*) среднее избыточное давление рm = ±0.9 бар. Пусть при этом значения Е, с/h такие, что q* = 2, α = ±1.2. Если при α = 1.2 реализуется относительный прогиб ξ < 1, то справедливо линейное решение (3.3) ξ = 0.155. При α = –1.2 прогиб не может быть определен по (3.3), необходимо обратиться к нелинейному решению (4.3), из которого находим ξ = 1.570. Отметим, по классической теории изгиба ξ = 0.341 (α = 0). Как видно, имеется не только количественное отличие между этими решениями. При вакуумировании поверхностей пластины, когда коэффициент α приближается к (–1) и меньше, прогиб нужно определять, исходя из нелинейной теории.
б) При шарнирном закреплении вместо (4.1) имеем
(4.5)
$\frac{{d\Phi }}{{dr}} = - \frac{{E{{f}^{2}}{{a}^{2}}{{r}^{3}}}}{{{{c}^{4}}}}\left( {1 - \frac{{2b{{r}^{2}}}}{{3{{c}^{2}}}} + \frac{{{{b}^{2}}{{r}^{4}}}}{{6{{c}^{4}}}}} \right) + \frac{{Cr}}{2}$Из второго условия (2.9) следует С = (Еf 2a2/3c2)(6 – 4b + b2). Тем же путем, что выше, получаем уравнение относительно ξ, которое при ν = 0.3 приводится к виду
(4.6)
$\begin{gathered} 0.377{{\xi }^{3}} + 1.437(1 + \alpha )\xi = q{\text{*}} \\ \alpha = 2.6\frac{{{{p}_{m}}}}{E}{{\left( {\frac{c}{h}} \right)}^{2}} \\ \end{gathered} $В случае α = –1 ± ε ($\varepsilon \ll 1$) решение уравнений (4.3) и (4.6) в двух приближениях
(4.7)
$\xi \approx {{(1.17q{\text{*}} \mp 7.18\varepsilon {{(q*)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}})}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{\text{,}}\quad \xi = {{(2.657q{\text{*}} \mp 5.26\varepsilon {{(q*)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}})}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}$В табл. 1 даны значения прогиба в центре пластины при рассмотренных граничных условиях (ГУ) для ряда значений модуля Юнга с учетом ($\alpha \ne 0$) и без учета ($\alpha = 0$) влияния среднего давления на линейный и нелинейный изгиб (подчеркнутые данные) пластины. Заданы близкие значения давлений ${{p}_{1}} = 1$ бар, ${{p}_{2}} = 1.001$ бар при параметрах: $c{\text{/}}h = 100$, $\nu = 0.3$, γ = 0. Из таблицы видно, что в данной задаче влияние среднего давления на прогиб в центре пластины из оргстекла для линейного решения при шарнирном закреплении достигает 56%, в случае защемленного края − 25%, а при нелинейном решении 29 и 21%, соответственно. Следует отметить, что влияние среднего давления на изгиб пластин, как из магниевого сплава, так и стали при ГУ защемления не наблюдается, а при шарнирном закреплении края пластины из магниевого сплава − не превышает 11%.
Таблица 1.
| ГУ | (2.7) | (2.8) | ||
|---|---|---|---|---|
| Е, бар | $\alpha \ne 0$ | $\alpha = 0$ | $\alpha \ne 0$ | $\alpha = 0$ |
| $2 \cdot {{10}^{4}}$ | 1.513 | 3.478 | 0.636 | 0.853 |
| 1.276 | 1.805 | 0.611 | 0.770 | |
| $2 \cdot {{10}^{5}}$ | 0.308 | 0.348 | 0.082 | 0.085 |
| 0.301 | 0.337 | 0.082 | 0.085 | |
| $2 \cdot {{10}^{6}}$ | 0.034 | 0.035 | 0.008 | 0.008 |
| 0.034 | 0.035 | 0.008 | 0.008 | |
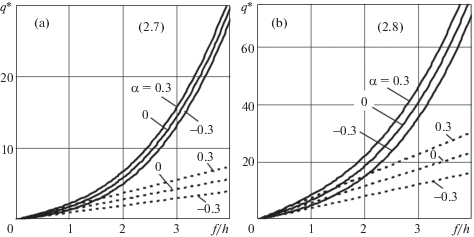
На фиг. 3a, 3b представлены зависимости безразмерного параметра нагрузки q* и прогиба в центре пластины для условий (2.7) и (2.8), соответственно. Сплошной линией отмечены решения с учетом геометрической нелинейности для $\alpha = - 0.3$; 0; 0.3, штриховой − линейные решения. Видно, что при фиксированном значении $q{\text{*}}$ при увеличении $\alpha $ максимальный прогиб уменьшается, а при отрицательном значении α − возрастает, при этом прогиб пластины в случае шарнирного опирания почти в четыре раза больше, чем при защемлении края пластины для всех рассмотренных значений параметра $\alpha $ линейного решения.
5. Заключение. 1. В классической теории изгиба тонких круглых пластин отношение стрелы прогиба f к толщине h определяется безразмерным параметром нагрузки q* = = (ре/Е)(h/с)4, зависящим от отношения распределенной поперечной силы ${{p}_{e}} = \gamma h + {{p}_{2}} - {{p}_{1}}$ к модулю упругости Е материала и от относительной толщины h/с (γ – удельный вес, p1, p2 – избыточные давления снизу и сверху пластины). Учет разности площадей выпуклой и вогнутой поверхностей пластины, среднего избыточного давления рm = (p1 + p2)/2 приводит к зависимости f /h также от безразмерного параметра α = (κрm/Е)(c/h)2. Здесь число κ зависит от условий закрепления пластины (для ν = 0.3 при защемлении κ = 0.68, шарнирном закреплении κ = 2.62).
2. При постоянном значении q* увеличение параметра α приводит к уменьшению прогиба (классической теории соответствует α = 0). Избыточные давления могут иметь и отрицательные значения, что имеет место при вакуумировании поверхностей пластины (должно быть p0 + p1 > 0, p0 + p2 > 0, где p0 – атмосферное давление). Поэтому рm и α также могут быть отрицательными, причем $\alpha > - 1$ в линейной задаче. В нелинейной задаче это ограничение снимается. При отрицательном значении α прогиб возрастает. Из условия $\alpha = - 1$ определяется критическое значение среднего избыточного давления $p_{m}^{*}$ при вакуумировании поверхностей пластины. Закритический изгиб происходит при α < –1, однако, рm должно оставаться меньше, чем атмосферное давление p0.
3. Наибольшее влияние среднего давления рm на изгиб имеет место при равенстве больших давлений p1 и p2, а наименьшее – при одностороннем давлении. В последнем случае поправка на значение прогиба за счет среднего давления может быть при малых отношениях с/h. Это объясняется ограничением допустимого значения разности p2 – p1 для данной пластины.
4. Имеется сильная зависимость прогиба пластины от действия давления на ее кромку. Приведенные выше результаты получены при действии на кромку только атмосферного давления p0. Если, например, при p1 = p2 = рm на кромку действует среднее избыточное давление рm, то исчезает его влияние на изгиб. Реализуется абсолютная устойчивость формы пластины, изогнутой под собственным весом. В целом, требуется дальнейшее изучение влияния среднего избыточного давления на изгиб круглой пластины и его экспериментальное исследование.
Авторы выражают благодарность М.С. Ганеевой за обсуждение.
Работа частично выполнена в рамках государственного задания (проекты № 0246-2019008, № 0049-2015-0040 и по грантам РФФИ № 17-41-02040017-р_а, № 18-01-00150.
Список литературы
Бубнов И.Г. Труды по теории пластин. М.: Гостехиздат, 1953. 423 с.
Timoshenko S. Deflection of a uniformly loaded circular plate with clamped edges // Collected Papers. New York, 1953. P. 401–410.
Панов Д.Ю. О больших прогибах круглой пластины // Труды ЦАГИ. 1939. № 450. С. 55–65.
Феодосьев В.И. О больших прогибах и устойчивости круглой мембраны с мелкой гофрировкой // ПММ. 1945. Т. 9. № 5. С. 389–395.
Феодосьев В.И. К расчету хлопающей мембраны // ПММ. 1946. Т. 10. № 2. С. 295–300.
Bodner S.R. The post buckling behavior of a clamped circular plate // Quart. Appl. Math. 1955. V. 12. № 4. P. 397–401.
Григолюк Э.И., Магеррамова Л.А. Устойчивость круговых однородных и неоднородных пластин // Изв. АН СССР. МТТ. 1981. № 2. С. 11–138.
Корнишин М.С., Исанбаева Ф.С. Гибкие пластины и панели. М.: Наука, 1968. 260 с.
Григолюк Э.И., Коршунова О.А. Устойчивость кольцевых пластин при сдвиге // Изв. АН СССР. МТТ. 1983. № 5. С. 156–161.
Вольмир А.С. Гибкие пластинки и оболочки. М.: Гостехиздат, 1956. 420 с.
Chen S.L., Guany J.C. The perturbation parameter in the problem of large deflection of clamped circular plates // Appl. Math. and Mech. 1981. № 2. P. 137–154.
Shen H.Sh. Postbuckling Behavior of Plates and Shells. Shanghai Jiao Tong University, 2017. 675 p.
Ганеева М.С., Ильгамов М.А., Моисеева В.Е. Нелинейный изгиб плоских предохранительных мембран под действием давления жидкости и температуры // Известия Уфимского научного центра РАН. 2014. № 2. С. 41–47.
Ганеева М.С., Моисеева В.Е., Скворцова З.В. Нелинейный изгиб и устойчивость круглых пластин под действием давления жидкости и температуры // Изв. вузов. Авиационная техника. 2016. № 1. С. 3–8.
Ильгамов М.А. Взаимодействие неустойчивостей в гидроупругой системе // ПММ. 2016. Т. 80. Вып. 5. С. 566–579.
Ильгамов М.А. Влияние давления окружающей среды на изгиб тонкой пластины и пленки // ДАН. 2017. Т. 476. № 4. С. 402–405.
Ильгамов М.А. Изгиб и устойчивость тонкой пластины при вакуумировании ее поверхностей // ДАН. 2018. Т. 480. № 5. С. 542–544.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела