Известия РАН. Механика твердого тела, 2019, № 3, стр. 108-117

1. Введение. Изучение процессов деформации ползучести при переменных температурах имеет большое значение при создании металлургического оборудования.

Методы расчета деформации ползучести рассмотрены в ряде работ, (см. например [1–4]).

Поскольку скорость деформации ползучести обычно значительно возрастает с повышением температуры, то многие детали металлургического оборудования: установок непрерывного литья металлов, печных конструкций, агломерационного оборудования приходится охлаждать, как правило, циркуляцией воды через деформируемые детали. Часто количество тепла, которое мы можем удалить от данной детали за определенное время, ограничено.

Эти ограничения определены или техническими условиями работы узлов оборудования, (например, кристаллизаторов, роликов систем вторичного охлаждения), или значительным увеличением их стоимости при увеличении расхода воды на охлаждение.

Поэтому возникает вопрос о том, как лучше использовать заданное количество тепла, которое мы можем удалить от детали за определенное время, чтобы наиболее существенно уменьшить деформацию ползучести.

В работе [5] была рассмотрена задача определения экстремального режима охлаждения, т.е. изменения температуры T(t), как функции времени t, обеспечивающей минимум величины деформации ползучести.

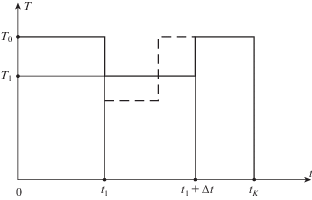
В данной работе рассмотрена задача поиска минимума величины деформации ползучести при частном виде функции T(t), а именно при постоянных величинах температуры в течение интервала времени 0 ≤ t ≤ t₁, см. фиг. 1. До момента t₁ температура постоянна и равна T₀.

При тепловом равновесии деталь получает количество тепловой энергии Q, которое удаляется за счет конвекции.

Уравнение баланса тепла в условиях конвективного теплообмена можно записать в виде:

где α₀ – коэффициент теплоотдачи Вт/м₂ ⋅ с ⋅ гр,

F – площадь теплообмена (м²),

T₀ – постоянная температура (град),

T_С – температура окружающей среды (величина Q/t₁ – это количество тепла, удаляемого в единицу времени).

В момент t₁ включают охлаждение, что обеспечивает быстрое уменьшение температуры на величину ΔT.

Примем, что

где Q – количество тепла, отведенное от тела до момента выключения охлаждения t = t₂, (т.е. за время Δt = t – t₁).

Запишем величину $\Delta Q$ в виде

При заданном количестве изменения тепловой энергии (за счет охлаждения):

Формулы (1.1) и (1.3) можно использовать обычно при Т < 800°С, при более высоких температурах тепловой поток пропорционален величинам T⁴, где T – абсолютная температура.

Приняв зависимость (1.3), полагаем, что можно при определенной величине $\Delta Q$ = = const, уменьшить время $\Delta t$, чтобы усилить эффект охлаждения, увеличив $\Delta T$, но на более короткое время, как показано на фиг. 1 штрихами.

Вопрос в том, как это повлияет на общую величину деформации ползучести, достигнутую за время t_k.

В момент t₂ – охлаждение выключают и при t₂ < t ≤ t_k – деформация продолжается при T = T₀.

Относительно выбора именно такого “ступенчатого” режима изменения температура (см. фиг. 1) по сравнению с произвольной функцией T(t), см. [5], укажем, что он является наиболее простым для реализации в промышленности и требует значительно меньших затрат, (по сравнению с точной функцией T(t), соответствующей экстремуму).

Действительно, достаточно использовать реле времени для включения системы охлаждения в момент t₁ и ее выключения при t = t₂.

Поэтому в данной работе ограничимся рассмотрением процесса ползучести при таком температурном режиме для решения вопросов об его эффективности и о выборе оптимального момента включения охлаждения с целью максимально возможного уменьшения деформации ползучести.

2. Основные уравнения. Для определения деформации ползучести используем известное, см. [1–3], уравнение

где p – деформация ползучести,

${\sigma }$ – напряжение при одноосном напряженном состоянии,

${\alpha \;}$ и γ – величины, для данного металла, сплава постоянные;

F(${\sigma }$) – функция, определяющая зависимость скорости деформации от напряжения.

Зависимость (2.1) применима с определенной точностью при одноосном напряженном состоянии. Ее можно использовать, как приближенную для некоторых условий, например тонкостенных труб, нагруженных внутренним давлением, колосников обжиговых машин, деталей систем вторичного экранного охлаждения установок непрерывного литья металлов и так далее.

Более точные зависимости деформации ползучести от напряжений и температуры приведены в работах [1–3].

Определению деформации при напряжениях, переменных по объему деформируемого тела, предполагается посвятить отдельную работу.

Допустим, что одноосная деформация p(t) происходит при постоянных температуре t₀ и напряжении, а в течение времени t_k. За это время произойдет деформация ползучести, равная

Если температура постоянна, а напряжение задано, как функция σ(t), то

Теперь рассмотрим процесс, при котором температура остается постоянной при $0 \leqslant t \leqslant {{t}_{1}}$, а затем уменьшается на величину $\Delta T$. В течение времени ${{t}_{1}} \leqslant t \leqslant {{t}_{2}}$ она остается постоянной и равной ${{T}_{0}} - \Delta T$, см. фиг. 1, где $\Delta t = {\;}{{t}_{1}} - {{t}_{2}}$. При $t = {\;}{{t}_{1}} + \Delta t$ охлаждение прекращают, и температура вновь возрастает до величины ${{T}_{0}}$. Такой же она остается в течение времени $\left( {{{t}_{k}} - {{t}_{2}}} \right)$, до конца процесса деформации.

За время ${{t}_{1}}$ будет достигнута деформация ${{p}_{1}}$:

Эта функция далее возрастет и при $t = {{t}_{2}}$ достигнет величины

После выключения охлаждения деформация при ${{t}_{2}} \leqslant t \leqslant {{t}_{k}}$ еще возрастет и достигнет конечной величины

Это выражение можно записать в виде

При малых величинах ${\gamma }\Delta T$, можно принять ${\text{exp}}\left( { - {\gamma }\Delta T} \right) \approx 1 - \left( {{\gamma }\Delta T} \right).$ Во многих случаях расчеты определяют величины ${{t}_{2}} > {{t}_{k}}$, что по условиям задачи не возможно, (t_k – полное время деформации).

В этих случаях в формулы входит только одна неизвестная величина ${{t}_{1}}$ и после начала охлаждения его реализуют все время до конца процесса деформации. В таких задачах конечная деформация равна:

Такие случаи имеют место при постоянных или монотонно возрастающих напряжениях в течение всего времени деформации, (другие случаи предполагается рассмотреть в отдельной работе).

Далее выразим величину ΔT, как функцию $\Delta t = {{t}_{k}} - {{t}_{1}}$. Если перейти к безразмерным переменным u₁ = t₁/t_k, u = t/t_k, также использовать безразмерную постоянную $B = {\gamma }\Delta Q{\text{/}}\left( {{{{\alpha }}_{0}}F{{t}_{k}}} \right)$, то для деформируемой детали, то вместо (2.6) получим зависимость

3. Примеры изменения напряжений. При постоянном напряжении из формулы (2.7) получим функцию:

где функция

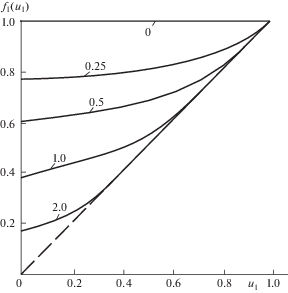
Графики функций $f\left( {{{u}_{1}}} \right)$ при некоторых величинах постоянной B приведены на фиг. 2 (величины B указаны индексами у кривых).

Понятно, что при B = 0, ${{f}_{1}}\left( {{{u}_{1}}} \right) = 1.0$, а если $B \to \infty $, то график $f\left( {{{u}_{1}}} \right)$ приближается к прямой $f\left( {{{u}_{1}}} \right) = {{u}_{1}}$, показанной на фиг. 2 штрихами. Если при $0 \leqslant {{u}_{1}} \leqslant 1.0$ производная $d{{f}_{1}}\left( {{{u}_{1}}} \right){\text{/}}d{{u}_{1}} > 0$ и минимальное значение функция $f\left( {{{a}_{1}}} \right)$ принимает, при ${{u}_{1}} = 0$, то в этом целесообразно включать охлаждение в начале процесса деформации.

Например, если $B = 1.0$, то при ${{u}_{1}} = 0$, f₁(0) = 0.367 и уменьшение деформации ползучести определено величиной ${{0.367}^{{\beta }}} = 0.715$ (при ${\beta } = 0.357$; α = 1.8) и при ${{u}_{1}} = 0$ охлаждение обеспечит уменьшение деформации ползучести на ~2.9%. Такая величина незначительна и режим охлаждения не эффективен.

Усиление охлаждения до величины, соответствующей параметру B = 2.0 уменьшению функции ${{f}_{1}}\left( 0 \right){\;}$ до f₁(0) = 0.135, а величина [f₁(0)]^0.357 ≈ 0.51 уменьшится почти в два раза. При $B < 0.5$ влияние охлаждения на деформацию незначительно.

Теперь рассмотрим случай, когда напряжение не остается в процессе деформации постоянным, а возрастает согласно функции

где ${{Q}_{m}}$, и ${{t}_{k}}$ характеризуют максимальное напряжение и время процесса за время ${{t}_{1}}$ будет достигнута деформация ${{p}_{1}}\left( {{{t}_{1}}} \right){\;}$ (при температуре ${{T}_{0}}$):

Далее произойдет охлаждение деформируемого тела на ΔT и в момент времени ${{t}_{2}} > {{t}_{1}}$ деформация ползучести достигнет величины ${{p}_{2}}\left( {{{t}_{2}}} \right)$, где

Конечная деформация при $t = {{t}_{k}}\left( {{{t}_{k}} \geqslant {{t}_{2}}} \right)$ равна в этом случае

Как правило, в задачах, в которых напряжение в течение всего времени монотонно возрастает, ${{t}_{2}} \geqslant {{t}_{k}}$ и следует принимать в (3.4) ${{t}_{2}} = {{t}_{k}}$. В этом случае можно выразить величину деформации в виде

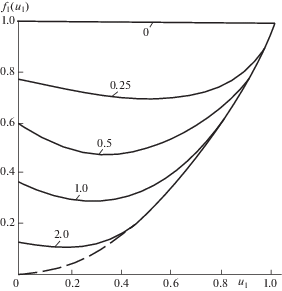
На фиг. 3 приведены графики функций $f\left( {{{u}_{1}}} \right)$ при n = 1.0 и величинах B, указанных индексами у кривых.

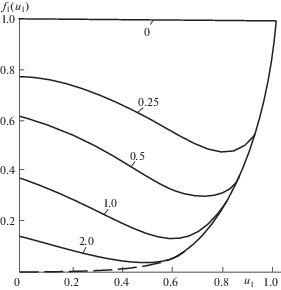
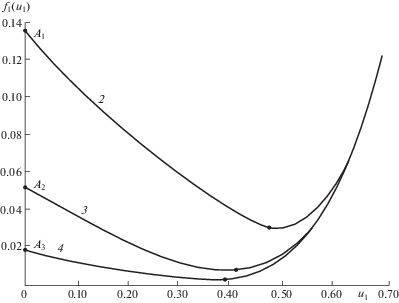
На фиг. 4 приведены графики ${{f}_{1}}\left( {{{u}_{1}}} \right){\;}$при n = 5 (на фиг. 4 при B = 0.25; 0.50; 0.10; 0.20, а на фиг. 5 при B = 2.0; 3.0 и 4.0 в увеличенном масштабе).

Чем больше величина B, тем меньше величины ${{u}_{1}}$ при которых имеет место минимум функции $f\left( {{{u}_{1}}} \right)$, а при $B \to \infty $ ${{u}_{1}} \to 0$.

Следовательно, чем больше “n” и “B” тем раньше следует включить охлаждение. Однако, при n = 1.0 величина “выигрыша” незначительна, например, если n = 1.0 и B = 2.0, то ${{f}_{1}}\left( 0 \right) = 0.1352$, а в точке минимума при ${{u}_{1}} = 0.17,{\;\;}{{f}_{1}}\left( {0.17} \right) = 0.110$. Отношение величин деформации при ${\beta } = 2.8{\;}$и ${\beta } = 0$ равно (0.1352/0.110)^0.35 = 1.07 и такое различие несущественно, поскольку разброс величин деформации намного больше. При $n < 5$ можно принимать ${{u}_{1}}$ = 0, т.е. начинать охлаждение в момент начала процесса деформации. Но с увеличением показателя степени “n” в формуле (3.3) влияние выбора величины ${{u}_{1}}$ усиливается.

Это видно из графиков, приведенных фиг. 4 и 5. Например, при $n = 5$, $B = 2.5{\;}$ отношение значений функции ${{f}_{1}}\left( {{{u}_{1}}} \right)$ при ${{u}_{1}}$ = 0 и ${{u}_{1}}$ = 50 равно 0.135/0.031 = 4.35 и 4.35^β ≈ 1.63 и уменьшение деформации ползучести в 1.63 раза может оказаться значительным.

Согласно расчетам, выбор величины ${{u}_{1}}$ при $n < 5.0$ оказывает незначительное влияние на величину ${{f}_{1}}\left( {{{u}_{1}}} \right)$. Поэтому можно в этих случаях принимать ${{u}_{1}} = 0$ и реализовать охлаждение детали в течение всего времени деформации.

Но при $n \geqslant 5$ влияние величины ${{u}_{1}}$ на функцию ${{f}_{1}}\left( {{{u}_{1}}} \right)$ усиливается.

Приведем пример охлаждения пластины экранного вторичного охлаждения установки непрерывного литья стали 91 кг из стали 08Ю за время ${{t}_{k}} = 5400$ c (90 мин), при величине тепловой энергии ΔQ = 2.25 ⋅ 10⁷ Дж.

При величине ${\alpha } = 1.8;{\;\gamma } = 0.01$ гр^–1 и n = 5.0 выберем величину a₀ = 22 Вт/(м² ⋅ град), по данным ([7] стр. 99) для теплообмена без обдува детали воздухом.

Определим для этих условий параметр B

Если использовать охлаждение в течение всего времени ${{t}_{k}}$, т.е. при ${{t}_{1}} = 0$, ${{u}_{1}} = 0$, то функция $f\left( 0 \right) = \exp \left( { - 3.79} \right) = 0.226$, а в точке минимума функции $f\left( {{{u}_{1}}} \right)$ при u₁ = 0.41 f₁(0.41) = 0.0027.

Такие результаты означают, что при использовании охлаждения в течение всего времени деформации (при ${{t}_{1}} = 0$) величину деформации ползучести можно уменьшить в ${{\left( {0.0226} \right)}^{{\beta }}} = {{\left( {0.0226} \right)}^{{ - 0.35}}}$ = 3.6 раза.

Если же начать охлаждение при ${{t}_{1}} = 0.14 \cdot 5400 = 2214\;{\text{с }}$, то за время $(1.00{\kern 1pt} - {\kern 1pt} 0.41){{t}_{k}}\quad$ = = 3186 c можно уменьшить величину деформации ползучести ${{\left( {0.0027} \right)}^{{ - 0.35}}} = 7.14{\;}$ раза. Отношение величин 7.14/3.6 = 1.98, что определяет возможный выигрыш в уменьшении деформации ползучести.

В каждом конкретном случае следует решать вопрос о выборе режима охлаждения детали.

Используя формулу (1.3), можно определить, что при времени охлаждения ${{t}_{k}} = 5400$ c, ${{{\alpha }}_{0}}$ = 22 Вт/(м² град), $F = 0.5$ м² можно уменьшить температуру детали на величину

А при включении системы охлаждения в момент t₁ = 2214 c:

Если начальная температура была равна 750°C, то в первом случае температура будет равна 371.2°C в течение всего времени ${{t}_{k}}$, а во втором при t₁ = 2214 c ее можно уменьшить до 108°C, что позволит почти в два раза уменьшить полную величину деформации ползучести, (по сравнению с деформацией, достигнутой при использовании охлаждения в течение всего времени деформации).

4. Усовершенствование способов уменьшения деформации ползучести. Уменьшение деформаций ползучести весьма актуально в черной и цветной металлургии при эксплуатации агломерационных и обжиговых машин, печного оборудования, установок непрерывного литья и других устройств. Одним из основных способов уменьшения такой деформации является охлаждение деталей водой, расход которой в черной и цветной металлургии очень велик. Между тем, дефицит воды в мире значительный и достигает I 230 млрд в год. Конечно, РФ имеет большие запасы пресной воды: 22–25% от мирового объема [6], занимая по ним второе место в мире, (уступая только Бразилии), однако эти ресурсы распределены неравномерно и во многих областях РФ малое количество воды создает серьезные трудности. Поэтому в одном из постановлений государственной думы РФ отмечено, что “неблагоприятное положение с развитием питьевого водоснабжения создает угрозу национальной безопасности РФ”, см. [8].

Помимо дефицита воды возникает другая проблема – отложение солей (кальция, магния и так далее) на поверхностях каналов для циркуляции воды. Уже слой накипи 1–2 мм может уменьшить тепловой поток на 50% и более. Это часто приводит к повышению температуры, резкому ускорению процесса ползучести и выходу оборудования из строя.

Приходится строить специальные цеха для химической очистки поверхностей каналов для движения воды воздействием кислот или щелочей [9, 10], что резко увеличивает затраты (и создает проблемы с соблюдением экологических требований). Во многих работах даны рекомендации: повысить требования к качеству охлаждающей воды, (например, снизить ее общую и карбонатную жесткость (см. [6] с. 310)). Повысить требования, конечно, можно но, как действовать металлургам, в распоряжении которых имеется только определенная вода, а затраты на ее химическую очистку очень велики.

Оптимальное решение этой проблемы дает система охлаждения с постоянным количеством охлаждающей жидкости (обычно воды), циркулирующей по замкнутому контуру [11]. При этом происходит нагрев, обычно если температура окружающей среды 20°, то можно допустить температуры до 90–95°. При нагреве на 70°С килограмм воды обеспечивает удаление тепла 2.94 ⋅ 10⁵ Дж/кг.

Поскольку этот объем постоянный отложения солей почти не происходит (а кроме того, однократная химическая очистка определенного количества воды допустима).

При этом возникает задача о том, можно ли оптимально использовать момент начала охлаждения.

В [11] предусмотрено использование двух контуров: в первом по замкнутой траектории движется жидкость (вода), а во втором – воздух. Часть труб является теплообменником, где тепло (частично или полностью) передается от воды к воздуху, (который движется по трубам теплообменника). Нагретый воздух удаляют в атмосферу, но конечно, лучше использовать его (для отопления зданий, в сушильных агрегатах, печах и так далее).

Никакого загрязнения воздуха или воды не происходит. Известно, что аварийные ситуации с прекращением водоснабжения цехов приводят к выходу из строя десятков тонн оборудования из-за деформации ползучести. Но при циркуляции охладителя по замкнутому контуру такого не произойдет.

При использовании резервных аккумуляторов можно обеспечить работу системы охлаждения даже и в случае отключения электричества. Оптимизация режимов охлаждения должна в каждом случае определяться с учетом функции, определяющей изменение напряжений в деформируемых деталях.

Отметим, что в ряде других случаев (и задач) обеспечение охлаждения деталей или узлов оборудования связано со значительными трудностями. Так А.А. Абрикосов указывал [12]: “… в обычном магните энергия тока в конечном итоге тратится на разогрев обмотки. Из-за этого приходится делать громоздкую и дорогостоящую систему охлаждения. Именно это обстоятельство ограничивает возможности электромагнитов с полями до 5–6 Тл.

Известно также, (из рекламного сообщения), что фирма “Unilabel AG Minimal-schmiertechnik” разрабатывает “системы охлаждения с минимальным количеством охлаждающего средства”, но конкретной информации по ним нет. Но видно, что вопросы охлаждения с минимизацией расхода охладителя становятся все более важными.

Рассмотренные здесь простые режимы изменения температуры не являются экстремальными, но могут оказаться полезными в ряде случаев и их легко реализовать при создании систем охлаждения металлургического оборудования.