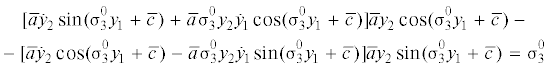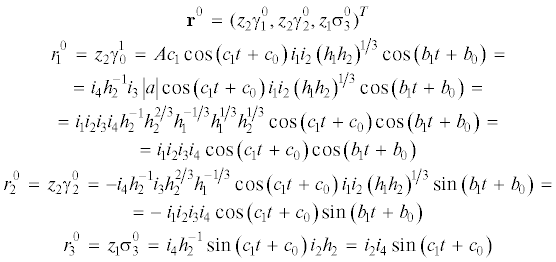Известия РАН. Механика твердого тела, 2019, № 3, стр. 16-29

СЕМЕЙСТВО ЭКСТРЕМАЛЬНЫХ ВЕКТОР-ФУНКЦИЙ УГЛОВЫХ СКОРОСТЕЙ С ПОСТОЯННОЙ АБСОЛЮТНОЙ ВЕЛИЧИНОЙ В ЗАДАЧЕ ОПТИМАЛЬНОЙ ПЕРЕОРИЕНТАЦИИ СФЕРИЧЕСКИ СИММЕТРИЧНОГО ТЕЛА С МИНИМАЛЬНЫМИ ЭНЕРГОЗАТРАТАМИ

А. Н. Сиротин^*

Московский авиационный институт (национальный исследовательский ун-т)
Москва, Россия

Поступила в редакцию 15.09.2017
После доработки 14.05.2018
Принята к публикации 04.06.2018

DOI: 10.1134/S0572329919030140

Аннотация

Исследуется задача оптимального управления переориентацией абсолютно твердого сферически симметричного тела. В качестве критерия эффективности маневра выбран интегрально-квадратичный функционал, характеризующий общие энергозатраты. Управлением служит главный момент приложенных внешних сил. В данной задаче впервые получено семейство аналитических экстремальных траекторий, которые определяются единственным образом в соответствии с требованием неизменности по времени абсолютной величины вектор-функции угловой скорости. Приведены иллюстрирующие примеры.

Ключевые слова: оптимальное управление, переориентация, сферически симметричное твердое тело, энергозатраты, принцип максимума

1. Введение. Задачи оптимального управления угловым движением абсолютно твердых тел относятся к классу нелинейных задач, вследствие чего провести исчерпывающий анализ свойств всего множества экстремальных траекторий (удовлетворяющих необходимым условиям принципа максимума) в настоящее время не представляется возможным. Сложность задачи существенным образом зависит от свойств симметрии, которым обладает вращающееся тело. Для частного случая сферически симметричного тела дифференциальные динамические уравнения Эйлера существенно упрощаются. Однако при этом структура кинематических дифференциальных уравнений не изменяется. Тем не менее, общая соответствующая задача оптимального управления угловым движением все же не сводится к традиционной линейной или другим известным решениям, а полное семейство экстремальных траекторий описать не удается.

Целью данной статьи является построение нового класса экстремальных траекторий в задаче оптимального управления переориентации сферически симметричного тела с минимальными энергозатратами. Изучаемые в статье экстремальные траектории не описывают все многообразие экстремалей. Показано, что если абсолютная величина вектор-функции угловой скорости неизменна по времени, то существует соответствующая экстремальная угловая скорость, по которой восстанавливается полная траектория. Координаты экстремальных траекторий углового движения описываются тригонометрическими функциями времени.

2. Формулировка задачи. Рассматривается вращение абсолютно твердого сферически симметричного тела относительно неподвижной точки, совпадающей с центром масс. Главный момент внешних сил, приложенных к телу, является управлением. Все используемые векторы определяются своими декартовыми прямоугольными координатами в связанной системе отсчета, оси которой совпадают с главными центральными осями инерции тела. Тензор инерции считается единичным. Предполагается, что в инерциальном пространстве выбрано m осей чувствительности ($m \geqslant 1$), определяемых соответствующими векторами ${{r}^{i}}\left( t \right) \in {{\mathbb{R}}^{3}}$, $i = 1,\; \ldots ,\;m$ единичной длины.

Уравнения углового движения (кинематические для $m$ ортов и динамические управления Эйлера-Пуансо для вектора угловой скорости) в таком случае имеют вид

(2.1)

${{\dot {r}}^{i}} = {{r}^{i}} \cdot \omega ,\quad i = 1,\; \ldots ,\;m;\quad \dot {\omega } = u,\quad t \in \left( {0,T} \right),\quad \left( {^{\centerdot } = \frac{d}{{dt}}} \right)$

где ${{r}^{i}}:\mathbb{R} \to {{S}^{2}}$; $\omega :\mathbb{R} \to {{\mathbb{R}}^{3}}$ – вектор-функция угловой скорости; $u:\mathbb{R} \to {{\mathbb{R}}^{3}}$ – вектор-функция управления. Считается, что заданы краевые условия

(2.2)

${{r}^{i}}\left( 0 \right),\quad {{r}^{i}}\left( T \right),\quad i = 1, \ldots ,m;\quad \omega \left( 0 \right),\quad \omega \left( T \right)$

определяющие требуемый маневр. Условия на левом и правом концах различны и соответствующее вращение не может быть абсолютным покоем.

Длительность управляемого процесса фиксирована. В качестве критерия эффективности маневра выбран интегрально-квадратичный функционал, который характеризует суммарные энергозатраты. Таким образом, изучается задача оптимального управления

(2.3)

$\min \frac{1}{2}\int\limits_{\left[ {0,T} \right]} {u\left( t \right) \cdot u\left( t \right)dt} $

где минимум ищется по всем допустимым управлениям и траекториям, удовлетворяющим дифференциальным уравнениям (2.1) и краевым условиям (2.2).

Предполагается, что в задаче (2.3) точная нижняя грань достигается и решение (управление) сформулированной задачи существует в классе кусочно-непрерывных функций времени.

Для рассматриваемой задачи оптимального управления вводится прямая и сопряженная системы уравнений принципа максимума [1, 2]

(2.4)

$\begin{gathered} {{{\dot {r}}}^{i}} = {{r}^{i}} \cdot \omega ,\quad {{{\dot {\psi }}}^{i}} = {{\psi }^{i}} \cdot \omega ,\quad i = 1, \ldots ,m \\ \dot {\omega } = u,\quad \dot {\gamma } = - \sum\limits_{i = 1}^m {{{\psi }^{i}} \cdot {{r}^{i}}} \\ \end{gathered} $

где ${{\psi }^{i}},\gamma :\mathbb{R} \to {{\mathbb{R}}^{3}}$ – непрерывные вектор-функции. Гамильтониан системы имеет вид

$H = \omega \cdot \sum\limits_{i = 1}^m {{{\psi }^{i}} \cdot {{r}^{i}} + \gamma \cdot u + \frac{1}{2}{{\psi }_{0}}u \cdot u,\quad {{\psi }_{0}} = \operatorname{const} \leqslant 0} $

и по построению

${{\dot {r}}^{i}} = \frac{{\partial H}}{{\partial {{\psi }^{i}}}},\quad \dot {\omega } = \frac{{\partial H}}{{\partial \gamma }},\quad {{\dot {\psi }}^{i}} = - \frac{{\partial H}}{{\partial {{r}^{i}}}},\quad \dot {\gamma } = - \frac{{\partial H}}{{\partial \omega }}$

В статье рассматриваются нормальные экстремальные траектории, для которых ${{\psi }_{0}} \ne 0$. Так как экстремаль можно умножить на любое положительное число, то для нормального случая верно ${{\psi }_{0}} = - 1$.

Для нормальной экстремали и экстремальной траектории получаем условия максимума по управлению

$\mathop {\max }\limits_u \left( {\omega \cdot \sum\limits_{i = 1}^m {{{\psi }^{i}} \cdot {{r}^{i}} + \gamma \cdot \omega - \frac{1}{2}u \cdot u} } \right)$

и, следовательно, экстремальное управление есть

(2.5)

$u = \gamma $

В силу уравнений (2.4) и (2.5) из предположения о существовании решения в классе кусочно-непрерывных функций времени по принципу математической индукции следует вывод о том, что решения системы (2.4), (2.5) можно выбирать из существования более узкого класса бесконечно дифференцируемых функций времени.

Введем вектор-функцию $s:\mathbb{R} \to {{\mathbb{R}}^{3}}$

$s = \sum\limits_{i = 1}^m {{{\psi }^{i}} \cdot {{r}^{i}}} $

Используя тождество Якоби для векторного произведения, получаем дифференциальное векторное уравнение

(2.6)

$\dot {s} = s \cdot \omega $

с первым интегралом $\left| s \right| = {{h}_{1}} = \operatorname{const} \geqslant 0$.

Структура дифференциальных уравнений (2.4), (2.5) такова, что можно перейти к исследованию негамильтоновой системы меньшей размерности

(2.7)

$\dot {\omega } = \gamma ,\quad \dot {\gamma } = - s,\quad \dot {s} = s \times \omega $

Каждое решение системы (2.4), (2.5) по построению удовлетворяет дифференциальным уравнениям (2.7) в силу (2.6). Обратное не очевидно, однако по решению (2.7) можно восстановить требуемую экстремальную траекторию для (2.4), (2.5).

Для системы дифференциальных уравнений (2.7) имеется семейство первых интегралов

(2.8)

$\omega \cdot s + \frac{1}{2}\gamma \cdot \gamma = {{h}_{0}} = \operatorname{const} $

(2.9)

$s + \gamma \cdot \omega = \sigma = \operatorname{const} \in {{\mathbb{R}}^{3}}$

Данные соотношения проверяются с помощью непосредственного дифференцирования и использования (2.7). Положим

(2.10)

$\left| \sigma \right| = {{h}_{2}} = \operatorname{const} \geqslant 0$

Изучение экстремальных траекторий из прямой и сопряженной системы принципа максимума может быть сведено к нахождению решений системы дифференциальных векторных уравнений (2.7), которая не является гамильтоновой канонической системой. Полное описание семейства всех экстремальных траекторий в данный момент автору не известно. Целью данной статьи является построение одного класса экстремальных траекторий.

3. Тригонометрические экстремальные угловые скорости. Задача оптимального управления переориентацией твердого тела является нелинейной и не разрешима явным образом. Для частного случая дифференциальные динамические уравнения существенно упрощаются, при этом уравнения кинематики не изменяются. Однако, задача оптимального управления угловым движением все же не сводится к линейной или другим известным решениям, а полное семейство экстремальных траекторий описать не удается.

Естественным способом получить новые неизвестные экстремальные траектории в рассматриваемой задаче является попытка ввести дополнительные связи (ограничения в виде дифференциальных уравнений или алгебраические соотношения) и проверить совместимость с уравнениями прямой и сопряженной систем принципа максимума. Эти дополнительные соотношения имеют иногда смысл в виде новых первых интегралов для частных случаев экстремальных траекторий, которые в некоторых случаях могут быть построены явно. Самым известным результатом [3] является использование плоского поворота. Введение нового уравнения для задачи оптимального управления угловым движением в виде дополнительной связи как поворота относительно неподвижной оси в инерциальной системе отсчета позволяет в некоторых случаях сильно упростить задачу. Соответствующие решения отвечают только узкому классу экстремальных угловых движений [4].

В статье предлагается расширить семейство новых экстремальных траекторий, вводя дополнительные ограничения. Первоначально предполагается, что абсолютная величина вектор-функции угловой скорости, как функция времени, является неизменной. Затем удается показать, что это соотношение удовлетворяет решениям уравнений прямой и сопряженных системы принципа максимума и, следовательно, порождает некоторое множество экстремальных траекторий в рассматриваемой задаче оптимального управления.

Теорема. Пусть ${{h}_{1}} > 0$, ${{h}_{2}} > 0$. Тогда для каждого $t \in \left[ {0,T} \right]$ справедливы эквивалентные утверждения:

(i) для некоторой матрицы $G \in SO\left( 3 \right)$ существуют экстремальные вектор-функции угловых скоростей, описываемые соотношениями

(3.1)

$\omega \left( t \right) = \left( {\begin{array}{*{20}{c}} {{{\omega }_{1}}\left( t \right)} \\ {{{\omega }_{2}}\left( t \right)} \\ {{{\omega }_{3}}\left( t \right)} \end{array}} \right) = {{G}^{T}}\left( {\begin{array}{*{20}{c}} {a\sin \left( {{{b}_{1}}t + {{b}_{0}}} \right)} \\ {a\cos \left( {{{b}_{1}}t + {{b}_{0}}} \right)} \\ {{{b}_{1}}} \end{array}} \right)$

(ii) абсолютная величина экстремальной вектор-функции угловой скорости не меняется со временем, т.е. ${{\left| {\omega \left( t \right)} \right|}^{2}} = {{a}_{0}} = \operatorname{const} \geqslant 0$.

Доказательство. (i) ⇒ (ii). Вектор-функция (3.1) определяет некоторую экстремальную угловую скорость в рассматриваемой задаче оптимального управления.

Действительно, из (2.7) следует дифференциальное уравнение $\dddot \omega = \ddot {\omega } \times \omega $, которое связано только с вектором угловой скорости и каждое решение такого уравнения совпадает с каким-либо экстремальным вектором угловой скорости. Непосредственно проверяется, что (3.1) есть решение построенного уравнения и поэтому является экстремальной угловой скоростью.

Теперь утверждение (i) ⇒ (ii) очевидно.

(ii) ⇒ (i). Рассмотрим произвольную экстремальную траекторию в рассматриваемой задаче оптимального управления. Соответствующие дифференциальные векторные уравнения (2.7) имеют ряд особенностей. Действительно, правые части уравнений представляют собой только линейные или билинейные функции. Это позволяет перейти от декартовых прямоугольных координат исследуемой системы к новым координатам. Эти координаты представляют собой всевозможные скалярные произведения вектор-функций, участвующие в уравнении (2.7). Получаемая соответствующая система дифференциальных уравнений оказывается замкнутой.

Введем обозначения

(3.2)

${{x}_{1}} = \omega \cdot \omega ,\quad {{x}_{2}} = \gamma \cdot \gamma ,\quad {{x}_{3}} = \omega \cdot s,\quad {{x}_{4}} = \omega \cdot \gamma ,\quad {{x}_{5}} = \gamma \cdot s$

Непосредственные вычисления с помощью соотношений (2.7) дают

(3.3)

$\begin{gathered} {{{\dot {x}}}_{1}} = 2\omega \cdot \dot {\omega } = 2\omega \cdot \gamma = 2{{x}_{4}},\quad {{{\dot {x}}}_{2}} = 2\gamma \cdot \dot {\gamma } = - 2\gamma \cdot s = - 2{{x}_{5}} \\ {{{\dot {x}}}_{3}} = \dot {\omega } \cdot s + \omega \cdot \dot {s} = \dot {\omega } \cdot s = \gamma \cdot s = {{x}_{5}} \\ {{{\dot {x}}}_{4}} = \dot {\omega } \cdot \gamma + \omega \cdot \gamma = \gamma \cdot \gamma - \dot {\omega } \cdot s = {{x}_{2}} - {{x}_{3}} \\ {{{\dot {x}}}_{5}} = \dot {\gamma } \cdot s + \gamma \cdot \dot {s} = - s \cdot s + \gamma \cdot (s \cdot \omega ) = - s \cdot (s + \gamma \cdot \omega ) = - s \cdot \sigma \\ \end{gathered} $

Здесь использовалось равенство (2.9). Воспользуемся тождеством Лагранжа для смешанных произведений и получим

$\begin{gathered} {{\left( {\sigma \cdot s} \right)}^{\centerdot }} = \sigma \cdot \dot {s} = \left( {s + \gamma \cdot \omega } \right) \cdot \left( {s \cdot \omega } \right) = \left( {\gamma \cdot \omega } \right) \cdot \left( {s \cdot \omega } \right) = \\ = \;\left( {\gamma \cdot \omega } \right)\left( {\omega \cdot \omega } \right) - \left( {\omega \cdot s} \right)\left( {\gamma \cdot \omega } \right) = {{x}_{1}}{{x}_{5}} - {{x}_{3}}{{x}_{4}} \\ \end{gathered} $

Таким образом, получается замкнутая система скалярных дифференциальных уравнений

(3.4)

${{\dot {x}}_{1}} = 2{{x}_{4}}$

(3.5)

${{\dot {x}}_{2}} = - 2{{x}_{5}}$

(3.6)

${{\dot {x}}_{4}} = {{x}_{2}} - {{x}_{3}} = \frac{3}{2}{{x}_{2}} - {{h}_{0}}$

(3.7)

${{\ddot {x}}_{5}} = {{x}_{3}}{{x}_{4}} - {{x}_{1}}{{x}_{5}} = \left( {{{h}_{0}} - \frac{1}{2}{{x}_{2}}} \right){{x}_{4}} - {{x}_{1}}{{x}_{5}}$

Здесь опущено в (3.3) уравнение для переменной ${{x}_{3}}$, которое не требуется в силу первого интеграла (2.8) в виде ${{x}_{3}} + {{x}_{2}}{\text{/}}2 = {{h}_{0}}$.

Выразим переменные ${{x}_{2}}$, ${{x}_{4}}$, ${{x}_{5}}$ через ${{x}_{1}}$ и соответствующие производные $x_{1}^{{\left( k \right)}}$. Тогда из (3.4) имеем

(3.8)

${{x}_{4}} = \frac{1}{2}{{\dot {x}}_{1}}$

Из (3.6) и (3.8) получаем

(3.9)

${{x}_{2}} = \frac{2}{3}\left( {{{{\dot {x}}}_{4}} + {{h}_{0}}} \right) = \frac{2}{3}\left( {\frac{1}{2}{{{\ddot {x}}}_{1}} + {{h}_{0}}} \right) = \frac{1}{3}{{\ddot {x}}_{1}} + \frac{2}{3}{{h}_{0}}$

Из (3.5) и (3.9) имеем

(3.10)

${{x}_{5}} = - \frac{1}{2}{{\dot {x}}_{2}} = - \frac{1}{6}{{\dddot x}_{1}}$

По предположению (ii) получаем равенство ${{x}_{1}} = {{\left| \omega \right|}^{2}} = \operatorname{const} $ и, следовательно, получаем цепочку уравнений из (3.10) и (3.3)

(3.11)

${{x}_{5}} = {{\dot {x}}_{5}} = 0$

В силу (3.11) и (3.3) получаем

(3.12)

$s \cdot \sigma = 0$

Дифференцируя это равенство, получаем

$0 = \dot {s} \cdot \sigma = \left( {s \cdot \omega } \right) \cdot \sigma = \left( {\sigma \cdot s} \right) \cdot \omega $

Таким образом, для каждого $t \in \left[ {0,T} \right]$ справедливо включение

(3.13)

$\omega \left( t \right) \in {\text{Lin}}\left\{ {\sigma ,s\left( t \right)} \right\},\quad s \bot \sigma $

Поэтому для вектор-функции $\omega $ верно разложение

(3.14)

$\omega = {{\dot {y}}_{1}}\sigma + {{y}_{2}}s$

где ${{y}_{1}},{{y}_{2}}:\mathbb{R} \to \mathbb{R}$ – некоторые скалярные функции соответствующей гладкости.

Выберем постоянную матрицу $G \in SO\left( 3 \right)$ так, чтобы было верно равенство

(3.15)

$G\sigma \in {\text{Lin}}\{ {{e}^{3}}\} ,\quad {{e}^{3}} = {{\left( {0,0,1} \right)}^{T}}$

Матрица $G$ определяется не единственным образом.

Положим ${{\omega }^{0}} = G\omega $, ${{\gamma }^{0}} = G\gamma $, ${{s}^{0}} = Gs$, ${{\sigma }^{0}} = G\sigma $. Используя уравнение (2.7) и разложение (3.14), получаем

$\dot {s} = s \cdot \omega = s \cdot \left( {{{{\dot {y}}}_{1}}\sigma + {{y}_{2}}s} \right) = {{\dot {y}}_{1}}s \cdot \sigma $

и далее

(3.16)

${{\dot {s}}^{0}} = {{\dot {y}}_{1}}{{s}^{0}} \cdot {{\sigma }^{0}}$

В силу (3.15) и (3.12) введем обозначения

${{\sigma }^{0}} = {{(0,0,\sigma _{3}^{0})}^{T}},\quad {{s}^{0}} = {{(s_{1}^{0},s_{2}^{0},0)}^{T}}$

поскольку по определению верно равенство $0 = s \cdot \sigma = {{s}^{0}} \cdot {{\sigma }^{0}}$. Включение (3.15) означает, что возможны два случая $\sigma _{3}^{0} = {{h}_{2}}{\text{ и л и }}\sigma _{3}^{0} = - {{h}_{2}}$. Запишем векторное дифференциальное уравнение (3.16) в координатной форме

(3.17)

$\dot {s}_{1}^{0} = {{\dot {y}}_{1}}\sigma _{3}^{0}s_{2}^{0},\quad \dot {s}_{2}^{0} = - {{\dot {y}}_{1}}\sigma _{3}^{0}s_{1}^{0}$

Непосредственная проверка доказывает справедливость соотношений

${{(s_{1}^{0})}^{2}} + {{(s_{2}^{0})}^{2}} = \operatorname{const} = {{\left| s \right|}^{2}} = h_{1}^{2}$

Следовательно, справедливо представление

(3.18)

$s_{1}^{0} = \bar {a}\sin g,\quad s_{2}^{0} = \bar {a}\cos g$

где $\bar {a}$ – некоторое число, $g:\mathbb{R} \to \mathbb{R}$ – соответствующая скалярная функция. Подставляем (3.18) в (3.17) и, следовательно, получаем

${{\bar {a}}^{2}} = h_{1}^{2},\quad \dot {g} = \sigma _{3}^{0}{{\dot {y}}_{1}},\quad g = \sigma _{3}^{0}{{y}_{1}} + \bar {c}$

где $\bar {c}$ – число. Таким образом, решение системы уравнений (3.17) есть

(3.19)

$s_{1}^{0} = \bar {a}\sin (\sigma _{3}^{0}{{y}_{1}} + \bar {c}),\quad s_{2}^{0} = \bar {a}\cos (\sigma _{3}^{0}{{y}_{1}} + \bar {c}),\quad s_{3}^{0} = 0$

Обозначим ${{\omega }^{0}} = {{(\omega _{1}^{0},\omega _{2}^{0},\omega _{3}^{0})}^{T}},{{\gamma }^{0}} = {{(\gamma _{1}^{0},\gamma _{2}^{0},\gamma _{3}^{0})}^{T}}$ и воспользуемся разложением (3.14) ${{\omega }^{0}} = {{\dot {y}}_{1}}{{\sigma }^{0}} + {{y}_{2}}{{s}^{0}}$. Поэтому из (3.19) получаем координатную запись

(3.20)

$\omega _{1}^{0} = \bar {a}{{y}_{2}}\sin (\sigma _{3}^{0}{{y}_{1}} + \bar {c}),\quad \omega _{2}^{0} = \bar {a}{{y}_{2}}\cos (\sigma _{3}^{0}{{y}_{1}} + \bar {c}),\quad \omega _{3}^{0} = {{\dot {y}}_{1}}\sigma _{3}^{0}$

Из уравнений (2.7) имеем $\dot {\omega } = \gamma ,{{\dot {\omega }}^{0}} = {{\gamma }^{0}}$. Следовательно, из формул (3.19) и (3.20) получаем

(3.21)

$\begin{gathered} \gamma _{1}^{0} = \bar {a}{{{\dot {y}}}_{2}}\sin (\sigma _{3}^{0}{{y}_{1}} + \bar {c}) + \bar {a}\sigma _{3}^{0}{{y}_{2}}{{{\dot {y}}}_{1}}\cos (\sigma _{3}^{0}{{y}_{1}} + \bar {c}) \\ \gamma _{2}^{0} = \bar {a}{{{\dot {y}}}_{2}}\cos (\sigma _{3}^{0}{{y}_{1}} + \bar {c}) - \bar {a}\sigma _{3}^{0}{{y}_{2}}{{{\dot {y}}}_{1}}\sin (\sigma _{3}^{0}{{y}_{1}} + \bar {c}) \\ \gamma _{3}^{0} = \sigma _{3}^{0}{{{\ddot {y}}}_{1}} \\ \end{gathered} $

Функции ${{y}_{1}}$ и ${{y}_{2}}$ из разложения (3.14) не являются произвольными и связаны несколькими соотношениями. Эти соотношения можно выбирать для нахождения ${{y}_{1}}$, ${{y}_{2}}$ по-разному. Здесь воспользуемся равенством (2.9), которое в нашем случае имеет вид

(3.22)

${{s}^{0}} + {{\gamma }^{0}} \cdot {{\omega }^{0}} = {{\sigma }^{0}}$

Непосредственные покоординатные преобразования с помощью (3.19), (3.20), (3.21) и (3.22) приводят к следующему результату

$\begin{gathered} \bar {a}\sin (\sigma _{3}^{0}{{y}_{1}} + \bar {c}) + [\bar {a}{{{\dot {y}}}_{2}}\cos (\sigma _{3}^{0}{{y}_{1}} + \bar {c}) - \bar {a}\sigma _{3}^{0}{{y}_{2}}{{{\dot {y}}}_{1}}\sin (\sigma _{3}^{0}{{y}_{1}} + \bar {c})]\sigma _{3}^{0}{{{\dot {y}}}_{1}} - \\ - \;\sigma _{3}^{0}{{{\ddot {y}}}_{1}}\bar {a}{{y}_{2}}\cos (\sigma _{3}^{0}{{y}_{1}} + \bar {c}) = 0 \\ \end{gathered} $

$\begin{gathered} \bar {a}\cos (\sigma _{3}^{0}{{y}_{1}} + \bar {c}) + \sigma _{3}^{0}{{{\ddot {y}}}_{1}}\bar {a}{{y}_{2}}\sin (\sigma _{3}^{0}{{y}_{1}} + \bar {c}) - \\ - \;[\bar {a}{{{\dot {y}}}_{2}}\sin (\sigma _{3}^{0}{{y}_{1}} + \bar {c}) + \bar {a}\sigma _{3}^{0}{{y}_{2}}{{{\dot {y}}}_{1}}\cos (\sigma _{3}^{0}{{y}_{1}} + \bar {c})]\sigma _{3}^{0}{{{\dot {y}}}_{1}} = 0 \\ \end{gathered} $

После соответствующих преобразований получаем в матричном виде

$\begin{gathered} \left( {\begin{array}{*{20}{c}} {\cos (\sigma _{3}^{0}{{y}_{1}} + \bar {c})}&{\sin (\sigma _{3}^{0}{{y}_{1}} + \bar {c})} \\ { - \sin (\sigma _{3}^{0}{{y}_{1}} + \bar {c})}&{\cos (\sigma _{3}^{0}{{y}_{1}} + \bar {c})} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\bar {a}\sigma _{3}^{0}\left( {{{{\dot {y}}}_{1}}{{{\dot {y}}}_{2}} - {{{\ddot {y}}}_{1}}{{y}_{2}}} \right)} \\ {\bar {a}(1 - {{{(\sigma _{3}^{0})}}^{2}}\dot {y}_{1}^{2}{{y}_{2}})} \end{array}} \right) = 0 \\ ({{{\bar {a}}}^{2}}{{{\dot {y}}}_{1}}y_{2}^{2} - 1)\sigma _{3}^{0} = 0 \\ \end{gathered} $

Матрица в левой части невырождена, соответствующие постоянные $\sigma _{3}^{0}$, $\bar {a}$ ненулевые (поскольку $\left| {\sigma _{3}^{0}} \right| = \left| \sigma \right| = {{h}_{2}} > 0$, $\left| {\bar {a}} \right| = {{h}_{1}} > 0$) и поэтому получается следующая система уравнений

(3.23)

${{\dot {y}}_{1}}{{\dot {y}}_{2}} - {{\ddot {y}}_{1}}{{y}_{2}} = 0$

(3.24)

${{(\sigma _{3}^{0})}^{2}}\dot {y}_{1}^{2}{{y}_{2}} = 1$

(3.25)

${{\bar {a}}^{2}}{{\dot {y}}_{1}}y_{2}^{2} = 1$

Из равенств (3.24) и (3.25) следует, что функции ${{y}_{1}}$, ${{y}_{2}}$ в нуль не обращаются для каждого $t \in \left[ {0,T} \right]$. Тогда, вычитая (3.24), из (3.25) после преобразований получаем равенство

${{(\sigma _{3}^{0})}^{2}}{{\dot {y}}_{1}} = {{\bar {a}}^{2}}{{y}_{2}}$

После подстановки этого соотношения в (3.24) и (3.25) получаем

$\dot {y}_{1}^{3} = \frac{{{{{\bar {a}}}^{2}}}}{{{{{(\sigma _{3}^{0})}}^{4}}}} = \frac{{h_{1}^{2}}}{{h_{2}^{4}}},\quad y_{2}^{3} = \frac{{{{{(\sigma _{3}^{0})}}^{2}}}}{{{{{\bar {a}}}^{4}}}} = \frac{{h_{2}^{2}}}{{h_{1}^{4}}}$

Как следствие, равенство (3.23) обращается в тождество.

Положим

$\bar {a} = {{i}_{1}}{{h}_{1}},\quad \sigma _{3}^{0} = {{i}_{2}}{{h}_{2}};\quad {{i}_{1}},{{i}_{2}} \in \left\{ { - 1,1} \right\}$

Окончательно получаются формулы для координат вектора экстремальной угловой скорости в виде

(3.26)

$\dot {\omega }_{1}^{0}\left( t \right) = a\sin \left( {{{b}_{1}}t + {{b}_{0}}} \right),\quad \omega _{2}^{0}\left( t \right) = a\cos \left( {{{b}_{1}}t + {{b}_{0}}} \right),\quad \omega _{3}^{0} = {{b}_{1}}$

где

(3.27)

$\begin{gathered} a = \bar {a}{{y}_{2}} = {{i}_{1}}{{h}_{1}}\sqrt[3]{{\frac{{h_{2}^{2}}}{{h_{1}^{4}}}}} = {{i}_{1}}\sqrt[3]{{\frac{{h_{2}^{2}}}{{h_{1}^{{}}}}}} = {{i}_{1}}h_{1}^{{ - \frac{1}{3}}}h_{2}^{{\frac{2}{3}}} \\ {{b}_{1}} = \sigma _{3}^{0}{{y}_{1}} = {{i}_{2}}{{h}_{2}}\sqrt[3]{{\frac{{h_{1}^{2}}}{{h_{2}^{4}}}}} = {{i}_{2}}\sqrt[3]{{\frac{{h_{1}^{2}}}{{h_{2}^{{}}}}}} = {{i}_{2}}h_{1}^{{\frac{2}{3}}}h_{2}^{{ - \frac{1}{3}}} \\ {{b}_{0}} - \;п р о и з в о л ь н о ; \\ \sigma _{3}^{0}{{y}_{1}} + \bar {c} = {{b}_{1}}t + {{b}_{0}} \\ \end{gathered} $

Наконец, верно равенство

$a_{0}^{2} = {{a}^{2}} + b_{1}^{2} = h_{2}^{{4/3}}h_{1}^{{ - 2/3}} + h_{1}^{{4/3}}h_{2}^{{ - 2/3}}$

Теорема доказана.

Таким образом, установлено, что в задаче оптимального управления переориентацией сферически симметричного тела с минимальными энергозатратами имеется некоторое аналитическое семейство экстремальных вектор-функций угловых скоростей. Это множество единственным образом порождается вектор-функциями угловой скорости с постоянной абсолютной величиной. Соответствующие координаты экстремальных угловых скоростей выражаются явным образом через тригонометрические функции времени.

Для удобства приведем подробные формулы для координат вектор-функций s⁰, ${{\gamma }^{0}}$, ${{\omega }^{0}}$

(3.28)

$\omega _{1}^{0}(t)\, = \,{{i}_{1}}h_{1}^{{ - 1/3}}h_{2}^{{2/3}}{\text{sin}}({{b}_{1}}t\, + \,{{b}_{0}}),\quad \omega _{2}^{0}(t)\, = \,{{i}_{1}}h_{1}^{{ - 1/3}}h_{2}^{{2/3}}{\text{cos}}({{b}_{1}}t\, + \,{{b}_{0}}),\quad \omega _{3}^{0}(t)\, = \,{{i}_{2}}h_{1}^{{2/3}}h_{2}^{{ - 1/3}}$

(3.29)

$s_{1}^{0}\left( t \right) = {{i}_{1}}{{h}_{1}}\sin \left( {{{b}_{1}}t + {{b}_{0}}} \right),\quad s_{2}^{0}\left( t \right) = {{i}_{1}}{{h}_{1}}\cos \left( {{{b}_{1}}t + {{b}_{0}}} \right),\quad s_{3}^{0}\left( t \right) = 0$

(3.30)

$\gamma _{1}^{0}\left( t \right) = {{i}_{1}}{{i}_{2}}{{\left( {{{h}_{1}}{{h}_{2}}} \right)}^{{1/3}}}\cos \left( {{{b}_{1}}t + {{b}_{0}}} \right),\quad \gamma _{2}^{0}\left( t \right) = - {{i}_{1}}{{i}_{2}}{{\left( {{{h}_{1}}{{h}_{2}}} \right)}^{{1/3}}}\sin \left( {{{b}_{1}}t + {{b}_{0}}} \right),\quad \gamma _{3}^{0}\left( t \right) = 0$

Здесь использовались формулы

${{\gamma }^{0}} = {{\dot {\omega }}^{0}},\quad {{s}^{0}} = - {{\ddot {\omega }}^{0}}$

Непосредственно также проверяется решение дифференциального уравнения

(3.31)

${{\dot {s}}^{0}} = {{s}^{0}} \times {{\omega }^{0}}$

4. Восстановление экстремальных траекторий. Экстремальная вектор-функция угловой скорости из п. 3 является только частью требуемой траектории. Оказывается можно восстановить соответствующие экстремальные кинематические параметры и для произвольного $m$ получить явные соотношения.

Пусть $m = 1$. Для удобства положим

${{r}^{1}} = r$

В силу (3.11) и соответствующих обозначений (3.2) имеем

(4.1)

$\gamma \cdot s = 0$

Вектор-функция $\gamma $ такова, что $\left| \gamma \right| = {{h}_{3}} = \operatorname{const} > 0$.

Действительно, равенство следует из (3.11), (3.5) и определений (3.2). По построению тогда верно неравенство ${{h}_{3}} > 0$ или ${{h}_{3}} = 0$. Если ${{h}_{3}} = 0$, то из (2.7) следует решение соответствующего дифференциального уравнения $\dot {\omega } = 0$ в виде ${{\omega }_{i}} = \operatorname{const} $, i = 1, 2, 3. Тогда из (3.1) следует условие ${{b}_{1}} = 0$, откуда ${{h}_{1}} = 0$. Это невозможно по условию и поэтому справедливо строгое неравенство ${{h}_{3}} > 0$.

Умножаем скалярно на $\gamma $ обе части уравнения (2.9), что приводит к равенствам

(4.2)

$\gamma \cdot \sigma = \gamma \cdot s = 0$

Таким образом, из уравнений (3.12) и (4.1)–(4.2) следует, что для каждого $t \in \left[ {0,T} \right]$ тройка векторов $\sigma $, $s\left( t \right)$, $\gamma \left( t \right)$ образует ортогональный базис в ${{\mathbb{R}}^{3}}$, т.е.

$\sigma \cdot s = \sigma \cdot \gamma = s \cdot \gamma = 0,\quad \left| s \right| = {{h}_{1}},\quad \left| \sigma \right| = {{h}_{2}},\quad \left| \gamma \right| = {{h}_{3}}$

По построению верно равенство $s = \psi \cdot r$ и, следовательно,

$s \cdot r = 0$

Поэтому справедливо включение $r\left( t \right) \in \operatorname{Lin} \left\{ {\sigma ,\gamma \left( t \right)} \right\}$ и соответствующее разложение

(4.3)

$r = {{z}_{1}}\sigma + {{z}_{2}}\gamma $

где ${{z}_{1}},{{z}_{2}}:\mathbb{R} \to \mathbb{R}$ – некоторые скалярные функции соответствующей гладкости.

Пусть ${{r}^{0}} = Gr = {{(r_{1}^{0},r_{2}^{0},r_{3}^{0})}^{T}}$, тогда справедливы уравнения

(4.4)

${{r}^{0}} = {{z}_{1}}{{\sigma }^{0}} + {{z}_{2}}{{\gamma }^{0}},\quad {{\dot {r}}^{0}} = {{\dot {z}}_{1}}{{\sigma }^{0}} + {{\dot {z}}_{2}}{{\gamma }^{0}} + {{z}_{2}}{{\dot {\gamma }}^{0}} = {{\dot {z}}_{1}}{{\sigma }^{0}} + {{\dot {z}}_{2}}{{\gamma }^{0}} - {{z}_{2}}{{s}^{0}}$

где использовались соотношения из (2.7)

${{\dot {\gamma }}^{0}} = G\dot {\gamma } = G\left( { - s} \right) = - {{s}^{0}}$

Воспользуемся кинематическими дифференциальными уравнениями (2.1) и представлениями (3.14), (4.4). Тогда из уравнения

(4.5)

${{\dot {r}}^{0}} = {{r}^{0}} \cdot {{\omega }^{0}}$

получаем соответственно векторные равенства

$\begin{gathered} {{{\dot {z}}}_{1}}{{\sigma }^{0}} + {{{\dot {z}}}_{2}}{{\gamma }^{0}} - {{z}_{2}}{{s}^{0}} = ({{z}_{1}}{{\sigma }^{0}} + {{z}_{2}}{{\gamma }^{0}}) \cdot ({{{\dot {y}}}_{1}}{{\sigma }^{0}} + {{y}_{2}}{{s}^{0}}) = \\ = \;{{y}_{2}}{{z}_{1}}{{\sigma }^{0}} \cdot {{s}^{0}} + {{{\dot {y}}}_{1}}{{z}_{2}}{{\gamma }^{0}} \cdot {{\sigma }^{0}} + {{y}_{2}}{{z}_{2}}{{\gamma }^{0}} \cdot {{s}^{0}} \\ \end{gathered} $

Умножаем скалярно на $\sigma $, $s$, $\gamma $ соответственно обе части полученного соотношения, что приводит к возникновению скалярных уравнений

(4.6)

${{\dot {z}}_{1}} = {\text{|}}{{\sigma }^{0}}{{{\text{|}}}^{{ - 2}}}{{y}_{2}}{{\sigma }^{0}} \cdot ({{\gamma }^{0}} \cdot {{s}^{0}}){{z}_{2}}$

(4.7)

$ - {{z}_{2}} = {\text{|}}{{s}^{0}}{{{\text{|}}}^{{ - 2}}}{{\dot {y}}_{1}}{{s}^{0}} \cdot ({{\gamma }^{0}} \cdot {{\sigma }^{0}}){{z}_{2}}$

(4.8)

${{\dot {z}}_{2}} = {\text{|}}{{\gamma }^{0}}{{{\text{|}}}^{{ - 2}}}{{y}_{2}}{{\gamma }^{0}} \cdot ({{\sigma }^{0}} \cdot {{s}^{0}}){{z}_{1}}$

Вычислим требуемую постоянную

$\begin{gathered} \sigma \cdot \left( {\gamma \times s} \right) = {{\sigma }^{0}} \cdot ({{\gamma }^{0}} \cdot {{s}^{0}}) = \sigma _{3}^{0} \cdot (\gamma _{1}^{0}s_{2}^{0} - \gamma _{2}^{0}s_{1}^{0}) = \\ = \;{{i}_{2}}{{h}_{2}} \cdot (i_{1}^{2}{{i}_{2}}{{h}_{1}}{{\left( {{{h}_{1}}{{h}_{2}}} \right)}^{{1/3}}}{{\cos }^{2}}\left( {{{b}_{1}}t + {{b}_{0}}} \right) + i_{1}^{2}{{i}_{2}}{{h}_{1}}{{\left( {{{h}_{1}}{{h}_{2}}} \right)}^{{1/3}}}{{\sin }^{2}}\left( {{{b}_{1}}t + {{b}_{0}}} \right)) = {{\left( {{{h}_{1}}{{h}_{2}}} \right)}^{{4/3}}} \\ \end{gathered} $

Здесь использовались соотношения (3.29), (3.30). Наконец, вычислим правые части равенств (4.6)–(4.8)

$\begin{gathered} {\text{|}}{{\sigma }^{0}}{{{\text{|}}}^{{ - 2}}}{{y}_{2}}{{\sigma }^{0}} \cdot ({{\gamma }^{0}} \cdot {{s}^{0}}) = h_{2}^{{2/3}}h_{1}^{{ - 4/3}}h_{2}^{{ - 2}}h_{1}^{{4/3}}h_{2}^{{4/3}} = 1 \\ {\text{|}}{{s}^{0}}{{{\text{|}}}^{{ - 2}}}{{{\dot {y}}}_{1}}{{s}^{0}} \cdot ({{\gamma }^{0}} \cdot {{\sigma }^{0}}) = - {\text{|}}{{s}^{0}}{{{\text{|}}}^{{ - 2}}}{{{\dot {y}}}_{1}}{{\sigma }^{0}} \cdot ({{\gamma }^{0}} \cdot {{s}^{0}}) = - h_{1}^{{ - 2}}h_{1}^{{2/3}}h_{2}^{{ - 4/3}}h_{1}^{{4/3}}h_{2}^{{4/3}} = - 1 \\ h_{3}^{2} = {{\left| \gamma \right|}^{2}} = {\text{|}}{{\gamma }^{0}}{{{\text{|}}}^{2}} = {{\left( {{{h}_{1}}{{h}_{2}}} \right)}^{{2/3}}} \\ {\text{|}}{{\gamma }^{0}}{{{\text{|}}}^{{ - 2}}}{{y}_{2}}{{\gamma }^{0}} \cdot ({{\sigma }^{0}} \cdot {{s}^{0}}) = - {\text{|}}{{\gamma }^{0}}{{{\text{|}}}^{2}}{{y}_{2}}{{\sigma }^{0}} \cdot ({{\gamma }^{0}} \cdot {{s}^{0}}) = - h_{2}^{{2/3}}h_{1}^{{ - 4/3}}h_{1}^{{ - 2/3}}h_{2}^{{ - 2/3}}h_{1}^{{4/3}}h_{2}^{{4/3}} = - h_{1}^{{ - 2/3}}h_{2}^{{4/3}} = - {{a}^{2}} \\ \end{gathered} $

Положим $c_{1}^{2} = {{a}^{2}}$. Таким образом, после преобразований уравнения (4.6) и (4.8) имеют вид

(4.9)

${{\dot {z}}_{1}} = {{z}_{2}},\quad {{\dot {z}}_{2}} = - c_{1}^{2}{{z}_{1}}$

Равенство (4.7) опущено, поскольку выполняется тождественно.

После дифференцирования и соответствующих преобразований оба уравнения системы (4.9) сводятся к несвязанным дифференциальным уравнениям

(4.10)

${{\ddot {z}}_{1}} = - c_{1}^{2}{{z}_{1}},\quad {{\ddot {z}}_{2}} = - c_{1}^{2}{{z}_{2}}$

Система (4.9) имеет первый интеграл $c_{1}^{2}z_{1}^{2} + z_{2}^{2} = \operatorname{const} $. Решения уравнений (4.10) могут быть записаны в одном из альтернативных видов:

(4.11)

${{z}_{1}}\left( t \right) = A\sin \left( {{{c}_{1}}t + {{c}_{0}}} \right),\quad {{z}_{2}}\left( t \right) = A{{c}_{1}}\cos \left( {{{c}_{1}}t + {{c}_{0}}} \right)$

или

(4.12)

${{z}_{1}}\left( t \right) = A\cos \left( {{{c}_{1}}t + {{c}_{0}}} \right),\quad {{z}_{2}}\left( t \right) = A{{c}_{1}}\sin \left( {{{c}_{1}}t + {{c}_{0}}} \right)$

где A, ${{c}_{0}}$, ${{c}_{1}}$ – постоянные

(4.13)

${{c}_{1}} = {{i}_{3}}\left| a \right| = {{i}_{3}}h_{1}^{{ - 1/3}}h_{2}^{{2/3}},\quad {{i}_{3}} \in \left\{ { - 1,1} \right\}$

Число A может быть определено точно.

Непосредственно проверяется, что решение (4.12) не удовлетворяет уравнениям (4.9). Следовательно, решением дифференциальных уравнений (4.9) может быть только соотношение (4.11).

Вычислим постоянную A. Для этого воспользуемся равенством ${\text{|}}{{r}^{0}}{{{\text{|}}}^{2}} = {{\left| r \right|}^{2}} = 1$. Используя разложение (4.3) и формулы (4.11), получаем

$\begin{gathered} 1 = z_{1}^{2}{\text{|}}{{\sigma }^{0}}{{{\text{|}}}^{2}} + z_{2}^{2}{\text{|}}{{\gamma }^{0}}{{{\text{|}}}^{2}} = {{A}^{2}}h_{2}^{2}{{\sin }^{2}}\left( {{{c}_{1}}t + {{c}_{0}}} \right) + {{A}^{2}}c_{1}^{2}h_{1}^{{2/3}}h_{2}^{{2/3}}{{\cos }^{2}}\left( {{{c}_{1}}t + {{c}_{0}}} \right) = \\ = \;{{A}^{2}}h_{2}^{2}{{\sin }^{2}}\left( {{{c}_{1}}t + {{c}_{0}}} \right) + {{A}^{2}}h_{1}^{{ - 2/3}}h_{2}^{{4/3}}h_{1}^{{2/3}}h_{2}^{{2/3}}{{\cos }^{2}}\left( {{{c}_{1}}t + {{c}_{0}}} \right) = {{A}^{2}}h_{2}^{2} \\ \end{gathered} $

Здесь использовались уравнения (3.27) и (4.13). Следовательно,

$A = {{i}_{4}}h_{2}^{{ - 1}},\quad {{i}_{4}} \in \left\{ { - 1,1} \right\}$

Таким образом, из разложения (4.4) получаем координаты вектор-функции ${{r}^{0}}$ в виде

(4.14)

Непосредственно проверяется, что соотношения (4.14) являются решениями дифференциального уравнения (4.5). Следовательно, для m = 1 формулы (4.14) для равенства

(4.15)

$r = {{G}^{T}}{{r}^{0}}$

описывают экстремальную траекторию для координат орта оси чувствительности.

Рассмотрим теперь построение решений кинематических уравнений (2.1) для m = 3. По построению имеем

${{(G{{r}^{i}})}^{\centerdot }} = (G{{r}^{i}}) \cdot \left( {G\omega } \right) = (G{{r}^{i}}) \cdot {{\omega }^{0}},\quad i = 1,2,3$

Введем обозначения

(4.16)

${{p}^{i}} = G{{r}^{i}},\quad {{r}^{i}} = {{G}^{T}}{{p}^{i}}$

и поэтому

(4.17)

${{\dot {p}}^{i}} = {{p}^{i}} \cdot {{\omega }^{0}},\quad i = 1,2,3$

К данному моменту вектор-функция времени ${{\omega }^{0}}$ известна и определена по формулам (3.28). Следовательно, система уравнений (4.17) является системой обычных линейных неавтономных дифференциальных векторных уравнений. Решение уравнений (4.17) можно записать с помощью фундаментальной матрицы $F\left( t \right) \in SO\left( 3 \right)$

(4.18)

${{p}^{i}}\left( t \right) = F\left( t \right){{p}^{i}}\left( 0 \right),\quad i = 1,2,3$

где

(4.19)

$\begin{gathered} \dot {F} = - S({{\omega }^{0}})F,\quad F\left( 0 \right) = {{I}_{3}} \\ S({{\omega }^{0}}) = \left( {\begin{array}{*{20}{c}} 0&{ - \omega _{3}^{0}}&{\omega _{2}^{0}} \\ {\omega _{3}^{0}}&0&{ - \omega _{1}^{0}} \\ { - \omega _{2}^{0}}&{\omega _{1}^{0}}&0 \end{array}} \right),\quad {{I}_{3}} = \operatorname{diag} \left( {1,1,1} \right) \\ \end{gathered} $

Для матрицы F введем обозначения

(4.20)

$F = ({{f}^{1}} \vdots {{f}^{2}} \vdots {{f}^{3}})$

По построению

(4.21)

${{f}^{i}} \cdot {{f}^{j}} = {{\delta }_{{ij}}};\quad i,j = 1,2,3$

Матричное дифференциальное уравнение (4.19) перепишем в векторном виде

(4.22)

${{\dot {f}}^{i}} = {{f}^{i}} \cdot {{\omega }^{0}},\quad i = 1,2,3$

с начальными условиями

${{f}^{i}}\left( 0 \right) = {{e}^{i}},\quad {{e}^{2}} = {{\left( {0,1,0} \right)}^{T}},\quad {{e}^{1}} = {{\left( {1,0,0} \right)}^{T}}$

Положим

(4.23)

${{f}^{1}} = {{r}^{0}},\quad {{f}^{2}} = h_{1}^{{ - 1}}{{s}^{0}},\quad {{f}^{3}} = h_{1}^{{ - 1}}{{r}^{0}} \cdot {{s}^{0}}$

Соотношения (4.21) выполнены в силу построений

${{r}^{0}} \cdot {{s}^{0}} = r \cdot s = 0$

Непосредственно проверяется равенство

$\begin{gathered} \det F = \det ({{r}^{0}} \vdots h_{1}^{{ - 1}}{{s}^{0}} \vdots h_{1}^{{ - 1}}{{r}^{0}} \cdot {{s}^{0}}) = \det (h_{1}^{{ - 1}}{{r}^{0}} \cdot {{s}^{0}} \vdots {{r}^{0}} \vdots h_{1}^{{ - 1}}{{s}^{0}}) = \\ = \;(h_{1}^{{ - 1}}{{r}^{0}} \cdot {{s}^{0}}) \cdot ({{r}^{0}} \cdot h_{1}^{{ - 1}}{{s}^{0}}) = h_{1}^{{ - 1}}{\text{|}}{{r}^{0}} \cdot {{s}^{0}}{{{\text{|}}}^{2}} = 1 \\ \end{gathered} $

Таким образом, матрица $F\left( t \right)$ – собственная ортогональная.

Дифференциальные уравнения (4.22) для i =1, 2 выполняются в силу построения (4.23) и уравнений (4.5) и (3.31). Дифференциальное уравнение (4.22) при i = 3 для (4.23) верно в силу тождества Якоби для векторного произведения. Таким образом, формулы (4.23) справедливы для уравнений (4.22).

Выберем для (4.23), (4.20) постоянные ${{b}_{0}} = {{c}_{0}} = 0$, ${{i}_{1}} = 1$, ${{i}_{2}}{{i}_{3}}{{i}_{4}} = 1$, тогда может быть построена матрица вида

(4.24)

$\begin{gathered} F\left( t \right) = \left( {\begin{array}{*{20}{c}} {{{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}}\cos {{c}_{1}}t\cos {{b}_{1}}t}&{{{i}_{1}}\sin {{b}_{1}}t}&{ - {{i}_{1}}{{i}_{2}}{{i}_{4}}\sin {{c}_{1}}t\cos {{b}_{1}}t} \\ { - {{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}}\cos {{c}_{1}}t\sin {{b}_{1}}t}&{{{i}_{1}}\cos {{b}_{1}}t}&{{{i}_{1}}{{i}_{2}}{{i}_{4}}\sin {{c}_{1}}t\sin {{b}_{1}}t} \\ {{{i}_{2}}{{i}_{4}}\sin {{c}_{1}}t}&0&{{{i}_{2}}{{i}_{3}}{{i}_{4}}\cos {{c}_{1}}t} \end{array}} \right) = \\ = \;\left( {\begin{array}{*{20}{c}} {\cos {{c}_{1}}t\cos {{b}_{1}}t}&{\sin {{b}_{1}}t}&{ - {{i}_{3}}\sin {{c}_{1}}t\cos {{b}_{1}}t} \\ { - \cos {{c}_{1}}t\sin {{b}_{1}}t}&{\cos {{b}_{1}}t}&{{{i}_{3}}\sin {{c}_{1}}t\sin {{b}_{1}}t} \\ {{{i}_{3}}\sin {{c}_{1}}t}&0&{\cos {{c}_{1}}t} \end{array}} \right) \\ \end{gathered} $

Следовательно, матрица (4.24) является решением матричного дифференциального уравнения с соответствующим начальным условием (4.19) и поэтому определяет соответствующую фундаментальную матрицу. В итоге, для m = 3 из (4.16), (4.18) получаем исходную экстремальную траекторию

(4.25)

${{r}^{i}}\left( t \right) = {{G}^{T}}F\left( t \right)G{{r}^{i}}\left( 0 \right),\quad i = 1,2,3$

определяемую матрицей (4.24). Полученная формула применима и для произвольного m.

Таким образом, если абсолютная величина вектор-функции экстремальной угловой скорости не меняется со временем, тогда все соответствующие координаты траекторий описываются тригонометрическими функциями времени.

5. Примеры и комментарии. Частный случай экстремальных угловых скоростей из (3.1) для задачи оптимальной переориентации сферически симметричного тела был первоначально получен в [5]. Для этих соотношений в (3.1) достаточно положить ${{b}_{1}} = - b$, ${{b}_{0}} = - 3{\text{/}}2\pi - c$.

Полученное множество экстремальных траекторий $({{r}^{i}},\omega )$ описывается формулами (3.28), (4.14), (4.24) и (4.25), если положить

${{r}^{i}} = {{G}^{T}}{{r}^{0}},\quad i = 1,\; \ldots ,\;m;\quad \omega = {{G}^{T}}{{\omega }^{0}}$

Свободными параметрами являются матрица $G \in SO\left( 3 \right)$, положительные числа ${{h}_{1}},{{h}_{2}} \in \left( {0,\infty } \right)$, вещественные числа ${{b}_{0}},{{c}_{0}} \in \mathbb{R}$ и индексы ${{i}_{1}},{{i}_{2}},{{i}_{3}},{{i}_{4}} \in \left\{ { - 1,1} \right\}$. Согласно построению, начальные и терминальные условия (2.2) не могут быть произвольными.

Приведем некоторые примеры соответствующих краевых условий. Пусть m = 1 и положим $G = {{I}_{3}}$, ${{h}_{1}} = {{h}_{2}} = 1$, ${{b}_{0}} = {{c}_{0}} = 0$. В этом случае получаем равенства ${{b}_{1}} = {{i}_{2}}$, ${{c}_{1}} = {{i}_{3}}$. Краевые условия, таким образом, могут быть получены в виде

$\begin{gathered} \omega \left( 0 \right) = {{\left( {0,{{i}_{1}},{{i}_{2}}} \right)}^{T}},\quad \omega \left( T \right) = {{\left( {{{i}_{1}}\sin \left( {{{i}_{2}}T} \right),{{i}_{1}}\cos \left( {{{i}_{2}}T} \right),{{i}_{2}}} \right)}^{T}},\quad r\left( 0 \right) = {{\left( {{{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}},0,0} \right)}^{T}}, \\ r\left( T \right) = {{\left( {{{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}}\cos \left( {{{i}_{3}}T} \right)\cos \left( {{{i}_{2}}T} \right), - {{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}}\cos \left( {{{i}_{3}}T} \right)\cos \left( {{{i}_{2}}T} \right),{{i}_{2}}{{i}_{4}}\sin \left( {{{i}_{3}}T} \right)} \right)}^{T}} \\ \end{gathered} $

Зафиксируем ${{i}_{1}} = {{i}_{2}} = 1$ и тем самым построим одну траекторию для вектор-функции угловой скорости

$\omega \left( 0 \right) = {{\left( {0,1,1} \right)}^{T}},\quad \omega \left( T \right) = {{\left( {\sin T,\cos T,0} \right)}^{T}}$

Для соответствующего экстремального управления для $t \in \left[ {0,T} \right]$ имеем

$u\left( t \right) = \gamma \left( t \right) = {{\left( {\cos t, - \sin t,0} \right)}^{T}}$

В этом случае имеются две различные траектории, соответствующие орту оси чувствительности. Действительно, параметры ${{i}_{3}}$, ${{i}_{4}}$ можно выбирать произвольно, что приводит к следующим результатам. Если ${{i}_{3}} = {{i}_{4}}$ (либо +1, либо –1), тогда

$r\left( 0 \right) = {{\left( {1,0,0} \right)}^{T}},\quad r\left( T \right) = {{({{\cos }^{2}}T, - \cos T\sin T,\sin T)}^{T}}$

Если ${{i}_{3}} = - {{i}_{4}}$ (либо +1, либо –1), тогда

$r\left( 0 \right) = {{\left( { - 1,0,0} \right)}^{T}},\quad r\left( T \right) = {{( - {{\cos }^{2}}T,\cos T\sin T, - \sin T)}^{T}}$

Построим теперь краевые условия для экстремальных траекторий при фиксированных индексах ${{i}_{3}} = {{i}_{4}} = 1$ и произвольных ${{i}_{1}}$, ${{i}_{2}}$. В этом случае для $t \in \left[ {0,T} \right]$, если ${{i}_{1}} = {{i}_{2}} = - 1$, тогда

$\begin{gathered} \omega \left( 0 \right) = {{\left( {0, - 1, - 1} \right)}^{T}},\quad \omega \left( T \right) = {{(\sin T, - \cos T, - 1)}^{T}},\quad u\left( t \right) = {{(\cos t,\sin t,0)}^{T}} \\ r\left( 0 \right) = {{\left( {1,0,0} \right)}^{T}},\quad r\left( T \right) = {{({{\cos }^{2}}T,\cos T\sin T, - \sin T)}^{T}} \\ \end{gathered} $

Если ${{i}_{1}} = - 1$, ${{i}_{2}} = 1$, тогда

$\begin{gathered} \omega \left( 0 \right) = {{\left( {0, - 1,1} \right)}^{T}},\quad \omega \left( T \right) = {{\left( { - \sin T, - \cos T,1} \right)}^{T}},\quad u\left( t \right) = {{\left( { - \cos t, - \sin t,0} \right)}^{T}} \\ r\left( 0 \right) = {{\left( { - 1,0,0} \right)}^{T}},\quad r\left( T \right) = {{( - {{\cos }^{2}}T,\cos T\sin T,\sin T)}^{T}} \\ \end{gathered} $

Если ${{i}_{1}} = 1$, ${{i}_{2}} = - 1$, тогда

$\begin{gathered} \omega \left( 0 \right) = {{\left( {0,1, - 1} \right)}^{T}},\quad \omega \left( T \right) = {{\left( { - \sin T,\cos T, - 1} \right)}^{T}},\quad u\left( t \right) = {{\left( { - \cos t, - \sin t,0} \right)}^{T}} \\ r\left( 0 \right) = {{\left( { - 1,0,0} \right)}^{T}},\quad r\left( T \right) = {{( - {{\cos }^{2}}T, - \cos T\sin T, - \sin T)}^{T}} \\ \end{gathered} $

Примеры экстремальных траекторий и соответствующих граничных условий для $m = 3$ приведены в [1].

Полученные экстремальные управления позволяют получить явный вид функционала качества (2.3) в рассматриваемой задаче оптимального управления. Действительно, из (3.30) имеем

$\begin{gathered} \frac{1}{2}\min \int\limits_{\left[ {0,T} \right]} {u\left( t \right) \cdot u\left( t \right)dt} = \frac{1}{2}\int\limits_{\left[ {0,T} \right]} {\gamma \left( t \right) \cdot \gamma \left( t \right)dt} = \frac{1}{2}\int\limits_{\left[ {0,T} \right]} {{{\gamma }^{0}}\left( t \right) \cdot {{\gamma }^{0}}\left( t \right)dt} = \\ = \;\frac{1}{2}\int\limits_{\left[ {0,T} \right]} {[{{{\left( {{{h}_{1}}{{h}_{2}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{{\cos }}^{2}}\left( {{{b}_{1}}t + {{b}_{0}}} \right) + {{{\left( {{{h}_{1}}{{h}_{2}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{{\sin }}^{2}}\left( {{{b}_{1}}t + {{b}_{0}}} \right)]} dt = \frac{T}{2}{{\left( {{{h}_{1}}{{h}_{2}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \\ \end{gathered} $

Следовательно, введенный в статье класс экстремальных тригонометрических траекторий обладает следующими свойствами:

– величина функционала минимальных энергозатрат линейно зависит от времени протекающего управляемого процесса;

– задача оптимального управления с бесконечным временем не разрешима в классе построенных экстремалей.

При m = 3 ортогональную матрицу из (4.24), соответствующую решению задачи Коши (4.19), удобно представить в виде произведения

$F\left( t \right) = \left( {\begin{array}{*{20}{c}} {\cos {{b}_{1}}t}&{\sin {{b}_{1}}t}&0 \\ { - \sin {{b}_{1}}t}&{\cos {{b}_{1}}t}&0 \\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\cos {{c}_{1}}t}&0&{ - \sin {{c}_{1}}t} \\ 0&1&0 \\ {\sin {{c}_{1}}t}&0&{\cos {{c}_{1}}t} \end{array}} \right)$

Данные матрицы отвечают поворотам относительно осей ортов e³, e² с соответствующими углами ${{b}_{1}}t$ и $ - {{c}_{1}}t$.

Полученное семейство экстремальных траекторий позволяет эффективно характеризовать соответствующие вектор-функции времени, если перейти от декартовых прямоугольных координат к криволинейным координатам. Действительно, вектор-функция экстремальной угловой скорости вполне удобно описывается с помощью цилиндрических координат, а кинематические параметры могут быть естественно использованы для сферических координат.

Заключение. Установлено, что в задаче оптимального управления переориентацией сферически симметричного тела с минимальными энергозатратами имеется семейство аналитических экстремальных угловых скоростей. Данное множество порождается единственным образом вектор-функциями угловой скорости с постоянной абсолютной величиной. Соответствующие координаты экстремальных траекторий выражаются явным образом исключительно через тригонометрические функции времени.

Работа выполнена при финансовой поддержке Российского Фонда фундаментальных исследований (17-01-00538).

Список литературы

Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. М.: Физматлит, 2005. 392 с.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Физматлит, 1961. 384 с.
Алексеев К.Б. Экстенсивное управление ориентацией космических летательных аппаратов. М.: Машиностроение, 1977. 123 с.
Сиротин А.Н. Плоский разворот как допустимая экстремаль в задаче оптимального управления вращением асимметрического тела // Изв. РАН. МТТ. 2012. № 1. С. 3–26.
Сиротин А.Н. Семейство тригонометрических экстремалей в задаче переориентации сферически симметричного тела с минимальными энергозатратами // ПММ. 2013. Т. 77. Вып. 2. С. 283–291.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал