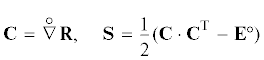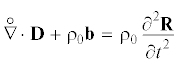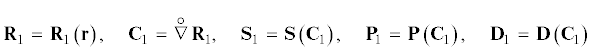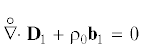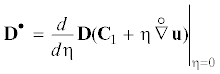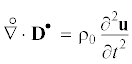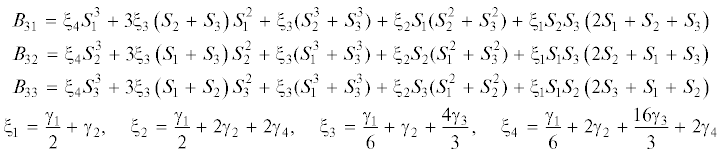1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 3, 2019

Известия РАН. Механика твердого тела, 2019, № 3, стр. 3-15

МОДУЛИ ВЫСШИХ ПОРЯДКОВ В УРАВНЕНИЯХ ДИНАМИКИ ПРЕДНАПРЯЖЕННОГО УПРУГОГО ТЕЛА

Т. И. Белянкова a, b, В. В. Калинчук a, b, *, Д. Н. Шейдаков a

a Южный научный центр Российской академии наук
Ростов-на-Дону, Россия

b Южный Федеральный университет
Ростов-на-Дону, Россия

* E-mail: kalin@ssc-ras.ru

Поступила в редакцию 28.08.2017
После доработки 28.08.2017
Принята к публикации 29.01.2018

Полный текст (PDF)

Аннотация

В терминах отсчетной конфигурации проведена линеаризация уравнений нелинейной механики первоначально изотропного упругого тела (ПИУТ) в окрестности некоторого преднапряженного состояния равновесия. При этом использовалось специальное представление упругого потенциала через алгебраические инварианты тензора деформации Коши–Грина, содержащее модули высших порядков. Построены линеаризованные определяющие соотношения и уравнения движения, учитывающие нелинейное влияние начальных деформаций на свойства ПИУТ.

Ключевые слова: модули высших порядков, преднапряженная среда, начальная деформация, алгебраические инварианты тензора деформации Коши–Грина

1. Введение. Технологическое развитие авиа- и машиностроения, приборостроения и электроники приводит к необходимости создания новых конструкционных материалов, а также подробного исследования их физических свойств, технологических и прочностных характеристик в зависимости от режимов и условий эксплуатации. Проведение подобных исследований сопряжено с необходимостью решения сложных прикладных задач теории упругости и привлечения механических моделей гиперупругой среды [1, 2], с той или иной степенью точности отражающих процессы, происходящие в изучаемых телах. В случае изотропного материала упругий потенциал представляется в виде скалярной функции инвариантов меры или тензора деформации [2–4]. Для жестких материалов широко используется предложенное Мурнаганом представление упругого потенциала в виде кубической функции инвариантов тензора деформации Коши–Грина [5] с константами III порядка. Значения последних определены для ряда металлов, сплавов и конструкционных материалов, кристаллов с различными классами симметрии [6–9], а также для некоторых горных пород [10]. Модель Мурнагана позволяет более точно описывать поведение предварительно напряженных тел. С ее помощью в [6, 10–19] исследованы эффекты второго порядка, а также изучены особенности динамики, распространения и локализации волн в преднапряженных средах. В [11] проведена линеаризация уравнений нелинейной механики деформируемого твердого тела в текущей и отсчетной конфигурациях. Полученные результаты в дальнейшем [11, 16–19] использованы при решении ряда конкретных задач динамической теории упругости. В [17–19] исследовано влияние характера начальных воздействий на возникновение, распространение и локализацию волновых полей в однородных и неоднородных предварительно напряженных средах. Развитие технологий, основанных на эксплуатации материалов и конструкций, допускающих большой уровень деформации, определяет необходимость усовершенствования привлекаемых моделей за счет использования более сложных форм упругого потенциала. Различные представления упругих потенциалов с константами III и IV порядков успешно использовались при моделировании мягких и резиноподобных материалов [20, 21]. Среди жестких материалов выделяются так называемые металлические стекла, перспективные в практических приложениях и обладающие уникальными физическими свойствами. Они способны до начала пластического течения выдерживать чрезвычайно высокий уровень упругой деформации, что требует привлечения констант IV порядка для адекватного описания их поведения. Результаты экспериментальных исследований по определению упругих модулей III и IV порядков для объемных металлических стекол на основе циркония (Zr) и палладия (Pd) представлены в [22–24]. Настоящая работа посвящена усовершенствованию развитой в [11] линеаризованной теории контактного взаимодействия предварительно напряженных тел путем учета модулей IV порядка в представлении упругого потенциала. В работе построены линеаризованные определяющие соотношения и уравнения движения преднапряженной среды, позволяющие учитывать нелинейные эффекты “второго” и “третьего” порядков при анализе влияния начальной деформации на упругие свойства исходного материала. Изучено влияние модулей высших порядков на характеристики предварительно напряженного материала при расчете начально-деформированного состояния.

2. Общая постановка задачи для преднапряженного ПИУТ. Введем в рассмотрение отсчетную $v$ и актуальную V конфигурации с радиус-векторами:

(2.1)
${\mathbf{r}} = {{x}_{k}}{{{\mathbf{i}}}_{k}},\quad {\mathbf{R}} = {{X}_{k}}{{{\mathbf{i}}}_{k}}$
где $\left\{ {{{{\mathbf{i}}}_{1}},{{{\mathbf{i}}}_{2}},{{{\mathbf{i}}}_{3}}} \right\}$ – ортонормированный декартовый векторный базис, ${{x}_{1}},{{x}_{2}},{{x}_{3}}$ и ${{X}_{1}},{{X}_{2}},{{X}_{3}}$ – лагранжевы и эйлеровы координаты, соответственно.

Деформацию среды характеризуют градиент деформации С и тензор деформации Коши–Грина ${\mathbf{S}}$ ( – набла оператор в отсчетной конфигурации, У – единичный тензор):

(2.2)
напряженное состояние – тензоры напряжений Кирхгофа ${\mathbf{P}}$ и Пиола В:

(2.3)
${\mathbf{P}} = \frac{{\partial W({\mathbf{S}})}}{{\partial {\mathbf{S}}}},\quad {\mathbf{D}} = {\mathbf{P}} \cdot {\mathbf{C}}$

В случае изотропного материала удельная потенциальная энергия деформации $W({\mathbf{S}})$ может быть выражена через алгебраические инварианты ${{I}_{k}} = tr{{{\mathbf{S}}}^{k}}$ $\left( {k = 1,2,3} \right)$ тензора деформации Коши–Грина [22–24]:

(2.4)
$W = \frac{1}{2}\lambda I_{1}^{2} + \mu {{I}_{2}} + \frac{1}{6}{{\beta }_{1}}I_{1}^{3} + {{\beta }_{2}}{{I}_{1}}{{I}_{2}} + \frac{4}{3}{{\beta }_{3}}{{I}_{3}} + \frac{1}{{24}}{{\gamma }_{1}}I_{1}^{4} + \frac{1}{2}{{\gamma }_{2}}I_{1}^{2}{{I}_{2}} + \frac{4}{3}{{\gamma }_{3}}{{I}_{1}}{{I}_{3}} + \frac{1}{2}{{\gamma }_{4}}I_{2}^{2}$

Здесь $\lambda ,\mu $ – упругие модули II порядка; ${{\beta }_{1}},{{\beta }_{2}},{{\beta }_{3}}$ и ${{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}},{{\gamma }_{4}}$ – упругие модули III и IV порядков, соответственно. Тензор Кирхгофа (2.3) с учетом представления (2.4) записывается в виде [3]:

(2.5)
${\mathbf{P}} = k{{\chi }_{k}}{{{\mathbf{S}}}^{{k - 1}}};\quad {{\chi }_{k}} = \frac{{\partial W}}{{\partial {{I}_{k}}}},\quad k = 1,2,3$
(2.6)
$\begin{gathered} {{\chi }_{1}} = \lambda {{I}_{1}} + \frac{1}{2}{{\beta }_{1}}I_{1}^{2} + {{\beta }_{2}}{{I}_{2}} + \frac{1}{6}{{\gamma }_{1}}I_{1}^{3} + {{\gamma }_{2}}{{I}_{1}}{{I}_{2}} + \frac{4}{3}{{\gamma }_{3}}{{I}_{3}} \\ {{\chi }_{2}} = \mu + {{\beta }_{2}}{{I}_{1}} + \frac{1}{2}{{\gamma }_{2}}I_{1}^{2} + {{\gamma }_{4}}{{I}_{2}},\quad {{\chi }_{3}} = \frac{4}{3}\left( {{{\beta }_{3}} + {{\gamma }_{3}}{{I}_{1}}} \right) \\ \end{gathered} $

Краевая задача нелинейной теории упругости для предварительно напряженного ПИУТ в лагранжевых координатах описывается уравнениями

(2.7)
и граничными условиями на поверхности тела $\Omega = {{\Omega }_{1}} + {{\Omega }_{2}}$:
(2.8)
$\begin{gathered} {{\Omega }_{1}}{\text{:}}\quad {\mathbf{n}} \cdot {\mathbf{D}} = {\mathbf{t}} \\ {{\Omega }_{2}}{\text{:}}\quad {\mathbf{R}} = {\mathbf{R}}{\text{*}} \\ \end{gathered} $
b и t – векторы массовых и поверхностных сил, соответственно; ${\mathbf{R}}{\text{*}}$ – радиус-вектор точек поверхности деформированного тела; ${{\rho }_{0}}$ – плотность материала в отсчетной конфигурации; n – единичный вектор нормали к поверхности недеформированного тела. Замыкает постановку задачи закон состояния гиперупругого изотропного материала (2.5), (2.6).

3. Линеаризованные уравнения движения для преднапряженного ПИУТ. Пусть существует некоторое равновесное начально-деформированное состояние ПИУТ и величины, характеризующие это состояние, не зависят явно от времени [3, 11]:

(3.1)

Уравнения равновесия в объеме и на поверхности $\Omega = {{\Omega }_{1}} + {{\Omega }_{2}}$ представляются соотношениями:

(3.2)
(3.3)
$\begin{gathered} {{\Omega }_{1}}{\text{:}}\quad {\mathbf{n}} \cdot {{{\mathbf{D}}}_{1}} = {{{\mathbf{t}}}_{1}} \\ {{\Omega }_{2}}{\text{:}}\quad {{{\mathbf{R}}}_{1}} = {\mathbf{R}}_{1}^{*} \\ \end{gathered} $

Рассмотрим малое возмущение начального состояния (3.1), вызванное небольшим изменением поверхностных или массовых сил (характеристики возмущенного состояния будем отмечать верхним индексом $^{ \times }$):

(3.4)
${{{\mathbf{b}}}^{ \times }} = {{{\mathbf{b}}}_{1}} + \eta {\mathbf{b}},\quad {{{\mathbf{t}}}^{ \times }} = {{{\mathbf{t}}}_{1}} + \eta {\mathbf{f}}$

Положение точек тела в таком состоянии определяется радиус-вектором

(3.5)
${{{\mathbf{R}}}^{ \times }} = {{{\mathbf{R}}}_{1}} + \eta {\mathbf{u}}$

Здесь $\eta $ – малый параметр, u – вектор добавочных перемещений. Для тензора Пиола в возмущенном состоянии справедливо представление:

(3.6)
${{{\mathbf{D}}}^{ \times }} = {{{\mathbf{D}}}_{1}} + \eta {{{\mathbf{D}}}^{ \bullet }} + o({{\eta }^{2}})$
(3.7)

Здесь и далее верхним индексом $^{ \bullet }$ обозначены конвективные производные соответствующих тензоров.

Величины (3.4)–(3.6), определяющие возмущенное состояние тела, удовлетворяют уравнениям движения (2.7) с граничными условиями (2.8). Учитывая соотношения (3.1)–(3.7), в отсутствие массовых сил получаем линеаризованные уравнения движения:

(3.8)
и линеаризованные граничные условия на поверхности $\Omega = {{\Omega }_{1}} + {{\Omega }_{2}}$:

(3.9)
$\begin{gathered} {{\Omega }_{1}}{\text{:}}\quad {\mathbf{n}} \cdot {{{\mathbf{D}}}^{ \bullet }} = {\mathbf{f}} \\ {{\Omega }_{2}}{\text{:}}\quad {\mathbf{u}} = {\mathbf{u}}{\text{*}} \\ \end{gathered} $

Путем линеаризации определяющих соотношений (2.3), (2.5) найдем конвективную производную тензора Пиола ${{{\mathbf{D}}}^{ \bullet }}$:

(3.10)
${{{\mathbf{D}}}^{ \bullet }} = {{{\mathbf{P}}}^{ \bullet }} \cdot {{{\mathbf{C}}}_{1}} + {{{\mathbf{P}}}_{1}} \cdot {{{\mathbf{C}}}^{ \bullet }}$

Здесь

(3.11)
${{{\mathbf{P}}}^{ \bullet }} = 2{{\chi }_{2}}{{{\mathbf{S}}}^{ \bullet }} + 3{{\chi }_{3}}({{{\mathbf{S}}}_{1}} \cdot {{{\mathbf{S}}}^{ \bullet }} + {{{\mathbf{S}}}^{ \bullet }} \cdot {{{\mathbf{S}}}_{1}}) + \chi _{1}^{ \bullet }{\mathbf{E}} + 2\chi _{2}^{ \bullet }{{{\mathbf{S}}}_{1}} + 3\chi _{3}^{ \bullet }{\mathbf{S}}_{1}^{2}$
где

(3.12)
$\begin{gathered} \chi _{k}^{ \bullet } = {{\chi }_{{km}}}I_{m}^{ \bullet };\quad {{\chi }_{{km}}} = \frac{{{{\partial }^{2}}W}}{{\partial {{I}_{k}}\partial {{I}_{m}}}},\quad I_{m}^{ \bullet } = \frac{{\partial {{I}_{m}}}}{{\partial {\mathbf{S}}}} \circ {{{\mathbf{S}}}^{ \bullet }} = m{\mathbf{S}}_{1}^{{m - 1}} \circ {{{\mathbf{S}}}^{ \bullet }},\quad k,m = 1,2,3 \\ {{{\mathbf{S}}}^{ \bullet }} = \frac{1}{2}({{{\mathbf{C}}}_{1}} \cdot {{{\mathbf{C}}}^{{\text{T}}}}^{ \bullet } + {{{\mathbf{C}}}^{ \bullet }} \cdot {\mathbf{C}}_{1}^{{\text{T}}}),\quad {{{\mathbf{C}}}^{ \bullet }} = \mathop \nabla \limits^{\text{o}} {\mathbf{u}} \\ \end{gathered} $

Здесь символом “$ \circ $” обозначена операция полного умножения.

Далее будем полагать, что начальное деформированное состояние ПИУТ однородно:

(3.13)
${{{\mathbf{R}}}_{1}} = {{v}_{k}}{{x}_{k}}{{{\mathbf{i}}}_{k}};\quad {{v}_{k}} = 1 + {{\delta }_{k}}{\text{,}}\quad k = 1,2,3$
где ${{\delta }_{1}},{{\delta }_{2}},{{\delta }_{3}}$ – относительные удлинения волокон, направленных вдоль координатных осей, совпадающих в естественной конфигурации с декартовыми координатами.

Градиент деформации и тензор деформации Коши–Грина (2.2) с учетом условия (3.13) записываются следующим образом:

(3.14)
${{{\mathbf{C}}}_{1}} = {{v}_{k}}{{{\mathbf{i}}}_{k}}{{{\mathbf{i}}}_{k}},\quad {{{\mathbf{S}}}_{1}} = {{S}_{k}}{{{\mathbf{i}}}_{k}}{{{\mathbf{i}}}_{k}};\quad {{S}_{k}} = \frac{1}{2}(v_{k}^{2} - 1),\quad k = 1,2,3$

Тензоры Кирхгофа и Пиола представляются выражениями:

(3.15)
${{{\mathbf{P}}}_{1}} = {{P}_{k}}{{{\mathbf{i}}}_{k}}{{{\mathbf{i}}}_{k}},\quad {{{\mathbf{D}}}_{1}} = {{v}_{k}}{{P}_{k}}{{{\mathbf{i}}}_{k}}{{{\mathbf{i}}}_{k}};\quad {{P}_{k}} = n{{\chi }_{n}}S_{k}^{{n - 1}},\quad k = 1,2,3$

Конвективные производные (3.10), (3.11) этих тензоров принимают вид (${{\delta }_{{km}}}$ – символ Кронекера):

(3.16)
$\begin{gathered} {{{\mathbf{P}}}^{ \bullet }} = P_{{km}}^{*}{{{\mathbf{i}}}_{k}}{{{\mathbf{i}}}_{m}},\quad {{{\mathbf{D}}}^{ \bullet }} = ({{v}_{m}}P_{{km}}^{*} + {{P}_{k}}{{u}_{{m,k}}}){{{\mathbf{i}}}_{k}}{{{\mathbf{i}}}_{m}} \\ P_{{km}}^{*} = \left[ {{{\chi }_{2}} + \frac{3}{2}{{\chi }_{3}}\left( {{{S}_{k}} + {{S}_{m}}} \right)} \right]\left( {{{v}_{k}}{{u}_{{k,m}}} + {{v}_{m}}{{u}_{{m,k}}}} \right) + {{\delta }_{{km}}}{{\theta }_{{kn}}}{{v}_{n}}{{u}_{{n,n}}} \\ {{\theta }_{{kn}}} = {{\chi }_{{11}}} + 2{{\chi }_{{12}}}\left( {{{S}_{k}} + {{S}_{n}}} \right) + {{\chi }_{{13}}}(4S_{k}^{2} + 3S_{n}^{2}) + 4{{\chi }_{{22}}}{{S}_{k}}{{S}_{n}} \\ {{u}_{{k,m}}} = \frac{{\partial {{u}_{k}}}}{{\partial {{x}_{m}}}},\quad {{u}_{{k,mn}}} = \frac{{{{\partial }^{2}}{{u}_{k}}}}{{\partial {{x}_{m}}\partial {{x}_{n}}}},\quad k,m,n = 1,2,3 \\ \end{gathered} $

Здесь использованы соотношения

$\begin{gathered} {{{\mathbf{S}}}^{ \bullet }} = \frac{1}{2}\left( {{{v}_{k}}{{u}_{{k,m}}} + {{v}_{m}}{{u}_{{m,k}}}} \right){{{\mathbf{i}}}_{k}}{{{\mathbf{i}}}_{m}},\quad I_{1}^{ \bullet } = {{v}_{k}}{{u}_{{k,k}}},\quad I_{2}^{ \bullet } = 2{{v}_{k}}{{S}_{k}}{{u}_{{k,k}}},\quad I_{3}^{ \bullet } = {\text{3}}{{v}_{k}}S_{k}^{2}{{u}_{{k,k}}} \\ \chi _{1}^{ \bullet } = ({{\chi }_{{11}}} + 2{{\chi }_{{12}}}{{S}_{n}} + 3{{\chi }_{{13}}}S_{n}^{2}){{v}_{n}}{{u}_{{n,n}}},\quad \chi _{2}^{ \bullet } = \left( {{{\chi }_{{12}}} + 2{{\chi }_{{22}}}{{S}_{n}}} \right){{v}_{n}}{{u}_{{n,n}}},\quad \chi _{3}^{ \bullet } = {{\chi }_{{13}}}{{v}_{n}}{{u}_{{n,n}}} \\ \end{gathered} $

Согласно представлениям (3.12), коэффициенты ${{\chi }_{{km}}}$ равны:

(3.17)
$\begin{gathered} {{\chi }_{{11}}} = \lambda + {{\beta }_{1}}{{I}_{1}} + \frac{1}{2}{{\gamma }_{1}}I_{1}^{2} + {{\gamma }_{2}}{{I}_{2}},\quad {{\chi }_{{12}}} = {{\chi }_{{21}}} = {{\beta }_{2}} + {{\gamma }_{2}}{{I}_{1}},\quad {{\chi }_{{22}}} = {{\gamma }_{4}} \\ {{\chi }_{{13}}} = {{\chi }_{{31}}} = \frac{4}{3}{{\gamma }_{3}},\quad {{\chi }_{{23}}} = {{\chi }_{{32}}} = {{\chi }_{{33}}} = 0;\quad {{I}_{m}} = S_{1}^{m} + S_{2}^{m} + S_{3}^{m},\quad m = 1,2,3 \\ \end{gathered} $

Линеаризованные уравнения движения (3.8) в скалярном виде представляются формулами ($m = 1,2,3$):

(3.18)
${{P}_{k}}{{u}_{{m,kk}}} + {{\theta }_{{mn}}}{{v}_{m}}{{v}_{n}}{{u}_{{n,mn}}} + {{v}_{m}}\left[ {{{\chi }_{2}} + \frac{3}{2}{{\chi }_{3}}\left( {{{S}_{k}} + {{S}_{m}}} \right)} \right]\left( {{{v}_{k}}{{u}_{{k,km}}} + {{v}_{m}}{{u}_{{m,kk}}}} \right) = {{\rho }_{0}}\frac{{{{\partial }^{2}}{{u}_{m}}}}{{\partial {{t}^{2}}}}$

Используя выражения (3.16), компоненты линеаризованного тензора напряжений Пиолы ${{{\mathbf{D}}}^{ \bullet }}$ могут быть представлены в компактной форме [2, 3, 11]:

(3.19)
${{{\mathbf{D}}}^{ \bullet }} = D_{{ij}}^{*}{{{\mathbf{i}}}_{i}}{{{\mathbf{i}}}_{j}};\quad D_{{ij}}^{*} = C_{{ijkl}}^{*}{{u}_{{k,l}}},\quad i,j = 1,2,3$
(3.20)
$\begin{gathered} C_{{iiii}}^{*} = {{P}_{i}} + {{\theta }_{{ii}}}v_{i}^{2} + 2\left( {{{\chi }_{2}} + 3{{\chi }_{3}}{{S}_{i}}} \right)v_{i}^{2},\quad C_{{ijij}}^{*} = \left( {{{\chi }_{2}} + \frac{3}{2}{{\chi }_{3}}\left[ {{{S}_{i}} + {{S}_{j}}} \right]} \right){{v}_{j}}{{v}_{i}} \\ C_{{ijji}}^{*} = {{P}_{i}} + \left( {{{\chi }_{2}} + \frac{3}{2}{{\chi }_{3}}\left[ {{{S}_{i}} + {{S}_{j}}} \right]} \right)v_{j}^{2},\quad C_{{iijj}}^{*} = {{\theta }_{{ij}}}{{v}_{i}}{{v}_{j}},\quad i \ne j \\ \end{gathered} $

Все остальные коэффициенты $C_{{ijkl}}^{*}$ равны нулю.

Представление (3.19) определяет влияние начальных деформаций на исходные свойства изотропного материала, т.е. $C_{{ijkl}}^{*}$ определяют свойства предварительно напряженного тела. В отсутствии начальных деформаций $\left( {{{v}_{1}} = {{v}_{2}} = {{v}_{3}} = 1} \right)$, согласно (2.6), (3.14)–(3.17) получаем

$C_{{iiii}}^{*} = \lambda + 2\mu ,\quad C_{{iijj}}^{*} = \lambda ,\quad C_{{ijij}}^{*} = \mu ,\quad C_{{ijji}}^{*} = \mu $

С учетом (3.19), (3.20) линеаризованные уравнения движения (3.18) преднапряженного первоначально изотропного тела принимают вид [1–3, 11]:

(3.21)
$C_{{ijkl}}^{*}{{u}_{{k,li}}} = {{\rho }_{0}}\frac{{{{\partial }^{2}}{{u}_{j}}}}{{\partial {{t}^{2}}}},\quad j = 1,2,3$

При решении краевых задач для полуограниченных сред задача (3.9), (3.21) замыкается дополнительными граничными условиями:

– для полупространства $\left| {{{x}_{1}}} \right|,\;\left| {{{x}_{2}}} \right| \leqslant \infty ,\,\,\,{{x}_{3}} \leqslant 0$

(3.22)
${{x}_{3}} \to - \infty {\text{:}}\quad {\mathbf{u}} \to 0$

– для слоя $\left| {{{x}_{1}}} \right|,\;\left| {{{x}_{2}}} \right| \leqslant \infty ,{{a}_{ - }} \leqslant {{x}_{3}} \leqslant {{a}_{ + }}$, нижняя грань которого жестко защемлена

(3.23)
${{x}_{3}} = {{a}_{ - }}{\text{:}}\quad {\mathbf{u}} = 0$

– на границе раздела n-го и (n + 1)-го элементов структуры с плоскопараллельными границами (при полном сцеплении):

(3.24)
${{x}_{3}} = {{a}_{n}}{\text{:}}\quad {{{\mathbf{u}}}^{{\left( n \right)}}} = {{{\mathbf{u}}}^{{\left( {n + 1} \right)}}},\quad D_{{3k}}^{{*\left( n \right)}} = D_{{3k}}^{{*\left( {n + 1} \right)}},\quad k = 1,2,3$

– на границе раздела (при контакте без трения):

(3.25)
${{x}_{3}} = {{a}_{n}}{\text{:}}\quad u_{3}^{{\left( n \right)}} = u_{3}^{{\left( {n + 1} \right)}} = 0,\quad D_{{3k}}^{{*\left( n \right)}} = D_{{3k}}^{{*\left( {n + 1} \right)}} = 0,\quad k = 1,2$

4. Различные типы начального напряженного состояния ПИУТ. Начальные напряжения в теле определяются тензором Кирхгофа, который в случае однородной начальной деформации (3.13) задан соотношениями (3.15) с коэффициентами (2.6). Группируя слагаемые по степеням тензора деформации ${\mathbf{S}}$, для компонент тензора Кирхгофа получаем:

(4.1)
$\begin{gathered} {{P}_{1}} = \left( {\lambda + 2\mu } \right){{S}_{1}} + \lambda \left( {{{S}_{2}} + {{S}_{3}}} \right) + {{B}_{{21}}} + {{B}_{{31}}} \\ {{P}_{2}} = \left( {\lambda + 2\mu } \right){{S}_{2}} + \lambda \left( {{{S}_{1}} + {{S}_{3}}} \right) + {{B}_{{22}}} + {{B}_{{32}}} \\ {{P}_{3}} = \left( {\lambda + 2\mu } \right){{S}_{3}} + \lambda \left( {{{S}_{1}} + {{S}_{2}}} \right) + {{B}_{{23}}} + {{B}_{{33}}} \\ \end{gathered} $

Если в представлении (2.4) удержать слагаемые с упругими модулями II и III порядков, то для ${{\chi }_{1}},{{\chi }_{2}},{{\chi }_{3}}$, согласно выражениям (2.6), получим:

${{\chi }_{1}} = \lambda {{I}_{1}} + \frac{1}{2}{{\beta }_{1}}I_{1}^{2} + {{\beta }_{2}}{{I}_{2}},\quad {{\chi }_{2}} = \mu + {{\beta }_{2}}{{I}_{1}},\quad {{\chi }_{3}} = \frac{4}{3}{{\beta }_{3}}$
и ${{B}_{{3k}}} = 0$ $\left( {k = 1,2,3} \right)$ в выражениях (4.1).

При сохранении в упругом потенциале (2.4) только слагаемых с модулями II порядка коэффициенты ${{\chi }_{1}},{{\chi }_{2}},{{\chi }_{3}}$ равны:

${{\chi }_{1}} = \lambda {{I}_{1}},\quad {{\chi }_{2}} = \mu ,\quad {{\chi }_{3}} = 0;\quad {{B}_{{2k}}} = {{B}_{{3k}}} = 0,\quad k = 1,2,3$

Компоненты тензора напряжений Кирхгофа в этом случае линейно связаны с компонентами тензора деформации Коши–Грина.

Слагаемые ${{B}_{{2k}}}$ и ${{B}_{{3k}}}$ $\left( {k = 1,2,3} \right)$ позволяют учитывать в соотношениях (4.1) влияние упругих модулей высших порядков:

(4.2)
$\begin{gathered} {{B}_{{21}}} = {{\zeta }_{2}}S_{1}^{2} + 2{{\zeta }_{1}}{{S}_{1}}\left( {{{S}_{2}} + {{S}_{3}}} \right) + {{\zeta }_{1}}(S_{2}^{2} + S_{3}^{2}) + {{\beta }_{1}}{{S}_{2}}{{S}_{3}} \\ {{B}_{{22}}} = {{\zeta }_{2}}S_{2}^{2} + 2{{\zeta }_{1}}{{S}_{2}}\left( {{{S}_{1}} + {{S}_{3}}} \right) + {{\zeta }_{1}}(S_{1}^{2} + S_{3}^{2}) + {{\beta }_{1}}{{S}_{1}}{{S}_{3}} \\ {{B}_{{23}}} = {{\zeta }_{2}}S_{3}^{2} + 2{{\zeta }_{1}}{{S}_{3}}\left( {{{S}_{1}} + {{S}_{2}}} \right) + {{\zeta }_{1}}(S_{1}^{2} + S_{2}^{2}) + {{\beta }_{1}}{{S}_{1}}{{S}_{2}} \\ {{\zeta }_{1}} = \frac{{{{\beta }_{1}}}}{2} + {{\beta }_{2}},\quad {{\zeta }_{2}} = \frac{{{{\beta }_{1}}}}{2} + 3{{\beta }_{2}} + 4{{\beta }_{3}} \\ \end{gathered} $
(4.3)

Выражения (4.1) представляют собой систему трех, в общем случае нелинейных, уравнений относительно трех неизвестных: $\left\{ {{{S}_{1}},{{S}_{2}},{{S}_{3}}} \right\}$, $\left\{ {{{P}_{1}},{{P}_{2}},{{P}_{3}}} \right\}$ или их сочетаний в зависимости от способа задания начального напряженно-деформированного состояния. При комбинированном задании начального состояния известной предполагается деформация вдоль одной оси (например, ${{v}_{1}}$) и два условия на напряжения. Деформации и напряжения вдоль других осей определяются из системы (4.1). Далее исследованы влияния предварительных напряжений при следующих видах начальных состояний $\left( {i,j,k = 1,2,3;i \ne j \ne k} \right)$:

$1{{x}_{i}} \Rightarrow \quad {{P}_{i}} = P,\quad {{P}_{j}} = {{P}_{k}} = 0$ (одноосное)
$2{{x}_{i}} \Rightarrow \quad {{P}_{i}} = 0,\,\quad {{P}_{j}} = {{P}_{k}} = P$ (двухосное)
$3{{x}_{i}} \Rightarrow \quad {{P}_{i}} = P,\,\quad {{P}_{j}} = {{P}_{k}} = G$ (трехосное, несимметричное)
$3x \Rightarrow \quad {{P}_{1}} = {{P}_{2}} = {{P}_{3}} = P$ (трехосное, гидростатическое)

В качестве материала использовано металлическое стекло со следующими параметрами [22]:

$\begin{gathered} \rho = 9300\,{\text{к г /}}{{{\text{м }}}^{{\text{3}}}},\quad \lambda = 145.3\,{\text{Г П а }},\quad \mu = 35.8\,{\text{Г П а }} \\ {{\beta }_{1}} = - 227\,{\text{Г П а }},\quad {{\beta }_{2}} = - 234\,{\text{Г П а }},\quad {{\beta }_{3}} = - 81.8\,{\text{Г П а }} \\ {{\gamma }_{1}} = - 105828\,{\text{Г П а }},\quad {{\gamma }_{2}} = 1555.6\,{\text{Г П а }},\quad {{\gamma }_{3}} = 181\,{\text{Г П а }},\quad {{\gamma }_{4}} = - 298\,{\text{Г П а }} \\ \end{gathered} $

Упругие коэффициенты и начальные напряжения в приведенных ниже численных результатах отнесены к модулю сдвига $\mu $ изотропного материала в естественном состоянии (далее штрихи опущены)

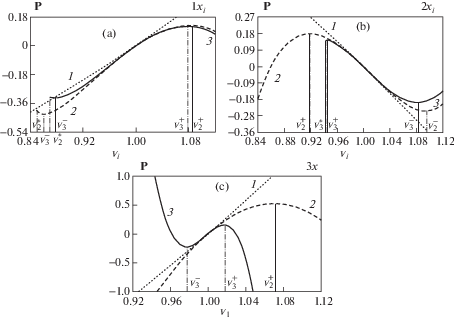
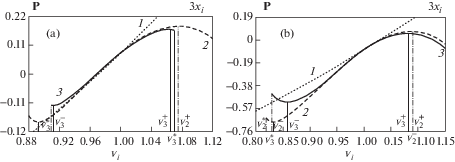
$P{\text{'}} = P{\text{/}}\mu ,\quad G{\text{'}} = G{\text{/}}\mu ,\quad C_{{ijkl}}^{{*'}} = C_{{ijkl}}^{*}{\text{/}}\mu $

На фиг. 1 и 2 приведены эпюры начальных напряжений, необходимых для достижения требуемой деформации, рассчитанные без учета модулей высших порядков (${{B}_{{2k}}} = {{B}_{{3k}}} = 0$, $k = 1,2,3$; пунктирные линии, кривые 1), с учетом упругих модулей III порядка (${{B}_{{2k}}} \ne 0,\;{{B}_{{3k}}} = 0$, штриховые линии, кривые 2) и с учетом модулей упругости III и IV порядков (${{B}_{{2k}}} \ne 0,\;{{B}_{{3k}}} \ne 0$, сплошные линии, кривые 3). На фиг. 1 представлены эпюры напряжений, рассчитанные для одноосных (1xi, фиг. 1, a), двухосных (2xi, фиг. 1, b) и гидростатического (3x, фиг. 1, c) состояний соответственно. Фиг. 2 иллюстрирует влияние учета модулей высших порядков на поведение напряжений для трехосных (3xi) состояний, осложненных наличием постоянной статической составляющей G, равной 0.1 (фиг. 2, a) и –0.1 (фиг. 2, b). Как следует из графиков, присутствие констант высших порядков приводит к значительной нелинейности зависимости “напряжения–деформации”. Символами $v_{k}^{*}$ на фиг. 1 и 2 обозначены критические значения удлинений соответствующих кривой k $\left( {k = 2,3} \right)$, при которых начальные напряжения становятся комплекснозначными. Символами $v_{k}^{ - }$ и $v_{k}^{ + }$ обозначены значения, при которых напряжения достигают локального минимума $P_{k}^{ - }$ или максимума $P_{k}^{ + }$, соответственно. В диапазоне $[v_{k}^{ - },v_{k}^{ + }]$ выполняется условие взаимно однозначного соответствия “напряжения–деформации”, что свидетельствует о выполнении в этом диапазоне критерия $\sigma _{{ii}}^{0} \Leftrightarrow \left( {{{x}_{3}},{{v}_{i}}} \right)$ [5], определяющего внутреннюю устойчивость материала. Как следует из графиков, наличие констант высших порядков ограничивает диапазон удлинений, при которых материал сохраняет устойчивость. Учет констант IV порядка в большей степени сужает диапазон устойчивости. Наиболее чувствительным к потере устойчивости является 9-ти константный материал в гидростатическом состоянии.

Фиг. 1
Фиг. 2

5. Влияние модулей высших порядков на свойства преднапряженного ПИУТ. В качестве тензора напряжений в предварительно напряженном упругом теле выступает тензор ${{{\mathbf{D}}}^{ \bullet }}$ (3.19) – линеаризованный тензор Пиола, участвующий в уравнениях движения (3.21) с граничными условиями (3.9), (3.22)–(3.25) в зависимости от задачи и типа среды. Влияние начальных напряжений на свойства первоначально изотропного материала отражают коэффициенты $C_{{ijkl}}^{*}$ (3.20). Перепишем их в следующем в виде [11]:

(5.1)
$C_{{ijkl}}^{*} = {{\delta }_{{jk}}}{{P}_{i}} + C_{{ijkl}}^{ \times }{{v}_{j}}{{v}_{k}},\quad i,j,k,l = 1,2,3$
Здесь $C_{{ijkl}}^{ \times }$ зависят от свойств материала и характера начальных воздействий

(5.2)
$\begin{gathered} C_{{iiii}}^{ \times } = \lambda + 2\mu + 4\left( {{{\beta }_{2}} + 2{{\beta }_{3}}} \right){{S}_{i}} + \left( {{{\beta }_{1}} + 2{{\beta }_{2}}} \right){{I}_{1}} + 4\left( {\frac{7}{3}{{\gamma }_{3}} + {{\gamma }_{4}}} \right)S_{i}^{2} + \\ + \;4\left( {{{\gamma }_{2}} + 2{{\gamma }_{3}}} \right){{I}_{1}}{{S}_{i}} + \left( {\frac{1}{2}{{\gamma }_{1}} + {{\gamma }_{2}}} \right)I_{1}^{2} + \left( {{{\gamma }_{2}} + 2{{\gamma }_{4}}} \right){{I}_{2}} \\ C_{{ijij}}^{ \times } = C_{{ijji}}^{ \times } = \mu + 2{{\beta }_{3}}\left( {{{S}_{i}} + {{S}_{j}}} \right) + {{\beta }_{2}}{{I}_{1}} + 2{{\gamma }_{3}}{{I}_{1}}\left( {{{S}_{i}} + {{S}_{j}}} \right) + {{\gamma }_{4}}{{I}_{2}} + \frac{1}{2}{{\gamma }_{2}}I_{1}^{2} \\ C_{{iijj}}^{ \times } = \lambda + 2{{\beta }_{2}}\left( {{{S}_{i}} + {{S}_{j}}} \right) + {{\beta }_{1}}{{I}_{1}} + \frac{4}{3}{{\gamma }_{3}}(4S_{i}^{2} + 3S_{j}^{2}) + 2{{\gamma }_{2}}\left( {{{S}_{i}} + {{S}_{j}}} \right){{I}_{1}} + \\ + \;4{{\gamma }_{4}}{{S}_{i}}{{S}_{j}} + {{\gamma }_{2}}{{I}_{2}} + \frac{1}{2}{{\gamma }_{1}}I_{1}^{2},\quad i,j = 1,2,3,\quad i \ne j \\ \end{gathered} $

Все остальные коэффициенты $C_{{ijkl}}^{ \times }$ равны нулю.

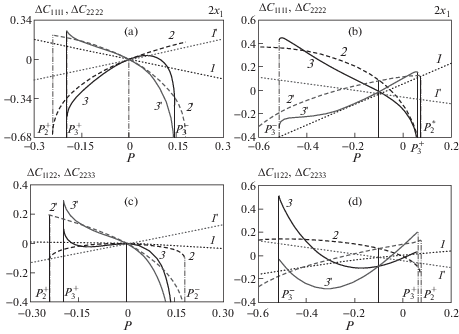
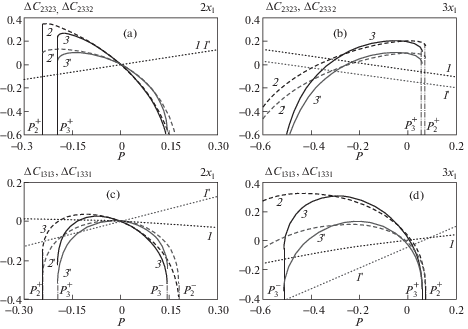
Фиг. 3 и 4 иллюстрируют влияние деформации на четыре типа упругих коэффициентов в предварительно напряженном теле. На рисунках представлена зависимость $\Delta {{C}_{{ijkl}}}$ ($\Delta {{C}_{{ijkl}}} = (C_{{ijkl}}^{*} - C_{{ijkl}}^{0}){\text{/}}C_{{ijkl}}^{0}$, где $C_{{ijkl}}^{0}$ – значения упругих модулей в естественном состоянии) от величины начальных напряжений для $C_{{iiii}}^{*},\,\,C_{{iijj}}^{*}$ (фиг. 3) и $C_{{ijij}}^{*},\,\,C_{{ijji}}^{*}$ (фиг. 4) при двухосном ($2{{x}_{1}}$, фиг. a и c) и трехосном ($3{{x}_{1}}$,$G = - 0.1$, фиг. b и d) начальных воздействиях. Как и ранее, учет упругих модулей II порядка, II и III, а также II, III и IV порядков отмечены на фигурах пунктирными (кривые 1), штриховыми (кривые 2) и сплошными (кривые 3) линиями, соответственно. Кривые с отметками 1, 2, 3 и 1', 2', 3' на фиг. 3, a, b соответствуют $\Delta C_{{1111}}^{{}}$ и $\Delta C_{{2222}}^{{}}$, на фиг. 3, c, d – $\Delta C_{{1122}}^{{}}$ и $\Delta C_{{2233}}^{{}}$, на фиг. 4, a, b – $\Delta C_{{2323}}^{{}}$ и $\Delta C_{{2332}}^{{}}$, на фиг. 4, c, d – $\Delta C_{{1313}}^{{}}$ и $\Delta C_{{1331}}^{{}}$.

Фиг. 3
Фиг. 4

Как видно из фиг. 3, 4 даже в области линейности по начальным напряжениям учет модулей высших порядков в предварительно напряженном теле приводит к существенным изменениям в поведении $C_{{ijkl}}^{*}$. Однако, при всех различиях в поведении $C_{{ijkl}}^{*}$ следует отметить, что при одноосных, двухосных и гидростатическом начальных напряженных состояниях пересечения $\Delta C_{{iiii}}^{{}}$, $\Delta C_{{iijj}}^{{}}$, $\Delta C_{{ijji}}^{{}}$ и $\Delta C_{{ijij}}^{{}}$ с учетом различных приближений происходит в нуле (P = 0, фиг. 3 и 4, a, c). При этом значение P = 0 отвечает естественному состоянию. В случае несимметричного трехосного напряженного состояния ($3{{x}_{1}},\,\,G = \pm 0.1$) или трехосного состояния общего вида значение P = 0 не соответствует естественному состоянию материала. Пересечение пар $\Delta C_{{1111}}^{{}}$ и $\Delta C_{{2222}}^{{}}$, $\Delta C_{{1122}}^{{}}$ и $\Delta C_{{2233}}^{{}}$, $\Delta C_{{2323}}^{{}}$ и $\Delta C_{{2332}}^{{}}$, $\Delta C_{{1313}}^{{}}$ и $\Delta C_{{1331}}^{{}}$ в случае $3{{x}_{1}},\,\,G = - 0.1$ происходит в некотором деформированном состоянии ($P \ne 0$, фиг. 3 и 4, b, d), значения в точках пересечения отлично от нуля и зависит как от характера начального напряженного состояния, так и от констант, учитываемых в соответствующих приближениях.

6. Линейное приближение. В случае малых начальных деформаций используется линейное приближение для инвариантов меры деформации:

${{v}_{k}} = 1 + {{\delta }_{k}},\quad v_{k}^{2} = 1 + 2{{\delta }_{k}},\quad {{v}_{k}}{{v}_{i}} = 1 + {{\delta }_{k}} + {{\delta }_{i}},\quad i,k = 1,2,3,\quad i \ne k$
${{S}_{k}} = {{\delta }_{k}},\quad {{I}_{1}} = s = {{\delta }_{1}} + {{\delta }_{2}} + {{\delta }_{3}},\quad {{I}_{2}} = {{I}_{3}} = 0$

Коэффициенты ${{\chi }_{k}}$ (2.6) и ${{\chi }_{{km}}}$ (3.17) $\left( {k,m = 1,2,3} \right)$ в линейном приближении выражаются формулами

$\begin{gathered} {{\chi }_{1}} = \lambda s,\quad {{\chi }_{2}} = \mu + {{\beta }_{2}}s,\quad {{\chi }_{3}} = \frac{4}{3}\left( {{{\beta }_{3}} + {{\gamma }_{3}}s} \right),\quad {{\chi }_{{11}}} = \lambda + {{\beta }_{1}}s \\ {{\chi }_{{12}}} = {{\chi }_{{21}}} = {{\beta }_{2}} + {{\gamma }_{2}}s,\quad {{\chi }_{{22}}} = {{\gamma }_{4}},\quad {{\chi }_{{13}}} = {{\chi }_{{31}}} = \frac{4}{3}{{\gamma }_{3}},\quad {{\chi }_{{23}}} = {{\chi }_{{32}}} = {{\chi }_{{33}}} = 0 \\ \end{gathered} $

Компоненты тензора Кирхгофа (2.5) имеют простой вид:

${{P}_{k}} = \lambda s + 2\mu {{\delta }_{k}},\quad k = 1,2,3$

Коэффициенты $C_{{ijkl}}^{*}$, входящие в выражения для компонент линеаризованного тензора напряжений Пиола (3.19), (3.20), при малых начальных деформациях записываются следующим образом $\left( {i,j = 1,2,3,i \ne j} \right)$:

(6.1)
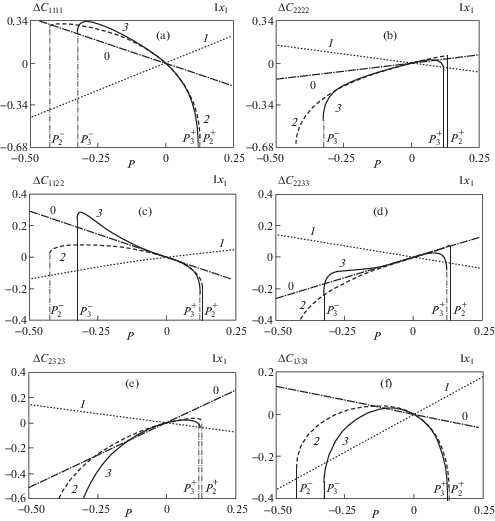
$\begin{gathered} C_{{iiii}}^{*} = {{P}_{i}} + \left( {\lambda + 2\mu } \right)\left( {1 + 2{{\delta }_{i}}} \right) + {{\beta }_{1}}s + 4{{\beta }_{2}}{{\delta }_{i}},\quad C_{{ijij}}^{*} = \mu + \left( {\mu + 2{{\beta }_{3}}} \right)\left( {{{\delta }_{i}} + {{\delta }_{j}}} \right) \\ C_{{iijj}}^{*} = \lambda + {{\beta }_{1}}s + \left( {\lambda + 2{{\beta }_{2}}} \right)\left( {{{\delta }_{i}} + {{\delta }_{j}}} \right),\quad C_{{ijji}}^{*} = {{P}_{i}} + \mu \left( {1 + 2{{\delta }_{j}}} \right) + 2{{\beta }_{3}}\left( {{{\delta }_{i}} + {{\delta }_{j}}} \right) \\ \end{gathered} $

На фиг. 5 показано влияние учета нелинейности деформации на различные свойства преднапряженного материала при одноосном (1x1) начальном воздействии. Как и на предыдущих графиках здесь представлены относительные изменения коэффициентов $\Delta C_{{ijkl}}^{{}}$, рассчитанных с учетом лишь упругих модулей II порядка (кривые 1), II и III порядков (кривые 2), и II, III и IV порядков (кривые 3), в зависимости от величины начальных напряжений. Цифрой 0 отмечены линейные по деформации приближения коэффициентов (6.1).

Фиг. 5

Из графиков следует, что чувствительность коэффициентов $C_{{ijkl}}^{*}$ к нелинейности деформации заметно различается, однако для большинства коэффициентов существует область малых деформаций, в которой нелинейностью можно пренебречь. Таким образом, при оценке динамических, эксплуатационных и прочностных характеристик деталей, выполненных из искусственных высокотехнологичных материалов, работающих под воздействием различного рода нагрузок, при решении широкого круга прикладных задач, а также задач контактного взаимодействия необходимо сочетать максимально точный учет свойств материала с возможностью получения достаточно простых и эффективных в использовании решений.

7. Заключение. В терминах отсчетной конфигурации проведена линеаризация уравнений нелинейной механики деформируемого твердого тела в окрестности некоторого преднапряженного состояния равновесия. Использовалось специальное представление упругого потенциала через алгебраические инварианты тензора деформации Коши–Грина, содержащее модули высших порядков. Построены линеаризованные определяющие соотношения и уравнения движения, учитывающие нелинейное влияние начальных деформаций на свойства ПИУТ. Исследовано влияние различных видов больших начальных деформаций на упругие коэффициенты первоначально изотропного материала. Показано значительное расхождение в поведении упругих модулей для предварительно напряженных двух-, пяти- и девятиконстантных материалов. При малых начальных деформациях для большей части упругих коэффициентов различия между линейным по деформации и нелинейными, связанными с учетом модулей высших порядков, приближениями в случае простых начальных воздействий незначительны. При сложных воздействиях разница в поведении коэффициентов становится существенной. Анализ показал, что использование линейного приближения при исследовании влияния начальных воздействий на упругие свойства первоначально изотропного материала более предпочтительно, чем использование модели двухконстантного материала.

Работа выполнена при финансовой поддержке Российского научного фонда (грант 14-19-01676) и Миннауки и высшего образования РФ (проект 01201354242).

Список литературы

  1. Трусделл К. Первоначальный курс рациональной механики сплошных сред. М.: Мир, 1975. 592 с.

  2. Maugin G.A. Continuum Mechanics of Electromagnetic solids. Elsevier science publishers. Amsterdam, New York, Oxford, Tokyo, 1968. 598 p.

  3. Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980. 512 с.

  4. Красильников В.А., Крылов В.В. Введение в физическую акустику. М.: Наука, 1984. 403 с.

  5. Murnaghan F.D. Finite deformations of an elastic solid // Am. J. of Math. 1937. V. 59. № 2. P. 235–260.

  6. Hughes D.S., Kelly J.L. Second-Order Elastic Deformation of Solids // Phys. Rev. 1953. V. 92. № 5. P. 1145–1149.

  7. Thurston R.N., Brugger K. Third-order elastic constants and the velocity of small amplitude elastic waves in homogeneously stressed media // Phys. Rev. 1964. V. 133. № 6A. P. A1604–A1610.

  8. Smith R.T., Stern R., Stephens R.W.B. Third-order elastic moduli of polycrystal line metals from ultrasonic velocity measurements // J. Acoust. Soc. Amer. 1966. V. 40. № 5. P. 1002–1008.

  9. Секоян С.С. О вычислении констант упругости третьего порядка по результатам ультразвуковых измерений // Акуст. журн. 1970. Т. 16. № 3. С. 453–457.

  10. Бакулин В.Н., Протосеня А.Г. О наличии нелинейных эффектов при распространении упругих волн в горных породах // ДАН СССР. 1982. Т. 263. № 2. С. 314–316.

  11. Калинчук В.В., Белянкова Т.И. Динамические контактные задачи для предварительно напряженных тел. М.: Физматлит, 2008. 240 с.

  12. Hayes M., Rivlin R.S. Propagation of plane wave in an isotropic elastic material subjected to pure homogeneous deformation //Arch. Ration Mech. and Analysis. 1961. V. 8. № 1. P. 15–22.

  13. Калинчук В.В., Полякова И.Б. О вибрации штампа на поверхности предварительно напряженного полупространства // Прикл. механика. 1982. Т. 18. № 6. С. 22–27.

  14. Гузь А.Н. Упругие волны в телах с начальными напряжениями. Т. 1. Киев: Наук. думка, 1986. 376 с.

  15. Гузь А.Н. Упругие волны в телах с начальными напряжениями. Т. 2. Киев: Наук. думка, 1986. 536 с.

  16. Белянкова Т.И., Калинчук В.В. О взаимодействии осциллирующего штампа с предварительно напряженным полупространством // ПММ. 1993. Т. 57. Вып. 4. С. 123–134.

  17. Калинчук В.В., Белянкова Т.И. Динамика поверхности неоднородных сред. М.: Физматлит, 2009. 312 с.

  18. Белянкова Т.И., Калинчук В.В. Особенности локализации волнового поля в преднапряженном функционально-градиентном слое // Физика и механика материалов. 2015. Т. 23. № 1. С. 25–30.

  19. Белянкова Т.И., Калинчук В.В. Особенности локализации волнового поля в преднапряженном функционально-градиентном слое // Акустический журнал. 2017. Т. 63. № 3. С. 219–234.

  20. Destrade M., Ogden R.W. On the third- and fourth-order constants of incompressible isotropic elasticity // J. Acoust. Soc. Am. 2010. V. 128. № 6. P. 3334–3344.

  21. Shams M., Destrade M., Ogden R.W. Initial stresses in elastic solids: Constitutive laws and acoustoelasticity // Wave Motion. 2011. V. 48. P. 552–567.

  22. Кобелев Н.П., Колыванов Е.Л., Хоник В.А. Упругие модули высших порядков объемного металлического стекла Zr52.5Ti5Cu17.9Ni14.6Al10 // ФТТ. 2007. Т. 49. Вып. 7. С. 1153–1158.

  23. Kobelev N.P., Khonik V.A., Makarov A.S., Afonin G.V., Mitrofanov Yu.P. On the nature of heat effects and shear modulus softening in metallic glasses: A generalized approach // J. of Appl. Phys. 2014. V. 115. P. 033513.

  24. Кобелев Н.П., Колыванов Е.Л., Хоник В.А. Упругие модули высших порядков металлического стекла Pd40Cu30Ni10P20 // ФТТ. 2015. Т. 57. Вып. 8. С. 1457–1461.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал