Известия РАН. Механика твердого тела, 2019, № 5, стр. 86-103
МАКСИМУМЫ НАПРЯЖЕНИЙ В ПРОДОЛЬНЫХ ВОЛНАХ ПОХГАММЕРА–КРИ
В. В. Мокряков *
Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: mokr@ipmnet.ru
Поступила в редакцию 07.03.2019
После доработки 15.03.2019
Принята к публикации 21.03.2019
Аннотация
В статье представлен расчет полей напряжений, которые возникают в цилиндрических стержнях круглого сечения, в случае волн Похгаммера–Кри. Рассмотрены примеры расчета полей для четырех низших мод волн в стальном стержне для двух случаев фазовых скоростей. Построены и рассмотрены структуры изостат главных напряжений в продольном сечении стержня. Построены поля первого главного напряжения и напряжения фон Мизеса.
1. Введение. Цилиндрические стержни с круглым сечением являются широко распространенным конструкционным элементом. Для расчета прочности любой конструкции требуется найти ее напряженно-деформированное состояние, особенно наибольшие значения (максимальное растяжение и максимальный сдвиг). Напряжения возникают не только от статических нагрузок, но и от вибраций, поэтому необходимо изучать напряженно-деформированное состояние, вызываемое упругими волнами.
Уравнения, описывающие поведение упругих волн в стержне круглого сечения, и дающие дисперсионные соотношения (отношение частоты к волновому числу) получили Похгаммер [1] и Кри [2, 3]. Численные решения уравнения были получены позже, в работах [4–14] и др., где были рассмотрены продольные осесимметричные, изгибные и крутильные моды.
Сейчас развитие этой задачи идет по нескольким направлениям: изменение геометрии (замена цилиндра на цилиндрическую полость, трубу или другую осесимметричную конструкцию), изменение свойств материала (замена упругого материала на упруго-вязкий, термоупругий), изменение распределения свойств конструкции (замена однородности на неоднородность, изотропности на анизотропность). Недавние работы [16–23] могут служить примерами описанных исследований.
Как видно из представленных работ, рассматриваются амплитудно-частотные характеристики круглых стержней. Поэтому в данной работе фокус исследования перенесен на прочностные свойства стержней в условиях вибрации, на структуру полей напряжений. Особое внимание уделено локализации максимальных величин напряжений (наибольшему растяжению и напряжению фон Мизеса).
В данной работе рассмотрен расчет напряженно-деформированного состояния в бесконечном цилиндрическом стержне круглого сечения в условиях продольной волны Похгаммера–Кри. Рассмотрены поля напряжений для первых мод волн для двух заданных фазовых скоростей.
2. Постановка задачи. Рассматривается бесконечный стержень радиусом a. Материал стержня имеет плотность ρ, модуль Юнга E, коэффициент Пуассона ν.
Поверхность стержня свободна от нагрузок.
Исследуются поля напряжений (с учетом главных напряжений и напряжения фон Мизеса), возбуждаемых продольными волнами Похгаммера–Кри.
3. Дисперсионное соотношение. Введем следующие обозначения:
ω – частота волны; γ – волновое число; c = ω/γ – фазовая скорость волны; c0 = = $\sqrt {{E \mathord{\left/ {\vphantom {E \rho }} \right. \kern-0em} \rho }} $ – скорость бесконечно длинных волн в бесконечном стержне; c1 = $\sqrt {{{\left( {\lambda + 2\mu } \right)} \mathord{\left/ {\vphantom {{\left( {\lambda + 2\mu } \right)} \rho }} \right. \kern-0em} \rho }} $ – скорость волн расширения в бесконечной среде; ${{c}_{2}} = \sqrt {{\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-0em} \rho }} $ – скорость волн сдви-га в бесконечной среде; cR – скорость волн Рэлея (поверхностных волн в полупространстве).
Также в формулах будем использовать следующие выражения: $h = \omega \sqrt {{1 \mathord{\left/ {\vphantom {1 {c_{1}^{2}}}} \right. \kern-0em} {c_{1}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} $, $\kappa = \omega \sqrt {{1 \mathord{\left/ {\vphantom {1 {c_{2}^{2}}}} \right. \kern-0em} {c_{2}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} $
(3.1)
$H = {{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {c_{1}^{2}}}} \right. \kern-0em} {c_{1}^{2}}} - 1 = {{{{h}^{2}}{{c}^{2}}} \mathord{\left/ {\vphantom {{{{h}^{2}}{{c}^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}},$ $K = {{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {c_{2}^{2}}}} \right. \kern-0em} {c_{2}^{2}}} - 1 = {{{{\kappa }^{2}}{{c}^{2}}} \mathord{\left/ {\vphantom {{{{\kappa }^{2}}{{c}^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}$Кроме того, запишем известные тождества для функций Бесселя, которые будем использовать в дальнейшем:
(3.2)
$2n{{J}_{n}}\left( x \right) = x\left( {{{J}_{{n - 1}}}\left( x \right) + {{J}_{{n + 1}}}\left( x \right)} \right),$ $2J_{n}^{'}\left( x \right) = {{J}_{{n - 1}}}\left( x \right) - {{J}_{{n + 1}}}\left( x \right)$Общее решение волны Похгаммера–Кри часто представляют в комплексной форме [7]:
Продифференцировав, получим
Чтобы получить поля деформаций и напряжений, нужно общее решение в комплексной форме перевести в действительную. Для этого нужно объединить действительную и мнимую части решения в линейную комбинацию, введя фазу φ:
Дисперсионное соотношение получаем исходя из граничных условий – поверхность стержня должна быть свободная от нагрузок:
Приравняв r = a, получим
или
Отсюда
Последнее равенство представляет собой дисперсионное соотношение, т.е. связь частоты ω с волновым числом γ (или с фазовой скоростью c, заменив $\gamma = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}$).
Запишем это выражение через c1 и c2, и раскроем J1 через J0 и J2.
Здесь необходимо отметить, что при c = c2 (т.е. κ = 0) оба числителя отношения становятся равны нулю, что приводит к вырождению уравнения.
Комплекс ${{\kappa c} \mathord{\left/ {\vphantom {{\kappa c} \omega }} \right. \kern-0em} \omega }$ перенесем в константу C.
Тогда запишем дисперсионное соотношение так:
Так перепишем формулы для смещений.
или
то есть
Используя дисперсионное соотношение, введем величину U:
Тогда можем записать:
Отсюда смещения:
Это выражение можно записать короче:
(3.3)
$\begin{gathered} {{u}_{r}} = 2U\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}\frac{H}{a}\left[ {\left( {K - 1} \right)\frac{{{{J}_{1}}\left( {\kappa a} \right)}}{\kappa }\frac{{{{J}_{1}}\left( {hr} \right)}}{h} + 2\frac{{{{J}_{1}}\left( {ha} \right)}}{h}\frac{{{{J}_{1}}\left( {\kappa r} \right)}}{\kappa }} \right]\sin \left( {\gamma z - \omega t + \varphi } \right) \\ {{u}_{z}} = 2U\frac{\omega }{{ca}}\left[ {\left( {1 - K} \right)\frac{{{{J}_{1}}\left( {\kappa a} \right)}}{\kappa }{{J}_{0}}\left( {hr} \right) + 2H\frac{{{{J}_{1}}\left( {ha} \right)}}{h}{{J}_{0}}\left( {\kappa r} \right)} \right]\cos \left( {\gamma z - \omega t + \varphi } \right) \\ \end{gathered} $Только нужно помнить, что при h = 0 или κ = 0 следует переходить к пределу, как это сказано выше.
4. Расчет напряженного состояния. Из (3.3) получаем компоненты тензора деформаций в осесимметричной изотропной задаче:
Таким образом, получаем первый инвариант деформаций:
Зная тензор деформаций, получаем компоненты тензора напряжений:
Формулы деформаций и напряжений для более общей задачи можно найти в монографии [15].
5. Расчет средней плотности энергии. Представим плотность полной энергии как сумму плотностей кинетической и упругой энергии:
Обозначим длину волны как $l = 2\pi {c \mathord{\left/ {\vphantom {c \omega }} \right. \kern-0em} \omega }$. Тогда средняя плотность энергии будет иметь следующий вид:
С учетом осесимметричности, плотность кинетической энергии равна
Отсюда получаем
Поскольку интегралы по dz равны l/2, то, учитывая (3.1), получаем:
Используем известные формулы интегрирования [24, 25]:
В итоге получаем
Плотность упругой энергии имеет следующий вид:
Получаем
Найдем интегралы:
Представив постоянные Ламе через фазовую скорость
Обращаем внимание, что выражения типа ${{{{J}_{1}}\left( x \right)} \mathord{\left/ {\vphantom {{{{J}_{1}}\left( x \right)} x}} \right. \kern-0em} x}$, ${{{{J}_{2}}\left( x \right)} \mathord{\left/ {\vphantom {{{{J}_{2}}\left( x \right)} {{{x}^{2}}}}} \right. \kern-0em} {{{x}^{2}}}}$ приводят к неопределенности при $x \to 0$. Вычислить их можно, используя (3.2):
Итак, получаем полную среднюю плотность энергии:
Это выражение позволяет выбрать амплитуду U такой, чтобы величина средняя плотность энергии была заданной. Далее, во всех рассматриваемых волнах U такова, чтобы средняя плотность энергии была одна и та же – 1 Дж/м3.
6. Параметры модельной задачи. Рассмотрим бесконечный стальной стержень радиусом a = 1 см со следующими параметрами: плотность ρ = 7.8 × 103 кг/м3; модуль Юнга E = 2.0 × 1011 Па; коэффициент Пуассона ν = 0.28 (отсюда c0 = 5065.7 м/с, c1 = = 5725.3 м/с, c2 = 3164.8 м/с, cR = 2925.1 м/с).
Поверхность стержня свободна от нагрузок. Исследуются поля напряжений (с учетом главных напряжений и напряжения фон Мизеса), возбуждаемых продольными волнами Похгаммера–Кри. Средняя плотность энергии волны – 1 Дж/м3.
7. Примеры расчета. В данном разделе рассмотрены несколько характерных полей напряжений мод волн Погхаммера–Кри. Обозначим конкретную волну как (c, n), где c – ее фазовая скорость, а n – номер моды.
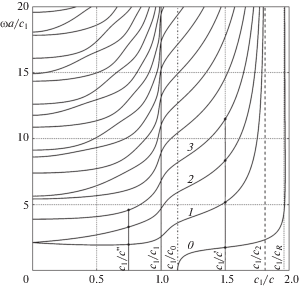
На рис. 1 представлено решение уравнения дисперсионного соотношения: по оси абсцисс – c1/c, безразмерная величина, обратно пропорциональная фазовой скорости, это позволяет охватить всю область определения; по оси ординат – ωa/c1, безразмерная величина, пропорциональная частоте.
Выбраны для рассмотрения два значения фазовой скорости. Первая скорость меньше c1, но больше с2: c' = 2/3 c1 ≈ 3.82 км/с; вторая больше с1: c'' = 4/3c1 ≈ 7.63 км/c. Эти значения достаточно далеки от значений особых скоростей (c0, c1, c2, cR). Для каждой выбранной скорости выбраны несколько частот, соответствующих модам от нулевой до третьей (в область определения нулевой моды попадает только скорость c'), величины частот ω (MГц) представлены в табл. 1. На рис. 1 жирные точки соответствуют рассматриваемым волнам, номера мод указаны цифрами рядом с соответствующими линиями.
На графиках, относящихся к волнам (c', 0), (c'', 1), (c'', 2), (c'', 3), представлен один период волны; на других ((c', 1), (c', 2), (c', 3)) – два периода. Горизонтальная ось (Oz) совпадает с осью цилиндра (т.е. на графиках представлено продольное сечение стержня), волна движется вдоль оси Oz. Шкалы осей указаны в миллиметрах. Ниже представлены поля смещений и напряжений для выбранных волн.
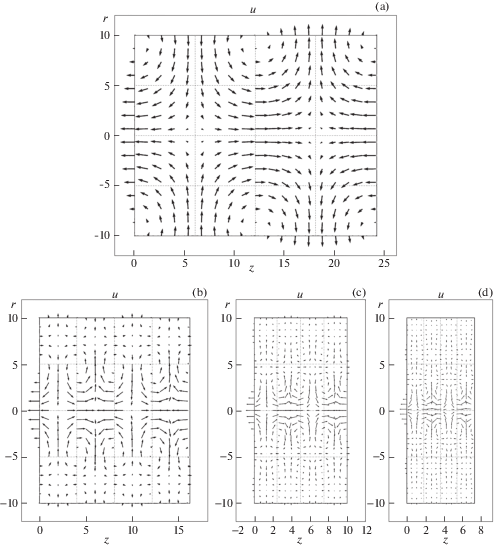
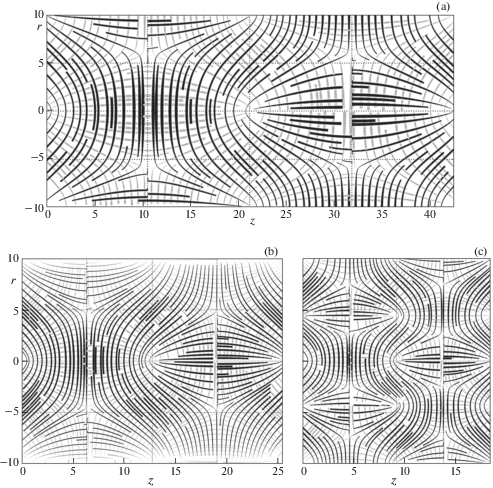
5.1. Смещения. На рис. 2a–2d представлены векторные поля смещений для фазовой скорости c' (на графике a – 0-я мода, b – 1-я, c – 2-я, d – 3-я). Аналогично, на рис. 3a–3c представлены поля для скорости c'' (a – 1-я мода, b – 2‑я, c – 3-я). Амплитуда величины смещений u (нм) представлены в табл. 2.
Рассмотрим смещения волн с фазовой скоростью c'. На графиках (рис. 2) видны периодические вихревые ячейки, закрученные взаимно-симметрично. При этом с увеличением номера моды (и величины частоты) характер движения материала в ячейках не меняется, но размер ячеек уменьшается пропорционально длине волны, и, соответственно, обратно пропорционально частоте. Также с увеличением номера моды волна все больше концентрируется в окрестности оси стержня.
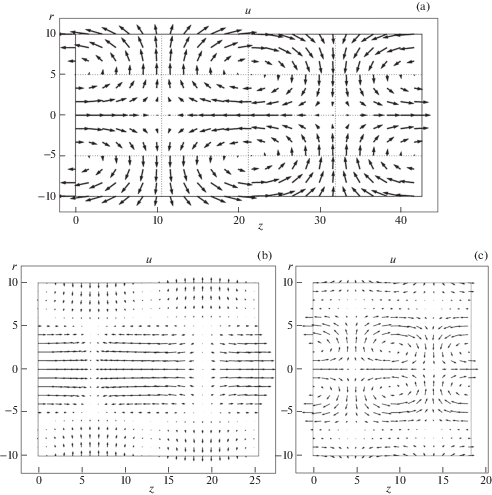
При сравнении с волнами (c', n), поля смещений в волнах (c'', n) существенно зависят от конкретной моды (рис. 3).
Структура поля смещений волны (c'', 1) похожа на структуры волны (c', 0), только ячейки вытянуты вдоль оси стержня, а не радиально.
В волне (c'', 2) структура поля смещений совершенно иная. Хорошо видны две области колебаний, на их границе (r ≈ 0.5a) смещения близки к нулю. Во внутренней области колебания среды близки к продольным, во внешней области – к радиальным.
Структура волны (c'', 3) также имеет разделение на внутреннюю и внешнюю области (граница между областями находится на r ≈ 0.75a). Структура внутренней области аналогична структуре поля волны (c'', 1), с поправкой на размер ячейки. Ячейки внешней области также имеют вихревой тип, но они не полные.
5.2. Изостаты. Поскольку рассматриваемая задача осесимметрична, одно из главных напряжений известно – это окружное напряжение σθθ. Остальные два главных напряжения перпендикулярны σθθ, то есть находятся в плоскости продольного сечения стержня и являются линейной комбинацией напряжений σrr и σzz. Обозначим эти два главных напряжения как σa и σb, при этом считаем, что σa ≥ σb. Здесь
Обозначим угол наибольшего растяжения как α (наибольшее растяжение вдоль оси стержня считается равным 0°, вдоль радиусов – 90°. Вычислить α можно с помощью формулы $\operatorname{tg} \alpha = {{\left( {{{\sigma }_{{rr}}} - {{\sigma }_{{zz}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\sigma }_{{rr}}} - {{\sigma }_{{zz}}}} \right)} {2{{\sigma }_{{rz}}}}}} \right. \kern-0em} {2{{\sigma }_{{rz}}}}} + \sqrt {{{1 + {{{\left( {{{\sigma }_{{rr}}} - {{\sigma }_{{zz}}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{1 + {{{\left( {{{\sigma }_{{rr}}} - {{\sigma }_{{zz}}}} \right)}}^{2}}} {4\sigma _{{rz}}^{2}}}} \right. \kern-0em} {4\sigma _{{rz}}^{2}}}} $, или в более простой форме tgα = ${{\left( {{{\sigma }_{a}} - {{\sigma }_{{zz}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\sigma }_{a}} - {{\sigma }_{{zz}}}} \right)} {{{\sigma }_{{rz}}}}}} \right. \kern-0em} {{{\sigma }_{{rz}}}}} = {{\left( {{{\sigma }_{{rr}}} - {{\sigma }_{b}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\sigma }_{{rr}}} - {{\sigma }_{b}}} \right)} {{{\sigma }_{{rz}}}}}} \right. \kern-0em} {{{\sigma }_{{rz}}}}}$.
Отсюда получаем поле единичных векторов, касающихся изостат σa
Для получения изостат σb нужно взять поле ортогональных векторов $\left( { - \sin \alpha ,\cos \alpha } \right)$.
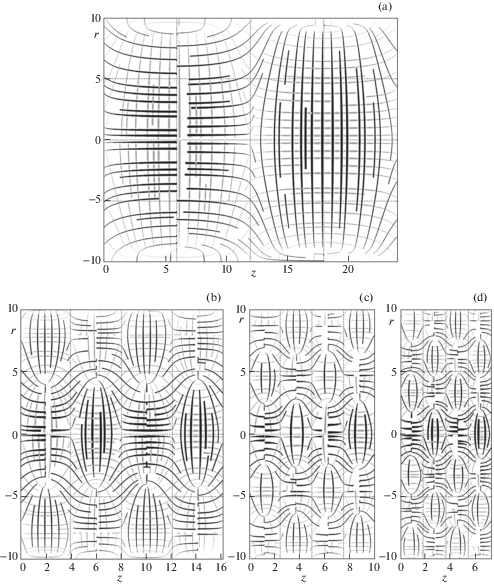
На рис. 4a–4d (c = c', моды n = 0–3), рис. 5a–5c (c = c'', моды n = 1–3) представлены изостаты – линии, касающиеся направлений главных напряжений в каждой точке. На рисунках черным цветом обозначены изостаты σa, серым – σb. Толщина изостат пропорциональны разнице главных напряжений σa – σb.
На рис. 4a для волны (c', 0) видно, как на каждой полуфазе стержень растягивается попеременно то вдоль, то поперек стержня. На графиках волн (c', 1–3) (рис. 4b–4d) хорошо видна периодическая структура не только вдоль оси стержня (z), но и вдоль радиуса (r). Размеры ячеек пропорциональны длине волны.
Для волн со скоростью c'' изостаты представлены на рис. 5a–5c (c = c'', n = 1–3). Периодическая структура изостат имеет место и в этом случае, размер ячеек также пропорционален длине волны, только ячейки вытянуты вдоль оси, а не по радиусу.
5.3. Первое главное напряжение σ1и напряжение фон Мизеса. Для расчета прочности конструкции требуются максимальное растяжение (σ1) и максимальный сдвиг (σMises) в каждой точке.
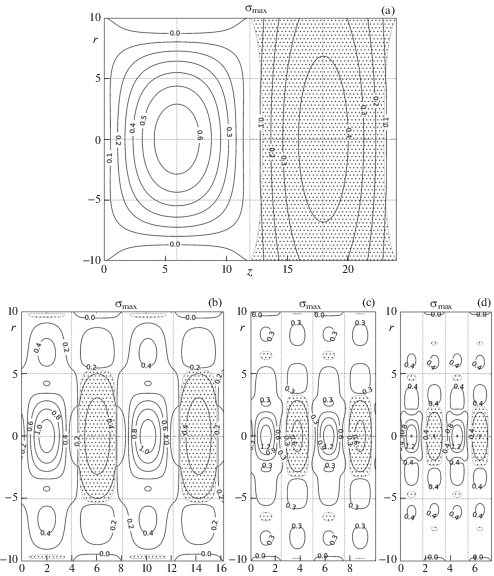
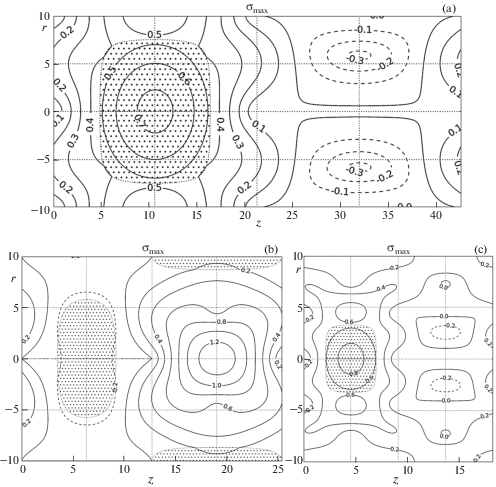
В данной задаче первое главное напряжение σ1 является наибольшим из σθθ и σa. Максимальная величина первого главного напряжения σI (МПа) для рассматриваемых волн представлена в табл. 3. На рис. 6a–6d (c = c', n = 0–3), рис. 7a–7c (c = c'', n = = 1–3) представлены поля первого главного напряжения для соответствующих волн. Штриховка показывает области, где σ1 = σθθ. В остальных областях σ1 = σa.
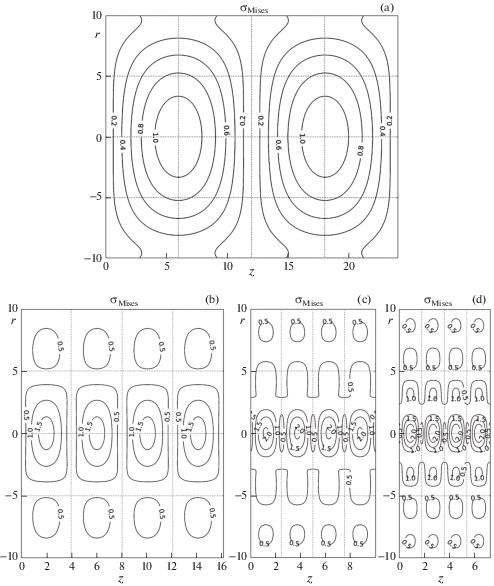
Напряжение фон Мизеса для осесимметричной задачи имеет вид
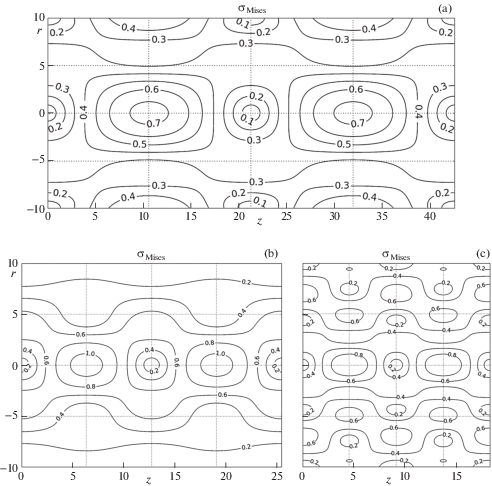
Максимальная величина σMises (МПа) для рассмотренных волн представлена в табл. 4. Поля напряжения фон Мизеса представлены на рис. 8a–8d (c = c', n = 0–3), рис. 9a–9c (c = c'', n = 1–3).
Обратим внимание, что наибольшие напряжения (и первое главное, и фон Мизеса) располагаются на оси стержня (для выбранных фазовых частот).
6. Заключение. Рассмотрен бесконечный упругий стержень круглого сечения, в котором возбуждены продольные волны Похгаммера–Кри.
Представлены формулы смещений, деформаций и напряжений для напряженно-деформированного состояния стержня. Рассмотрены напряженно-деформированные состояния для первых четырех мод волн Похгаммера–Кри (n = 0,..3), при двух значения фазовых скоростей c' = 2/3 · c1 ≈ 3.82 км/с и c'' = 4/3 · c1 ≈ 7.63 км/c. Построены поля смещений и картины изостат в продольном сечении стержня. Также рассчитаны поля первого главного напряжения и напряжения фон Мизеса.
Отмечено, что в рассмотренных волнах картина изостат для каждой заданной фазовой скорости имеет характерную структуру. Масштаб структуры пропорционален периоду продольной волны, то есть обратно пропорционален частоте волны. Также результаты показывают, что для рассмотренных фазовых скоростей наибольшие напряжения (и растягивающие, и сдвиговые) располагаются на оси стержня. То есть, для контроля прочности стержневых конструкций недостаточно знания напряжений на поверхности, так как разрушение может локализоваться в центре стержней.
Автор выражает благодарность профессору С.В. Кузнецову и профессору Ю.Н. Радаеву за ценные консультации.
Работа поддержана Программой РАН I.2.27 “Фундаментальные проблемы решения сложных практических задач с помощью суперкомпьютеров”.
Список литературы
Pochhammer L. Ueber die Fortpflanzungsgeschwindigkeiten kleiner Schwingungen in einem unbegrenzten isotropen Kreiscylinder // J. Reine Angew. Math. 1876. V. 81. S. 324–336.
Chree C. Longitudinal vibrations of a circular bar // Quart. J. Pure Appl. Math. 1886. V. 21. P. 287–298.
Chree. C. The equations of an isotropic elastic solid in polar and cylindrical coordinates, their solutions and applications // Trans. Cambridge Philos. Soc. 1889. V. 14. P. 250–309.
Field G.S. Velocity of sound in cylindrical rods // Canadian J. Research. 1931. V. 5. P. 619–624.
Shear S.K., Focke A.B. The dispersion of supersonic waves in cylindrical rods of polycrystalline silver, nickel, and magnesium // Phys. Rev. 1940. V. 57. P. 532–537.
Hudson G.E. Dispersion of elastic waves in solid circular cylinders // Phys. Rev. 1943. V. 63. P. 46–51.
Кольский Г. Волны напряжения в твердых телах. М.: Изд-во иностранной литературы, 1955. 194 с.
Redwood M., Lamb J. On propagation of high frequency compressional waves in isotropic cylinders // Proc. Phys. Soc. Section B. London.1957. V. 70. № 1. P. 136–143.
Onoe M., McNiven H.D., Mindlin R.D. Dispersion of axially symmetric waves in elastic rods // Trans. ASME J. Appl. Mech. 1962. V. 29. P. 729–734.
Hutchinson J.R., Percival C.M. Higher modes of longitudinal wave propagation in thin rod // J. Acoust. Soc. Amer. 1968. V. 44. P. 1204–1210.
Zemanek J. An experimental and theoretical investigation of elastic wave propagation in a cylinder // J. Acoust. Soc. Amer. 1972. V. 51. P. 265–283.
Graff K.F. Wave motion in elastic solids. New York: Dover, 1991. 692 p.
Abramson H.N. Flexural waves in elastic beams of circular cross section // J. Acoust. Soc. Amer. 1957. V. 29. P. 1284–1286.
Pao Y.-H., Mindlin R.D. Dispersion of flexural waves in an elastic, circular cylinders // Trans. ASME. J. Appl. Mech. 1960. V. 27. P. 513–520.
Ковалев В.А., Радаев Ю.Н. Волновые задачи теории поля и термомеханика. Саратов: Изд-во Саратовского университета, 2010. 340 с.
Ватульян А.О., Юров В.О. Волновые процессы в полом цилиндре в поле неоднородных предварительных напряжений // ПМТФ. 2016. Т. 57. № 4. С. 182–191.
Zhou W. et al. Guided torsional wave generation of a linear in-plane shear piezoelectric array in metallic pipes // Ultrasonics. 2016. V. 65. P. 69–77.
Муравьева О.В., Леньков С.В., Мурашов С.А. Крутильные волны, возбуждаемые электромагнитно-акустическими преобразователями, при акустическом волноводном контроле трубопроводов // Акустический журнал. 2016. Т. 62. № 1. С. 117–124.
Garcia-Sanchez D. et al. Acoustic confinement in superlattice cavities // Phys. Rev. A. 2016. V. 94. P. 033813-1–033813-6.
Othman R. A fractional equation to approximate wave dispersion relation in elastic rods // Strain. 2017. V. 53. № 4. e12228. P. 1–10.
Li Zh., Jing L., Murch R. Propagation of monopole source excited acoustic waves in a cylindrical high-density polyethylene pipeline // J. Acoust. Soc. Amer. 2017. V. 142. P. 3564–3579.
Zima B., Rucka M. Guided ultrasonic waves for detection of debonding in bars partially embedded in grout // Constr. Build. Mat. 2018. V. 168. P. 124–142.
Ilyashenko A.V., Kuznetsov S.V. Pochhammer–Chree waves: polarization of the axially symmetric modes // Arch. Appl. Mech. 2018. V. 88. № 8. P. 1385–1394.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз, 1962. 1100 с.
Ватсон Г.Н. Теория бесселевых функций. Часть 1. М.: Изд. иностранной литературы, 1949. 798 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела