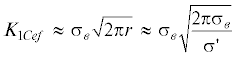Известия РАН. Механика твердого тела, 2019, № 5, стр. 70-85

1. Введение. Для ледяного покрова и других материалов (гипс, бетон, парафин и др.), характерно развитие структур разрушения в локальном и региональном масштабах. Это происходит в условиях взаимодействия процессов в сценариях разрушения, реализующихся в разных масштабах, отличающихся друг от друга на несколько порядков, что может влиять на параметры эффективной трещиностойкости. Обращаясь к области задач механики разрушения для таких систем, можно выделить наметившийся интерес к масштабной зависимости эффективной сопротивляемости развитию трещин.

Одним из базовых положений линейной механики разрушения является допущение о малости концевой области трещины (в частности, трещины нормального разрыва) по сравнению с размерами трещины, и ее автономности. Это предполагает независимость механизма локального деформирования и разрушения в этой области в состоянии предельного равновесия (во внутренней задаче теории трещин) от локальных условий нагружения и геометрии внешней задачи, масштаб которой задается размером трещины и границами тела. Такая постановка задачи дает возможность характеризовать напряженное состояние в вершине трещины нормального разрыва одним параметром – коэффициентом интенсивности напряжений, предельная величина которого (K_IC – для трещин нормального разрыва) характеризует сопротивляемость среды развитию трещин и является фиксируемым свойством материала. Вместе с тем существуют ситуации, в которых такие условия соблюдаются не для всех сценариев разрушения. К ним относится, в частности, изменение масштаба разрушения. Заметим, что влияние масштабного фактора на параметры прочности для таких материалов, как горные породы, бетон и лед являются объектом внимания достаточно давно [1]. Интерес к этой теме в последнее время связан, в том числе, с противоположными тенденциями в масштабных эффектах для различных свойств материалов – уменьшением удельной прочности при росте размеров нагружаемого тела и увеличением эффективной трещиностойкости в той же ситуации. Основные направления этих исследований обозначены в [2]. Отметим также недавнюю работу [3], в которой показанo масштабное изменение трещиностойкости снега.

2. Масштабные вариации при определении трещиностойкости морского льда. Рассмотрим имеющиеся данные об изменении эффективной трещиностойкости, связанные с изменением масштаба, на примере механики разрушения морского льда. Морской лед со столбчатозернистой структурой и порами, заполненными рассолом (тип S2 [4]) имеет несколько характерных масштабных уровней, которые влияют на развитие трещин в морском ледяном покрове, начиная с размера зерна и расстояния между капиллярными порами и дренажными каналами до размеров ледовых образований. Напряженное состояние в структуре льда при сжатии в масштабе окрестности одиночного капилляра близко к таковому в пластине с отверстием в однородно нагруженном упругом теле (плоская деформация). Такая система может служить отдельным структурным элементом, способным преобразовать приложенные к телу внешние напряжения. Модель разрушения пористого тела была в основных чертах предложена ранее [5–7]. Для большинства однородных и слабопористых материалов, для которых такое представление справедливо, характерно развитие трещин нормального разрыва вдоль оси нагружения на контуре пор [8]. Очаг разрушения образуется в области локальных растягивающих напряжений в окрестности контура отверстия радиуса (R) в направлении вдоль оси сжатия, что соответствует положению максимума нормальных упругих напряжений на контуре отверстия. В результате при внешнем сжатии в этой области образуется устойчиво развивающаяся трещина нормального разрыва (l). Разрушение происходит при слиянии трещин, растущих от соседних пор, когда величина L = l + R близка к половине среднего расстояния между порами. При таком условии в капиллярной структуре средняя пористость n может быть связана с соотношением размеров структуры.

Для оценки эффективной трещиностойкости морского льда в масштабе капиллярной пористой структуры ранее была предложена модель разрушения [9]. По условиям предельного равновесия симметричных микротрещин выходящих на контур одиночной поры взаимосвязь между прочностью при одноосном сжатии поперек оси капилляров и капиллярной пористостью может быть представлена в виде

где $K_{{IC}}^{*}$ – эффективный критический коэффициент интенсивности напряжений – трещиностойкость льда в масштабе единичной поры, n – капиллярная пористость.

Сравнение полученного выражения с эмпирическим соотношением, приведенным в [10] и [11] для столбчато-зернистого морского льда, сжатого поперек оси капилляров, показывает, что уровень эффективных значений $K_{{IC}}^{*} \approx 5\;кРа \cdot \sqrt м $.

Обратимся далее к экспериментальным данным критического коэффициента интенсивности напряжений – эффективной трещиностойкости льда ${{K}_{{1C}}}$ – при увеличении масштаба разрушения:

– При использовании малых (лабораторных) образцов (характерный размер L ~ ~ $0.05{\kern 1pt} - {\kern 1pt} 0.1$ м [9, 12, 13]) при температуре ∼ –10°С величина ${{K}_{{1С}}} \approx 60{\kern 1pt} - {\kern 1pt} 80\;кПа\sqrt м $. Образцы в этих испытаниях имели конфигурации, рекомендованные для конструкционных материалов.

– По данным испытаний, проведенных в [13, 14, 16], на фрагментах морского ледяного покрова толщиной до ∼1.8 м, при развитии трещин в льдинах с характерным размером в плане от 0.5 до 3 м величина ${{K}_{{1C}}}$ возрастает до значения ${{К}_{{1С}}}_{{ef}} \approx 250\;кПа\sqrt м $.

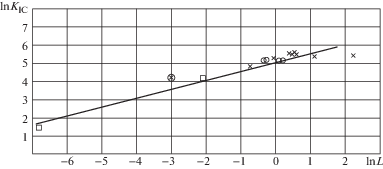
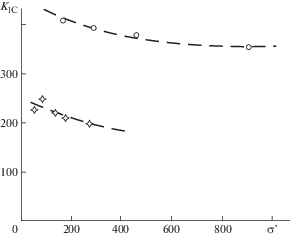
На рис. 1 в логарифмических координатах показана совокупность данных о влиянии масштаба разрушения на изменение эффективной трещиностойкости морского льда (□ – данные авторов [9, 12], – сводные данные из работ [14, 15]). Также отражено ограничение величины эффективной трещиностойкости при наибольших размерах образцов (в ситуации, когда размер плоского образца значительно больше его толщины ($L \gg h$)). При L > 10 м и $h \leqslant 0.8$ м трещиностойкость практически не меняется [13]. Далее будем интересоваться диапазоном условий, при которых проявляется зависимость эффективной трещиностойкости ${{K}_{{1C}}}$ от размера образца. Линейная аппроксимация соотношения $\ln {{K}_{{{\text{IC}}}}}$ и $\ln L$ на участке $L < 10$ м (прямая на рис. 1) дает соотношение, связывающее трещиностойкость и характерный размер в виде

или

Базовые эксперименты в масштабе лабораторного образца и выше, на которых была найдена зависимость эффективной трещиностойкости от размера образца [13, 14] выполнялись с соблюдением рекомендуемого геометрического подобия образцов (в плане) при увеличении размеров. При этом был отмечен ряд важных деталей. Увеличение эффективной трещиностойкости K_1С сопровождалось ростом предельного раскрытия вершины надреза (радиус исходного надреза оставался постоянным) и множественным нарушением связей в области концентрации растягивающих напряжений [16–18]. Это указывает на формирование увеличивающейся области предразрушения – концевой зоны трещины – в ситуации возрастания измеряемого параметра. Детали механизма такого явления представляют предмет отдельного исследования (относятся к внутренней задаче механики разрушения). Обсуждение этого вопроса для льда можно найти в [15]. Соглашаясь с выводами [15] о неправомерности предположения об одинаковости механизмов предразрушения, определяющих энергозатраты в концевых зонах при распространении трещины при такой разнице масштабов разрушения, можно по приведенным экспериментальным данным заключить, что имеется аналогия реакции материала на некоторый определяющий параметр нагружения в разных масштабах. Здесь уместно отметить, что этот вопрос нуждается в уточнении, в том числе и в силу недостаточности данных в диапазоне промежуточных размеров объектов (1–100 мм).

Отметим также возможный вариант обобщенного подхода (со стороны внешней задачи) в виде связи уровня трещиностойкости с размером образца и размером концевой области трещины. В силу такой связи при изменении размера эффективной концевой зоны (зоны предразрушения) по мере роста трещины в предельно-равновесном режиме в рамках внешней задачи для характеристики напряженного состояния в этой области перестает строго действовать асимптотика решений задачи теории упругости для малых расстояний от вершины трещины. Поэтому изменяются условия разрушения. Рассмотрим для немалой концевой области некоторые из них, полагая, что в рамках внешней задачи сохраняется упруго-хрупкий характер разрушения.

Возрастание размеров концевой зоны при увеличении размеров образца подтверждается измерениями раскрытия в вершине надреза (CTOD) к моменту страгивания трещины. Так по данным [13] при увеличении размера компактного образца морского льда от 0.5 до 3 м величина CTOD изменялась от 9–12 мкм до 36–45 мкм.

Для оценки характерного размера концевой обрасти в ледяном покрове в рамках подхода внешней задачи теории трещин воспользуемся известным соотношением для трещины в предельно-равновесном состоянии [19].

Напомним, что характерный линейный размер концевой области может быть использован и в качестве характеристики трещиностойкости (параметр L_1C [20]).

Для оценки локальной прочности при изменении масштаба концевой зоны воспользуемся соотношением Базанта [21, 22]

где $\Sigma $ и В – постоянные (по данным [13] для морского льда $\Sigma \approx 0.59$ [МПа], $B \approx 0.37$ [м]).

Связывая размер L с размером образца, и учитывая (2.4), получим из (2.5) и (2.7) оценку размера концевой обрасти

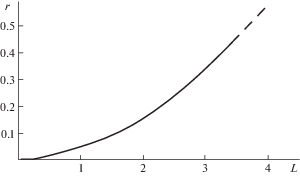
Вид этой функции показан на рис. 2 (размеры даны в метрах). Можно видеть, что при характерных размерах ледяных образований порядка 1 м и выше ожидаемый эффективный размер концевой зоны, оставаясь значительно меньше размеров образца в плане, значительно больше, чем размеры структурных элементов материала (зерен, пор) и порядка толщины образцов. Поэтому при развитии трещин нормального разрыва в концевых зонах в этих масштабах могут иметь значение промежуточные структуры разрушения малого масштаба, образующиеся при взаимодействии между элементами исходной структуры льда, а при $L > 10$ м размер концевой зоны сопоставим с толщиной образца и в этой области меняется напряженное состояние.

Поясним это на примере развития трещины в балке под действием изгибающего момента. Согласно [24] для этого случая нагружения имеем

где $\ell $ – длина трещины, Н – толщина балки, t – ее ширина, М – изгибающий момент.

Полагая, как обычно, условие предельного равновесия ${{K}_{I}} = {{K}_{{IC}}}$ учтем взаимосвязь K_IC и масштабного эффекта льда в форме (2.4). Будем считать в качестве параметра, определяющего масштаб процесса разрушения, размер неповрежденной части изгибаемой балки L ∼ $\left( {H - \ell } \right)$ на продолжении надреза. Критическая величина изгибающего момента определится соотношением

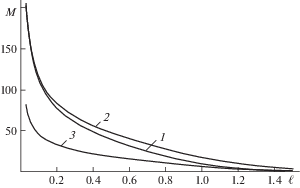
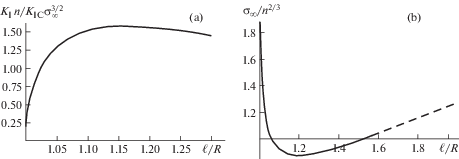
На рис. 3 показана оценка критической величины изгибающего момента по (2.10) для балки шириной 1 м и толщиной 1.5 м с трещиной, имеющей размер $\ell $ (кривая 1). Для сравнения приведена оценка для варианта с уровнем трещиностойкости (K_IC = = 200 кПа м^–0.5 – кривая 2) и трещиностойкостью, измеренной в масштабе лабораторных образцов (K_IC ∼ 80 кПа м^–0.5– кривая 3).

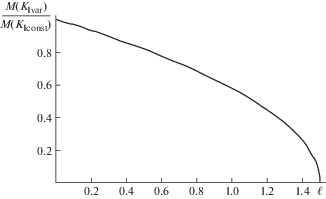
Кривая 1 занимает промежуточное положение. Поэтому, например, оценка глубины необходимого начального надреза для обламывания ледяной балки по данным лабораторного определения K_IC (кривая 3) дает заниженную величину эффективной трещиностойкости. Соотношение критического изгибающего момента в варианте учета масштабного изменения трещиностойкости по (2.10) и при постоянной ее величине, соответствующей максимальному уровню K_IC для рассматриваемого примера показано на рис. 4 для балки толщиной 1.5 м.

Эксперименты по определению трещиностойкости горных пород, льда и других хрупких материалов обычно проводятся по методике с использованием локально нагружаемых “компактных образцов”, в том числе и образцов большого размера [13], либо при изгибе образцов – балочек. При этом обычно соблюдаются рекомендации по определенному соотношению размеров исходного надреза (зародышевого нарушения) и размеров образца.

Поэтому при пропорциональном увеличении масштаба – размеров образцов и исходных надрезов – фактические условия нагружения в области концевой области исходного надреза (трещины), такие как градиент внешних напряжений на продолжении исходного надреза, изменяются. В этом случае можно ожидать влияния этого фактора на эффективную трещиностойкость по мере развития индивидуальной трещины в образце, когда эффективный масштаб будет задаваться расстоянием до свободной границы. Отражением такого влияния может быть и отмеченное в [23] влияние границ нагружаемой области на измеряемые параметры. В такой ситуации представляет интерес учет влияния градиента напряжений от внешних нагрузок на параметры и механизм предразрушения в концевой области трещины.

3. Влияние градиента напряжений. Качественное объяснение эффекта для трещин с немалой концевой областью представляется следующим. Размер концевой области, в которой происходит затрата энергии при подготовке локального разрыва испытывает влияние вариаций поля внешних напряжений, приходящихся на эту область. В частности, при резком изменении внешних напряжений (возрастании) по мере приближения к вершине исходного нарушения в концевой области трещины, локальные процессы предразрушения стягиваются к этой вершине. Происходит уменьшение размера концевой области и, соответственно, уменьшение потребления энергии в окрестности вершины надреза. По мере выполаживания внешних напряжений размер концевой области растет, приближаясь к асимптотике, задаваемой линейной механикой разрушения (вариант с возрастанием напряжений на продолжении разреза в квазистатической постановке практически не реализуется).

Роль локальной неоднородности напряженного состояния в определении критических условий разрушения конструкций и природных объектов давно привлекает внимание. Среди подходов к этому вопросу, обзор которых можно найти, например, в [24] выделим область интереса к влиянию градиентов напряжений. Так в [25] показано, что неравномерность напряженного состояния приводит к снижению разрушающей способности напряжения в области максимальных значений. Согласно градиентным критериям для определения разрушающей нагрузки нужно сравнивать не максимальное значение первого главного напряжения ${{\sigma }_{1}}$ с пределом прочности материала ${{\sigma }_{в}}$ (принятого в качестве эквивалентного), а максимальное значение эффективного напряжения ${{\sigma }_{{ef}}}$, которое при неоднородном напряженном состоянии меньше эквивалентного. Поэтому эффективное напряжение ${{\sigma }_{{ef}}}$ пропорционально ${{\sigma }_{1}}$ и зависит от степени неравномерности поля напряжений в окрестности рассматриваемой точки тела и неоднородности материала. К настоящему времени вопрос о влиянии такого эффекта не может считаться исчерпанным. Коротко остановимся на известных подходах. В [26] предложена форма зависимости

где ${{g}_{1}}$ – градиент первого главного напряжения.

В отличие от классических однопараметрических критериев градиентный критерий разрушения содержит еще параметры L₁ и $\beta $. Параметр L₁ находится из условия соответствия градиентного критерия с линейной механикой разрушения и сводится к известной задаче об одноосном растяжении плоскости с эллиптическим отверстием (перпендикулярно большой оси эллипса). Связь параметра L₁ с критическим коэффициентом интенсивности напряжений ${{K}_{{{\text{I}}\,c}}}$ и пределом прочности ${{\sigma }_{в}}$ дается в виде

Таким образом, параметр L₁ выражается через известные характеристики материала и приравнивается к известному в механике разрушения критическому размеру дефекта в виде трещины Гриффитса. Безразмерный параметр β, изменяющийся от нуля до единицы, учитывает квазихрупкий характер разрушения: β = σ_в/(E${{\varepsilon }_{*}}$), где ${{\varepsilon }_{*}}$ – деформация в момент разрушения при одноосном однородном растяжении; E – модуль упругости.

В другом варианте градиентного подхода [27, 28] локальная прочность материала предполагается зависящей от размера зоны концентрации напряжений L_e. Если размер L_e достаточно велик по сравнению с размерами структурных составляющих материала, то величина локальной прочности мало отличается от величины предельного напряжения σ₀, определенной в условиях однородного распределения напряжений. Наоборот, если L_e сопоставим с размерами структурных элементов, их влияние на локальную прочность становится заметным. Причем это влияние тем больше, чем меньше размер L_e по отношению к характерному размеру структуры материала L₀. Таким образом, локальная прочность материала зависит не просто от размера зоны концентрации напряжений L_e, а от соотношения L₀/L_e, которое характеризует масштаб в рассматриваемой задаче.

Приведем некоторые оценки, предполагая основным влияющим фактором градиент напряжений на потенциальной траектории трещины. Вернемся к компактному образцу, служившему прототипом образца для натурных испытаний в работах со льдом [13, 14]. Свяжем ${{K}_{{{\text{IC}}}}}$ с уровнем градиента внешнего поля напряжений в области вершины трещины. В компактном образце, нагружаемом сосредоточенными силами на внешнем конце надреза градиент напряжений на продолжении исходного надреза создается в основном изгибающим моментом в плоскости образца. В балочном приближении компактный образец можно представить в виде двух полубалочек, передающих изгибающий момент в область прямолинейной траектории трещины на продолжении исходного надреза.

где Р – сосредоточенное усилие от нагружающего устройства, $L{\text{*}}$ – плечо (в экспериментах на квадратном компактном образце эта величина близка к сумме длины исходного надреза и полуразмера оставшейся части образца. $L* \approx (\ell + L){\text{/}}2$, где $L$ – полный размер образца, $\ell $ – длина надреза (трещины).

По решению задачи теории упругости [29] для такого образца

В случае $\ell {\text{/}}L$ ∼ 0.5 величина $f(\ell {\text{/}}L)$ ∼ 9.66.

Изгибные напряжения на траектории трещины в том же приближении

Градиент внешних напряжений

Для варианта $\ell {\text{/}}L$ ∼ 0.5

Согласно (2.4) и (3.7), в предельно-равновесном состоянии для морского льда получим

Отсюда, используя (2.5), в рамках внешней задачи можно, таким образом, представить масштабную зависимость трещиностойкости морского льда в виде функции градиента внешних напряжений на продолжении трещины в момент страгивания трещины

Можно отметить, что если в (3.2) при определении характеристического размера L₁ в качестве ${{K}_{{{\text{IC}}}}}$ используется эффективная трещиностойкость материала по (3.9), влияние градиента напряжений в (3.1) нивелируется. Механизм влияния градиента внешних напряжений на условия предельного равновесия в концевой области можно проиллюстрировать, представляя его в виде вклада вариации внешних напряжений в окрестности вершины трещины в оценку размеров концевой области. На ее границе будем по-прежнему считать напряжение близким к предельному ${{\sigma }_{в}}$, так что условие, определяющее размер концевой зоны запишется в виде

Для случая немалой концевой области при постоянном градиенте напряжений можно записать приближенное соотношение ${{f}_{2}}(\operatorname{var} \sigma ,r{\text{)}}\sim \sigma {\text{'}}r$.

Отметим, что такая форма условия предельного равновесия по смыслу близка к предложенной в [30] модификации соотношения (2.7), в которое добавлен свободный член, отвечающий за дополнительные затраты энергии при изменении масштаба. Соотношение (3.10) при высоких уровнях градиента напряжений и размеров концевой области, (то есть в ситуации преобладания процессов деформирования, связанных с искажением поля напряжений в концевой области) стремится к асимптотике

Для такого варианта уровень эффективной трещиностойкости определится, как

Отмечая совпадение формы взаимосвязи эффективной трещиностойкости с градиентом напряжений в (3.9) и (3.12) можно получить для морского льда оценку $n \approx \sqrt {2\pi \sigma _{в}^{3}} \approx 0.2$ [(МПа)^1.5], и ${{\sigma }_{в}} \approx 0.185$ мПа, что близко к уровню прочности морского льда на разрыв [31].

Экспериментальное моделирование ситуации. Приведенные модельные представления могут быть применены и к другим структурированным материалам, для которых характерно развитие немалой концевой зоны трещин при квазихрупком разрушении в рамках внешней задачи. Для подтверждения правомерности данного подхода были проведены эксперименты по определению трещиностойкости структурированных (зернистых) модельных материалов (гипс, парафин) в условиях сохранения внешних размеров образцов и вариаций размера начального надреза.

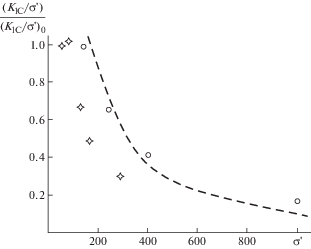
Эксперименты проводились на компактных образцах размером (49 × 49 мм в плане). Толщина гипсовых образцов – 15 мм, парафиновых – 10 мм. Изменялась длина исходного надреза в серии экспериментов при сохранении остальных размеров образцов, что вызывало различие градиента напряжений при страгивании трещин. Результаты измерений показаны на рис. 5 (обозначения: _o – гипс, ₊ – парафин). Можно видеть устойчивую тенденцию снижения эффективной трещиностойкости при увеличении градиента напряжений. На рис. 6 показаны относительные изменения параметра ${{K}_{{1C}}}{\text{/}}\sigma {\text{'}}$ при росте $\sigma {\text{'}}$ для тех же образцов модельных материалов в сравнении с оценкой для льда (3.9) по данным, представленным выше (пунктир). Здесь ${{({{K}_{{{\text{IC}}}}}{\text{/}}\sigma {\text{'}})}_{0}}$ отражает значения параметров для экспериментов при минимальном уровне градиента напряжений в эксперименте. Можно видеть, близкие тенденции понижения относительного уровня значений при росте градиента напряжений для всех испытанных материалов, что позволяет считать значимой принятую взаимосвязь характеристик трещиностойкости структурированных (зернистых, пористых) материалов с масштабом градиента внешних напряжений.

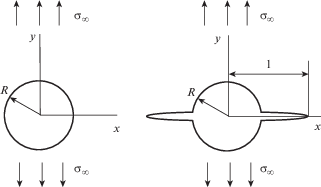
4. Оценка возможных эффектов. Рассмотренная модель расширяет количество возможных сценариев развития разрушения для структурированных материалов с масштабной чувствительностью трещиностойкости. В качестве примера рассмотрим плоскую модельную задачу о начале распространения трещин в окрестности кругового отверстия в упругой пластине при статическом одноосном растяжении (рис. 7). Эта задача, в частности, моделирует разрушение морского льда, содержащего капиллярные поры, в окрестности капилляров. Ограничимся при этом приближением таких размеров концевой зоны, при которых градиент внешних напряжений по ее длине можно считать постоянным.

Напомним, что в обычном представлении сценария разрушения при росте трещин, выходящих на контур отверстия при растяжении, по мере удаления вершины трещины от края отверстия коэффициент интенсивности напряжений в ее концевых областях монотонно возрастает, вследствие чего при достижении им величины ${{K}_{I}} = {{K}_{{IC}}}$ = const наступает неустойчивая фаза и переход к динамическому разрушению.

Изменение величины ${{K}_{{IC}}}$ под воздействием градиента напряжений меняет сценарий разрушения. Приведем некоторые оценки, основываясь на полученных соотношениях.

Распределение упругих напряжений в области концентрации напряжений в окрестности отверстия в плоскости имеет вид [32]

где R – радиус отверстия.

При формировании концевой зоны зародышевого нарушения (малой трещины) на границе отверстия основную роль играет градиент напряжений, создаваемый отверстием. Отсюда и из (3.9) следует характер изменения эффективной трещиностойкости для трещины на начальном этапе удаления от отверстия в виде

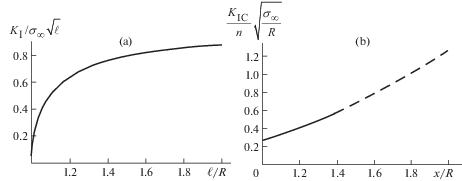
На рис. 8b показан характер предполагаемого изменения эффективной трещиностойкости материала (льда) под влиянием градиента напряжений в окрестности отверстия. На рис. 8a показан характер изменения K_IC при удлинении трещины для такой схемы нагружения (по [29]). Эта зависимость для малых величин $\left( {\ell {\text{/}}R - 1} \right)$ может быть приближенно представлена в виде

Учитывая (4.2) и (4.3) запишем в таком же приближении условие предельного равновесия

Это соотношение иллюстрирует характер развития трещины в непосредственной близости от контура отверстия. В описываемом сценарии разрушения по мере роста трещины происходит возрастание эффективной трещиностойкости на фоне роста коэффициента интенсивности напряжений по мере удаления от границы отверстия.

В результате характер соотношения предельного равновесия для малой трещины в окрестности отверстия (рис. 9а) становится немонотонным. Появление экстремума в области $\ell {\text{/}}L$ ∼ 1.15 означает возможность торможения и остановки трещины на начальном этапе после ее инициирования и начального неустойчивого развития, что отражается и на изменении предельных внешних напряжений ${{\sigma }_{\infty }}$ (рис. 9b) по уровню критического напряжения (4.2). Необходимо напомнить, что рассматриваемый эффект относится только к диапазону высоких градиентов внешних напряжений. По мере его уменьшения эффект ослабления локальной трещиностойкости падает, ${{K}_{{ICef}}} \to {{K}_{{IC}}} \approx $ const, и сценарий разрушения возвращается к схемам с постоянным уровнем трещиностойкости. В данном варианте задачи это означает выход на неустойчивый режим развития трещины при большом удалении ее вершины от отверстия. Оценим реальную границу возможного устойчивого роста микротрещин в образцах морского льда для рассматриваемой ситуации. По данным [13] при проведении крупномасштабных экспериментов локальная прочность льда при растяжении (изгибе) ${{\sigma }_{t}}\sim {{\sigma }_{\infty }} \approx 0.5$ МПа. Для этого уровня напряжений величина ${{\sigma }_{\infty }}{\text{/}}n \approx 1.47$. По (26) можно оценить в тех же допущениях, что он соответствует устойчивому подрастанию трещины до размера $\ell {\text{/}}R \approx 2.3$. Поскольку трещина такого размера значительно влияет на распределение напряжений у отверстия, приводимая оценка является качественной оценкой сверху. При обозначенной в [13] солености льда на уровне 4–7 промилле пористость льда, заполненная рассолом, по данным [31] составляет n ∼ 0.04–0.06, отношение полурасстояния между порами к радиусу пор для такой пористости $\ell {\text{*/}}R \approx 4.1{\kern 1pt} - {\kern 1pt} 5.0$. Следовательно, устойчивое подрастание трещин до размера $\ell {\text{/}}R \approx 2.33$ должно смениться неустойчивым ростом до слияния с соседними при $\ell {\text{*/}}R \approx $ 4.1–5.0.

Приведенные оценки показывают и возможный сценарий разрушения пористой структуры морского льда при растяжении в направлении поперек оси параллельных капилляров с образованием зоны предразрушения. В связи с этим упомянем результаты крупномасштабных экспериментов в [13], в которых было отмечено частичное сохранение несущей способности льда в объеме немалой концевой области магистрального разрыва, что свидетельствует о развитии в ней структуры разрушения в устойчивом режиме. Большую роль в развитии такой несущей структуры может играть этап устойчивого подрастания трещин в окрестности элементов исходной структуры материала (пор, кристаллов) при возрастании нагрузки за счет увеличения ${{K}_{{1Cef}}}$ при снижении уровня градиента напряжений в локальных процессах разрушения. При этом в пористой среде в окрестностях растущих микротрещин возможно провоцирование роста трещин у соседних пор. Это приводит к образованию систем (эшелонов) трещин, образующих связанную систему нарушений. Механизм образования упорядоченных систем трещин частично рассмотрен в [33] для вариантов ситуаций, в которых увеличение сопротивления развитию отдельной трещины связано с падением уровня коэффициента интенсивности напряжений от внешних нагрузок при постоянстве уровня трещиностойкости. Тот же эффект может быть получен, как было показано выше, и при увеличении коэффициента интенсивности напряжений, если возрастает локальная трещиностойкость материала. Описанные явления увеличивают многообразие возможных сценариев разрушения. Дополнительные вариации также дает влияние исходной нарушенности контура отверстия (поры). В самом деле, если контур поры достаточно гладкий (для нашего примера $\ell {}_{0}/R < 1.2$ – рис. 9b), инициирование разрушения происходит на падающем участке кривой критического напряжения. Поэтому сначала, после страгивания зародышевого нарушения, ожидается неустойчивый рост трещин до размера, определяемого восходящей ветвью кривой на рис. 9. Затем рост трещин проходит в устойчивом режиме, описанном выше. Размер области устойчивого режима развития трещин и, тем самым, возможность образования регулярной структуры множественного разрушения, таким образом, зависит от механического состояния контура капилляров. В частности, при начально-гладком контуре отверстия (при $\ell {}_{0}/R \to 1$) возможно отсутствие этапа устойчивого роста. В этом случае можно прогнозировать развитие магистрального разрыва без образования области предразрушения.

Описанный механизм возрастания эффективной трещиностойкости может давать вклад и в тенденцию увеличения прочности морского льда на разрыв (изгиб) по мере уменьшения пористости (содержания рассола в капиллярных порах). Поясним это на примере.

Полагая в (4.4) $\ell {\text{/}}R \approx {{\nu }^{{ - 0.5}}}$ , где $\nu $ – объем рассола в капиллярных порах, и аппроксимируя возрастающую ветвь функции ${{\sigma }_{\infty }}(\ell {\text{/}}R)$ линейной функцией, получим

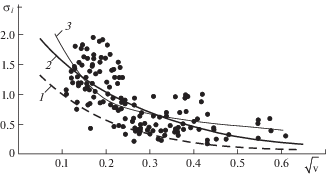
На рис. 10 показан вид этой функции (при n ∼ 0.2 [(МПа)^1.5]) в сравнении с функцией, предложенной в [34] (кривая 1), а также данными экспериментов (точки на рисунке) и обобщающей функцией по [35] (кривая 2). Заметим, что среди многочисленных работ по исследованию прочности морского льда при изгибе нет единого представления о виде определяющих соотношений, связывающих прочность и пористость. Найденные зависимости влияния объема рассола варьируются от линейных функций [36] до экспоненциальных [34]. Введение процессов, характеризующих множественное разрушение при подготовке разрыва может облегчить анализ сценария разрушения. Эффект немонотонного изменения эффективной трещиностойкости, когда при страгивании микротрещины в условиях растяжения происходит скачкообразное ее подрастание, сменяющееся на некотором участке устойчивым ростом, может также служить основой механизма развития регулярной структуры разрушения в условиях крупномасштабной концентрации растягивающих напряжений. Существование этапа возрастания эффективной трещиностойкости может приводить к устойчивому подрастанию многих очагов разрушения, образующих упорядоченную структуру разрушения при взаимодействии трещин, растущих в окрестности отдельных элементов исходной структуры. В частности, это относится к развитию структуры предразрушения в немалой концевой зоне в окрестностях вершины магистрального разрыва или сдвига. Такой механизм дополняет возможные сценарии микроразрушения в описанных условиях, обычно относимые к влиянию статистической неоднородности прочностных свойств материалов.

5. Заключение. Проведенный анализ показывает, что можно выделить класс материалов, к которым, в частности, относится морской лед и другие структурированные материалы (гипс, бетон, парафин и др.), на эффективную трещиностойкость которых при хрупком разрушении влияет масштабный фактор, в роли которого выступает градиент внешних напряжений. Данное воздействие, возмущая напряженное состояние в немалой концевой области вершины трещины, создает возможность изменения эффективной трещиностойкости для процессов разрушения в областях концентрации напряжений.

Такие области в структурированных материалах содержат нарушения, предшествующие развитию магистральных разрывов. К ним относятся, в частности, концевые зоны магистральных разрывов, в которых материал содержит множественные нарушения (микротрещины, приуроченные к элементам микроструктуры), сохраняя при этом некоторую долю несущей способности. Аналогичные явления наблюдаются при развитии магистрального разрыва в крупномасштабных фрагментах морского ледяного покрова, имеющего столбчатозернистую структуру и капиллярную пористость [15]. Описанный процесс объясняет генезис структуры концевой зоны крупномасштабных разрывов в ледяном покрове.

Этот механизм также создает принципиальную возможность ранней диагностики повреждений в окрестностях концентраторов напряжений для материалов, обладающих аналогичной тенденцией изменения эффективной трещиностойкости, поскольку появление малых трещин в условиях высокого градиента напряжений (и пониженной локальной трещиностойкости), обозначая инициирование разрушения, не приводит к их распространению в неустойчивом режиме. Работа выполнена при финансовой поддержке программы Президиума РАН № I.2.55П: “Арктика – научные основы новых технологий освоения, сохранения и развития”.