Известия РАН. Механика твердого тела, 2019, № 6, стр. 20-29
ДИНАМИЧЕСКОЕ ВОЗДЕЙСТВИЕ НА ТРУБОПРОВОД С УЧЕТОМ СУХОГО ТРЕНИЯ НА ЕГО ПОВЕРХНОСТИ
А. Н. Филиппов *
Федеральное государственное автономное образовательное учреждение высшего образования
“Российский государственный университет нефти и газа
(национальный исследовательский университет) имени И.М. Губкина”
Москва, Россия
* E-mail: filippov.a@gubkin.ru
Поступила в редакцию 09.01.2019
После доработки 09.01.2019
Принята к публикации 30.01.2019
Аннотация
Получено точное аналитическое решение задачи о волновом движении трубчатого полубесконечного стержня, взаимодействующего с окружающей его упругой средой по закону сухого трения Кулона, при действии на его торце экспоненциально падающей динамической нагрузки (моделирование подрыва заряда ВВ) и в случае удара жестким телом конечной массы по этому торцу. Исследована картина волнового движения в зависимости от параметров нагружения: определены передний и задний фронты упругой волны, найдено распределение остаточных деформаций при ее прохождении по стержню. Полученные результаты могут быть использованы при расчете деформации нефте- и газопроводов в случае ударных нагружений.
1. Введение. На практике часто приходится сталкиваться с проблемами расчета волновых процессов в телах удлиненной формы, находящихся в контакте с окружающей средой или другими телами. При этом, как правило, картина движения качественно (не говоря уже о количественной стороне вопроса) зависит от вида, характера и степени взаимодействия названных объектов. К задачам подобного рода можно отнести движение заглубленного в грунт трубопровода, исследование процесса забивки свай, скольжение протяженных тел в каналах при воздействии ударной нагрузки, динамическое контактное взаимодействие армирующих волокон и матрицы композитных материалов и т.п. Поскольку решение таких задач в точной постановке даже в рамках линейной теории упругости встречает значительные математические трудности, то обычный подход к преодолению последних основывается на включении в уравнения движения исследуемого тела реакций контактирующих с ним объектов.
Ряд интересных и важных задач в случае взаимодействия упругого стержня и жесткой среды при постоянной по величине силе сухого трения, действующей на контактной поверхности при наличии относительного движения, детально исследован в работах [1–12], в том числе применительно к заглубленному в грунт трубопроводу [4, 11]. В упомянутых работах сила трения не зависела от деформации ни самого стержня, ни окружающей его среды. В работе [13] этот пробел был устранен, и сила сухого трения в динамическом режиме была принята пропорциональной продольной деформации стержня в случае его сжатия из-за наличия окружающей стержень среды типа Винклера [14]. В монографии Л.В. Никитина [15] приведен детальный обзор работ, опубликованных до 1997 года, и даны точные аналитические решения задач статики и динамики упругих и упругопластических тел с сухим трением, в том числе по моделированию ударного воздействия на трубопровод, находящийся в упругой среде. Следует отметить, что все краевые задачи в [15] были рассмотрены в одномерной постановке. В последние годы интерес к задачам подобного типа не ослабевает: в работе [16], например, представлены модели сейсмического режима и блоковой динамики, основанные на фрикционных автоколебаниях в системах с нелинейным сухим трением. При этом получено семейство моделей Барриджа и Кнопова для описания генерации землетрясений при относительном движении бортов разлома. Развиваются двумерные модели динамики стержней [17], в том числе с учетом деформации окружающей среды [18] при наличии сухого трения на боковой поверхности. Рассматривается и совместное движение пары контактирующих стержней [19]. Однако решение краевых задач ведется в основном численными методами. Между тем наличие аналитических решений даже в простых случаях позволяет верифицировать численные алгоритмы и схемы.
В данной работе применительно к перечисленным выше явлениям используется модель взаимодействия длинного тонкого упругого тела (трубчатого стержня) с окружающей его упругой же средой, представляющей собой линейное винклеровское основание, предложенная в работе [13]. При этом в случае проскальзывания между телом и средой, на поверхности контакта действует сила сухого трения, величина которой зависит от амплитуды проходящего по трубе импульса напряжений.
2. Постановка задачи и анализ решения. Одномерное уравнение движения тонкого однородного линейно-упругого трубчатого стержня, взаимодействующего по закону сухого трения Кулона с окружающей его средой типа Винклера, имеет следующий вид [13]:
(2.1)
$a_{0}^{2}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + 2\kappa {\lambda }\frac{{\partial u}}{{\partial x}} = \frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}}$Предполагается, что в начальный момент времени полубесконечный трубчатый стержень был не напряжен, не деформирован и κ = 0:
(2.2)
$u\left( {0,x} \right) = \frac{{\partial u}}{{\partial t}}\left( {0,x} \right) = 0,\quad x > 0$Здесь рассматриваются только сжимающие нагрузки, которые не приводят к прерыванию контакта стержня и среды. В этом наиболее простом случае можно строго показать, что передний фронт упругой волны как сильного, так и слабого разрывов распространяется со скоростью звука ${{a}_{0}}$11. Поэтому, в квазилинейном дифференциальном уравнении (2.1) следует положить $\kappa = \operatorname{H} \left( {t - {x \mathord{\left/ {\vphantom {x {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}} \right)$, избавившись таким образом от нелинейности (H(t) – единичная функция Хевисайда).
Для дальнейшего рассмотрения удобно ввести безразмерные переменные:
При этом уравнение движения (2.1) запишется в виде:
(2.3)
$\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + 2{\text{H}}\left( {t - x} \right)\frac{{\partial u}}{{\partial x}} = \frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}}$Здесь и всюду далее тильда над безразмерными величинами опущена.
В случае задания динамических граничных условий на конце $x = 0$ трубы
(2.4)
$\frac{{\partial u}}{{\partial x}}\left( {t,0} \right) = - f\left( t \right) \cdot \operatorname{H} \left( t \right),\quad t \geqslant 0,\quad f\left( t \right) \geqslant 0$(2.5)
${\varepsilon }\left( {t,x} \right) = - {{\operatorname{e} }^{{ - x}}}\left\{ {f\left( {t - x} \right) - x\int\limits_x^t {\frac{{{{J}_{1}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} )}}{{\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} }}f\left( {t - {\tau }} \right)d{\tau }} } \right\}\operatorname{H} \left( {t - x} \right)$(2.6)
$\begin{gathered} {v}\left( {t,x} \right) = {{\operatorname{e} }^{{ - x}}}\operatorname{H} \left( {t - x} \right)\left\{ {f\left( {t - x} \right) - \int\limits_x^t {\frac{{{{J}_{1}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} )}}{{\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} }}f\left( {t - {\tau }} \right){\tau }d{\tau }} } \right. + \\ + \;\int\limits_x^t {\left( {\int\limits_x^{\tau } {{{J}_{0}}(\sqrt {{{{\xi }}^{2}} - {{x}^{2}}} )f\left( {{\tau } - {\xi }} \right)d{\xi }} } \right)d{\tau }} + \\ \left. { + \;\int\limits_x^t {\left( { - f\left( {{\tau } - x} \right) + x\int\limits_x^{\tau } {\frac{{{{J}_{1}}(\sqrt {{{{\xi }}^{2}} - {{x}^{2}}} )}}{{\sqrt {{{{\xi }}^{2}} - {{x}^{2}}} }}f\left( {{\tau } - {\xi }} \right)d{\xi }} } \right)d{\tau }} } \right\} \\ \end{gathered} $3. Динамическое воздействие на торец стержня убывающей во времени нагрузкой. При задании экспоненциально падающей концевой нагрузки
(3.1)
$f\left( t \right) = A\exp \left( { - ct} \right),\quad t \geqslant 0,\quad A,c = \operatorname{const} \geqslant 0$(3.2)
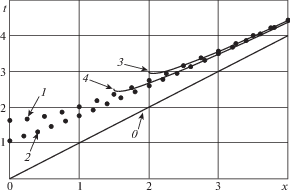
$\begin{gathered} \exp \left( { - c\left( {{\varphi }\left( x \right) - x} \right)} \right) + c{{J}_{0}}(\sqrt {{{{\varphi }}^{2}}\left( x \right) - {{x}^{2}}} ) - \\ - \;{{c}^{2}}\int\limits_x^{{\varphi }\left( x \right)} {{{J}_{0}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} )} \exp \left( { - c\left( {{\varphi }\left( x \right) - {\tau }} \right)} \right)d{\tau + } \\ + \;\int\limits_x^{{\varphi }\left( x \right)} {\left\{ {{{J}_{0}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} ) + x\frac{{{{J}_{1}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} )}}{{\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} }}} \right\}\left( {1 - \exp \left( { - c\left( {{\varphi }\left( x \right) - {\tau }} \right)} \right)} \right)d} {\tau = 1} \\ \end{gathered} $На рис. 1 представлены расчеты фронта остановки $t = {\varphi }\left( x \right)$ для значений с равных 0 (точки 1, соответствующие ступенчатой нагрузке $f\left( t \right) = A\operatorname{H} \left( t \right)$) и 0.5 (точки 2). Прямая 0 определяет передний фронт волны $t = x$. Увеличение параметра c (более быстрое падение во времени концевой нагрузки) приводит к более раннему прохождению фронтом остановки сечений стержня. При больших значениях t и x (t > x) имеет место асимптотика:
которая для фронтов 1 и 2 показана соответственно кривыми 3 и 4, и с высокой точностью приближает $t = {\varphi }\left( x \right)$ при x > 2.5. Несмотря на то, что скорость заднего фронта $t = {\varphi }\left( x \right)$ упругой волны остается все время больше скорости распространения переднего фронта t = x, он не может догнать передний фронт и истощения волны не происходит. Как показывает анализ, после прохождения фронта остановки $t = {\varphi }\left( x \right)$ в стержне устанавливается состояние статического равновесия между силами упругости и трения, определяемое уравнением(3.4)
$\frac{{d{\varepsilon *}}}{{dx}} + 2\kappa \left( x \right){\varepsilon *}\left( x \right) = 0$4. Удар жестким телом по торцу стержня. Изменим граничное условие задачи. Пусть в полубесконечный трубчатый стержень попадает летящее со скоростью ${{{v}}_{0}} = \operatorname{const} $ абсолютно жесткое тело массы m. Краевое условие запишется при этом в виде:
(4.1)
$\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}}\left( {t,0} \right) = s\frac{{\partial u}}{{\partial x}}\left( {t,0} \right),\quad \frac{{\partial u}}{{\partial t}}\left( {0,0} \right) = B$(4.2)
$\begin{gathered} {v}\left( {t,x} \right) = B\frac{{\exp \left( { - x} \right)}}{{s - 2}}\operatorname{H} \left( {t - x} \right)\left\{ {\int\limits_x^t {\left( {1 - {{{\left( {s - 1} \right)}}^{2}}\operatorname{ch} \left( {{\omega }\left( {t - {\tau }} \right)} \right)} \right){{J}_{0}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} )d{\tau }} } \right. - \\ \left. { - \;1 + \left( {s - 1} \right)\operatorname{ch} \left( {{\omega }\left( {t - x} \right)} \right) + x\int\limits_x^t {\left( {1 - \left( {s - 1} \right)\operatorname{ch} \left( {{\omega }\left( {t - {\tau }} \right)} \right)} \right)\frac{{{{J}_{1}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} )}}{{\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} }}d{\tau }} } \right\} \\ \end{gathered} $(4.3)
$\begin{gathered} {v}\left( {t,x} \right) = B\frac{{\exp \left( { - x} \right)}}{{2 - s}}\operatorname{H} \left( {t - x} \right) \cdot \\ \cdot \;\left\{ {1 + \int\limits_x^t {({{{\left( {1 - s} \right)}}^{2}}\cos (\sqrt {2s - {{s}^{2}}} \left( {t - {\tau }} \right)) - 1){{J}_{0}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} )d{\tau }} } \right. + \\ + \;\left( {1 - s} \right)\cos (\sqrt {2s - {{s}^{2}}} \left( {t - x} \right)) - \\ - \;\left. {x\int\limits_x^t {(\left( {1 - s} \right)\cos (\sqrt {2s - {{s}^{2}}} \left( {t - {\tau }} \right)) + 1)\frac{{{{J}_{1}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} )}}{{\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} }}d{\tau }} } \right\} \\ \end{gathered} $Формулы для “переходного” случая s = 2 могут быть получены из формул (4.2) или (4.3) с помощью аккуратного предельного перехода:
В частном случае s = 1 выражения для деформации и скорости (4.3) существенно упрощаются:
(4.4)
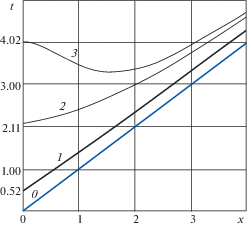
${v}\left( {t,x} \right) = B\exp \left( { - x} \right)\operatorname{H} \left( {t - x} \right)\left\{ {1 - \int\limits_x^t {\left( {{{J}_{0}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} ) + x\frac{{{{J}_{1}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} )}}{{\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} }}} \right)d{\tau }} } \right\}$Из формулы для деформации следует, что фронт смены ее знака представляет собой гиперболу $\sqrt {{{t}^{2}} - {{x}^{2}}} = {{{\mu }}_{1}}$, где ${{{\mu }}_{1}} = 2.4048$ – первый нуль функции Бесселя J0. Однако, прежде чем успеет пройти этот фронт, пройдет фронт остановки сечений стержня $t = {\varphi }\left( {x,1} \right)$ (он располагается между кривыми 1 и 2 на рис. 3), так что деформации останутся сжимающими.
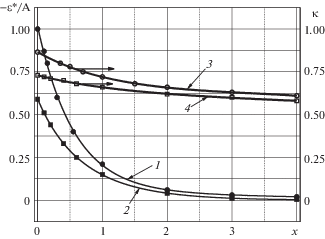
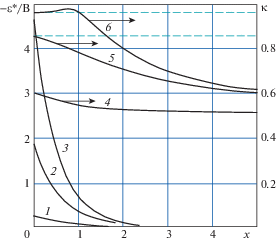
Анализ показывает, что при $s > {{s}_{*}}$ в стержне существует лишь одна область движения, задний фронт $t = {\varphi }\left( {x,s} \right)$ которой для различных значений s изображен на рис. 3 (кривая 0 – передний фронт t = x упругой волны, кривые 1, 2, 3 – задние фронты для значений s = 3.5; 0.3 и 0.08, соответственно). Остаточные распределения приведенных деформаций ${{ - {\varepsilon }*\left( {x,s} \right)} \mathord{\left/ {\vphantom {{ - {\varepsilon }*\left( {x,s} \right)} B}} \right. \kern-0em} B}$ по области застоя и графики функций ${\kappa }\left( {x,s} \right)$, определяемые из уравнения (10), при тех же s представлены на рис. 4 (кривые 1, 2, 3 – для ${{ - {\varepsilon *}} \mathord{\left/ {\vphantom {{ - {\varepsilon *}} B}} \right. \kern-0em} B}$ и 4, 5, 6 – для κ). Значение ${{s}_{*}}$ определяется как наименьший параметр, при котором уравнение ${{d\varphi \left( {x,s} \right)} \mathord{\left/ {\vphantom {{d\varphi \left( {x,s} \right)} {dx}}} \right. \kern-0em} {dx}} = - 1$ имеет хотя бы одно решение: оценка дает $0.05 < {{s}_{*}} < 0.08$. Отметим, что асимптотическое разложение функции $t = {\varphi }\left( {x,s} \right)$ при больших значениях x имеет вид:
Приведенная выше формула при $x > 5$ для $s > {{s}_{*}}$ с точностью не хуже 2% описывает истинную кривую.
Интересно заметить, что при условии ${{s}_{*}} < s < {{s}_{0}}$ (${{s}_{0}} \approx 0.188$) первым останавливается не концевое, а некоторое сечение внутри стержня с последующим распространением области застоя в обе стороны (см., например, кривую 3 на рис. 3); при этом распределение сил трения по длине стержня является немонотонным (кривая 6 на рис. 4). В случае же $0 \leqslant s \leqslant {{s}_{*}}$ в стержне возникнут зоны вторичного движения, решение задачи в которых должно строиться отдельно. Поясним эту ситуацию на примере случая, когда s = 0, что соответствует удару по трубчатому стержню бесконечной массой (удар стержня о неподвижную жесткую преграду). Тогда выражения для деформации и скорости значительно упрощаются:
(4.5)
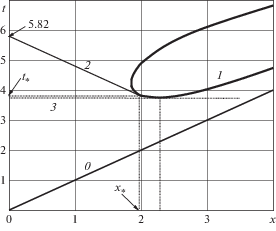
${v}\left( {t,x} \right) = B\exp \left( { - x} \right)\left\{ {1 - x\int\limits_x^t {\frac{{{{J}_{1}}(\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} )}}{{\sqrt {{{{\tau }}^{2}} - {{x}^{2}}} }}d{\tau }} } \right\}\operatorname{H} \left( {t - x} \right)$Примерная картина волнового движения для этого случая показана на рис. 5. Первым здесь останавливается сечение $x \approx 2.3$, где касательная к фронту остановки $t = {\varphi }(x,0{\text{)}}$ горизонтальна (пунктирная прямая 3). Далее фронт остановки (кривая 1) распространяется в обе стороны, достигая в сечении ${{x}_{*}} \approx 1.97$ в момент времени ${{t}_{*}} \approx 3.85$ максимальной скорости упругой волны и асимптотически приближаясь к переднему фронту (прямая 0). При этом решение (4.5) остается справедливым ниже характеристики $t + x = {{t}_{*}} + {{x}_{*}} \approx 5.82$ (прямая 2) и фронта остановки $t = {\varphi }\left( {x,0} \right)$ (кривая 1). На рис. 5 для наглядности показана вся кривая, на которой скорость (4.5) формально обращается в ноль. При этом верхняя часть этой кривой ($t > 3.85$) должна быть отброшена, как не имеющая физического смысла. В области выше характеристики $t + x = {{t}_{*}} + {{x}_{*}}$ и фронта остановки $t = {\varphi }\left( {x,0} \right)$ решение должно строиться с учетом возникновения вторичной упругой волны, бегущей с переменной скоростью по предварительно поджатому стержню. Фронт вторичной волны заранее неизвестен и должен определяться из решения задачи. Этому будет посвящена следующая статья.
5. Заключение. Представлено точное аналитическое решение краевой задачи о распространении упругой волны в трубчатом полубесконечном стержне, взаимодействующем с окружающей средой по закону сухого трения, при действии на его торце экспоненциально убывающей во времени динамической нагрузки, а также в случае удара жестким телом конечной массы по этому торцу. Подробно исследована картина волнового движения в зависимости от параметров нагружения. Определены передний и задний фронты упругой волны, найдено распределение остаточных деформаций после прохождения фронта остановки сечений. Полученные результаты могут быть использованы при расчете деформации нефте- и газопроводов в случае ударных нагружений.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 16-01-00138).
Список литературы
Никитин Л.В. Распространение волн в упругом стержне при наличии сухого трения // Инж. ж. 1963. Т. 3. Вып. 1. С. 126–130.
Никитин Л.В., Тюреходжаев А.Н. Поведение под нагрузкой упругого стержня, заглубленного в грунт // Проблемы механики горных пород. Алма-Ата: Наука, 1966. С. 304–311.
Никитин Л.В. Удар жестким телом по упругому стержню с внешним сухим трением // Инж. ж. МТТ. 1967. № 2. С. 166–170.
Ильюшин А.А., Рашидов Т.Р. О действии сейсмической волны на подземный трубопровод // Изв. АН УзССР. Сер. техн. наук. 1971. Т. 1. С. 3–11.
Тарханов Г.В. Распространение волн по упругому полубесконечному стержню при наличии сухого трения // Виброакустическая активность механизмов с зубчатыми передачами. М.: Наука, 1971. С. 184–187.
Никитин Л.В. Продольные колебания упругих стержней при наличии сухого трения // Изв. АН СССР. МТТ. 1978. № 6. С. 137–145.
Тарханов Г.В. Влияние предварительного смещения на распространение упругой волны по стержню при наличии сухого трения // Изв. АН СССР. МТТ. 1982. № 2. С. 173–178.
Веклич Н.А., Малышев Б.М. Распространение волн в упругих стержнях, находящихся в среде с сухим трением // Задачи механики твердого деформируемого тела. М.: МГУ, 1985. С. 64–99.
Никитин Л.В., Тюреходжаев А.Н. Демпфирование сухим трением динамических нагрузок в волокнистом композите // Механика композитных материалов. 1986. № 1. С. 28–37.
Никитин Л.В. Динамика упругих стержней с внешним сухим трением // Успехи механики. 1988. Т. 11. Вып. 4. С. 53–106.
Никитин Л.В., Рашидов А.Т. Трубопровод под воздействием стационарного конечного импульса в окружающей среде // Актуальные проблемы механики деформируемого твердого тела. Алма-Ата: Гылым, 1992. С. 12–18.
Mogilevsky R.I., Ormonbekov T.O., Nikitin L.V. Dynamics of rods with interfacial dry friction // J. Mech. Behav. Mater. 1993. V. 5. № 1. P. 85–93.
Филиппов А.Н. Распространение продольных упругих волн в стержне, окруженном средой типа Винклера // Вестн. Моск. ун-та. Сер. 1. Математика. Механика. 1983. № 1. С. 74–78.
Winkler E. Die Lehre von der Elasticität und Festigkeit mit besonderer Rücksicht auf ihre Anwendung in der Technik. Prag: H. Dominicus, 1867. 431 p.
Никитин Л.В. Статика и динамика твердых тел с внешним сухим трением. М.: Московский лицей, 1998. 261 с.
Захаров В.С. Модели сейсмотектонических систем с сухим трением // Вестн. Моск. ун-та. Сер. 4. Геология. 2011. № 1. С. 22–28.
Александрова Н.И. Численно-аналитическое исследование процесса ударного погружения трубы в грунт с сухим трением. Ч. I: Внешняя среда не деформируема // Физ.-техн. пробл. разраб. полез. ископ. 2012. № 5. С. 104–119.
Александрова Н.И. Численно-аналитическое исследование процесса ударного погружения трубы в грунт с сухим трением. Ч. II. Внешняя среда деформируема // Физ.-техн. пробл. разраб. полез. ископ. 2013. № 3. С. 91–106.
Яновская Е.А., Сосенушкин Е.Н., Иванова О.К. Динамическая модель распространения волн от ударного импульса в составном стержне с учетом трения // Изв. Самарского НЦ РАН. 2016. Т. 18. № 1–2. С. 349–357.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела