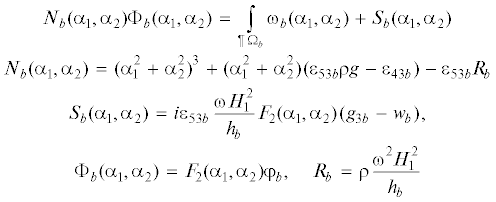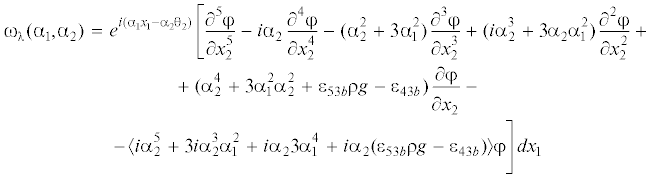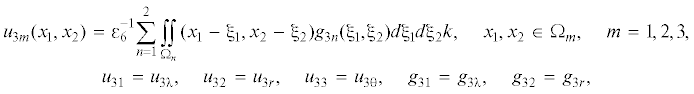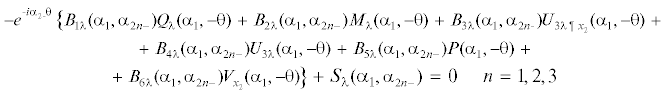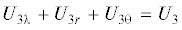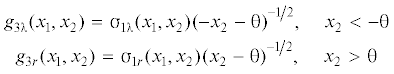1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 6, 2019

Известия РАН. Механика твердого тела, 2019, № 6, стр. 47-53

О ПРОЧНОСТНЫХ СВОЙСТВАХ СМАЗЫВАЕМЫХ ПОДШИПНИКОВ С ДЕФЕКТНЫМИ ПОКРЫТИЯМИ

В. А. Бабешко a, b, *, О. М. Бабешко b, О. В. Евдокимова a, Ю. Б. Елецкий a, С. Б. Уафа a

a Южный научный центр РАН
Ростов-на-Дону, Россия

b Кубанский государственный университет
Краснодар, Россия

* E-mail: babeshko41@mail.ru

Поступила в редакцию 17.06.19
После доработки 29.06.19
Принята к публикации 29.07.19

Полный текст (PDF)

Аннотация

Рассматривается модель подшипника с дефектом, имеющая целью выявление прочностных свойств блочной структуры, включающей обойму подшипниковой пары и сам подшипник со смазкой. Обойма представляет деформируемое основание с тонким покрытием, имеющим дефекты. Покрытие находится под воздействием смазки, которая в условиях функционирования утрачивает вязкость и может моделироваться тонким слоем идеальной несжимаемой жидкости, на который оказывается вертикальное внешнее давление подшипника. Для исследования локальных свойств подшипника в окрестности дефекта основание обоймы рассматривается в форме деформируемого слоя с дефектным покрытием, содержащим сверху слой идеальной несжимаемой жидкости. Предполагается, что покрытие имеет наиболее сложный скрытый дефект, описываемый трещиной, плоскость которой перпендикулярна границе покрытия. Описанная блочная структура исследуется методом блочного элемента, и выявляются особенности дальнейшего поведения подшипника.

Ключевые слова: блочный элемент, пластины, топология, внешние формы, блочные структуры, граничные задачи, скрытые дефекты, подшипники

Введение. В связи с важностью подшипниковых пар в машиностроении и других отраслях, всестороннее исследование в мире этих объектов ведется многие годы и в разных направлениях. Глубокие обобщающие исследования по фрикционным явлениям и примыкающей теории подшипников выполнены в работах [1–4]. В последние годы особое внимание уделяется проблемам трения в подшипниковых парах, что связано с проблемами прочности их эксплуатационной энергоемкостью [5–7]. Важное место занимают проблемы создания подшипниковых пар на основе материалов разной реологии, в том числе, с применением смазочных материалов [1–4, 8]. Одно из основных мест в этой теории занимают проблемы прочности подшипниковых пар, в том числе, с покрытиями [9–13]. В железнодорожном транспорте фрикционные проблемы возникли в связи с использованием рельсов нового поколения, имеющих больший ресурс прочности, чем старого типа. Перечисленные объекты практически постоянного функционирования рано или поздно обязательно выходят из строя. Имеется обширный теоретический и экспериментальный материал, связанный с разрушением подшипниковых пар и поверхностей, подвергающихся различным воздействиям. Ищутся пути и способы упреждения разрушения этих объектов и способов индикации их прочностного состояния. Для этого применяется широкий спектр различных современных методов как исследований и расчетов, так и диагностики и экспериментирования. Изучение исследований в области прочности подшипниковых пар показало, что, практически нет работ, связанных с изучением прочностных свойств дефектных подшипниковых пар, имеющих покрытия и смазку при наличии в качестве дефектов скрытых трещин, плоскости которых перпендикулярны покрытиям. Дефекты, которые рассматриваются в работе, относятся к категории скрытых, поскольку их вертикальная плоскость является мало доступной для обнаружения ультразвуковыми или рентгеновскими методами, сканирующими в вертикальном направлении. Наличие слоя жидкости усложняет выявление дефектов. Результат работы показывает важность их обнаружения, поскольку уже единичные дефекты могут приводить к необратимым последствиям в таких конструкциях. В основе исследования лежит метод блочного элемента, достаточно удачно зарекомендовавших себя в задачах со скрытыми дефектами.

1. Основные уравнения. Описанная проблема рассматривается в четырехблочной структуре, состоящей из деформируемого слоя, моделирующего тело, двух полубесконечных пластин Кирхгофа, между торцами которых может отсутствовать или присутствовать некоторое расстояние, и слоя жидкости. В каждом блоке такой структуры поставлены соответствующие граничные задачи. Методом блочного элемента исследование сводится к изучению системы функциональных уравнений, позволяющих выявить концентрацию напряжений в блочной структуре. Считаем, что на смазывающий материал – слой идеальной жидкости и пластины действуют внешние гармонические во времени силы, направленные вертикально. Покрытие жестко соединено с основанием, однако касательными силами в контакте с основанием, можно пренебречь, поскольку смазка считается идеальной жидкостью. В локальной системе координат ${{x}_{1}}{{x}_{2}}{{x}_{3}}$ с началом в плоскости ${{x}_{1}}{{x}_{2}}$, совпадающей со срединной плоскостью пластины, осью ox3, направленной вверх по нормали к пластине, осью ox1, направленной по касательной к границе торца пластины, осью ox2 – по нормали к его границе. Область, занятая левой пластиной обозначается ${\lambda }$, и описывается соотношениями $\left| {{{x}_{1}}} \right| \leqslant \infty $, ${{x}_{2}} \leqslant - {\theta }$, а занятая правой – индексом r и координатами $\left| {{{x}_{1}}} \right| \leqslant \infty $, ${\theta } \leqslant {{x}_{2}}$ . Для пластин уравнение Кирхгофа для фрагментов $b$ $b = {\lambda },r$, занимающих области ${{\Omega }_{b}}$ с границами $\partial {{{\Omega }}_{b}}$, при вертикальных гармонических воздействиях напряжением ${{t}_{{3b}}}{{e}^{{ - i{\omega }t}}}$ сверху и ${{g}_{{3b}}}{{e}^{{ - i{\omega }t}}}$ снизу после исключения временного параметра имеют вид

${{{\mathbf{R}}}_{b}}{\text{(}}\partial x_{1}^{{}},\partial x_{2}^{{}}{\text{)}}{{u}_{{3b}}} + {{\varepsilon }_{{53b}}}({{t}_{{3b}}} - {{g}_{{3b}}}) \equiv \left( {\frac{{{{\partial }^{4}}}}{{\partial x_{1}^{4}}} + 2\frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial x_{2}^{2}}} + \frac{{{{\partial }^{4}}}}{{\partial x_{2}^{4}}} - {{\varepsilon }_{{43b}}}} \right){{u}_{{3b}}} + {{\varepsilon }_{{53b}}}({{g}_{{3b}}} - {{t}_{{3b}}}) = 0$
$\begin{gathered} {{{\mathbf{R}}}_{b}}( - i{{\alpha }_{1}}, - i{{\alpha }_{2}}){{U}_{{3b}}} = [{{(\alpha _{1}^{2} + \alpha _{2}^{2})}^{2}} - {{\varepsilon }_{{43b}}}]{{U}_{{3b}}}, \\ {{U}_{{3b}}} = {{{\mathbf{F}}}_{{\mathbf{2}}}}{{u}_{{3b}}},\quad {{G}_{{3b}}} = {{{\mathbf{F}}}_{{\mathbf{2}}}}{{g}_{{3b}}},\quad {{T}_{{3b}}} = {{{\mathbf{F}}}_{{\mathbf{2}}}}{{t}_{{3b}}},\quad b = {\lambda },r \\ \end{gathered} $
$\begin{gathered} {{m}_{b}} = - {{D}_{{b1}}}\left( {\frac{{{{\partial }^{2}}{{u}_{{3b}}}}}{{\partial x_{2}^{2}}} + {{{\nu }}_{b}}\frac{{{{\partial }^{2}}{{u}_{{3b}}}}}{{\partial x_{1}^{2}}}} \right) = {{f}_{{3b}}}(\partial {{\Omega }_{b}}),\quad {{D}_{{b1}}} = \frac{{{{D}_{b}}}}{{{{Н}^{2}}}}, \\ {{D}_{{b2}}} = \frac{{{{D}_{b}}}}{{{{Н}^{3}}}},\quad {{x}_{{k0}}} = H{{x}_{k}},\quad k = 1,2 \\ {{q}_{b}} = - {{D}_{{b2}}}\left( {\frac{{{{\partial }^{3}}{{u}_{{3b}}}}}{{\partial x_{2}^{3}}} + (2 - {{{\nu }}_{b}})\frac{{{{\partial }^{3}}{{u}_{{3b}}}}}{{\partial x_{1}^{2}\partial {{x}_{2}}}}} \right) = {{f}_{{4b}}}(\partial {{\Omega }_{b}}) \\ {\text{ }}{{u}_{{3b}}} = {{f}_{{1b}}}(\partial {{{\Omega }}_{b}}),\quad \frac{{\partial {{u}_{{3b}}}}}{{Н\partial {{x}_{2}}}} = {{f}_{{2b}}}(\partial {{\Omega }_{b}}),\quad {{D}_{b}} = \frac{{{{E}_{b}}h_{b}^{3}}}{{12(1 - \nu _{b}^{2})}} \\ \end{gathered} $
${{{\varepsilon }}_{{43b}}} = {{{\omega }}^{2}}{{{\rho }}_{b}}\frac{{(1 - {{{\nu }}_{b}}^{2})12{{Н}^{4}}}}{{E{{h}_{b}}^{2}}},\quad {{{\varepsilon }}_{{53b}}} = \frac{{(1 - {{{\nu }}_{b}}^{2})12{{Н}^{4}}}}{{{{E}_{b}}{{h}_{b}}^{3}}},\quad {\varepsilon }_{6}^{{ - 1}} = \frac{{(1 - {\nu })H}}{{\mu }}$

Здесь для пластин приняты обозначения: ${{{\nu }}_{b}}$ – коэффициент Пуассона, ${{E}_{b}}$ – модуль Юнга, ${{h}_{b}}$ – толщины пластин , ${{{\rho }}_{b}}$ – плотность, ${\omega }$ – частота колебаний. ${{g}_{{3b}}}$, ${{t}_{{3b}}}$ – значения контактных напряжений со стороны основания и давлений на пластины слоя жидкости сверху, действующих вдоль оси ${{x}_{3}}$ в области ${{\Omega }_{b}}$. ${{{\mathbf{F}}}_{2}} \equiv {{{\mathbf{F}}}_{2}}({{{\alpha }}_{{\text{1}}}}{\text{,}}{{{\alpha }}_{{\text{2}}}})$ и ${{{\mathbf{F}}}_{1}} \equiv {{{\mathbf{F}}}_{1}}({{{\alpha }}_{1}})$ двумерный и одномерный операторы преобразования Фурье соответственно, ${{m}_{b}}$ и ${{q}_{b}}$ – изгибающий момент и перерезывающая сила, ${{f}_{1}}(\partial {{\Omega }_{b}})$ – вертикальное перемещение на границе ${{f}_{2}}(\partial {{\Omega }_{b}})$; угол поворота срединной плоскости вокруг оси ${{x}_{1}}$, в системе координат ${{x}_{1}}o{{x}_{2}}$; ${{h}_{b}}$ – толщины пластин, $H$ – размерный параметр подложки, например, толщина деформируемого слоя материала.

Поведение блочного элемента, которым является слой толщины ${{H}_{1}}$ несжимаемой жидкости ${{\Omega }_{0}}$ на поверхности, описывается уравнениями мелкой воды следующего вида

$p = \left( {i{\omega \rho \varphi } + {\rho g}\frac{{i{{h}_{b}}}}{{{\omega }H_{1}^{2}}}{\Delta \varphi }} \right){{e}^{{ - i{\omega }t}}} - w{{e}^{{ - i{\omega }t}}}$

Здесь $p$ – давление в слое жидкости, ${\rho }$ – плотность жидкости, $g$ – ускорение свободного падения, φ – потенциал скоростей в жидкости, $w$ – внешнее воздействие на слой. Учитывая, что на верхней границе литосферной плиты на нее оказывается давление слоя жидкости, с учетом взятой модели необходимо принять

${{t}_{{3b}}} = p,\quad {{u}_{{3b}}} = \frac{{{{h}_{b}}}}{{i{\omega }H_{1}^{2}}}{\Delta }{{{\varphi }}_{b}}$

В результате, дифференциальное уравнение относительно потенциала скоростей принимает вид

${{\Delta }^{3}}{{\varphi }_{b}} + ({{\varepsilon }_{{53b}}}\rho g - {{\varepsilon }_{{43b}}})\Delta {{\varphi }_{b}} + {{\varepsilon }_{{53b}}}\rho \frac{{{{\omega }^{2}}H_{1}^{2}}}{{{{h}_{b}}}}{{\varphi }_{b}} - i{{\varepsilon }_{{53b}}}\frac{{\omega H_{1}^{2}}}{{{{h}_{b}}}}({{g}_{{3b}}} - {{w}_{b}}) = 0$

2. Метод решения. Для использования метода блочного элемента необходимо применить его алгоритм, включающий этапы внешней алгебры, внешнего анализа и фактор – топологии. На этапе внешней алгебры граничная задача сводится к функциональному уравнению следующего вида

(2.1)

Здесь ${{{\omega }}_{b}}{\text{(}}{{{\alpha }}_{{\text{1}}}}{\text{,}}{{{\alpha }}_{{\text{2}}}}{\text{)}},$ $b = {\lambda },r$ – внешние формы, отвечающая рассматриваемой граничной задаче, которые достаточно просто строятся. Для $b = {\lambda }$ она имеет вид

Аналогичный вид имеет внешняя форма для левой полупластины.

Связь между граничными напряжениями и перемещениями на поверхности упругой среды, на которой находятся пластины, в случае полного сцепления слоя с жестким основанием, имеют вид

$\begin{gathered} {{{\mathbf{u}}}_{{3m}}}({{x}_{1}},{{x}_{2}}) = \frac{1}{{4{{\pi }^{2}}\varepsilon _{6}^{{}}}}\sum\limits_{n = 1}^2 {\int\limits_{ - \infty }^\infty {\int {{\mathbf{K}}({{\alpha }_{1}},{{\alpha }_{2}}){{{\mathbf{G}}}_{{{\mathbf{3n}}}}}({{\alpha }_{1}},{{\alpha }_{2}}){{e}^{{ - i\,\langle \,\alpha ,x\,\rangle \,}}}d{{\alpha }_{1}}d{{\alpha }_{2}}} } } , \\ {\mathbf{K}}({{\alpha }_{1}},{{\alpha }_{2}}) = {{{\mathbf{F}}}_{2}}({{\alpha }_{1}},{{\alpha }_{2}}){\mathbf{k}}({{x}_{1}},{{x}_{2}})\quad \left\langle {\alpha ,x} \right\rangle = {{\alpha }_{1}}{{x}_{1}} + {{\alpha }_{2}}{{x}_{2}}, \\ \end{gathered} $
$K({{\alpha }_{1}},{{\alpha }_{2}}) = \left\| {\begin{array}{*{20}{c}} {\alpha _{1}^{2}M + \alpha _{2}^{2}N}&{{{\alpha }_{1}}{{\alpha }_{2}}(M - N)}&{i\alpha _{1}^{{}}P} \\ {{{\alpha }_{1}}{{\alpha }_{2}}(M - N)}&{\alpha _{1}^{2}N + \alpha _{2}^{2}M}&{i\alpha _{2}^{{}}P} \\ { - i\alpha _{1}^{{}}P}&{ - i\alpha _{2}^{{}}P}&R \end{array}} \right\|,$
$\begin{gathered} M\left( u \right) = \frac{{\chi _{2}^{2}({{\sigma }_{2}}{\text{sh}}2{{\sigma }_{2}}{\text{ch}}2{{\sigma }_{1}} - \sigma _{1}^{{ - 1}}{{u}^{2}}{\text{sh}}2{{\sigma }_{1}}{\text{ch}}2{{\sigma }_{2}})}}{{2{{u}^{2}}\Delta \left( u \right)}}, \\ N\left( u \right) = \frac{{2{\text{sh}}2{{\sigma }_{2}}}}{{{{u}^{2}}{{\sigma }_{2}}{\text{ch}}2{{\sigma }_{2}}}}, \\ R\left( u \right) = \frac{{\chi _{2}^{2}({{\sigma }_{1}}{\text{sh}}2{{\sigma }_{1}}{\text{ch}}2{{\sigma }_{2}} - \sigma _{2}^{{ - 1}}{{u}^{2}}{\text{sh}}2{{\sigma }_{2}}{\text{ch}}2{{\sigma }_{1}})}}{{2\Delta \left( u \right)}}, \\ \end{gathered} $
$P(u) = \frac{{(2{{u}^{2}} - 0.5\chi _{2}^{2})\left( {1 - {\text{ch}}2{{\sigma }_{1}}{\text{ch}}2{{\sigma }_{2}}} \right) + \sigma _{1}^{{ - 1}}\sigma _{2}^{{ - 1}}[2{{u}^{4}} - {{u}^{2}}(1.5\chi _{2}^{2} + \chi _{1}^{2}) + \chi _{2}^{2}\chi _{1}^{2}]{\text{sh}}2{{\sigma }_{1}}{\text{sh}}2{{\sigma }_{2}}}}{{\Delta (u)}},$
$\begin{gathered} \Delta \left( u \right) = {{u}^{2}}(2{{u}^{2}} - \chi _{2}^{2}) - (2{{u}^{4}} - {{u}^{2}}\chi _{2}^{2} + 0.25\chi _{2}^{4}){\text{ch}}2{{\sigma }_{1}}{\text{ch}}2{{\sigma }_{2}} + \\ \, + \sigma _{1}^{{ - 1}}\sigma _{2}^{{ - 1}}{{u}^{2}}[2{{u}^{4}} - {{u}^{2}}(2\chi _{2}^{2} + \chi _{1}^{2}) + \chi _{1}^{2}\chi _{2}^{2} + 0.25\chi _{2}^{4}]{\text{sh}}2{{\sigma }_{1}}{\text{sh}}2{{\sigma }_{2}} \\ u = \sqrt {\alpha _{1}^{2} + \alpha _{2}^{2}} \\ \end{gathered} $

Матрица-функция ${\text{K(}}{{\alpha }_{1}},{{\alpha }_{2}}{\text{)}}$ – двух комплексных переменных ${{\alpha }_{1}},{{\alpha }_{2}}$, с мероморфными элементам, с учетом пренебрежения касательными контактными напряжениями между основанием и покрытием упрощается до одного уравнения и принимает вид

$\begin{gathered} {{\Omega }_{1}} \equiv {{\Omega }_{{\lambda }}}(\left| {{{x}_{1}}} \right| \leqslant \infty ;{{x}_{2}} \leqslant - {\theta }),\quad {{\Omega }_{2}} \equiv {{\Omega }_{r}}(\left| {{{x}_{1}}} \right| \leqslant \infty ;{\theta } \leqslant {{x}_{2}}), \\ {{\Omega }_{3}} \equiv {{\Omega }_{\theta }}(\left| {{{x}_{1}}} \right| \leqslant \infty ; - {\theta } \leqslant {{x}_{2}} \leqslant {\theta }) \\ \end{gathered} $

Применим к исследованию функциональных уравнений этап внешнего анализа, названного так, поскольку дифференциальные операции совершаются над внешними формами. С этой целью представим функциональные уравнения в виде

${{U}_{{3b}}}{\text{(}}{{{\alpha }}_{{\text{1}}}}{\text{,}}{{{\alpha }}_{{\text{2}}}}{\text{)}}\,{\text{ = }}\,N_{b}^{{ - 1}}{\text{(}}{{{\alpha }}_{{\text{1}}}}{\text{,}}{{{\alpha }}_{{\text{2}}}}{\text{)[}}{{{\omega }}_{b}}{\text{(}}{{{\alpha }}_{{\text{1}}}}{\text{,}}{{{\alpha }}_{{\text{2}}}}{\text{)}} + {{{\varepsilon }}_{{{\text{53}}b}}}{{S}_{{3b}}}{\text{(}}{{{\alpha }}_{{\text{1}}}}{\text{,}}{{{\alpha }}_{{\text{2}}}}{\text{)]}}$

Потребуем выполнение автоморфизма, одним из способов осуществления которого, является обращение в ноль форм-вычетов Лере лишь в тех нулях ${{\alpha }_{{2n \pm }}} = {{\alpha }_{{2n \pm }}}({{\alpha }_{1}})$ функции $N_{b}^{{ - 1}}({{\alpha }_{1}},{{\alpha }_{2}})$, которые обеспечивают каждой из граничных задач в качестве носителей только свои пластины. Псевдодифференциальные уравнения, вырождающееся в алгебраические. С учетом принятых обозначений, уравнение для левой пластины можно представить в форме

Аналогичный вид имеет второе псевдодифференциальное уравнение для правой. Неизвестными в функциональных уравнениях являются задаваемые на торцах пластин, являющихся дефектами, то есть при ${{x}_{2}} = \pm {\theta }$ внешние воздействия. Их граничные значения в форме преобразований Фурье, представленные группами для левой и правой пластин имеют вид

$\begin{gathered} {{Q}_{\lambda }}({{\alpha }_{1}}, - \theta ),\;{{M}_{\lambda }}({{\alpha }_{1}}, - \theta ),\;{{U}_{{3\lambda {{x}_{2}}}}}({{\alpha }_{1}}, - \theta ),\;{{U}_{{3\lambda }}}({{\alpha }_{1}}, - \theta ),\;{{P}_{\lambda }}({{\alpha }_{1}}, - \theta ),\;{{V}_{{\lambda {{x}_{2}}}}}({{\alpha }_{1}}, - \theta ), \\ {{Q}_{r}}({{\alpha }_{1}},\theta ),\;{{M}_{r}}({{\alpha }_{1}},\theta ),\;{{U}_{{3r\partial {{x}_{2}}}}}({{\alpha }_{1}},\theta ),\;{{U}_{{3r}}}({{\alpha }_{1}},\theta ),\;{{P}_{r}}({{\alpha }_{1}},\theta ),\;{{V}_{{r{{x}_{2}}}}}({{\alpha }_{1}},\theta ) \\ \end{gathered} $

В каждой из двух групп псевдодифференциальных уравнений, в соответствии с постановки той или иной граничной задачи, можно задавать по три граничных условия на торцах пластин и на сечениях водного слоя, определяемых по торцам пластин. Остальные неизвестные определяются в результате решения псевдодифференциальных уравнений. После внесения найденных неизвестных во внешние формы в (2.1), получаем упакованные блочные элементы для пластин и слоев жидкости над ними. Таким образом, этап внешнего анализа для рассматриваемой блочной структуры завершен, поскольку по построению, блочный элемент основания, имеющий неограниченный носитель, является всегда упакованным. Таким же можно было считать и слой жидкости. Однако, полагая, что левая и правая пластины могут иметь разные толщины, рассматривается более сложная граничная задача с учетом этого разделения. Этап фактор-топологии предполагает осуществление сопряжения друг с другом блочных элементов как топологических многообразий с краем. Отношениями эквивалентности являются, продиктованные интересами исследования, принятые в рассматриваемых граничных задачах граничные условия. Для сопряжения блочных элементов с основанием сопрягаются граничные перемещения и контактные напряжения пластин и основания. Для перемещений, имеем

Здесь 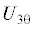объем жидкости в области между торцами пластин и верхней границей поверхности жидкости. При сблизившихся торцах пластин функция ${{U}_{{3\theta }}}$ исчезает. Последнее соотношение можно, выделив контактные напряжения 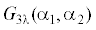, ${{G}_{{3r}}}({{\alpha }_{1}},{{\alpha }_{2}})$, ${{G}_{3}}({{\alpha }_{1}},{{\alpha }_{2}})$, представить в виде

$\begin{gathered} N_{\lambda }^{{ - 1}}({{\alpha }_{1}},{{\alpha }_{2}})\left\langle {{{\omega }_{\lambda }}({{\alpha }_{1}},{{\alpha }_{2}}) + {{\varepsilon }_{{53\lambda }}}i{{R}_{\lambda }}[{{G}_{{3\lambda }}}({{\alpha }_{1}},{{\alpha }_{2}}) - {{W}_{\lambda }}]} \right\rangle + {{U}_{{3\theta }}} + \\ \, + N_{r}^{{ - 1}}({{\alpha }_{1}},{{\alpha }_{2}})\left\langle {{{\omega }_{r}}({{\alpha }_{1}},{{\alpha }_{2}}) + {{\varepsilon }_{{53r}}}i{{R}_{r}}[{{G}_{{3r}}}({{\alpha }_{1}},{{\alpha }_{2}}) - {{W}_{r}}]} \right\rangle = \varepsilon _{6}^{{ - 1}}K({{\alpha }_{1}},{{\alpha }_{2}}){{G}_{3}}({{\alpha }_{1}},{{\alpha }_{2}}) \\ \end{gathered} $

Приняв во внимание, что ${{G}_{3}}({{\alpha }_{1}},{{\alpha }_{2}}) = - {{G}_{{3{\lambda }}}}({{\alpha }_{1}},{{\alpha }_{2}}) - {{G}_{{3r}}}({{\alpha }_{1}},{{\alpha }_{2}})$, и введя обозначения ${{G}_{{3\lambda }}}({{\alpha }_{1}},{{\alpha }_{2}}) = {{G}^{ - }}({{\alpha }_{1}},{{\alpha }_{2}})$, ${{G}_{{3r}}}({{\alpha }_{1}},{{\alpha }_{2}}) = {{G}^{ + }}({{\alpha }_{1}},{{\alpha }_{2}})$, получим следующие функциональные уравнения типа Винера–Хопфа для определения контактных напряжений для двух случаев: $\theta > 0$; $\theta = 0$ при ${{U}_{{3{\theta \lambda }}}} = 0$ в виде

${{M}_{{r\lambda }}}({{\alpha }_{1}},{{\alpha }_{2}}){{G}^{ + }}({{\alpha }_{1}},{{\alpha }_{2}}) = {{G}^{ - }}({{\alpha }_{1}},{{\alpha }_{2}}) + {{T}_{{r\lambda }}}({{\alpha }_{1}},{{\alpha }_{2}}) + {{U}_{{3\theta \lambda }}}$

Функции ${{G}^{ + }}({{\alpha }_{1}},{{\alpha }_{2}})$, ${{G}^{ - }}({{\alpha }_{1}},{{\alpha }_{2}})$ регулярны по параметру ${{\alpha }_{2}}$ в верхней и нижней полуплоскостях соответственно. Здесь приняты обозначения

$\begin{gathered} - [N_{\lambda }^{{ - 1}}({{\alpha }_{1}},{{\alpha }_{2}}){{\varepsilon }_{{53\lambda }}}i{{R}_{\lambda }} + \varepsilon _{6}^{{ \sim 1}}K({{\alpha }_{1}},{{\alpha }_{2}})] = {{M}_{\lambda }}({{\alpha }_{1}},{{\alpha }_{2}}), \\ [N_{r}^{{ - 1}}({{\alpha }_{1}},{{\alpha }_{2}}){{\varepsilon }_{{53r}}}i{{R}_{r}} + \varepsilon _{6}^{{ - 1}}K({{\alpha }_{1}},{{\alpha }_{2}})] = {{M}_{r}}({{\alpha }_{1}},{{\alpha }_{2}}) \\ N_{\lambda }^{{ \sim 1}}({{\alpha }_{1}},{{\alpha }_{2}}){{\omega }_{\lambda }}({{\alpha }_{1}},{{\alpha }_{2}}) - N_{\lambda }^{{ - 1}}({{\alpha }_{1}},{{\alpha }_{2}}){{\varepsilon }_{{53\lambda }}}i{{R}_{\lambda }}{{W}_{\lambda }} = {{T}_{\lambda }}({{\alpha }_{1}},{{\alpha }_{2}}) \\ N_{r}^{{ \sim 1}}({{\alpha }_{1}},{{\alpha }_{2}}){{\omega }_{r}}({{\alpha }_{1}},{{\alpha }_{2}}) - N_{r}^{{ - 1}}({{\alpha }_{1}},{{\alpha }_{2}}){{\varepsilon }_{{53r}}}i{{R}_{r}}{{W}_{r}} = {{T}_{r}}({{\alpha }_{1}},{{\alpha }_{2}}) \\ {{M}_{{r\lambda }}}({{\alpha }_{1}},{{\alpha }_{2}}) = {{M}_{r}}({{\alpha }_{1}},{{\alpha }_{2}})M_{\lambda }^{{ - 1}}({{\alpha }_{1}},{{\alpha }_{2}}),\quad {{U}_{{3\theta \lambda }}} = {{U}_{{3\theta }}} \\ {{T}_{{r\lambda }}}({{\alpha }_{1}},{{\alpha }_{2}}) = [{{T}_{\lambda }}({{\alpha }_{1}},{{\alpha }_{2}}) - {{T}_{r}}({{\alpha }_{1}},{{\alpha }_{2}})]M_{\lambda }^{{ - 1}}({{\alpha }_{1}},{{\alpha }_{2}}) \\ \end{gathered} $

Дальнейший анализ полученных функциональных уравнений и их решение детально изложено в работах [14, 15]. Анализ полученных функциональных уравнений, которые являются более сложными, чем в случае отсутствия слоя жидкости. Поведение контактных напряжений в зоне сближения пластин описывается функциями, приведенными ниже. При исследовании решения первого уравнения, ${\theta } > 0$, то есть в случае не скрытого дефекта, а легко наблюдаемого, имеются следующие свойства контактных напряжений между пластинами и основанием.

При ${\theta } = 0$, то есть, когда дефект является скрытым, контактные напряжения в зоне близости фрагментов лопнувшего покрытия приобретают сингулярную составляющую и имеют поведение вида

$\begin{gathered} {{g}_{{3{\lambda }}}}({{x}_{1}},{{x}_{2}}) \to {{{\sigma }}_{{2{\lambda }}}}({{x}_{1}},{{x}_{2}})x_{2}^{{ - 1}} \\ {{g}_{{3r}}}({{x}_{1}},{{x}_{2}}) \to {{{\sigma }}_{{2r}}}({{x}_{1}},{{x}_{2}})x_{2}^{{ - 1}} \\ \end{gathered} $

Вещественные напряжения с учетом гармонических воздействий имеют вид

${{{\sigma }}_{{3b}}}({{x}_{1}},{{x}_{2}},t) = \operatorname{Re} {{{\sigma }}_{{3b}}}({{x}_{1}},{{x}_{2}}){{e}^{{ - i{\omega }t}}} \equiv \operatorname{Re} {{{\sigma }}_{{3b}}}({{x}_{1}},{{x}_{2}})\cos {\omega }t + \operatorname{Im} {{{\sigma }}_{{3b}}}({{x}_{1}},{{x}_{2}})\sin {\omega }t$

Выводы. Принимая во внимание результаты работ по исследованию стартовых землетрясений, на основании последних формул можно сделать следующие выводы. В том случае, если покрытие состоит из материала с более высокими прочностными свойствами, то появление скрытого дефекта влечет за собой разрушение основания подшипника прочными частями покрытия. В этом случае менее разрушительным является образование не скрытого дефекта с ${\theta } > 0$. В этом случае исчезает целый фрагмент покрытия, но контактные напряжения в зоне покрытия оказываются энергетическими. В том случае, если прочностные свойства материала покрытия уступают материалу основания, то такое покрытие при появлении скрытого дефекта имеет меньше шансов разрушить более прочное основание. В работе исследован простейший вариант из большого разнообразия разрушения смазываемого подшипника при наличии защитного покрытия, а также и без него. Особый интерес возникает в связи с выявлением трещин нового типа [16], которые разрушают материал по иным закономерностям, чем трещины Гриффитса–Ирвина, что будет объектом дальнейших исследований.

Отдельные фрагменты работы выполнены в рамках реализации Госзадания Минобрнауки на 2019 г., проекты ( 9.8753.2017/8.9), ЮНЦ РАН на 2019 г., проекта (00-18-04) № госрег. 01201354241, программ президиума РАН №7, проект (00-18-21) и №20, проект (00-18-29), и при поддержке грантов РФФИ (19-41-230003), (19-41-230004), (19-48-230014), (17-08-00323), (18-08-00465), (18-01-00384), (18-05-80008).

Список литературы

  1. Крагельский И.В., Добычин М.Н., Комбалов В.С. Основы расчетов на трение и износ. М.: Машиностроение, 1977. 526 с.

  2. Горячева И.Г. Горячев А.П. Контактные задачи о скольжении штампа с периодическим рельефом по вязкоупругой полуплоскости // ПММ.2016. Т. 80. Вып. 1. С. 103–116.

  3. Горячева И.Г. Механика фрикционного взаимодействия. М.: Наука, 2001. 478 с.

  4. Горячева И.Г., Добычин М.Н. Контактные задачи в трибологии. М.: Машиностроение, 1988. 256 с.

  5. Горячева И.Г., Маховская Ю.Ю. Моделирование трения на разных масштабных уровнях // Изв. РАН. МТТ. 2010. № 3. С. 117–127.

  6. Ноздрин М.А., Маховская Ю.Ю., Шептунов Б.В. Расчет деформационной составляющей силы трения при скольжении тела по вязкоупругому основанию // Вестник ИГЭУ. 2009. № 3. С. 48–50.

  7. Александров В.М., Горячева И.Г., Торская Е.В. Пространственная задача о движении гладкого штампа по вязкоупругому полупространству // Докл. РАН. 2010. Т. 430. № 4. С. 490–493.

  8. Kuznetsov Ye.A. Effect of fluid lubricant on the contact characteristics of rough elastic bodies in compression // Wear. 1985. V. 102. № 3. P. 177–194.

  9. Горячева И.Г., Фельдштейн И.В. Анализ влияния внутренней системы дефектов на напряженное состояние упругих тел // Изв. РАН. МТТ. 1996. № 5. С. 55–61.

  10. Торская Е.В., Курбаткин И.И., Мезрин А.М., Морозов А.В., Муравьева Т.И., Фролов Н.Н., Сахаров В.В. Механические и трибологические свойства наноструктурированных покрытий на основе многокомпонентных оксидов // Трение и износ. 2013. Т. 34. № 2. С. 129–137.

  11. Горячева И.Г., Торская Е.В., Корнев Ю.В., Григорьев А.Я., Ковалева И.Н., Мышкин Н.К. Теоретикооэкспериментальное исследование механических свойств бикомпонентных покрытий, конденсируемых из паров металлов // Трение и износ. 2015. Т. 36. № 3. С. 340–343.

  12. Горячева И.Г., Фельдштейн И.В. Анализ влияния внутренней системы дефектов на напряженное состояние упругих тел // Изв. РАН. МТТ. 1996. № 5. С. 55–61.

  13. Goryacheva I.G., Torskaya E.V. The effect of interface imperfection and external loading on the axisymetric contact with a coated solid // Wear. 2003. V. 254. № 5–6. P. 538–545.

  14. Babeshko V.A., Evdokimova O.V., Babeshko O.M. On the possibility of predicting some types of earthquake by a mechanical approach // Acta Mechanica. 2018. V. 229. № 5. P. 2163–2175. https://doi.org/10.1007/s00707-017-2092-0

  15. Babeshko V.A., Evdokimova O.V., Babeshko O.M. On a mechanical approach to the prediction of earthquakes during horizontal motion of litospheric plates // Acta Mechanica. 2018. V. 229. № 1. P. 4727–4739. https://doi.org/10.1007/s00707-018-2255-7

  16. В.А.Бабешко, О.М.Бабешко, О.В.Евдокимова Об одном новом типе трещин, дополняющих трещины Гриффитса–Ирвина //ДАН. 2019. Т. 485. № 2. С. 34–38. https://doi.org/10.1134/S1028335819030042

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал