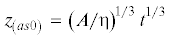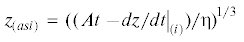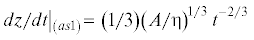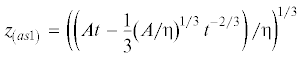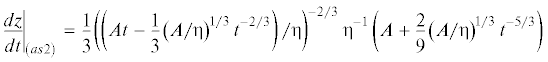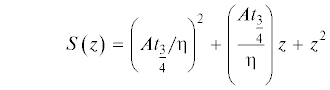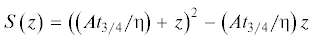Известия РАН. Механика твердого тела, 2020, № 1, стр. 149-157

1. Введение. Процесс нуклеации [1] является сложным многостадийным процессом фазового превращения. Адекватное описание каждой стадии необходимо в силу того, что предыдущая стадия воздействует на протекание последующей эволюции системы. Естественно, в некоторых случаях удается наблюдать редукцию описания системы, но практически во всех случаях число образований новой фазы является важнейшим параметром, управляющим последующей эволюцией.

Пример такого рода демонстрируется и эволюцией системы после окончания формирования образований новой фазы, в том числе твердых зарождений на подложках и в свободном пространстве. На первый взгляд кажется, что процесс формирования зародышей завершен и нет нужды в описании дальнейшей эволюции. Но если в системе существует некоторое малое количество активных центров (гетерогенных центров), то после окончания нуклеации на гетерогенных центрах произойдет процесс гомогенной нуклеации. Для описания гомогенной нуклеации в этом случае необходимо по крайней мере знать решение уравнения баланса при известном количестве образований новой фазы (в данном случае оно равно числу гетерогенных центров). Некоторые весьма эффективные методы построения такого решения и приведены ниже. Естественно, процесс гомогенного образования зародышей новой фазы будет деформировать чистую эволюцию системы при известном числе зародышей. Однако, возможно показать, что эта деформация будет достаточно мала [2]. Проблема построения описания гомогенной нуклеации (или же нуклеации на гетерогенных центрах с существенно меньшей активностью) может быть разделена на два шага – на построение пересыщения без гомогенной нуклеации и на построение решения, которое описывает гомогенную нуклеацию при построенном ранее решении как при внешнем пересыщении [3]. Таким образом, задача построения решения уравнения баланса при известном числе образований новой фазы является достаточно актуальной. Она и будет являться предметом обсуждения и решения ниже.

2. Какая ситуация является наихудшей для описания? При малом количестве гетерогенных центров (а именно в такой ситуации и важно изучение эволюции системы) описать начальные условия к дальнейшей эволюции достаточно легко. Число образований новой фазы совпадает с полным числом гетерогенных центров ${\eta }$. Можно показать, что спектр размеров зародышей новой фазы является практически монодисперсным (аргументы вполне аналогичны представленным в [4]). Идеальное пересыщения Φ (т.е. пересыщение, которое возникло бы в системе при отсутствии потребления метастабильной фазы зародышами новой фазы) является величиной, характеризующей внешние условия. Оно является известной функцией времени t. Возьмем простейшую аппроксимацию

с постоянным коэффициентом A. Форма функции ${\Phi }\left[ t \right]$ может быть весьма различна. Естественно, что $d{\Phi /}dt > 0$. Обобщение на произвольный закон для ${\Phi }$ как функции времени достаточно формально и достоинство предлагаемых ниже методов как раз в том и состоит, что они обобщаются на достаточно произвольный закон зависимости идеального пересыщения от времени. Они оказываются эффективными для зависимостей, при которых не происходит лавинного нарастания пересыщения во времени даже при зарождении частиц новой фазы. Легко определить предельные законы для таких зависимостей. Если считать, что спектр зародышей новой фазы финитный, то предельной зависимостью будет время в кубе, а если считать, что зарождение образований новой фазы продолжается, то предельной зависимостью будет время в четвертой степени. Здесь и в дальнейшем режим роста зародышей считается свободномолекулярным.

Уравнение баланса может быть записано в следующем виде

где ${\zeta }$ является действительным пересыщением и слагаемое ${\eta }{{z}^{3}}$ является числом молекул в образованиях новой фазы. В последнем члене $z$ является линейным размером образований новой фазы, а ${\eta }$ является полным числом образований новой фазы, которое уже не изменяется со временем и равно полному числу гетерогенных центров. В различных типах внешних условий могут появляться множители перед последним членом. Эти множители вызываются типом эволюции, навязанным внешними условиями. Если процесс нуклеации вызван изотермическим охлаждением системы, то возникнет один множитель, если адиабатическим расширением – то другой. В любом случае этот множитель известен, примем для него обозначение W[t]. Тогда

Можно рассмотреть ситуацию, в которой W[t] = 1 (это ситуация исключительно источника пара), остальные физически значимые ситуации рассматриваются аналогично. При напылении на подложку мы имеем, естественно, источник пара в чистом виде и вводить данный множитель нет нужды.

В обезразмеренном времени пересыщение ζ связано с изменением линейного размера как ${\zeta }~~ = dz{\text{/}}dt$.

Данное соотношение замыкает соотношение (2.1) и оно становится обыкновенным дифференциальным уравнением первого порядка (но нелинейным, уравнением Абеля в случае отсутствия множителя, отвечающего типу внешних условий). Необходимо поставить начальное условие, которое выглядит как $z\left( {{{t}_{{init}}}} \right) = 0$, где ${{t}_{{init}}}$ является моментом времени, в который произошла гетерогенная нуклеация (здесь можно говорить именно о моменте гетерогенной нуклеации, поскольку спектр размеров образований новой фазы является монодисперсным). Естественно, ${{t}_{{init}}} > 0~$ (поскольку t = 0 является моментом, в который ${\Phi }$ стало положительным и раньше никакого зародышеобразования в стабильной на этот момент фазе происходить не могло). Какая же ситуация является наихудшей для применения методов, представленных ниже? Ответом является ${{t}_{{init}}} = 0$. Чем больше ${{t}_{{init}}}$, тем сильнее оценки, лежащие в основе приближенных методов, представленных ниже. Эта часть анализа выполнена в [2] и нет нужды повторять ее здесь. Поворотной точкой анализа является выделение параметра

Здесь ${{t}_{{max}}}$ является моментом, в который достигается максимум пересыщения, ${{\zeta }_{{max}}}$ является величиной этого максимума. Параметр Q оказывается достаточно малым. Именно малость этого параметра играет ключевую роль в быстрой сходимости итераций, построенных ниже. Можно показать, что этот параметр управляет точностью дальнейших построений вплоть до наступления асимптотического периода эволюции. Можно записать все формулы, представленные ниже, также и для произвольного значения произвольного ${{t}_{{init}}}$, но они будут достаточно длинными. Запишем поэтому формулы только для наихудшей ситуации. Парадоксально, но они будут самыми короткими. Естественно, простейший в принципиальном плане путь обоснования применимости формул для произвольного случая заключается в том, чтобы записать их в явном виде для произвольного ${{t}_{{init}}}$.

3. Случай ${{t}_{{init}}} = 0$. Выбираем наихудший из возможных случаев. Тогда эволюционное уравнение записывается в виде

с начальным условием

Будем называть $dz{\text{/}}dt$ просто пересыщением ${\zeta }$. Перенормировкой приходим к

с тем же начальным условием.

3.1. Определение максимума пересыщения. В этом случае построение итераций вполне логично и естественно. Итерации определяются рекуррентными формулами

с начальным приближением в виде

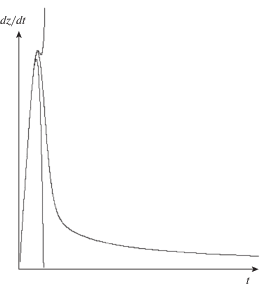
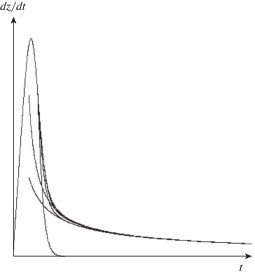
Итерации и точное решение (оно стремится к оси абсцисс на больших временах) представлены на рис. 1 . Чем выше номер итерации, тем точнее она приближается к решению. Мы видим, что первая итерация достаточно хорошо описывает качественное поведение решения, но не может дать достаточно точного значения для амплитуды пересыщения. Вторая итерация уже может обеспечить нахождение достаточно точного амплитудного значения пересыщения (для случая интенсивной нуклеации). Можно аналитически посчитать все итерации более высокого порядка, которые будут еще точнее описывать решение на стадии возрастания пересыщения и будут все точнее определять положение максимума пересыщения и его значение. Но описать сколько-нибудь точно и эффективно этап падения пересыщения данным способом не получается. Причина этого кроется в изменении скорости сходимости итераций. Действительно, сила итерационной процедуры основывается на малости параметра

После падения пересыщения мы имеем обратную ситуацию

что показывает неэффективность итерационного подхода к описанию обратной стороны горба пересыщения.

3.2. Обратная сторона горба пересыщения по соседству с максимумом. Задача получить решение на всем периоде спадания пересыщения оказывается слишком сложна, чтобы предложить аппроксимацию, пригодную всюду на данном периоде. Поэтому разобьем данный период на несколько подпериодов. Первый подпериод будет ограничен спаданием пересыщения до трех четвертей от максимального значения

На этом подпериоде имеется по крайней мере два эффективных подхода. Первый состоит в перенормировке первой итерации так, чтобы иметь правильное (точное) положение максимума (это положение определяется в рамках второй первоначальной итерации). Затем на основе перенормированной первой итерации строится вторая итерация. Второй подход оказывается еще проще. Определим положение максимума ${{t}_{{max}}}$ и амплитудного значения ${{{\zeta }}_{{max}}}$ на основе первоначальных итераций. Для второй производной ${{d}^{2}}{\zeta /}d{{t}^{2}}$ получаем

Около максимума ${\zeta }$ второй член в правой части предыдущего выражения должен быть мал и первый член приближенно пропорционален $z$, поскольку ${\zeta }$ около своего максимума меняется незначительно. Итак, ${{d}^{2}}{\zeta /}d{{t}^{2}}$ пропорционально $z$

Первая первоначальная итерация является хорошей оценкой снизу для t_max, ${{{\zeta }}_{{max}}}$, ${{z}_{{max}}}$. Явные вычисления дают

Условие на максимум записывается в виде

и тогда

${{t}_{{max}}} = {{(8{\text{/}}(6{\eta }{{A}^{2}}))}^{{1/25}}}$. Это означает, что в перенормированных величинах выполняется оценка

Тогда, чтобы отклонить ${{d}^{2}}{\zeta /}d{{t}^{2}}$ существенно необходимо изменить z тоже существенно. Но согласно (3.3) для $z > 1$ получаем, что существенное отклонение $~z$ означает радикальное падение ${\zeta }$. Тогда ${{d}^{2}}{\zeta /}d{{t}^{2}}$ может рассматриваться как квазиинтеграл эволюции в период после ${{t}_{{max}}}$ и до полного падения ${\zeta }$ (в действительности до существенного, а не до полного падения ${\zeta }$, поскольку согласно (3.2) именно изменение ${\zeta }$ отклонит ${{d}^{2}}{\zeta /}d{{t}^{2}}$ от величины максимума пересыщения. Следует отметить, что невозможно проинтегрировать (3.1) напрямую, положив здесь $z = {{z}_{{max}}}$

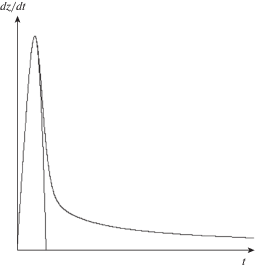
поскольку именно отклонение $z$ от ${{z}_{{max}}}$ является причиной отклонения ${\zeta }$ от ${{{\zeta }}_{{max}}}$ в самом начале падения сразу же после ${{t}_{{max}}}$. В результате приходим в оправданию применимости аппроксимации для $t > {{t}_{{max}}}$ вплоть до падения ζ. В действительности эта аппроксимация хорошо работает вплоть до ${{t}_{{3/4}}}$, определяемого из

Квадратичная аппроксимация (нижняя кривая) и точное решение (верхняя кривая) показаны на рис. 2.

3.3. Асимптотики. Чтобы описать эволюцию после ${{t}_{{3/4}}}$ можно предложить набор методов. Различные подпериоды должны описываться различными методами. Вначале опишем асимптотический подпериод, который соответствует $t \to \infty $. В этом случае можно приближенно записать

Тогда

Рекуррентная процедура является следующей:

и

Вычисления приводят к

и в первом приближении и к во втором приближении. Первое и второе асимптотические приближения и точное решение (кривая выходит из начала координат) показаны на рис. 3. Чем выше номер приближения, тем оно точнее.

Видно, что уже первое приближение для $dz{\text{/}}dt$ работает хорошо, второе приближение еще точнее. Совместно с квадратичной аппроксимацией можно считать, что решение – это комбинация асимптотики и квадратичного приближения, причем квадратичное приближение берется там, где оно выше асимптотики, а асимптотика берется там, где она выше квадратичного приближения. Полученное решение вполне применимо, но оно страдает одним очевидным недостатком. Оно не может обеспечить плавной релаксации решения к асимптотике. Чтобы увидеть эту релаксацию необходимо рассмотреть подпериод эффективной релаксации и использовать другие специфические черты решения.

3.4. Релаксация и деформированная релаксация. Уже даже первая первоначальная итерация оказывается способна описать процесс качественно и показать одну важную черту процесса. Этой чертой является быстрое спадание |dz/dt| вскоре после достижения максимума. Это поведение обеспечивается большой степенью $6$ (именно, $6 \gg 1$) в законе для dz/dt. Рассмотрим моменты времени, которые больше чем ${{t}_{{3/4}}}$. Тогда моменты времени t, на которых dz/dt отклоняется от асимптотического значения ${{\left. {dz{\text{/}}dt} \right|}_{{as}}}$ удовлетворяют неравенству

Последнее неравенство позволяет приближенно рассмотреть действие источника At как $A{{t}_{{3/4}}}$. Тогда эволюционное уравнение становится следующим

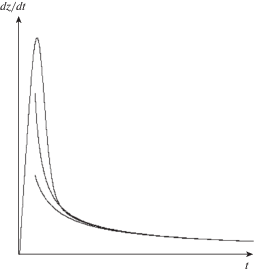
Последнее выражение позволяет аналитически вычислить интеграл. Это позволяет получить кривые ${{z}_{{rel}}}\left( t \right)$ и ${{(dz{\text{/}}dt)}_{{rel}}}\left( t \right)$. Естественно, что ${{(dz{\text{/}}dt)}_{{rel}}}$ приближается к нулю. На рис. 4 можно заметить кривую, приближающуюся к нулевому уровню. Это ${{(dz{\text{/}}dt)}_{{rel}}}$.

Слабейшим местом в построенном решении ${{(dz{\text{/}}dt)}_{{rel}}}$ является то, что оно стремится точно к нулю. На самом деле оно должно было бы приближаться к ${{(dz{\text{/}}dt)}_{{as}}}$. Чтобы получить необходимое свойство нужно предложить приближенную деформацию решения. Мы записываем релаксацию, но не к нулю, а к асимптотике. После проведения подобной деформации релаксационная кривая будет обозначаться ${{\left. {\left( {dz{\text{/}}dt} \right)} \right|}_{{rel~as}}}$. Она выглядит как

В этом случае можно взять асимптотику любого порядка. На рис. 4 можно увидеть кривые, приближающиеся к ${{(dz{\text{/}}dt)}_{{\left( {as1} \right)}}}$ и к ${{(dz{\text{/}}dt)}_{{\left( {as2} \right)}}}$. Эти кривые соответствуют релаксационным решениям ${{(dz{\text{/}}dt)}_{{relas\left( 1 \right)}}}$ и ${{(dz{\text{/}}dt)}_{{relas\left( 2 \right)}}}$ (решения известны по предыдущему рисунку). Видно, что соответствие между настоящим решением (кривая выходит из начала координат) и аппроксимациями идеально (в масштабах рисунка отличить практически невозможно).

Можно предложить также приближенное вычисление интеграла

Легко заметить, что величина

не приходит при $z > {{z}_{{3/4}}}$ к нулю. Тогда можно положить $S\left( {{{z}_{{3/4}}}} \right)$ вместо $S\left( z \right)$ и интеграл сведется к чистому логарифму. Это дает выражение для времени релаксации ${{t}_{{rel}}}$. Деформационный метод основан на том факте, что асимптотики при $t > {{t}_{{3/4}}}$ имеют достаточно малую производную ${{(dz{\text{/}}dt)}_{{as}}}$. А именно,

Данный метод достаточно эффективен для построения решения эволюционного уравнения.

4. Заключение. Представленные выше подходы позволяют построить адекватное решение уравнения баланса во все моменты времени. Это позволит достаточно точно описать стадию последующего зарождения (гомогенное зарождение). Действительно, гомогенное зародышеобразование может иметь место только при возрастании идеального пересыщения. При этом достаточно описать период возрастания пересыщения, что достигается построением первоначальных итераций. Но ведь зарождение может происходить и на гетерогенных центрах, которые могут быть впрыснуты в систему в любой момент (например, можно осветить камеру с пересыщенной фазой и создать ионы для конденсации). Таким образом, нужно уметь строить решение уравнения баланса во все моменты времени, что и реализовано выше. Достоинством приведенных выше методов является то, что они могут использоваться при достаточно произвольных функциональных зависимостях идеального пересыщения от времени, а не только линейного, использованного выше исключительно в целях наглядности.