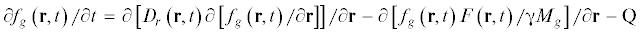Известия РАН. Механика твердого тела, 2020, № 1, стр. 137-148
СТОХАСТИЧЕСКАЯ МОДЕЛЬ ЗАРОЖДЕНИЯ ПОР ПРИ ОБЛУЧЕНИИ ОБРАЗЦА ИОНАМИ ИНЕРТНОГО ГАЗА
Г. И. Змиевская *
Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
* E-mail: zmig@mail.ru
Поступила в редакцию 01.07.2019
После доработки 04.08.2019
Принята к публикации 18.09.2019
Аннотация
Неточечные вакансионно-газовые дефекты (ВГД) (поры, блистеры) в кристаллической решетке возникают в результате ее облучения инертным газом Xe++, процесс рассмотрен как образование зародышей фазового перехода 1-го рода средствами вычислительной математики, кинетической теории, а также теории стохастических динамических переменных и Винеровских случайных процессов. Рассчитаны характеристики неупорядоченной пористости в образцах, состоящих из слоев (“диэлектрик/металл”) при различных толщинах слоев. Формирование дефектов сферической формы в материалах на временах порядка 10–4 cек, когда зарождается пористость материала, предшествует или сопровождает появление микротрещин. Облучение поверхностей инертным газом с энергиями ионов 5–10 kэB относится к процессам низкотемпературного блистеринга, в модели постоянство воздействия радиационных потоков, стимулирующих фазовый переход, создает условие “открытой” физической системы, в которой возможно объединение дефектов решетки в структуры, вызывающие локальные напряжения, а постоянство температуры образца, давления импланитруемых “мономеров” газа и пересыщения (подобных параметрам конденсации пара) характерны для флуктуационной неустойчивой стадии фазового перехода. Кинетические уравнения в частных производных с нелинейными коэффициентами (Колмогорова–Феллера и Эйнштейна–Смолуховского) решаются методом стохастической молекулярной динамики, устанавливающей связь решения стохастических уравнений Ито в смысле Стратоновича с кинетическими уравнениями, используются устойчивые численные методы. Определены условия образования ВГД с учетом влияния упругих свойств решетки, а также рассчитаны пористость и локальные напряжения в тонких слоях облучаемых материалов.
Введение. Современные перспективные теоретико-экспериментальные исследования нелинейной оптики [1], материаловедения [2], фотоники [3], лазерной физики [4] и других направлений привлекают внимание вычислителей, так новые возможности вычислительной техники стимулировали появление численного эксперимента в плазме и плазмоподобных средах [5] на основе кинетической теории и математической физики для изучения механизмов неравновесных быстропротекающих процессов в бесстолкновительной среде с самосогласованными электромагнитными полями. Физико-химические процессы столкновительной и флуктуационной природы в поверхностных слоях твердого тела приводят к фазовым превращениям, повреждениям порами и микротрещинами, самосогласованно меняются упругие свойства материала.
Имплантацию ионов в поверхность чаще всего представляют каскадами точечных дефектов, распространяющихся вглубь облучаемого материала без создания объемных дефектов.
Внедрение инертного газа и вакансий (или ВГД), создает нанопористость, плотность которой и распределение пор по размерам и расстояниям от облучаемой поверхности с оценкой локальных упругих напряжений представляет интерес для управления свойствами пористых полупроводников, для создания матриц диэлектриков с включениями наночастиц металла в интересах плазмоники.
Устройства на основе пористых полупроводников можно интегрировать с существующими полупроводниковыми оптическими и электронными элементами. Показатель преломления и диэлектрическая проницаемость пористых полупроводников меньше, чем у объемных материалов. Это может быть использовано для создания сред с низкой диэлектрической проницаемостью, что актуально, в частности, в связи с уменьшением размеров компонентов компьютеров. Учитывая развитую поверхность пористых сред и возможность их заполнения различными газами или жидкостями пористые среды возможно использовать в качестве сенсоров. Меняя толщину пористых слоев, можно создавать различные оптические среды и устройства, включая фотонные кристаллы.
1. Уравнения стохастической модели. Развитие численных методов для решения краевых задач математической физики методом физико-вероятностных аналогов [6] требует численного решения стохастических уравнений (СДУ) и вычисления интегралов от ансамбля траекторий случайных процессов, которые ассоциируются с конденсацией паров и ионной имплантацией. Алгоритмы метода стохастической молекулярной динамики [7] устойчивы и эффективны, а включение броуновского движения (БД) центров масс ВГД в решетке в модель позволяет рассматривать фазовый переход, происходящим в плазмоподобной среде. Зарождение газового пузырька в решетке возмущает колебания акустических фононов во всех материалах и фриделевские осцилляции плотности электронов решетки металлов и полупроводников, что учитывается дальнодействующим потенциалом косвенного упругого взаимодействия ВГД друг с другом и границами слоев, через возмущение колебаний акустических фононов, зависит от плотности ВГД и расстояния до границ слоев и до включений твердофазных дефектов (зерен), являющихся стоками для движущихся ВГД.
Пористость находится численным интегрированием функции распределения (ФР) размера кластера пор и ФР координат, то есть решением квазилинейных кинетических уравнений в частных производных [8], формулируемых относительно ФР стохастических динамических переменных [9]. В модели начальной стадии фазового перехода это g – размер сферического дефекта решетки и x, y, z – декартовы координаты центра масс ВГД, эволюция которых определяется расчетом конечного числа N траекторий винеровских случайных процессов, причем рассчитываются сами переменные (как точки фазовых пространств {G} и {R} размеров пор и их координат, соответственно) и плотности переходных вероятностей случайных процессов, которые ассоциируются с уравнениями математической физики для кинетических ФР. Как моменты ФР получены характеристики пористости и локальных напряжений в модельном объеме, возникающих при образовании пор из-за скачка давления на границе пузырька газа сферической формы.
Размеры пор и нанокластеров в этих материалах составляют от единиц нанометров до долей микрометра в зависимости от условий формирования [10]. Численные модели неравновесной кинетики фазового перехода [6, 7] используют модифицированные алгоритмы решения систем линейных СДУ Ито в смысле Стратоновича устойчивыми методами семейства методов Розенброка и суперпозицию диффузионных и скачкообразных случайных процессов [11, 12]. Выбранный материал для моделирования – карбид кремния, радиационностойкий алмазоподобный, достаточно дорогой, находящий применение и как источник упрочения в композиционных материалах и как широкозонный полупроводник, механизмы создания и свойств которого разносторонне представлены в [10].
1.1. Кластеризация дефектов. Кинетические уравнения в частных производных Колмогорова–Феллера и Эйнштейна–Смолуховского с нелинейными коэффициентами решаются новыми устойчивыми численными методами. Теория стохастических динамических переменных [9, 8 ] устанавливает связь решения уравнений Ито в смысле Стратоновича для траекторий винеровских случайных процессов с плотностью переходной вероятности этих процессов, или функциями распределения кинетических уравнений ${{f}_{r}}\left( {g,t} \right)$ и ${{f}_{g}}\left( {{\mathbf{r}},t} \right)$, ФР ${{f}_{g}}\left( {{\mathbf{r}},t} \right)$ зависит от r – положения зародышей кластеров в ортогональной системе координат. Область изменения переменных в (1): $g \in [2,{{g}_{{\max }}}]$, $t \in \left[ {0,{{t}_{\infty }}} \right]$. Функция ${{f}_{r}}\left( {g,t} \right)$ нормирована так, чтобы в единице объема находился хотя бы один кластер, состоящий не менее чем из двух частиц. Макроскопические характеристики (число кластеров в единице объема и др.) могут быть вычислены с учетом функции ${{f}_{r}}\left( {g,t} \right)$. Вычислительная реализация математической модели кластеризации (уравнения Колмогорова) требует решения квазилинейного интегро-дифференциального уравнения в частных производных второго порядка. Уравнение Колмогорова–Феллера для кластеризации формулируется относительно функции распределения /ФР/ зародышей пор по размерам в точке ${\mathbf{r}} = \sqrt {{{x}^{2}} + {{y}^{2}} + {{z}^{2}}} $ объема решетки:
(1.1)
$\begin{gathered} \partial {{f}_{r}}\left( {g,t} \right){\text{/}}\partial t = \partial \left[ {{{D}_{g}}\left( {g,t} \right)\left( {\partial {{f}_{r}}\left( {g,t} \right){\text{/}}dg} \right)} \right]{\text{/}}\partial g + \\ + \;\frac{1}{{{{k}_{B}}T}}\partial \left[ {{{D}_{g}}\left( {g,t} \right){{f}_{r}}\left( {g,t} \right)\partial \Delta \Phi \left( {g,r,t} \right){\text{/}}\partial g} \right]\partial g + {{S}_{\alpha }} + {{\Omega }_{{b{v}}}} \\ {{f}_{r}}\left( {g,0} \right) = {{f}_{{0g}}},\quad d{{f}_{r}}\left( {g,t} \right){\text{/}}{{\left. {dg} \right|}_{{g = 2}}} = 0,\quad {{f}_{r}}{{\left. {\left( {g,t} \right)} \right|}_{{g = 2}}} = 0 \\ \end{gathered} $Постоянный поток инертного газа образует ${{S}_{{\alpha }}} = S({{f}_{{\alpha }}}({v}))$ – источник частиц, формирующих блистер, ${{f}_{{\alpha }}}\left( V \right)$ – равновесная ФР “мономеров” по скоростям ${v}$, ${\alpha }$ обозначает газ и/или вакансию; ${{f}_{{0g}}}$ – ФР ВГД по размерам в слое в начальный момент времени, g – размер ВГД, измеряемый в единичных несжимаемых объемах атомов ксенона, ${{\Omega }_{{b{v}}}}$ – оператор столкновения и рекомбинации блистеров и вакансий, моделируется скачкообразным случайным процессом [11, 12], T – температура слоя, ${{k}_{{\text{B}}}}$ – постоянная Больцмана.
В (1.1) функционал-коэффициент диффузии ${{D}_{g}}\left( {g,t} \right)$ в пространстве размеров {G}, зависит от температуры T и давления “мономеров” (паров) ${{p}_{{v}}}$, определен в модели как D(g, t) = $D\left( {\left\langle g \right\rangle ,t} \right) \sim {{\left\langle g \right\rangle }^{{2/3}}}$, зависит от частоты колебаний атома решетки и ее упругих свойств. Здесь 〈g〉 – математическое ожидание среднего размера зародыша в точке r, $\left\langle g \right\rangle = \left\langle {g\left( t \right)} \right\rangle = \int_{g = 2}^{g\max } {g{{f}_{r}}\left( {g,t} \right)} dg$, рассчитанное в соответствии с ФР ${{f}_{r}}\left( {g,t} \right)$ из (1.1). Выражение для свободной энергии Гиббса $\Delta \Phi \left( {\left\langle g \right\rangle ,{\mathbf{r}},t} \right)$ – термодинамического потенциала образования зародыша, $\Delta \Phi $ измерен в ${{k}_{{\text{B}}}}T$.
Полная свободная энергия Гиббса формирования ВГД $\Delta \Phi $ в процессе кластеризации “мономеров” может состоять из слагаемых
(1.2)
$\Delta \Phi \left( {g,{\mathbf{r}},t} \right) = \Delta {{\Phi }_{I}} + \Delta {{\Phi }_{K}} + \Delta {{\Phi }_{Z}} + \Delta {{\Phi }_{b}} + \Delta {{\Phi }_{r}} + \Delta {{\Phi }_{g}}$ учтено поверхностное натяжение на границе “газ в поре – материал слоя”, $\Delta {{\Phi }_{b}}$ – упругая реакция решетки на образование зародыша, зависящая от K – модуля сжимаемости материала слоя, ${{V}_{{sub}}}$ – объема, приходящегося на атом материала слоя, и ${{V}_{{gas}}}$ – объема атома внедренного материала, $\Delta {{\Phi }_{Z}}$ – вклад в свободную энергию Гиббса, вызванный несоразмерностью параметров решеток
материалов слоев в точке центра масс зарождающегося ВГД, зависит от расстояния до
границы раздела слоев, $\Delta {{\Phi }_{r}}$ – положение ВГД в узлах – междоузлиях матрицы материала слоя и условие разрыва упругих
связей решетки. Для вакансионных кластеров еще учитывается заряд кластера $\Delta {{\Phi }_{g}}$. Запишем стохастическое дифференциальное уравнение (СДУ) для случайного процесса
$\left\{ {g\left( t \right),t \geqslant 0} \right\}$, плотность переходной вероятности которого является решением кинетического уравнения.
учтено поверхностное натяжение на границе “газ в поре – материал слоя”, $\Delta {{\Phi }_{b}}$ – упругая реакция решетки на образование зародыша, зависящая от K – модуля сжимаемости материала слоя, ${{V}_{{sub}}}$ – объема, приходящегося на атом материала слоя, и ${{V}_{{gas}}}$ – объема атома внедренного материала, $\Delta {{\Phi }_{Z}}$ – вклад в свободную энергию Гиббса, вызванный несоразмерностью параметров решеток
материалов слоев в точке центра масс зарождающегося ВГД, зависит от расстояния до
границы раздела слоев, $\Delta {{\Phi }_{r}}$ – положение ВГД в узлах – междоузлиях матрицы материала слоя и условие разрыва упругих
связей решетки. Для вакансионных кластеров еще учитывается заряд кластера $\Delta {{\Phi }_{g}}$. Запишем стохастическое дифференциальное уравнение (СДУ) для случайного процесса
$\left\{ {g\left( t \right),t \geqslant 0} \right\}$, плотность переходной вероятности которого является решением кинетического уравнения.
Уравнению соответствует СДУ Ито в смысле Стратоновича, СДУ запишем для простоты без источника газа и вакансий ${{S}_{\alpha }} = 0$
(1.3)
$\begin{gathered} dg\left( t \right) = {{f}_{1}}\left( {g,t} \right)dt + {\sigma }\left( {g,t} \right)dw(t),\quad g({{t}_{0}}) = {{g}_{0}} \\ {{f}_{1}}\left( {g,t} \right) = \left( {\frac{{D\left( {g,t} \right)}}{{kT}}\frac{{d\Delta \Phi \left( {g,t} \right)}}{{\partial g}} - \frac{1}{2}\frac{{\partial D\left( {g,t} \right)}}{{\partial g}}} \right);\quad {\sigma }(g,t) = \sqrt {2D(g,t)} \\ \end{gathered} $Здесь dw – приращение случайного процесса, моделирование которого относится к алгоритмической реализации численного эксперимента, эффективность и особенности обсуждаются в [6, 11].
1.2. Стохастическая диффузия. БД блистеров в кристаллической решетке описывается уравнением Эйнштейна–Смолуховского относительно ФР ${{f}_{g}}\left( {{\mathbf{r}},t} \right)$, зависящей от ${\mathbf{r}}$ – расположения центров масс кластеров зародышей пор с размером 〈g〉 в ортогональной системе координат {0, x, y, z} в образце:
Потенциал $U({\mathbf{r}})$ нормирован на величину $({{N}_{e}}\left| {{{V}_{F}}\left( {2{{k}_{F}}} \right)} \right|{\text{/}}(2\pi {{\varepsilon }^{2}}) + {{W}_{{elast}}})\Omega {\text{/}}{{k}_{{\text{B}}}}T$ где $\Omega $ – объем элементарной ячейки ${{N}_{e}}$ – электронная плотность, ${\varepsilon }$ – диэлектрическая проницаемость, ${{W}_{{elast}}}$ – модули упругости соответствующего слоя материала, ${{k}_{{\text{F}}}}$ – импульс Ферми электрона, ${{V}_{{\text{F}}}}\left( {2{{k}_{{\text{F}}}}} \right)$ – фурье-компонента потенциала взаимодействие электрона с точечным дефектом. Вывод формул для $U({\mathbf{r}})$ был сделан для слабоанизотропной решетки, точечных дефектов и сферической поверхности энергии Ферми [14].
Кинетическому уравнению (1.4) в частных производных Эйнштейна–Смолуховского для функции распределения ${{f}_{g}}\left( {{\mathbf{r}},t} \right)$ будет соответствовать стохастический аналог – СДУ Ито в смысле Стратоновича, где $dw(t)$ приращение винеровского процесса, не конкретизируем стоки (Q = 0)
(1.5)
$\begin{gathered} d{\mathbf{r}}(t) = \left( {\frac{{F\left( {{\mathbf{r}},t} \right)}}{{{{M}_{g}}{\gamma }}} - \frac{1}{2}\frac{{\partial {{D}_{r}}\left( {{\mathbf{r}},t} \right)}}{{\partial {\mathbf{r}}}}} \right) \cdot dt + \sqrt {2{{D}_{r}}\left( {{\mathbf{r}},t} \right)} \cdot dw(t) \\ {\mathbf{r}}\left( {t = 0} \right) = {{{\mathbf{r}}}_{0}},\quad \forall {\mathbf{r}} \in \left\{ {\mathbf{R}} \right\},\quad t \in \left[ {0,{{T}_{{fin}}}} \right] \\ \end{gathered} $Методы традиционной молекулярной динамики применяются в решении многих задач [13]. Стохастические уравнения (1.3) и (1.5) решаются численным методом стохастической молекулярной динамики [6, 7], заметно отличающимся постановкой задач, устойчивостью метода решения СДУ и выбором потенциала взаимодействия броуновских частиц, вывод формул для которого и идеи кластеризации дефектов в решетке [14] были модифицированы для расчетов блистеринга в [6], модель потенциала востребована и в настоящее время [15] связь пористости с напряжениями в материалах рассмотрена в [16].
Стандартный расчет вариантов: количество траекторий составляет 106, шаг по времени составляет ${{{\tau }}_{g}} = {{10}^{{ - 8}}}$ с количество шагов по времени на $\left[ {0,{{T}_{{fin}}}} \right]$ составляет 105. При этом кинетические уравнения в частных производных заменены уравнениями стохастического аналога в форме систем СДУ Ито–Стратоновича с нелинейными коэффициентами, их решение проводится на основе модификации [6] устойчивого обобщенного метода типа Розенброка.
2. Обсуждение результатов численных экспериментов. Задачи кластеризации ВГД с учетом их БД рассматривались в работах [17–19], дальнейшая обработка, анализ численных экспериментов, их визуализация [20] предоставляют дополнительную информацию о свойствах зарождения пористости.
Пористость ВГД в случае присутствия в образце и пузырьков газа и вакансий рассчитывается как:
(2.1)
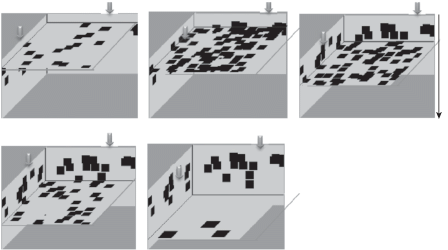
$por = \frac{{4\pi {{{\left( {{{r}_{b}} + {{r}_{{v}}}} \right)}}^{3}}}}{{3{{V}_{1}}}}\int {({{{\left\langle {{{g}_{b}}} \right\rangle }}^{3}}{{f}_{b}}\left( {\left\langle {{{g}_{b}}} \right\rangle ,x,y,z} \right) + {{{\left\langle {{{g}_{{v}}}} \right\rangle }}^{3}}{{f}_{{v}}}\left( {\left\langle {{{g}_{{v}}}} \right\rangle ,x,y,z} \right))dgdxdydz} $На рис. 1 приведены результаты перколяционного анализа ФР ${{f}_{b}}\left( {{\mathbf{r}},t = {{T}_{{fin}}}} \right)$ в момент окончания расчета ФР ВГД в нескольких сечениях образца Mo/Si, перпендикулярных направлению потока ионов инертного газа, различающихся глубиной от облучаемой поверхности. Черным изображены кластеры дефектов, серым – бездефектные области, пористость в образце сформировалась при облучении его ионами Ar с энергией 5 кэВ, доза облучения 1015 см–2 температура образца 800 K. Поры неравномерно распределены по глубине в образце.
По распределениям ВГД (по размерам пор и их координатам) можно рассчитать среднюю протяженность дефектов в решетке, образца SiC/Mo для плоскостей, перпендикулярных потоку ${\text{X}}{{{\text{e}}}^{{ + + }}}$.
Расчет средних размеров структур пор в объеме 1 × 1 × 0.5 мкм материала 3C-SiC в зависимости от температур образца (серия расчетов приведена при одинаковых условиях облучения) приведены на рис. 2. По оси ординат графика отложена средняя протяженность структур пор в долях размера по оси x, по оси абсцисс температуры $T{\text{/}}{{T}_{{melt}}}$, где ${{T}_{{melt}}}$ температура плавления карбида кремния (момент окончания расчетов 1.5 мс). Энергия ионов ксенона 4 кэВ и доза 1016 см–2.
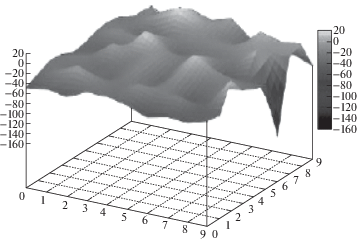
Рисунок 3 иллюстрирует поверхность равных значений $U\left( {x,y,{{z}_{k}}} \right)$ потенциала косвенного упругого взаимодействия кластеров зародышей ВГД между собой и с границами образца (через акустические фононы решеток и фриделевские осцилляции плотности электронов) приведена в сечении, совпадающем с межслойной границей в численном эксперименте облучения образца 400 × 400 × 400 нм, где ${{z}_{k}} = 180$ нм. Температура образца 0.53Тmelt 3C–SiC, в модели плотность дефектов 103 см–3, значения потенциала безразмерные, $U\left( {x,y,{{z}_{k}}} \right){\text{/}}{{U}_{0}}\left( {x,y,{{z}_{k}}} \right)$ где ${{U}_{0}}\left( {x,y,{{z}_{k}}} \right)$ – значения в начальный момент. Локальные напряжения, создаваемые ВГД (блистерами) в j-м слое образца вычисляется по формуле:
(2.2)
${{{\sigma }}_{j}} = 0.195r_{{at}}^{2}\frac{{{{{\mu }}_{{cd}}}{{b}_{b}}}}{{\left( {1 - {v}} \right){{a}_{m}}}}\int {\sum\limits_i {\frac{{\frac{1}{3}\ln \left( {\left\langle {{{g}_{i}}} \right\rangle } \right) + \ln \left( {\frac{{{{r}_{{at}}}}}{{{{b}_{b}}}}} \right) + \frac{{4{\pi }{{{\sigma }}_{{surf}}}}}{{{{{\mu }}_{{cd}}}{{b}_{b}}}}}}{{{{{({{{(x - {{x}_{i}})}}^{2}} + {{{(y - {{y}_{i}})}}^{2}} + {{{(z - {{z}_{i}})}}^{2}})}}^{{3/2}}}}}} } \left( {\left\langle g \right\rangle } \right)_{i}^{{2/3}}dxdydz$Напряжения, возникающие при ионной имплантации, достигают значений 109 Па и способствуют дальнейшему формированию протяженных структур дефектов и последующему развитию трещин. При этом максимум напряжений, возникающих в слое карбида кремния соответствует температуре, равной 0.55${{T}_{{melt}}}$ (температуры плавления материала). Напряжение от несоразмерности параметров решеток слоев рассчитывается отдельно и сравнивается с вкладом в напряжение вызванное ВГД. Облучение образца ведется ионами ксенона с энергией 5 кэВ, падение по нормали к поверхности карбида кремния, доза облучения 1015 см–2 [17].
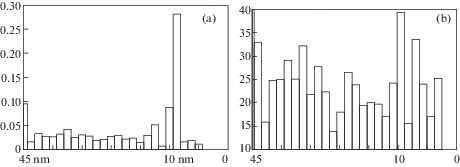
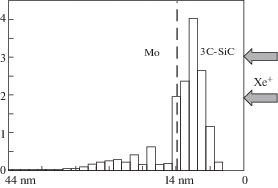
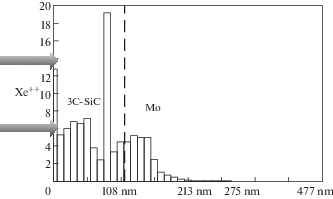
В работе [19] были приведены расчеты ФР по размерам и глубине от поверхности облучения, начальное равномерное распределение ВГД за время расчета становится бимодальным по размерам. На рис. 4а и рис. 4б приведены графики изменения долей объемов пор, отнесенных к общему объему, распределенных по глубине (рис. 4а) и распределение диаметров кластеров ВГД по глубине, сформировавшиеся в слоях карбида (толщина 14 нм) и молибдена (30 нм) при T = 1200 K, энергии ионов Xe = 5 кэВ и дозе 1015 см–2 за время расчета, число траекторий 104.
На рис. 5 приведена гистограмма средних напряжений в слоях образца (для условий рис. 4), возникающие при ионной имплантации в двухслойном образце “карбид кремния/металл”
в момент окончания расчета (1.5 мс). Разработанная методика визуализации пористости,
напряжения и ФР ВГД по координатам, позволяет анализировать распределение слоев увеличенной
пористости в объеме модели и связать их с упругими свойствами материалов слоев. На
рис. 6 приведено изменение дисперсности вакансионных кластеров (верхняя кривая) и газовых
в объеме расчетной области с размерами 400 × 400 × 400 нм, время в шагах алгоритма,
результат при 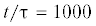 , соответствует ФР ВГД в объеме из работы [18], шаг алгоритма моделирования БД ${{{\tau }}_{r}}$ = 10–7 c.
, соответствует ФР ВГД в объеме из работы [18], шаг алгоритма моделирования БД ${{{\tau }}_{r}}$ = 10–7 c.
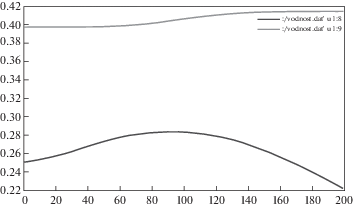
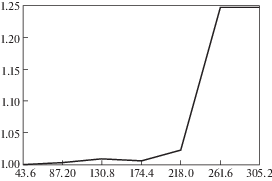
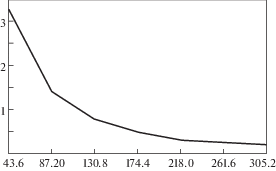
На рис. 7 изображена суммарная пористость облучаемого карбида кремния при T = 1530 K дозе облучения Xe = 1016 и энергии ионов 7 кэВ в зависимости от его толщины от 130.8 нм до 261.6 нм, пористость в относительных единицах. Рисунок 8 иллюстрирует отношение суммарной пористости слоя металла (под облучаемым слоем карбида кремния) к пористости одномерного фотонного кристалла (с мезапористой структурой), с размерами 44 нм ⋅ 436 нм ⋅ 436 нм высокой удельной поверхностью пор. Пример расчета пористости образца приведены на рис. 9. В начальный момент времени дефекты расположены только в слое карбида кремния, характеристики пористости в двухслойном образце “карбид кремния/металл” с облучаемой площадью 240 × 240 нм кристаллографической (001) плоскости при температуре 1530 K и дозе облучения Xe++ = 1016 см–2 при энергии ионов 7 кэВ. Причем для образца 3C–SiC (толщина слоя 125 нм)/молибден (толщина слоя 110 нм) средняя пористость карбида кремния 18%, в то время как средняя пористость молибдена 13%, а при толщине слоя молибдена 352 нм его средняя пористость составляет 4%. За время протекания существенно неравновесной флуктуационной стадии формирования зародышей дефектов средняя пористость образца возросла в 6.31 раза. Среднее значение пористости карбида кремния в момент окончания флуктуационной стадии при концентрации ВГД 105 см–3 превосходит среднее значение пористости карбида кремния при концентрации ВГД 103 см–3 в 8 раз.
Заключение. Решение квазилинейных кинетических уравнений для стохастической модели начальной стадии фазового перехода – образования ВГД в форме уравнения Колмогорова–Феллера для кластеризации зародышей и уравнения Смолуховского для броуновского движения центров масс зародышей позволяет получить неравновесные и нестационарные распределения дефектов по размерам и по глубине в слоях образца в зависимости от температуры образца и характеристик облучения. Численные эксперименты проведены устойчивыми алгоритмами решения систем СДУ моделей процесса взаимодействия потока ионов Хе++ со слоем карбида кремния на металле. Для СДУ Ито ранее были доказаны теоремы существования и единственности решения, это важно для оценки степени аморфизация кристаллической решетки материалов слоев, возможности потери планируемых прочностных свойств поверхностей, граничащих с радиационными потоками. Размеры пор позволяют оценить распределение локальных напряжений в объеме слоя (по величине скачка давления на границе нанопоры по закону Лапласа 1/R, где R – радиус поры, размеры пор в материале зависят от расстояния от границы слоев диэлектрика и металла из-за несоразмерности параметров кристаллических решеток слоев), на основе анализа пористости в тонком слое карбида кремния при имплантации инертного газа с энергией ионов 5–10 кэВ, в расчетах обнаружены цепочки ВГД или “структуры” (близко расположенных пор), сравнение структур пористости в карбиде кремния по направлению потока имплантации и перпендикулярно ему позволяет судить о роли границ расчетной области и толщин слоев. Описание кинетики физико-химических процессов быстропротекающей начальной стадии зарождения неточечных радиационно стимулируемых дефектов обращает внимание на модель броуновского движения центров масс сферических ВГД в решетке, которое вызывается потенциалами их косвенного упругого взаимодействия через возмущение дефектами колебаний акустических фононов решетки и фриделевских осцилляций электронов решетки и на то, что характеристики материалов получены осреднением неравновесных функций распределения ВГД по размерам и глубине от облучаемой поверхности порядка микрометров.
Благодарности. Автор признательна С.А. Кукушкину за ту пищу для ума, те идеи для численного моделирования, которые дают его публикации и за щедрость, с которой он делает доступными эти работы.
Список литературы
Головань Л.А., Тимошенко В.Ю., Кашкаров П.К. Оптические свойства нанокомпозитов на основе пористых систем // УФН. 2007. Т. 177. С. 619–638.
Kukushkin S.A., Osipov A.V. Theory andpractice of SiC grovth on Si and its applications to wide-gap semiconductor films // J. Phys. D: Appl. Phys. 2014. V. 47. P. 313001–313043.
Wiersma D.S. Disprdered photonics // Nature Photonics. 2013. V. 7. P. 188–196.
Wu Ch., Christensen M. S., Savolainen J.-M., Balling P. and Zhigilei L.V. Generation of subsurface voids and a nanocrystalline surface layer in femtosecond laser irradiation of a single-crystal Ag target // Phys. Rev. B. 2015. V. 91. P. 035 413.
Сигов Ю.С. Вычислительный эксперимент: мост между прошлым и будущим физики плазмы. Избранные труды / Сост. Змиевская Г.И., Левченко В.Д. М.: ФИЗМАТЛИТ, 2001. 288 с.
Змиевская Г.И. Флуктуационная стадия фазового перехода // “Энциклопедия низкотемпературной плазмы”: (Сер. Б) / Ред. В.Е. Фортов, VII, Матем. моделирование в низкотемпературной плазме (кн. 3. Ред. Ю.П. Попов), 2009. С. 58–83.
Zmievskaya G.I., Averina T.A., Bondareva A.L. Numerical solution of stochastic differential equations in the sense of Stratonovich in an amorphization crystal lattice model // Applied Numerical Math. 2015. V. 93. P. 15–29.
Скороход А.В. Стохастические уравнения для сложных систем. М.: Наука, 1983. 192 с.
Arnold L. Random dynamic system. Springer Monographs in Math., Springer, 1998. 586 p.
Кукушкин С.А. Начальные стадии хрупкого разрушения твердых тел // Успехи механики. 2003. Т. 2. № 2. С. 21–43.
Аверина Т.А. Статистическое моделирование решений стохастических дифференциальных уравнений и систем со случайной структурой / Рос. акад. наук, Сиб. отд., ИВМиМГ. Новосибирск: Изд-во СО РАН, 2019. 350 с.
Змиевская Г.И., Аверина Т.А. Флуктуации заряда на каплях расплава карбила кремния в процессе конденсации / Препринт ИПМ им. М.В. Келдыша Рос. акад. наук. Москва, 2018. № 280. 21 с. URL: http://library.keldysh.ru/preprint.asp?id=2018-280
Норман Г.Э., Стегайлов В.В. Метод классической молекулярной динамики: замысел и реальность // Наноструктуры. Матем. физика и моделирование. 2011. Т. 4. № 1. С. 31–58.
Бeрзин А.А., Морозов А.И., Сигов А.С. Диффузия легких атомов на поверхности кристалла и процессы кластеризации // ФТТ. 1996. Т. 38. № 5. С. 1349–1356.
Морозов А.И. Дефектонный вклад в высокотемпературную сверхпроводимость гидридов // ФТТ. 2019. Т. 61. Вып. 7. С. 1236–1239.
Bruno G., Efremov A.M., Levandovskyi A.N., Clausen B., Efremov A.M., Levandovskyi A.N., Clausen B. Connecting the macro- and microstrain responses in technical porous ceramics: modeling and experimental validations // J. Mater. Sci. 2011. V. 46. P. 161–173.
Змиевская Г.И., Бондарева А.Л. Кинетика возникновения пористости и изменение свойств материалов в численных моделях // Поверхность. Рентгеновские, синхротронные и нейтронные исследования. 2016. № 8. С. 33–40.
Змиевская Г.И., Бондарева А.Л. Численное моделирование кинетики возникновения пористости в многослойных средах // Физические и математические модели плазмы и плазмоподобных сред. Избранные научные труды / Под ред. Д. Майно и Г. Змиевской. М.: ИПМ им. М.В. Келдыша РАН, С. 16–30.
Zmievskaya G.I. Computer simulation of phase transition nonequilibrium processes, in book “Nonequilibrium processes”. V. 1. Kinetics and plasma / Ed. by S.M. Frolov, A.I. Lanshin. Torus Press, 2018. P. 130–139.
Иванов А.В. Использование библиотеки aiwlib на примере численного моделирования стохатического резонанса. Препринты ИПМ им. М.В. Келдыша, 2018. 089, 30 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела