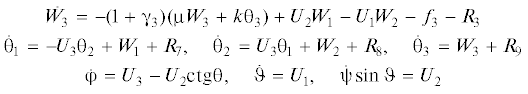Известия РАН. Механика твердого тела, 2020, № 2, стр. 96-111

1. Постановка задачи. Уравнения движения. Ранее [1–3] в рамках модели М.А. Лаврентьева исследованы свойства вращательного движения спутника на круговой орбите под влиянием только диссипативных внутренних сил. В настоящей работе исследуется эволюция вращательного движения спутника при учете как диссипативных, так и упругих внутренних сил.

Рассматривается спутник, состоящий из твердой оболочки и шарового демпфера (модель М.А. Лаврентьева) [4, 5]. Обозначим через ${\mathbf{J}} = {\text{diag}}(A,B,C)$ центральный тензор инерции всего спутника (оболочки вместе с демпфером) в главных центральных осях ${{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}},{{{\mathbf{e}}}_{3}}$, а через I – момент инерции демпфера относительно его центральной оси. Предполагается, что при относительных перемещениях демпфера на него действует диссипативный момент ${{{\mathbf{M}}}_{d}}$ и момент упругих сил ${{{\mathbf{M}}}_{e}}$, определяемые формулами [6]

Здесь ${\mathbf{\omega }}$ и ${\mathbf{\Omega }}$ – абсолютные угловые скорости оболочки и демпфера, $\tilde {\mu }$ и $\tilde {k}$ – коэффициенты демпфирования и жесткости, ${\mathbf{\theta }}$ – вектор конечного поворота демпфера относительно оболочки, ${\mathbf{\xi }}$ – орт оси конечного поворота, $\chi $ – угол конечного поворота. Действующий на спутник гравитационный момент имеет вид [7]

где ${{{\mathbf{\omega }}}_{0}}$ – вектор угловой скорости орбитального базиса, направленный по нормали n к плоскости орбиты, ${\mathbf{r}} = {{\mathbf{R}} \mathord{\left/ {\vphantom {{\mathbf{R}} R}} \right. \kern-0em} R}$, R – радиус-вектор, соединяющий центр притяжения с центром масс спутника.

Вращательное движение спутника описывается системой уравнений [6]

Здесь E – единичная матрица, ${\mathbf{u}} = {{\mathbf{\omega }} \mathord{\left/ {\vphantom {{\mathbf{\omega }} {{{{\omega }}_{0}}}}} \right. \kern-0em} {{{{\omega }}_{0}}}}$ и ${\mathbf{w}} = {{({\mathbf{\Omega }} - {\mathbf{\omega }})} \mathord{\left/ {\vphantom {{({\mathbf{\Omega }} - {\mathbf{\omega }})} {{{{\omega }}_{0}}}}} \right. \kern-0em} {{{{\omega }}_{0}}}}$ – безразмерные переменные (приведенная угловая скорость оболочки и приведенная относительная угловая скорость демпфера), ${\mu } = {{{\tilde {\mu }}} \mathord{\left/ {\vphantom {{{\tilde {\mu }}} {{{{\omega }}_{0}}}}} \right. \kern-0em} {{{{\omega }}_{0}}}}$ и $k = {{\tilde {k}} \mathord{\left/ {\vphantom {{\tilde {k}} {{\omega }_{0}^{2}}}} \right. \kern-0em} {{\omega }_{0}^{2}}}$ – безразмерные коэффициенты демпфирования и жесткости, ${\mathbf{\Lambda }}$ – кватернион единичной нормы, задающий положение связанного с оболочкой базиса главных осей инерции спутника ${{{\mathbf{e}}}_{1}},\;{{{\mathbf{e}}}_{2}},\;{{{\mathbf{e}}}_{3}}$ относительно базиса Кëнига ${{{\mathbf{i}}}_{1}},\;{{{\mathbf{i}}}_{2}},\;{{{\mathbf{i}}}_{3}}$. Точкой обозначена производная по безразмерному времени ${\tau } = {{{\omega }}_{0}}t.$ В уравнениях (1.3) все векторы задаются своими компонентами в базисе ${{{\mathbf{e}}}_{1}},\;{{{\mathbf{e}}}_{2}},\;{{{\mathbf{e}}}_{3}}$.

В рамках рассматриваемой модели, как и в рамках некоторых других моделей [7–9], предельными движениями несимметричного спутника на круговой орбите являются только положения равновесия относительно орбитального базиса, а для динамически симметричного спутника – стационарные вращения вокруг оси симметрии, сонаправленной с нормалью ${\mathbf{n}}$ к плоскости орбиты [6]. Ниже исследуется эволюция вращательного движения спутника в зависимости от значений параметров и начальных условий. Основной интерес в этой задаче представляет поведение оси вращения спутника и величины угловой скорости.

Эволюцию вращательного движения спутника можно исследовать с помощью численного интегрирования уравнений (1.3). Однако, как показал предварительный анализ, скорость эволюции так зависит от значений параметров и фазовых переменных, что во многих случаях для получения с достаточной точностью только одной полной траектории эволюции для одной комбинации значений параметров требуется неприемлемо большое время работы программы численного интегрирования уравнений (1.3). Поэтому ниже для получения подробной картины эволюции в широком диапазоне значений параметров и фазовых переменных будут выведены осредненные (эволюционные) уравнения.

Для определенности положим, что главные центральные моменты инерции спутника подчиняются условиям

Геометрия масс спутника может быть описана следующими безразмерными параметрами [3]:

В качестве независимых будем использовать следующие три параметра:

Параметры (1.5) выражаются через независимые параметры (1.6) формулами

Из соотношений (1.4)–(1.7) следует

Значение ${\delta } = 0$ соответствует динамически симметричному спутнику, сплюснутому вдоль оси симметрии ${{{\mathbf{e}}}_{3}}$, а значение ${\delta } = {\varepsilon }$ – динамически симметричному спутнику, вытянутому вдоль оси симметрии ${{{\mathbf{e}}}_{1}}$.

При ${\varepsilon } \ll 1$ (для спутника, близкого к сферически симметричному) будем иметь

Обозначим через ${{r}_{k}}$ проекцию вектора ${\mathbf{r}}$ на ось ${{{\mathbf{e}}}_{k}}$. Тогда для компонент приведенного гравитационного момента в осях ${{{\mathbf{e}}}_{k}}$ получим выражения

Для вывода осредненных уравнений вращательного движения спутника на круговой орбите применим алгоритм, использованный ранее [3] для решения аналогичной задачи, где учитывались только диссипативные внутренние силы. Запишем уравнения движения (1.3) в проекциях на оси базиса Резаля ${\mathbf{e}}_{1}^{'},\;{\mathbf{e}}_{2}^{'},\;{{{\mathbf{e}}}_{3}}$ (${\mathbf{e}}_{1}^{'}$ – орт линии узлов, ${\mathbf{e}}_{2}^{'} = {{{\mathbf{e}}}_{3}} \times {\mathbf{e}}_{1}^{'}$), задаваемого углами Эйлера ${\psi }$ и $\vartheta $. Обозначив через ${{U}_{k}},\,\,{{W}_{k}},\,\,{{\theta }_{k}}$ проекции векторов ${\mathbf{u}},\,\,{\mathbf{w}},\,\,{\mathbf{\theta }}$ на указанные оси, получим следующую систему уравнений:

Здесь ${\varphi }$ – угол собственного вращения, а через $m$ и c обозначены “агрегированные” параметры

Функции ${{R}_{k}}$, фигурирующие в уравнениях (1.11), выражаются формулами

а функции ${{f}_{k}}$ определяются выражениями

Система (1.11) отличается от полученной ранее [3] системы наличием членов, соответствующих моментам внутренних упругих сил, и дополнительных уравнений, описывающих кинематику относительного вращения демпфера.

2. Осредненные уравнения. Далее будем рассматривать спутник, близкий к сферически симметричному, т.е. положим ${\varepsilon } \ll 1$. При выводе осредненных уравнений будем, как и в работе [3], исходить из того, что при ${\varepsilon } \ll 1$ и ${\mu } \ne 0$ эволюционный процесс состоит из двух фаз. Первая фаза (быстрая эволюция) представляет собой сравнительно быстрый переходной процесс, в конце которого устанавливается вращение, близкое к вращению вокруг оси ${{{\mathbf{e}}}_{3}}$ наибольшего момента инерции, с кинетическим моментом, близким к начальному. Далее наступает режим медленной эволюции, в котором все переменные ${{U}_{k}},\;{{W}_{k}},\;{{{\theta }}_{k}}$, кроме переменной $\,{{U}_{3}}$, будут ограниченными функциями малого параметра ε, вследствие чего все правые части системы (1.11) будут ограниченными функциями ε. Это свойство дает возможность применить к системе (1.11) метод осреднения [10, 11] без приведения ее к стандартной форме.

Введем следующие обозначения для фазовых переменных:

Первые девять уравнений системы (1.11) перепишем в виде

Здесь

Решение системы будем искать в виде ${\mathbf{Z}} = {\mathbf{V}} + {\mathbf{S}}$, а компоненты вектор-функции ${\mathbf{S}}$ определим из условия, чтобы уравнение

удовлетворялось с точностью до $O({{{\varepsilon }}^{2}})$.

Выражения для производных ${{{\dot {\sigma }}}_{k}}$ представим в виде суммы двух слагаемых ${{{\dot {\sigma }}}_{k}} = {{{\nu }}_{k}}$ + + λ_k, где через ${{{\nu }}_{k}}$ обозначено значение производной, вычисленное с точностью до $O({\varepsilon })$, а слагаемое ${{{\lambda }}_{k}}$ – ограниченная функция ε. Учитывая, что в режиме медленной эволюции переменные ${{Z}_{j}},\,j \ne 3$ – ограниченные функции ε, из кинематических уравнений системы (1.11) получим

Здесь и далее $U = {{V}_{3}}$.

Оставляя в уравнении (2.2) члены первого порядка малости по ${\varepsilon }$, получим уравнение

где через ${\mathbf{L}}({\mathbf{S}})$ обозначены линейные по ${\varepsilon }$ члены функции ${\mathbf{D}}({\mathbf{S}})$ с компонентами а через ${{{\mathbf{P}}}_{k}}$ и ${{{\mathbf{Q}}}_{k}}$ – векторы с компонентами

Решение уравнения (2.4) записывается гармоническими по переменным ${{{\sigma }}_{k}}$ функциями вида

а коэффициенты ${{x}_{{j\,k}}}$ и ${{y}_{{j\,k}}}$ ($j = 1,\,2,\,...\,,9$) определяются из линейных систем

Вычисленные из системы (2.7) выражения для коэффициентов ${{x}_{{j\,k}}}$ и ${{y}_{{j\,k}}}$ ввиду их громоздкости здесь не приводятся. Они будут использоваться на последнем этапе для вычисления правых частей осредненных уравнений. Отметим только, что указанные коэффициенты зависят от переменных $U,\;\vartheta $ и являются ограниченными функциями ${\varepsilon }$.

В предположении, что в режиме медленной эволюции движение близко к вращению вокруг оси ${{{\mathbf{e}}}_{3}}$ наибольшего момента инерции, анализ эволюции сводится к изучению поведения фазовых переменных ${{U}_{3}},\,\,\vartheta $ и ${\psi }$. Для получения эволюционных уравнений найдем выражения для средних значений производных по времени от указанных переменных. Искомые выражения определим, полагая, что в режиме медленной эволюции средние значения производных по времени от всех переменных Z_j, кроме ${{U}_{3}}$, равны нулю с точностью до $O({{{\varepsilon }}^{3}})$. При этом будем учитывать, что для переменных Z_j средние ${{\bar {Z}}_{j}}$ выражаются суммой двух слагаемых: ${{\bar {Z}}_{j}} = {{\bar {V}}_{j}} + {{\bar {S}}_{j}}$, а средние от функций ${{f}_{k}}$ и ${{S}_{j}}$ с точностью до $O({{{\varepsilon }}^{2}})$ равны нулю.

Из уравнений (1.11), полагая ${{\dot {\bar {Z}}}_{j}} = 0$, $j \ne 3$, получим систему

Отсюда с точностью до $O({{{\varepsilon }}^{2}})$ найдем

Из последнего уравнения (1.11) при учете выражений (2.9) и (1.15) определяется среднее для угловой скорости прецессии спутника формулой

Таким образом, средняя скорость прецессии спутника с демпфером линейна по ${\varepsilon }$ и не зависит от значений параметров ${\mu },\,k$. Она совпадает с выражением для средней скорости прецессии спутника, моделируемого одним твердым телом [7].

В свою очередь, из третьего и одиннадцатого уравнений (1.11) при учете соотношений (2.10) следует, что для определения главных членов в выражениях для средних ${{\dot {\bar {U}}}_{3}}$ и $\dot {\bar {\vartheta }}$ необходимо проводить вычисления с точностью до $O({{{\varepsilon }}^{3}})$.

Далее при выполнении соответствующих вычислительных процедур используются вычисленные из системы (2.7) выражения для коэффициентов ${{x}_{{j\,k}}}$ и ${{y}_{{j\,k}}}$ в функциях (2.6), формулы для среднего от произведения (среднее обозначается угловыми скобками)

и следующее свойство, установленное для функций (1.13):

Из третьего и шестого уравнений (1.11), полагая ${{\dot {\bar {W}}}_{3}} = 0$, получим

Отсюда, учитывая соотношения (2.9), (2.10), (2.12), (2.13) и (1.9), получим с точностью до $O({{{\varepsilon }}^{3}})$

Из второго и пятого уравнений (1.11) при ${{\dot {\bar {U}}}_{2}} = {{\dot {\bar {W}}}_{2}} = 0$ будем иметь

Отсюда, учитывая равенство $\dot {\bar {\vartheta }} = {{\bar {U}}_{1}}$, с точностью до $O({{{\varepsilon }}^{3}})$ найдем

При вычислении правых частей в уравнениях (2.14) и (2.15) следует отдельно рассматривать резонансный и нерезонансный случаи. В рассматриваемой задаче резонансный случай определяется условием

где ${{n}_{k}}$ – целые числа. Главные резонансы ${{{\nu }}_{0}}\, = {{{\nu }}_{1}}$ и ${{{\nu }}_{0}}\, = {{{\nu }}_{2}}$ реализуются, когда величина угловой скорости спутника достигает значений U = 1 и U = 2, соответственно.

Далее рассматривается нерезонансный случай. В этом случае фигурирующие в уравнениях (2.14) и (2.15) слагаемые $\left\langle {{{S}_{i}}\,{{S}_{j}}} \right\rangle $ вычисляются с точностью до $O({{{\varepsilon }}^{3}})$ формулами

Для вычисления средних ${{\bar {f}}_{2}}$ и ${{\bar {f}}_{3}}$ от функций (1.14) с точностью до $O({{{\varepsilon }}^{3}})$ выведем формулу для среднего от функции ${{p}_{j}}\sin {{{\sigma }}_{j}}$, где ${{p}_{j}} = {{p}_{j}}(U,\vartheta )$, ${{{\sigma }}_{j}} = {{{\sigma }}_{j}}({\tau },{\varphi },{\psi })$. Учитывая, что $\dot {U} = O({{{\varepsilon }}^{2}})$ и пренебрегая членами второго порядка по ${\varepsilon }$, получим

Здесь через ${{\bar {p}}_{j}}$ обозначено среднее по времени, а штрихом – производная по углу нутации $\vartheta $.

Аналогичной процедурой при учете соотношений (2.3) на основании формулы σ_j = ${{{\nu }}_{j}}{\tau } + \int {{{{\lambda }}_{j}}} d{\tau }$ получим с точностью до $O({{{\varepsilon }}^{2}})$

Здесь

где ${{{\bar {\nu }}}_{j}}$ – средняя скорость изменения переменной ${{{\sigma }}_{j}}$.

Из формул (2.18), (2.19) с точностью до $O({{{\varepsilon }}^{2}})$будем иметь

На основании формул (2.20), (1.14), (1.15) при учете соотношений

получим с точностью до $O({{{\varepsilon }}^{3}})$

После выполнения всех вычислительных процедур уравнения (2.14), (2.15) приводятся к следующему виду (средние ${{\bar {U}}_{3}}$ и $\bar {\vartheta }$ далее обозначаются символами $U$ и $\vartheta $):

Здесь использованы обозначения

Уравнения (2.24), (2.25) образуют замкнутую систему относительно переменных U и $\vartheta $. Они описывают поведение величины угловой скорости спутника и угла между осью вращения ${{{\mathbf{e}}}_{3}}$ и нормалью ${\mathbf{n}}$ к плоскости орбиты в зависимости от безразмерного времени ${\tau } = {{{\omega }}_{0}}t$. При $c \ne 0$ эти уравнения не вырождаются ни при каких значениях переменных, кроме U = 0. Для построения фазовых траекторий эволюции вращательного движения спутника в плоскости переменных U и $\vartheta $ достаточно исследовать решения системы в области U > 0, $\vartheta \in [0,\,{\pi }]$.

Как следует из уравнений (2.24), (2.25), скорость эволюции пропорциональна ${{{\varepsilon }}^{2}}$ и существенно зависит от значений параметров m, c, ${\gamma }$ и величины U. При $U \gg 1$ скорость эволюции обратно пропорциональна U², при $m \gg 1$ – обратно пропорциональна $m$, при $с \gg 1$ – обратно пропорциональна c². Эти оценки свидетельствуют о том, что при ${\varepsilon } \ll 1$ для значений параметров $m \gg 1$, $с \gg 1$ и в области $U \gg 1$ эта скорость весьма мала. Поэтому получить с должной точностью полную картину эволюционного процесса численным интегрированием точных уравнений (1.3) затруднительно.

В уравнениях (2.24), (2.25) можно перейти к новому безразмерному времени ${\tau '}$, определенному формулой

Тогда для получения с требуемой точностью фазовых траекторий численным интегрированием этих уравнений потребное время работы программы окажется существенно (в 1/ε² раз) меньше, чем при использовании точных уравнений (1.3).

Кроме того, из уравнений (2.24), (2.25) можно исключить время и получить одно уравнение

описывающее зависимость $\vartheta (U)$. Покажем, что это уравнение не имеет особенностей в области U > 2. Для этого сначала докажем, что при U > 2, c > 0 выполняется неравенство

Действительно, выражение (2.29) представляет собой квадратичную форму переменных x = 1 и $y = \cos \vartheta $. Матрица этой квадратичной формы имеет вид

Условие положительной определенности этой матрицы описывается неравенствами

которые выполняются при U > 2, поскольку при $c > 0$ функции ${{g}_{2}},{{D}_{2}}$ и ${{D}_{3}}$ строго положительны.

Из уравнения (2.24) при учете неравенства (2.29) следует, что при ${\delta } > 0$ в области U > 2 угловая скорость $U$ будет монотонно убывающей функции времени и поэтому уравнение (2.28) в указанной области не имеет особенностей. Ввиду того, что в этом уравнении $U$ – независимая переменная, для построения фазовых портретов эволюции вращательного движения спутника с помощью этого уравнения потребное время работы программы численного интегрирования оказывается на много порядков меньше, чем при использовании точных уравнений (1.3), причем это время практически не зависит от значений параметров m, c и ${\alpha }$.

При c = 0 уравнения (2.24), (2.25) совпадают с полученными ранее [3] уравнениями, описывающими эволюцию вращательного движения спутника под влиянием только диссипативных внутренних сил.

При δ = 0 уравнения (2.24), (2.25) описывают эволюцию вращательного движения динамически симметричного спутника.

3. Плоские вращения спутника. Осредненные уравнения (2.24), (2.25), также, как и точные уравнения (1.3), допускают решения, соответствующие плоским вращениям вокруг оси наибольшего момента инерции, сонаправленной с нормалью к плоскости орбиты. Этим решениям соответствуют значения угла $\vartheta = 0$ (прямые вращения) и $\vartheta $ = π (обратные вращения). Для динамически симметричного спутника (δ = 0) эти вращения стационарные, а для несимметричного спутника с демпфером угловая скорость U на указанных плоских вращениях меняется с течением времени и в финале эволюции становится равной единице (спутник приходит в положение равновесия относительно орбитального базиса).

На основании уравнения (2.24) при учете формул (2.26) получим, что средняя угловая скорость для плоских вращений спутника описывается уравнением

Этим одним уравнением описываются и прямые и обратные плоские вращения. При этом прямым вращениям соответствуют значения U > 0, а обратным – значения U < 0. Решение уравнения (3.1) записывается в виде

где ${{U}_{0}}$ – начальное значение угловой скорости спутника. Время, необходимое для достижения спутником угловой скорости $U{\text{*}}$, отличной от угловой скорости орбитального базиса на величину ${\Delta }$, т.е. $\left| {U{\text{*}} - 1} \right| = {\Delta }$, определяется формулой

Если $c > 0$, то при ${\Delta } \to \,\,0$ ${\tau *} \to \infty $.

Вывод условий устойчивости плоских вращений спутника проведем, основываясь на осредненных равнениях (2.24), (2.25). Обозначим через ${{U}_{X}} = U\sin \vartheta $ и ${{U}_{Z}} = U\cos \vartheta $ проекции угловой скорости спутника на плоскость орбиты и на нормаль к плоскости орбиты, соответственно. Тогда вопрос об устойчивости плоских вращений сведется к исследованию устойчивости решений уравнений (2.24), (2.25) по отношению к переменной U_X. Полагая, как и ранее, U > 0, $0 \leqslant \vartheta \leqslant {\pi }$, получим, что если при достаточно малом ${{U}_{X}} > 0$ значение производной ${{\dot {U}}_{X}} < 0$, то плоское вращение асимптотически устойчиво по переменной ${{U}_{X}}$ (возмущенные траектории “прижимаются” к траекториям плоских вращений), а если ${{\dot {U}}_{X}} > 0$, то неустойчиво. Характер устойчивости плоского вращения зависит не только от значений параметров, но и от величины угловой скорости. Поэтому за счет изменения угловой скорости в процессе эволюции знак производной ${{\dot {U}}_{X}}$ может меняться, вследствие чего траектории плоских вращений могут делиться на интервалы асимптотически устойчивых и неустойчивых вращений.

При учете уравнений (2.24), (2.25) и формулы

для “прямых” вращений, полагая U > 0, $0 < \vartheta \ll 1$ и пренебрегая членами выше первого порядка малости по $\vartheta $, получим условие асимптотической устойчивости в виде неравенства

Полагая $U > 0$, $\vartheta = {\pi } - {\xi }$, где $0 < {\xi } \ll 1$, получим условие асимптотической устойчивости для обратных вращений

Значения U > 0, при которых записанные неравенства выполняются с обратным знаком, соответствуют неустойчивым плоским вращениям.

Для динамически симметричного спутника условия устойчивости прямых стационарных вращений принимают вид

Корни уравнения  f = 0 определяют границы интервалов асимптотической устойчивости и неустойчивости. Проведенный анализ показал, что это уравнение в области U  > 0 может иметь только два вещественных корня: ${{U}_{1}} > 2$ и $\,{{U}_{2}} < {{({{m}^{2}} + 4)} \mathord{\left/ {\vphantom {{({{m}^{2}} + 4)} 2}} \right. \kern-0em} 2}$. Такие корни существуют только при $c < {{{{m}^{2}}} \mathord{\left/ {\vphantom {{{{m}^{2}}} 2}} \right. \kern-0em} 2}$. При этом в диапазоне ${{U}_{1}} < U < {{U}_{2}}$ прямые стационарные вращения будут неустойчивыми, а для остальных значений U > 0 – асимптотически устойчивыми. При $c \geqslant {{{{m}^{2}}} \mathord{\left/ {\vphantom {{{{m}^{2}}} 2}} \right. \kern-0em} 2}$ все прямые стационарные вращения будут асимптотически устойчивыми.

Условия устойчивости обратных стационарных вращений динамически симметричного спутника записываются в виде

В этом случае уравнение  f = 0 имеет единственный вещественный корень ${{U}_{3}}$ в области U > 0. При этом для значений $U > {{U}_{3}}$ обратные стационарные вращения асимптотически устойчивы, а в интервале $0 < U < {{U}_{3}}$ – неустойчивы.

Подробный анализ условий (3.7), (3.8) показал, что при увеличении значения коэффициента демпфирования $m$ увеличивается длина интервала $({{U}_{1}},{{U}_{2}})$ неустойчивости прямых стационарных вращений спутника и уменьшается длина интервала $(0,{{U}_{3}})$ неустойчивости обратных вращений. При увеличении коэффициента жесткости c, наоборот, уменьшается длина интервала $({{U}_{1}},{{U}_{2}})$ и увеличивается длина интервала $(0,{{U}_{3}})$.

Было проведено сопоставление условий (3.7), (3.8) с условиями устойчивости стационарных вращений спутника, получаемыми на основе результатов численного анализа корней характеристического уравнения линеаризованной системы [6]. Установлено совпадение определяемых этими условиями границ интервалов асимптотической устойчивости и неустойчивости для прямых стационарных вращений в области U > 1 и для обратных вращений в области $U > O(\varepsilon )$. Исключение составляет лишь интервал $0 < U < 1$ для прямых вращений. Из условия (3.7) следует, что в этом интервале стационарные вращения асимптотически устойчивы, в то время как результаты численного анализа корней характеристического уравнения линеаризованной системы показывают при $c > 0$ наличие области неустойчивости $U{\text{*}} < U < 1$. При этом с ростом параметра $c$ левая граница $U{\text{*}}$ интервала смещается влево, достигая значения $U{\text{*}} = 0$, а при дальнейшем увеличении $c$ становятся неустойчивыми и обратные вращения в интервале $0 < U < U_{3}^{*}$, причем $U_{3}^{*} \to {{U}_{3}}$.

Обнаруженное в интервале $0 < U < 1$ несовпадение условий устойчивости может быть объяснено тем, что в правых частях осредненных уравнений (2.24), (2.25) учитываются только члены второго порядка по $\varepsilon $. Поэтому не исключено, что некоторые из членов третьего порядка по $\varepsilon $ не содержат множителей вида $\sin \vartheta $. Тогда при $\left| {\sin \vartheta } \right| < \varepsilon $ эти члены могут оказаться доминирующими по сравнению с членами ${{{\varepsilon }}^{2}}\sin \vartheta $, за счет чего поведение фазовых траекторий в малой $\varepsilon $-окрестности плоских вращений может отличаться от поведения траекторий осредненных уравнений (2.24), (2.25). В пользу такого объяснения свидетельствуют результаты численного интегрирования, проведенного с привлечением точных уравнений (1.3). Установлено, что за границей $\varepsilon $-окрестности, т.е. при $\left| {\sin \vartheta } \right| > {\rm O}(\varepsilon )$, осредненные уравнения адекватно описывают поведение фазовых траекторий динамически симметричного спутника и в интервале 0 < $U$ < 1.

Аналитическое исследование интервалов асимптотической устойчивости и неустойчивости плоских вращений несимметричного спутника ($\alpha > 0$) на основе условий (3.5), (3.6) проблематично ввиду того, что границы этих интервалов определяются вещественными корнями полиномов пятнадцатой степени. Поэтому был проведен численный анализ границ этих интервалов.

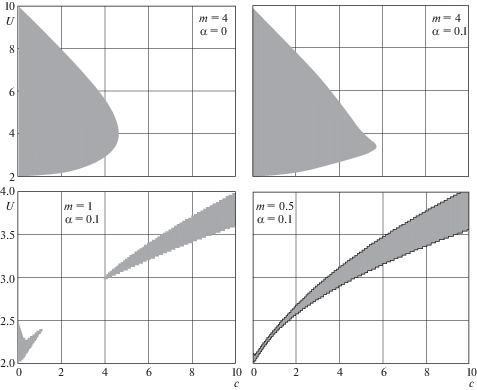
На рис. 1, 2 приведены диаграммы, показывающие границы интервалов асимптотической устойчивости и неустойчивости плоских вращений для динамически симметричного спутника (α = 0) и несимметричного спутника (α = 0.1) в зависимости от значений параметра $c$ при фиксированных значениях параметра $m$. Интервалы неустойчивости затемнены.

Из приведенных диаграмм следует, что для прямых вращений (рис. 1) при $c \leqslant \,{{m}^{2}}$ длина и расположение интервалов неустойчивости для симметричного и несимметричного спутника близки друг к другу. Но при α > 0 и значениях $c$, существенно превышающих величину ${{m}^{2}}$, “рождаются” области неустойчивости, отсутствующие у симметричного спутника.

Для обратных вращений (рис. 2) диаграммы для симметричного и несимметричного спутника существенно различаются только тем, что в области $0 < U < {{U}_{3}}$, где стационарные вращения симметричного спутника неустойчивы, при α > 0 и $c \gg {{m}^{2}}$ имеются небольшие по размерам интервалы асимптотически устойчивых плоских вращений.

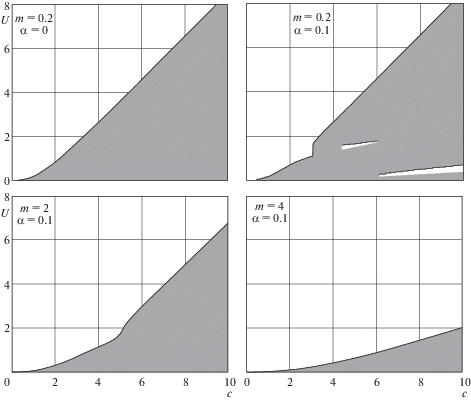
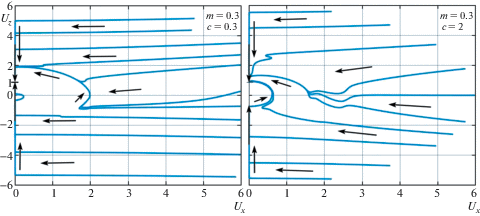
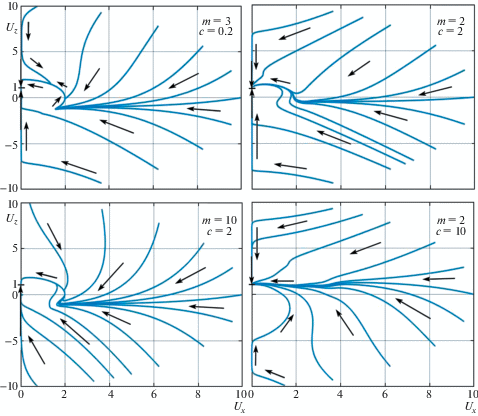
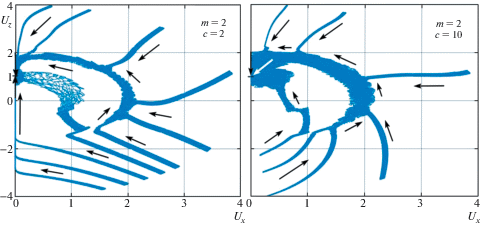
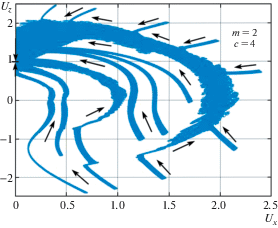
4. Фазовые траектории эволюции вращательного движения спутника. На рис. 3–6 приведены фазовые траектории (ФТ) вращательного движения спутника для разных комбинаций значений параметров $m,\;c$ и разных начальных условий. ФТ на рис. 3, 4 построены на основе результатов численного интегрирования осредненных уравнений (2.24), (2.25), а на рис. 5, 6 – на основе точных уравнений (1.3). Через ${{U}_{X}}$ и ${{U}_{Z}}$ обозначены проекции приведенной угловой скорости спутника на плоскость орбиты и на нормаль к плоскости орбиты, соответственно. Стрелками показано направление эволюции.

Сравнительный анализ диаграмм, изображенных в правых частях рис. 4 и на рис. 5, а также результаты других расчетов, показывают идентичность ФТ осредненных и точных уравнений в области U > 2. Из приведенных диаграмм следует также, что при c < ${{m}^{2}}$ ФТ незначительно отличаются от траекторий вращательного движения спутника под влиянием только диссипативных внутренних сил [3].

При $m \ll 1$ и $c \ll 1$ (рис. 3, слева) для большинства начальных условий из области U > 2 ось вращения спутника сначала поворачивается в сторону нормали к плоскости орбиты (${{U}_{X}} \to 0$), а затем спутник эволюционирует к положению относительного равновесия в режиме плоского вращения (${{U}_{X}} = 0$, ${{U}_{Z}} \to 1$). Существующие при указанных значениях параметров интервалы неустойчивости для прямых и обратных плоских вращений малы и к заметному отклонению движений спутника от плоских вращений не приводят. При $m \ll 1$ и $c \ll 1$ только для небольшой части начальных условий из области U > 2 ФТ попадают на окружность U = 2. После этого наступает режим резонансного вращения 2:1, в процессе которого величина угловой скорости спутника остается постоянной, а ось вращения поворачивается против часовой стрелки в сторону нормали к плоскости орбиты. Третий этап эволюции для таких траекторий представляет собой “прямое” плоское вращение, в процессе которого величина угловой скорости меняется от 2 до 1.

При $m \ll 1$ и $c \sim 1$ (рис. 3, справа) длина интервала неустойчивости для “обратных” плоских вращений составляет уже значительную величину ${{U}_{3}} \sim c$. Поэтому, когда величина угловой скорости U попадает в интервал неустойчивости, спутник выходит из режима плоского обратного вращения и дальнейшая эволюция к положению относительного равновесия происходит по “обходной” траектории. Аналогичные примеры “входа” спутника в режим плоского вращения и “выхода” из этого режима представлены на рис. 4 (верхняя левая и нижняя правая части рисунка). Такое поведение спутника подтверждается и результатами численного интегрирования точных уравнений (1.3).

С ростом значения параметра $m$ увеличивается область начальных условий, для которых ФТ попадают на резонансную окружность U = 2. При $m \gg 1$ большинство ФТ имеют своей составной частью этап резонансного вращения 2:1. При этом, если $c \ll {{m}^{2}}$ (левая часть рис. 4), это резонансное вращение адекватно описывается и траекториями осредненных уравнений. Но в случае $c \gg {{m}^{2}}$ (нижняя правая часть рис. 4) ФТ осредненных уравнений в окрестности резонансного значения U = 2 отличаются от ФТ точных уравнений (рис. 5, справа). Объясняется это различие тем, что осредненные уравнения (2.24), (2.25) выведены для нерезонансного случая.

На рис. 6 представлен полученный численным интегрированием точных уравнений (1.3) типичный фазовый портрет вращательного движения спутника в области U < 2 и ее окрестности. Видно, что ФТ из области U > 2 захватываются в резонансное вращение 2:1 и в этом режиме спутник движется вплоть до того, когда угол между осью вращения и нормалью к плоскости орбиты становится близким к нулю. Но ярко выраженного притягивающего резонансного вращения 1:1, какое существует при c = 0 [3], не наблюдается.

Фазовые портреты вращательного движения для динамически симметричного и несимметричного спутника существенно отличаются только тем, что для симметричного спутника ФТ заканчиваются стационарными вращениями вокруг нормали к плоскости орбиты, а для несимметричного спутника имеются еще финальные куски ФТ, по которым спутник приходит в положение относительного равновесия.