1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 3, 2020

Известия РАН. Механика твердого тела, 2020, № 3, стр. 69-79

ЭФФЕКТИВНАЯ МОДЕЛЬ НЕСУЩИХ СЛОЕВ ДЛЯ ПОСЛОЙНОГО АНАЛИЗА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ТРЕХСЛОЙНЫХ ЦИЛИНДРИЧЕСКИХ НЕРЕГУЛЯРНЫХ ОБОЛОЧЕК ВРАЩЕНИЯ

В. Н. Бакулин *

Институт прикладной механики РАН
Москва, Россия

* E-mail: vbak@yandex.ru

Поступила в редакцию 17.01.2020
После доработки 27.01.2020
Принята к публикации 28.01.2020

Полный текст (PDF)

Аннотация

Рассматривается применение эффективных аппроксимаций, повышающих скорость сходимости численных результатов, при построении конечно-элементной модели несущих слоев для уточненного послойного анализа напряженно-деформированного состояния трехслойных нерегулярных цилиндрических оболочек. Считается, что несущие слои являются достаточно тонкими и жесткими, и для моделирования напряженно-деформированного состояния в них применяются двумерные конечные элементы естественной кривизны, построенные на основе классической теории моментных оболочек. Предполагается, что слой заполнителя может моделироваться по толщине необходимым числом трехмерных конечных элементов, что позволяет учесть изменение геометрических и физико-механических характеристик, а также параметров напряженно-деформированного состояния не только по меридиональной и окружной координатам, но и по толщине оболочки и слоя заполнителя. Рассмотренные конечно-элементные аппроксимации позволяют уменьшить порядок систем уравнений, т.е. понизить размерность решаемых задач по сравнению с традиционно используемыми аппроксимациями, что особенно актуально при послойном анализе слоисто-неоднородных конструкций. Высокая скорость сходимости численных результатов, полученных с помощью рассмотренной конечно-элементной модели несущих слоев, подтверждена приведенным сравнением с другими известными конечными элементами.

Ключевые слова: нерегулярные трехслойные оболочки вращения, несущие слои, напряженно-деформированное состояние, послойный анализ, конечно-элементные аппроксимации, конечно-элементная модель

1. Введение. Для повышения удельной жесткости конструкций современной ракетной и авиационной техники растет использование оболочек слоисто-неоднородной структуры, в том числе трехслойных цилиндрических нерегулярных оболочек вращения [1–4]. Модели для анализа напряженно-деформированного состояния (НДС) конструкций современной техники, отличающейся многими конструктивными особенностями и сложными видами нагрузок, должны позволять провести расчет с высокой степенью точности и детализации.

Из анализа работ, посвященных исследованиям напряженно-деформированного состояния слоисто-неоднородных оболочек, следует, что в основном рассмотрены задачи для ограниченного круга видов нагружения и условий закрепления слоев, а также следует отметить, что распространены модели, часто не удовлетворяющие требованиям по степени детализации расчетов НДС несущих слоев и слоев заполнителя и не позволяющие провести анализ с необходимой точностью в общем случае нерегулярных ортотропных слоистых оболочек, при учете таких особенностей, как неоднородная структура стенки оболочки с учетом неоднородности, в том числе на уровне слоев заполнителя, переменные геометрические и физико-механические свойства и изменение их и параметров НДС не только по меридиональной и окружной координатам, но и по толщине слоя заполнителя. Учет многих из этих особенностей можно обеспечить послойным моделированием напряженно-деформированного состояния слоистых, в том числе трехслойных оболочек.

Послойный анализ слоисто-неоднородных элементов конструкций [5] заключается в том, что стенка конструкции разбивается на слои, а при необходимости и слои, и особенно заполнитель, разбиваются по толщине на дополнительные слои (уточненный послойный анализ), которые затем стыкуются между собой. При таком подходе можно в зависимости от геометрических и физико-механических характеристик слоев и условий задач создавать и применять разные модели для расчета слоев, используя аналитические и численные методы. При послойном анализе получение аналитических решений для большого числа актуальных научных и важных прикладных задач по расчету напряженно-деформированного состояния слоисто-неоднородных элементов конструкций сталкивается с трудностями математического характера, часто непреодолимыми сложностями.

Одним из методов для решения указанных задач, позволяющим с необходимой степенью детализации проводить уточненные расчетные исследования, является метод конечных элементов (МКЭ) [6–9 и др.]. Некоторые конечно-элементные модели (КЭМ) слоистых оболочек рассматривались в [10–18] и других работах. В основном эти модели построены на гипотезах, применяемых к пакету слоев. Расчет напряженно-деформированного состояния слоисто-неоднородных элементов конструкций с помощью таких моделей часто не удовлетворяет современным требованиям к точности результатов моделирования.

2. Постановка задачи. Предлагаемый подход [19–23] позволяет провести послойное моделирование напряженно-деформированного состояния слоисто-неоднородных оболочечных конструкций с высокой степенью точности и детализации. Подход состоит в построении модели из оболочечных конечных элементов (КЭ) несущих слоев и необходимого (для достижения требуемой точности и степени детализации) числа КЭ заполнителя для моделирования напряженно-деформированного состояния по толщине оболочки, а при необходимости и ее слоев, и особенно заполнителя (уточненный послойный анализ). Такой подход позволяет использовать различные по точности модели (в зависимости от условий задач) для анализа напряженно-деформированного состояния в слоях, учесть в них изменение геометрических и физико-механических свойств материалов и параметров НДС по всем трем координатам, к которым отнесена оболочка, а также проводить расчет при разнообразных граничных условиях и различных нарушениях сплошности слоев.

Однако модели, построенные на основе предлагаемого подхода послойного анализа [19–23], отличаются большой размерностью, зависящей от числа слоев и числа КЭ, на которые разбиваются слои оболочки по толщине в случае уточненного послойного анализа, а также от числа степеней свободы конечных элементов и эффективности функций, аппроксимирующих искомые параметры (перемещения, деформации, напряжения) внутри конечных элементов. Эффективными будем называть аппроксимации, повышающие скорость сходимости численных результатов, а, следовательно, позволяющие уменьшить порядок систем уравнений, то есть, понизить размерность задач по сравнению с традиционно используемыми аппроксимациями. Обычно при расчете как однородных, так и неоднородных оболочек используют конечные элементы с базисными функциями на основе аппроксимации полей перемещений полиномами первого и второго порядков [7, 10, 11].

Использование таких аппроксимаций в виде полиномов приводит к громоздким конечно-элементным моделям, что значительно затрудняет и ограничивает разработку и применение таких моделей, приходится заниматься с большими массивами информации, что сильно осложняет работу, в том числе обработку полученных численных результатов. При большой размерности задач растут погрешности вычислений, необходимые ресурсы ЭВМ, время расчета. Это значительно затрудняет, а нередко делает невозможным проведение исследований таких конструкций с надлежащей точностью. В связи с этим актуальной является проблема снижения размерности КЭМ для расчета слоисто-неоднородных особенно оболочечных элементов конструкций.

И.Ф. Образцов отмечал в работе [24] “… основная проблема при рассмотрении сложных конструкций заключается в создании эффективных математических моделей исследуемых систем, которые не только обеспечивают выполнение заданных требований к информативности и точности исследований, но и одновременно являются экономичными, способствуя, в частности, минимизации затрат машинного времени и памяти ЭВМ”.

Об эффективности аппроксимаций при построении конечно-элементных моделей для уточненного прочностного анализа слоистых оболочек говорится в [25].

Все более распространенным становится мнение, высказанное в монографии Г. Стренга, Д. Фикса [26]: “конечные элементы стали наиболее употребительным средством вычислительной математики во всем мире, но будет еще лучше, если мы научимся решать те же задачи с меньшими затратами”.

Построению эффективных моделей деформирования тонкостенных конструкций, слоисто-неоднородных и трехслойных оболочек, в том числе с прямоугольными отверстиями посвящены работы [4, 27–39]. В этих работах построение эффективных моделей осуществляется и на основе метода конечных элементов, и на основе комбинированных с методом конечных элементов подходов, а также на других аналитико-численных и численно-аналитических подходах (метод конечных тел и др.) решения краевых задач.

В представленной работе для понижения размерности создаваемых моделей уточненного послойного анализа напряженно-деформированного состояния трехслойных цилиндрических нерегулярных оболочек вращения предлагается применить эффективные функции, аппроксимирующие обобщенные деформации, и точно учесть аналитически полученные перемещения как жесткого тела при построении конечных элементов несущих слоев рассматриваемых слоисто-неоднородных оболочек. Предложенные подходы построения эффективных аппроксимаций и на их основе создания моделей уточненного анализа напряженно-деформированного состояния несущих слоев трехслойных цилиндрических нерегулярных оболочек вращения позволили повысить скорость сходимости получаемых численных результатов, а, следовательно, уменьшить порядок систем уравнений, т.е. понизить размерность задач по сравнению с традиционно используемыми аппроксимациями. Это подтверждено проведенными расчетами и приведенным сравнением сходимости результатов, полученных с помощью рассматриваемого КЭ и других известных конечных элементов.

3. Эффективные аппроксимации для построения конечно-элементной модели несущих слоев трехслойных цилиндрических нерегулярных оболочек. Будем рассматривать трехслойные оболочки с тонкими и жесткими несущими слоями (индекс “c”) и толстым промежуточным слоем заполнителя (индекс “f”). Для упрощения записи эти индексы у коэффициентов, составляющих вектора и матрицы, указывать не будем.

Конечные элементы несущих слоев и заполнителя образованы сечением слоев оболочки двумя плоскостями, перпендикулярными оси вращения, и двумя плоскостями, проходящими через ось оболочки. Узлы расположены в угловых точках конечных элементов.

Местные системы координат конечных элементов несущих слоев находятся на срединных поверхностях КЭ с началом координат, расположенном на пересечении двух линий, одна из которых проходит на одинаковом расстоянии от криволинейных границ элементов, а другая от прямолинейных.

Будем считать справедливыми для несущих слоев гипотезы Кирхгофа–Лява, тогда компоненты линейной составляющей вектора обобщенных деформаций моментной цилиндрической оболочки

${\mathbf{\varepsilon }}_{{\mathbf{i}}}^{{\mathbf{c}}} = {{\{ \varepsilon _{1}^{{}},\varepsilon _{2}^{{}},\gamma ,{\unicode{230} }_{1}^{{}},{\unicode{230} }_{2}^{{}},\chi \} }^{{\text{т}}}}$
связаны с компонентами вектора перемещений точек срединной поверхности
${\mathbf{\delta }}_{{\mathbf{i}}}^{{\mathbf{c}}} = {{\{ u,{v},w\} }^{{\text{т}}}}$
соотношениями [40]
(3.1)
${\mathbf{\varepsilon }}_{i}^{с} = {\mathbf{B}}_{{\mathbf{i}}}^{с}{\mathbf{\delta }}_{i}^{с}$
${\mathbf{B}}_{{\mathbf{i}}}^{{\mathbf{c}}} = \left[ {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial x}}}&0&0 \\ 0&{\frac{1}{R}\frac{\partial }{{\partial \varphi }}}&{\frac{1}{R}} \\ {\frac{1}{R}\frac{\partial }{{\partial \varphi }}}&{\frac{\partial }{{\partial x}}}&0 \\ 0&0&{ - \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}} \\ 0&{\frac{1}{{{{{(R)}}^{2}}}}\frac{\partial }{{\partial \varphi }}}&{ - \frac{1}{{{{{(R)}}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{\varphi }^{2}}}}} \\ 0&{\frac{1}{R}\frac{\partial }{{\partial x}}}&{ - \frac{1}{R}\frac{{{{\partial }^{2}}}}{{\partial x\partial \varphi }}} \end{array}} \right]$
х, φ – линейная и угловая координаты; R – радиус срединной поверхности i-го несущего слоя, i – номер слоя, начиная с внутренней поверхности оболочки.

Аппроксимирующие функции перемещений (АФП) для оболочечных конечных элементов должны учитывать перемещения как жесткого тела [5, 7, 17–23, 34, 39, 41, 42], которые получаются интегрированием соотношений (3.1) при нулевых значениях деформаций.

Эти функции перемещений как жесткого тела будут записаны с помощью неопределенных коэффициентов α1, …, α6 (постоянных интегрирования) и приведены в первых шести строках табл. 1.

Таблица 1
αi u v w
α1 0 sin φ –cos φ
α2 Rcos φ x sin φ –x cos φ
α3 0 –cos φ –sin φ
α4 Rsin φ –xcos φ –x sin φ
α5 1 0 0
α6 0 1 0
α7 x 0 0
α8 xφ –1/(2R)x2 0
α9 0 0 R
α10 0 0 Rx
α11 Rφ 0 0
α12 0 0 –1/2x2
α13 0 0 –1/6x3
α14 0 0 –1/2x2φ
α15 0 0 –1/6x3φ
α16 0 R2φ –R2
α17 –1/2R3φ2 R2xφ –R2x
α18 0 1/2R2φ2 –R2φ
α19 R3φ(–1/6φ2 + 1) R2x(1/2φ2 – 1) –R2xφ
α20 –R2φ Rx 0

Наиболее эффективными, т.е. приводящими к высокой скорости сходимости численных результатов, являются функции формы, построенные на основе аналитических решений задач теории оболочек [43–47]. Но разработать такой подход удалось только для осесимметричных трехслойных цилиндрических оболочек.

Проведенные исследования показали, что наиболее эффективными с точки зрения скорости сходимости получаемых результатов для анализа напряженно-деформированного состояния трехслойных нерегулярных цилиндрических оболочек являются конечно-элементные модели, построенные на основе аппроксимации функций обобщенных деформаций с последующим удовлетворением уравнениям неразрывности (совместности) деформаций.

Сложность и особенность оболочечных конечных элементов, построенных на основе аппроксимации функций обобщенных деформаций, заключается в необходимости удовлетворения этих функций уравнениям неразрывности (совместности) деформаций [40, 48].

При записи аппроксимирующих функций деформаций (АФД) для рассматриваемого конечного элемента несущих слоев трехслойной цилиндрической нерегулярной оболочки, узловыми перемещениями которого служат u, ${v}$, w и два угла поворота нормали к срединной поверхности (т.е. пять степеней свободы в узле), используются четырнадцать неопределенных коэффициентов α7, …, α20

(3.2)
${\mathbf{\varepsilon }}_{{\mathbf{i}}}^{{\mathbf{c}}} = {\mathbf{\Omega }}_{{\mathbf{i}}}^{{\mathbf{c}}}{\mathbf{\alpha }}_{{\mathbf{i}}}^{{\mathbf{c}}}$
где ${\mathbf{\Omega }}_{{\mathbf{i}}}^{{\mathbf{c}}}$ – матрица (6 × 20) (см. табл. 2), ${\mathbf{\alpha }}_{{\mathbf{i}}}^{{\mathbf{c}}}$ – вектор неопределенных коэффициентов α1, …, α20. Коэффициенты матрицы ${\mathbf{\Omega }}_{{\mathbf{i}}}^{{\mathbf{c}}}$ удовлетворяют уравнениям неразрывности деформаций. В пустых клеточках табл. 2 коэффициенты матрицы ${\mathbf{\Omega }}_{{\mathbf{i}}}^{{\mathbf{c}}}$ равны нулю.

Таблица 2
  ε1 ε2 γ ${{\unicode{230} }_{1}}$ ${{\unicode{230} }_{2}}$ χ
α1            
α2            
α3            
α4            
α5            
α6            
α7 1          
α8 φ         –x/R2
α9   1        
α10   x        
α11     1      
α12 –x2/2R   1    
α13 –x3/6R   x    
α14 –x2φ/2R   φ   x/R
α15 –x3φ/6R   xφ   x2/2R
α16         1  
α17         x Rφ
α18         φ  
α19         xφ Rφ2/2
α20           1

Аппроксимирующие функции перемещений для рассматриваемого конечного элемента несущих слоев, вызванных деформированием КЭ, получаются интегрированием соотношений (3.1) с учетом (3.2). Тогда полные функции перемещений будут иметь вид

(3.3)
$\delta _{i}^{c} = {\mathbf{T}}_{i}^{c}\alpha _{i}^{c}$
где ${\mathbf{T}}_{i}^{c}$ (3 × 20) – матрица аппроксимирующих функций перемещений КЭ несущих слоев трехслойной цилиндрической нерегулярной оболочки (табл. 1).

Используя процедуры и алгоритмы, аналогичные [47], проводится построение конечно-элементной модели для анализа напряженно-деформированного состояния несущих слоев трехслойных цилиндрических нерегулярных оболочек.

4. Сравнение эффективности аппроксимаций рассматриваемого конечного элемента и известных конечных элементов на тестовом примере. Перед применением моделей, особенно основанных на численных методах, необходимо оценить достоверность, сходимость, точность результатов, полученных с помощью рассмотренных моделей. Погрешности аппроксимации исследовались в работах [49–51]. Алгоритм оценки сходимости решения в конечно-элементных задачах предложен в [52–55].

Достоверность, сходимость, точность результатов, полученных с помощью рассмотренной модели, и эффективность (скорость сходимости численного решения) конечного элемента исследовалась на известном и широко распространенном для оболочечных конечных элементов тесте сопоставлением с аналитическим решением и численными результатами, полученными с помощью известных конечных элементов других авторов.

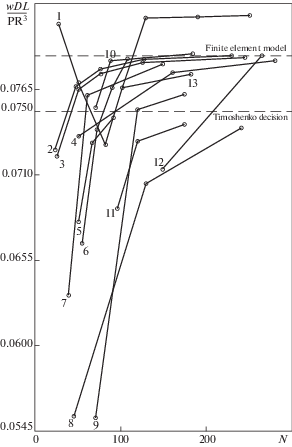
На рис. 1 на примере решения задачи С.П. Тимошенко для свободной круговой цилиндрической оболочки, нагруженной двумя симметричными диаметрально противоположными и расположенными на одинаковом расстоянии от торцов сосредоточенными радиальными силами [56], приведено сравнение сходимости численных результатов, полученных с помощью рассматриваемого конечного элемента цилиндрической оболочки (цифра 2 у графика на рис. 1 ) и известных конечных элементов других авторов, представленных в работе [57]. Приведены численные решения, полученные с помощью известных конечных элементов следующих авторов [57], соответствующих цифрам у графиков на рис. 1 : Henshell R.D. – 1; Ashwell D.G., Sabir A.B. – 3; Dawe D.J. – 4; Wempner G.A., Oden J.T., Kross D.A. – 5; Altman W., Iguti F. – 6; Murthy S.S., Gallagher R.H. (1986 г.) – 7; Morley L.S.D. – 8; Bogner F.K., Fox R.L. and Schmit L.A. – 9; Murthy S.S., Gallagher R.H. (1983 г.) – 10; Cantin G., Clough R.W. – 11, Сахаров А.С., Cоловей Н.А. – 12; Thomas G.R., Gallagher R.H. – 13.

Рис. 1

На рис. 1 показаны зависимости безразмерного прогиба от порядка решаемой системы уравнений N. Обозначения на рис. 1 : w – прогиб оболочки в точке приложения сил Р, направленных к оси оболочки, D, l, R, h – цилиндрическая жесткость, длина, радиус, толщина оболочки соответственно.

На рис. 1 приведены также аналитическое решение С.П. Тимошенко для свободной круговой цилиндрической оболочки, нагруженной двумя симметричными диаметрально расположенными на одинаковом расстоянии от торцов сосредоточенными радиальными силами, направленными к оси оболочки (нижняя пунктирная линия) [56] и конечно-элементное решение (верхняя пунктирная линия).

Сопоставление скорости сходимости численных результатов, полученных с помощью рассматриваемого конечного элемента круговой цилиндрической оболочки и известных конечных элементов, показало эффективность (высокую скорость сходимости численных результатов, что позволило уменьшить необходимое для расчета число КЭ) применяемого конечного элемента, имеющего 20 степеней свободы, по сравнению с распространенными конечными элементами других авторов, приведенными в работе [57], результаты расчетов которых представлены на рис. 1 в виде графических зависимостей с цифрами 1, 3–13 у графиков.

5. Построение конечно-элементной модели слоя заполнителя. Как уже отмечалось выше, эффективность функций, аппроксимирующих искомые параметры (перемещения, деформации, напряжения) внутри конечных элементов, приводящих к высокой скорости сходимости численных результатов, особенно актуальна при послойном анализе, когда размерность моделей зависит от числа слоев и числа КЭ, на которые разбиваются оболочки, в т.ч. по толщине. Рассмотренные эффективные аппроксимирующие функции перемещений конечного элемента несущих слоев используем при построении КЭ для послойного анализа напряженно-деформированного состояния заполнителя трехслойных нерегулярных цилиндрических оболочек. Для этого аппроксимирующие функции перемещений конечного элемента несущих слоев приводятся к соответствующей поверхности стыковки со слоем заполнителем. В качестве узловых выберем обе цилиндрические поверхности трехмерного конечного элемента слоя заполнителя. Таким образом, у конечного элемента слоя заполнителя будет восемь узлов. Применение аппроксимирующих функций перемещений конечного элемента несущих слоев при построении КЭ слоя заполнителя позволило избежать разрыва перемещений на поверхностях контакта конечных элементов слоев трехслойной нерегулярной цилиндрической оболочки.

Приняв линейный закон изменения перемещений по толщине КЭ заполнителя, получим аппроксимирующие функции перемещений конечного элемента слоя заполнителя. Используя соотношения связи деформаций с перемещениями и физические соотношения, связывающие деформации с напряжениями, для толстостенного заполнителя и применив процедуру и алгоритмы, аналогичные [21, 39, 47], проводится построение конечно-элементной модели заполнителя для послойного анализа напряженно-деформированного состояния трехслойных нерегулярных цилиндрических оболочек.

Заключение. Для понижения размерности создаваемых моделей уточненного послойного анализа напряженно-деформированного состояния трехслойных цилиндрических нерегулярных оболочек вращения применены эффективные функции, аппроксимирующие обобщенные деформации, и точно учтены аналитически полученные перемещения как жесткого тела при построении конечных элементов тонких и жестких несущих слоев рассматриваемых слоисто-неоднородных оболочек. Указанные подходы построения эффективных аппроксимаций и на их основе создания моделей уточненного анализа напряженно-деформированного состояния несущих слоев трехслойных цилиндрических нерегулярных оболочек вращения позволили повысить скорость сходимости получаемых численных результатов, а, следовательно, уменьшить порядок систем уравнений по сравнению с традиционно используемыми аппроксимациями (аппроксимация перемещений). Это подтверждено проведенными расчетами и приведенным сравнением сходимости результатов, полученных с помощью рассматриваемого конечного элемента и других известных конечных элементов.

Работа выполнена в рамках государственного задания, номер государственной регистрации темы АААА-А19-119012290177-0.

Список литературы

  1. Образцов И.Ф., Булычев Л.А., Васильев В.В. и др. Строительная механика летательных аппаратов. М.: Машиностроение, 1986. 536 с.

  2. Бакулин В.Н., Образцов И.Ф., Потопахин В.А. Динамические задачи нелинейной теории многослойных оболочек: действие интенсивных термосиловых нагрузок, концентрированных потоков энергии. М.: Наука, Физматлит, 1998. 464 с.

  3. Бакулин В.Н., Острик А.В. Комплексное действие излучений и частиц на тонкостенные конструкции с гетерогенными покрытиями. М.: Физматлит, 2015. 280 с.

  4. Bakulin V.N. Investigation of the Influence of the Cutout Dimensions on the Stress-strain State of Three-layer Shells with Load-bearing Layers of Composite Materials // Journal of Physics: Conference Series: Materials Science and Engineering. 714, 012002 (2020). https://doi.org/10.1088/1757-899X/714/1/012002

  5. Бакулин В.Н. Уточненная модель послойного анализа трехслойных нерегулярных конических оболочек // Доклады Академии наук. 2017. Т. 472. № 3. С. 272–277.

  6. Образцов И.Ф., Савельев Л.М., Хазанов Х.С. Метод конечных элементов в задачах строительной механики летательных аппаратов. М.: Высшая школа, 1985. 392 с.

  7. Бакулин В.Н., Рассоха А.А. Метод конечных элементов и голографическая интерферометрия в механике композитов. М.: Машиностроение, 1987. 312 с.

  8. Зенкевич О., Морган К. Конечные элементы и аппроксимация. М.: Мир, 1986. 318 с.

  9. Бакулин В.Н., Каледин В.О., Каледин Вл.О., Кузнецова Е.В., Репинский В.В. Объектно-ориентированная реализация метода конечных элементов для решения задач механики конструкций // Математическое моделирование. 2003. Т. 15. № 2. С. 77–82.

  10. Бакулин В.Н., Кривцов В.С., Рассоха А.А. Алгоритм получения матрицы жесткости конечного элемента анизотропной оболочки // Изв. вузов. Авиационная техника. 1983. № 4. С. 14–18.

  11. Алфутов Н.А., Зиновьев П.А., Попов Б.Г. Расчет многослойных пластин и оболочек из композиционных материалов. М.: Машиностроение, 1984. 263 с.

  12. Пискунов В.Г., Вериженко В.Е., Присяжнюк В.К. и др. Расчет неоднородных пологих оболочек и пластин методом конечных элементов. Киев: Вища школа, 1987. 200 с.

  13. Рикардс Р.Б. Метод конечных элементов в теории оболочек и пластин. Рига: Зинатне, 1988. 284 с.

  14. Фомичев Ю.И., Перевозчикова В.М., Бакулин В.Н. Устойчивость многослойных ортотропных оболочек вращения при неосесимметричном температурно-силовом нагружении // Прикладная механика. 1986. № 12. С. 54–60.

  15. Фомичев Ю.И., Перевозчикова В.М., Бакулин В.Н. Исследование напряженно-деформированного состояния конструктивно-ортотропной оболочечной конструкции под действием не осесимметричных нагрузок // Проблемы прочности. 1986. № 5. С. 117–122.

  16. Каледин В.О., Аульченко С.М., Миткевич А.Б., Решетникова Е.В., Седова Е.А., Шпакова Ю.В. Моделирование статики и динамики оболочечных конструкций из композиционных материалов. М.: Физматлит, 2014. 196 с.

  17. Бакулин В.Н., Репинский В.В. Конечно-элементные модели деформации однослойных и трехслойных конических оболочек // Математическое моделирование. 2001. Т. 13. № 6. С. 39–46.

  18. Бакулин В.Н. Конечно-элементные модели для расчета слоистых оболочек вращения ненулевой гауссовой кривизны // Математическое моделирование. 2002. Т. 14. № 8. С. 37–43.

  19. Бакулин В.Н. Блочная конечно-элементная модель для послойного анализа напряженно-деформированного состояния трехслойных оболочек с нерегулярной структурой // Изв. РАН. МТТ. 2018. № 4. С. 66–73.

  20. Бакулин В.Н. Эффективная модель послойного анализа трехслойных нерегулярных оболочек вращения цилиндрической формы // Доклады Академии наук. 2018. Т. 478. № 2. С. 148–152.

  21. Бакулин В.Н. Модель для уточненного расчета напряженно-деформированного состояния трехслойных конических нерегулярных оболочек // Прикладная математика и механика. 2019. Т. 83. № 2. С. 315–327.

  22. Бакулин В.Н. Блочная конечно-элементная модель послойного анализа трехслойных в общем случае нерегулярных оболочек вращения двойной кривизны // Доклады Академии наук. 2019. Т. 484. № 1. С. 35–40.

  23. Бакулин В.Н. Модель для послойного анализа напряженно-деформированного состояния трехслойных нерегулярных оболочек вращения двойной кривизны // Изв. РАН. МТТ. 2020. № 2. С. 112–122.

  24. Образцов И.Ф. О некоторых перспективных прикладных проблемах механики, имеющих народнохозяйственное значение // Изв. АН СССР. Механика твердого тела. 1982. № 4. С. 3–9.

  25. Бакулин В.Н. Неклассические уточненные модели в механике трехслойных оболочек // Вест. Нижегородского университета им. Н.И. Лобачевского. Н. Новгород: Изд-во ННГУ им. Н.И. Лобачевского, 2011. № 4. Ч. 5. С. 1989–1991.

  26. Strang G., Fix G.J. An Analysis of the Finite Element Method. Englewood Cliffs, N. J.: Prentice-Hall, 1973 = Стренг Г., Фикс Д. Теория метода конечных элементов. М.: Мир, 1977. 392 с.

  27. Бакулин В.Н., Мысык Д.А. К расчету трехслойных оболочек с переменной толщиной заполнителя // Механика композитных материалов. 1980. № 5. С. 933–935.

  28. Бакулин В.Н. Исследование напряженно-деформированного состояния трехслойных оболочек при действии радиальной нагрузки, неравномерно распределенной по полукольцевой площадке // Проблемы прочности. 1985. № 5. С. 78–81.

  29. Бакулин В.Н., Каледин В.О., Рассоха А.А. Анализ термоупругих напряжений в слоистых оболочках двоякой кривизны // Механика композитных материалов. 1987. № 6. С. 1028–1033.

  30. Бакулин В.Н. и др. Численный анализ температурных полей в слоистых анизотропных оболочках // Математические методы и физико-химические поля: Республ. межвед. сб. научн. тр. Киев. 1987. № 26. С. 98–101.

  31. Бакулин В.Н., Каледин Вл.О. Конечный элемент круговой арки с конечной сдвиговой жесткостью // Механика композитных материалов. 1988. № 5. С. 915–919.

  32. Бакулин В.Н., Каледин В.О. Численно-аналитический подход к исследованию деформирования оболочечных конструкций из композитов // Изв. АН СССР. МТТ. 1989. № 4. С. 184–188.

  33. Образцов И.Ф., Иванов Ю.И., Нерубайло Б.В., Зайцев В.Н. О поcтроении эффективных моделей деформирования тонкостенных конструкций // Прикладная механика. 1985. Т. 21. № 7. С. 61–67.

  34. Бакулин В.Н. Уточненная модель для расчета напряженно-деформированного состояния трехслойных конических оболочек вращения // Вестник Московского авиационного института. 2011. Т. 18. № 2. С. 211–218.

  35. Бакулин В.Н., Острик А.В. Совместное тепловое и механическое действие излучений и ударных волн на многослойную ортотропную оболочку с гетерогенным покрытием // Прикладная математика и механика. 2014. Т. 78. Вып. 2. С. 225–235.

  36. Преображенский И.Н., Голда Ю.Л., Дмитриев В.Г. Численный метод исследования напряженно-деформированного состояния гибких композитных оболочек вращения, ослабленных вырезами различной формы // Механика композитных материалов. 1985. № 6. С. 1030–1035.

  37. Бакулин В.Н., Ревенко В.П. Аналитико-численный метод конечных тел решения краевой задачи для цилиндрической ортотропной оболочки с немалым прямоугольным отверстием // Известия вузов. Математика. 2016. № 6. С. 3–14.

  38. Revenko V.P., Bakulin V.N. Method of Finite Bodies for Mathematical Modeling of the Stress-strain State of Cylindrical Orthotropic Shell with the Reinforced Rectangular Hole // Journal of Physics: Conference Series 1392, 012021 (2019). IOP Publishing https://doi.org/10.1088/1742-6596/1392/1/012021

  39. Бакулин В.Н. Послойный анализ напряженно-деформированного состояния трехслойных оболочек с вырезами // Изв. РАН. МТТ. 2019. № 2. С. 111–125.

  40. Балабух Л.И., Колесников К.С., Зарубин В.С. и др. Основы строительной механики ракет. М.: Высшая школа, 1969. 494 с.

  41. Железнов Л.П., Кабанов В.В. Функции перемещений конечных элементов оболочки вращения как твердых тел // Изв. РАН. МТТ. 1990. № 1. С. 131–136.

  42. Репинский В.В. Эффективные конечные элементы для расчета устойчивости тонких анизотропных оболочек вращения. Вопр. оборон. техники. Сер. 15. Вып. 1 (117). 1997. С. 3–7.

  43. Бакулин В.Н., Каледин Вл.О. О подходе к построению конечно-элементной аппроксимации для эффективного решения задач теории слоистых оболочек // Третья Всесоюзная конференция Механика неоднородных структур. Львов: Ин-т прикл. проблем мех. и матем. АН УССР, 1991. С. 17–18.

  44. Каледин Вл.О., Шпиталь С.В. Выбор расчетной схемы при исследовании осесимметричного краевого эффекта в трехслойных цилиндрических оболочках с легким заполнителем // Мех. композ. матер. 1993. № 5. С. 657–665.

  45. Бакулин В.Н. Аппроксимации для моделирования напряженно-деформированного состояния слоистых цилиндрических оболочек // Математическое моделирование. 2004. Т. 16. № 6. С. 101–105.

  46. Образцов И.Ф., Бакулин В.Н. Уточненные модели для исследования напряженно-деформированного состояния трехслойных цилиндрических оболочек // Доклады Академии наук. 2006. Т. 407. № 1. С. 36–39.

  47. Бакулин В.Н. Конечно-элементная модель для анализа напряженно-деформированного состояния трехслойных оболочек // Математическое моделирование. 2006. Т. 18. № 1. С. 3–9.

  48. Новожилов В.В. Теория тонких оболочек. Л.: Судпромгиз, 1951. 344 с.

  49. Оден Дж. Конечные элементы в нелинейной механике сплошных сред. М. Мир, 1976. 464 с.

  50. Годунов С.К., Рябенький В.С. Разностные схемы. М.: Наука, 1977. 439 с.

  51. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функций. М.: Наука, 1980. 352 с.

  52. Бакулин В.Н., Инфлянскас В.В. Алгоритм оценки сходимости решения в конечно-элементных задачах // Вестник Московского авиационного института. 2009. Т. 16. № 6. С. 222–227.

  53. Бакулин В.Н., Инфлянскас В.В. О выборе параметров конечно-элементной сетки в задачах с локальной нагрузкой // Машиностроение и техносфера XXI века. Сборник трудов XVIII международной научно-технической конференции в г. Севастополе 12–17 сентября 2011 г. В 4-х томах. Донецк: ДонНТУ, 2011. Т. 1. С. 48–50.

  54. Бакулин В.Н., Инфлянскас В.В. К вопросу о достаточной плотности конечно-элементной сетки // Материалы XVII Международной конференции по вычислительной механике и современным прикладным программным системам (ВМСППС 2011), 25–31 мая 2011 г. Алушта. М.: Изд-во МАИ-ПРИНТ, 2011. С. 40–44.

  55. Бакулин В.Н., Инфлянскас В.В. Оценка локальных параметров сетки в конечно-элементных задачах // Вычислительная механика сплошных сред. 2013. Т. 6. № 1. С. 70–77.

  56. Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. М.: Физматгиз, 1963. 635 с.

  57. Голованов А.И., Корнишин М.С. Введение в метод конечных элементов статики тонких оболочек. Казань, 1990. 270 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал