Известия РАН. Механика твердого тела, 2020, № 3, стр. 80-91
ПРОСТРАНСТВЕННАЯ НЕСТАЦИОНАРНАЯ КОНТАКТНАЯ ЗАДАЧА ДЛЯ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ И АБСОЛЮТНО ТВЕРДОГО ТЕЛА
А. С. Оконечников a, Д. В. Тарлаковский a, b, Г. В. Федотенков a, b, *
a Московский авиационный институт (национальный исследовательский университет)
Москва, Россия
b НИИ механики МГУ имени М.В. Ломоносова
Москва, Россия
* E-mail: greghome@mail.ru
Поступила в редакцию 10.12.2019
После доработки 18.12.2019
Принята к публикации 23.12.2019
Аннотация
Рассмотрена пространственная нестационарная контактная задача с подвижными границами области взаимодействия для тонкой упругой цилиндрической оболочки и абсолютно твердого ударника, ограниченного гладкой выпуклой поверхностью. Приведена замкнутая математическая постановка и построена система разрешающих уравнений. В основе последней лежит пространственно-временное интегральное уравнение, вытекающее из принципа суперпозиции и условий контакта. Ядром этого уравнения является функция влияния для цилиндрической оболочки. До замкнутой системы разрешающих уравнений оно дополняется кинематическим соотношением для определения подвижной границы области контакта и уравнением движения ударника как абсолютно твердого тела. Построен и реализован алгоритм решения пространственной нестационарной контактной задачи для бесконечно длинной цилиндрической оболочки и абсолютно твердого ударника в случае нормального удара по боковой поверхности оболочки. Приведены примеры расчетов.
Введение. В настоящее время, нестационарные контактные задачи механики деформируемого твердого тела приобретают все большую актуальность как в теоретическом, так и прикладном отношении. Это связано с возрастающими требованиями к точности расчетов на прочность и несущую способность основных элементов инженерных конструкций, работающих под воздействием нестационарных нагрузок. Исследование волновых процессов в тонких оболочках является актуальным для современной космической и авиационной техники, судостроения, строительства инженерных сооружений и т.д. В этой связи контактные задачи для оболочек являются одним из наиболее бурно развивающихся научных направлений. Среди них одними из наименее исследованных являются пространственные нестационарные контактные задачи. Имеется ограниченный круг работ, посвященных решению плоских и осесимметричных нестационарных контактных задач для оболочек [1–7]. Присутствуют работы, посвященные численным методам решения пространственных нестационарных задач для оболочек [8–14]. Работы, направленные на аналитическое или численно-аналитическое решение пространственных нестационарных контактных задач, практически отсутствуют. В данной статье разработан метод и реализован алгоритм решения пространственной нестационарной контактной задачи с подвижными границами для цилиндрической оболочки типа Тимошенко и абсолютно твердого ударника.
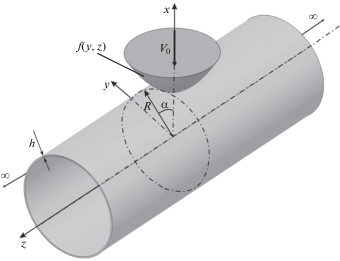
1. Постановка задачи. В начальный момент времени абсолютно твердый ударник, двигаясь с заданной начальной скоростью V0, входит в контакт с боковой поверхностью бесконечно длиной тонкой упругой круговой цилиндрической оболочки. Ударник ограничен гладкой выпуклой поверхностью, вектор его начальной скорости направлен по нормали к боковой поверхности оболочки (рис. 1).
Для описания движения оболочки используются уравнения движения модели С.П. Тимошенко в перемещениях, записанные в главных ортогональных координатах, связанных с направлениями главных кривизн срединной поверхности [15]:
(1.1)
$\begin{gathered} \frac{{{{\partial }^{2}}W}}{{\partial {{\tau }^{2}}}} = {\mathbf{L}}W + P \\ {\mathbf{L}} = {{\left( {{{L}_{{ij}}}} \right)}_{{5 \times 5}}},\quad W = {{\left( {u,v,w,{{\chi }_{\alpha }},{{\chi }_{z}}} \right)}^{{\text{T}}}},\quad P = {{\left( {0,0,p,0,0} \right)}^{{\text{T}}}} \\ \end{gathered} $Здесь и далее все функции, переменные и параметры приведены к безразмерной форме с использованием системы безразмерных величин (штрихом обозначены размерные параметры):
Уравнение движения ударника как абсолютно твердого тела имеет следующий вид:
(1.2)
$\begin{gathered} {{m}_{u}}{{{\ddot {u}}}_{c}}\left( \tau \right) = P\left( \tau \right) = \iint\limits_{\Omega \left( \tau \right)} {p\left( {\xi ,\zeta ,\tau } \right)d\xi d\zeta } \\ {{u}_{c}}\left( 0 \right) = 0,\quad {{{\dot {u}}}_{c}}\left( 0 \right) = {{V}_{0}} \\ \end{gathered} $Полагаем, что контакт между оболочкой и ударником происходит в условиях свободного проскальзывания.
Пусть ${{\Pi }_{1}}$ и ${{\Pi }_{2}}$ – поверхности, ограничивающие оболочку и ударник в момент времени $\tau > 0$, в инерциальной декартовой прямоугольной системе координат, ось $Oz$ которой совпадает с осью оболочки, задаются уравнениями
Тогда истинная область контакта ${{\Pi }_{*}}$ определяется следующими условиями:
(1.3)
$\begin{gathered} {{\Pi }_{*}}:\Delta \left( {y,z,\tau } \right) = {{f}_{1}}\left( {y,z,\tau } \right) - {{f}_{2}}\left( {y,z,\tau } \right) = 0 \\ p\left( {y,z,\tau } \right) < 0,\quad \left( {y,z} \right) \in {{\Omega }_{k}} \\ \end{gathered} $Из (1.3) следуют уравнения, неявно определяющие границу области контакта $\partial {{\Pi }_{*}}$:
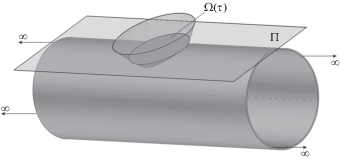
В линеаризованной постановке задачи истинная область контакта ${{\Pi }_{*}}$ заменяется фиктивной областью $\Omega \left( \tau \right)$, принадлежащей плоскости, являющейся общей касательной к поверхностям ${{\Pi }_{1}}$ и ${{\Pi }_{2}}$ в начальный момент времени контактного взаимодействия (рис. 2).
Положим, что положение поверхности, ограничивающей ударник, в текущий момент времени $\tau $ задается явным уравнением в системе координат $Oxyz$:
Граница $\partial \Omega \left( \tau \right)$ области $\Omega \left( \tau \right)$ определяются из условия пересечения поверхности ограничивающей ударник, с плоскостью $\Pi $:
(1.5)
$\partial \Omega \left( \tau \right){\text{: }}\;\;{\text{ }}f\left( {y,z} \right) + {{u}_{c}}\left( \tau \right) = 1$С учетом (1.4) условия контакта ударника и оболочки имеют вид
(1.6)
${\text{ }}f\left( {y,z} \right) + {{u}_{c}}\left( \tau \right) = w\left( {\alpha ,z,\tau } \right),\quad p\left( {\alpha ,z,\tau } \right) < 0,\quad y,z \in \Omega \left( \tau \right),\quad y = \sin \alpha $В начальный момент времени оболочка находится в недеформированном состоянии, что соответствует нулевым начальным условиям
(1.7)
${{\left. u \right|}_{{\tau = 0}}} = {{\left. v \right|}_{{\tau = 0}}} = {{\left. w \right|}_{{\tau = 0}}} = {{\left. {{{\chi }_{\alpha }}} \right|}_{{\tau = 0}}} = {{\left. {{{\chi }_{z}}} \right|}_{{\tau = 0}}} = {{\left. {\dot {u}} \right|}_{{\tau = 0}}} = {{\dot {v}}_{{\tau = 0}}} = {{\left. {\dot {w}} \right|}_{{\tau = 0}}} = {{\left. {{{{\dot {\chi }}}_{\alpha }}} \right|}_{{\tau = 0}}} = {{\left. {{{{\dot {\chi }}}_{z}}} \right|}_{{\tau = 0}}} = 0$Здесь и далее точка над величиной означает ее производную по времени τ.
Уравнения и соотношения (1.1), (1.2), (1.4)–(1.7) составляют замкнутую математическую постановку нестационарной контактной задачи с подвижными границами для цилиндрической оболочки и абсолютно твердого ударника.
2. Система разрешающих уравнений. Для сведения постановки контактной задачи к разрешающим уравнениям используется функция влияния ${{G}_{w}}\left( {\alpha ,z,\tau } \right)$ для бесконечно длинной круговой цилиндрической оболочки типа Тимошенко. Она представляет собой нормальные перемещения оболочки как решения следующей задачи:
Функция влияния ${{G}_{w}}\left( {\alpha ,z,\tau } \right)$ найдена и исследована в работе [17].
Основываясь на принципе суперпозиции [16–18], нормальные перемещения связаны с контактным давлением посредством интегрального оператора свертки
(2.1)
$w\left( {\alpha ,z,\tau } \right) = \int\limits_0^\tau {dt\iint\limits_{{{\Pi }_{*}}\left( t \right)} {{{G}_{w}}\left( {\alpha - \xi ,z - \zeta ,\tau - t} \right)p\left( {\xi ,\zeta ,t} \right)dS}} $Заменим область контакта ${{\Pi }_{*}}(\tau )$ фиктивной областью Ω(τ). С учетом малости размера пятна контакта $\left( {{\text{diam}}\Omega \left( \tau \right) \ll 1} \right)$ полагаем
(2.2)
$\sin \alpha \approx \alpha \approx y,\quad \left( {y,z} \right) \in \Omega \left( \tau \right)$Из условия контакта (1.4) с учетом выражения (2.2) и интегрального соотношения (2.1), вытекает основное разрешающее интегральное уравнение относительно искомого контактного давления $p\left( {y,z,\tau } \right)$:
(2.3)
$\int\limits_0^\tau {dt\iint\limits_{\Omega \left( t \right)} {{{G}_{w}}\left( {y - \xi ,z - \zeta ,\tau - t} \right)p\left( {\xi ,\zeta ,t} \right)dS}} = f\left( {y,z} \right) + {{u}_{c}}\left( \tau \right)$В уравнении (2.3) кроме контактного давления неизвестными являются также область контакта Ω(τ) и перемещение центра масс ударника ${{u}_{c}}\left( \tau \right)$.
Для получения замкнутой системы к (2.3) добавим соотношение (1.5), определяющее положение границы области контакта $\Omega \left( \tau \right)$ и уравнение движения ударника (1.2), записанное в интегральной форме
(2.4)
${{u}_{c}}\left( \tau \right) = {{V}_{0}}\tau + \frac{1}{{{{m}_{u}}}}\int\limits_0^\tau {\left( {\tau - t} \right)dt\iint\limits_{\Omega \left( t \right)} {p\left( {y,z,t} \right)dS}} $Уравнения (2.3), (2.4) и (1.5) составляют замкнутую систему разрешающих уравнений пространственной нестационарной контактной задачи для цилиндрической оболочки и абсолютно твердого ударника.
3. Численно-аналитический алгоритм решения. Для решения системы разрешающих уравнений используем численно-аналитический алгоритм, основанный на методе механических квадратур.
Временной интервал $\left[ {0,\tau } \right]$ разделим на M равномерных шагов ${{\Delta }_{t}} = {\tau \mathord{\left/ {\vphantom {\tau M}} \right. \kern-0em} M}$:
(3.1)
${{t}_{m}} = m{{\Delta }_{t}},\quad m = 1{\kern 1pt} - {\kern 1pt} M,\quad {{t}_{M}} = M{{\Delta }_{t}} = \tau $Интегралы по времени в уравнениях (2.3) и (2.4) заменим суммой интегралов по интервалам $\left[ {{{\tau }_{{m - 1}}},{{\tau }_{m}}} \right]$ и положим, что в пределах каждого временного интервала контактное давление остается постоянным:
(3.2)
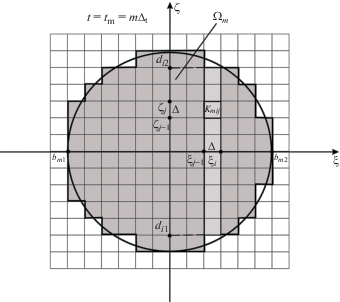
$\begin{gathered} \sum\limits_{m = 1}^M {\int\limits_{{{t}_{{m - 1}}}}^{{{t}_{m}}} {dt\iint\limits_{\Omega \left( t \right)} {{{G}_{w}}\left( {y - \xi ,z - \zeta ,\tau - t} \right){{p}_{m}}\left( {\xi ,\zeta } \right)dS}} } = f\left( {y,z} \right) + {{u}_{{cM}}} \\ {{u}_{{cM}}} = {{V}_{0}}\tau + \frac{1}{{{{m}_{u}}}}\sum\limits_{m = 1}^M {\int\limits_{{{\tau }_{{m - 1}}}}^{{{\tau }_{m}}} {\left( {\tau - t} \right)dt\iint\limits_{\Omega \left( t \right)} {{{p}_{m}}\left( {\xi ,\zeta } \right)dS}} } \\ {{u}_{{cM}}} = {{u}_{c}}\left( \tau \right),\quad {{p}_{m}}\left( {\xi ,\zeta } \right) = p\left( {\xi ,\zeta ,{{t}_{m}}} \right),\quad {{t}_{m}} = m{{\Delta }_{t}} \\ \end{gathered} $Область контакта $\Omega \left( t \right) \in \Pi $ приближенно заменим объединением прямоугольных подобластей ${{K}_{{mij}}}$ (рис. 3):
(3.3)
$\begin{gathered} \Omega \left( t \right) \approx {{\Omega }_{m}} \in \Pi ,\quad {{\Omega }_{m}} = \bigcup\limits_{i,j} {{{K}_{{mij}}}} \\ {{K}_{{mij}}} = \left\{ {\left( {\xi ,\zeta } \right):{{\xi }_{{i - 1}}} \leqslant \xi \leqslant {{\xi }_{i}},{{\zeta }_{{j - 1}}} \leqslant \zeta \leqslant {{\zeta }_{j}},t = {{t}_{m}}} \right\} \\ {{\xi }_{i}} - {{\xi }_{{i - 1}}} = {{\zeta }_{j}} - {{\zeta }_{{j - 1}}} = \Delta ,\quad {{\xi }_{i}} = {{b}_{{m1}}} + i\Delta ,\quad {{\zeta }_{j}} = {{d}_{{i1}}} + j\Delta \\ i \in \left[ {1,I} \right],\quad I = \left[ {\frac{{{{b}_{{m2}}} - {{b}_{{m1}}}}}{\Delta }} \right];\quad j \in \left[ {1,{{J}_{i}}} \right],\quad {{J}_{i}} = \left[ {\frac{{{{d}_{{i2}}} - {{d}_{{i1}}}}}{\Delta }} \right] \\ \end{gathered} $Из соображений, касающихся устойчивости численной схемы, шаг Δ по пространственным переменным выбирается из условия $\Delta > {{\Delta }_{t}}$ [19]. В частности, можно положить $\Delta = 2{{\Delta }_{t}}$. Границы ${{b}_{{m1}}}$, ${{b}_{{m2}}}$, ${{d}_{{i1}}}$, ${{d}_{{i2}}}$ изменения дискретных значений пространственных переменных ${{\xi }_{i}}$ и ${{\zeta }_{j}}$ являются решениями уравнений
(3.4)
$f\left( {{{b}_{m}},0} \right) + {{u}_{{cm}}} = 1{\text{ }} \Rightarrow {{b}_{{m1}}},\quad {{b}_{{m2}}},{\text{ }}f\left( {{{\xi }_{i}},{{d}_{i}}} \right) + {{u}_{{cm}}} = 1{\text{ }} \Rightarrow {{d}_{{i1}}},\quad {{b}_{{i2}}},\quad {{u}_{{cm}}} = u\left( {{{t}_{m}}} \right)$С применением аппроксимации (3.3), получим численные аналоги уравнений (3.2). Для этого положим, что в пределах элементарного квадрата ${{K}_{{mij}}}$ контактное давление остается постоянным:
(3.5)
${{\left. {{{p}_{m}}\left( {\xi ,\zeta } \right)} \right|}_{{\left( {\xi ,\zeta } \right) \in {{K}_{{ij}}}}}} = {{p}_{{mij}}} = {\text{const}}$Тогда из (3.1)–(3.5) следует
(3.6)
$\begin{gathered} f\left( {{{b}_{m}},0} \right) + {{u}_{{cm}}} = 1{\text{ }} \Rightarrow {{b}_{{m1}}},{{b}_{{m2}}},{\text{ }}f\left( {{{\xi }_{i}},{{d}_{i}}} \right) + {{u}_{{cm}}} = 1{\text{ }} \Rightarrow {{d}_{{i1}}},{{d}_{{i2}}} \\ k,i \in \left[ {1,I} \right],\quad I = \left[ {\frac{{{{b}_{{m2}}} - {{b}_{{m1}}}}}{\Delta }} \right];\quad l,j \in \left[ {1,{{J}_{i}}} \right],\quad {{J}_{i}} = \left[ {\frac{{{{d}_{{i2}}} - {{d}_{{i1}}}}}{\Delta }} \right] \\ \end{gathered} $Уравнения (3.6) составляют численный аналог системы разрешающих уравнений пространственной нестационарной контактной задачи для абсолютно твердого ударника и тонкой упругой круговой цилиндрической оболочки типа Тимошенко.
Построения решений системы (3.6) проводится пошагово по времени. Отметим, что система уравнений (3.6) является нелинейной, так как третье и четвертое уравнения содержат искомые значения контактного давления ${{p}_{{Mij}}}$ на M-ном шаге по времени. Для линеаризации системы уравнений (3.6) предлагается использовать итерационную процедуру. На нулевой итерации второе уравнение системы (3.6) заменяется следующим аналогом
Это позволяет определить перемещение ${{u}_{{cM}}}$ без учета поля давления на шаге с номером M. Затем из третьего и четвертого уравнения определяются границы области интегрирования, а затем верхние значения I и Ji сумм в первом уравнении. После этого из первого уравнения вытекает система $I \times J$ линейных алгебраических уравнений, где $J = \sum\limits_{i = 1}^I {{{J}_{i}}} $, относительно $I \times J$ искомых значений контактного давления на M-ном шаге по времени. После их определения перемещение ударника ${{u}_{{cM}}}$ уточняется с использованием второго уравнения системы (3.6). Затем уточняются границы области интегрирования, а также пределы верхних значений сумм I и ${{J}_{i}}$. После этого происходит пересчет поля значений контактного давления как решений первого уравнения в системе (3.6), эквивалентного системе $I \times J$ линейных алгебраических уравнений.
Таким образом, алгоритм решения системы (3.6) включает следующие операции.
1. На первом шаге определяется поле дискретных значений контактного давления ${{p}_{{1ij}}}$ на элементарных квадратах ${{K}_{{1ij}}}$.
2. На втором и последующих шагах по времени первое уравнение системы (3.6) записывается в виде
(3.7)
$\sum\limits_{i = 1}^I {\sum\limits_{j = 1}^{{{J}_{i}}} {{{G}_{{Mijkl}}}{{p}_{{Mij}}}} } = {{f}_{{kl}}} + {{u}_{{cM}}} - {{F}_{M}},\quad {{F}_{M}} = \sum\limits_{m = 1}^{M - 1} {\sum\limits_{i = 1}^I {\sum\limits_{j = 1}^{{{J}_{i}}} {{{G}_{{mijkl}}}{{p}_{{mij}}}} } } $3. На каждом шаге по времени перемещение ударника и положение границ области интегрирования уточняется с помощью описанной выше итерационной процедуры.
4. Коэффициенты ${{G}_{{mijkl}}}$ вычисляются численно-аналитически по формуле
(3.8)
${{G}_{{mijkl}}} \approx {{\tilde {G}}_{{mijkl}}} = {{\Delta }_{t}}\int\limits_{{{\xi }_{{i - i}}}}^{{{\xi }_{i}}} {\int\limits_{{{\zeta }_{{j - i}}}}^{{{\zeta }_{j}}} {{{G}_{w}}\left[ {{{y}_{k}} - \xi ,\;{{z}_{l}} - \zeta ,\left( {M - \frac{{2m - 1}}{2}} \right){{\Delta }_{t}}} \right]d\xi d\zeta } } $При этом структура функции влияния и методы для ее получения, описанные в работе [17], позволяют аналитически вычислить интегралы в правой части (3.8).
5. После определения положения границы области контакта и поля контактного давления в дискретные моменты времени, истинные нормальные перемещения оболочки снова определяются интегральным соотношением (2.1). Его дискретный аналог имеет вид
4. Примеры расчетов. В качестве примера рассмотрим нестационарное контактное взаимодействие круговой цилиндрической оболочки, радиуса R = 1 и толщиной $h = 0.025$ с абсолютно твердым ударником, ограниченным поверхностью, имеющей форму параболоида вращения: $f\left( {y,z} \right) = {{y}^{2}} + {{z}^{2}} + 1.$ В качестве материала оболочки примем сталь со следующими характеристиками: $\rho = 7850$ кг/м3, $\lambda = 1.15$ × 1011 Па, $\mu = {\text{7}}{\text{.69}}$ × 1010 Па, чему соответствуют безразмерные параметры: $\eta = 0.53$, $\gamma = 1.3$ × 10–6.
Рассмотрим влияние начальной скорости ударника на процесс нестационарного контактного взаимодействия. Примем к анализу три ее возможных значения ${{V}_{0}}$ = 0.01, ${{V}_{0}} = 0.05$ и ${{V}_{0}} = 0.1$. Поверхность контакта в данном случае представляет собой круг, граница которого совпадает с сечением поверхности $x = {{y}^{2}} + {{z}^{2}} + 1 - {{u}_{c}}\left( \tau \right)$ плоскостью x = 1 в текущий момент времени $\tau $.
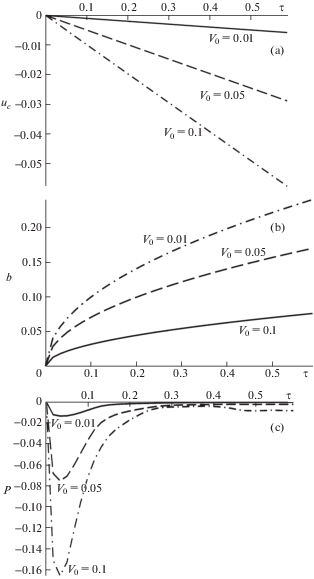
На рис. 4a–4c представлены зависимости перемещения центра масс ударника ${{u}_{c}}\left( \tau \right)$ от времени (рис. 4a), радиуса области контакта от времени (рис. 4b) и результирующей контактной силы $P\left( \tau \right)$ от времени (рис. 4c). Здесь сплошные кривые соответствуют ${{V}_{0}}$ = 0.01, штриховая – ${{V}_{0}} = 0.05$, штрихпунктирная – ${{V}_{0}} = 0.1$.
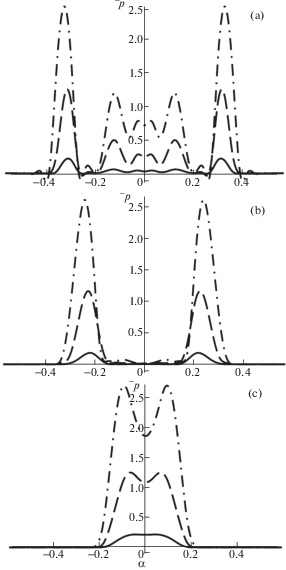
На рис. 5a–5c представлены распределения контактного давления по угловой координате α в момент времени $\tau = 0.3$. Рис. 5a соответствует значение координаты $z = 0$, 5b – $z = 0.15$, 5c – $z = 0.3$. Сплошные кривые соответствуют ${{V}_{0}} = 0.01$, штриховые – ${{V}_{0}} = 0.05$, штрихпунктирные – ${{V}_{0}} = 0.1$.
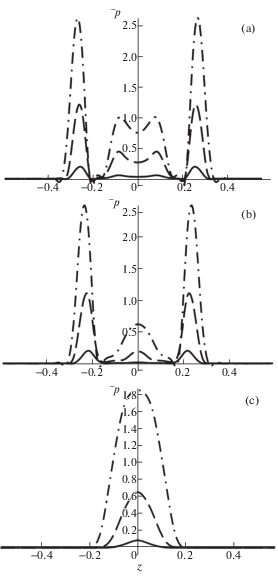
На рис. 6a–6c представлены распределения контактного давления по продольной координате $z$ в момент времени $\tau = 0.3$. Рис. 6а соответствует значение координаты $\alpha = 0$, 6b – $\alpha = 0.15$, 6c – $\alpha = 0.3$. Сплошные кривые соответствуют ${{V}_{0}} = 0.01$, штриховые – ${{V}_{0}} = 0.05$, штрихпунктирные – ${{V}_{0}} = 0.1$.
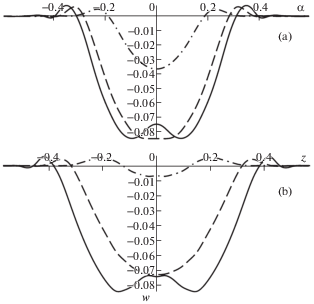
На рис. 7a и 7b представлены распределения нормальных перемещений по угловой координате (рис. 7a) и по продольной координате (рис. 7b). Здесь результаты соответствуют моменту времени $\tau = 0.6$ и начальной скорости ${{V}_{0}} = 0.1$. На рис. 7a сплошные кривые соответствуют z = 0, штриховые – z = 0.15, штрихпунктирные – z = 0.3. Сплошные кривые на рис. 7b соответствуют α = 0, штриховые – $\alpha = 0.15$, штрихпунктирные – $\alpha = 0.3$.
Заключение. Предложен метод решения пространственной нестационарной контактной задачи с подвижными границами задач для тонкой упругой цилиндрической оболочки и абсолютно твердого ударника. Разработан и реализован численно-аналитический алгоритм решения. Приведены примеры расчетов.
Работа выполнена при поддержке РФФИ, номер проекта 19-08-00438 А.
Список литературы
Тарлаковский Д.В., Федотенков Г.В. Двумерный нестационарный контакт упругих цилиндрических или сферических оболочек // Проблемы машиностроения и надежности машин. 2014. № 2. С. 69–76.
Михайлова Е.Ю., Тарлаковский Д.В., Федотенков Г.В. Нестационарный контакт сферической оболочки и упругого полупространства // Труды МАИ. 2014. № 78.
Fedotenkov G.V., Mikhailova E.Yu., Kuznetsova E.L., Rabinskiy L.N. Modeling the unsteady contact of spherical shell made with applying the additive technologies with the perfectly rigid stamp // IJPAM. 111. 2016. V. 111. № 2. P. 331–342.
Михайлова Е.Ю., Федотенков Г.В. Нестационарная осесимметричная задача об ударе сферической оболочки по упругому полупространству (начальный этап взаимодействия) // Изв. РАН. МТТ. 2011. № 2. С. 98–108.
Тарлаковский Д.В., Федотенков Г.В. Воздействие нестационарного давления на цилиндрическую оболочку с упругим заполнителем // Ученые записки Казанского университета. Серия физико-математические науки. 2016. Т. 158. Кн. 1. С. 141–151.
Шевляков А.Г. Колебания цилиндрических трубопроводов, заполненных жидкостью, обусловленные поперечным импульсом внешнего давления // Строительная механика инженерных конструкций и сооружений. 2009. № 2. С. 65–74.
Бешенков С.Н., Бешенкова В.И. Нестационарное отрывное деформирование вложенных цилиндрических оболочек // Современная наука: актуальные проблемы и пути их решения. 2014. № 9. С. 29–32.
Игоничева Е.В., Кибец А.И., Кибец Ю.И., Самыгин А.Н. Численное решение трехмерной задачи соударения трубопровода с плитой // Вестник Нижегородского университета им. Н.И. Лобачевского. Серия: Механика. 2000. № 2 (2). С. 87–97.
Демарева А.В., Иванов В.А., Жестков М.Н., Кибец А.И., Кибец Ю.И., Шошин Д.В. Численное решение динамических задач деформирования многослойных оболочек с пористым заполнителем // Проблемы прочности и пластичности. 2014. Т. 76. № 1. С. 46–54.
Резанова Е.В. Численное исследование динамики сферической газосодержащей оболочки // Известия Алтайского государственного университета. 2013. № 1–2 (77). С. 042–047.
Kulikov G.M., Plotnikova S.V. The contact problem for a geometrically non-linear Timoshenko-type shell // Journal of Applied Mathematics and Mechanics. 2003. V. 67. Issue 6. P. 825–836.
Бочкарев С.А., Лекомцев С.В., Сенин А.Н. Анализ пространственных колебаний коаксиальных цилиндрических оболочек, частично заполненных жидкостью // Вычислительная механика сплошных сред. 2018. Т. 11. № 4. С. 448–462.
Jiabei S., Zhuyong L., Jiazhen H. Dynamic contact model of shell for multibody system applications // Multibody System Dynamics. 2018. V. 44. Issue 4. P. 335–366.
Kamran K., Rossi R., Onate E. A contact algorithm for shell problems via Delaunay-based meshing of the contact domain // Computational Mechanics. 2013. V. 52. Issue 1. P. 1–16.
Михайлова Е.Ю., Тарлаковский Д.В., Федотенков Г.В. Обобщенная линейная модель динамики тонких упругих оболочек // Ученые записки Казанского университета. Серия физико-математические науки. 2018. Т. 160. Кн. 3. С. 561–577.
Тарлаковский Д.В., Федотенков Г.В. Пространственное нестационарное движение упругой сферической оболочки // Известия Российской академии наук. Механика твердого тела. 2015. № 2. С. 118–128.
Mitin A.Yu., Fedotenkov G.V., Kalinchuk V.V. Three-dimensional non-stationary motion of Timoshenko-type circular cylindrical shell // Lobachevskii Journal of Mathematics. 2019. V. 40. № 3. P. 311–320.
Митин А.Ю., Тарлаковский Д.В., Федотенков Г.В. Нестационарный контакт цилиндрической оболочки и абсолютно твердого эллиптического параболоида // Труды МАИ. 2019. № 107. С. 5.
Горшков А.Г., Тарлаковский Д.В. Динамические контактные задачи с подвижными границами. М.: Наука. Физматлит, 1995. 352 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела