Известия РАН. Механика твердого тела, 2020, № 3, стр. 48-57
О ПАРАДОКСЕ АНОМАЛЬНОЙ ОТНОСИТЕЛЬНОЙ ИЗГИБНОЙ ЖЕСТКОСТИ СВЕРХТОНКИХ БАЛОК В ГРАДИЕНТНОЙ ТЕОРИИ УПРУГОСТИ
С. А. Лурье *
Институт прикладной механики РАН
Москва, Россия
* E-mail: salurie@mail.ru
Поступила в редакцию 29.11.2019
После доработки 15.12.2019
Принята к публикации 19.12.2019
Аннотация
Рассматривается проблема уточненного моделирования сверхтонких стержней, возникшая в связи с необходимостью объяснения известных экспериментальных данных о существенной зависимости изгибной жесткости таких сверхтонких структур от их толщины в случае если толщина становится весьма малой, соизмеримой как считают некоторые авторы с характерными размерами микроструктуры материала. Для моделирования таких эффектов в теории тонких стержней Кирхгофа используются градиентные теории, нелокальные, микрополярные теории упругости, включающие масштабные параметры по построению. Однако полученные результаты моделирования являются весьма противоречивыми, остается нерешенным вопрос о достоверности полученных результатов и о природе эффекта масштабозависимости эффективных изгибных свойств сверхтонких стержней. В работе показывается, что указанные эффекты для стержней Кирхгофа и Тимошенко можно объяснить путем учета поверхностных свойств для сверхтонких стержней (пластин).
1. Введение. На протяжении последних лет значительный интерес проявляется к учету масштабных факторов при оценке эффективных характеристик жесткости стержней и пластин при уменьшении их толщины [1–6]. Масштабные эффекты нашли экспериментальное подтверждение при исследовании изгибной жесткости консольных стержней из алюминия, полипропилена и эпоксидной смолы [7–12]. Естественно, что для объяснения подобных эффектов были привлечены градиентные теории упругости, включающие дополнительные параметры размерности квадрата длины. Анализ исследований работ, посвященных построению градиентных теорий изгиба стержней Бернулли приведен в исследованиях [13–16], где для анализа привлекаются корректные прикладные варианты градиентных теорий, используются различные подходы для формулировки прикладных теорий изгиба стержней включая вариационный, асимптотический и полуобратный метод. Отмечено что для построения уравнений равновесия прикладной теории изгиба стержней, как правило, используется вариационная процедура получения уравнений равновесия. При таком подходе для стержней Бернулли–Эйлера можно отметить два основных направления в области моделирования изгиба сверхтонких стержней. В работах первого направления [17] рассматривается приближенная модель, в которой считается, что для сверхтонких стержней трансверсальные перемещения по отношению к оси стержня, а также соответствующие деформации настолько малы, что их можно принять равными нулю. В таком случае полагается, что плотность потенциальной энергии U для градиентной теории сверхтонких стержней связана только с продольной деформацией ${{\varepsilon }_{{11}}}$ ее производной по осевой координате.
где ${{\tau }_{{11}}},{{\varepsilon }_{{11}}},$ осевые напряжения и деформации, ${{\varepsilon }_{{11}}} = {{R}_{{1,1}}},{{\tau }_{{11}}} = (\lambda + 2\mu ){{\varepsilon }_{{11}}},$ и ${{R}_{1}}$ – осевое перемещение, ${{R}_{{i,j}}} = \partial {{R}_{i}}{\text{/}}\partial {{x}_{j}}$ $\lambda ,\mu $ – коэффициенты Ламе.В работах второго направления [18, 19] учитываются все компоненты тензора деформаций, так что потенциальная энергия в градиентной теории балок записывается с учетом гипотез Бернулли в следующей более общей форме
Для получения уравнений равновесия обычно используется формальная процедура, сводящаяся к интегрированию функционала Лагранжа по толщине стержня. После введения определяющих уравнений для усилий уравнений равновесия изгиба записываются относительно прогиба балки $w$. При использовании более простой одномерной модели уравнения изгиба имеют вид:
Отметим, что в этом случае изгибные свойства балки контролируются классической изгибной цилиндрической жесткостью ${{D}_{0}} = EI$, а градиентные, масштабные эффекты уточняют характер распределения перемещений (и напряжений) на торцах стержня в зависимости от вида граничных условий.
Для второго направления указанный выше формальный подход приводит к иному варианту модели изгиба, с уравнением равновесия вида
где $D = {{D}_{0}}(1 + k{{(l{\text{/}}h)}^{2}})$, k – некоторый постоянный коэффициент, который зависит от типа применяемой градиентной теории.Последний результат был встречен с большим энтузиазмом, ибо указывали на масштабозависимость свойств изгибаемых тонких структур и позволяли объяснить соответствующие экспериментальные результаты [8–12]. Однако с другой стороны они вызывают сомнение из-за того, что решение для полиномиальной, медленно-меняющейся части, полученное по градиентной теории стержней отличается от решения, построенного в соответствии с классической теорией упругости, приводит к несоответствию с теоремой об общей структуре градиентного решения [20, 21]. В работах [13, 14] на основе аналитического и численного анализа показано, что причина ошибочного эффекта масштабозависимости изгибной жесткости сверхтонких стержней Бернулли может быть связана с невыполнением граничных условий в градиентной упругости на лицевых поверхностях изгибаемых балок.
2. Граничные условий на лицевых поверхностях балок. Как правило, процедура получения равнений изгиба балок на основе вариационного подхода фактически игнорирует граничные условия на лицевых поверхностях стрежней для усилий и моментов в градиентной теории, в силу интегрирования функционала Лагранжа по толщине балки. Проверка предположения о том, что ошибочная оценка изгибной жесткости может быть связана с невыполнением граничных условий на поверхностях изгибаемого стержня приведена для стержней Бернулли в [13]. В связи с указанной возможностью появления погрешности при оценке изгибной жесткости порядка $ + k(l{\text{/}}h)_{{}}^{2}$ следует отметить, что такого порядка же неточности могут возникнуть в связи с более тонкими эффектами, порожденными использованием некорректных градиентных моделей [21, 22]. Действительно, в работе [8] градиентная теория изгиба стержней Бернулли строится с использованием прикладной однопараметрической градиентной теории упругости. Причем, в отличие от большинства других исследований делается попытка учесть граничные условия на лицевых поверхностях стержней Бернулли. При этом рассматривается прикладная теория, в которой плотность энергии деформации определяется симметричным тензором кривизн ${{\chi }_{{ij}}}$, найденным по тензору кривизн поворотов ${{\omega }_{i}} = - (1{\text{/}}2){{\varepsilon }_{{kli}}}{{R}_{{k,l}}}$: ${{\chi }_{{ij}}} = (1{\text{/}}2)({{\omega }_{i}}{{_{,}}_{j}} + {{\omega }_{j}}{{_{,}}_{i}}) = - (1{\text{/}}4)({{e}_{{kli}}}{{R}_{k}}{{_{,}}_{{lj}}} + {{e}_{{kli}}}{{R}_{k}}{{_{,}}_{{li}}})$, ${{e}_{{kli}}}$ – символ Леви–Чивита. В таком случае градиентная часть плотности потенциальная энергия имеет вид $U = {{l}^{2}}\mu {{\chi }_{{ij}}}{{\chi }_{{ij}}}$, где $\mu $ – модуль сдвига, l – масштабный параметр. Нетрудно проверить, что градиентная часть потенциальной энергии $U = {{l}^{2}}\mu {{\chi }_{{ij}}}{{\chi }_{{ij}}}$ может быть записана в традиционной форме через кривизны вектора перемещений ${{R}_{i}}{{_{,}}_{{jk}}}$ в следующем виде:
где градиентный тензор модулей упругости шестого ранга ${{С}_{{ijklmn}}}$ имеет вид:(2.2)
${{С}_{{ijklmn}}} = (1{\text{/}}4){{l}^{2}}\mu ({{e}_{{lmp}}}{{e}_{{ijp}}}{{\delta }_{{kn}}} + {{e}_{{lmk}}}{{e}_{{ijn}}})$Легко убедиться, что ${{С}_{{ijklmn}}}$ в (2.1), (2.2) удовлетворяет условиям потенциальности (условия симметрии по первой и второй тройке индексов), но не удовлетворяет условию симметрии порядка дифференцирования [21], т.е. симметрии по второй паре индексов в каждой из троек индексов.. В этом нетрудно убедиться, вычислив, например выражение ${{С}_{{123132}}} - {{С}_{{132123}}} = - (1{\text{/}}2){{l}^{2}}\mu $.
Следовательно, не выполняются условия корректности градиентных теорий, обсуждаемые в работах [20, 21]. Градиентная теория, привлекаемая в [8] к построению теории изгиба балок, является некорректной. Покажем, что паразитные составляющие в тензоре модулей упругости шестого ранга ${{С}_{{ijklmn}}}$ возникающие в силу несимметрии относительно последних индексов в каждой из троек ijk и lmn остаются в граничных условиях. Это, по видимому, является причиной ошибочной оценки изгибной жесткости. Действительно, следуя [22, 23], нетрудно показать, что краевая задача для градиентной упругости определяется уравнением равновесия
и краевыми условиями на гладкой поверхности(2.4)
${{\tau }_{{ij}}}{{n}_{j}} - {{\left( {{{\mu }_{{ijk}}}{{n}_{k}}} \right)}_{{,j}}} + {{\left( {{{\mu }_{{ijk}}}{{n}_{k}}{{n}_{l}}} \right)}_{{,l}}}{{n}_{j}} = {{t}_{i}}\quad {\text{и}}\quad {{R}_{i}} = {{\bar {R}}_{i}}$(2.5)
${{\mu }_{{ijk}}}{{n}_{j}}{{n}_{k}} = 0\quad {\text{и}}\quad {{R}_{{i,j}}}{{n}_{j}} = \partial {{\bar {R}}_{i}}{\text{/}}\partial n$Отметим, что паразитные слагаемые, которые могли бы возникнуть из-за отсутствия указанной симметрии в тензоре модулей упругости шестого ранга в определяющих соотношениях для моментов ${{\mu }_{{ijk}}}\, = {{С}_{{ijklmn}}}{{R}_{{l,mn}}}$ отсутствуют и в уравнении равновесия (2.3) и во втором граничном условии (2.5) (для моментов) в силу сверток с соответствующими симметричными выражениями по индексам jk. Однако паразитные слагаемые остаются в первом граничном условии (2.4) из-за слагаемого ${{\left( {{{\mu }_{{ijk}}}\,{{n}_{k}}} \right)}_{{,j}}}$ в котором такой свертки нет. Это паразитное слагаемое, очевидно, вносит погрешность в краевое условие порядка $(l{\text{/}}h)_{{}}^{2}$ и является причиной ошибки в оценке эффективных изгибных жесткостей как показано в результате анализа полуобратных решений в задачах изгиба балок [14, 16].
3. Корректная вариационная модель изгиба балок в градиентной упругости. Рассмотрим задачу чистого изгиба тонкого стержня прямоугольного сечения (рис. 1.) Полагаем что длина стержна равна L, а высота и толщина поперечного сечения равны соответственно 2h и b. Считаем, что при чистом изгибе тонкой балки в плоской постановке реализуется следующая кинематика стержней Тимошенко для дисторсий
(3.1)
${{R}_{{1,1}}} = \theta {\text{'}}y,\quad {{R}_{{1,2}}} = \theta ,\quad {{R}_{{2,1}}} = w{\text{'}},\quad {{R}_{{2,2}}} = 0$Здесь ${{R}_{{1,1}}} = \theta {\text{'}}y,$ ${{R}_{{1,2}}} = \theta ,$ ${{R}_{{2,1}}} = w{\text{'}},$ индексы 1 и 2 соответствуют проюдольной и поперечной координатам x и y соответственно, $\theta $ – угол поворота сечения стержня при изгибе, w – прогиб балки в направлении оси y, штрихом обозначается производная по продольной координате x.
Запишем компоненты вторых производных перемещений
(3.2)
${{R}_{{1,11}}} = \theta {\text{''}}y,\quad {{R}_{{1,12}}} = {{R}_{{1,21}}} = \theta {\text{'}},\quad {{R}_{{1,22}}} = 0,\quad {{R}_{{2,11}}} = w{\text{''}},\quad {{R}_{{2,12}}} = 0,\quad {{R}_{{2,22}}} = 0$Будем в дальнейшем рассматривать наиболее общую корректную градиентную модель Миндлина в форме 1 (см. [23]), для которой тензор градиентных модулей упругости $A_{{ijklmn}}^{{}}$ имеет вид:
(3.3)
$\begin{gathered} A_{{ijklmn}}^{{}} = {{a}_{1}}\left( {{{\delta }_{{ij}}}{{\delta }_{{kl}}}{{\delta }_{{mn}}} + {{\delta }_{{in}}}{{\delta }_{{jk}}}{{\delta }_{{lm}}} + {{\delta }_{{ik}}}{{\delta }_{{jl}}}{{\delta }_{{mn}}} + {{\delta }_{{im}}}{{\delta }_{{jk}}}{{\delta }_{{ln}}}} \right) + {{a}_{2}}{{\delta }_{{il}}}{{\delta }_{{jk}}}{{\delta }_{{mn}}} \\ \, + {{a}_{3}}\left( {{{\delta }_{{ij}}}{{\delta }_{{km}}}{{\delta }_{{ln}}} + {{\delta }_{{ik}}}{{\delta }_{{jn}}}{{\delta }_{{lm}}} + {{\delta }_{{ij}}}{{\delta }_{{kn}}}{{\delta }_{{lm}}} + {{\delta }_{{ik}}}{{\delta }_{{jm}}}{{\delta }_{{ln}}}} \right) \\ \, + {{a}_{4}}\left( {{{\delta }_{{il}}}{{\delta }_{{jm}}}{{\delta }_{{kn}}} + {{\delta }_{{il}}}{{\delta }_{{jn}}}{{\delta }_{{km}}}} \right) + {{a}_{5}}\left( {{{\delta }_{{im}}}{{\delta }_{{jl}}}{{\delta }_{{kn}}} + {{\delta }_{{im}}}{{\delta }_{{jn}}}{{\delta }_{{kl}}} + {{\delta }_{{in}}}{{\delta }_{{jl}}}{{\delta }_{{km}}} + {{\delta }_{{in}}}{{\delta }_{{jm}}}{{\delta }_{{kl}}}} \right) \\ \end{gathered} $(3.4)
${{\tau }_{{ij}}} = \lambda e{{\delta }_{{ij}}} + \mu ({{R}_{{i,j}}} + {{R}_{{j,i}}})\,\,\,\,(e = {{R}_{{l,l}}}),\quad \mu _{{ijk}}^{{}} = {{A}_{{ijklmn}}}{{R}_{{l,mn}}}$Следуя (3.2), (3.4), определяющие уравнения для моментов запишем в виде
(3.5)
$\begin{gathered} \mu _{{ijk}}^{{}} = \mu _{{ikj}}^{{}} = {{a}_{1}}\left( {{{\delta }_{{ij}}}{{R}_{{k,ll}}} + {{\delta }_{{ik}}}{{R}_{{j,ll}}} + 2{{\delta }_{{jk}}}{{e}_{{,i}}}} \right) + {{a}_{2}}{{\delta }_{{jk}}}{{R}_{{i,ll}}} \\ \, + 2{{a}_{3}}\left( {{{\delta }_{{ij}}}{{e}_{{,k}}} + {{\delta }_{{ik}}}{{e}_{{,j}}}} \right) + 2{{a}_{4}}{{R}_{{i,jk}}} + 2{{a}_{5}}\left( {{{R}_{{j,ki}}} + {{R}_{{k,ij}}}} \right) \\ \end{gathered} $Учитывая кинематическую модель (3.1), (3.2), получим систему физических соотношений для напряжений Коши и моментов в терминах угла поворота сечения при изгибе и прогибе
(3.6)
$\mu _{{111}}^{{}} = [4({{a}_{1}} + {{a}_{3}} + {{a}_{5}}) + {{a}_{2}} + 2{{a}_{4}}]\theta {\text{''}}y,\quad \mu _{{112}}^{{}} = ({{a}_{1}} + 2{{a}_{5}})w{\text{''}} + (2{{a}_{3}} + 2{{a}_{4}} + 2{{a}_{5}})\theta {\text{'}}$Уравнения (3.1)–(3.6) полностью определяют кинематическую и физическую модель градиентной упругости для стрежней несжимаемых в поперечном направлении. Учтем (3.1), (3.2) и запишем выражение вариации потенциальной энергии для наиболее общего варианта корректной градиентной теории дисторсий Миндлина [23]
(3.7)
$\begin{gathered} \delta U = b\int\limits_0^L {\int\limits_{ - h}^h {(({{\tau }_{{11}}}\delta {{R}_{{1,1}}} + {{\tau }_{{12}}}\delta {{R}_{{1,2}}} + {{\tau }_{{21}}}\delta {{R}_{{2,1}}} + } } \\ \, + \mu _{{111}}^{{}}\delta {{R}_{{1,11}}} + (\mu _{{112}}^{{}} + {{\mu }_{{121}}})R{{u}_{{1,12}}} + {{\mu }_{{211}}}\delta {{R}_{{2,11}}})dydx \\ \end{gathered} $В случае теории стержней Бернулли–Эйлера, т.е. когда $\theta = - w{\text{'}}$ вместо (3.7) получим
(3.8)
$\delta U = b\int\limits_0^L {\int\limits_{ - h}^h {({{\tau }_{{11}}}\delta {{R}_{{1,1}}} + \mu _{{111}}^{{}}\delta {{R}_{{1,11}}} + \mu _{{112}}^{{}}\delta {{R}_{{1,12}}})} } dydx$Вариационная форма (3.7) определяет градиентную модель изгиба балок с кинематикой стержней, учитывающих средний сдвиг. Действительно, уравнение равновесия и граничные условия для этой модели могут быть получены используя вариационный принцип Лагранжа, $\delta L = 0,L = U - A$, где A – работа сил заданных в объеме и на поверхности стержня. Если лицевые поверхности стержня свободны от нагрузки, а на торцах стержня действует только изгибающий момент, то интегрирование вариационного уравнения (3.7) по толщине стержня приводит к уравнениям равновесия
гдеУравнения (3.9) очевидно можно переписать в терминах кинематических переменных θ и w если учесть (3.6). Исключая в полученных уравнениях $\theta $, можно получить уравнение равновесия в прогибах
Первое слагаемое в полученном уравнении указывает на масштабозависимость эффективной жесткости, а второе определяет градиентный эффект в задаче изгиба. Множитель при первом слагаемом в записанном уравнении показывает, что градиентные эффекты вносят поправку порядка $\tilde {k}{{(l{\text{/}}h)}^{2}}$ в цилиндрическую жесткость как это отмечалось ранее для стержней Бернулли–Эйлера. Такой результат является следствием использования интегрирования функционала Лагранжа по толщине при выводе уравнений равновесия. В результате граничные условия на лицевых поверхностях балки игнорируются.
Рассмотрим теперь уравнение (3.8) и проведем интегрирование по частям в последнем слагаемом в отношении поперечной координаты. Получим
(3.10)
$\delta U = b\int\limits_0^L {\int\limits_{ - h}^h {({{\tau }_{{11}}}\delta {{R}_{{1,1}}} + \mu _{{111}}^{{}}\delta {{R}_{{1,11}}} - \mu _{{112,2}}^{{}}\delta {{R}_{{1,1}}})} } dzdx + b\int\limits_0^L {(\mu _{{112}}^{{}}{{R}_{{1,1}}})_{{z = - h}}^{{z = h}}\,dx} $Принимая во внимание, что $\delta {{R}_{{1,1}}}$ является произвольной в (3.10) получаем, что на нижней и верхней границе балки должны выполняться следующие граничные условия
Условие (3.11) является одним из необходимых условий стационарности функционала Лагнранжа $\delta L = 0$ имеет смысл уравнения равновесия и не может игнорироваться. При условии (3.11) потенциальная энергия приобретает вид
(3.12)
$\delta U = b\int\limits_0^L {\int\limits_{ - h}^h {({{\tau }_{{11}}}\delta {{R}_{{1,1}}} + \mu _{{111}}^{{}}\delta {{R}_{{1,11}}} - \mu _{{112,2}}^{{}}\delta {{R}_{{1,1}}})dz\,dx} } $Последнее слагаемое в записанном выражении следует принять равным нулю в силу того, что для стержней Бернулли–Эйлера (и для стержней Тимошенко) $\mu _{{112,2}}^{{}}$ = 0. Поэтому с учетом того, что вдали от торцов балки $\mu _{{112,1}}^{{}}$ является фактически постоянной, выражение (3.12) сводится к выражению потенциальной энергии для модели балок, кинематика которых определяется только продольной деформацией. Следовательно величина $\mu _{{112}}^{{}}$ должна быть исключена из вариационного равенства (3.8). Это положение имеет и физическое обоснование: если функция $\mu _{{112}}^{{}}$ равна нулю на лицевых поверхностях балки, то для тонких структур она должна быть равной нулю и в любой промежуточной точке сечения. В результате показано, что эффективная изгибная жесткость не зависит от масштабного параметра. Аналогично, только несколько более сложно, показывается, что и для теории стрежней Тимошенко использование градиентной теории оставляет неизменным изгибную жесткость. Отметим, что полученные здесь оценки вполне соответствуют результатам, найденным с использованием полуобратных решений, в которых граничные условия на лицевых поверхностях балки выполняются точно, а также результатам численного моделирования [13].
4. Адгезионная природа масштабных эффектов для сверхтонких балок (пластин). Мы показали, что для градиентной модели изгиба балок не наблюдается эффекта зависимости эффективной изгибной жесткости от толщины балки. Тем не менее результаты экспериментов, приведенных в работах на микростержнях [8–12] показывают, что эффект масштабозависимости имеет место для изгибной жесткости. Попытаемся объяснить этот эффект влиянием поверхностных взаимодействий, роль которых возрастает при уменьшении толщины балки (пластинки). В работах [24, 25] дана вариационная модель адгезионных взаимодействий твердых деформируемых тел, как варианта теории упругости поверхностей тел. Воспользуемся этой моделью. Рассмотрим классическую теорию упругости для упругих тел с дополнительными свойствами адгезионно-активной поверхности и запишем потенциальную энергию, которая при решении в перемещениях полностью определяет математическую модель поверхностных взаимодействий
(4.1)
$L = A - \iiint {{{U}_{V}}dV} - \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc} {{{U}_{F}}dF} = A - \frac{1}{2}\iiint {{{C}_{{ijmn}}}{{R}_{{i,j}}}{{R}_{{m,n}}}dV - \frac{1}{2}\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc} {{{A}_{{ijmn}}}{{R}_{{i,j}}}{{R}_{{m,n}}}} dF}$Физические соотношения для напряжений в объеме тела ${{\sigma }_{{ij}}}$ и на поверхности тела ${{a}_{{ij}}}$ очевидно, определяются расширенными формулами Грина
(4.2)
${{\sigma }_{{ij}}} = \frac{{\partial {{U}_{V}}}}{{\partial {{R}_{{i,j}}}}} = {{C}_{{ijmn}}}{{R}_{{m,n}}},\quad {{a}_{{ij}}} = \frac{{\partial {{U}_{F}}}}{{\partial {{R}_{{i,j}}}}} = {{A}_{{ijmn}}}{{R}_{{m,n}}}$В соответствии с (4.1) и (4.2) математическая модель упругих тел с адгезионно-активной поверхностью полностью определяется следующим вариационным равенством
(4.3)
$\begin{gathered} \delta L = \delta A - \iiint {{{\sigma }_{{ij}}}\delta {{R}_{{i,j}}}dV} - \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc} {{{a}_{{ij}}}\delta {{R}_{{i,j}}}dF} = \iiint {({{\sigma }_{{ij,j}}} + P_{i}^{V})\delta {{R}_{i}}dV} + \\ \, + \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc} {[(P_{i}^{F} - {{\sigma }_{{ij}}}{{n}_{j}} + {{a}_{{ij}}}_{{,p}}\delta _{{pj}}^{*})\delta {{R}_{i}} + ( - {{a}_{{ij}}}{{n}_{j}})\delta ({{R}_{{i,p}}}{{n}_{p}})]dF = 0} \\ \end{gathered} $Мы будем использовать модель адгезии для классических линейно упругих изотропных тел, которая полностью определяется соотношениями (4.3) и равенствами
(4.4)
$\begin{gathered} A_{{ijmn}}^{{}} = {{\lambda }^{F}}\delta _{{ij}}^{*}\delta _{{mn}}^{*} + {{\mu }^{F}}(\delta _{{im}}^{*}\delta _{{jn}}^{*} + \delta _{{in}}^{*}\delta _{{jm}}^{*}) + {{\delta }^{F}}{{n}_{i}}{{n}_{m}}\delta _{{jn}}^{*} \\ {{a}_{{ij}}} = {{A}_{{ijmn}}}{{R}_{{m,n}}} = ({{\lambda }^{F}} + {{\mu }^{F}}) \cdot R_{{n,m}}^{{}}\delta _{{nm}}^{*}\delta _{{ij}}^{*} + \\ \, + 2{{\mu }^{F}} \cdot (R_{{n,m}}^{\,}\delta _{{in}}^{*}\delta _{{jm}}^{*} - (1{\text{/}}2)R_{{n,m}}^{\,}\delta _{{ij}}^{*}\delta _{{nm}}^{*}) + {{\delta }^{F}} \cdot R_{{n,m}}^{\,}n_{n}^{\,}\delta _{{mj}}^{*}{{n}_{i}} \\ \end{gathered} $Рассмотрим теперь изгиб изотропной тонкой пластины с адгезионно-активной поверхностью [24], [26]. Уравнение изгиба теории пластин Кирхгофа, полученное для этого случая на основе (4.3), (4.4), имеет вид
(4.5)
$\begin{gathered} D{\text{*}}{{\nabla }^{2}}{{\nabla }^{2}}W - {{\delta }^{F}}{{\nabla }^{2}}W = q \\ D{\text{*}} = \frac{{E{{h}^{3}}}}{{12(1 - {{{v}}^{2}})}} + \frac{{(2{{\mu }^{F}} + {{\lambda }^{F}}){{h}^{2}}}}{2} = {{D}_{0}}\left[ {1 + \tilde {k}\left( {\frac{l}{h}} \right)} \right],\quad {{D}_{0}} = \frac{{E{{h}^{3}}}}{{12(1 - {{v}^{2}})}} \\ \end{gathered} $Нетрудно записать и уравнение чистого изгиба изотропной пластины с адгезионно- активной поверхностью в случае кинематики Тимошенко ${{R}_{1}} = z{{\theta }_{x}},$ ${{R}_{2}} = z{{\theta }_{y}}$, ${{R}_{z}}$ = = w(x, y). Например, в случае цилиндрического изгиба (θy = 0) имеем
(4.6)
$D{\text{*}}\frac{{{{\partial }^{2}}{{\theta }_{x}}}}{{\partial {{x}^{2}}}} - \mu h\left( {{{\theta }_{x}} + \frac{{\partial w}}{{\partial x}}} \right) = 0,\quad \mu h\left( {\frac{{\partial {{\theta }_{x}}}}{{\partial x}} + \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}} \right) + 2{{\delta }^{F}}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + p = 0$Для сравнения с экспериментом, рассмотрим, уравнение изгиба балки прямоугольного сечения с адгезионно-активными лицевыми поверхностями, которое для случая цилиндрического изгиба следует из уравнений теории пластин (4.5) или (4.6). Положим, что в дальнейшем ${{\delta }^{F}} = 0$. Получим
(4.7)
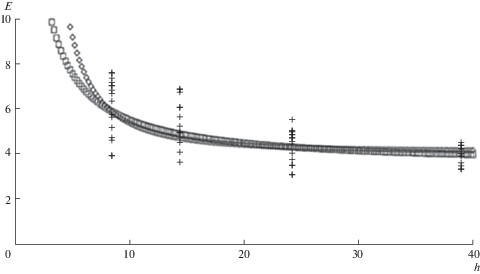
$D{\text{*}}{{w}^{{IV}}} = p,\quad D{\text{*}}{{D}_{0}}\left[ {1 + \tilde {k}\left( {\frac{l}{h}} \right)} \right],\quad {{D}_{0}} = EI,\quad I = \frac{{{{h}^{3}}}}{{12}}$В работе [27], (см. также [8]) представлены результаты эксперимента изгибной жесткости консольных микростержней заданной толщины. Полученные результаты измерений представлялись в форме зависимостей приведенных модулей упругости. Ранее именно эти зависимости использовались в качестве подтверждения справедливости градиентного эффекта масштабозависимости эффективных изгибных характеристик тонких изгибаемых балок, так как экспериментальные зависимости достаточно хорошо приближались квадратичной гиперболической зависимостью. На рис. 2 приведены кривые, характеризующие поведение квадратичной гиперболической функцией $\left( {1 + 6{{{\left( {l{\text{/}}h} \right)}}^{2}}} \right)$ (обозначена точками ◇) и хорошо описывающие данные эксперимента для балки с модулем упругости ≈2.5 ГПа. На том же графике приведена кривая, показывающая изменение гиперболической функции ($\left[ {1 + \tilde {k}\left( {l{\text{/}}h} \right)} \right]$, соответствующая модели адгезии (4.5), (4.7) и обеспечивающая минимум среднеквадратичного отклонения от первой кривой в заданном диапазоне толщин (обозначена точками □). Экспериментальные точки (обозначены крестиками +) указывают диапазон данных эксперимента. В результате, мы можем заключить, что для наиболее характерного диапазона толщин модель адгезии с высокой точностью соответствует данным эксперимента.
5. Заключение. Дано объяснение эффекту масштабозависимости эффективной изгибной жесткости сверхтонких стержней не за счет градиентных эффектов, а за счет влияния поверхностных эффектов, влияние которых усиливается при уменьшении толщины. Так как истинный модуль упругости при растяжении фактически не зависит от толщины (см. [8]), то удается идентифицировать масштабный параметр ${{k}_{f}}l$ = = 4.76 мкм и определить затем модуль упругости поверхностных взаимодействий ${{\mu }^{f}} + 2{{\mu }^{f}} \approx 11.9$ × 103 Па ⋅ м. Наконец отметим, что параметр поверхностных взаимодействий ${{\delta }^{F}}$ также может быть учтен при описании экспериментальных данных, однако для оценки его влияния, особенно при изменении длины микростержней, должны быть приведены дополнительные экспериментальные исследования.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, грант № 18-01-00553a и государственного задания ИПРИМ РАН AAAA-A17-117032010137-0.
Список литературы
Yang F., Chong A.C.M., Lam D.C.C., Tong P. Couple stress based strain gradient theory for elasticity// Int. Journal of Solids and Structures. 2002. V. 39. P. 2731–2743.
Wang C.M., Zhang Y.Y., He X.Q. Vibration of nonlocal Timoshenko beams // Nanotechnology. 2007. V. 18. 105401.
Ma H.M.,Gao X.-L., Reddy J.N. A microstructure-dependent Timoshenko beam model based on a modified couple stress theory // Journal of the Mechanics and Physics of Solids. 2008. V. 56. № 12. P. 3379–3391.
Ma H.M.,Gao X.-L., Reddy J.N. A non-classical Mindlin plate model based on a modified couple stress theory // Acta Mech. 2011. V. 220. № 1–4. P. 217–235.
Kong S., Shou S., Nie Z., Wang K. Static and dynamic analysis in micro-beams based on strain gradient elasticity // Int. J. Engng. Sci. 2009. V. 47. № 4. P. 487–498.
Lazoupulos K.A., Lazoupulos A.K. On a strain gradient elastic Timoshenko beam model, Zeitschrift für Angenwandte Mathematik und Mechanik // ZAMM. 2011. V. 91. P. 591–882.
Kakunai S., Masaki J., Kuroda R., Iwata K., Nagata R. Measurement of apparent Young’s modulus in the bending of cantilever beam by heterodyne holographic interferometry // Exp. Mech. 1985. V. 25. № 4. P. 408–412.
Lam D.C.C., Yang F., Chong A.C.M., Wang J., Tong P. Experiments and theory in strain gradient elasticity // J. Mech. Phys. Solids. 2003. V. 51. P. 1477–1508.
McFarland A.W., Colton J.S. Role of material microstructure in plate stiffness with relevance to microcantilever sensors // J. Micromech. Microeng. 2005. V. 15. № 5. P. 1060–1067.
Liebold C., Muller W.H. Measuring material coefficients of higher gradient elasticity by using AFM techniques and Raman-spectroscopy // Advanced Structured Materials. 2013. V. 22. P. 255–271.
Lakes R., Drugan W.J. Bending of a Cosserat elastic bar of square cross section: Theory and experiment // Journal of Applied Mechanics. 2015. V. 82. № 9. 091002.
Lakes R. Experimental methods for study of Cosserat elastic solids and other generalized elastic continua // Ed. H. Mhlhaus, J. Wiley, N.Y. Ch. 1995. V. 1. P. 1–22.
Lurie S.A., Solyaev Y.O. Revisiting bending theories of elastic gradient beams. // Int. Journal of Engineering Science 2018. V 126. P. 1–21. https://doi.org/10.1016/j.ijengsci.2018.01.002
Lomakin E.V., Lurie S.A., Rabinskiy L.N., Solyaev Y.O. Semi-Inverse Solution of a Pure Beam Bending Problem in Gradient Elasticity Theory. The Absence of Scale Effects // Doklady Physics 2018. V. 63. № 4. P. 161–164.https://doi.org/10.1134/S1028335818040031
Lurie S.A., Volkov-Bogorodsky D.B., Belov P.A., Lykosova E.D. Do nanosized rods have abnormal mechanical properties? On some fallacious ideas and direct errors related to the use of the gradient theories for simulation of scale-dependent rods.// Nanomechanics Science and Technology: An International Journal. 2016. V. 7. № 4. P. 261–295. https://doi.org/10.1615/NanomechanicsSciTechnolIntJ.v7.i4.10
Lurie S., Solyaev Y., Volkov A., Volkov-Bogorodskiy D. Bending problems in the theory of elastic materials with voids and surface effects. // Mathematics and Mechanics of Solids. 2017. V. 23. № 5. P. 787–804.
Papargyri-Beskou S., Tsepoura K.G., Polyzos D., Beskos D.E. Bending and stability analysis of gradient elastic beams. International // Journal of Solids and Structures. 2003. V. 40. № 2. P. 385–400. https://doi.org/10.1016/S0020-7683(02)00522-X
Lazopoulos K.A. Post-buckling problems for long elastic beams. //Acta Mechanica. 2003. V. 164. № 3–4. P. 189–198. https://doi.org/10.1007/s00707-003-0023-8
Lazopoulos K.A., Lazopoulos A.K. Stability of a gradient elastic beam compressed by non-conservative forces // ZAMM 2010. V. 90. № 3. P. 174–184. https://doi.org/10.1002/zamm.200900231
Belov P.A., Lurie S.A. Mathematical theory of damaged media. Gradient theory of elasticity. Formulations hierarchy comparative analysis. In: Analysis and Applications. Palmarium Academic Publishing; 2014. 336 p. ISBN: 978-3-639-73761-5
Gusev A.A., Lurie S.A. Symmetry conditions in strain gradient elasticity //Mathematics and Mechanics of Solids. 2015. V. 22. № 4. P. 683–691. https://doi.org/10.1177/1081286515606960
Vasiliev V.V., Lurie S.A. On correct nonlocal generalized theories of elasticity // Physilac Mezomechanics. 2016. V. 19. № 3. P. 269–281.
Gao X.L., Park S.K. Variational formulation of a simplified strain gradient elasticity theory and its application to a pressurized thick-walled cylinder problem // Int. Journal of Solids and Structures. 2007. V. 44. № 22–23. P. 7486–7499.
Belov P.A., Lurie S.A. Theory of ideal adhesion interactions // J. Compos. Mech. Des. 2007. V. 14. P. 545–561.
Lurie S., Belov P., Lykosova E. Extended Model of Surface-related Effects in Second Gradient Elasticity. Surface Waves Related to the Nature of Adhesion., Ch 10 in book Nonlinear Wave Dynamics of Materials and Structures Ed.: Altenbach, H., Eremeyev, V.A., Pavlov, I.S., Porubov, A.V. (Eds.), Series Title Advanced Structured Materials. 2019. V. 122. https://doi.org/10.1007/978-3-030-38708-2
Eremeyev V.A. On effective properties of materials at the nano- and microscales considering surface effects. // Acta Mechanica 2016. V. 227. P. 29–42.
Liebold C., Müller W.H. Applications of Strain Gradient Theories to the Size Effect in Submicro-Structures incl. Experimental Analysis of Elastic Material Parameters // Bulletin of TICMI. 2015. V. 19. № 1. P. 45–55.
Liebold C., Müller W.H. Comparison of gradient elasticity models for the bending of micromaterials.//Computational Materials Science. 2016. V. 116. P. 52–61. https://doi.org/10.1016/j.commatsci.2015.10.031
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела