Известия РАН. Механика твердого тела, 2020, № 3, стр. 39-47

1. Введение. Пористые материалы находят широкое применение в различных отраслях современного машиностроения и позволяют создавать легкие и достаточно прочные конструкции, обладающие высокими характеристиками абсорбирования энергии. Поэтому исследование характерных особенностей распределения напряжений в окрестности различных отверстий имеет важное значение и в этом заключается основная цель настоящей работы.

Изучению влияния неоднородности структуры данных конструкционных материалов на их деформационные, пластические и прочностные свойства посвящены исследования многих авторов [1–5]. При формулировке условий пластичности в большинстве моделей влиянием третьего инварианта тензора напряжений пренебрегали и поверхность текучести представлялась в виде функции второго инварианта девиатора напряжений и первого инварианта тензора напряжений, коэффициенты которой зависели от параметра пористости, представляющего собой отношение объема пустот к общему объему материала [1, 6–10]. При квадратичной зависимости условия текучести от компонентов тензора напряжений поверхность текучести в пространстве главных напряжений представляла собой поверхность вытянутого эллипсоида. Данные предположения были подтверждены результатами экспериментальных исследований, полученных в условиях трехосного сжатия различных пористых материалов. Для анализа поведения грунтов часто используется линейная зависимость между вторым инвариантом девиатора напряжений и первым инвариантом напряжений. При этом поверхность текучести представляет собой коническую поверхность [11]. Данная модель находит широкое применение при решении многих практически важных задач.

Поведение неоднородностей существенным образом зависит от вида внешних воздействий, поэтому механические характеристики неоднородных материалов, включая пористые, зависят от вида напряженного состояния, создаваемого в телах при нагружении [12, 13]. Исследована зависимость деформационных и прочностных характеристик пористых алюминиевых сплавов, полимеров, конструкционных графитов и других материалов от пористости и структурных особенностей [6–10, 14].

В данной работе получено полуаналитическое решение задачи о круговом отверстии под действием внутреннего давления в пористой среде для случая плоской деформации. Решение получено для жесткопластической среды в пренебрежении упругими деформациями с использованием условия пластичности Грина [1]. Поскольку при формулировке данного условия пластичности считалось, что его коэффициенты зависят от пористости среды, то для получения аналитических зависимостей рассматривалось предельное состояние среды с некоторым определенным значением параметра пористости.

2. Определяющие соотношения. В работе [12] показано, что условие пластичности для материалов с зависящими от вида напряженного состояния свойствами, к которым относятся и пористые материалы, может быть представлено в следующем обобщенном виде:

В таком виде могут быть представлены многие из известных условий пластичности. Здесь параметр ${\xi } = {\sigma /}{{{\sigma }}_{0}}$ характеризует соотношение между нормальными и касательными напряжениями в точке сплошной среды, где ${\sigma } = \frac{1}{3}{{{\sigma }}_{{ii}}}$ – среднее нормальное напряжение, а ${{{\sigma }}_{0}} = \sqrt {3{\text{/}}2{{S}_{{ij}}}{{S}_{{ij}}}} $ – эффективное напряжение, которое определяет среднюю величину касательного напряжения, где ${{S}_{{ij}}} = {{{\sigma }}_{{ij}}} - {\sigma }{{{\delta }}_{{ij}}}$. Для конкретизации условия (2.1) можно принять, что при чистом сдвиге (ξ = 0) функция $f\left( 0 \right) = 1$. Тогда $k = \sqrt 3 {{{\tau }}_{s}}$, где τ_s – предел текучести при сдвиге. Функция $F({{{\sigma }}_{{ij}}})$ из (2.1) должна быть невогнутой, т.е. ${{d}^{2}}F \geqslant 0$. Вычисляя второй дифференциал функции $F({{{\sigma }}_{{ij}}})$ и учитывая, что $3{\text{/}}2{{S}_{{ij}}}d{{S}_{{ij}}}$ = σ₀dσ₀, получим

Коэффициенты, стоящие в правой части выражения (2.2) равны

Тогда ${{d}^{2}}F = f{\kern 1pt} ''{\kern 1pt} {\text{/}}{{{\sigma }}_{0}}{{\left( {d{\sigma } - {\xi }d{{{\sigma }}_{0}}} \right)}^{2}} - \left( {f - {\xi }f{\kern 1pt} '} \right){\text{/}}{{{\sigma }}_{0}}~{{\left( {d{{{\sigma }}_{0}}} \right)}^{2}} + \left( {f - {\xi }f{\kern 1pt} '} \right){\text{/}}{{{\sigma }}_{{0~}}}3{\text{/}}2~d{{S}_{{ij}}}d{{S}_{{ij}}}$.

Учитывая, что $f - {\xi }f{\kern 1pt} ' = {\lambda }\left( {\xi } \right) > 0$, поскольку является коэффициентом пропорциональности в выражении для интенсивности скоростей пластических деформаций [12], и $3{\text{/}}2d{{S}_{{ij}}}d{{S}_{{ij}}}~ \geqslant d{\sigma }_{0}^{2}$ получим ${{d}^{2}}F \geqslant f{\kern 1pt} ''\frac{{{{{\left( {d{\sigma } - {\xi }d{{{\sigma }}_{0}}} \right)}}^{2}}}}{{{{{\sigma }}_{0}}}} \geqslant 0$. Из этого следует, что для обеспечения выпуклости функции $F\left( {{{{\sigma }}_{{ij}}}} \right)$ достаточно, чтобы

Рассмотрим следующее выражение для функции $f\left( {\xi } \right)$:

из которого получается условие пластичности Грина ${\sigma }_{0}^{2} + {\alpha }{{{\sigma }}^{2}} = {{k}^{2}}$, которое часто используется при решении задач для пористых материалов. Параметры α и k представляют собой функции параметра пористости сплошной среды. Для выполнения условия (2.3) достаточно, чтобы ${\alpha } \geqslant 0$. Разными авторами предлагались различные аналитические зависимости для коэффициентов от пористости среды, например 1/(1 + + ${{({\alpha /}3)}^{2}})({\sigma }_{0}^{2} + {{{\alpha }}^{2}}{{{\sigma }}^{2}})$ = k [8]. Данный критерий позволяет учесть зависимость предела текучести от параметра пористости.

Принимая ассоциированный с условием (2.1) закон течения ${{\dot {\epsilon }}_{{ij}}} = h{\kern 1pt} '\partial F{\text{/}}\partial {{{\sigma }}_{{ij}}}$ в случае жесткопластического тела связь между скоростями деформаций и напряжениями можно представить в следующем виде:

где ${\Lambda }\left( {\xi } \right) = f{\kern 1pt} '\left( {\xi } \right),{\lambda }\left( {\xi } \right) = f\left( {\xi } \right) - {\xi }f{\kern 1pt} '\left( {\xi } \right),h{\kern 1pt} ' = \frac{H}{{{\chi }\left( {\xi } \right)}},H = \sqrt {{{{\dot {\epsilon }}}_{{ij}}}{{{\dot {\epsilon }}}_{{ij}}}} ,{\chi }\left( {\xi } \right) = \sqrt {\frac{1}{3}{{{\Lambda }}^{2}}\left( {\xi } \right) + \frac{3}{2}{{{\lambda }}^{2}}\left( {\xi } \right)} $

Функции ${\Lambda }\left( {\xi } \right)$ и ${\lambda }\left( {\xi } \right)$ и их производные взаимосвязаны и для них выполняются соотношения ${\lambda }\left( {\xi } \right) + {\xi \Lambda }\left( {\xi } \right) = f\left( {\xi } \right),{\lambda }{\kern 1pt} '\left( {\xi } \right) + {\xi \Lambda }{\kern 1pt} '\left( {\xi } \right) = 0$. Из (2.5) можно получить выражения для интенсивности скоростей пластических деформаций $\Gamma = \sqrt {2{\text{/}}3{{{\dot {e}}}_{{ij}}}{{{\dot {e}}}_{{ij}}}} = h{\kern 1pt} '{\lambda }\left( {\xi } \right)$, где ${{\dot {e}}_{{ij}}} = {{\dot {\epsilon }}_{{ij}}} - 1{\text{/}}3\epsilon {{\dot {\delta }}_{{ij}}}$ и скорости объемной деформации $\dot {\epsilon } = {{\dot {\epsilon }}_{{ij}}}{{{\delta }}_{{ij}}} = h{\kern 1pt} '{\Lambda }\left( {\xi } \right)$. Отсюда видно, что функция λ(ξ) должна быть положительно определена. В таком случае скорость остаточной объемной деформации пропорциональна интенсивности скоростей деформаций .

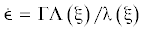В общем случае коэффициент пропорциональности 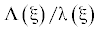зависит от вида напряженного состояния ξ, принимает различные значения для различных соотношений между нормальными и касательными напряжениями в сплошной среде.

3. Плоская деформация. Рассмотрим случай плоской деформации: ${{\dot {\epsilon }}_{{33}}} = {{\dot {\epsilon }}_{{13}}} = {{\dot {\epsilon }}_{{23}}}$ = 0. С помощью определяющих соотношений (2.5) можно исключить напряжение σ₃₃ из условия (2.1), выразив его через ${{{\sigma }}_{{11}}},{{{\sigma }}_{{22}}},{{{\sigma }}_{{12}}}$. Получаются следующие выражения:

Чтобы исключить из всех выражений напряжение σ₃₃, введем параметр ${\zeta } = S{\text{/}}{{S}_{0}}$ далее выразим ζ через ξ, используя (3.1):

Тогда условие пластичности (2.1), используя (3.2) и (3.1), можно представить в следующем виде:

Так как ${\zeta } = S{\text{/}}{{S}_{0}} = S{{f}_{1}}\left( {\zeta } \right){\text{/}}k$, то ζ и напряжение S₀ можно выразить через S, а зависимость ${\zeta } = {\xi }\left( S \right)$ – взаимнооднозначная при выполнении условий 3λ(ξ) > $\left| {{\Lambda }\left( {\xi } \right)} \right|$, ${\Lambda }{\kern 1pt} '{\kern 1pt} \left( {\xi } \right) \geqslant 0$, при этом напряжение S₀ также можно выразить через S, S₀ = $\sqrt 3 kF\left( S \right)$, где $F\left( S \right) = {{3}^{{ - \frac{1}{2}}}}f_{1}^{{ - 1}}\left[ {{\zeta }\left( S \right)} \right]$. Выражения для напряжений в случае плоской деформации можно представить в следующем виде:

В (3.4) угол θ представляет собой угол между осью x₁ и направлением площадки, на которой действует максимальное касательное напряжение. Для случая плоской деформации система уравнений, описывающая напряженное состояние, включает в себя условие пластичности (2.1) и уравнения равновесия:

Подставив напряжения (3.4) в уравнения равновесия (3.5), получим систему уравнений для определения S и θ:

В (3.6) штрихом обозначается дифференцирование по переменной S. Важно отметить, что система (3.6) является гиперболической при $\left| {kF'} \right| < 1.$ Этот факт накладывает ограничения на значения функции, характеризующей степень чувствительности пластических свойств среды к изменению вида напряженного состояния. Выпишем характеристики системы уравнений (3.6) и обозначим их индексами α и β, а также выпишем соотношения вдоль них:

Легко заметить, что характеристики (10) будут ортогональны только в случае, если $f\left( {\xi } \right) \equiv {\text{const}}$, когда условие (2.1) совпадает с условием пластичности Губера–Мизеса.

4. Распределение напряжений в окрестности кругового отверстия. Будем рассматривать задачу о неограниченном теле с круговым вырезом. По всему контуру выреза приложено нормальное давление, равное p. Перейдем к безразмерным величинам, для этого радиальные координаты отнесем к радиусу отверстия a, а напряжения – к k. Рассмотрим критерий пластичности (2.1) для функции $f\left( {\xi } \right)$, представленной выражением (2.4). Введем полярную систему координат $\left( {r,~{\psi }} \right)$. Формулы для напряжений (3.4) в полярной системе координат будут следующие:

При осевой симметрии напряжения ${{\sigma }_{{rr}}}$ и ${{\sigma }_{{{\psi \psi }}}}~$ являются главными и уравнения равновесия (3.5) в полярной системе координат сведутся к одному уравнению:

Граничное условие в этой задаче будет следующим: $\begin{array}{*{20}{c}} {{{\sigma }_{{rr}}}{{{\text{|}}}_{{\bar {r} = 1}}} = - p{\text{/}}k} \end{array}$, где $\bar {r} = r{\text{/}}a$. В  случае (2.4) при ${\alpha } \geqslant 0$ поверхность текучести (2.1) выпуклая. Случай α = 0 соответствует условию Губера–Мизеса. Из соотношения (3.2) получим ξ = =  $\zeta {\text{/}}\sqrt {{{{\left( {1\, + \,\alpha {\text{/}}9} \right)}}^{2}}\, + \,{{\alpha }^{2}}{{\zeta }^{2}}{\text{/}}9} $. Функция ${{f}_{1}}\left( {\zeta } \right)$ из (3.3) имеет вид ${{f}_{1}}\left( {\zeta } \right) = \sqrt {1 + {\beta }{{{\zeta }}^{2}}} $, где коэффициент β выражается через параметр пористости среды

Функцию F(S) с учетом (4.3) можно представить в виде

Система (3.6) гиперболична при выполнении следующего неравенства $\left| {kF'} \right| < 1.$ Продифференцировав (4.4) по переменной $S$ и подставив в это неравенство находим, что ${{(S{\text{/}}k)}^{2}} < 3{\text{/}}\left[ {{\beta }\left( {3 + {\beta }} \right)} \right]$ – условие гиперболичности системы (3.6) для критерия пластичности Грина (2.4). Подставим (4.4) в (4.1), затем полученные выражения подставим в уравнение равновесия (4.2) и проинтегрировав получим следующее уравнение:

где C₁ константа интегрирования, которая определяется из граничного условия, $\bar {r}$ – безразмерный радиус пластической области. Уравнения характеристик и соотношения вдоль них имеют следующий вид:

Далее необходимо определить радиус пластической области. Максимальный радиус будет при ${{{\psi }}_{0}} = \pm {\pi /}2$, θ = ψ₀ + π/4, подставим эти значения в (4.6) и получим $\bar {r} = {{e}^{{\sqrt {\left( {1 + k{{F}_{1}}} \right)/\left( {1 - k{{F}_{1}}} \right)} }}}$, где $\bar {r}~$– безразмерный радиус пластической области, а ${{F}_{1}} = F'$(S).

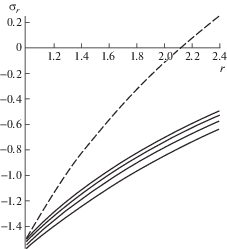
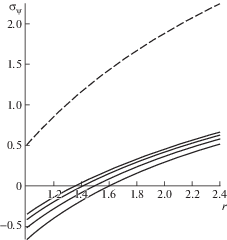
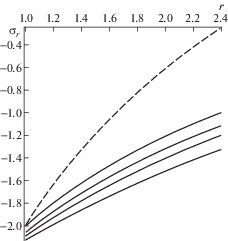
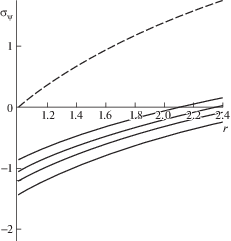
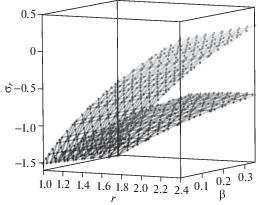
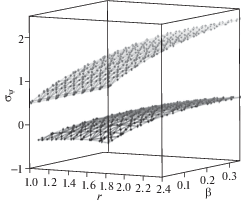
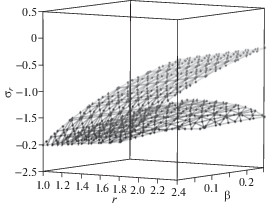
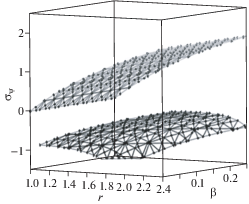
Можно построить графики зависимости напряжений от радиуса в пластической области при различных значениях коэффициента β, который через (4.3) связан с параметром пористости ${\alpha }$ из условия пластичности (2.4), и нагрузок, приложенных на внутреннем радиусе выреза, $p{\text{/}}k = \left\{ {1.5;~\,\,2} \right\}$, и сравнить их с классическим случаем Губера–Мизеса. Радиус пластических деформаций определяется конечной точкой на диаграммах напряжений, которые изображены на графиках, из которых видно, что в исследованном диапазоне нагрузок радиус пластической области меняется незначительным образом. При этом распределение напряжений заметно изменяются с увеличением нагрузки. На рис. 1 и 2 приведены зависимости распределения напряжений от коэффициента β для p/k = 1.5 для значений параметра ${\beta } = \left\{ {0.01,\,\,~0.1,~\,\,0.2,~\,\,0.3} \right\}$, на рис. 3 и 4 эти зависимости представлены для p/k = 2 и значений ${\beta } = \left\{ {0.01,~\,\,0.1,~\,\,0.15,~\,\,0.2} \right\}$. На рис. 5 и 6 приведены поверхности, характеризующие распределения напряжений ${{{\sigma }}_{r}}$ и ${{{\sigma }}_{{\psi }}}$ в зависимости от r и β для p/k = 1.5, а на рис. 7 и 8 – аналогичные поверхности для p/k = 2.

5. Заключение. В работе получено полуаналитическое решение задачи о действии внутреннего давления на поверхности цилиндрического канала в пористом теле. Исследована зависимость распределения напряжений от значения параметра, характеризующего пористость материала, и установлено, что распределение напряжений существенным образом зависит от значения этого параметра. Показано, что распределение напряжений и их уровень существенно отличаются от значений для сплошного материала с инвариантными к виду внешних воздействий пластическими свойствами, для которого может быть использован критерий Губера–Мизеса. Кроме того, установлено, что размер пластической области незначительно зависит от величины давления на поверхности отверстия, но распределения напряжений весьма чувствительно к величине нагрузки.

Работа выполнена при поддержке Российского научного фонда (грант 20-11-20230).