1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 3, 2020

Известия РАН. Механика твердого тела, 2020, № 3, стр. 134-145

Трибомеханические эффекты неоднородности упругого покрытия (упрощенная деформационная модель)

И. А. Солдатенков *

Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: iasoldat@hotmail.com

Поступила в редакцию 15.11.2019
После доработки 25.11.2019
Принята к публикации 28.12.2019

Полный текст (PDF)

Аннотация

Рассматривается неоднородное по глубине упругое покрытие, для которого в рамках концепции асимптотически тонкого слоя предлагается упрощенная деформационная модель. На основе такой модели для неоднородного покрытия строится решение контактной задачи при наличии межмолекулярного взаимодействия и выполняется расчет кинетики изнашивания в упорном подшипнике скольжения. Показано, что характер неоднородности покрытия может оказывать существенное влияние на его напряженно-деформированное состояние и кинетику изнашивания.

Ключевые слова: упругость, напряженно-деформированное состояние, контактная задача, неоднородное покрытие, межмолекулярное взаимодействие, изнашивание

Введение. Неоднородные (в том числе многослойные) покрытия являются эффективным средством повышения эксплуатационных характеристик различных узлов трения [1, 2]. Существует ряд подходов к моделированию упругого поведения неоднородных покрытий, среди которых можно отметить метод дискретных слоев [3, 4], двухсторонний асимптотический метод [5], метод граничных элементов и двойное преобразование Фурье [6]. Процесс изнашивания неоднородного по длине покрытия описывался на основе метода возмущений [7] и проекционного метода [8]. Расчет изнашивания неоднородного по глубине покрытия выполнялся с использованием численной разностной схемы [3].

Строгая постановка контактной задачи при наличии межмолекулярного взаимодействия предполагает существование некоторого зазора между контактирующими телами. Величина этого зазора должна обеспечивать баланс сил, обусловленных контактной деформацией тел и их межмолекулярным взаимодействием (самосогласованный подход по Дерягину [9]). В рамках такого подхода рассмотрен ряд контактных задач для однородного покрытия, в том числе при объемном приложении сил межмолекулярного взаимодействия [10, 11].

Настоящая работа посвящена анализу влияния неоднородности упругих и износостойких свойств по глубине покрытия на его напряженно-деформированное состояние (НДС) и кинетику изнашивания.

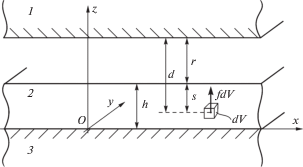
1. Упрощенная деформационная модель для неоднородного покрытия. Рассмотрим упругий слой (покрытие) 2 толщины $h$, сцепленный с абсолютно жестким основанием (подложкой) 3 и взаимодействующий с абсолютно жестким телом (индентором) 1 (рис. 1). Зададим систему координат $Oxyz$, плоскость $Oxy$ которой совместим с поверхностью подложки (рис. 1). В дальнейшем также будут использоваться обозначения координат с индексом: ${{x}_{1}} = x$, ${{x}_{2}} = y$, ${{x}_{3}} = z$. Покрытие считается изотропным и неоднородным по глубине. Упругие свойства такого покрытия можно задать параметрами Ламе $\lambda ,\;\mu $, зависящими от координаты z. Покрытие находится в напряженно-деформированном состоянии, обусловленном действием внешних контактных и объемных сил со стороны индентора.

Рис. 1

В дальнейшем будет использоваться концепция асимптотически тонкого слоя, согласно которой НДС покрытия в продольном направлении (в плоскости $Oxy$) на расстояниях ~h изменяется незначительно [12]. Пренебрегая этим изменением НДС, будем считать, что компоненты вектора перемещений ${{u}_{i}}$, тензора деформаций ${{\varepsilon }_{{ij}}}$ и тензора напряжений ${{\sigma }_{{ij}}}$ зависят только от координаты z. В этом случае, как нетрудно убедиться на основе формул Коши и закона Гука [13], все компоненты НДС равны нулю, кроме

(1.1)
$\begin{gathered} {{\varepsilon }_{{i3}}} = {{\varepsilon }_{{3i}}} = \frac{1}{2}u_{i}^{'},\quad {{\sigma }_{{i3}}} = {{\sigma }_{{3i}}} = \mu u_{i}^{'},\quad i = 1,2;\quad {{\varepsilon }_{{33}}} = u_{3}^{'} \\ {{\sigma }_{{\left\{ \begin{subarray}{l} 11 \\ 22 \end{subarray} \right\}}}} = \lambda u_{3}^{'},\quad {{\sigma }_{{33}}} = (\lambda + 2\mu )u_{3}^{'} \\ \end{gathered} $
при этом справедливы уравнения равновесия

(1.2)
$\sigma _{{i3}}^{'} + {{f}_{i}} = 0,\quad i = 1,2,3$

Здесь и далее ${{f}_{i}}$ – компоненты объемных сил, а штрихом обозначается производная по z.

Имеют место граничные условия

(1.3)
${{\left. {{{u}_{i}}} \right|}_{{z = 0}}} = 0,\quad {{\left. {{{\sigma }_{{3i}}}} \right|}_{{z = h}}} = {{q}_{i}};\quad i = 1,2,3$
первое из которых является следствием сцепления покрытия с абсолютно жесткой подложкой, а второе – наличия контактных напряжений ${{q}_{i}}$, приложенных к верхней границе покрытия. Здесь и далее не делается различия между толщиной покрытия в исходном и деформированном состояниях, что допустимо при малых деформациях.

Равенства (1.1) определяют линейные зависимости производных $u_{i}^{'}$ от напряжений ${{\sigma }_{{3i}}}$, интегрирование которых по z с учетом первого граничного условия (1.3) позволяет установить, что

(1.4)
${{u}_{i}}(z) = \int\limits_0^z {{{C}^{{(i)}}}(\xi ){{\sigma }_{{3i}}}(\xi )d\xi ,} \quad {{C}^{{(i)}}}(z) = \left\{ \begin{gathered} {{\mu }^{{ - 1}}}(z),\quad i = 1,2 \hfill \\ {{(\lambda (z) + 2\mu (z))}^{{ - 1}}},\quad i = 3 \hfill \\ \end{gathered} \right.$

Присутствующие в первом равенстве (1.4) напряжения ${{\sigma }_{{3i}}}$ находятся путем интегрирования уравнений (1.2) по z с учетом второго граничного условия (1.3):

(1.5)
${{\sigma }_{{3i}}}(z) = \int\limits_z^h {{{f}_{i}}(\xi )d\xi } + {{q}_{i}}$

Остальные отличные от нуля напряжения ${{\sigma }_{{11}}}$, ${{\sigma }_{{22}}}$ выражаются через компоненту ${{\sigma }_{{33}}}$ на основе двух последних равенств (1.1), так что

(1.6)
${{\sigma }_{{\left\{ \begin{subarray}{l} 11 \\ 22 \end{subarray} \right\}}}}(z) = \frac{{\lambda (z)}}{{\lambda (z) + 2\mu (z)}}{{\sigma }_{{33}}}(z)$

Записанные выше соотношения свидетельствуют о том, что НДС асимптотически тонкого покрытия расщепляется на три независимых системы, зависящие от отдельных компонент внешних нагрузок:

1) ${{u}_{1}},\;{{\varepsilon }_{{13}}} = {{\varepsilon }_{{31}}},\;{{\sigma }_{{13}}} = {{\sigma }_{{31}}}$ – зависит от ${{q}_{1}},\;{{f}_{1}}$;

2) ${{u}_{2}},\;{{\varepsilon }_{{23}}} = {{\varepsilon }_{{32}}},\;{{\sigma }_{{23}}} = {{\sigma }_{{32}}}$ – зависит от ${{q}_{2}},\;{{f}_{2}}$;

3) ${{u}_{3}},\;{{\varepsilon }_{{33}}},\;{{\sigma }_{{11}}} = {{\sigma }_{{22}}},\;{{\sigma }_{{33}}}$ – зависит от ${{q}_{3}},\;{{f}_{3}}$.

Отметим, что расщепление НДС на независимые системы имеет место при контактном взаимодействии с круговым и однонаправленным трением скольжения [14, 15].

В дальнейшем в связи с рассмотрением контактного взаимодействия при наличии межмолекулярного взаимодействия и изнашивания будет использоваться только третья из указанных выше систем НДС покрытия. Введем для этой системы специальные обозначения: $\sigma = {{\sigma }_{{33}}}$, $p = - {{q}_{3}}$ – контактное давление, $B = {{(\lambda + 2\mu )}^{{ - 1}}}$ – коэффициент податливости и, пользуясь равенствами (1.4) и (1.5), запишем соотношения

(1.7)
${{u}_{3}}(z) = \int\limits_0^z {B(\xi ){\kern 1pt} {\kern 1pt} \sigma (\xi )d\xi } ,\quad \sigma (z) = \int\limits_z^h {{{f}_{3}}(\xi )d\xi } - p$

Согласно второму равенству (1.7): $\sigma {\text{'}}(z) = - {{f}_{3}}(z)$. Учитывая это и выполняя в первом равенстве (1.7) интегрирование по частям, можно установить, что

(1.8)
${{u}_{3}}(z) = A(z){\kern 1pt} {\kern 1pt} \sigma (z) + \int\limits_0^z {A(\xi ){\kern 1pt} {\kern 1pt} {{f}_{3}}(\xi )d\xi } $
(1.9)
$A(z) = \int\limits_0^z {B(\xi )d\xi } ,\quad A'(z) = B(z)$

Полагая в равенстве (1.8) z = h и принимая во внимание граничное условие $\sigma (h)$ = –p, получим следующее выражение для нормального граничного перемещения:

(1.10)
$w \equiv {{u}_{3}}(h) = - \bar {B}hp + \int\limits_0^h {A(\xi ){\kern 1pt} {\kern 1pt} {{f}_{3}}(\xi )d\xi } $
причем $\bar {B} = A(h){\text{/}}h$ – среднее значение коэффициента B по глубине покрытия. В частности, при отсутствии объемной силы ${{f}_{3}}$ имеет место линейная зависимость граничного перемещения $w$ от контактного давления:
(1.11)
$w = - \bar {B}hp \equiv - A(h)p$
которая отвечает модели Винклера с коэффициентом постели $\bar {B}h$ [12]. Такая же зависимость была установлена ранее путем предельного перехода от многослойного покрытия к покрытию с непрерывным изменением упругих параметров [3].

Полученные выше выражения для компонент ${{\sigma }_{{ij}}}$ тензора напряжений позволяют рассчитывать определенные комбинации этих компонент, которые используются в различных критериях разрушения [16]. Примером такой комбинации является интенсивность касательных напряжений

(1.12)
${{\tau }_{i}} = \frac{1}{{\sqrt 6 }}{{\left[ {{{{({{\sigma }_{{11}}} - {{\sigma }_{{22}}})}}^{2}} + {{{({{\sigma }_{{11}}} - {{\sigma }_{{33}}})}}^{2}} + {{{({{\sigma }_{{22}}} - {{\sigma }_{{33}}})}}^{2}} + 6(\sigma _{{12}}^{2} + \sigma _{{13}}^{2} + \sigma _{{23}}^{2})} \right]}^{{1/2}}}$

С учетом выражений (1.5), (1.6) для отличных от нуля компонент тензора напряжений и второго равенства (1.7), формула (1.12) позволяет установить, что в рассматриваемом случае

(1.13)
${{\tau }_{i}}(z) = \frac{1}{{\sqrt 3 }}\left| {{{\sigma }_{{33}}}(z) - {{\sigma }_{{11}}}(z)} \right| = \frac{2}{{\sqrt 3 }}\mu (z)B(z)\left| {\sigma (z)} \right| = \frac{2}{{\sqrt 3 }}\rho (z)\left| {\int\limits_z^h {{{f}_{3}}(\xi )d\xi } - p} \right|$
где $\rho = \mu {\kern 1pt} B = \frac{\mu }{{\lambda + 2\mu }} = \frac{{1 - 2\nu }}{{2(1 - \nu )}}$, $\nu $ – коэффициента Пуассона [13]. Согласно выражению (1.13), интенсивность касательных напряжений в рассматриваемом случае зависит от единственного параметра упругих свойств покрытия – коэффициента Пуассона.

2. Контакт при наличии межмолекулярного взаимодействия. Рассмотрим контакт неоднородного по глубине покрытия с однородным индентором при наличии парного взаимодействия их молекул. Считается, что индентор и покрытие разделены контактным зазором $r$, обеспечивающим баланс сил межмолекулярного и упругого взаимодействия контактирующих тел (самосогласованный подход) [9] (рис. 1).

При определенных допущениях [17, 18] суммирование сил парных взаимодействий молекул позволяет для каждой точки покрытия рассчитать объемную силу ${{f}_{i}}$, обусловленную межмолекулярным взаимодействием. Эта сила направлена вдоль оси $z$ и зависит от расстояния d между точкой ее приложения и индентором (рис. 1). Кроме того, для неоднородного покрытия с изменяющимися по глубине свойствами объемная сила зависит от расстояния $s$ точки ее приложения до поверхности покрытия. Таким образом, в рассматриваемом случае

(2.1)
${{f}_{1}} = {{f}_{2}} \equiv 0,\quad {{f}_{3}} = f(d,s);\quad d = r + s = r + h - z,\quad s = h - z$

В свою очередь, суммирование объемных сил по глубине покрытия и подложки позволяет определить силу p воздействия индентора на покрытие, приходящуюся на единицу площади его поверхности:

(2.2)
$p = \Phi (r),\quad \Phi (r) = - \int\limits_0^\infty f (r + s,s){\mkern 1mu} {\kern 1pt} ds$
которая в рамках самосогласованного подхода интерпретируется как контактное давление [9, 11, 17].

Существуют различные формы зависимости силы $F$ парного взаимодействия молекул от расстояния $l$ между ними, среди которых наиболее известен закон Леннард–Джонса [19]. В рассматриваемом случае взаимодействия молекул покрытия и индентора этот закон имеет вид:

(2.3)
$F(l,s) = \frac{{{{a}_{1}}(s)}}{{{{l}^{m}}}} - \frac{{{{a}_{2}}(s)}}{{{{l}^{n}}}}$
где ${{a}_{1}},\,\,{{a}_{2}},\,\,m,\,\,n$ – параметры взаимодействия, причем обычно полагают m = 7, n = 13. При наличии зависимости (2.3) объемная сила f определяется по формуле [20]
(2.4)
$f(d,s) = \frac{{{{b}_{{{\kern 1pt} 1}}}(s)}}{{{{d}^{{m - 3}}}}} - \frac{{{{b}_{{{\kern 1pt} 2}}}(s)}}{{{{d}^{{n - 3}}}}},\quad d \in [r,r + h]$
где
${{b}_{1}}(s) = \frac{{2\pi {{N}_{*}}N(s){{a}_{1}}(s)}}{{(m - 1)(m - 3)}},\quad {{b}_{2}}(s) = \frac{{2\pi {{N}_{*}}N(s){{a}_{2}}(s)}}{{(n - 1)(n - 3)}}$
${{N}_{*}}$ и N – концентрации молекул индентора и покрытия.

Традиционная постановка контактной задачи при наличии межмолекулярного взаимодействия подразумевает, что определяемое по формуле (2.2) контактное давление p прикладывается к поверхности покрытия, в результате чего оно деформируется [9, 10, 17]. Ниже используется уточненная постановка, в которой естественным образом предполагается, что деформация покрытия порождается объемными силами ${{f}_{i}}$ вида (2.1), распределенными по его глубине, тогда как поверхность покрытия свободна от нагрузок [11, 20, 21]. В качестве параметра нагружения покрытия в обеих постановках выступает зазор $r$, однозначно определяющий объемные силы и контактное давление по формулам (2.1) и (2.2).

Замечание 1. Вопрос метода реализации заданного значения $r$ здесь не рассматривается. Отметим только, что зазор $r$ связан равенством (2.2) с контактным давлением p, совпадающим с удельной нагрузкой на индентор, поэтому имеется возможность подбором этой нагрузки получить требуемое значение $r$.

В дальнейшем будет рассматриваться бесконечно протяженный плоский индентор, для которого НДС покрытия в плоскости $Oxy$ не меняется и в точности отвечает концепции асимптотически тонкого слоя, т.е. описывается равенствами (1.1).

Используя уточненную постановку задачи, положим p = 0 в равенствах (1.7)–(1.10) и учтем в них выражение (2.1) для объемной силы ${{f}_{3}}$. В результате получим:

(2.5)
$\begin{gathered} \sigma (z) = \int\limits_z^h {f(r + h - \xi ,h - \xi )d\xi } \\ {{u}_{3}}(z) = A(z){\kern 1pt} \sigma (z) + \int\limits_0^z {A(\xi )f(r + h - \xi ,h - \xi )d\xi } \\ w = \int\limits_0^h {A(\xi )f(r + h - \xi ,h - \xi )d\xi } \\ \end{gathered} $

Преследуя цель выявить эффекты неоднородности упругих свойств покрытия, будем далее считать его физические свойства неизменными. Это означает, что правые части равенств (2.3) и (2.4) не зависят от величины $s$, т.е. $F(l,s) = F(l),$ $f(d,s) = f(d)$. Кроме того, положим для определенности, что коэффициент податливости $B$ изменяется по глубине покрытия линейно:

(2.6)
$B(z) = \frac{1}{h}({{B}^{ + }} - {{B}^{ - }})z + {{B}^{ - }};\quad {{B}^{ - }} = B(0),\quad {{B}^{ + }} = B(h)$
поэтому, согласно формуле (1.9):

(2.7)
$A(z) = \frac{1}{{2h}}({{B}^{ + }} - {{B}^{ - }}){{z}^{2}} + {{B}^{ - }}z$

Подставим выражения (2.4) и (2.7) в третью формулу (2.5) и вычислим полученные интегралы. В результате, после несложных преобразований определим граничное перемещение w как функцию контактного зазора $r$:

(2.8)
$w = - \bar {B}h\,\Psi (r)$
где

$\Psi (r) = - \frac{{{{A}_{1}}}}{{r_{e}^{k}}}\left( {{{s}_{0}}{{\Pi }_{{k,\,l}}} + {{s}_{1}}{{\Pi }_{{k - 1,\,l - 1}}} + {{s}_{2}}{{\Pi }_{{k - 2,\,l - 2}}}} \right)$
$\begin{gathered} {{r}_{e}} = {{\left( {\frac{{{{A}_{1}}}}{{{{A}_{2}}}}} \right)}^{{\frac{1}{{m - n}}}}},\quad {{A}_{1}} = \frac{{{{b}_{1}}}}{k},\quad {{A}_{2}} = \frac{{{{b}_{2}}}}{l},\quad k = m - 4,\quad l = n - 4 \\ {{s}_{0}} = \left( {1 + \frac{r}{h}} \right)\left( {1 + {{\chi }_{B}}\frac{r}{h}} \right),\quad {{s}_{1}} = - \frac{{{{r}_{e}}}}{h}\left[ {1 + {{\chi }_{B}}\left( {1 + 2\frac{r}{h}} \right)} \right],\quad {{s}_{2}} = {{\chi }_{B}}{{\left( {\frac{{{{r}_{e}}}}{h}} \right)}^{2}},\quad {{\chi }_{B}} = \frac{{{{B}^{ + }} - {{B}^{ - }}}}{{2\bar {B}}} \\ {{\Pi }_{{i,j}}} = \frac{k}{i}(R_{1}^{i} - R_{2}^{i}) - \frac{l}{j}(R_{1}^{j} - R_{2}^{j}),\quad {{R}_{1}} = \frac{{{{r}_{e}}}}{r},\quad {{R}_{2}} = \frac{{{{r}_{e}}}}{{r + h}} \\ \end{gathered} $

Подстановка выражений (2.1), (2.4) для объемной силы в формулу (1.13) приводит к следующему выражению для интенсивности касательных напряжений:

(2.9)
$\begin{gathered} {{\tau }_{i}}(z) = \frac{2}{{\sqrt 3 }}\rho (z)\left| {\tilde {\Phi }(z,r)} \right| \\ \tilde {\Phi }(z,r) = - \int\limits_z^h {f(r + h - \xi )d\xi } = - \frac{{{{A}_{1}}}}{{r_{e}^{k}}}\left\{ {\left[ {{{{\left( {\frac{{{{r}_{{\text{e}}}}}}{r}} \right)}}^{k}} - {{{\left( {\frac{{{{r}_{e}}}}{{r + h - z}}} \right)}}^{k}}} \right] - \left[ {{{{\left( {\frac{{{{r}_{{\text{e}}}}}}{r}} \right)}}^{l}} - {{{\left( {\frac{{{{r}_{e}}}}{{r + h - z}}} \right)}}^{l}}} \right]} \right\} \\ \end{gathered} $

Замечание 2. При использовании традиционной постановки контактной задачи при наличии межмолекулярного взаимодействия в равенствах (1.7)–(1.10), (1.13) следует положить ${{f}_{3}} = 0$ и учесть выражение (2.2) для контактного давления p. В результате вместо равенств (2.5) и (2.9) получим

$\sigma (z) = - \Phi (r),\quad {{u}_{3}}(z) = - A(z)\Phi (r),\quad w = - \bar {B}h\Phi (r),\quad {{\tau }_{i}}(z) = \frac{2}{{\sqrt 3 }}\rho (z)\left| {\Phi (r)} \right|$

На основе формул (2.8) и (2.9) были выполнены численные расчеты граничного перемещения w и интенсивности ${{\tau }_{i}}$ касательных напряжений. Дополнительно проводился расчет внедрения $\delta $ индентора в покрытие, отсчитываемого от поверхности покрытия в недеформированном состоянии. Это внедрение связано с граничным перемещением $w$ и контактным зазором $r$ соотношением $\delta + r = - w$, которое с учетом выражения (2.8) позволяет установить, что

(2.10)
$\delta = \bar {B}h\,\Psi (r) - r$

Согласно выражению (2.10), зависимость $\delta (r)$ является монотонной при условии $\bar {B}h\,\mathop {\max }\limits_{r \in (0,\infty )} \Psi {\kern 1pt} '(r)$ < 1, выполнение которого контролировалось в ходе расчетов. Данное обстоятельство позволяет использовать внедрение $\delta $, наряду с контактным зазором r, в качестве параметра взаимодействия индентора и покрытия.

Расчеты проводились при $h = 1$ нм, $\bar {B} = {{10}^{{ - 9}}}$ Па–1, $m = 7,$ $n = 13$ , ${{r}_{e}} = 1$ нм. Кроме того, полагалось, что ${{A}_{{{\kern 1pt} 1}}} = {{(6\pi )}^{{ - 1}}}{{A}_{H}}$ [9], где ${{A}_{H}}$ – постоянная Гамакера, ${{A}_{H}} = {{10}^{{ - 19}}}$ Дж. Значения остальных параметров указываются отдельно для каждого численного примера.

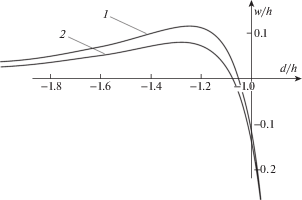
На рис. 2 представлены зависимости граничного перемещения $w$ от внедрения $\delta $, рассчитанные по формулам (2.8), (2.10) и отвечающие двум вариантам линейного распределения (2.6) коэффициента податливости $B$ по глубине покрытия: ${{B}^{ + }} = 0.3\bar {B}$, ${{B}^{ - }} = 1.7\bar {B}$ – возрастание податливости покрытия по глубине (кривая 1); ${{B}^{ + }} = 1.7\bar {B}$, ${{B}^{ - }} = 0.3\bar {B}$ – снижение податливости покрытия по глубине (кривая 2). Среднее значение $({{B}^{ + }} + {{B}^{ - }}){\text{/}}2$ коэффициента податливости для обоих вариантов одинаковое и совпадает с заданным значением $\bar {B}$.

Рис. 2

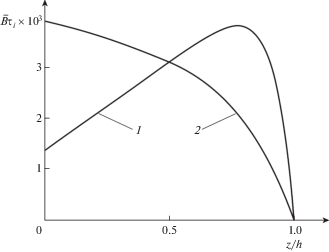
На рис. 3 показано распределение интенсивности ${{\tau }_{i}}$ касательных напряжений по глубине покрытия, рассчитанное по формуле (2.9) при $r = 0.9{\kern 1pt} {\kern 1pt} {{r}_{e}}$ и линейной зависимости коэффициента Пуассона $\nu $ от координаты $z$ вида:

(2.11)
$\nu (z) = \frac{1}{h}({{\nu }^{ + }} - {{\nu }^{ - }})z + {{\nu }^{ - }},\quad {{\nu }^{ - }} = \nu (0),\quad {{\nu }^{ + }} = \nu (h)$
Рис. 3

Показанные распределения отвечают двум вариантам зависимости (2.11): ${{\nu }^{ + }} = 0.1$, ${{\nu }^{ - }} = 0.4$ – возрастание коэффициента Пуассона по глубине покрытия (кривая 1); ${{\nu }^{ + }}$ = = 0.4, ${{\nu }^{ - }} = 0.1$ – снижение коэффициента Пуассона по глубине покрытия (кривая 2). Среднее значение $({{\nu }^{ + }} + {{\nu }^{ - }}){\text{/}}2$ коэффициента Пуассона для обоих вариантов одинаковое и совпадает со значением $\bar {\nu } = 0.25$.

Представленные на рис. 2 и 3 результаты расчетов свидетельствуют о возможности существенного влияния характера распределения по глубине упругих свойств неоднородного покрытия на его НДС.

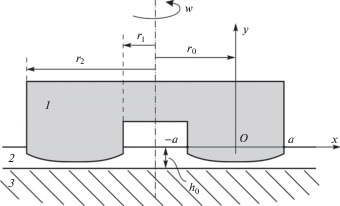
3. Контакт при наличии изнашивания. Пусть неоднородное по глубине покрытие 2, сцепленное с подложкой 3, находится в прямом контакте с вращающейся пятой 1 упорного подшипника, ${{r}_{1}}$ и ${{r}_{2}}$ – внутренний и внешний радиус пяты (рис. 4). Угловая скорость $\omega $ вращения пяты и нагрузка P на нее считаются неизменными во времени. В результате такого взаимодействия покрытие изнашивается и его толщина $h$ уменьшается. Аналогичная задача для однородного покрытия рассматривалась в работе [22].

Рис. 4

Пользуясь осевой симметрией задачи, расположим начало $O$ системы координат посередине кольцевой области контакта (на расстоянии ${{r}_{0}} = ({{r}_{1}} + {{r}_{2}}){\text{/}}2$ от оси вращения пяты), а координатную ось ${\kern 1pt} x$ совместим с неизношенной поверхностью покрытия и сориентируем ее в произвольном радиальном направлении (рис. 4). Область контакта пяты с покрытием будем считать неизменной и представлять отрезком $[ - a,a]$ оси $x$. Форму подошвы пяты в выбранной системе координат зададим уравнением $y = g(x),$ $g(0) = 0$.

Примем элементарный закон изнашивания покрытия в форме $dW{\text{/}}dl = F(p,V,h)$, где $W$ – линейный износ покрытия, $l$ – путь трения, $V$ – скорость скольжения, $p$ – как и прежде, контактное давление. Аргументом $h$ здесь учитывается изменение износостойкости покрытия по глубине. Если принять во внимание соотношение $dl = Vdt$ и функциональные зависимости рассматриваемых величин от координаты $x$ и времени $t$, то выбранный закон изнашивания можно представить в следующем виде:

(3.1)
$\frac{{\partial W(x,t)}}{{\partial t}} = V(x)F\left( {p(x,t),\,\,V(x),h(x,t)} \right),\quad W(x,0) = 0$

Здесь и далее $x \in [ - a,a]$,

(3.2)
$h(x,t) = {{h}_{0}} - W(x,t),\quad V(x) = \omega ({{r}_{0}} + x)$,
${{h}_{0}}$ – толщина покрытия в неизношенном состоянии.

Имеют место условия контакта и равновесия [22]:

(3.3)
$ - w(x,t) + W(x,t) = \delta (t) - g(x)$
(3.4)
$2\pi \int\limits_{ - a}^a {({{r}_{0}} + x)p(x,t)\,dx} = P = \operatorname{const} $
где $\delta $ – внедрение пяты в покрытие.

Для определения граничного перемещения $w$ воспользуемся соотношением (1.11), подстановка которого в условие контакта (3.3) с учетом первого равенства (3.2) приводит к следующему выражению для контактного давления:

(3.5)
$p(x,t) = \frac{1}{{A(h(x,t))}}\left[ {\delta (t) - g(x) - {{h}_{0}} + h(x,t)} \right]$

В частности, учитывая, что $h(x,0) = {{h}_{0}}$, из выражения (3.5) можно получить начальное распределение контактного давления:

(3.6)
${{p}_{0}}(x) \equiv p(x,0) = \frac{1}{{A({{h}_{0}})}}\left[ {{{\delta }_{0}} - g(x)} \right]$
при этом начальное значение ${{\delta }_{0}} = \delta (0)$ внедрения находится подстановкой правой части равенства (3.6) в условие контакта (3.4).

Следуя известной процедуре [22], продифференцируем равенство (3.5) по $t$ с учетом закона изнашивания (3.1) и подставим полученное выражение для производной $\partial p{\text{/}}\partial t$ в продифференцированное по $t$ условие равновесия (3.4). В результате можно получить выражение для скорости внедрения, обеспечивающей выполнение условия равновесия (3.4):

(3.7)
$\frac{{d\delta (t)}}{{dt}} = {{\left[ {\int\limits_{ - a}^a {\frac{{({{r}_{0}} + x)\,dx}}{{A(h(x,t))}}} } \right]}^{{{\kern 1pt} - 1}}}\int\limits_{ - a}^a {\frac{{({{r}_{0}} + x){\kern 1pt} {\kern 1pt} \varphi \left( {x,p(x,t),h(x,t)} \right)\,dx}}{{A(h(x,t))}}} $
где $\varphi (x,p,h) = V(x)F(p,V(x),h)(1 - B(h)p)$.

Дифференциальные уравнения (3.1) и (3.7) совместно с выражением (3.5) допускают несложную численную реализацию с использованием разностной схемы. Это позволяет рассчитать функции $h(x,t)$, $\delta (t)$ и $p(x,t)$, описывающие кинетику изнашивания покрытия.

Расчеты проводились для случая плоской пяты $(g(x) \equiv 0)$ при следующих значениях параметров задачи: ${{h}_{{{\kern 1pt} 0}}} = 2$ мм, ${{r}_{{{\kern 1pt} 1}}} = 2$ мм, ${{r}_{{{\kern 1pt} 2}}} = 22$ мм, $P \simeq 1.2$ кН, $\omega = 100$ с–1. Изменение коэффициента податливости $B$ по глубине покрытия и соответствующая функция $A(z)$ определялись согласно равенствам (2.6) и (2.7) при ${{B}^{ + }} = 0.5\bar {B}$, ${{B}^{ - }} = 1.5\bar {B}$, $\bar {B} = 1.5$ × 10–7 Па–1. Отметим, что для рассматриваемой задачи в равенствах (2.6), (2.7) следует формально положить $h = {{h}_{0}}$.

Функция $F(p,V,h)$ в законе изнашивания (3.1) рассчитывалась по формулам

(3.8)
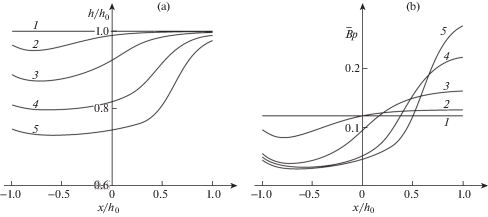
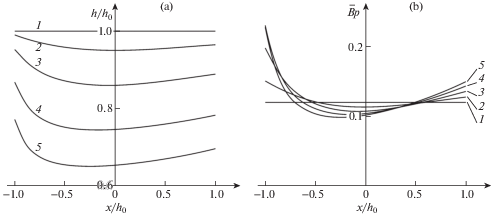
$F(p,V,h) = \alpha {{p}_{w}}{{\left( {\frac{p}{{{{p}_{w}}}}} \right)}^{\gamma }}{{F}_{2}}(V,h),\quad {{F}_{2}}(V,h) = \frac{V}{{{{V}_{m}}(h)}}\exp \left( {\frac{{{{V}_{m}}(h) - V}}{{{{V}_{m}}(h)}}} \right)$
которые определяют немонотонную зависимость скорости изнашивания $dW/d{\kern 1pt} l$ от скорости скольжения $V$. Подобные зависимости характерны для изнашивания некоторых материалов в условиях сухого и граничного трения [23]. Параметры $\alpha ,{{p}_{w}},\gamma $ здесь считались постоянными: $\alpha = {{10}^{{ - 10}}}$ Па–1, ${{p}_{w}} = 1$ ГПа, $\gamma = 2$, тогда как изменение параметра ${{V}_{m}}$ по глубине покрытия описывалось линейной функцией (ср. с (2.6)):

${{V}_{m}}(z) = \frac{1}{{{{h}_{0}}}}(V_{m}^{ + } - V_{m}^{ - })z + V_{m}^{ - };\quad V_{m}^{ - } = {{V}_{m}}(0),\quad V_{m}^{ + } = {{V}_{m}}({{h}_{0}})$

На рис. 5 и 6 показаны распределения толщины $h$ изношенного покрытия (a) и контактного давления $p$ (b) в различные моменты времени $t$, с: 0 (1), $0.70842$ × 104 (2), $0.40755$ × 105(3), $0.12284$ × 106(4), $0.19306$ × 106 (5) – рис. 5 и 0 (1), $0.18596$ × 104 (2), $0.58959$ × 104 (3), $0.12025$ × 105 (4), $0.17885$ × 105 (5) – рис. 6. Рис. 5 отвечает случаю $V_{m}^{ + } = 0.5{\kern 1pt} {\kern 1pt} {{\bar {V}}_{m}}$, $V_{m}^{ - } = 1.5{\kern 1pt} {\kern 1pt} {{\bar {V}}_{m}}$ (– возрастание параметра ${{V}_{m}}$ по глубине покрытия), тогда как рис. 6 – случаю $V_{m}^{ + } = 1.5{\kern 1pt} {\kern 1pt} {{\bar {V}}_{m}}$, $V_{m}^{ - } = 0.5{\kern 1pt} {\kern 1pt} {{\bar {V}}_{m}}$ (– снижение параметра ${{V}_{m}}$ по глубине покрытия), причем для обоих случаев ${{\bar {V}}_{m}} = 0.4$ м/с.

Рис. 5
Рис. 6

Представленные на рис. 5 и 6 результаты расчетов свидетельствуют о возможности существенного влияния характера распределения по глубине износостойких свойств неоднородного покрытия на кинетику его изнашивания и соответствующую эволюцию контактного давления.

4. Выводы. 1. В рамках концепции асимптотически тонкого слоя для неоднородного покрытия предложена упрощенная деформационная модель. Получены выражения для компонент НДС покрытия, обусловленного действием внешних контактных и объемных сил.

2. Построено решение контактной задачи для неоднородного покрытия при наличии межмолекулярного взаимодействия. Показано, что характер распределения по глубине упругих свойств такого покрытия может оказывать существенное влияние на его НДС и, в частности, на распределение интенсивности касательных напряжений по глубине покрытия.

3. Выполнен расчет кинетики изнашивания покрытия в упорном подшипнике скольжения, который свидетельствует о возможности существенного влияния характера распределения износостойких свойств по глубине покрытия на его износ и контактное давление.

Работа выполнена по теме государственного задания (№ госрегистрации АААА-А17-117021310379-5) и при частичной финансовой поддержке Российского научного фонда (19-19-00548).

Список литературы

  1. Holmberg K., Matthewa A. Coatings Tribology: Properties, Mechanisms, Techniques and Applications in Surface Engineering. Amsterdam: Elsevier Science, 2009. 560 p.

  2. Khadem M., Penkov O.V., Yang H.K., Kim D.E. Tribology of multilayer coatings for wear reduction: A review // Friction. 2017. V. 5. № 3. P. 248–262.

  3. Солдатенков И.А. К анализу процесса изнашивания многослойного покрытия // Трение и износ. 1991. Т.12. № 2. С. 204–209.

  4. Tokovyy Y., Ma C.C. Elastic Analysis of Inhomogeneous Solids: History and Development in Brief // Journal of Mechanics. 2019. P. 1–14. https://doi.org/10.1017/jmech.2018.57

  5. Vasiliev A.S., Volkov S.S., Belov A.A., Litvinchuk S.Yu., Aizikovich S.M. Indentation of a hard transversely isotropic functionally graded coating by a conical indenter // International Journal of Engineering Science. 2017. V. 112. P. 63–75.

  6. Торская Е.В. Моделирование накопления контактно-усталостных повреждений в двухслойном полупространстве при неполном сцеплении слоев // Изв. РАН. МТТ. 2011. № 6. С. 122–130.

  7. Александров В.М., Кудрова Ф.В. Точное решение периодической контактной задачи для упругого слоя при учете износа // ПММ. 2002. Т. 66. Вып. 4. С. 647–654.

  8. Манжиров А.В., Казаков К.Е. Контактная задача с износом для основания с поверхностно неоднородным покрытием // ДАН. 2017. Т. 475. № 1. С. 39–44.

  9. Muller V.M., Yushchenko V.S., Derjaguin B.V. On the influence of molecular forces on the deformation of an elastic sphere and its sticking to a rigid plane // J. Coll. Interface Sci. 1980. V. 77. № 1. P. 91–101.

  10. Солдатенков И.А. Применение метода последовательных приближений к расчету упругого контакта при наличии молекулярной адгезии // ПММ. 2012. Т. 76. Вып. 5. С. 734–743.

  11. Солдатенков И.А. Контактная задача при объемном приложении сил межмолекулярного взаимодействия (уточненная постановка) // ПММ. 2013. Т. 77. Вып. 6. С. 877–893.

  12. Александров В.М., Мхитарян С.М. Контактные задачи для тел с тонкими покрытиями и прослойками. М.: Наука, 1983. 487 с.

  13. Ломакин В.А. Теория упругости неоднородных тел. М.: Ленанд, 2014. 376 с.

  14. Галин Л.А. Контактные задачи теории упругости и вязкоупругости. М.: Наука, 1980. 303 с.

  15. Солдатенков И.А. О релаксации касательного контактного напряжения в задачах с трением скольжения // ПММ. 2005. Т. 69. Вып. 1. С. 106–116.

  16. Collins J.A. Failure of Materials in Mechanical Design. Analysis, Prediction, Prevention. New York: The Ohio State University, John Wiley & Sons, 1981. Коллинз Дж. Повреждение материалов в конструкциях. Анализ, предсказание, предотвращение. М.: Мир, 1984. 624 с.

  17. Greenwood J.A. Adhesion of small spheres // Phil. Mag. 2009. V. 89. № 11. P. 945–965.

  18. Israelachvili J.N. Intermolecular and Surface Forces. 3-rd ed. London: Academic, 2011. 674 p.

  19. Kaplan I.G. Intermolecular interactions: physical picture, computational methods and model potentials. Chichester: Wiley, 2006. 367 p.

  20. Солдатенков И.А. Контактная задача при объемном приложении сил межмолекулярного взаимодействия: функция влияния для неоднородного упругого полупространства // ПММ. 2018. Т. 82. Вып. 3. С. 358–371.

  21. Sauer R.A., Li S. A contact mechanics model for quasi-continua // Int. J. Numer. Meth. Engng. 2007. V. 71. № 8. P. 931–962.

  22. Солдатенков И.А. Об особенностях эволюции контактного давления при изнашивании покрытия в упорном подшипнике скольжения // Трение и износ. 2010. Т. 31. № 2. С. 144–149.

  23. Modern Tribology Handbook. Vol. 1: Principles of Tribology / Eds by B. Bhushan. Boca Raton: CRC Press, 2001. 1690 p.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал