Известия РАН. Механика твердого тела, 2020, № 3, стр. 146-161

1. Введение. Расчетная схема для определения напряженно-деформированного состояния (НДС) корпуса летательного аппарата (ЛА) принимается в виде цилиндрической оболочки, на которую действует сосредоточенная нагрузка через шпангоут. Шпангоут моделируется кольцевой линией, наделенной жесткостными характеристиками шпангоута, которая располагается на краю оболочки или в сечении на удалении от него.

Исследуется НДС оболочки и шпангоута в зависимости от их параметров и нагрузки в виде сил и моментов.

Исследование выполняется аналитическим методом сопряжения интервалов в матричной форме, удобной для реализации на ЭВМ. Метод обеспечивает устойчивость счета на ЭВМ.

Эффективность метода в том, что аналитическое решение не содержит постоянных интегрирования и параметрический анализ ограничивается решением системы алгебраических уравнений при смене параметров расчетной схемы. Решение системы обыкновенных дифференциальных уравнений (ОДУ), полученной методом Фурье разделения переменных в дифференциальных уравнениях с частными производными, выполняется при параметрическом счете один раз аналитически, как начальной, а не краевой задачи.

Внимание при исследовании уделено влиянию жесткостных характеристик шпангоута на его НДС и НДС оболочки.

2. Математическая модель механики деформирования цилиндрической оболочки. Исследования выполнены на основе математической модели В.З. Власова [1] механики деформирования цилиндрической оболочки.

u_n, ${{v}_{n}}$, w_n – функциональные коэффициенты тригонометрических рядов разложений u, $v$ и w; ${{c}^{2}} = {{h}^{2}}{\text{/}}(12{{R}^{2}})$ – малый параметр; R и h – радиус и толщина цилиндрической оболочки; ${\xi } = x{\text{/}}R~$ – безразмерная координата вдоль ее оси.

Систему линейных обыкновенных дифференциальных уравнений (2.1) приводим к матричной форме. Для этого каждое из уравнений разрешаем относительно старшей производной от u_n, ${{v}_{n}}$ и w_n. Добавляем к ним тождества $u_{n}^{'} = u_{n}^{'}$, $v_{n}^{'} = v_{n}^{'}$, $w_{n}^{'} = w_{n}^{'}$, $w_{n}^{{''}} = w_{n}^{{''}}$ и $w_{n}^{{'''}} = w_{n}^{{'''}}$. Формируем столбец y = |u_n, $u_{n}^{'}$, ${{{v}}_{n}}$, ${v}_{n}^{'}$, w_n, $w_{n}^{'}$, $w_{n}^{{''}}$, $w_{n}^{{'''}}$|^T и переписываем систему уравнений (2.1) в матричной форме

Физические соотношения В.З. Власова [1] с учетом представления погонных усилий T₁, S, Q₁ и M₁ в виде рядов Фурье принимают вид:

$B = Eh{\text{/}}(1 - {{{\nu }}^{2}}),D = E{{h}^{3}}{\text{/}}(12(1 - {{{\nu }}^{2}})){\text{\;}}$, E – модуль упругости, ν – коэффициент Пуассона, ${\xi } = x{\text{/}}R$ – безразмерная координата вдоль оси оболочки, R – радиус средней поверхности оболочки, $Q_{1}^{*}$, S* – приведенные по Кирхгофу перерезывающие и сдвигающие погонные усилия в оболочке.

Добавляя тождества u_n = u_n, ${{{v}}_{n}} = {{{v}}_{n}}$, w_n = w_n, $w_{n}^{'} = w_{n}^{'}$, физические соотношения представляем в матричной форме

Ненулевые элементы матрицы G имеют вид:

При решении краевых задач для каждого номера n гармоники определяются функциональные коэффициенты ${{u}_{n}},{{{v}}_{n}},{{w}_{n}},w_{n}^{'},{{T}_{{1n}}},S_{n}^{*},Q_{{1n}}^{*},{{M}_{{1n}}}$ тригонометрических рядов искомых величин, характеризующих состояние сечения оболочки при ξ = const. Параметры T_2n и M_2n для сечения φ = const определяются из соотношений В.З. Власова [1].

Тригонометрические ряды метода Фурье разделения переменных начинаются при n = 1. Нулевой член n = 0 опущен, так как он соответствует осесимметричному нагружению оболочки. При этом математическая модель – обыкновенные дифференциальные уравнения шестого порядка. При матричной записи уравнений ненулевые элементы матрицы А = ${\text{||}}aij{\text{||}}_{1}^{6}$ определяются из матрицы А = ${\text{||}}aij{\text{||}}_{1}^{8}$, если положить n = 0, а из столбца у исключить ${{{v}}_{n}} = 0$ и ${v}_{n}^{'} = 0$. Тогда

Аналогично определяются ненулевые элементы матрицы G = ${\text{||}}{{g}_{{ij}}}{\text{||}}_{1}^{6}.$

3. Математическая модель механики деформирования шпангоута. Уравнения равновесия элемента шпангоута имеют вид:

Q_y, Q_z, Q_x – соответственно усилия растяжения кольцевой линии и перерезывающие усилия, направленные по радиусу и перпендикулярно плоскости кольцевой линии; M_y, M_z, M_x – моменты в сечении шпангоута, векторы которых направлены соответственно по касательной y к кольцевой линии, по нормали z и бинормали x; q_y, q_z, q_x – интенсивности внешних усилий, направленных соответственно по касательной y, нормали z и бинормали x к упругой кольцевой линии шпангоута; m_y, m_z, m_x – интенсивности внешних моментов, изгибающих упругую кольцевую линию шпангоута в ее плоскости, из ее плоскости и закручивающий ее момент.

Исключая перерезывающие силы Q_x, Q_z из уравнений равновесия (3.1), получаем

R – радиус упругой кольцевой линии.

Физические соотношения имеют вид:

$EF,E{{J}_{x}},E{{J}_{z}},G{{J}_{{tor}}}$ – жесткости шпангоута на растяжение (сжатие), на изгиб в плоскости кольцевой линии и из ее плоскости и на закручивание соответственно; ${\varepsilon },~{{{\chi }}_{1}},~{{{\chi }}_{2}},~{\Theta }$ – линейная, изгибные и угловая деформации.

Геометрические соотношения имеют вид

Исключая деформации в физических соотношениях (3.3) с помощью геометрических соотношений (3.4), подставляя полученные выражения для усилия растяжения (сжатия) и моментов в уравнения равновесия, получаем систему линейных обыкновенных дифференциальных уравнений в перемещениях (математическую модель механики деформирования шпангоута).

$u,v,w$ – составляющие перемещения точек упругой кольцевой линии; β – угол закручивания сечения шпангоута; ${{J}_{x}},~{{J}_{y}},{{J}_{{tor}}},~F$ – моменты инерции и площадь сечения шпангоута, E – модуль упругости материала шпангоута.

Как для оболочек, которые подкрепляют шпангоуты, решение системы уравнений (3.5) ищется в форме тригонометрических рядов

При этом внешняя нагрузка, например в виде сосредоточенных сил и моментов, разлагается в ряды

В итоге система дифференциальных уравнений (3.5) приводится к системе алгебраических уравнений

Разложения (3.6) и (3.7) справедливы, если внешняя нагрузка на шпангоут симметрична относительно начала координаты φ.

В результате решения системы алгебраических уравнений для каждого номера n гармоники определяют параметры u_n, ${{v}_{n}}$, w_n, β_n тригонометрических рядов (3.6) искомых величин u, $v$, w, β.

Усилия и моменты в шпангоуте определяются с помощью рядов

Значения коэффициентов Q_yn, M_xn, M_yn, M_zn этих рядов определяются выражениями

которые получены с использованием физических, геометрических соотношений и представления перемещений в виде рядов.

При математическом моделировании подкрепления оболочки шпангоутом, он представляется упругой кольцевой линией, наделенной всеми жесткостными характеристиками шпангоута. Предполагается, что упругая кольцевая линия совпадает со средней поверхностью оболочки.

Взаимодействие оболочки и шпангоута моделируется действием сил и моментов, которые возникают в деформированной оболочке, на упругую кольцевую линию. Эти силы и моменты имеют смысл внешней нагрузки.

Систему алгебраических уравнений (3.8) представляем в матричной форме

В сокращенной записи

f – столбец параметров сил и моментов, действующих на упругую кольцевую линию со стороны сопряженных с ней оболочек; p – столбец параметров перемещений и угла закручивания; G – матрица жесткости упругой кольцевой линии, элементами которой являются параметры

Преодолевая проблему устойчивости счета, строится соответствующий алгоритм аналитического решения краевой задачи.

4. Алгоритм устойчивого счета. Основной интервал [x₀, x_n], равный длине оболочки вдоль образующей, промежуточными точками x₁, x₂, …, x_{n – 1} делится на n интервалов.

Решение дифференциального уравнения (2.2) на произвольном интервале определяется формулой [2] и записывается в виде:

${\mathbf{y}} = {\text{||}}{{u}_{n}},~u_{n}^{'},~{{{v}}_{n}},~{v}_{n}^{'},~{{w}_{n}},~w_{n}^{'},~w_{n}^{{''}}~,w_{n}^{{'''}}{\text{|}}{{{\text{|}}}^{T}}$, а индексы “s”, “e” обозначают соответственно начало и конец произвольного интервала

Алгоритм решения краевой задачи для основного интервала строится сопряжением интервалов, на которые он делится [3]. Для сопряжения необходимо определить столбец ${\mathbf{t}} = {\text{||}}{{u}_{n}},~{{{v}}_{n}},~{{w}_{n}},~w_{n}^{'},~{{T}_{{1n}}},~S_{n}^{*},Q_{{1n}}^{*},~{{M}_{{1n}}}{\text{|}}{{{\text{|}}}^{T}}$, который характеризует состояние сечения оболочки. Для этого используем физические соотношения (2.4) в матричной форме, которые справедливы при любых значениях аргумента x на основном интервале и, следовательно, на произвольно выбранном.

Исключая столбец y из соотношений (2.2) и (2.4), находим связь между столбцами t, характеризующими состояния сечений начала и конца произвольно выбранного интервала. Иначе – связь параметров сечений оболочки

Если разрешающая система обыкновенных дифференциальных уравнений записана в канонической матричной форме

ее решение определяет связь между столбцами t, характеризующими состояния сечений начала и конца произвольно выбранного интервала

Для того, чтобы выполнить сопряжение интервалов $\left[ {{{x}_{{i - 1}}},~~{{x}_{i}}} \right]$, столбец t, характеризующий состояния сечений оболочки, делим на геометрический ${\mathbf{p}} = {\text{||}}{{u}_{n}},{{{v}}_{n}},{{w}_{n}},w_{n}^{'}{\text{|}}{{{\text{|}}}^{T}}$ и силовой ${\mathbf{q}} = {\text{||}}{{T}_{{1n}}},~S_{n}^{{\text{*}}},Q_{{1n}}^{{\text{*}}},{{M}_{{1n}}}{\text{|}}{{{\text{|}}}^{T}}$.

Матрицы решений (4.3), (4.5) однородных дифференциальных уравнений делим на блоки

В результате решения (4.3), (4.5) могут быть записаны в виде системы матричных уравнений

Полученная система матричных уравнений преобразуется к виду:

Здесь приписан индекс $i$ на том основании, что решения (4.3), (4.5) дифференциальных уравнений справедливы для произвольно выбранного интервала $i$, на которые делится основной.

B_ji (j = 1, 2, 3, 4; i = 1, 2, …, n) – по физическому смыслу характеризуют жесткость i‑го (i = 1, 2, …, n) интервала.

Матричные уравнения (4.6) позволяют выполнить сопряжение интервалов, на которые делился основной интервал. По физическому смыслу при этом длина оболочки набирается из длин коротких, на которые она предварительно делилась.

Геометрические условия сопряжения имеют вид:

Силовые условия сопряжения имеют вид:

Используя силовые условия сопряжения интервалов и принятые обозначения столбцов ${{{\mathbf{p}}}_{i}}~~\left( {i = 0,1, \ldots ,n} \right)$ геометрических параметров, получаем n + 1 матричных алгебраических уравнений, каждое из которых записано для сечений оболочки, включая крайние.

Здесь ${{{\mathbf{r}}}_{i}}~~\left( {i = 0,1, \ldots ,n} \right)$ – столбцы силовых параметров в сечениях оболочки, включая крайние. Если в этих сечениях оболочка не нагружена силами сосредоточенными или распределенными по линии окружной координаты, то ${{{\mathbf{r}}}_{i}} = 0$. Если же в сечении на оболочку действует сила или момент, то они отождествляется со скачком в соответствующем силовом факторе в данном сечении и, таким образом, математически моделируют нагружение оболочки сосредоточенное или локальное по линии.

Решение краевой задачи сводится к решению системы алгебраических уравнений (4.7).

Обратим внимание на то, что в предложенном методе система алгебраических уравнений (4.7) построена без использования краевых условий и не для определения постоянных. Искомыми в системе матричных [4] алгебраических уравнений являются столбцы p_i геометрических параметров краевой задачи.

Число матричных уравнений (4.7) равняется числу сечений сопряжения интервалов и краевых, так как они для этих сечений и записаны.

5. Математическое моделирование подкрепления оболочки шпангоутом. Допустим, что оболочка в i-м сечении подкреплена шпангоутом, механика деформирования которого математически моделируется матричным уравнением (3.10). Тогда оболочка в этом сечении помимо внешней нагрузки r_i воспринимает еще и реакцию f упругой кольцевой линии. Следовательно, матричное уравнение для i-го сечения системы уравнений (4.7) можно записать в виде:

Исключая столбец f в уравнении с помощью (3.10) и учитывая, что упругая кольцевая линия шпангоута сопрягается со средней поверхностью оболочки (p_i = p), получаем

Полученный результат физически понятен. Матрицы B_ji характеризуют жесткость интервала оболочки. Следовательно, учет матрицы G – жесткости шпангоута увеличивает жесткость конструкции.

Таким образом, подкрепление оболочки в i-м сечении шпангоутом математически моделируется (5.1) учетом матрицы G его жесткости в соответствующем матричном уравнении системы матричных алгебраических уравнений (4.7).

6. Моделирование нагрузки. Нагрузка может передаваться на оболочку по относительно малым площадкам. С целью упрощения решения задач нагрузку математически моделируют, представляя ее сосредоточенной или распределенной по линии.

Допустим, что действие сосредоточенных сил P_x, P_z и момента M_y, а также начало окружной координаты совпадают. Тогда силы и момент разлагаются в тригонометрические ряды по четным функциям

k – число сил или моментов, приложенных к оболочке.

Для силы ${{P}_{i}}~~\left( {i = x,~z} \right)$, приложенной к оболочке в начале координаты φ, разложение имеет вид:

R – радиус средней поверхности оболочки.

Если сила P_i  приложена в точке φ = φ₀, то разложение имеет вид:

Допустим, что оболочка нагружена двумя самоуравновешенными направленными, например, по диаметру силами P_z в точках φ = 0 и ${\varphi } = {\pi }$. Тогда суммарная самоуравновешенная нагрузка на оболочку принимает вид:

При действии на оболочку сосредоточенных моментов M_x и M_z их следует заменить статически эквивалентными

7. Эффективность алгоритма исследования. Очевидно, что число неизвестных столбцов p_i соответствует числу матричных алгебраических уравнений системы (4.7). Граничные условия учитываются при решении этой полной системы алгебраических уравнений.

Если оболочка имеет свободные края и нагружена самоуравновешенными воздействиями, то систему алгебраических уравнений (4.7) решают без изменений и определяют столбцы ${{{\mathbf{p}}}_{i}}~~\left( {i = 1,2, \ldots ,n} \right)$ параметров перемещений точек средней поверхности оболочки во всех сечениях, включая краевые.

Если один край оболочки, например левый, защемлен, а другой, правый, свободен, то p₀ = 0. При этом условии первое матричное уравнение системы (4.7), как лишнее, опускаем.

Если защемлены оба края оболочки, то p₀ = 0, p_n = 0, тогда первое и последнее матричные уравнения системы (4.7) опускаем как лишние.

Аналогично реализуется алгоритм при решении краевых задач.

Вариантные расчеты, связанные с выбором числа и мест установки шпангоутов для подкрепления оболочки, ограничиваются решением системы алгебраических уравнений (4.7). При этом в уравнениях для сечений, где устанавливают шпангоуты, учитываются матрицы их жесткости.

Вариантные расчеты, связанные с нагружением конструкции, также ограничиваются решениями системы алгебраических уравнений. При этом, например, сосредоточенную нагрузку или нагрузку по линии окружной координаты учитывают в столбцах ${{{\mathbf{r}}}_{i}}~~\left( {i = 1,2, \ldots ,n} \right)$ для соответствующих сечений оболочки. Если, например, оболочка нагружена в i-м сечении радиальной силой P_z, то, учитывая (6.1), столбец r_i достаточно записать в виде ${{{\mathbf{r}}}_{i}} = {\text{||}}0,~0,~1,~0{\text{|}}{{{\text{|}}}^{{\text{T}}}}$. Если заносится единица, то результат масштабируется величиной ${\pi }R{\text{/}}{{P}_{z}}$.

Таким образом, сосредоточенное нагружение оболочки или оболочки через шпангоут, а также нагружение гладкой или подкрепленной оболочки шпангоутом по линиям окружной координаты реализуется в вариантных вычислениях учетом параметров нагрузки в столбцах r_i.

Во всех случаях после решения системы алгебраических уравнений (4.7) определяются столбцы ${{{\mathbf{p}}}_{i}}~~\left( {i = 1,2, \ldots ,n} \right)$ параметров перемещений, для которых матричные уравнения (4.6) позволяют вычислить столбцы q_i параметров внутренних силовых факторов оболочки.

Таким образом, строится алгоритм эффективного аналитического исследования жесткости и прочности конструкции.

8. Вычислительный алгоритм. 1. Линейные обыкновенные дифференциальные уравнения задачи записывают в виде системы уравнений первого порядка и представляют в матричной форме (2.2).

2. Вычисляют решение матричного дифференциального уравнения (2.2) по формуле (4.1).

3. Физические соотношения задачи представляют в матричной форме (2.4).

4. Вычисляют произведение матриц ${\mathbf{G}}({{x}_{e}}){\mathbf{K}}_{{{{x}_{s}}}}^{{{{x}_{e}}}}({\mathbf{A}}(x)){{{\mathbf{G}}}^{{ - 1}}}({{x}_{s}})$ или используют матрицу B(x), (4.4).

5. Матрицы решений (4.3) или (4.5) делят на блоки A₁₁, A₁₂, A₂₁, A₂₂.

6. Вычисляют матрицы B_ji, $\left( {i = 1,2, \ldots ,n;j = 1,2,3,4} \right)$, (4.6).

7. Формируют систему матричных алгебраических уравнений (4.7).

8. Вариантные расчеты: повторное решение системы алгебраических уравнений (4.7) при изменении краевых условий, внешнего воздействия на оболочку (конструкцию), и подкрепления ее шпангоутом (шпангоутами) с различными жесткостными характеристиками.

Система матричных алгебраических уравнений (4.7) формируется с образованием квазидиагональной матрицы коэффициентов B_ji, а в ЭВМ запоминается в плотно упакованном виде с целью экономии оперативной памяти и времени решения задачи.

9. Вычислительные исследования. Расчетная схема – консольно закрепленная цилиндрическая оболочка, подкрепленная шпангоутом на свободном торце. К шпангоуту приложена радиальная сосредоточенная сила P_z. Исследования выполнены для оболочки с параметрами $l{\text{/}}R = 3$ и $R{\text{/}}h = 50$ и шпангоута с квадратным поперечным сечением $0.5h \times 0.5h$; $5h \times 5h$; $20h \times 20h$; $30h \times 30h$; $50h \times 50h$ при следующих условиях:

a) шпангоут наделен всеми жесткостными характеристиками;

b) отсутствует жесткость шпангоута на изгиб из его плоскости, $E{{J}_{z}} = 0$;

c) отсутствует жесткость при закручивании шпангоута, $G{{J}_{y}} = 0$;

d) шпангоут обладает изгибной жесткостью только в своей плоскости, $G{{J}_{y}} = 0$, $E{{J}_{z}}$ = 0.

Моменты инерции J_x, J_y, J_z для шпангоута определяли по формулам [5]

Изменения искомых величин в безразмерном виде

вдоль образующей оболочки, проходящей через точку приложения силы P_z, в малой ее окрестности $0 \leqslant \xi \leqslant l{\text{/}}\left( {5R} \right)$ или $0 \leqslant x{\text{/}}l \leqslant 0.2$, и шпангоута, сечение которого $30h \times 30h$, показаны на рис. 1–3 утолщенными линиями. Для наглядного сопоставления с результатами для неподкрепленной оболочки величина момента $\overline {{{M}_{1}}} $ показана умноженная на коэффициент 10, а величина момента $\overline {{{M}_{2}}} $ – на коэффициент 4.

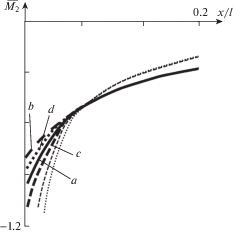
Определено, что значения искомых величин для оболочки, подкрепленной шпангоутом с сечением $0.5h \times 0.5h$, совпадают (что и следовало ожидать) с соответствующими величинами для неподкрепленной оболочки. Они приведены на рис. 1–3 тонкими штриховой и точечной линиями.

Из графиков рис. 1–3 следует, что необоснованные часто используемые допущения при построении математических моделей механики деформирования шпангоутов для расчета подкрепленных оболочек могут приводить к результатам, даже качественно отличающимися от тех, которые находят без каких-либо допущений.

10. Усилия с рулей на корпус через шпангоут. Задача часто возникает при движении объекта в водной или воздушной среде, а управление движением осуществляется рулями, закрепленными на корпусе объекта. Часто объект имеет корпус в виде цилиндрической оболочки, а усилия с рулей передаются на корпус через шпангоут. Расчетная схема – цилиндрическая оболочка, заделанная по торцам, силы P_x, P_z и момент M_y действуют на оболочку через шпангоут, который установлен на расстоянии x/R = 0.63 от левого края.

Параметры объекта:

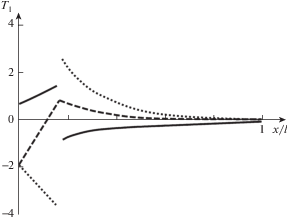
Изменения по ξ искомых величин, характеризующих напряженно-деформированное состояние конструкции, в безразмерном виде приведены для φ = 0 на рис. 4–8.

Начало координат ξ для графиков совпадает с точкой воздействия на шпангоут.

Нагрузка P_x, P_z, M_y на шпангоут может быть в различных сочетаниях по величине их значений. Результаты приводятся, когда действует одна из них: сплошные линии соответствуют нагрузке P_x, штриховые – P_z, точечные – M_y. Принцип независимости действия сил позволяет определять результаты при совместном действии. Для сопоставления результатов некоторые величины на графиках представлены умноженными на коэффициенты:

• Перемещение $\bar {w}$ для нагрузки P_z показано умноженным на коэффициент 0.5.

• Момент $\overline {{{M}_{1}}} $ для нагрузки P_x показан умноженным на коэффициент 50, а для нагрузки M_y – на коэффициент 0.5.

• Момент $\overline {{{M}_{2}}} $ для нагрузки P_x показан умноженным на коэффициент 50, а для нагрузки P_z – на коэффициент 2.5.

• Усилие $\overline {{{T}_{2}}} $ для нагрузки P_x показано умноженным на коэффициент 10, а для нагрузки P_z – на коэффициент 5.

Достоверность полученных результатов и погрешности счета легко проверяются использованием теоремы о взаимности работ. Рассматривая рассчитанные значения перемещений $u,{v},w,w'$ шпангоута в точке приложения сил P_x, P_z и момента $\overline {{{M}_{y}}} $, приходим к выводу, что теорема о взаимности перемещений, при единичных воздействиях, удовлетворяется совпадением результатов до трех значащих цифр включительно

Таким образом, при выполнении НИОКР исследование напряженно-деформированного состояния конструкции методом сопряжения интервалов с контролируемой погрешностью не вызывает затруднений.

Краткий анализ полученных результатов показывает, что

a) при действии сил P_z, направленных вдоль образующей оболочки, наибольшие напряжения, вычисленные по тангенциальным усилиям T_i $i = 1,2$ в оболочке, на порядок превышают напряжения от изгибающих моментов M_i $i = 1,2$. В шпангоуте наибольшим оказался момент ${{M}_{z}}$, возникающий при его изгибе из своей плоскости;

b) при действии радиальных сил P_z напряжения в оболочке от изгибающих моментов и тангенциальных усилий оказались почти равными. В шпангоуте наибольшим оказался момент M_x, возникающий при его изгибе в своей плоскости;

c) при действии момента $\overline {{{M}_{y}}} $ напряжения в оболочке от изгибающих моментов более чем в 6 раз превышают напряжения от тангенциальных усилий. В шпангоуте наибольшими оказались закручивающий его момент M_y и момент M_z, возникающий при его изгибе из своей плоскости.

Заключение. Предлагается аналитический метод с эффективным алгоритмом реализации на ЭВМ исследования НДС корпуса ЛА при заданных рулевых нагрузках через шпангоут, часто востребованный при выполнении НИОКР для определения прочности конструкции.

Метод реализован при многопараметрическом вычислительном анализе принятой расчетной схемы, подтверждая свою эффективность.

Работа выполнена при поддержке РФФИ, грант № 18-08-00840/18.