Известия РАН. Механика твердого тела, 2020, № 3, стр. 5-11
ОПТИМАЛЬНОЕ ПРОЕКТИРОВАНИЕ КОМПОЗИТНОЙ СЕТЧАТОЙ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ, НАГРУЖЕННОЙ ВНЕШНИМ ДАВЛЕНИЕМ
В. В. Васильев *
Институт проблем механики РАН им. Ишлинского
Москва, Россия
* E-mail: vvvas@dol.ru
Поступила в редакцию 16.12.2019
После доработки 15.02.2020
Принята к публикации 22.02.2020
Аннотация
Рассматриваются сетчатые цилиндрические оболочки, изготовленные из современных композитных материалов методом автоматической непрерывной намотки, обладающие высокой степенью весового совершенства и получившие широкое применение в аэрокосмической технике. Обсуждается проблема использования таких конструкций в качестве корпусов глубоководных аппаратов, работающих не внешнее давление. Рассматривается задача оптимального проектирования сетчатых цилиндрических оболочек на основе критерия минимума массы при ограничениях по прочности и устойчивости. Методом минимизации коэффициентов безопасности по возможным формам разрушения получено аналитическое решение, определяющее оптимальные проектные параметры композитной сетчатой оболочки.
1. Введение. Сетчатые композитные конструкции. Вариант сетчатой композитной конструкции, рассматриваемый в настоящей работе, имеет форму трехслойной цилиндрической оболочки, состоящей из наружного и внутреннего композитных слоев, армированных в кольцевом направлении, и среднего слоя, образованного системой спиральных ребер, изготавливаемых методом намотки однонаправленного композитного материала на основе углеродных волокон. Процесс намотки ребер показан на рис. 1. Пространство между ребрами заполняется пенопластом или полимером, наполненным стеклянными микросферами. Обшивки изготавливаются методом кольцевой намотки.
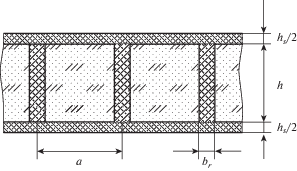
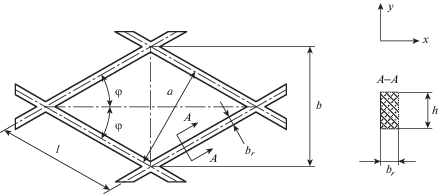
Сечение стенки плоскостью ортогональной осям ребер показано на рис. 2, а сетчатая структура – на рис. 3. Обзор исследований по композитным сетчатым конструкциям, применяемым в аэрокосмической технике, представлен в работе [1]. В настоящей работе рассматривается возможность применения таких конструкций в качестве корпусов глубоководных аппаратов [2, 3].
2. Постановка задачи оптимального проектирования. Рассмотрим цилиндрическую оболочку с радиусом $R$ и длиной $l,$ нагруженную всесторонним внешним давлением q. Осевая и кольцевая деформации безмоментной оболочки связаны с давлением следующим образом:
(2.1)
${{B}_{{11}}}{{e}_{x}} + {{B}_{{12}}}{{e}_{y}} = - \frac{1}{2}qR,\quad {{B}_{{12}}}{{e}_{x}} + {{B}_{{22}}}{{e}_{y}} = - qR$Коэффициенты жесткости стенки имеют вид (индексы “$r$” и “$s$” относятся к ребрам и обшивке)
(2.2)
${{B}_{{11}}} = 2{{E}_{r}}h{{\bar {b}}_{r}}{{c}^{4}},\quad {{B}_{{12}}} = 2{{E}_{r}}h{{\bar {b}}_{r}}{{c}^{2}}{{s}^{2}},\quad {{B}_{{22}}} = h(2{{E}_{r}}{{\bar {b}}_{r}}{{s}^{4}} + {{E}_{s}}{{\bar {h}}_{s}})$(2.3)
${{\bar {b}}_{r}} = \frac{{{{b}_{r}}}}{a},\quad {{\bar {h}}_{s}} = \frac{{{{h}_{s}}}}{h},\quad s = \sin {\varphi ,}\quad c = \cos {\varphi }$Найдем деформации из уравнений (2.1)
(2.4)
${{{\sigma }}_{r}} = {{E}_{r}}({{e}_{x}}{{c}^{2}} + {{e}_{y}}{{s}^{2}}) = - \frac{{qR}}{{4h{{{\bar {b}}}_{r}}{{c}^{2}}}},\quad {{{\sigma }}_{s}} = {{E}_{s}}{{e}_{y}} = - \frac{{qR(2{{c}^{2}} - {{s}^{2}})}}{{2h{{{\bar {h}}}_{s}}{{c}^{2}}}}$В обшивке, армированной в кольцевом направлении, действуют только кольцевые напряжения. При угле ребер, определяемом равенством ${{s}^{2}}{\text{/}}{{c}^{2}} = 2$ $({{{\varphi }}_{0}} = 54.735^\circ )$ напряжение в обшивке отсутствует и давление воспринимается только спиральными ребрами [4].
Сформулируем ограничения, накладываемые на проектные параметры оболочки. Ограничения по прочности ребер и обшивки записываются в виде
(2.5)
$\left| {{{{\sigma }}_{r}}} \right| \leqslant {{{\bar {\sigma }}}_{r}},\quad \left| {{{{\sigma }}_{s}}} \right| \leqslant {{{\bar {\sigma }}}_{s}}$(2.6)
${{q}_{{cr}}} = \frac{{4{\pi }}}{{Rl}}\sqrt[4]{{\frac{{{{B}_{{11}}}D_{y}^{3}}}{{27{{R}^{2}}}}}}$Здесь
(2.7)
${{D}_{y}} = \frac{{{{h}^{3}}}}{2}\left( {\frac{1}{3}{{E}_{r}}{{{\bar {b}}}_{r}}{{s}^{4}} + \frac{1}{2}{{E}_{s}}{{{\bar {h}}}_{s}}} \right)$(2.8)
${{q}_{{cr}}} = \frac{{4{\pi }c}}{{Rl}}\sqrt[4]{{\frac{{{{h}^{{10}}}{{E}_{r}}{{{\bar {b}}}_{r}}}}{{108{{R}^{2}}}}{{{\left( {\frac{1}{3}{{E}_{r}}{{{\bar {b}}}_{r}}{{s}^{4}} + \frac{1}{2}{{E}_{s}}{{{\bar {h}}}_{s}}} \right)}}^{3}}}}$Сжатые спиральные ребра могут потерять устойчивость между узлами их пересечения (рис. 3). Пренебрегая возможным влиянием обшивок и легкого заполнителя, расположенного в пространстве между ребрами, запишем критическое напряжение, соответствующее местной форме потери устойчивости, с помощью формулы Эйлера, то есть
где $l = a{\text{/}}(2cs)$ – расстояние между узлами пересечения ребер (рис. 3). Заметим, что этот результат справедлив если ребра теряют устойчивость в касательной плоскости, то есть если $h \geqslant {{b}_{r}}.$ Используя равенство (2.4) для ${{{\sigma }}_{r}}$, получим следующее выражение для критического давления, соответствующего местной форме потери устойчивости спиральных ребер:Ограничения по общей и местной формам потери устойчивости принимают вид
Масса оболочки, состоящей из двух систем спиральных ребер и двух обшивок, определяется равенством [1]
где ${\rho }$ – плотность материала и ${\bar {\rho }} = {{{\rho }}_{s}}{\text{/}}{{{\rho }}_{r}}.$Таким образом, необходимо определить проектные параметры оболочки, удовлетворяющие ограничениям (2.5) и (2.10) и обеспечивающие минимальное значение массы (2.11). Проектными параметрами являются – толщины сетчатого слоя и обшивки $h$ и ${{h}_{s}}$ (или $h$ и ${{\bar {h}}_{s}} = {{h}_{s}}{\text{/}}h$), угол ориентации спиральных ребер ${\varphi }$ и отношение ширины сечения спиральных ребер к расстоянию между ребрами ${{\bar {b}}_{r}} = {{b}_{r}}{\text{/}}a$.
3. Оптимизация сетчатой цилиндрической оболочки, нагруженной внешним давлением. Для оптимизации конструкции используем метод минимизации массы по коэффициентам безопасности, соответствующим возможным формам разрушения оболочки [6]. Существо метода заключается в следующем. Для всех возможных форм разрушения оболочки вводятся коэффициенты безопасности – ${{n}_{r}} = {{{\bar {\sigma }}}_{r}}{\text{/}}{{{\sigma }}_{r}}$, ${{n}_{s}} = {{{\bar {\sigma }}}_{s}}{\text{/}}{{{\sigma }}_{s}}$ по прочности ребер и обшивки и ${{n}_{0}} = {{q}_{{cr}}}{\text{/}}q$, ${{n}_{m}} = q_{{cr}}^{m}{\text{/}}q$ по общей и местной формам потери устойчивости. С помощью этих коэффициентов ограничения (2.5) и (2.10), имеющие форму неравенств, преобразуются в равенства, которые используются для выражения проектных параметров через коэффициенты безопасности. В результате масса оболочки (2.11) оказывается функцией этих коэффициентов и минимизируется по ним. Минимизация по коэффициентам безопасности является более эффективной чем минимизация по проектным параметрам, так как диапазон изменения этих параметров неизвестен, а коэффициенты безопасности удовлетворяют неравенству $n \geqslant 1.$ Если масса оказывается монотонно возрастающей функцией коэффициента $n,$ то n = 1 и соответствующее ограничение является активным. Таким образом, оказывается возможным снизить число варьируемых параметров и получить аналитическое решение задачи оптимизации.
Для рассматриваемой оболочки ограничения (2.5) и (2.10) преобразуются в результате введения коэффициентов безопасности к следующим равенствам:
(3.2)
$\frac{{qR{{n}_{s}}}}{{2h{{{\bar {h}}}_{s}}{{{{\bar {\sigma }}}}_{s}}{{c}^{2}}}}(2{{c}^{2}} - {{s}^{2}}) = 1$(3.3)
$\frac{{4{\pi }{{n}_{0}}c}}{{qRl}}\sqrt[4]{{\frac{{{{E}_{r}}{{h}^{{10}}}{{{\bar {b}}}_{r}}}}{{108{{R}^{2}}}}{{{\left( {\frac{1}{3}{{E}_{r}}{{{\bar {b}}}_{r}}{{s}^{4}} + \frac{1}{2}{{E}_{s}}{{{\bar {h}}}_{s}}} \right)}}^{3}}}} = 1$Из ограничений по прочности (3.1) и (3.2) имеем
(3.5)
$h{{\bar {b}}_{r}} = \frac{{qR{{n}_{r}}}}{{4{{{{\bar {\sigma }}}}_{r}}{{c}^{2}}}},\quad h{{\bar {h}}_{s}} = \frac{{qR{{n}_{s}}}}{{2{{{{\bar {\sigma }}}}_{s}}{{c}^{2}}}}(2{{c}^{2}} - {{s}^{2}})$Подставляя эти равенства в выражение (2.11) для массы, получим
(3.6)
$M = {\pi }q{{R}^{2}}l{{{\rho }}_{r}}\left[ {\frac{{{{n}_{r}}}}{{2{{{{\bar {\sigma }}}}_{r}}{{c}^{2}}}} + \frac{{2{\bar {\rho }}{{n}_{s}}}}{{{{{{\bar {\sigma }}}}_{s}}{{c}^{2}}}}(2{{c}^{2}} - {{s}^{2}})} \right]$Отсюда следует, что масса является возрастающей функцией коэффициентов ${{n}_{r}}$ и ${{n}_{s}}$. Из условия минимума массы следует, что ${{n}_{r}} = {{n}_{s}} = 1$, то есть ограничения по прочности ребер и обшивки являются активными. Тогда выражение (3.6) принимает вид
(3.7)
$M = {\pi }q{{R}^{2}}l{{{\rho }}_{r}}\left[ {\frac{1}{{2{{{{\bar {\sigma }}}}_{r}}{{c}^{2}}}} + \frac{{2{\bar {\rho }}}}{{{{{{\bar {\sigma }}}}_{s}}{{c}^{2}}}}(2{{c}^{2}} - {{s}^{2}})} \right]$Это равенство показывает, что масса является монотонной функцией угла ${\varphi }$ и уменьшается при возрастании этого угла. Максимальным является значение ${\varphi } = {{{\varphi }}_{0}}$, при котором оболочка не имеет обшивки, а при ${\varphi } > {{{\varphi }}_{0}}$ толщина обшивки оказывается отрицательной и этот случай не рассматривается. При ${{n}_{r}} = {{n}_{s}} = 1$ из равенств (3.5) следует
(3.8)
$h{{\bar {b}}_{r}} = \frac{{qR}}{{4{{{{\bar {\sigma }}}}_{r}}{{c}^{2}}}},\quad h{{\bar {h}}_{s}} = \frac{{qR}}{{2{{{{\bar {\sigma }}}}_{s}}{{c}^{2}}}}(2{{c}^{2}} - {{s}^{2}})$С учетом первого из этих соотношений из ограничения (3.4) найдем
(3.9)
${{h}^{2}} = \frac{{{{{\pi }}^{2}}{{q}^{2}}{{R}^{2}}{{E}_{r}}{{n}_{m}}{{s}^{2}}}}{{48{\bar {\sigma }}_{r}^{3}{{c}^{2}}}}$Возводя ограничение (3.3) в четвертую степень и подставляя равенства (3.8) и (3.9), получим
где(3.11)
$с = \frac{{{{{\pi }}^{3}}R{{E}_{r}}{{E}_{s}}}}{{144l{\bar {\sigma }}_{r}^{3}{{{{\bar {\sigma }}}}_{s}}}}\sqrt[3]{{\frac{{{\pi }R{{E}_{r}}}}{{4{{{{\bar {\sigma }}}}_{r}}l}}}},\quad n = n_{0}^{{4/3}}{{n}_{m}},\quad F({\varphi }) = \frac{{\sqrt[3]{{1 + {\text{t}}{{{\text{g}}}^{2}}{\varphi }}}}}{{\left[ {2 - {\text{t}}{{{\text{g}}}^{2}}{\varphi } + \frac{{{{E}_{r}}{{{{\bar {\sigma }}}}_{s}}{\text{t}}{{{\text{g}}}^{2}}{\varphi }}}{{3{{E}_{s}}{{{{\bar {\sigma }}}}_{r}}(1 + {\text{t}}{{{\text{g}}}^{2}}{\varphi })}}} \right]}}$Продемонстрируем процесс проектирования на примере оболочки из углепластика с параметрами
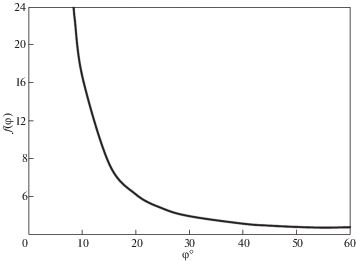
Для такой оболочки в уравнении (3.10) имеем $с = 0.009117$ (МПа)–2 и зависимость $f({\varphi })$ показана на рис. 4 из которого следует, что при ${\varphi } = {{{\varphi }}_{0}}$ эта зависимость достигает минимального значения ${{f}_{0}} = 0.7$. Возможны два варианта оптимальных проектов. Примем в уравнении (3.10) ${{n}_{0}} = {{n}_{m}} = n = 1$, то есть предположим, что все ограничения являются активными. Полагая $f = {{f}_{0}}$, из уравнения (3.10) получим ${{q}_{0}} = \sqrt {{{f}_{0}}{\text{/}}c} = 8.76$ МПа. Таким образом, при ${{n}_{0}} = {{n}_{m}} = 1$ решение уравнения (3.10) существует если $q > {{q}_{0}}$. В качестве примера рассмотрим оболочку с параметрами (3.12) при $q = 10$ МПа. При n = 1 из уравнения (3.10) имеем $f({{{\varphi }}_{q}}) = 0.912$ и рис. 4 дает ${{{\varphi }}_{q}} = 45^\circ $. Из равенства (3.9) при ${{n}_{m}} = 1$ и ${\varphi } = {{{\varphi }}_{q}}$ найдем h = 170 мм. Тогда из соотношений (3.8) получим ${{\bar {b}}_{r}}$ = 0.0916 и ${{h}_{s}} = 7$ мм. Для того, чтобы определить ширину сечения ребра ${{b}_{r}}$, необходимо задать число спиральных ребер, проходящих через сечение оболочки, ${{m}_{r}}$. Примем ${{m}_{r}} = 90$. Тогда расстояние между узлами пересечения спиральных ребер $b = 4{\pi }R{\text{/}}{{m}_{r}}$ = 279 мм (рис. 3), а расстояние между осями ребер $a = bc = 197$ мм. В результате получим ${{b}_{r}} = a{{\bar {b}}_{r}} = 18$ мм. Таким образом, оболочка с диаметром 4 м и длиной 5 м, спроектированная на давление 10 МПа, имеет общую толщину 177 мм и состоит из наружных кольцевых слоев углепластика с толщиной 3.5 мм и внутреннего сетчатого слоя с толщиной 170 мм, состоящего из спиральных ребер с углами $ \pm 45^\circ $. Согласно равенству (3.7), теоретическая масса оболочки (без учета массы днищ и соединений) составляет 1937 кг при водоизмещении 50300 кг.
Рассмотрим случай $q < {{q}_{0}}$. Для оболочки с параметрами (3.12) примем, например, q = 5 МПа. Для такой оболочки при n = 1 из уравнения (3.10) получим $f({\varphi }) = 0.223$, что меньше минимального значения ${{f}_{0}}$ (рис. 4). Таким образом, уравнение (3.10) не имеет решения при n = 1. Для определения $n$ можно воспользоваться уравнением (3.10), в котором следует задать угол ${\varphi }$. Теоретически минимальная масса оболочки достигается при ${\varphi } = {{{\varphi }}_{0}} = 54.735^\circ $, однако такая оболочка не имеет обшивки. Для реальной оболочки угол ${{{\varphi }}_{q}}$ выбирается из конструктивных соображений так, что ${{{\varphi }}_{q}} < {{{\varphi }}_{0}}$. Примем, например, φq = 50°. Тогда $f({{{\varphi }}_{q}}) = 0.774$ и уравнение (3.10) дает $n = 3.4$. Таким образом, при $q < {{q}_{0}}$ ограничения по устойчивости не являются активными и выполняются с некоторыми запасами. При этом, так как $n$ определяется вторым равенством (3.11), коэффициенты безопасности по общей и местной формам потери устойчивости могут быть выбраны произвольно, но так, чтобы они были больше единицы и удовлетворяли условию $n_{0}^{{4/3}}{{n}_{m}} = 3.4$. Все такие оболочки имеют одинаковую массу, которая определяется равенством (3.7) и составляет 1225 кг, но разные проектные параметры. Примем, например, ${{n}_{0}} = {{n}_{m}} = 1.69$. Тогда из равенств (3.8) и (3.9) получим $h = 109$ мм, ${{\bar {b}}_{r}}$ = 0.0854, и ${{h}_{s}} = 20.5$ мм.
4. Заключение. Представлен метод оптимального проектирования трехслойной цилиндрической оболочки, нагруженной внешним давлением. Оболочка состоит из наружных кольцевых слоев и внутреннего слоя из спиральных ребер, изготовленных из однонаправленного волокнистого композитного материала методом намотки. Получены соотношения, определяющие проектные параметры и массу оболочки. Установлено пороговое значение давления, ниже которого активными являются ограничения по прочности слоев, а выше – ограничения по прочности и устойчивости. Полученные результаты свидетельствуют о перспективности применения рассматриваемых конструкций в качестве корпусов глубоководных аппаратов.
Список литературы
Азаров А.В. Проблема проектирования аэрокосмических сетчатых композитных конструкций // Изв. РАН. МТТ. 2018. № 4. С. 85–93.
Васильев В.В., Разин А.Ф., Никитюк В.А. Корпус для внешнего давления из композиционных материалов // Патент РФ, 2010. № 2441798.
Васильев В.В., Разин А.Ф., Сисаури В.И. Корпус глубоководного аппарата из композиционных материалов // Патент РФ, 2018. № 2649117.
Образцов И.Ф., Васильев В.В., Бунаков В.А. Оптимальное армирование оболочек вращения из композиционных материалов. М.: Машиностроение. 1977. 144 с.
Васильев В.В. Механика конструкций из композиционных материалов. М.: Машиностроение. 1988. 270 с.
Vasiliev V.V., Razin A.F. Optimum design of filament-wound anisogrid lattice structures / Proc. of the 16-th Annual Techn. Conf. of American Soc. Of Composites. Blacksbutg, USA. 2001. C. 1–8 (CD).
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела