Известия РАН. Механика твердого тела, 2020, № 4, стр. 140-151
ФЕНОМЕНОЛОГИЧЕСКАЯ МОДЕЛЬ ИЗМЕНЕНИЯ ФАЗОВО-СТРУКТУРНЫХ ДЕФОРМАЦИЙ В СПЛАВАХ С ПАМЯТЬЮ ФОРМЫ
А. А. Мовчан *
Институт прикладной механики РАН
Москва, Россия
* E-mail: movchan47@mail.ru
Поступила в редакцию 09.01.2020
После доработки 13.01.2020
Принята к публикации 17.01.2020
Аннотация
Предложена объединенная модель фазово-структурного деформирования сплавов с памятью формы, в рамках которой неупругая деформация этих материалов может изменяться, как за счет фазовых превращений, так и за счет структурных переходов. Модель развития деформаций за счет структурного перехода использует понятие поверхности нагружения, изотропного и трансляционного упрочнения, ассоциированного закона течения. Модель развития деформации за счет термоупругих фазовых (прямых или обратных) превращений не апеллирует к понятию поверхности нагружения, адекватно описывая развитие фазовых деформаций, которое наблюдается при постоянных и даже уменьшающихся напряжениях. В рамках модели учитывается наблюдаемое в экспериментах влияние второго механизма на первый (перекрестное упрочнение), состоящее в том, что при изменении деформаций за счет фазового превращения изменяется радиус поверхности нагружения, определяющий процесс деформирования при структурном переходе. В рамках модели наблюдается ряд необычных для теории пластического течения явлений, как то уменьшение радиуса поверхности нагружения, которое может происходить даже при увеличении неупругих деформаций, рост этого радиуса в том числе при уменьшении неупругих деформаций, изменение радиуса поверхности нагружения в ситуации, когда точка, изображающая напряженное состояние, движется, или даже покоится в упругой области.
1. Введение. Для некоторых классов материалов механики деформируемого твердого тела характерна ситуация наличия двух (или более) механизмов неупругого деформирования, принципиально различающихся, в том числе, и по своим макроскопическим проявлениям, и в то же время влияющих друг на друга. Здесь речь может идти о пластических деформациях и деформациях ползучести сталей и сплавов [1], мгновенных нелинейных деформациях и линейных вязкоупругих деформациях полимеров [2, 3], фазовой и пластической деформации TRIP – сталей [4].
Ярким примером таких материалов являются сплавы с памятью формы (СПФ), изменение неупругих деформаций в которых может происходить по механизмам прямых или обратных термоупругих фазовых превращений и (или) структурных переходов. Известно [5, 6], что для процесса деформирования, связанного со структурными переходами (раздвойникованием и переориентацией мартенситной фазы), характерны все признаки явления деформационного упрочнения (наличие упругой области в пространстве девиатора напряжений и ограничивающей эту область поверхности нагружения, изменение размеров этой поверхности и смещение ее центра при изменении неупругих деформаций), что делает эти процессы сходными с процессами пластического деформирования. В то же время, экспериментально установлено [7], что для процессов деформирования СПФ, связанных с термоупругими фазовыми превращениями (прямым из аустенитной фазы в мартенситную и обратным) явление деформационного упрочнения не характерно, неупругие деформации в таких процессах меняются при постоянных и убывающих напряжениях, что напоминает процесс ползучести. В [8, 9] обнаружен эффект перекрестного упрочнения, свидетельствующий о влиянии процессов деформирования, связанных с фазовыми переходами на структурные превращения.
Необходимо отметить, что описанные выше особенности процесса неупругого деформирования СПФ в большинстве известных моделей поведения этих материалов (обзор таких моделей, опубликованных до 2015 г., приведен в [10]) не учитываются. Так, в [11–13] моделируется только фазовый механизм деформирования СПФ, проявления структурного механизма не рассматриваются. В [14] наоборот, с помощью аналога теории пластичности с изотропным и трансляционным упрочнением моделируется структурный механизм деформирования СПФ, но не рассматривается фазовый. В работах [15–17] понятие поверхности нагружения вообще не используется. В работах [18–21] учитываются, как фазовый, так и структурный механизмы деформирования, однако не отражена упомянутая выше принципиальная разница между этими механизмами. В [22] изложена модель фазового и структурного деформирования СПФ, с учетом специфических свойств этих механизмов, а также влияния фазового механизма на структурный. Однако, в этой работе для структурного механизма деформирования учитывается только изотропное упрочнение, хотя приведенные в [23] диаграммы прямого и обратного нагружения СПФ в режиме мартенситной неупругости (кручение) явно демонстрируют наличие эффекта Баушингера.
В данной работе предлагается вариант объединенной модели фазово-структурного деформирования СПФ, лишенный этого недостатка, т.е. учитывающий не только изотропное, но и трансляционное упрочнение СПФ при деформировании этих материалов по структурному механизму.
2. Формулировка модели. Предлагаемая система определяющих соотношений для фазово-структурного деформирования СПФ имеет вид:
(2.1)
$d\varepsilon _{{ij}}^{{{\text{ph'}}}} = \frac{3}{2}{{\rho }_{{D1}}}\frac{{{{S}_{{ij}}}}}{{{{S}_{i}}}}{{\varphi }_{1}}\left( {{{S}_{i}}} \right)dq,\quad dq > 0$(2.2)
$d\varepsilon _{{ij}}^{{{\text{ph'}}}} = \frac{{\varepsilon _{{ij}}^{{{\text{phst'}}}}}}{q}dq,\quad dq < 0$(2.3)
${{\rho }_{{D2}}}q{{\varphi }_{2}}\left( {S{\text{*}}} \right) = \int {\frac{{{{S}_{{ij}}}}}{{{{S}_{i}}}}d\varepsilon _{{ij}}^{{{\text{phst'}}}}} ,\quad {{S}_{i}} = \sqrt {\frac{3}{2}{{S}_{{ij}}}{{S}_{{ij}}}} $(2.4)
$d\varepsilon _{{ij}}^{{{\text{st}}}} = d\lambda {{S}_{{ij}}}$ при $d\lambda > 0$ и ${{S}_{i}} = S{\text{*}}$, $d\varepsilon _{{ij}}^{{{\text{st}}}} = 0$ при $d\lambda \leqslant 0$ или ${{S}_{i}} < S{\text{*}}$(2.5)
$\sigma _{{ij}}^{'} = {{S}_{{ij}}} + {{r}_{{ij}}},\quad qd{{r}_{{ij}}} = gd\varepsilon _{{ij}}^{{{\text{st}}}},\quad g > 0$Здесь $d\varepsilon _{{ij}}^{{{\text{phst'}}}}$ – приращение девиатора фазово-структурной деформации, складывающееся из приращения за счет фазового $d\varepsilon _{{ij}}^{{ph{\text{'}}}}$ и за счет структурного $d\varepsilon _{{ij}}^{{{\text{st}}}}$ переходов; $\sigma _{{ij}}^{{\text{'}}}$, ${{S}_{{ij}}}$, ${{r}_{{ij}}}$ – девиаторы напряжений, активных напряжений и микронапряжений (${{r}_{{ij}}}$ – координаты центра поверхности нагружения в пространстве девиатора напряжений). Приращение девиатора деформации за счет фазового перехода происходит при изменении объемной доли мартенситной фазы q, определяется формулами (2.1) для прямого и (2.2) для обратного превращения и не связано с понятием деформационного упрочнения. Изменение деформации за счет структурного перехода происходит лишь в случае, когда точка, изображающая напряженное состояние находится на Мизесовской поверхности нагружения, радиус которой S* определяется соотношением (2.3); (2.4) представляет собой ассоциированный закон для приращения деформаций за счет структурного перехода; (2.5) является уравнением, определяющим движение центра поверхности нагружения; здесь $g$ в простейшем случае, является постоянной (линейное трансляционное упрочнение). Согласно (2.5) центр поверхности нагружения для структурных деформаций смещается только при изменении неупругих деформаций за счет структурного перехода. Материальные функции ${{\varphi }_{1}}$ и ${{\varphi }_{2}}$ определены и непрерывны для неотрицательных значений аргумента, ${{\varphi }_{1}}(0) = {{\varphi }_{2}}(0) = 0$, монотонно возрастают и стремятся к единице при аргументе, стремящемся к бесконечности, т.е. обладают свойствами интегральных функций распределения.
В случае, когда весь рассматриваемый процесс состоит только из фазовых (прямых или обратных) переходов без структурных превращений, $d\varepsilon _{{ij}}^{{{\text{st}}}} \equiv 0$, поэтому, согласно (2.5) $d{{r}_{{ij}}} \equiv 0$, ${{S}_{{ij}}} = \sigma _{{ij}}^{'}$ и процесс прямого превращения описывается так же, как и в рамках модели, не учитывающей трансляционное упрочнение [22]: $d\varepsilon _{{ij}}^{{{\text{ph}}'}} = \frac{3}{2}{{\rho }_{{D1}}}\frac{{\sigma _{{ij}}^{'}}}{{{{\sigma }_{i}}}}{{\varphi }_{1}}\left( {{{\sigma }_{i}}} \right)dq$.
Согласно (2.3), (2.1) и (2.4) для прямого превращения, происходящего совместно со структурным переходом должно выполняться неравенство $d\lambda > 0$ и условие
(2.6)
${{\rho }_{{{\text{D}}2}}}q{{\varphi }_{2}}\left( {S_{i}^{{}}} \right) = \int {\left[ {{{\rho }_{{{\text{D}}1}}}{{\varphi }_{1}}\left( {{{S}_{i}}} \right)dq + \frac{2}{3}{{S}_{i}}d\lambda } \right]} $Дифференцируя соотношение (2.6) получаем для $d\lambda $ выражение
(2.7)
$d\lambda = \frac{3}{2}\frac{{3Aq{{S}_{{mn}}}d\sigma _{{mn}}^{'} - {{S}_{i}}{{B}^{ + }}dq}}{{(3Ag + 2)S_{i}^{2}}},\quad {{B}^{ + }} = 2\left[ {{{\rho }_{{{\text{D}}1}}}{{\varphi }_{1}}\left( {{{S}_{i}}} \right) - {{\rho }_{{{\text{D}}2}}}{{\varphi }_{2}}\left( {{{S}_{i}}} \right)} \right],\quad A = {{\rho }_{{{\text{D}}2}}}\varphi _{2}^{'}\left( {{{S}_{i}}} \right)$Дифференциальное условие активного нагружения $d\lambda > 0$ сводится к неравенству
Согласно (2.8), в случае нарушения неравенства
(2.9)
${{\rho }_{{{\text{D}}1}}}{{\varphi }_{1}}\left( {{{S}_{i}}} \right) > {{\rho }_{{{\text{D}}2}}}{{\varphi }_{2}}\left( {{{S}_{i}}} \right)$Согласно (2.2), (2.3) и (2.4) для одновременного осуществления обратного превращения и структурного перехода должно выполняться соотношение
В случае структурного перехода при отсутствии фазовых превращений, в приведенных выше формулах следует положить dq = 0; соотношения для неупругих деформаций и условие (2.8) упрощаются:
3. Случай пропорционального нагружения. Рассмотрим случай, вообще говоря, немонотонного пропорционального изменения девиатора напряжений $\sigma _{{ij}}^{'}$:
(3.1)
$\sigma _{{ij}}^{'} = \sigma \cdot \sigma _{{ij}}^{0},$ $\sigma _{{ij}}^{0} = {\text{const,}}$ $\sigma _{{kk}}^{0} = 0,$ $\frac{3}{2}\sigma _{{ij}}^{0}\sigma _{{ij}}^{0} = 1,$ ${{\sigma }_{i}} = \left| \sigma \right|$Для определенности предполагается, что для первого нагружения девиатор $\sigma _{{ij}}^{0}$ выбран так, чтобы было σ > 0, $\sigma = {{\sigma }_{i}}$. Легко видеть, что при таком нагружении в общем случае, девиатор фазово-структурной деформации также будет изменяться пропорционально:
(3.2)
$\varepsilon _{{ij}}^{{{\text{phst}}'}} = \varepsilon \cdot \varepsilon _{{ij}}^{0},$ $\varepsilon _{{ij}}^{0} = {\text{const,}}$ $\varepsilon _{{kk}}^{0} = 0,$ $\frac{2}{3}\varepsilon _{{ij}}^{0}\varepsilon _{{ij}}^{0} = 1,$ $\left| \varepsilon \right| = {{\varepsilon }_{i}},$ $\varepsilon _{{ij}}^{0} = \frac{3}{2}\sigma _{{ij}}^{0}$Подстановка (3.1), (3.2) в уравнения модели приводят к соотношениям
(3.3)
${{r}_{{ij}}} = r\sigma _{{ij}}^{0},$ $dr = \frac{3}{2}gd{{\varepsilon }^{{{\text{st}}}}},$ ${{S}_{{ij}}} = S\sigma _{{ij}}^{0},$ $S = \sigma - r,$ ${{S}_{i}} = \left| S \right|,$ $d{{\varepsilon }^{{{\text{st}}}}} = \frac{2}{3}Sd\lambda $Для прямого ($dq > 0$) или обратного ($dq < 0$) фазовых превращений соответственно выполняется
(3.4)
$d{{\varepsilon }^{{{\text{ph}}}}} = {\text{sign}}\left( S \right){{\rho }_{{{\text{D}}1}}}{{\varphi }_{1}}\left( {\left| S \right|} \right)dq,$ $d{{\varepsilon }^{{{\text{ph}}}}} = \frac{\varepsilon }{q}dq$Согласно (3.3), (3.4) приращение параметра деформации за счет прямого фазового перехода ($dq > 0$) или за счет структурного превращения ($d\lambda > 0$) всегда имеет тот же знак, что и величина $S$, а за счет обратного превращения ($dq < 0$) знак, противоположный знаку ε.
Уравнение для определения радиуса поверхности нагружения S* (2.3) в общем случае пропорционального нагружения принимает вид
(3.5)
${{\rho }_{{{\text{D}}2}}}q{{\varphi }_{2}}\left( {S{\text{*}}} \right) = \int {d\chi ,\quad d\chi = {\text{sign}}\left( S \right)d\varepsilon } $На участке процесса, где знак S не меняется, $\Delta \chi = {\text{sign}}\left( S \right)\Delta \varepsilon $. Если во всем рассматриваемом процессе знак S не меняется, то соотношение (3.5) можно представить в форме
(3.6)
${{\rho }_{{{\text{D}}2}}}q{{\varphi }_{2}}\left( {S{\text{*}}} \right) = {\text{sign}}\left( S \right)\varepsilon $Пусть рассматриваемый процесс на содержит этапов обратного превращения. Тогда знаки $S$ и $d\varepsilon $ совпадают и (3.5) переходит в соотношение
(3.7)
${{\rho }_{{{\text{D}}2}}}q{{\varphi }_{2}}\left( {S{\text{*}}} \right) = L,\quad L = \int {\left| {d\varepsilon } \right|} $(3.8)
$\left| S \right| = \varphi _{2}^{{ - 1}}\left( {\frac{L}{{{{\rho }_{{{\text{D}}2}}}q}}} \right)$Здесь $\varphi _{2}^{{ - 1}}$ – функция, обратная ${{\varphi }_{2}}$, однозначная и непрерывная в силу монотонности и непрерывности ${{\varphi }_{2}}$ и напряжение постоянно. На тех участках рассматриваемого процесса, на которых не будет структурного перехода, выполняется $S = {\text{const}}$. Для процесса, не включающего в себя обратного превращения, справедливы, кроме того, следующие дифференциальные соотношения
Дифференциальное условие активного нагружения, дополняющее зависимость (3.8) имеет в рассматриваемом случае вид
(3.10)
$Aq{\text{sign}}\left( S \right)d\sigma > \left[ {{{\rho }_{{{\text{D}}1}}}{{\varphi }_{1}}\left( {\left| S \right|} \right) - {{\rho }_{{{\text{D}}2}}}{{\varphi }_{2}}\left( {\left| S \right|} \right)} \right]dq$В случае обратного превращения, сопровождаемого структурным переходом справедливы соотношения
(3.11)
$d{{\varepsilon }^{{{\text{st}}}}} = 2\frac{{\left[ {{{\rho }_{{{\text{D}}2}}}q{{\varphi }_{2}}\left( {\left| S \right|} \right){\text{sign}}\left( S \right) - \varepsilon } \right]dq{\text{/}}q + Aqd\sigma }}{{3Ag + 2}}$(3.12)
$\left[ {{{\rho }_{{{\text{D}}2}}}q{{\varphi }_{2}}\left( {\left| S \right|} \right) - {\text{sign}}\left( S \right)\varepsilon } \right]\frac{{dq}}{q} + Aq{\text{sign}}\left( S \right)d\sigma > 0$Если в рассматриваемом процессе знак S не меняется, то для этапа этого процесса, на котором происходят обратное превращение и структурный переход, должно выполняться соотношение (3.6), в котором S* заменено на S. Сопоставление (3.11) и (3.6) позволяет в этом случае существенно упростить выражение для $d{{\varepsilon }^{{{\text{st}}}}}$ и $d\varepsilon $, и дифференциальное условие активного нагружения (3.12):
(3.13)
$d{{\varepsilon }^{{{\text{st}}}}} = \frac{{2Aqd\sigma }}{{3Ag + 2}},$ $d\varepsilon = \frac{{2Aqd\sigma }}{{3Ag + 2}} + \frac{\varepsilon }{q}dq,$ $Sd\sigma > 0$В случае, если происходит структурный переход без фазового, справедливы соотношения (3.13) при dq = 0.
4. Прямое и обратное превращение под действием постоянного напряжения.
Пусть происходит прямое и обратное термоупругое фазовое превращение под действием напряжения с постоянным девиатором: $\sigma _{{ij}}^{'} = {\text{const}}$, $d\sigma _{{ij}}^{'} = 0$. Такой процесс можно считать частным случаем пропорционального нагружения.
На этапе прямого превращения дифференциальное условие активного нагружения (3.10) при $d\sigma = 0$ с учетом выполнения неравенства (2.9) не выполняется, т.е. структурный переход происходить не может. Тогда $d{{\varepsilon }^{{{\text{st}}}}} = 0$, dr = 0, в аустенитном состоянии r = 0, следовательно r = 0 для всего этапа прямого превращения, то есть центр поверхности нагружения находится в начале координат. Поэтому для первого этапа процесса $S = \sigma > 0$, $d\varepsilon = d{{\varepsilon }^{{{\text{ph}}}}}$ и решение уравнения для неупругой деформации (3.9) имеет вид
Поскольку знак S > 0 на этапе прямого превращения не изменялся, то для радиуса поверхности нагружения справедливо, согласно (3.6), (4.1) выражение
(4.2)
$S* = \varphi _{2}^{{ - 1}}\left[ {\frac{{{{\rho }_{{{\text{D}}1}}}}}{{{{\rho }_{{{\text{D}}2}}}}}{{\varphi }_{1}}\left( \sigma \right)} \right]$Согласно (4.2), радиус поверхности нагружения при прямом превращении, происходящем под действием постоянного напряжения сохраняет постоянное значение (не зависит от $q$), несмотря на то, что с ростом $q$ растет неупругая деформация (за счет прямого превращения). В силу неравенства (2.9) и свойств функций ${{\varphi }_{1}}$ и ${{\varphi }_{2}}$ в процессе прямого превращения выполняется неравенство
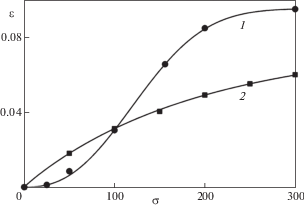
то есть точка, изображающая напряженное состояние находится в упругой области.Сравнение полученного экспериментально графика зависимости неупругой деформации при полном прямом превращении под действием постоянного напряжения от величины этого напряжения с зависимостью (4.1) при q = 1 позволяет найти параметр материала ${{\rho }_{{D1}}}$ как асимптотическое значение, к которому стремится интенсивность накопленной деформации при интенсивности напряжений, стремящейся к бесконечности, и материальную функцию ${{\varphi }_{1}}\left( \sigma \right)$, соответствующую графику зависимости $\varepsilon {\text{/}}{{\rho }_{{{\text{D}}1}}}$ от σ.
На рис. 1 приведены экспериментальные данные по полному прямому превращению под действием постоянного одноосного растягивающего напряжения (точки) и сжимающего напряжения (квадраты) образцов из равноатомного никелида титана, отожженного при температуре 800°C в течение 1 часа с последующей закалкой в воду комнатной температуры. По оси абсцисс отложены значения напряжений (модуля напряжений при сжатии), под действием которых производился соответствующий эксперимент в МПа, по оси ординат – неупругие деформации, полученные при полном прямом превращении под действием соответствующего напряжения. Линия 1 соответствует аппроксимации экспериментальных данных для случая растяжения с помощью функции распределения Вейбулла $\varepsilon = {{\rho }_{{{\text{D}}1}}}[1 - \exp ( - {{(\sigma {\text{/}}{{\sigma }_{{01}}})}^{\alpha }})]$. Методом наименьших квадратов получены следующие значения параметров ${{\rho }_{{{\text{D}}1}}} = 0.095$, ${{\sigma }_{{01}}} = 147$ МПа, $\alpha = 2.5$. Линия 2 соответствует аппроксимации экспериментальных данных для сжатия с помощью функции γ – распределения: $\varepsilon = {{\rho }_{{{\text{D}}1}}}{{\varphi }_{1}}\left( {\sigma {\text{/}}{{\sigma }_{{01}}}} \right)$, φ1(x) = $\frac{1}{{\Gamma (\alpha )}}\int_0^x {{{t}^{{\alpha - 1}}}\exp ( - t)dt} $. Методом наименьших квадратов получаются следующие значения параметров ${{\rho }_{{{\text{D}}1}}} = 0.076$, ${{\sigma }_{{01}}} = 204.3$, $\alpha = 0.955$.
При прямом превращении под действием монотонно убывающего без изменения знака напряжения, $d\sigma < 0$, $dq > 0$, условие (2.8) не выполнено и структурный переход также не возможен. В этом случае неупругая деформация возрастает за счет фазового перехода, точка, описывающая напряженное состояние перемещается в упругой области, а радиус поверхности нагружения уменьшается [22]. Тем самым, в рамках феноменологической теории описывается микроструктурный эффект неоднородного упрочнения мартенситной части представительного объема СПФ [24]. При прямом превращении под действием возрастающего напряжения радиус поверхности нагружения на некоторых участках процесса не меняется, несмотря на возрастание неупругих деформаций, а на некоторых участках возрастает [22].
Пусть прямое превращение под действием постоянного напряжения происходит до значения параметра q, равного $0 < {{q}_{0}} \leqslant 1$, после чего под действием того же напряжения $\sigma = {\text{const}}$ происходит обратное превращение. В начальной точке обратного превращения $S* > \sigma = S > 0$. В процессе обратного превращения dσ = dS + dr = = $dS + 3gd{{\varepsilon }^{{{\text{st}}}}}$ = 0, то есть величина $S$ может меняться только в случае структурного перехода, однако структурный переход может иметь место только при выполнении равенства $S = S{\text{*}}$. В процессе обратного фазового перехода при отсутствии структурного, величина S* также меняться не может. Действительно, в начальной точке обратного превращения неупругая деформация, согласно (4.1) будет равна ${{\varepsilon }_{0}} = {{\rho }_{{{\text{D}}1}}}\varphi \left( \sigma \right){{q}_{0}}$. Решая второе уравнение (3.4) при начальном условии $\varepsilon ({{q}_{0}}) = {{\varepsilon }_{0}}$, получаем $\varepsilon = {{\rho }_{{{\text{D}}1}}}{{\varphi }_{1}}\left( \sigma \right)q$. Поскольку на рассматриваемом участке S сохраняет положительный знак, то уравнение (3.6) для определения S* имеет вид ${{\rho }_{{{\text{D}}2}}}q{{\varphi }_{2}}\left( {S{\text{*}}} \right) = {{\rho }_{{{\text{D}}1}}}q{{\varphi }_{1}}\left( \sigma \right)$ и величина S* определяется уравнением (4.2), т.е., не меняется, если не начался структурный переход. Следовательно, разница $S{\text{*}} - S$ до тех пор, пока не начался структурный переход, сохраняет постоянное значение, а начаться структурный переход может лишь в случае $S = S{\text{*}}$. В то же время, при обратном фазовом превращении под действием возрастающего напряжения радиус поверхности нагружения может расти при уменьшающейся неупругой деформации [22].
Таким образом, установлено, что для прямого превращения из полностью аустенитного состояния и последующего обратного превращения, происходящих под действием одного и того же постоянного напряжения структурный переход не имеет места, r = 0, $S = \sigma $, радиус поверхности нагружения $S* = {\text{const}}$, $S* > \sigma $ и определяется из уравнения (4.2).
5. Пропорциональное нагружение в режиме мартенситной неупругости. Пусть материал переводится из аустенитного в мартенситное состояние в отсутствии напряжений (первый этап), после чего происходит пропорциональное нагружение в режиме мартенситной неупругости (второй этап). В конце первого этапа, в силу того, что ${{\varphi }_{1}}(0) = {{\varphi }_{2}}(0) = 0$ получается $\sigma = S = r = S* = \varepsilon = 0$. На этапе мартенситной неупругости q = 1, $dq = 0$ и дифференциальное условие активного нагружения $d\lambda > 0$ сводится к неравенству $Sd\sigma > 0$. На этапе монотонного нагружения $\sigma > 0$, $d\sigma > 0$, $S > 0$, $d{{\varepsilon }^{{{\text{st}}}}}$ > 0, $r > 0$.
В отсутствии фазового превращения при q = 1 уравнение поверхности нагружения (3.7) сводится к соотношению $S* = \varphi _{2}^{{ - 1}}\left( {L{\text{/}}{{\rho }_{{{\text{D}}2}}}} \right)$. В каждой точке монотонного пропорционального нагружения в режиме мартенситной неупругости будут выполняться оба условия активного нагружения, $S = S{\text{*}}$, $L = {{\varepsilon }^{{{\text{st}}}}} = \varepsilon $, ${{\varepsilon }^{{{\text{st}}}}} = {{\rho }_{{{\text{D}}2}}}{{\varphi }_{2}}\left( S \right)$, и, согласно (3.3) уравнение диаграммы мартенситной неупругости при монотонном наружении есть
(5.1)
$\sigma = \frac{3}{2}g{{\varepsilon }^{{{\text{st}}}}} + \varphi _{2}^{{ - 1}}({{\varepsilon }^{{{\text{st}}}}}{\text{/}}{{\rho }_{{{\text{D}}2}}})$Здесь учтено, что при постоянном $q$ соотношение (2.5) интегрируется, в результате чего для пропорционального нагружения при нулевых начальных условиях получается $r = 3g{{\varepsilon }^{{{\text{st}}}}}{\text{/}}2$.
Соотношение (5.1) можно использовать для идентификации модели – определения функции ${{\varphi }_{2}}$ и параметров $g$ и ${{\rho }_{{{\text{D}}2}}}$ по известной диаграмме мартенситной неупругости СПФ в координатах ${{\varepsilon }^{{{\text{st}}}}}$, $\sigma $. В случае, если $g$ не считается константой, а предполагается функцией $\sigma $, то (5.1) представляет собой не явное выражение для $\sigma $, а уравнение для этой величины.
Пусть нагружение происходит до значения ${{\varepsilon }^{{{\text{st}}}}} = {{\varepsilon }_{{\max }}}$, после чего осуществляется разгрузка и нагружение в обратную сторону. Радиус поверхности нагружения в момент начала разгрузки и до момента начала неупругого деформирования в обратную сторону сохраняет постоянное значение, равное $S* = \varphi _{2}^{{ - 1}}\left( {{{\varepsilon }_{{\max }}}{\text{/}}{{\rho }_{{{\text{D}}2}}}} \right)$, неупругое деформирование в обратную сторону начинается при $\sigma _{1}^{ - } = 3g{{\varepsilon }_{{\max }}} - \varphi _{2}^{{ - 1}}\left( {{{\varepsilon }_{{\max }}}{\text{/}}{{\rho }_{{{\text{D}}2}}}} \right)$ и уравнение диаграммы обратного неупругого деформирования в режиме мартенситной неупругости имеет вид
(5.2)
${{\sigma }^{ - }} = - \varphi _{2}^{{ - 1}}\left( {\frac{{2{{\varepsilon }_{{\max }}} - {{\varepsilon }^{{{\text{st}}}}}}}{{{{\rho }_{{{\text{D}}2}}}}}} \right) + \frac{3}{2}g{{\varepsilon }^{{{\text{st}}}}},\quad {{\sigma }^{ - }} < \sigma _{1}^{ - },\quad {{\varepsilon }^{{{\text{st}}}}} < {{\varepsilon }_{{\max }}}$Вычитание (5.2) из (5.1) позволяет исключить трансляционную часть упрочнения и получить соотношение для определения материальной функции $\varphi _{2}^{{ - 1}}$ по экспериментальным данным на прямое и обратное пропорциональное нагружение в режиме мартенситной неупругости:
(5.3)
$\sigma - {{\sigma }^{ - }} = \varphi _{2}^{{ - 1}}\left( {\frac{{{{\varepsilon }^{{{\text{st}}}}}}}{{{{\rho }_{{{\text{D}}2}}}}}} \right) + \varphi _{2}^{{ - 1}}\left( {\frac{{2{{\varepsilon }_{{\max }}} - {{\varepsilon }^{{{\text{st}}}}}}}{{{{\rho }_{{{\text{D}}2}}}}}} \right),$ $0 \leqslant {{\varepsilon }^{{{\text{st}}}}} \leqslant {{\varepsilon }_{{\max }}}$6. Обратное превращение после нагружения в режиме мартенситной неупругости. Пусть после того, как параметр структурной деформации в процессе монотонного нагружения достиг некоторого значения $\varepsilon _{{\max }}^{{{\text{st}}}} > 0$ и параметры $\sigma $, S, $r$ при монотонном нагружении достигли максимальных значений ${{S}_{{\max }}} = \varphi _{2}^{{ - 1}}(\varepsilon _{{\max }}^{{st}}{\text{/}}{{\rho }_{{D2}}}) > 0$, rmax = = $3g\varepsilon _{{\max }}^{{{\text{st}}}}{\text{/}}2$, ${{\sigma }_{{\max }}} = {{S}_{{\max }}} + {{r}_{{\max }}} = \varphi _{2}^{{ - 1}}(\varepsilon _{{\max }}^{{{\text{st}}}}{\text{/}}{{\rho }_{{D2}}}) + 3{{g}_{0}}\varepsilon _{{\max }}^{{{\text{st}}}}{\text{/}}2$, причем радиус поверхности нагружения равен ${{S}_{{\max }}}$, начинается нагрев и соответствующее обратное превращение при постоянном напряжении $\sigma = {{\sigma }_{{\max }}}$. До тех пор, пока знак $S$ не изменится, будет справедливо соотношение (3.6) и, следовательно, дифференциальное условие активного нагружения (3.12) сведется к неравенству $d\sigma > 0$ и выполняться не будет, так как $d\sigma $ = 0. Таким образом, структурного перехода не будет, пока знак S не изменится. Изменения S при $\sigma = {\text{const}}$ не возможны без структурного перехода, поскольку в отсутствии структурного перехода $r$ согласно (2.5) не меняется, следовательно, не меняется и $S = \sigma - r$. Таким образом, при обратном превращении структурный переход места не имеет, решение второго уравнения (3.4) при начальном условии $\varepsilon (1) = {{\varepsilon }_{{\max }}}$ имеет вид $\varepsilon = q{{\varepsilon }_{{\max }}}$, т.е. деформации линейно убывают до нуля при $q$, убывающем до нуля. То же самое решение будет справедливо и в случае, если перед началом нагрева действующее напряжение было уменьшено до любого значения ${{\sigma }_{0}} > {{r}_{{\max }}}$ с тем, чтобы при этом не изменился положительный знак $S = \sigma - r$, и после этого нагрев происходил при постоянном уменьшенном напряжении. Дело в том, что при неизменном знаке S будет по-прежнему справедливо дифференциальное условие активного нагружения (последняя формула (3.13)), которое не может выполняться при постоянном напряжении. Более того, при еще более глубокой разгрузке до значения ${{r}_{{\max }}} > {{\sigma }_{0}} > {{r}_{{\max }}}$ – Smax, что гарантирует нахождение точки, изображающей напряженное состояние после разгрузки внутри поверхности нагружения, структурный переход опять не будет наблюдаться, поскольку в этом случае первое слагаемое правой части дифференциального условия активного нагружения (3.12) будет отрицательно (так как в данном случае $S < 0$ и для обратного превращения $dq < 0$), а второе слагаемое будет равно нулю. В рассмотренном в данном пункте процессе обратного превращения радиус поверхности нагружения будет сохранять постоянное значение $S* = {{S}_{{\max }}}$.
7. Доориентация мартенсита после полного прямого превращения. Процесс состоит из трех этапов. Этап № 1 – полное прямое превращение под действием постоянного напряжения ${{\sigma }_{1}}$. В конечной точке этого этапа $q = 1$, $\varepsilon = {{\varepsilon }_{1}} = {{\rho }_{{{\text{D}}1}}}{{\varphi }_{2}}\left( {{{\sigma }_{1}}} \right)$, $\sigma = {{\sigma }_{1}}$, $r = 0$, $S{\text{*}}$ определяется по формуле (4.2). Этап № 2 – упругое догружение – рост напряжения от ${{\sigma }_{1}}$ до $S{\text{*}}$ в процессе которого будет изменяться лишь упругая составляющая деформации. В конце второго этапа $\varepsilon = {{\varepsilon }_{1}}$, $\sigma = S{\text{*}}$, $r = 0$. Этап № 3 – догружение в режиме мартенситной неупругости. Точка, изображающая напряженное состояние находится на поверхности нагружения, $S > 0$, $d\sigma > 0$, выполняются все условия активного нагружения в режиме мартенситной неупругости, фазового перехода нет, $dq = 0$, неупругая деформация, согласно (3.13) при q = 1 подчиняется дифференциальному уравнению
(7.1)
$d{{\varepsilon }^{{{\text{st}}}}} = \frac{{2{{\rho }_{{{\text{D}}2}}}\varphi _{2}^{'}\left( S \right)d\sigma }}{{3{{\rho }_{{{\text{D}}2}}}\varphi _{2}^{'}\left( S \right)g + 2}}$Подставляя в (7.1) $d\sigma = dS + dr = dS + \frac{3}{2}gd{{\varepsilon }^{{{\text{st}}}}}$, получаем уравнение dεst = $d[{{\rho }_{{D2}}}{{\varphi }_{2}}(S)]$, решение которого, удовлетворяющее начальному условию ${{\varepsilon }^{{{\text{st}}}}}\left( {S{\text{*}}} \right) = {{\varepsilon }_{1}}$ имеет вид
К (7.2) добавляется соотношение $dS = d\sigma - dr$, приводящее после исключения $r$ к дифференциальному уравнению $d\sigma = d\left[ {S + \frac{3}{2}g{{\rho }_{{{\text{D}}2}}}{{\varphi }_{2}}\left( S \right)} \right]$, решение которого при начальном условии $\sigma \left( {S{\text{*}}} \right) = S{\text{*}}$ дает
(7.3)
$\sigma = S + \frac{3}{2}g\left[ {{{\rho }_{{{\text{D}}2}}}{{\varphi }_{2}}\left( S \right) - {{\varepsilon }_{1}}} \right]$Исключая из (7.3) величину S с помощью (7.2) получаем диаграмму доориентации
(7.4)
$\sigma = \varphi _{2}^{{ - 1}}\left( {\frac{{{{\varepsilon }^{{{\text{st}}}}}}}{{{{\rho }_{{{\text{D}}2}}}}}} \right) + \frac{3}{2}g({{\varepsilon }^{{{\text{st}}}}} - {{\varepsilon }_{1}}),\quad {{\varepsilon }^{{{\text{st}}}}} \geqslant {{\varepsilon }_{1}}$Сравнение уравнения диаграммы доориентации (7.4) с исходной диаграммой мартенситной неупругости (5.1) показывает, что диаграмма доориентации (7.4) для одних и тех же значений ${{\varepsilon }^{{{\text{st}}}}}$ должна отличаться от исходной диаграммы мартенситной неупругости на постоянную для $g = {\text{const}}$ величину $\Delta \sigma = 3{{g}_{0}}{{\varepsilon }_{1}}{\text{/}}2$, т.е. эти диаграммы должны быть эквидистантны. Этот вывод вполне естественен, так как при описании опыта в рамках применяемой модели слагаемое r величины $\sigma $ равно нулю для $\varepsilon \in \left[ {0,{{\varepsilon }_{1}}} \right]$ и начинает расти линейно с ростом $\varepsilon $ лишь после достижения этой величиной значения ${{\varepsilon }_{1}}$, тогда как для исходной диаграммы мартенситной неупругости величина r растет с ростом $\varepsilon $ начиная с $\varepsilon = 0$.
8. Обратное нагружение в режиме мартенситной неупругости после прямого превращения под действием постоянного напряжения. Пусть на первом этапе процесса происходит полное прямое превращение под действием постоянного напряжения ${{\sigma }_{1}}$, накапливается неупругая деформация, равная, согласно (4.1) величине ${{\varepsilon }_{{\max }}} = {{\rho }_{{{\text{D}}1}}}{{\varphi }_{1}}\left( {{{\sigma }_{1}}} \right)$. Радиус поверхности нагружения в момент окончания процесса прямого превращения, согласно (4.2) равен $S* = \varphi _{2}^{{ - 1}}\left( {{{\rho }_{{{\text{D}}1}}}{{\varphi }_{1}}\left( {{{\sigma }_{1}}} \right){\text{/}}{{\rho }_{{{\text{D}}2}}}} \right)$. Поскольку структурного превращения не происходило, то центр поверхности нагружения находится в начале координат, ${{r}_{1}} = 0$. На втором этапе происходит разгрузка до $\sigma = 0$ и дальнейший рост $\sigma $ в отрицательную сторону. До тех пор, пока напряжение не достигнет значения ${{\sigma }_{2}} = - S{\text{*}}$ будет происходить упругий процесс. При $\sigma = - S{\text{*}}$ точка, изображающая напряженное состояние выходит на поверхность нагружения. Кроме того, в этой точке $S < 0$, $d\sigma < 0$, то есть выполнится дифференциальное условие активного нагружения, которое в отсутствии фазовых переходов имеет вид $Sd\sigma > 0$, т.е. начнется процесс структурного деформирования.
Так как обратное превращение при этом отсутствует, то справедливо соотношение (3.8), т.е. $S = - \varphi _{2}^{{ - 1}}((2{{\varepsilon }_{{\max }}} - {{\varepsilon }^{{{\text{st}}}}}){\text{/}}{{\rho }_{{{\text{D}}2}}})$, а дифференциальное уравнение для определения r (3.3) при начальном условии $r\left( {{{\varepsilon }_{{\max }}}} \right) = 0$ имеет решение $r = - 3g({{\varepsilon }_{{\max }}} - {{\varepsilon }^{{{\text{st}}}}})$. В результате для параметра напряжения $\sigma = S + r$ получается уравнение диаграммы обратного нагружения в режиме мартенситной неупругости после прямого превращения в виде
(8.1)
$\sigma = - \varphi _{2}^{{ - 1}}\left( {\frac{{2{{\varepsilon }_{{\max }}} - {{\varepsilon }^{{st}}}}}{{{{\rho }_{{{\text{D}}2}}}}}} \right) - \frac{3}{2}g({{\varepsilon }_{{\max }}} - {{\varepsilon }^{{{\text{st}}}}})$Сравнивая соотношение (8.1) с уравнением диаграммы обратного нагружения в режиме мартенситной неупругости после прямого нагружения в том же режиме мартенситной неупругости (5.2) получаем
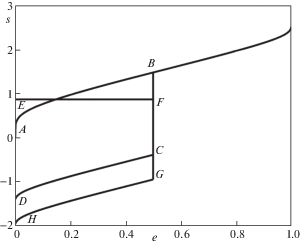
т.е. диаграмма обратного нагружения в режиме мартенситной после прямого превращения располагается эквидистантно и ниже по оси напряжений диаграммы обратного нагружения после прямого нагружения в режиме мартенситной неупругости до того же значения деформации εmax. Различие диаграмм (8.1) и (5.2) является еще одним, ранее не известным проявлением эффекта перекрестного упрочнения [9]. Имея обе такие диаграммы и составив разность (8.2) можно определить параметр материала g.На рис. 2 представлены графики зависимостей (5.1), (5.2) и (8.1). Кривые построены в безразмерных координатах $e = {{\varepsilon }^{{{\text{st}}}}}{\text{/}}{{\rho }_{{{\text{D}}2}}}$, $s = \sigma {\text{/}}{{\sigma }_{{02}}}$ для следующих значений безразмерных переменных $G = g{{\rho }_{{{\text{D}}2}}}{\text{/}}{{\sigma }_{{20}}} = 0.75$, ${{\gamma }_{1}} = {{\sigma }_{{20}}}{\text{/}}{{\sigma }_{{10}}} = 2.04$, ${{\gamma }_{2}} = {{\rho }_{{{\text{D}}1}}}{\text{/}}{{\rho }_{{{\text{D}}2}}} = 1.27$ ${{\alpha }_{1}} = 2.5$, ${{\alpha }_{2}} = 5.6$ (данные соответствуют никелиду титана). Линия $AB$ представляет собой диаграмму монотонного нагружения в режиме мартенситной неупругости (5.1), линия BC соответствует разгрузке и обратному нагружению в пределах упругой области, линия $CD$ – диаграмма последующего обратного наружения в режиме мартенситной неупругости (5.2).
Линия $EF$ соответствует накоплению деформаций прямого превращения под действием постоянного напряжения, величина которого подобрана таким образом, чтобы в конце этого этапа процесса была достигнута величина фазовой деформации, равная структурной деформации в точке B окончания этапа прямого нагружения в режиме мартенситной неупругости. Линия $FG$ соответствует разгрузке после окончания прямого превращения и нагружению в противоположную сторону в упругой области. Линия $GH$ представляет собой диаграмму обратного нагружения (8.1) в режиме мартенситной неупругости, осуществляемого после прямого превращения и разгрузки.
Выводы. Сформулирована система определяющих соотношений для описания фазово-структурного деформирования СПФ, учитывающая принципиальные различия процессов деформирования этих материалов за счет фазовых и структурных переходов и влияние первого процесса на второй. В отличие от известного аналога [22] модель учитывает не только изотропное, но и экспериментально наблюдаемое трансляционное упрочнение мартенситной части представительного объема СПФ.
Модель качественно правильно описывает характерные для СПФ явления: накопление деформаций прямого превращения при постоянном, убывающем или возрастающем напряжении, памяти формы, мартенситной неупругости при монотонном и реверсивном нагружении, эффект перекрестного упрочнения, эффект неоднородного упрочнения мартенситной части представительного объема материала.
Работа выполнена в рамках госбюджетной темы, государственная регистрация № АААА-А19-119012290118-3 при частичной финансовой поддержке РФФИ грант № 20-01-00240.
Список литературы
Работнов Ю.Н. Ползучесть элементов конструкций. М.: Наука, 1966. 752 с.
Суворова Ю.Н. О нелинейно-наследственном уравнении Ю.Н. Работнова и его приложениях // Изв. РАН. МТТ. 2004. № 1. С. 174–181.
Работнов Ю.Н. Элементы наследственной механики твердых тел. М.: Наука, 1977. 384 с.
Cherkaoni M., Berveiller M., Lemoine X. Coplings betyween plasticity amd martensitic phase transformation: overal behavior of polycrystalline TRIP steels // International Journal of Plasticity. 2000. V. 16. P. 1215–1241.
Thamburaja P. Constitutive equations for martensitic reorientation and detwinning in shape-memory alloys // Journal of the Mechanics and Physics of Solids. 2005. V. 53. P. 825–856.
Liu Y., Xie Z. Detwinning in shape memory alloy // In: Progress in Smart Materials and Structures. Editor: Peter L. Reece, 2007. Chapter 3. P. 29–65. Nova Science Publishers.
Мовчан А.А., Казарина С.А. Материалы с памятью формы как объект механики деформируемого твердого тела: экспериментальные исследования, определяющие соотношения, решение краевых задач // Физическая мезомеханика. 2012. Т. 15. № 1. С. 105–116.
Казарина С.А., Мовчан А.А., Сильченко А.Л. Экспериментальное исследование взаимодействия фазовых и структурных деформаций в сплавах с памятью формы // Механика композиционных материалов и конструкций. 2016. Т. 22. № 1. С. 85–98.
Мовчан А.А., Сильченко А.Л., Казарина С.А. Экспериментальное исследование и теоретическое моделирование эффекта перекрестного упрочнения сплавов с памятью формы // Деформация и разрушение материалов. 2017. № 3. С. 20–27.
Cisse C., Zaki W., Zineb T.B. A review of constitutive models and modeling techniques for shape memory alloys // International Journal of Plasticity 2015. https://doi.org/10.1016/j.ijplas.2015.08.006
Sadjadpour A., Bhattacharya K. A micromechanics inspired constitutive model for shape-memory alloys: the one-dimensional case // Smart Mater. Struct. 2007. V. 16. P. 51–62.
Xiao H., Bruhns O.T., Meyers A. Finite elasto-plastic ${{J}_{2}}$-flow models with strain recovery effects . Acta Mech. 2010. V. 210. P. 13–25. .https://doi.org/10.1007/s00707-009-0192-1
Olsen J.S., Zhang Z.L., Hals J.K., Lu H. Effect of notches on the behavior of superelastic round-bar NiTi specimens // Smart Mater. Struct. 2011. V. 20. 025014 (12 p.).
Мишустин И.В., Мовчан А.А. Аналог теории пластического течения для описания деформации мартенситной неупругости в сплавах с памятью формы // Изв. РАН. МТТ. 2015. № 2. С. 78–95.
Du X.W., Sun G., Sun S.S. Piecewise linear constitutive relation for pseudo-elasticity of shape memory alloys (SMA) // Mater. Sci. and Eng. A. 2005. V. 393. № 1–2 . P. 332–337.
Wang R., Cho C., Kim C., Pan Q. A proposed phenomenological model for shape memory alloys // Smart Mater. Struct. 2006. V. 15. P. 393–400.
Sadjadpour A., Bhattacharya K. A micromechanics inspired constitutive model for shape-memory alloys: the one-dimensional case // Smart Mater. Struct. 2007. V. 16. P. 51–62.
Arghavani J., Auricchio F., Naghdabadi R., Reali A., Sohrabpour S. A 3-D phenomenological constitutive model for shape memory alloys under multiaxial loadings // Int. J. of Plasticity. 2010. V. 26. P. 976–991.
Lexcellent Ch., Boubakar M.L., Bouvet Ch., Calloch S. About modeling the shape memory alloy behaviour based on the phase transformation surface identification under proportional loading and anisothermal conditions // Int. J. Solids and Struct. 2006. V. 43. № 3–4. P. 613–626.
Auricchio F., Bonetti E., Scalet G., Uberitini F. Theoretical and numerical modeling of shape memory alloys accounting for multiple phase transformations and martensite reorientation // Int. J. of Plasticity. 2014. V. 59. P. 30–54.
Xiaojun Gu, Weihong Zhang, Wael Zaki and Ziad Moumni. An extended thermomechanically coupled 3D rate-dependent model for pseudoelastic SMAs under cyclic loading // Smart Mater. Struct. 2017. V. 26. 095047 (16 p.).
Мовчан А.А. Модель влияния фазового механизма деформирования на структурный в сплавах с памятью формы // Деформация и разрушение материалов. 2019. № 7. С. 14–23.
Каменцева З.П., Кузьмин С.Л., Лихачев В.А. Исследование деформационного упрочнения никелида титана // Проблемы прочности. 1980. № 9. С. 87–91.
Мишустин И.В., Мовчан А.А. Моделирование фазовых и структурных превращений в сплавах с памятью формы, происходящих под действием немонотонно меняющихся напряжений // Изв. РАН. МТТ. 2014. № 1. С. 37–53.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела