Известия РАН. Механика твердого тела, 2020, № 5, стр. 64-75

1. Введение. Необходимость построения модели контактного взаимодействия жесткого тела с относительно мягким слоем, лежащим на жестком основании, возникает во многих практических областях, например, при анализе результатов индентирования мягких биологических тканей, полимерных материалов и т.д. При этом рассматриваются различные условия закрепления слоя на основании, формы контактирующей поверхности индентора, а также механические свойства самого слоя. Сам процесс индентирования может содержать несколько стадий: погружение индентора в ткань, удержание его на определенной глубине, извлечение из слоя мгновенно или за определенное время. Так как многие материалы, в том числе биологические ткани, проявляют релаксационные свойства, то при построении модели контактного взаимодействия возникает необходимость использовать модели вязкоупругих тел.

Построению решений контактных задач для упругого слоя посвящено большое количество работ. Весомый вклад в эту область внес советский и российский механик и математик Иосиф Израилевич Ворович. Им со своими учениками разработан асимптотический метод решения смешанных задач теории упругости [1–4], который был применен, в частности, при решении осесимметричных контактных задач для относительно толстого (“метод больших $\lambda $”, где $\lambda = {h \mathord{\left/ {\vphantom {h a}} \right. \kern-0em} a}$, $a$ – радиус области контакта, $h$ – толщина слоя) и тонкого (“метод малых $\lambda $”) упругих слоев.

Известные решения контактных задач для вязкоупругого слоя в большинстве случаев построены с использованием принципа Вольтерра и решений соответствующих по постановке контактных задач для упругих оснований. В [5, 6] рассматривалось внедрение с постоянной скоростью цилиндра и сферы в вязкоупругий слой, а затем мгновенное их извлечение. При этом исследовалась зависимость остаточной деформации от времени. В качестве основы бралось упругое решение, полученное в работе [7], где отдельным множителем выделялся зависящий от относительной толщины слоя параметр, значение которого находилось численно. На основе этого упругого решения в работе [8] получена зависимость глубины внедрения от приложенной силы при взаимодействии конуса с вязкоупругим слоем. Внедрение индентора различной формы (цилиндр, конус, сфера) в вязкоупругий слой при заданном законе изменения глубины рассмотрено в работе [9]. За основу при этом берется решение, которое получается из выражений для упругого полупространства с помощью поправочных коэффициентов, что накладывает ограничение на относительную толщину слоя. Анализ построенных решений показал, что основные характеристики процесса нагружения и разгрузки индентора оказывают существенное влияние на характер изменения во времени контактных характеристик.

Исследуются и обратные задачи, например, в работе [10] на основе решения задачи о внедрении цилиндра с плоским основанием в вязкоупругий слой с учетом влияния трения предложена методика определения механических характеристик слоя.

В большинстве упомянутых работ для описания механического поведения слоя используется модель линейно вязкоупругого материала с не зависящим от времени коэффициентом Пуассона и функциями релаксации экспоненциального вида [5, 6, 8, 10]. Отметим также, что в ряде работ (например, [11–13]) при исследовании взаимодействия индентора с вязкоупругим слоем использовались упрощенные стерженьковые модели.

В данном исследовании моделируется внедрение с постоянной скоростью и удержание в вязкоупругом слое цилиндра с плоским основанием. Решение строится с применением принципа Вольтерра и известных решений контактных задач для упругого слоя, полученных “методами больших и малых $\lambda $”. Для описания механического поведения слоя используются модели сплошной среды с двумя функциями релаксации (экспоненциальная и степенная), отражающими разные особенности механического поведения вязкоупругих материалов. С целью анализа возможности использования более простых механических моделей слоя проводится сравнение полученных зависимостей с результатами моделирования на основе упрощенной “стерженьковой” модели основания.

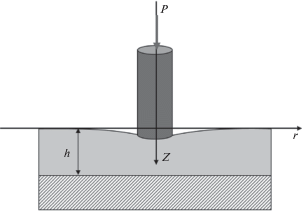
2. Постановка задачи. Рассматривается задача о внедрении жесткого цилиндра в вязкоупругий слой, лежащий без трения на жестком основании (рис. 1). Цилиндр имеет плоское основание радиуса $R$. Рассматриваются две асимптотики: тонкий и толстый слой. Для этого вводится коэффициент относительной толщины слоя $\lambda $, который равен отношению толщины слоя $h$ к радиусу области контакта, то есть $\lambda = {h \mathord{\left/ {\vphantom {h R}} \right. \kern-0em} R}$. Таким образом, для тонкого слоя имеем условие, что $\lambda < 1$, а для толстого – $\lambda > 1$.

Процесс внедрения состоит из двух стадий: погружение с постоянной скоростью $V$ до заданной глубины ${{\delta }_{*}}$, а затем удержание цилиндра на фиксированной глубине ${{\delta }_{*}}$, т.е. функция внедрения $\delta (t)$ имеет вид (${{t}_{*}} = {{{{\delta }_{*}}} \mathord{\left/ {\vphantom {{{{\delta }_{*}}} V}} \right. \kern-0em} V}$):

причем величина максимального внедрения ${{\delta }_{*}} = V{{t}_{*}}$ удовлетворяет условию малости деформаций.

Материал слоя является однородным, изотропным и линейно вязкоупругим, обладающим не зависящим от времени коэффициентом Пуассона. Заметим, что такое предположение является распространенным в задачах линейной вязкоупругости и применяется не только к биологическим тканям, но и к некоторым другим материалам (например, асфальтобетонам, полимерам). Для описания ядра релаксации материала слоя используются экспоненциальная и степенная функции (см. пп. 4.1 и 4.2).

3. Метод решения контактной задачи. Поскольку радиус области контакта постоянен и равен радиусу основания цилиндра, тип граничных условий остается неизменным в течение всего процесса нагружения. Поэтому для решения контактной задачи можно воспользоваться принципом Вольтерра [14], позволяющим строить решение вязкоупругой задачи на основании решения соответствующей контактной задачи для упругого материала с заменой упругих постоянных интегральными операторами.

В упругом случае основное уравнение, связывающее вертикальные перемещения поверхности основания $w(r,t)$ и контактные давления $p(r,t)$, при осесимметричном нагружении имеет вид [4]

где $K(x,y) = \int\limits_0^\infty {L\left( u \right){{J}_{0}}\left( {xu} \right){{J}_{0}}\left( {yu} \right)du} $, $L\left( u \right) = {{\left( {\cosh 2u - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\cosh 2u - 1} \right)} {\left( {\sinh 2u + 2u} \right)}}} \right. \kern-0em} {\left( {\sinh 2u + 2u} \right)}}$, а ${{J}_{0}}$ – функции Бесселя первого рода. Здесь $E$ и $\nu $ – модуль Юнга и коэффициент Пуассона основания. Время $t$ в соотношении (3.1) для упругого случая рассматривается как параметр. Приближенные решения упругой задачи для случаев относительно больших и малых значений коэффициента $\lambda $ построены в [4, 15] с использованием асимптотических методов. На основе этих решений ниже изучается процесс изменения во времени контактных характеристик (распределения давлений и зависимость нагрузки от времени) при разных скоростях внедрения штампа в вязкоупругий слой.

3.1. Внедрение цилиндра в толстый вязкоупругий слой. Рассмотрим случай больших $\lambda $. Из полученного в [4, 15] приближенного решения интегрального уравнения (3.1) для случая толстого упругого слоя следуют асимптотические выражения для контактного давления и приложенной нагрузки при заданной форме контактирующей поверхности штампа, т.е. при $w\left( {r,t} \right) = \delta \left( t \right)$:

где ${{a}_{m}} = \left( {{{{{{\left( { - 1} \right)}}^{m}}} \mathord{\left/ {\vphantom {{{{{\left( { - 1} \right)}}^{m}}} {{{{\left( {2m!!} \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {2m!!} \right)}}^{2}}}}} \right)\int\limits_0^\infty {\left( {1 - L\left( u \right)} \right){{u}^{{2m}}}du} $, $m = 0,\;1,\; \ldots $, – постоянные коэффициенты. Заметим, что если слой жестко сцеплен с основанием, эти коэффициенты зависят от коэффициента Пуассона $\nu $ через функцию $L\left( u \right)$.

В [4] указано, что для $\lambda \geqslant 2$ погрешность формул (3.2) и (3.3) не превышает 3%. Также из результатов следует, что при стремлении $\lambda $ к бесконечности, то есть когда толщина слоя значительно больше радиуса пятна контакта, решение (3.2) и (3.3) стремится к решению для случая полупространства, которое имеет вид

Перейдем к вязкоупругому случаю. Учитывая, что коэффициент Пуассона материала слоя не зависит от времени, для контактного давления и нагрузки получим

где ${{q}_{1}} = 1 + {{b}_{0}} + b_{0}^{2} + b_{0}^{3} + b_{0}^{4} - {{b}_{1}}(1 - 3\left( {1 + {{b}_{0}}} \right){{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}})$, ${{Q}_{1}} = 1 + {{b}_{0}} + b_{0}^{2} + b_{0}^{3} + b_{0}^{4}$ + b₁(1 + + 2b₀) – коэффициенты, зависящие от относительной толщины слоя, ${{b}_{0}} = {{2{{a}_{0}}} \mathord{\left/ {\vphantom {{2{{a}_{0}}} {\pi \lambda }}} \right. \kern-0em} {\pi \lambda }}$, b₁ = ${{8{{a}_{1}}} \mathord{\left/ {\vphantom {{8{{a}_{1}}} {3\pi {{\lambda }^{3}}}}} \right. \kern-0em} {3\pi {{\lambda }^{3}}}}$. При заданной функции релаксации соотношения (3.4) и (3.5) определяют контактные давления и нагрузку в разные моменты процесса нагружения в зависимости от механических и геометрических характеристик вязкоупругого слоя.

3.2. Внедрение цилиндра в тонкий вязкоупругий слой. Для малых $\lambda $ воспользуемся решением, которое получено с помощью метода симметричной асимптотики [4]. Из этого решения следуют выражения для контактного давления $p\left( {r,t} \right)$ под штампом с плоским основанием при внедрении его на величину $\delta \left( t \right)$ в тонкий упругий слой, лежащий на жестком основании без сил трения, а также для действующей на штамп суммарной силы P(t):

Здесь ${\text{erf}}(x)$ – функция ошибок (или интеграл вероятности). Для $\lambda \leqslant {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ погрешность в определении контактных давлений и силы по приближенным формулам (3.6) и (3.7) в упругом случае, как указано в [4], не превышает 4%. С использованием упругого решения в вязкоупругом случае для контактного давления и нагрузки получим следующие выражения

где введены коэффициенты ${{q}_{2}} = {{{\text{erf}}\sqrt {{{({{R}^{2}} - {{r}^{2}})} \mathord{\left/ {\vphantom {{({{R}^{2}} - {{r}^{2}})} {2\lambda {{R}^{2}}}}} \right. \kern-0em} {2\lambda {{R}^{2}}}}} } \mathord{\left/ {\vphantom {{{\text{erf}}\sqrt {{{({{R}^{2}} - {{r}^{2}})} \mathord{\left/ {\vphantom {{({{R}^{2}} - {{r}^{2}})} {2\lambda {{R}^{2}}}}} \right. \kern-0em} {2\lambda {{R}^{2}}}}} } \lambda }} \right. \kern-0em} \lambda } + \sqrt {{{{{R}^{2}}} \mathord{\left/ {\vphantom {{{{R}^{2}}} {\pi \lambda ({{R}^{2}} - {{r}^{2}})}}} \right. \kern-0em} {\pi \lambda ({{R}^{2}} - {{r}^{2}})}}} {{e}^{{{{ - ({{R}^{2}} - {{r}^{2}})} \mathord{\left/ {\vphantom {{ - ({{R}^{2}} - {{r}^{2}})} {2\lambda {{R}^{2}}}}} \right. \kern-0em} {2\lambda {{R}^{2}}}}}}}$ и ${{Q}_{2}} = ({1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0em} \lambda } + \sqrt 2 - 1){\text{erf}}\sqrt {{1 \mathord{\left/ {\vphantom {1 {2\lambda }}} \right. \kern-0em} {2\lambda }}} + \sqrt {{2 \mathord{\left/ {\vphantom {2 {\pi \lambda }}} \right. \kern-0em} {\pi \lambda }}} {{e}^{{ - {1 \mathord{\left/ {\vphantom {1 {2\lambda }}} \right. \kern-0em} {2\lambda }}}}}$.

Заметим, что структура зависимостей контактного давления и нагрузки от времени одинакова для случаев тонкого и толстого вязкоупругих слоев, что объясняется линейностью соответствующих зависимостей в упругом случае.

4. Анализ изменения во времени контактных характеристик для различных моделей вязкоупругого слоя. Вид функции релаксации зависит от выбранной вязкоупругой модели материала слоя. В данном исследовании рассмотрены две модели: с экспоненциальной и со степенной функциями релаксации.

4.1. Экспоненциальная функция релаксации. Рассмотрим экспоненциальную функцию релаксации, которая имеет вид

где $\alpha = {1 \mathord{\left/ {\vphantom {1 {{{T}_{\sigma }}}}} \right. \kern-0em} {{{T}_{\sigma }}}} - {1 \mathord{\left/ {\vphantom {1 {{{T}_{\varepsilon }}}}} \right. \kern-0em} {{{T}_{\varepsilon }}}}$, $\beta = {1 \mathord{\left/ {\vphantom {1 {{{T}_{\sigma }}}}} \right. \kern-0em} {{{T}_{\sigma }}}}$, а ${{E}_{0}}$ – мгновенный модуль упругости [16]. Величины ${{T}_{\sigma }}$ и ${{T}_{\varepsilon }}$ – времена релаксации и ползучести вязкоупругого слоя, соответственно. При этом должно выполняться условие ${{{{T}_{\varepsilon }}} \mathord{\left/ {\vphantom {{{{T}_{\varepsilon }}} {{{T}_{\sigma }}}}} \right. \kern-0em} {{{T}_{\sigma }}}} \geqslant 1$, где равенство соответствует упругому случаю. Эту модель также называют стандартным вязкоупругим телом. Регулярные модели, у которых функция релаксации содержит различные комбинации экспоненциальных слагаемых, чаще всего используются для описания механического поведения биологических тканей. Подставив выражения (2.1) и (4.1) в формулы (3.4), (3.5) и (3.8), (3.9), получим

для толстого слоя

для тонкого слоя

Здесь $E = {{E}_{0}}{{\left( {\beta - \alpha } \right)} \mathord{\left/ {\vphantom {{\left( {\beta - \alpha } \right)} \beta }} \right. \kern-0em} \beta }$ соответствует длительному модулю упругости. Стандартное вязкоупругое тело обладает ограниченной релаксацией, что характерно для твердых деформируемых тел.

При расчетах контактных характеристик использовались следующие безразмерные величины: $\tilde {p} = {{p(1 - {{\nu }^{2}})} \mathord{\left/ {\vphantom {{p(1 - {{\nu }^{2}})} E}} \right. \kern-0em} E}$, $\tilde {P} = {{P(1 - {{\nu }^{2}})} \mathord{\left/ {\vphantom {{P(1 - {{\nu }^{2}})} {{{R}^{2}}E}}} \right. \kern-0em} {{{R}^{2}}E}}$, $T = {{{{T}_{\varepsilon }}} \mathord{\left/ {\vphantom {{{{T}_{\varepsilon }}} {{{T}_{\sigma }}}}} \right. \kern-0em} {{{T}_{\sigma }}}} = {\beta \mathord{\left/ {\vphantom {\beta {\left( {\beta - \alpha } \right)}}} \right. \kern-0em} {\left( {\beta - \alpha } \right)}}$, $\tilde {t} = \beta t$ и $\tilde {r} = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R}$.

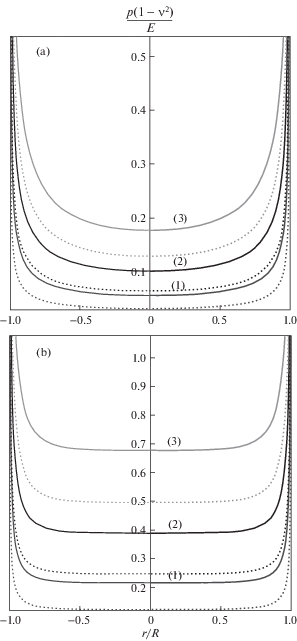
На рис. 2a и 2b представлены графики распределения давления $\tilde {p}\left( {\tilde {r},\tilde {t}} \right)$ в разные моменты времени для тонкого ($\tilde {h}$ = 1/2) и толстого ($\tilde {h} = 2$) слоев, соответственно, рассчитанные из соотношений (4.2) и (4.3) при $\tilde {V} = 0.1$ и T = 2. Для сравнения приведены графики распределения давления для упругого слоя (T = 1, изображены точками) при тех же величинах внедрения цилиндра (1 – $\tilde {\delta }$ = 1/16, 2 – $\tilde {\delta }$ = 1/8, 3 – $\tilde {\delta }$ = 1/4). Из результатов расчетов следует, что как и в упругом случае, с уменьшением толщины слоя давление в центральной части области контакта выравнивается. В центральной части области контакта цилиндра с вязкоупругим слоем при одинаковых внедрениях давление выше, чем в случае упругого слоя. Расчеты, проведенные для стадии удержания, показали, что со временем значение контактного давления в каждой точке снижается и на больших временах удержания стремится к значению, характерному для упругого слоя с длительным модулем упругости E.

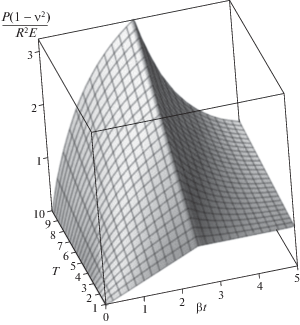
Для исследования влияния вязкоупругих свойств слоя на изменение нагрузки при внедрении и удержании цилиндра были построены трехмерные графики временной зависимости нагрузки $\tilde {P}\left( {\tilde {t}} \right)$ для значений отношения времен релаксации и ползучести $T \in \left[ {1;10} \right]$ для толстого слоя c $\tilde {h} = 2$ при $\tilde {V} = 0.1$ (рис. 3). Анализ стадии нагружения показал, что значение параметра $T$ влияет как на величину силы, действующей на индентор при достижении им заданной глубины внедрения ${{\delta }_{*}} = V{{t}_{*}}$, так и на скорость изменения нагрузки в течение всего процесса взаимодействия. Как следует из (4.3), скорость изменения нагрузки в стадии внедрения удовлетворяет соотношению:

из которого следует, что скорость роста нагрузки со временем падает, а с увеличением вязкости материала эта скорость растет.

В стадии удержания скорость релаксации нагрузки удовлетворяет соотношению:

показывающему, что скорость релаксации прямо пропорциональна параметру $\left( {T - 1} \right)$, характеризующему вязкость материала слоя, и скорости внедрения индентора $V$. Таким образом, поведение функции $P\left( t \right)$ на стадии удержания позволяет сделать выводы о релаксационных свойствах материала. Также экспериментальные данные, полученные на этой стадии процесса, позволяют определить длительный модуль упругости материала по значению горизонтальной асимптоты, соответствующей упругому решению с длительным модулем упругости.

Результаты для тонкого слоя аналогичны, поскольку выражения для изменения нагрузки от времени (4.2) и (4.3) в асимптотическом приближении для тонкого и толстого слоя отличаются лишь коэффициентом, зависящим от относительной толщины слоя. Из результатов расчетов следует, что чем толще слой, тем меньше значение нагрузки в заданный момент времени (при заданной глубине внедрения).

4.2. Степенная функция релаксации. Рассмотрим степенную функцию релаксации, которая имеет вид $G\left( t \right) = {A \mathord{\left/ {\vphantom {A {{{{\left( {\theta t} \right)}}^{\gamma }}}}} \right. \kern-0em} {{{{\left( {\theta t} \right)}}^{\gamma }}}} + E$, где $A$ имеет размерность [Па], $\theta $ – $[{{{\text{с}}}^{{ - 1}}}]$, $\gamma \in (0;1)$, а $E$ соответствует длительному модулю упругости слоя [16]. Эта модель используется для описания релаксации и ползучести полимеров [17]. Подставив выражение для функции релаксации в (3.4), (3.5) и (3.8), (3.9), а также используя выражение для внедрения (2.1), получим

для толстого слоя

для тонкого слоя

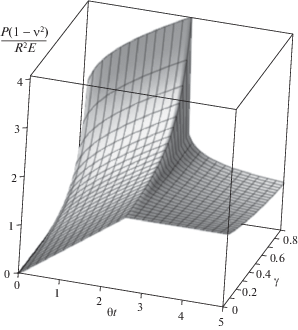
Для расчетов рассматривались следующие безразмерные величины: $\tilde {p}$ = p(1 – ν²)/E, $\tilde {P} = {{P(1 - {{\nu }^{2}})} \mathord{\left/ {\vphantom {{P(1 - {{\nu }^{2}})} {{{R}^{2}}E}}} \right. \kern-0em} {{{R}^{2}}E}}$, $\tilde {A} = {A \mathord{\left/ {\vphantom {A E}} \right. \kern-0em} E}$, $\tilde {t} = \theta t$ и $\tilde {r} = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R}$. На рис. 4 представлен график зависимости нагрузки от времени $\tilde {P}\left( {\tilde {t}} \right)$ при $\tilde {V} = 0.1$ и $\gamma \in \left( {0;1} \right)$ для толстого слоя ($\tilde {h} = 2$). Результаты показывают, что для рассматриваемой модели характерна высокая скорость роста нагрузки в начальный период внедрения цилиндра и высокая скорость релаксации контактных давлений в начале удержания цилиндра на заданной глубине. Эта скорость увеличивается с увеличением параметра $\gamma $. Этот вывод вытекает и из анализа производной функции изменения нагрузки со временем на разных стадиях процесса внедрения:

В стадии же удержания скорость релаксации при $t \to {{t}_{*}} + 0$, в отличие от модели с экспоненциальным ядром релаксации, стремится к бесконечности. Горизонтальной асимптотой при больших временах является прямая, т.е. ${{\left. {P(t)} \right|}_{{t \to + \infty }}} = \pi R{{Q}_{2}}(\lambda )E{{\delta }_{*}}{\text{/}}(1 - {{\nu }^{2}})$, что соответствует упругому решению с длительным модулем упругости.

Зависимость нагрузки от глубины внедрения в стадии нагружения имеет вид:

Отсюда следует, что на заданной глубине внедрения с увеличением скорости погружения возрастает и значение нагрузки, действующей на индентор.

5. Сравнение с одномерной моделью. Рассмотрим упрощенную модель основания, а именно, одномерную модель стандартного вязкоупругого тела. Определяющее соотношение, связывающее контактное давление на поверхности слоя и вертикальное перемещение границы, для данной модели имеет вид [16]

Зависимость контактного давления и нагрузки от времени для такой модели получена в [12] и имеет следующий вид

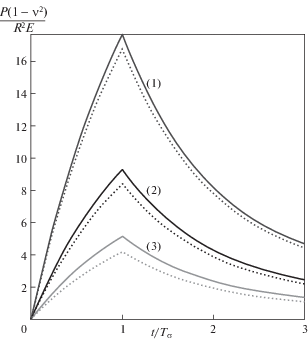
При использовании упрощенной модели мы получаем равномерное распределение давления в области контакта, в отличие от модели сплошной среды. Для сравнения выражений для нагрузок, полученных с использованием стерженьковой модели и модели сплошной среды с экспоненциальной функцией релаксации (см. (4.3)), на рис. 5 представлена зависимость нагрузки от времени $\tilde {P}\left( {\tilde {t}} \right)$ при $\tilde {V} = 0.1$, T = 10 для тонкого слоя разной толщины (1 – $\tilde {h} = {1 \mathord{\left/ {\vphantom {1 8}} \right. \kern-0em} 8}$, 2 – $\tilde {h} = {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}$, 3 – $\tilde {h} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$), где сплошные линии соответствуют модели сплошной среды, а точки – стерженьковой модели. Из полученных результатов следует, что для толщин слоя $h < {R \mathord{\left/ {\vphantom {R 4}} \right. \kern-0em} 4}$ ошибка при использовании упрощенной модели нахождения зависимости нагрузки от времени не превосходит 10%.

6. Заключение. Построена модель, позволяющая изучить внедрение с постоянной скоростью жесткого цилиндра в вязкоупругий слой, лежащий на жестком основании без трения, в предположении, что коэффициент Пуассона слоя не зависит от времени. Модель использована для анализа процесса взаимодействия индентора с основанием, состоящего из двух этапов: внедрения индентора до определенной глубины и его удержание на этой глубине, что позволило исследовать релаксацию контактных напряжений и суммарной силы в зависимости от скорости нагружения и механических характеристик слоя. При этом рассмотрены два вида функций релаксации, характеризующих релаксационное поведение напряжений в различных материалах, обладающих вязкоупругими свойствами: экспоненциальный и степенной.

Полученные в аналитическом виде решения для толстого и тонкого слоя позволили изучить характер изменения контактных напряжений во времени как для относительно малых, так и больших толщин слоя. Проведенный анализ зависимости нагрузки от времени в стадии удержания (скорость релаксации, асимптотика на больших временах) позволил выделить признаки, характерные для каждого вида функции релаксации. Показано, что скорость релаксации в начале стадии удержания и асимптотика графика при больших временах дают возможность определить, какая вязкоупругая модель наиболее адекватно может описать экспериментальные данные по индентированию материала.

Полученные результаты предполагается использовать для анализа экспериментальных результатов индентирования вязкоупругих материалов, а также для решения обратной задачи по определению механических характеристик материалов, в частности, биологических тканей и полимеров, на основе экспериментальных зависимостей.

Работа выполнена при поддержке Российского научного фонда, грант 18-19-00574.