Известия РАН. Механика твердого тела, 2020, № 5, стр. 76-86
НЕЛИНЕЙНЫЕ ЭФФЕКТЫ, МОДЕЛИРУЕМЫЕ ВЯЗКОУПРУГОЙ МОДЕЛЬЮ МАКСВЕЛЛОВСКОГО ТИПА ПРИ КОНЕЧНЫХ ДЕФОРМАЦИЯХ
Н. С. Стеценко *
Московский государственный университет им. М.В. Ломоносова
Москва, Россия
* E-mail: stetsenkonina@mail.ru
Поступила в редакцию 14.10.2019
После доработки 18.10.2019
Принята к публикации 21.10.2019
Аннотация
Для вязкоупругих материалов исследуется обобщение элементарной модели Максвелла на случай конечных деформаций с использованием однопараметрического семейства объективных производных Гордона–Шоуолтера. С помощью полученных определяющих соотношений рассматриваются задачи о простом сдвиге, одноосном растяжении-сжатии и сдвиговых колебаниях, заданных пилообразной функцией. Показано, что полученные аналитические решения этих задач существенно зависят от параметров модели, и, таким образом, рассмотрение семейства объективных производных, частными случаями которого являются производные Олдройда, Коттер–Ривлина и Яуманна, расширяет возможности описания поведения материала. Показано, что анализируемая модель прогнозирует появление эффектов Пойнтинга, Кельвина и Вейссенберга, проявляет неньютоновскую вязкость, обнаруживает ненулевую разность нормальных напряжений (normal stress differences) в задаче о простом сдвиге, моделирует явления уменьшения вязкости как функции скорости сдвига при увеличении скорости сдвига (shear thinning), а также увеличение вязкости как функции скорости деформации растяжения при увеличении скорости деформации одноосного растяжения (extensional thickening).
1. Введение. Широкое использование в промышленности резиноподобных материалов и изделий из них, а также задачи улучшения моделирования поведения материалов, применяемых в огнеметах со времен Второй мировой войны, дали толчок развитию математического аппарата для построения вязкоупругих моделей при конечных деформациях. К нелинейным явлениям, наблюдаемым в экспериментах при конечных деформациях [1–12], можно отнести наличие ненулевой разности нормальных напряжений при сдвиге (в англоязычной литературе – normal stress differences), уменьшение сдвиговой вязкости как функции скорости сдвига при увеличении скорости сдвига (shear thinning – псвевдопластичность) и увеличение продольной вязкости как функции скорости деформации растяжения при увеличении скорости деформации растяжения (extensional thickening – объемное утолщение). Таким образом, одной из важнейших целей, возникающей при построении определяющих соотношений при конечных деформациях вязкоупругих материалов, является моделирование этих эффектов.
Существует множество работ, исследующих обобщение элементарной модели Максвелла на область больших деформаций [10, 11, 13–15]. Такой подход является частным случаем общего метода обобщения определяющих соотношений при малых деформациях на область конечных деформаций. Согласно этому методу новые пары тензорных мер напряжений, деформаций и меры скорости их изменения подставляются в форму определяющих соотношений для малых деформаций [16, 17]. Эти тензорные меры выбираются таким образом, чтобы соблюдался принцип материальной независимости от системы отсчета [18, 19]. Так как использование материальной производной не всегда приводит к реалистичному описанию поведения среды, в дальнейшем мы будем использовать так называемые объективные производные тензора напряжений [20–23]. Корректный выбор объективной производной и тензорных мер напряжений и деформаций позволяет построить модель, удовлетворяющую принципу объективности.
В качестве базовой модели при малых деформациях рассмотрим дифференциальную форму элементарной модели Максвелла [24]:
где E, T – параметры модели. В соответствии с исследуемым подходом $\sigma $ из (1.1) далее заменяется, например, тензором истинных напряжений Коши S, $\dot {\varepsilon }$ из (1.1) – тензором скорости деформации V, а производная по времени от напряжения из (1.1) заменяется однопараметрическим семейством объективных производных Гордона–Шоуолтера, которое исследуется, например, в [25–29]:(1.3)
${\mathbf{D}}_{\alpha }^{{}}[{\mathbf{S}}] = {\mathbf{\dot {S}}} - {\mathbf{\Omega }} \cdot {\mathbf{S}} + {\mathbf{S}} \cdot {\mathbf{\Omega }} - \alpha ({\mathbf{V}} \cdot {\mathbf{S}} + {\mathbf{S}} \cdot {\mathbf{V}})$2. Определяющее соотношение при конечных деформациях для несжимаемого вязкоупругого материала. Преобразуем выражение (1.3) к виду:
(2.1)
${\mathbf{\dot {S}}} = - {{{\mathbf{Z}}}^{T}} \cdot {\mathbf{S}} - {\mathbf{S}} \cdot {\mathbf{Z}} + E{\mathbf{V}} - {{T}^{{ - 1}}}{\mathbf{S}}$Далее будем считать рассматриваемый вязкоупругий материал несжимаемым. В этом случае тензор напряжения Коши находится с точностью до неопределенного шарового тензора –pI и может быть представлен в виде:
3. Кинематические соотношения и соответствующее им напряженное состояние в задаче о простом сдвиге вязкоупругого слоя. Закон движения сплошной среды при простом сдвиге вдоль оси x2 в плоскости $O{{x}_{2}}{{x}_{3}}$ имеет вид [31]:
(3.1)
${{x}_{1}} = x_{1}^{0},\quad {{x}_{2}} = x_{2}^{0} + k(t)x_{3}^{0},\quad {{x}_{3}} = x_{3}^{0}$Здесь $x_{i}^{0}$ и xi – декартовы координаты материальной точки в начальный и текущий моменты времени. Компоненты введенных выше матриц для движения среды (3.1) имеют вид:
Подставляя полученную матрицу Z в выражение (2.1), придем к системе дифференциальных уравнений относительно компонент тензора ${\mathbf{S}}$:
(3.2)
$\begin{gathered} {{{\dot {S}}}_{{11}}} = - {{S}_{{11}}}{\text{/}}T,\quad {{{\dot {S}}}_{{23}}} = - {{S}_{{23}}}{\text{/}}T + \dot {k}(t)((\alpha + 1){{S}_{{33}}} - (1 - \alpha ){{S}_{{22}}}){\text{/}}2 + E\dot {k}(t){\text{/}}2 \\ {{{\dot {S}}}_{{22}}} = - {{S}_{{22}}}{\text{/}}T + \dot {k}(t)(\alpha + 1){{S}_{{23}}},\quad {{{\dot {S}}}_{{33}}} = - {{S}_{{33}}}{\text{/}}T - \dot {k}(t)(1 - \alpha ){{S}_{{23}}} \\ {{{\dot {S}}}_{{12}}} = - {{S}_{{12}}}{\text{/}}T + \dot {k}(t)(\alpha + 1){{S}_{{13}}}{\text{/}}2,\quad {{{\dot {S}}}_{{13}}} = - {{S}_{{13}}}{\text{/}}T - \dot {k}(t)(1 - \alpha ){{S}_{{12}}}{\text{/}}2 \\ \end{gathered} $Заметим, что ${{S}_{{22}}}(1 - \alpha ) = - {{S}_{{33}}}(\alpha + 1).$ При начальном условии ${\mathbf{S}}(0) = 0$ получим ${{S}_{{11}}}(t) = {{S}_{{12}}}(t)$ = S13(t) = 0, а для компонент S22, S23 имеем линейную неоднородную систему обыкновенных дифференциальных уравнений с переменными коэффициентами с матрицей B(t) и правой частью b(t):
Так как произведение матрицы B(t) и интеграла от этой матрицы $\int_0^t {{\mathbf{B}}(\tau )} d\tau $ коммутативно (выполняется условие Лаппо-Данилевского [32]), то фундаментальная матрица этой системы имеет вид ${\mathbf{\Phi }}(t) = {{e}^{{\int_0^t {{\mathbf{B}}(\tau )d\tau } }}} = {\mathbf{H}}(t) \cdot {{{\mathbf{e}}}^{{{\mathbf{J}}(t)}}} \cdot {\mathbf{H}}{{(t)}^{T}}$, где H(t) – матрица перехода матрицы от $\int_0^t {{\mathbf{B}}(\tau )} d\tau $ к ее жордановой форме ${\mathbf{J}}(t) = {\mathbf{H}}{{(t)}^{{ - 1}}} \cdot \int_0^t {{\mathbf{B}}(\tau )d\tau \cdot } {\mathbf{H}}(t)$. Вычисления дают:
Общее решение исходной неоднородной системы находится как ${\mathbf{S}}(t) = {\mathbf{\Phi }}(t) \cdot {\mathbf{C}}(t)$, где
(3.3)
${\mathbf{\dot {C}}}(t) \sim \left( \begin{gathered} - E\dot {k}(t){{e}^{{t/T}}}\sin (k(t)\sqrt {1 - {{\alpha }^{2}}} )(\alpha + 1){\text{/}}(2\sqrt {1 - {{\alpha }^{2}}} ) \\ E\dot {k}(t){{e}^{{t/T}}}\cos (k(t)\sqrt {1 - {{\alpha }^{2}}} ){\text{/}}2 \\ \end{gathered} \right)$В частных случаях k(t) компоненты (3.3) удается аналитически проинтегрировать и получить точное решение задачи о сдвиге. Для $k(t) = ut$, u = const из (3.3) получим:
Тогда аналитическое решение системы (3.2) имеет вид:
(3.4)
$\begin{gathered} {{S}_{{11}}}(t) = {{S}_{{12}}}(t) = {{S}_{{13}}}(t) = 0,\quad {{S}_{{22}}}(t)(1 - \alpha ) = - {{S}_{{33}}}(t)(\alpha + 1) \\ {{S}_{{23}}}(t) = 1{\text{/}}2ETu{{\{ 1 - {{e}^{{ - t/T}}}\cos (Xt) + TX{{e}^{{ - t/T}}}\sin (Xt)\} } \mathord{\left/ {\vphantom {{\{ 1 - {{e}^{{ - t/T}}}\cos (Xt) + TX{{e}^{{ - t/T}}}\sin (Xt)\} } {[1 + {{T}^{2}}{{X}^{2}}]}}} \right. \kern-0em} {[1 + {{T}^{2}}{{X}^{2}}]}} \\ {{S}_{{33}}}(t) = 1{\text{/}}2(1 - \alpha )ETu\{ [{{e}^{{ - t/T}}}\sin (Xt){\text{/}}\sqrt {1 - {{\alpha }^{2}}} ] - \\ - \;{{Tu[1 - {{e}^{{ - t/T}}}\cos (Xt)]\} } \mathord{\left/ {\vphantom {{Tu[1 - {{e}^{{ - t/T}}}\cos (Xt)]\} } {[1 + {{T}^{2}}{{X}^{2}}]}}} \right. \kern-0em} {[1 + {{T}^{2}}{{X}^{2}}]}} \\ \end{gathered} $Нормальные компоненты тензора напряжений находятся лишь с точностью до гидростатического давления [31]: ${{\sigma }_{{\beta \beta }}}(t) = {{S}_{{\beta \beta }}}(t) - p$, β = 1–3.
Из (3.4) получим, что в задаче о простом сдвиге исследуемая модель демонстрирует наличие не равного нулю среднего нормального напряжения, отличные от нуля разности нормальных напряжений (что отвечает ортогональным эффектам Кельвина и Пойнтинга для твердых тел и эффекту Вейссенберга для жидкостей соответственно [28, 31, 33–35]), проявляет неньютоновскую сдвиговую вязкость [10, 11]. Ниже в (3.5) эти величины приведены в неустановившемся и в установившемся состоянии:
(3.5)
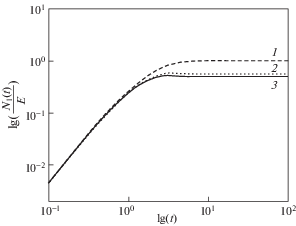
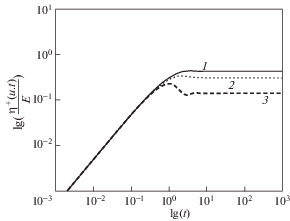
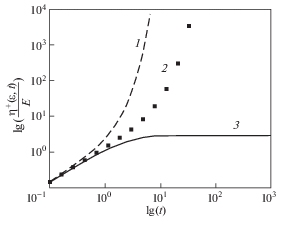
$\begin{gathered} {{N}_{1}}(t) = {{\sigma }_{{22}}}(t) - {{\sigma }_{{33}}}(t) = \\ = \; - ETu{{\{ [{{e}^{{ - t/T}}}{{\sin (Xt)} \mathord{\left/ {\vphantom {{\sin (Xt)} {\sqrt {1 - {{\alpha }^{2}}} }}} \right. \kern-0em} {\sqrt {1 - {{\alpha }^{2}}} }}] - Tu[1 - {{e}^{{ - t/T}}}\cos (Xt)]\} } \mathord{\left/ {\vphantom {{\{ [{{e}^{{ - t/T}}}{{\sin (Xt)} \mathord{\left/ {\vphantom {{\sin (Xt)} {\sqrt {1 - {{\alpha }^{2}}} }}} \right. \kern-0em} {\sqrt {1 - {{\alpha }^{2}}} }}] - Tu[1 - {{e}^{{ - t/T}}}\cos (Xt)]\} } {[1 + {{T}^{2}}{{X}^{2}}]}}} \right. \kern-0em} {[1 + {{T}^{2}}{{X}^{2}}]}} \\ {{N}_{1}} = \mathop {\lim }\limits_{t \to \infty } {{N}_{1}}(t) = E{{T}^{2}}{{u}^{2}}{\text{/}}(1 + {{T}^{2}}{{u}^{2}}(1 - {{\alpha }^{2}})) \\ {{N}_{2}}(t) = {{\sigma }_{{33}}}(t) - {{\sigma }_{{11}}}(t) = - 1{\text{/}}2(1 - \alpha ){{N}_{1}}(t),\quad {{N}_{2}} = - 1{\text{/}}2(1 - \alpha ){{N}_{1}} \\ {{\eta }^{ + }}(u,t) = {{\sigma }_{{23}}}(t){\text{/}}u = 1{\text{/}}2ET{{\{ 1 - {{e}^{{ - t/T}}}\cos (Xt) + TX{{e}^{{ - t/T}}}\sin (Xt)\} } \mathord{\left/ {\vphantom {{\{ 1 - {{e}^{{ - t/T}}}\cos (Xt) + TX{{e}^{{ - t/T}}}\sin (Xt)\} } {[1 + {{T}^{2}}{{X}^{2}}]}}} \right. \kern-0em} {[1 + {{T}^{2}}{{X}^{2}}]}} \\ \eta (u) = \mathop {\lim }\limits_{t \to \infty } {{\eta }^{ + }}(u,t) = 1{\text{/}}2ET{\text{/}}(1 + {{T}^{2}}{{u}^{2}}(1 - {{\alpha }^{2}})) \\ \end{gathered} $Из (3.5) получаем ненулевые значения ${{N}_{1}}$, ${{N}_{2}}$ для $\alpha \in ( - 1,\;1)$ (${{N}_{2}} = 0$ для α = 1). Зависимость $\lg ({{N}_{1}}(t){\text{/}}E)$ как функция $\lg (t)$ при различных значениях параметра α показана на рис. 1: кривая 1 соответствует $\alpha = \pm 1$, кривая 2 – $\alpha = \pm 0.5$, кривая 3 – α = 0. Поскольку разности нормальных напряжений и сдвиговая вязкость находятся из экспериментов, причем существуют методы их измерения как в установившемся, так и неустановившемся состоянии, то по данным испытаний можно найти параметры модели, наилучшим образом подходящие исследуемому материалу. Из (3.5) имеем $ - {{N}_{1}}{\text{/}}{{N}_{2}}$ = 0.5(1 – α), т.е. для рассматриваемых определяющих уравнений отношение $ - {{N}_{1}}{\text{/}}{{N}_{2}}$ не зависит от скорости сдвига. Известно, что, например, для полимеров отношение $ - {{N}_{1}}{\text{/}}{{N}_{2}} \in [0.05,\;0.3]$ [10], таким образом, мы можем получить значения параметра α, удовлетворяющие этому отрезку и соответствующие полимерам: $\alpha \in [0.4$, 0.9]. Из (3.5) видно, что функция $\eta (u)$ убывает, что говорит о качественном описании явления псевдопластичности (shear thinning [9–11]) рассматриваемой моделью в установившемся состоянии. В качестве примера для α = 0.6, как для частного случая отрезка [0.4, 0.9], на рис. 2 изображена величина $\lg ({{\eta }^{ + }}(u,t){\text{/}}E)$ для фиксированных значений скорости сдвига в зависимости от lg(t): кривая 1 для $u = 0.5$ c–1, кривая 2 – $u = 1$ c–1, кривая 3 – $u = 2$ c–1. Таким образом, проиллюстрировано прогнозирование явления сдвигового утончения в измерениях, проводимых и в неустановившемся состоянии. Можно получить условия на параметр α в зависимости от скорости сдвига такие, что компоненты напряжения (3.4) будут монотонными функциями времени. И, обратно, можно получить условия на скорость сдвига так, чтобы для заданного значения $\alpha $ компоненты напряжения были монотонными функциями времени [28].
4. Случай сдвиговых колебаний, задаваемых пилообразной функцией. Рассмотрим случай сдвиговых колебаний таких, что функция k(t) из (3.1) имеет вид k(t) = $A\arcsin \sin (\omega t)$. Обозначим далее для удобства $f(t): = A\arcsin \sin (\omega t)$, G(t) := := $A\omega {\text{sign}}\cos (\omega t)$, $B: = \sqrt {1 - {{\alpha }^{2}}} $. При колебаниях такого вида компоненты вектора (3.3) также могут быть аналитически проинтегрированы:
Тогда в рассматриваемом случае аналитическое решение системы (3.2) имеет вид:
(4.1)
$\begin{gathered} {{S}_{{11}}}(t) = {{S}_{{12}}}(t) = {{S}_{{13}}}(t) = 0,\quad {{S}_{{22}}}(t)(1 - \alpha ) = - {{S}_{{33}}}(t)(\alpha + 1) \\ {{S}_{{23}}}(t) = \frac{{0.5ETG(t)}}{{1 + {{T}^{2}}{{B}^{2}}G{{{(t)}}^{2}}}} \times \\ \times \;\{ G(t) - G(t){{e}^{{ - t/T}}}\cos (Bf(t)) + TG{{(t)}^{2}}B{{e}^{{ - t/T}}}\sin (Bf(t))\} \\ {{S}_{{33}}}(t) = \frac{{0.5(1 - \alpha )ETG(t)}}{{1 + {{T}^{2}}{{B}^{2}}G{{{(t)}}^{2}}}}\{ [{{e}^{{ - t/T}}}{\text{sin}}(Bf(t)){\text{/}}B] - TG(t)[1 - {{e}^{{ - t/T}}}{\text{cos}}(Bf(t))]\} \\ \end{gathered} $Здесь также нормальные компоненты тензора напряжений находятся с точностью до гидростатического давления.
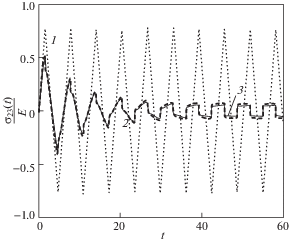
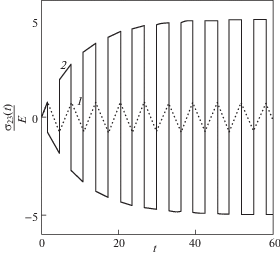
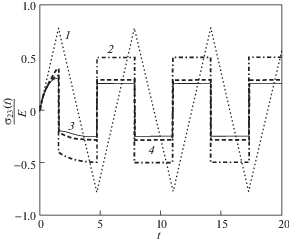
Из рис. 3–5 видно, что полученное решение (4.1) существенно зависит от параметров модели. Так на рис. 3 материал демонстрирует уменьшение амплитуды колебаний касательного напряжения в ответ на рассматриваемую сдвиговую кинематику: кривая 1 на рис. 3–5 соответствует компоненте ${{\varepsilon }_{{23}}}(t)$ тензора деформации Коши–Грина, пунктирная кривая 2 – компоненте ${{\sigma }_{{23}}}(t){\text{/}}E$ при $\alpha = \pm 0.5$, T = 10 с, сплошная кривая 3 – компоненте ${{\sigma }_{{23}}}(t){\text{/}}E$ при α = 0, T = 10 с. На рис. 4 материал, напротив, проявляет увеличение амплитуды колебаний компоненты ${{\sigma }_{{23}}}(t){\text{/}}E$ в зависимости от времени: сплошная кривая 2 соответствует ${{\sigma }_{{23}}}(t){\text{/}}E$ при $\alpha = \pm 1$, T = 10 с. На рис. 5 заметна лишь небольшая зона роста амплитуды ${{\sigma }_{{23}}}(t){\text{/}}E$: штрих-пунктирная кривая 2 отвечает $\alpha = \pm 1$, T = 1 с, сплошная кривая 3 – $\alpha = \pm 0.5$, T = 1 с, пунктирная кривая 4 – $\alpha = 0$, T = 1 с.
5. Одноосное растяжение–сжатие. Рассмотрим движение среды, задаваемое кинематическими соотношениями вида:
(5.1)
${{x}_{1}} = {{\lambda }_{1}}(t)x_{1}^{0},\quad {{x}_{2}} = {{\lambda }_{2}}(t)x_{2}^{0},\quad {{x}_{3}} = {{\lambda }_{3}}(t)x_{3}^{0}$Компоненты введенных выше матриц имеют вид:
Подставляя полученную матрицу $\hat {Z}$ в выражение (2.1), придем к неоднородной системе линейных обыкновенных дифференциальных уравнений с переменными коэффициентами относительно компонент тензора $\hat {S}$:
(5.2)
$\begin{gathered} {{{\dot {S}}}_{{11}}} = 2\alpha \frac{{\dot {\lambda }(t)}}{{\lambda (t)}}{{S}_{{11}}} + E\frac{{\dot {\lambda }(t)}}{{\lambda (t)}} - \frac{{{{S}_{{11}}}}}{T},\quad {{{\dot {S}}}_{{12}}} = - \frac{{{{S}_{{12}}}}}{T} \\ {{{\dot {S}}}_{{13}}} = - \frac{{{{S}_{{13}}}}}{T},\quad {{{\dot {S}}}_{{23}}} = - \frac{{{{S}_{{23}}}}}{T} \\ {{{\dot {S}}}_{{\beta \beta }}} = - \alpha \frac{{\dot {\lambda }(t)}}{{\lambda (t)}}{{S}_{{\beta \beta }}} - \frac{E}{2}\frac{{\dot {\lambda }(t)}}{{\lambda (t)}} - \frac{{{{S}_{{\beta \beta }}}}}{T} \\ \end{gathered} $(5.3)
$\begin{gathered} {{S}_{{11}}}(t) = E\dot {\varepsilon }{{e}^{{( - 1/T + 2\alpha \dot {\varepsilon })t}}}{\text{/}}(2\alpha \dot {\varepsilon } - 1{\text{/}}T) - E\dot {\varepsilon }{\text{/}}(2\alpha \dot {\varepsilon } - 1{\text{/}}T) \\ {{S}_{{22}}}(t) = {{S}_{{33}}}(t) = E\dot {\varepsilon }{{e}^{{( - 1/T - \alpha \dot {\varepsilon })t}}}{\text{/}}[2(\alpha \dot {\varepsilon } + 1{\text{/}}T)] - E\dot {\varepsilon }{\text{/}}[2(\alpha \dot {\varepsilon } + 1{\text{/}}T)] \\ \end{gathered} $Как и ранее имеем ${{\sigma }_{{\beta \beta }}} = {{S}_{{\beta \beta }}} - p$, $\beta = 1 - 3$, p – гидростатическое давление.
Из решения (5.3) получим условие на параметры модели, необходимые для того, чтобы решение было физично: $(2\alpha \dot {\varepsilon } - 1{\text{/}}T) < 0$, $ - 1{\text{/}}T - \alpha \dot {\varepsilon } < 0$. В установившемся состоянии для нормальных компонент напряжения и вязкости получим:
(5.4)
$\begin{gathered} {{\sigma }_{{11}}} = E\dot {\varepsilon }{\text{/}}(1{\text{/}}T - 2\alpha \dot {\varepsilon }) - p,\quad {{\sigma }_{{22}}} = {{\sigma }_{{33}}} = - E\dot {\varepsilon }{\text{/}}[2(\alpha \dot {\varepsilon } + 1{\text{/}}T)] - p \\ {{\eta }^{ + }}(\dot {\varepsilon },t) = [{{\sigma }_{{11}}}(t) - {{\sigma }_{{22}}}(t)]{\text{/}}\dot {\varepsilon }, \\ \eta (\dot {\varepsilon }) = \mathop {\lim }\limits_{t \to \infty } {{\eta }^{ + }}(\dot {\varepsilon },t) = 3E{\text{/}}[2(1{\text{/}}T - 2\alpha \dot {\varepsilon })(\alpha \dot {\varepsilon } + 1{\text{/}}T)] \\ \end{gathered} $Видим из (5.4), что вязкость $\eta (\dot {\varepsilon })$ значительно увеличивается по мере приближения величины $\dot {\varepsilon }$ к 1/2αT. Таким образом, из $(2\alpha \dot {\varepsilon } - 1{\text{/}}T) < 0$ можно для заданного $\dot {\varepsilon }$ получить условия на параметры модели, при которых будет наблюдаться явление объемного утолщения (extensional thickening [6, 9–11]): $2\alpha T < 1{\text{/}}\dot {\varepsilon }$. И, наоборот, для заданных α, T получим условие для $\dot {\varepsilon }$, при соблюдении которого вязкость $\eta (\dot {\varepsilon })$ будет возрастать как функция $\dot {\varepsilon }$: $\dot {\varepsilon } < 1{\text{/}}2\alpha T$ (за исключением случая α = 0, при котором вязкость из (5.4) не зависит от $\dot {\varepsilon }$). На рис. 6 для α = 0.6 показана величина $\lg ({{\eta }^{ + }}(\dot {\varepsilon },t){\text{/}}E)$ при нескольких фиксированных значениях $\dot {\varepsilon }$ в зависимости от $\lg (t)$: кривая 1 построена при $\dot {\varepsilon } = 2$ c–1, кривая 2 – $\dot {\varepsilon } = 1$ c–1, кривая 3 – $\dot {\varepsilon } = 0.5$ c–1. Видим, что в неустановившемся состоянии также проявляется явление объемного утолщения.
В случае одноосного сжатия получим выражение для продольной вязкости в виде:
(5.5)
$\eta (\dot {\varepsilon }) = \mathop {\lim }\limits_{t \to \infty } {{\eta }^{ - }}(\dot {\varepsilon },t) = 3E{\text{/}}[2(1{\text{/}}T + 2\alpha \dot {\varepsilon })( - \alpha \dot {\varepsilon } + 1{\text{/}}T)]$Таким образом, получаем, что в рассматриваемой модели вязкость при растяжении отличается от вязкости при сжатии, что характерно для неньютоновских вязких жидкостей. Однако, при малых значениях $\dot {\varepsilon }$ выражения (5.4) и (5.5) дают одно и тоже значение для вязкости, что справедливо для линейной теории. Кроме того, при малых значениях скорости сдвига и кратности удлинения получим, что сдвиговая вязкость связана с продольной в соответствии с законом Трутона: $\eta (u) = 3\eta (\dot {\varepsilon })$ [35].
Выводы. В работе рассмотрен метод построения определяющих соотношений вязкоупругих материалов при конечных деформациях. Предложенная модель удовлетворяет принципу материальной объективности, обобщает элементарную модель Максвелла и использует семейство объективных производных Гордона–Шоуолтера.
Для случаев простого сдвига, сдвиговых колебаний, заданных пилоообразной функцией, и одноосного растяжения–сжатия вязкоупругой среды получены аналитические решения уравнений, заданных построенными определяющими соотношениями. В задаче о сдвиге с постоянной скоростью показано, что модель качественно описывает эффекты Пойнтинга и Кельвина для твердых тел и эффект Вейссенберга для жидкостей, проявляет неньютоновскую вязкость, которая уменьшается при увеличении скорости сдвига. Для случая колебаний, заданных пилообразной функцией, существенная зависимость полученного решения от параметров модели позволяет получить увеличение и уменьшение амплитуды касательного напряжения, а также близкий к стабильному отклик в ответ на рассматриваемую кинематику. В задаче об одноосном растяжении–сжатии получены условия на параметры модели, при которых наблюдается явление увеличения вязкости при увеличении кратности удлинения.
Список литературы
Weissenberg K. A continuum theory of rheological phenomena // Nature. 1947. V. 159. № 4035. P. 310–311.
Pollett W.F.O., Cross A.H. A continuous-shear rheometer for measuring total stress in rubber-like materials // J. Sci. Instrum. 1950. V. 27. № 8. P. 209–212.
Christiansen E.B., Leppard W.R. Steady-state and oscillatory flow properties of polymer solutions // Trans. Soc. Rheol. 1974. V. 18. № 1. P. 65–86.
Meissner J., Garbella R.W., Hostettler J. Measuring normal stress differences in polymer melt shear flow // J. Rheol. 1989. V. 33. № 6. P. 843–864.
Cross M.M. Relation between viscoelasticity and shear-thinning behaviour in liquids // Rheol. Acta. 1979. V. 18. № 5. P. 609–614.
Meissner J. Experimental aspects in polymer melt elongational rheometry // Chem. Eng. Commun. 1985. V. 33. P. 159–180.
Bird R.B., Carreau P.J. A nonlinear viscoelastic model for polymer solutions and melts-I // Chem. Eng. Sci. 1968. V. 23. № 5. P. 427–434.
Keentok M., Georgescu A.G., Sherwood A.A., Tanner R.I. The measurement of the second normal stress difference for some polymer solutions // J. Non-Newtonian Fluid. 1980. V. 6. P. 303–324.
Wagner M.H. Analysis of time-dependent non-linear stress-growth data for shear and elongational flow of a low-density branched polyethylene melt // Rheol. Acta 1976. V. 15. № 2. P. 136–142.
Macosco C.W. Rheology: principles, measurements and applications. N. Y.: WILEY-VCH, 1993. 568 p.
Cho K.S. Viscoelasticity of polymers: Theory and numerical algorithms. D.: Springer, 2016. V. 241. 612 p.
Бегун А.С., Ковтанюк Л.В., Лемза А.О. Смена механизмов накопления необратимых деформаций материалов на примере их вискозиметрического деформирования // Изв. РАН. МТТ. 2018. № 1. С. 103–112.
Spriggs T.W. A four-constant model for viscoelastic fluids // Chem. Eng. Sci. 1965. V. 20. № 11. P. 931–940.
Olsson F., Ystr$\ddot {o}$m J. Some properties of the upper-convected Maxwell model for viscoelastic fluid flow // J. Non-Newtonian Fluid. 1993. V. 48. P. 125–145.
Giacomin A.J., Bird R.B., Johnson L.M., Mix A.W. Large-amplitude oscillatory shear flow from the corotational Maxwell model // J. Non-Newtonian Fluid. 2011. V. 166. P. 1081–1099.
Бровко Г.Л. Определяющие соотношения механики сплошной среды. Pазвитие математического аппарата и основ общей теории. М.: Наука, 2017. 432 с.
Шуткин А.С. Подходы к обобщению определяющих соотношений деформируемых твердых тел на область конечных деформаций // МКМК. 2010. Т. 16. № 2. С. 166–180.
Ильюшин А.А. Механика сплошной среды. М.: Изд-во Моск. ун-та, 1990. 310 с.
Noll W. A mathematical theory of the mechanical behavior of continuous media // Arch. Rat. Mech. Anal. 1958. V. 2. P. 197–226.
Oldroyd J.G. On the formulation of rheological equations of state // Proc. R. Soc. 1950. V. 200. P. 523–541.
Cotter B.A., Rivlin R.S. Tensors associated with time-dependent stress // Quart. Appl. Math. 1955. V. 13. № 2. P. 177–188.
Dienes J.K. On the analysis of rotation and stress rate in deforming bodies // Acta Mech. 1979. V. 32. № 4. P. 217–232.
Gordon, R.J., Schowalter W.R. Anisotropic fluid theory: a different approach to the dumbbell theory of dilute polymer solutions // Trans. Soc. Rheol. 1972. V. 16. P. 79–97.
Ильюшин А.А., Победря Б.Е. Математические основы термовязкоупругости. М.: Наука, 1970. 280 с.
Da Costa Mattos H.S. Some remaks about the use of Gordon-Schowalter time derivative in rate-type viscoelastic constitutive equations // Int. J. Eng. Sci. 2013. V. 73. P. 56–66.
Johnson M.W., Jr., Segalman D. Model for viscoelastic fluid behavior which allows non-affine deformation // J. Non-Newtonian Fluid. 1977. V. 2. № 3. P. 255–270.
Lee Y.J., Xu J. New formulations, positivity preserving discretizations and stability analysis for non-Newtonian flow models // Comput. Method. Appl. M. 2006 V. 195. P. 1180–1206.
Мартынова Е.Д., Стеценко Н.С. Использование объективных производных Гордона–Шоуолтера для описания конечных деформаций вязкоупругих тел // Вестн. МГУ. Сер. 1. Мат. Мех. 2017. № 6. С. 64–68.
Мартынова Е.Д. Процессы кручения цилиндрических образцов из несжимаемых вязкоупругих материалов максвелловского типа // ПММ. 2019. Т. 83. № 1. С. 95–106.
Бровко Г.Л. Свойства и интегрирование некоторых производных по времени от тензорных процессов в механике сплошной среды // Изв. АН СССР. МТТ. 1990. № 1. С. 54–60.
Truesdell C. A First Course in Rational Continuum Mechanics. N.Y.: Academic Press, 1977. 304 p. = Трусдел К. Первоначальный курс рациональной механики сплошных сред. М.: Мир, 1975. 572 с.
Демидович Б.П. Лекции по математической теории устойчивости. М.: Наука, 1967. 472 с.
Георгиевский Д.В. Порядок малости эффекта Пойнтинга с позиций аппарата тензорно нелинейных функций // Изв. РАН. МТТ. 2018. № 4. С. 29–33.
Георгиевский Д.В. Об ортогональных эффектах напряженно-деформированного состояния в механике сплошной среды // Вестн. КНУ Сер. 2013. № 3. С. 114–116.
Виноградов Г.В., Малкин А.А. Реология полимеров. М.: Химия, 1977. 440 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела