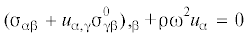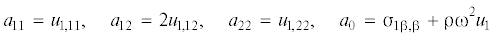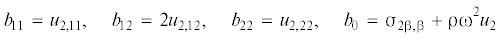Известия РАН. Механика твердого тела, 2020, № 5, стр. 27-37
К ВОССТАНОВЛЕНИЮ ХАРАКТЕРИСТИК ПЛОСКОГО НАЧАЛЬНОГО НАПРЯЖЕННОГО СОСТОЯНИЯ
А. О. Ватульян a, b, *, Р. Д. Недин a, **
a Южный федеральный университет
Ростов-на-Дону, Россия
b Южный математический институт ВНЦ РАН
Владикавказ, Россия
* E-mail: vatulyan@math.rsu.ru
** E-mail: rdn90@bk.ru
Поступила в редакцию 23.03.2020
После доработки 28.03.2020
Принята к публикации 18.04.2020
Аннотация
Сформулирована модель планарных колебаний плоской области при наличии полей предварительных напряжений. Представлены различные постановки двумерных обратных задач о восстановлении предварительного напряженного состояния. Предложены и обсуждены методики и алгоритмы решения поставленных обратных задач.
1. Введение. Анализ и оценка предварительного напряженного состояния (ПНС) в технических деталях и компонентах может значительно повысить точность прогнозирования отказов элементов конструкций. Оценка уровня остаточных напряжений обычно проводится с помощью различных экспериментальных методов – разрушающих, полуразрушающих и неразрушающих. Наиболее перспективными из них являются неразрушающие методы. Вместе с тем такие методы требуют построения адекватных, экспериментально подтвержденных, теоретических моделей неоднородных предварительных напряжений (ПН) для конкретных материалов; также необходимо создание математического аппарата, позволяющего достоверно идентифицировать внутреннее неоднородное распределение ПН в телах в рамках различных концепций неразрушающего контроля.
Зачастую поля ПН образуются в деталях в процессе поверхностной обработки, такой как дробеструйный наклеп, лазерная ударная обработка, шлифовка и др. В работе [1] представлена методика, основанная на методе собственных деформаций и методе конечных элементов, которая позволяет прогнозировать поля остаточных напряжений, возникающие в результате обработки поверхности произвольного трехмерного тела. Представлена упрощенная методика, которая значительно снижает вычислительные затраты на этапе предварительной обработки экспериментальных данных. Показано, что характерная общая обработка поверхности, включающая термомеханическую деформацию, может быть описана простой непрерывной функцией, которая зависит от глубины поверхностной обработки. В работе [2] предлагаются подходы к определению поля остаточных напряжений, образованных в результате процесса шлифовки образцов, выполненных из однородных материалов. Разработана математическая модель, учитывающая влияние упрочнения на прогнозирование хода распределения продольного растягивающего напряжения в прямоугольном линейном направляющем устройстве. Подход к измерению остаточных напряжений на поверхности апробирован с помощью применения метода дифракции рентгеновских лучей.
Одним из широко применяемых и развивающихся в настоящее время неразрушающих методов определения параметров ПНС является индентирование, весьма популярное за счет его простоты использования и применимости в макро-, микро- и наномасштабе. Авторы работы [3] впервые сформулировали связь между параметрами вдавливания и остаточным напряжением; при этом поле остаточных напряжений считалось одноосным. С тех пор развиваются теоретические подходы к определению более сложных типов остаточного напряженного состояния с помощью технологии индентирования. Например, авторы работы [4] провели методом конечных элементов (МКЭ) обширный анализ с целью изучения влияния осесимметричного поля остаточных напряжений и пластических параметров на реакцию на вдавливание в конструкционную сталь. В работе [5] проанализировано влияние предела текучести и отношения компонент двухосного поля ПН на точность процедуры определения остаточных напряжений в металлах с помощью индентирования.
МКЭ на основе метода перемещений активно используется в последнее время для определения полей ПН механических деталей. Этот метод наиболее пригоден для восстановления полей остаточных напряжений путем моделирования реальных производственных процессов, таких как литье, механическая обработка и сварка. Например, в [6] авторы проанализировали распределение остаточных напряжений при сварке с помощью создания полноразмерной точной конечноэлементной модели; в работе [7] проведена симуляция натурных экспериментов по микроиндентированию для анализа остаточных напряжений в стальном образце. В работе [8] описан метод прогнозирования остаточного напряженного состояния по измерениям на поверхности с использованием МКЭ и применен к балочному образцу.
Отметим, что существует множество подходов к моделированию ПН в твердых телах. Ряд моделей основан на линеаризации нелинейных соотношений механики сплошных сред и описан в работах [9–13]. На основе такого подхода в серии работ [13–20] предложены теоретические основы для определения неоднородных полей ПН (одноосных и плоских) в упругих телах на основе метода акустического зондирования. Предложенные методы главным образом базируются на итеративно-регуляризационных схемах решения соответствующих некорректных коэффициентных обратных задач. Преимущества таких подходов связаны с использованием дополнительной информации об измерении полей перемещений на части поверхности тела, которая может быть получена в рамках неразрушающих методов зондирования, а также с возможностью восстанавливать переменные материальные свойства и изменения компонент ПН по координатам. В настоящей работе представлены различные постановки плоских обратных задач о восстановлении параметров ПНС; предложены и обсуждены новые методики и алгоритмы решения поставленных обратных задач.
2. Планарные колебания плоской предварительно напряженной области. Рассмотрим задачу об установившихся планарных колебаниях плоской области S в рамках линеаризованной модели предварительно напряженного тела, наиболее употребительной в литературе [9–12]:
(2.2)
${{T}_{{{\alpha \beta }}}} = {{{\sigma }}_{{{\alpha \beta }}}} + {{u}_{{{\alpha ,\gamma }}}}{\sigma }_{{{\gamma \beta }}}^{{\text{0}}}$(2.3)
${{{\sigma }}_{{{\alpha \beta }}}} = {\lambda }{{{\delta }}_{{{\alpha \beta }}}}{{u}_{{{\gamma ,\gamma }}}} + {\mu }({{u}_{{{\alpha ,\beta }}}} + {{u}_{{{\beta ,\alpha }}}})$(2.4)
${{\left. {{{u}_{{\alpha }}}} \right|}_{{{{l}_{u}}}}} = 0,\quad {{\left. {{{T}_{{{\alpha \beta }}}}{{n}_{{\beta }}}} \right|}_{{{{l}_{{\sigma }}}}}} = {{P}_{{\alpha }}}$Изучим возможности восстановления компонент поля ПН по некоторой дополнительной информации. При этом наиболее адекватной процессу реконструкции поля ПН с помощью акустического зондирования является постановка, в которой заданы (измерены) компоненты смещений, возникающих от действия заданной нагрузки, и измеренных на поверхности тела в некотором частотном диапазоне. Эта постановка приводит к нелинейной коэффициентной обратной задаче (ОЗ) для системы трех функций; в случае простых конфигураций тела (таких как стержень, прямоугольник и др.), и в случае однокомпонентного поля ПН подобные задачи изучены ранее. Некоторые общие аспекты изучения таких задач будут описаны ниже. Иная постановка (промежуточная в смысле исследования возникающих операторных уравнений) состоит в задании компонент смещений внутри исследуемой области. Начнем исследование с этой постановки.
3. Обратная задача в первой постановке. Будем считать, что внутри области заданы компоненты поля смещений от действия заданных нагрузок. Поставим обратную задачу об определении самоуравновешенного поля ПН ${\sigma }_{{{\alpha \beta }}}^{{\text{0}}}(x)$ (т.е. удовлетворяющего уравнениям равновесия) по заданному полю перемещений ${{u}_{{\alpha }}}(x)$ во всей области S. В такой постановке ОЗ является линейной; как и в других типах коэффициентных ОЗ в такой постановке, возможно для их решения использовать наработанные схемы, однако имеются некоторые специфические особенности. В рамках этой постановки можно следовать двумя путями. Опишем последовательно оба этих подхода.
Подход на основе вспомогательных задач Коши. Подставим определяющие соотношения (2.2) в уравнения движения (2.1):
Считая, что поле ПН является самоуравновешенным, и учитывая уравнения равновесия для начальной среды ${\sigma }_{{{\gamma \beta ,\beta }}}^{{\text{0}}} = 0$, получим базовую систему уравнений
(3.2)
${{a}_{{11}}}{\sigma }_{{{\text{11}}}}^{{\text{0}}} + {{a}_{{12}}}{\sigma }_{{12}}^{0} + {{a}_{{22}}}{\sigma }_{{22}}^{0} + {{a}_{0}} = 0,\quad {{b}_{{11}}}{\sigma }_{{11}}^{0} + {{b}_{{12}}}{\sigma }_{{12}}^{0} + {{b}_{{22}}}{\sigma }_{{22}}^{0} + {{b}_{0}} = 0$Компоненты напряжений σαβ определяются согласно (2.3). Вместе с уравнениями равновесия
(3.3)
${\sigma }_{{11,1}}^{0} + {\sigma }_{{12,2}}^{0} = 0,\quad {\sigma }_{{12,1}}^{0} + {\sigma }_{{22,2}}^{0} = 0$(3.4)
${{\left. {({{{\sigma }}_{{11}}} + {{u}_{{1,1}}}{\sigma }_{{11}}^{0} + {{u}_{{1,2}}}{\sigma }_{{12}}^{0}){{n}_{1}} + ({{{\sigma }}_{{12}}} + {{u}_{{1,1}}}{\sigma }_{{12}}^{0} + {{u}_{{1,2}}}{\sigma }_{{22}}^{0}){{n}_{2}}} \right|}_{{{{l}_{{\sigma }}}}}} = {{P}_{1}}$(3.5)
${{\left. {({{{\sigma }}_{{12}}} + {{u}_{{2,1}}}{\sigma }_{{11}}^{0} + {{u}_{{2,2}}}{\sigma }_{{12}}^{0}){{n}_{1}} + ({{{\sigma }}_{{22}}} + {{u}_{{2,1}}}{\sigma }_{{12}}^{0} + {{u}_{{2,2}}}{\sigma }_{{22}}^{0}){{n}_{2}}} \right|}_{{{{l}_{{\sigma }}}}}} = {{P}_{2}}$Сформулированная задача является изначально переопределенной, поэтому для построения приближенного решения используем следующий подход. На начальном этапе сформулируем две вспомогательные задачи Коши.
Задачи Коши. 1) Исключим из уравнений (3.2) компоненту ${\sigma }_{{22}}^{0}$ с помощью стандартных преобразований, найдя
(3.6)
${\sigma }_{{12}}^{0} = - \frac{{{{D}^{{\text{I}}}}}}{{{{C}^{{\text{I}}}}}} - \frac{{{{A}^{{\text{I}}}}}}{{{{C}^{{\text{I}}}}}}{\sigma }_{{11}}^{0}$Подставив (3.6) в первое уравнение равновесия для начальной среды (3.3), получим:
(3.7)
${\sigma }_{{11,1}}^{0} + {{\tilde {A}}^{{\text{I}}}}{\sigma }_{{11,2}}^{0} + {{\tilde {A}}^{{\text{I}}}}{{,}_{2}}{\sigma }_{{11}}^{0} + {{\tilde {D}}^{{\text{I}}}}{{,}_{2}} = 0,\quad {{\tilde {D}}^{{\text{I}}}} = - {{D}^{{\text{I}}}}{\text{/}}{{C}^{{\text{I}}}},\quad {{\tilde {A}}^{{\text{I}}}} = - {{A}^{{\text{I}}}}{\text{/}}{{C}^{{\text{I}}}}$(3.8)
${{\left. {{\sigma }_{{11}}^{0}} \right|}_{{{{l}_{{\sigma }}}}}} = F({{P}_{{\alpha }}},{{u}_{{\alpha }}})$Тогда (3.7)–(3.8) образует задачу Коши о нахождении функции ${\sigma }_{{11}}^{0}$, которая может быть решена либо с помощью разностных аппроксимаций оператора в (3.7), либо с помощью схемы, описанной в [24] при решении задачи Коши.
2) Исключая аналогичным образом из уравнений (3.2) компоненту ${\sigma }_{{11}}^{0}$, получим
(3.9)
${\sigma }_{{12}}^{0} = - \frac{{{{D}^{{{\text{II}}}}}}}{{{{C}^{{{\text{II}}}}}}} - \frac{{{{A}^{{{\text{II}}}}}}}{{{{C}^{{{\text{II}}}}}}}{\sigma }_{{22}}^{0}$Подставив это выражение во второе уравнение равновесия (3.3), найдем
(3.10)
${\sigma }_{{22,2}}^{0} + {{\tilde {A}}^{{{\text{II}}}}}{\sigma }_{{22,1}}^{0} + {{\tilde {A}}^{{{\text{II}}}}}{{,}_{1}}{\sigma }_{{22}}^{0} + {{\tilde {D}}^{{{\text{II}}}}}{{,}_{1}} = 0,\quad {{\tilde {D}}^{{{\text{II}}}}} = - \frac{{{{D}^{{{\text{II}}}}}}}{{{{C}^{{{\text{II}}}}}}},\quad {{\tilde {A}}^{{{\text{II}}}}} = - \frac{{{{A}^{{{\text{II}}}}}}}{{{{C}^{{{\text{II}}}}}}}$Также аналогично сформулируем граничное условие
(3.11)
${{\left. {{\sigma }_{{22}}^{0}} \right|}_{{{{l}_{{\sigma }}}}}} = F({{P}_{{\alpha }}},{{u}_{{\alpha }}})$Решая 2 задачи Коши (3.7)–(3.8) и (3.10)–(3.11), единственным образом найдем независимо две компоненты ПН ${\sigma }_{{11}}^{0}$ и ${\sigma }_{{22}}^{0}$. Оставшуюся 3-ю компоненту касательных ПН ${\sigma }_{{12}}^{0}$, которая выражается 2 различными соотношениями ${\sigma }_{{12}}^{{0({\text{I}})}}$ и ${\sigma }_{{12}}^{{0({\text{II}})}}$ согласно (3.6) и (3.9), определим с помощью минимизации функционала невязки J = $\int_S {[{{{({\sigma }_{{12}}^{0} - {\sigma }_{{12}}^{{0({\text{I}})}})}}^{2}}} $ + + ${{({\sigma }_{{12}}^{0} - {\sigma }_{{12}}^{{0({\text{II}})}})}^{2}}]dS$.
Подход, основанный на введении функции напряжений. Выразим компоненты ПН через функцию напряжений $\Phi $:
(3.12)
${\sigma }_{{11}}^{0} = \Phi {{,}_{{22}}},\quad {\sigma }_{{12}}^{0} = - \Phi {{,}_{{12}}},\quad {\sigma }_{{22}}^{0} = \Phi {{,}_{{11}}}$Тогда уравнения равновесия (3.3) для начальной среды будут выполнены автоматически. Отметим, что для однородной изотропной среды функция $\Phi $ является бигармонической; в общем случае неоднородного ПНС о характере этой функции ничего не известно. Из уравнений движения (3.1) получим
(3.13)
${{u}_{{1,11}}}\Phi {{,}_{{22}}} - 2{{u}_{{1,12}}}\Phi {{,}_{{12}}} + {{u}_{{1,22}}}\Phi {{,}_{{11}}} + {{{\sigma }}_{{11,1}}} + {{{\sigma }}_{{12,2}}} + {\rho }{{{\omega }}^{2}}{{u}_{1}} = 0$(3.14)
${{u}_{{2,11}}}\Phi {{,}_{{22}}} - 2{{u}_{{2,12}}}\Phi {{,}_{{12}}} + {{u}_{{2,22}}}\Phi {{,}_{{11}}} + {{{\sigma }}_{{12,1}}} + {{{\sigma }}_{{22,2}}} + {\rho }{{{\omega }}^{2}}{{u}_{2}} = 0$При таком подходе для определения функции Ф получаем систему уравнений в частных производных второго порядка. Граничные условия (3.4)–(3.5) примут вид
(3.15)
${{\left. {\left( {{{{\sigma }}_{{11}}} + {{u}_{{1,1}}}\Phi {{,}_{{22}}} - {{u}_{{1,2}}}\Phi {{,}_{{12}}}} \right){{n}_{1}} + \left( {{{{\sigma }}_{{12}}} - {{u}_{{1,1}}}\Phi {{,}_{{12}}} + {{u}_{{1,2}}}\Phi {{,}_{{11}}}} \right){{n}_{2}}} \right|}_{{{{l}_{{\sigma }}}}}} = {{P}_{1}}$(3.16)
${{\left. {\left( {{{{\sigma }}_{{12}}} + {{u}_{{2,1}}}\Phi {{,}_{{22}}} - {{u}_{{2,2}}}\Phi {{,}_{{12}}}} \right){{n}_{1}} + \left( {{{{\sigma }}_{{22}}} - {{u}_{{2,1}}}\Phi {{,}_{{12}}} + {{u}_{{2,2}}}\Phi {{,}_{{11}}}} \right){{n}_{2}}} \right|}_{{{{l}_{{\sigma }}}}}} = {{P}_{2}}$Сведение к системе для двух функций. Сведем систему (3.2) для 3-х функций ПН к системе для 2-х функций. Для этого введем в рассмотрение функции F1, F2 такие, что F1 = $\Phi {{,}_{1}}$, ${{F}_{2}} = \Phi {{,}_{2}}$. Тогда $\Phi {{,}_{{22}}} = {{F}_{{2,2}}}$, $\Phi {{,}_{{12}}} = \Phi {{,}_{{21}}} = {{F}_{{1,2}}} = {{F}_{{2,1}}}$, $\Phi {{,}_{{11}}} = {{F}_{{1,1}}}$, и система (3.2) примет вид
(3.17)
${{a}_{{11}}}{{F}_{{2,2}}} - {{a}_{{12}}}{{F}_{{1,2}}} + {{a}_{{22}}}{{F}_{{1,1}}} + {{a}_{0}} = 0,$(3.18)
${{b}_{{11}}}{{F}_{{2,2}}} - {{b}_{{12}}}{{F}_{{1,2}}} + {{b}_{{22}}}{{F}_{{1,1}}} + {{b}_{0}} = 0$(3.19)
${{\left. {\left( {{{{\sigma }}_{{11}}} + {{u}_{{1,1}}}{{F}_{{2,2}}} - {{u}_{{1,2}}}{{F}_{{1,2}}}} \right){{n}_{1}} + \left( {{{{\sigma }}_{{12}}} - {{u}_{{1,1}}}{{F}_{{1,2}}} + {{u}_{{1,2}}}{{F}_{{1,1}}}} \right){{n}_{2}}} \right|}_{{{{l}_{{\sigma }}}}}} = {{P}_{1}}$(3.20)
${{\left. {\left( {{{{\sigma }}_{{12}}} + {{u}_{{2,1}}}{{F}_{{2,2}}} - {{u}_{{2,2}}}{{F}_{{1,2}}}} \right){{n}_{1}} + \left( {{{{\sigma }}_{{22}}} - {{u}_{{2,1}}}{{F}_{{1,2}}} + {{u}_{{2,2}}}{{F}_{{1,1}}}} \right){{n}_{2}}} \right|}_{{{{l}_{{\sigma }}}}}} = {{P}_{2}}$Одним из возможных вариантов решения задачи в постановке (3.17)–(3.18) с граничными условиями (3.19)–(3.20) является использование слабой постановки и последующая ее дискретизация на основе метода конечных элементов. Другой способ решения этой задачи основывается на конечно-разностных аппроксимациях [22].
Проекционный метод. Слабая постановка задачи (2.1)-(2.4) имеет вид [14]
(3.21)
$\int\limits_{{{l}_{{\sigma }}}} {{{P}_{i}}{{{v}}_{i}}dl - \int\limits_S {({\lambda }{{u}_{{i,i}}}{{{v}}_{{j,j}}} + 2{\mu \varepsilon }_{{ij}}^{u}{\varepsilon }_{{ij}}^{{v}} + {{u}_{{i,m}}}{\sigma }_{{mj}}^{0}{{{v}}_{{i,j}}} - {{{\omega }}^{2}}{\rho }{{u}_{i}}{{{v}}_{i}})dS} = 0} $(3.22)
$\left. {_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}} + \;\Phi {{,}_{{22}}}{{u}_{{i,1}}}{{{v}}_{{i,1}}} - \Phi {{,}_{{12}}}\left( {{{u}_{{i,1}}}{{{v}}_{{i,2}}} + {{u}_{{i,2}}}{{{v}}_{{i,1}}}} \right) + \Phi {{,}_{{11}}}{{u}_{{i,2}}}{{{v}}_{{i,2}}} - {\rho }{{{\omega }}^{2}}{{u}_{i}}{{{v}}_{i}}} \right]dS = 0$Воспользуемся идеей проекционных методов и будем искать функцию напряжений Φ в виде разложения $\Phi = \sum\limits_{k = 1}^N {{{{\tilde {a}}}_{k}}{{{\varphi }}_{k}}} $, где ${{{\varphi }}_{k}}({{x}_{1}},{{x}_{2}})$ – полиномы степени выше первой. Тогда (3.22) преобразуется следующим образом:
(3.23)
$ - \sum\limits_{k = 1}^N {{{{\tilde {a}}}_{k}}\int\limits_S {\left( {{{{\varphi }}_{{k,22}}}{{u}_{{i,1}}}{{{v}}_{{i,1}}} - {{{\varphi }}_{{k,12}}}\left[ {{{u}_{{i,1}}}{{{v}}_{{i,2}}} + {{u}_{{i,2}}}{{{v}}_{{i,1}}}} \right] + {{{\varphi }}_{{k,11}}}{{u}_{{i,2}}}{{{v}}_{{i,2}}}} \right)} } dS = 0$Выбирая набор пробных функций ${v}_{i}^{l}$, $l = 1 \div M$, получим систему линейных алгебраических уравнений (СЛАУ) относительно коэффициентов ${{\tilde {a}}_{k}}$:
В качестве простого примера рассмотрим прямоугольную область S = [0, l] × $\left[ { - b{\text{/}}2,b{\text{/}}2} \right]$; граница ${{x}_{1}} = 0$ – закреплена, ${{x}_{2}} = \pm b{\text{/}}2$ – свободны от нагрузок, на границе ${{x}_{1}} = l$ приложена касательная нагрузка. Будем выбирать пробные функции в виде полиномов, удовлетворяющих следующим условиям: ${v}_{i}^{l}(0,{{x}_{2}}) = 0$, ${v}_{1}^{l}({{x}_{1}}, - {{x}_{2}})$ = $ - {v}_{1}^{l}({{x}_{1}},{{x}_{2}})$, ${v}_{2}^{l}({{x}_{1}}, - {{x}_{2}}) = {v}_{2}^{l}({{x}_{1}},{{x}_{2}})$. В качестве пробных функций выберем следующие полиномы:
Ниже в качестве примера рассмотрим модельную ОЗ по реконструкции однородного поля ПН. Зададим поле ПН в виде трех постоянных величин ${\sigma }_{{11}}^{0}$, ${\sigma }_{{22}}^{0}$, ${\sigma }_{{12}}^{0}$. Функцию напряжений Ф будем соответственно искать в виде квадратичного полинома: Φ = = ${{\tilde {a}}_{1}}{{{\varphi }}_{1}} + {{\tilde {a}}_{2}}{{{\varphi }}_{2}} + {{\tilde {a}}_{3}}{{{\varphi }}_{3}}$, где ${{{\varphi }}_{1}} = x_{1}^{2}$, ${{{\varphi }}_{2}} = x_{1}^{{}}x_{2}^{{}}$, ${{{\varphi }}_{3}} = x_{2}^{2}$. Отсюда ${\sigma }_{{11}}^{0} = {{\Phi }_{{,22}}} = 2{{\tilde {a}}_{3}}$, ${\sigma }_{{22}}^{0}$ = = Φ,11 = $2{{\tilde {a}}_{1}}$, ${\sigma }_{{12}}^{0} = - {{\Phi }_{{,12}}} = - {{\tilde {a}}_{2}}$. В качестве пробных функций рассмотрим 3 пары функций:
Тогда на основе (3.24) получим квадратную СЛАУ размера 3 × 3. Для численной реализации выбраны следующие параметры: l = 100 см, b = 50 см, ν = 0.28 (коэффициент Пуассона), E = 2 × 106 кгс/см2, ρ = 0.007 кг/см3; τ2 = 104 кгс/см2, ω = 20 Гц (частота установившихся колебаний в окрестности первого резонанса).
Вычислительный эксперимент 1. Истинное поле ПН: ${\sigma }_{{11}}^{0} = {{10}^{{ - 3}}}E$, ${\sigma }_{{12}}^{0} = {\text{2}} \times {\text{1}}{{{\text{0}}}^{{ - 3}}}E$, ${\sigma }_{{22}}^{0} = {\text{3}} \times {\text{1}}{{{\text{0}}}^{{ - 3}}}E$. В табл. 1 приведены результаты решения ОЗ для двух разбиений конечноэлементной сетки.
Таблица 1
| ${\sigma }_{{{\text{11}}}}^{{\text{0}}}$ | ${\sigma }_{{{\text{12}}}}^{{\text{0}}}$ | ${\sigma }_{{{\text{22}}}}^{{\text{0}}}$ | |
|---|---|---|---|
| Истинное поле | 2000 | 4000 | 6000 |
| Реконструкция | 2000.01 | 4005.13 | 6000 |
| Отн. погр. (%) КЭ сетка 80 × 40 | 0.00039 | 0.1282 | 0.000053 |
| Отн. погр. (%) КЭ сетка 160 × 120 | 0.00003 | 0.0075 | 0.000006 |
Вычислительный эксперимент 2. Истинное поле ПН с амплитудой в 10 раз меньше, чем в эксперименте 1: ${\sigma }_{{11}}^{0} = {{10}^{{ - 4}}}E$, ${\sigma }_{{12}}^{0} = {\text{2}} \times {\text{1}}{{{\text{0}}}^{{ - 4}}}E$, ${\sigma }_{{22}}^{0} = {\text{3}} \times {\text{1}}{{{\text{0}}}^{{ - 4}}}E$. В табл. 2 приведены результаты решения ОЗ.
Таблица 2
| ${\sigma }_{{{\text{11}}}}^{{\text{0}}}$ | ${\sigma }_{{{\text{12}}}}^{{\text{0}}}$ | ${\sigma }_{{{\text{22}}}}^{{\text{0}}}$ | |
|---|---|---|---|
| Истинное поле | 200 | 400 | 600 |
| Реконструкция | 200.008 | 451.529 | 600.003 |
| Отн. погр. (%) | 0.0039 | 12.88 | 0.0005 |
Как можно видеть из этих вычислительных экспериментов, компонента касательных ПН ${\sigma }_{{12}}^{0}$ восстанавливается значительно хуже двух других компонент, причем чем меньше уровень ${\sigma }_{{12}}^{0}$, тем хуже проходит реконструкция. С другой стороны, при увеличении амплитуды этой компоненты точность реконструкции возрастает. Отметим, что плотность конечноэлементной сетки положительно влияет на точность решения ОЗ, причем существенно. Подбор частоты колебаний также значительно влияет на точность реконструкции; отметим, что желательно выбрать несколько частот, близких к резонансам, поскольку вблизи резонансных частот влияние ПН наиболее выражено. Численный анализ структур, входящих в уравнение (3.22), показал, что коэффициент при $\Phi {{,}_{{12}}}$ для широкого класса пробных функций на 2–3 порядка меньше коэффициентов при $\Phi {{,}_{{11}}}$, $\Phi {{,}_{{22}}}$. Это одна из возможных причин относительно низкой точности реконструкции компоненты ${\sigma }_{{12}}^{0}$.
При задании истинных полей ПН в других классах функций (линейные, квадратичные, экспоненциальные) наблюдались те же тенденции реконструкции.
Для выбранного набора базисных функций описанный метод позволяет с приемлемой точностью восстановить гладкие поля ПН в классах постоянных и линейных функций. При рассмотрении большего количества базисных функций в представлении функции напряжений Ф (т.е. при попытке восстановить ПН в классах квадратичных, кубических и других полиномиальных разложений высокого порядка), точность реконструкции значительно ухудшается.
4. Обратная задача во второй постановке. Рассмотрим обратную задачу об идентификации поля ПНС на основе дополнительной информации о данных акустического зондирования. Пусть известно поле смещений на части границы в конечном наборе частот. В работе [14] приведено два способа вывода соотношения для решения обратной задачи в случае плоской области. Это соотношение позволяет реализовать итерационный процесс по определению поправок компонент тензора ПН по отношению к некоторому выбранному начальному состоянию (один из них основан на использовании слабой постановки исходной прямой задачи и применении обобщенного соотношения взаимности).
В работе [17] в результате применения обобщенного соотношения взаимности для трехмерного упругого тела было получено операторное уравнение для исследования описанной ОЗ. Аналогичным образом можно получить уравнение для плоской задачи, например, исходя из слабой постановки для плоской задачи (3.21):
(4.1)
$\int\limits_S {\sigma }_{{{\mu \beta }}}^{{0(n)}}u_{{{\alpha ,\beta }}}^{{(n - 1)}}u_{{{\alpha ,\mu }}}^{{(n - 1)}}dS + \int\limits_{{{l}_{{\sigma }}}} {{P}_{{\alpha }}}({{f}_{{\alpha }}} - u_{{\alpha }}^{{(n - 1)}})dl = 0$Здесь индексы (n), (n – 1) – номера итерации; ${\sigma }_{{11}}^{{0(n)}}$, ${\sigma }_{{22}}^{{0(n)}}$, ${\sigma }_{{12}}^{{0(n)}}$ – поправки к соответствующим компонентам ПН на текущей итерации; ${{\left. {{{f}_{i}}} \right|}_{{{{S}_{{\sigma }}}}}}$ – измеренные смещения под зондирующей нагрузкой из дополнительной информации в ОЗ. Таким образом, можно построить итерационный процесс, на каждом шаге которого решается краевая задача для текущего приближения для ПН ${\sigma }_{{ij}}^{{0(n - 1)}}$ и вычисляется соответствующее поле смещений $u_{i}^{{(n - 1)}}$, после чего из интегрального уравнения Фредгольма 1-го рода (4.1) находятся поправки ${\sigma }_{{ij}}^{{0(n)}}$, и текущее приближение уточняется: ${\sigma }_{{ij}}^{0} = {\sigma }_{{ij}}^{{0(n - 1)}} + {\sigma }_{{ij}}^{{0(n)}}$. Такой подход требует знания начального приближения ${\sigma }_{{ij}}^{{0(0)}}$, поиск которого можно осуществлять в каком-нибудь узком классе функций (например, линейных или постоянных) с помощью минимизации функционала невязки в пространстве небольшой размерности. Детально подобные итерационные процессы рассмотрены в работах [14, 15, 17]. Отметим, что при этом не накладывалось ограничений на малость компонент ПН. На самом деле максимальные значения компонент полей ${\sigma }_{{ij}}^{0}$ на несколько порядков меньше характерных значений модуля упругости; использование этого факта значительно упрощает решение ОЗ.
Представим ${\sigma }_{{{\alpha \beta }}}^{0} = {\tau }{{s}_{{{\alpha \beta }}}}$, где τ – малый параметр. Используем разложение по ${\tau }$ для представления функций перемещений и напряжений
(4.2)
${{u}_{{\alpha }}} = u_{{\alpha }}^{0} + {\tau }u_{{\alpha }}^{1} + o({\tau }),\quad {{{\sigma }}_{{{\alpha \beta }}}} = {\sigma }_{{{\alpha \beta }}}^{{(0)}} + {\tau \sigma }_{{{\alpha \beta }}}^{{(1)}} + o({\tau })$Линеаризуя согласно (4.2) уравнения (2.1) с учетом представления (2.2) и приравнивая коэффициенты при одинаковых степенях ${{{\tau }}^{0}}$ и ${{{\tau }}^{1}}$, получим две группы уравнений:
(4.3)
${\sigma }_{{{\alpha \beta ,\beta }}}^{{(0)}} + {\rho }{{{\omega }}^{2}}u_{{\alpha }}^{0} = 0,\quad ({\sigma }_{{{\alpha \beta }}}^{{(1)}} + u_{{{\alpha ,\gamma }}}^{0}{{s}_{{{\gamma \beta }}}}){{,}_{{\beta }}}{\text{ + }}\,{\rho }{{{\omega }}^{2}}u_{{\alpha }}^{1} = 0$Соответствующие граничные условия имеют вид
(4.4)
${{\left. {u_{{\alpha }}^{0}} \right|}_{{{{l}_{u}}}}} = 0,\quad {{\left. {u_{{\alpha }}^{1}} \right|}_{{{{l}_{u}}}}} = 0,\quad {{\left. {{\sigma }_{{{\alpha \beta }}}^{{(0)}}{{n}_{{\beta }}}} \right|}_{{{{l}_{{\sigma }}}}}} = {{P}_{{\alpha }}},\quad {{\left. {({\sigma }_{{{\alpha \beta }}}^{{(1)}} + u_{{{\alpha ,\gamma }}}^{0}{{s}_{{{\gamma \beta }}}}){{n}_{{\beta }}}} \right|}_{{{{l}_{{\sigma }}}}}} = 0$Далее, используя стандартную технику, описанную в работе [17], из уравнений (4.3) с учетом граничных условий (4.4) можно получить соотношение
(4.5)
$\int\limits_S {u_{{{\alpha ,\gamma }}}^{0}u_{{{\alpha ,\beta }}}^{0}{{s}_{{{\gamma \beta }}}}} dS = \int\limits_{{{l}_{{\sigma }}}} {{{P}_{{\alpha }}}({{f}_{{\alpha }}} - u_{{\alpha }}^{0})dl} = F({\omega })$(4.6)
${{F}_{k}}^{{}}({\omega }) = \int\limits_{{{l}_{k}}} P_{\alpha }^{{(k)}}(f_{\alpha }^{{(k)}} - u_{{\alpha }}^{0})d{{l}_{k}},\quad k = \overline {1,3} ,~\quad {\omega } \in [{{{\omega }}_{ - }},{{{\omega }}_{ + }}]$Здесь в качестве формального аргумента указана частота установившихся колебаний $\omega $. Система интегральных уравнений Фредгольма с гладким ядром 1-го рода решается стандартным образом на основе метода регуляризации А.Н. Тихонова [23]. Здесь итерационный процесс ограничивается одним шагом, и начальное приближение для ПН задается нулевым.
Отметим, что при рассмотрении ОЗ о восстановлении материальных параметров, таких как переменный модуль Юнга, имеется априорная информация о его положительности, что упрощает процесс реконструкции. В случае же идентификации компонент ПНС такой априорной информации нет, однако можно поставить дополнительное условие о самоуравновешенности поля ПН, что приводит к переопределенной задаче.
Проекционный метод. Если считать, что поле ПН самоуравновешено, то можно выразить компоненты ПН через функцию напряжений $\Phi $, тогда уравнение (4.1) примет вид
(4.7)
$\int\limits_S^{} {[\Phi {{,}_{{22}}}K_{{11}}^{{}} + \Phi {{,}_{{11}}}K_{{22}}^{{}} - \Phi {{,}_{{12}}}K_{{12}}^{{}}]dS = F({\omega }),\quad {\omega } \in [{{{\omega }}_{ - }},{{{\omega }}_{ + }}]} $Исследование операторного уравнения (4.7) представляет собой более сложную задачу, чем исследование классического уравнения Фредгольма 1-го рода с непрерывным ядром. Одним из способов его изучения представляет собой проекционный метод, схожий с описанным в пункте 3 и основанный на отыскании функции Φ в виде линейной комбинации базисных функций ${{{\varphi }}_{k}}$, определяемых в классе гладких ортогональных функций [15]. Тогда из уравнения (4.7) можно получить уравнение, содержащее конечное число $m$ параметров ak:
(4.8)
$\sum\limits_{k = 1}^m {{{a}_{k}}B_{k}^{{}}} ({\omega }) = F({\omega }),\quad {\omega } \in [{{{\omega }}_{ - }},{{{\omega }}_{ + }}]$Заключение. Представлены различные постановки плоских обратных задач об идентификации предварительного напряженного состояния в плоских областях. При этом рассмотрены обратные задачи 2-х типов, при наличии дополнительной информации об измеренном поле перемещений: 1) в наборе точек области при фиксированной частоте колебаний; 2) на части границы области в диапазоне частот. Предложены и обсуждены методики и алгоритмы решения сформулированных обратных задач.
Благодарности. Исследование выполнено при финансовой поддержке Российского научного фонда (грант 18-71-10045).
Список литературы
Salvati E., Korsunsky A.M. A simplified FEM eigenstrain residual stress reconstruction for surface treatments in arbitrary 3D geometries // International Journal of Mechanical Sciences. 2018. V. 138–139. P. 457–466.
Ling H., Yang Ch., Feng Sh., Lu H. Predictive model of grinding residual stress for linear guideway considering straightening history // International Journal of Mechanical Sciences. 2020. V. 176. P. 105536.
Suresh S., Giannakopoulos A.E. A new method for estimating residual stresses by instrumented sharp indentation // Acta Mater. 1998. V. 46. № 16. P. 5755–5767.
Pham T.-H., Kim S.-E. Determination of equi-biaxial residual stress and plastic properties in structural steel using instrumented indentation // Mater Sci Eng A. 2017. V. 688. P. 352–363.
Moharrami R., Sanayei M. Numerical study of the effect of yield strain and stress ratio on the measurement accuracy of biaxial residual stress in steels using indentation // J Mater Res Technol. 2020. https://doi.org/10.1016/j.jmrt.2020.02.021
Deng D., Kiyoshima S. Numerical simulation of welding temperature field, residual stress and deformation induced by electro slag welding // Comput Mater Sci. 2012. V. 62. P. 23–34.
Yonezu A., Kusano R., Hiyoshi T., Chen X. A method to estimate residual stress in austenitic stainless steel using a microindentation test // J Mater Eng Perform. 2015. V. 24. P. 362–72.
Wang F., Mao K., Li B. Prediction of residual stress fields from surface stress measurements // International Journal of Mechanical Sciences. 2018. V. 140. P. 68–82.
Truesdell C.A. A first course in rational continuum mechanics. Baltimore. Maryland: The John Hopkins University, 1972. 417 p.
Hoger A. On the determination of residual stress in an elastic body // Journal of Elasticity. 1986. V. 16. P. 303–324.
Robertson R.L. Determining residual stress from boundary. Measurements: A linearized approach // Journal of Elasticity. 1998. V. 52. P. 63–73.
Гузь А.Н., Махорт Ф.Г., Гуща О.И. Введение в акустоупругость. Киев: Наукова думка, 1977. 151 с.
Nedin R.D., Dudarev V.V., Vatulyan A.O. Some aspects of modeling and identification of inhomogeneous residual stress // Engineering Structures. 2017. V. 151. P. 391–405.
Nedin R.D., Vatulyan A.O. Inverse Problem of Non-homogeneous Residual Stress Identification in Thin Plates // Int J Solids Struct. 2013. V. 50. P. 2107–2114.
Nedin R.D., Vatulyan A.O. Concerning one approach to the reconstruction of heterogeneous residual stress in plate // ZAMM: Z. angew. Math. Mech. V. 94. № 1–2. 2014. P. 142–149.
Dudarev V.V., Nedin R.D., Vatulyan A.O. Nondestructive identification of inhomogeneous residual stress state in deformable bodies on the basis of the acoustic sounding method // Advanced Materials Research. 2014. V. 996. P. 409–414.
Ватульян А.О., Дударев В.В., Недин Р.Д. Предварительные напряжения: моделирование и идентификация. Монография. Ростов-на-Дону: Изд-во ЮФУ, 2015. 206 с.
Nedin R.D., Vatulyan A.O., Bogachev I.V. Direct and inverse problems for prestressed functionally graded plates in the framework of the Timoshenko model // Mathematical Methods in the Applied Sciences. 2018. V. 41. № 4. P. 1600–1618.
Vatulyan A., Nedin R., Dudarev V. Modelling and analysis of prestress field in a thin plate with a nonuniform coating // IOP Conf. Series: Journal of Physics: Conf. Series. 2019. V. 1203. P. 012027.
Ватульян А.О., Недин Р.Д. К идентификации неоднородных предварительных напряжений // Вестник СПбГУ. Сер. 1. Математика, механика, астрономия. 2011. № 1. С. 38–44.
Недин Р.Д. Моделирование и частотный анализ предварительно напряженных функционально-градиентных пластин с отверстиями // Вычислительная механика сплошных сред. 2019. Т. 12. № 2. С. 192–201.
Ватульян А.О., Гукасян Л.С. О задаче Коши для уравнения в частных производных первого порядка и ее приложениях в теории обратных задач // Вестник ДГТУ. 2012. Т. 12. № 7 (68). С. 11–20.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1986. 287 с.
Гюнтер Н.М. Интегрирование уравнений первого порядка в частных производных. Ленинград, М.: ОНТИ, 1934. 360 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела