Известия РАН. Механика твердого тела, 2020, № 6, стр. 50-58
ОБ ОДНОМ СПОСОБЕ РАСЧЕТА ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЙ В ФУНКЦИОНАЛЬНО-ГРАДИЕНТНОМ УПРУГОПЛАСТИЧЕСКОМ МАТЕРИАЛЕ
Е. Т. Акинлаби a, Е. П. Дац b, c, Р. М. Махамуд d, Е. В. Мурашкин e, *
a Институт жизни и наук о Земле Панафриканского университета
Ибадан, Нигерия
b Институт прикладной математики ДВО РАН
Владивосток, Россия
c Владивостокский государственный университет экономики и сервиса
Владивосток, Россия
d Университет Йоханнесбурга
Йоханнесбург, ЮАР
e Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: murashkin@ipmnet.ru
Поступила в редакцию 12.02.2020
После доработки 28.02.2020
Принята к публикации 29.02.2020
Аннотация
В работе рассматривается последовательность решений одномерных задач о необратимом деформировании функционально-градиентного материала в условиях неравномерного теплового расширения. Получены численные решения задач о нагреве упругопластической сферы, константы материала которой являются линейными функциями радиуса, и точные решения, в которых константы материала аппроксимированы кусочно-постоянными функциями. Показано, что деформирование функционально-градиентного упругопластического материала, в котором константы материала заданы кусочно-постоянными распределениями, может быть качественно описано численными решениями, в которых константы материала являются непрерывными аппроксимациями соответствующих кусочно-постоянных функций. Полученные численные и аналитические решения краевых задач графически анализируются.
Введение. В современной технологической практике все больше используются материалы с необнородно распределенными механическими характеристиками [1–4]. К таким материалам, в частности, относятся и функционально-градиентные материалы. Функционально-градиентные материалы являются, прежде всего, сплавами, состоящие из твёрдых гранул и микронеоднородностей (карбидов, нитридов и боридов переходных металлов (карбид вольфрама, карбид титана, карбонитрид титана, диборид титана и др.). Такие неоднородности образуют прочный сплошной каркас. Металлической связкой при этом выступают добавки кобальта, никеля, титана, алюминия). Ее содержание непрерывно изменяется в объёме материала, что легко задается параметрами процессов аддитивного производства (прежде всего ). В результате функционально-градиентные материалы обладают высокой твёрдостью и большой ударной вязкостью. Благодаря этому функционально-градиентные материалы используются при производстве военной техники, авиации, в горнодобывающей промышленности и медицине.
Конструкции, собранные из функционально-градиентных материалов и сплавов, эксплуатируются в широком диапазоне температур. Поэтому одной из основных актуальных задач при расчете напряженно-деформированного состояния и остаточных напряжений в таких изделиях и конструкциях является учет теплового расширения материала. В условиях температурного воздействия различные коэффициенты теплового расширения в многослойной структуре являются причиной возникновения градиентов температурных напряжений и деформаций даже в условиях равномерного нагрева изделия. Высокие уровни напряжений способны приводить к возникновению областей необратимого деформирования и разрушения.
Теоретические исследования напряженно-деформированного состояния упругопластического материала, подверженного интенсивному тепловому воздействию, представлены в точных решениях ряда задач в рамках теории температурных напряжений [5] и теории пластического течения [6]. В работах [7–9] получены численно-аналитические одномерные решения для напряженно-деформированного состояния материала в упругопластическом шаре при учете температурной зависимости предела текучести. Формирование температурных напряжений при пластическом течении и разгрузке в условиях осесимметричного распределения температуры исследованы в работах [10–13]. В [14, 15] проведено сравнение решений для температурных напряжений в упругопластическом цилиндре, полученных для трех различных условий пластичности. В работе [16] показана возможность получения аналитических решений для напряженно-деформированного состояния упругопластического материала в условиях тороидальной симметрии. В работах [17, 18] получены точные решения задач об определении остаточных напряжений в двухслойном упругопластическом материале сферической и цилиндрической формы при различных уровнях теплового расширения в каждом слое.
В настоящем исследовании рассматриваются численные и аналитические решения задач термоупругопластичности в многослойном материале сферической формы с различными механическими параметрами материала для каждого слоя. Предложен новый подход к определению напряженно-деформированного состояния функционально-градиентного упругопластического материала с использованием линейных аппроксимаций параметров материала. Ход получения аналитических решений краевых задач теории термоупругопластичности аналогичен методике описанной Д.Д. Ивлевым в [6] для упругопластических задач.
1. Основные соотношения. Дальнейшие рассмотрения проводятся в рамках классической модели малых упругопластических деформаций типа Прандтля–Рейса [5], в которой тензор полных деформаций εij состоит из термоупругой (обратимой) eij и пластической (необратимой) pij частей:
(1.1)
${{\varepsilon }_{{ij}}} = {{e}_{{ij}}} + {{p}_{{ij}}} = \frac{1}{2}({{\partial }_{j}}{{u}_{i}} + {{\partial }_{i}}{{u}_{j}})$Связь между компонентами тензора температурных напряжений и термоупругих деформаций определяется законом Дюамеля–Неймана:
(1.2)
${{\sigma }_{{ij}}} = 2\mu {{e}_{{ij}}} + (\lambda {{e}_{{kk}}} - (3\lambda + 2\mu )\alpha \Delta ){{\delta }_{{ij}}}$В рамках модели упругопластических деформаций возможен процесс необратимого деформирования, начало которого связано с выполнением в некоторых областях условия пластичности
Согласно принципу максимума диссипации энергии Мизеса поверхность, определяемая неявной зависимостью (1.3) оказывается пластическим потенциалом, из чего следуют соотношения ассоциированного закона пластического течения:
(1.4)
${{\partial }_{t}}{{\varepsilon }_{{ij}}} = \xi \frac{{\partial f}}{{\partial {{\sigma }_{{ij}}}}},\quad \xi = \sqrt {{{\partial }_{t}}{{\varepsilon }_{{kl}}}{{\partial }_{t}}{{\varepsilon }_{{lk}}}} {{\left( {\frac{{\partial f}}{{\partial {{\sigma }_{{mn}}}}}\frac{{\partial f}}{{\partial {{\sigma }_{{nm}}}}}} \right)}^{{ - \frac{1}{2}}}},\quad {{\partial }_{t}} = \frac{\partial }{{\partial t}}$В условиях медленного изменения температуры в сферическом слое справедливо уравнение равновесия, которое при отсутствии массовых сил можно принять в виде
Система уравнений (1.1)–(1.5) с учетом краевых условий и уравнения теплопроводности полностью описывает напряженно-деформированное состояние термоупругопластического материала.
2. Постановка и решение задачи о деформировании многослойной конструкции в условиях сферической симметрии. С целью получения наиболее простых аналитических зависимостей постановка задачи реализована в одномерном варианте. Исследуется композитный сферический слой, в котором напряженно-деформированное состояние в каждой точке материала зависит только от радиальной координаты и степени равномерного нагрева. Функционально-градиентный материал сферической формы представляет из себя многослойную структуру, состоящую из $n$ слоев заданной толщины, в каждом из которых параметры материала являются постоянными, а их значения меняются при переходе от слоя к слою. Запишем основные соотношения теории (1.1)–(1.5) для слоя под номером $v$ ($1 \leqslant v \leqslant n$) в условиях сферической симметрии:
(2.1)
$\begin{array}{*{20}{c}} {\varepsilon _{{rr}}^{{(v)}} = e_{{rr}}^{{(v)}} + p_{{rr}}^{{(v)}} = \frac{{\partial u_{r}^{{(v)}}}}{{\partial r}},\quad \varepsilon _{{\theta \theta }}^{{(v)}} = \varepsilon _{{\varphi \varphi }}^{{(v)}} = e_{{\theta \theta }}^{{(v)}} + p_{{\theta \theta }}^{{(v)}} = \frac{{u_{r}^{{(v)}}}}{r}} \\ {\sigma _{{rr}}^{{(v)}} = ({{\lambda }_{v}} + 2{{\mu }_{v}})e_{{rr}}^{{(v)}} + 2{{\lambda }_{v}}e_{{\theta \theta }}^{{(v)}} - (3{{\lambda }_{v}} + {{\mu }_{v}}){{\alpha }_{v}}\Delta } \\ {\sigma _{{\theta \theta }}^{{(v)}} = 2({{\lambda }_{v}} + {{\mu }_{v}})e_{{\theta \theta }}^{{(v)}} + {{\lambda }_{v}}e_{{rr}}^{{(v)}} - (3{{\lambda }_{v}} + {{\mu }_{v}}){{\alpha }_{v}}\Delta } \end{array}$Проинтегрировав систему уравнений (2.1), получим общие решения в условиях термоупругого равновесия
(2.2)
$\begin{array}{*{20}{c}} {\sigma _{{rr}}^{v} = {{A}_{v}} + \frac{1}{{B_{v}^{3}}},\quad \sigma _{{\theta \theta }}^{v} = \sigma _{{\varphi \varphi }}^{{(v)}} = {{A}_{v}} - \frac{1}{{2B_{v}^{3}}}} \\ {u_{r}^{{(v)}} = r{{\alpha }_{v}}\Delta + \frac{{{{A}_{v}}r}}{{3{{\lambda }_{v}} + 2{{\mu }_{v}}}} - \frac{{{{B}_{v}}}}{{4{{\mu }_{v}}{{r}^{2}}}}} \end{array}$Здесь ${{A}_{v}}$, ${{B}_{v}}$ – неизвестные константы интегрирования, определяемые из граничных условий задачи.
Размер слоя $v$ определяется внутренним и внешним радиусами ${{R}_{{v - 1}}} \leqslant r \leqslant {{R}_{v}}$. Таким образом, нумерация слоев происходит в направлении увеличения радиальной координаты. Для нахождения констант интегрирования в (2.2) зададим граничные условия задачи. В многослойном материале условия непрерывности радиальных перемещений и напряжений на контактных поверхностях можно принять в форме:
(2.3)
$\sigma _{{rr}}^{{(v)}}({{R}_{v}}) = \sigma _{{rr}}^{{(v + 1)}}({{R}_{v}}),\quad u_{r}^{{(v)}}({{R}_{v}}) = u_{r}^{{(v + 1)}}({{R}_{v}}),\quad 1 \leqslant v \leqslant n - 1$На внутренней поверхности R0 первого слоя и на внешней поверхности Rn последнего слоя заданы условия свободного теплового расширения
Предполагается, что многослойный материал подвержен равномерному увеличению температуры. В условиях свободного теплового расширения единственной причиной возникновения температурных напряжений является различный уровень теплового расширения разных слоев, вызванный различными значениями коэффициентов линейного теплового расширения ${{\alpha }_{v}}$. На распределение температурных напряжений при различном тепловом расширении так же оказывает влияние распределение значений параметров Ламе и размеры каждого слоя. Далее в расчетах будет использоваться трехслойный материал с одинаковой толщиной для каждого слоя, а распределения констант материала будут являться кусочно-постоянными функциями радиуса с одинаковой разницей между значениями при последовательном переходе от слоя к слою. Очевидно, что в термоупругом случае решения при кусочно-постоянных распределениях констант материала могут быть элементарным образом аппроксимированы решениями, в которых константы материала являются некоторыми непрерывными распределениями. Гораздо больший интерес представляет случай нелинейного поведения функционально-градиентного материала. В частности, различное тепловое расширение слоев может приводить к таким уровням температурных напряжений, при которых может наблюдаться процесс пластического течения на контактных поверхностях. Как отмечалось ранее, начало пластического течения определяется при помощи условия пластичности (1.3), которое в случае сферической симметрии имеет вид
(2.5)
$f(\sigma _{{ij}}^{{(v)}}) = {{(\sigma _{{rr}}^{{(v)}} - \sigma _{{\theta \theta }}^{{(v)}})}^{2}} - 4k_{v}^{2} = 0$Из ассоциированного закона пластического течения при условии (2.5) следуют соотношения пластической несжимаемости материала:
(2.6)
$p_{{rr}}^{{(v)}} + p_{{\theta \theta }}^{{(v)}} + p_{{\varphi \varphi }}^{{(v)}} = 0,\quad p_{{\theta \theta }}^{{(v)}} = p_{{\varphi \varphi }}^{{(v)}}$Проинтегрировав уравнения равновесия (2.1) с учетом соотношений (2.5)–(2.6), получим решения для напряжений и перемещений в областях необратимого деформирования ${{R}_{{v - 1}}} \leqslant r \leqslant {{a}_{v}}$, где ${{a}_{v}}$ – упругопластическая граница:
(2.7)
$\begin{gathered} \sigma _{{rr}}^{{(v)}} = {{F}_{v}} - 4{{s}_{v}}{{k}_{v}}\ln (r),\quad \sigma _{{\theta \theta }}^{{(v)}} = \sigma _{{\varphi \varphi }}^{{(v)}} = {{F}_{v}} - 4{{s}_{v}}{{k}_{v}}\ln (r) - 2{{s}_{v}}{{k}_{v}} \\ u_{r}^{{(v)}} = \frac{{{{G}_{v}}}}{{{{r}^{2}}}} - \frac{{4{{s}_{v}}{{k}_{v}}}}{{3{{\lambda }_{v}} + 2{{\mu }_{v}}}}r\ln (r) + r\left( {\frac{{{{F}_{v}}}}{{3{{\lambda }_{v}} + 2{{\mu }_{v}}}} + {{\alpha }_{v}}\Delta } \right) \\ {{s}_{v}} = {\text{sign}}(\sigma _{{rr}}^{{(v)}}({{a}_{v}}) - \sigma _{{\theta \theta }}^{{(v)}}({{a}_{v}})) \\ \end{gathered} $Для определения констант ${{F}_{v}}$, ${{G}_{v}}$ и констант из (2.2) необходимо к граничным условиям (2.4) и условиям на контактных поверхностях (2.3) добавить условия непрерывности радиальных напряжений и перемещений на упругопластических границах ${{a}_{v}}$:
(2.8)
${{\mathop \sigma \limits^ - }_{{rr}}}({{a}_{v}}) = {{\mathop \sigma \limits^ + }_{{rr}}}({{a}_{v}}),\quad {{\mathop u\limits^ - }_{r}}({{a}_{v}}) = {{\mathop u\limits^ + }_{r}}({{a}_{v}}),\quad v = 0 \ldots m$(2.9)
${{\mathop \sigma \limits^ - }_{{\theta \theta }}}({{a}_{v}}) = {{\mathop \sigma \limits^ + }_{{\theta \theta }}}({{a}_{v}}),\quad v = 0 \ldots m$Таким образом, для определения констант интегрирования ${{A}_{v}}$, ${{B}_{v}}$, ${{F}_{v}}$, ${{G}_{v}}$ в n-слойном материале с m зонами пластического течения необходимо сначала решить систему из $2(n + m)$ уравнений (2.3), (2.4), (2.8), после чего используя найденные выражения, решить систему из m уравнений (2.9) для определения положения упругопластических границ ${{a}_{v}}$.
3. Непрерывные распределения констант материала и численное решении задачи. Расчет напряженно-деформированного состояния многослойного материала является непростой задачей с точки зрения численной реализации. Известно, что решения упругопластических задач, в которых имеют место контактные граничные условия, для своей сходимости требуют значительных вычислительных ресурсов. Стандартный алгоритм Шварца при учете пластических свойств материала может приводить к высоким погрешностям и как следствие к неверным решениям для напряжений в области контакта. Чаще всего для упрощения процедуры вычисления прибегают к способу описания функционально-градиентного материала, который заключается в представлении многослойной структуры в виде одного сплошного слоя, в котором задано дискретное распределение констант материала, соответствующее различному материалу заданной толщины. При исследовании в рамках линейных моделей, в частности в условиях термоупругого деформирования, данный подход позволяет получить решения, не усложняя процедуру расчета и не приводя к значительным погрешностям в вычислениях. Однако в случае учета нелинейных эффектов, таких как пластическое течение в окрестности точек разрыва распределений констант материала, данный подход приводит к вычислительным трудностям, связанным с корректировкой решений при развитии нескольких зон необратимого деформирования на контактных поверхностях. Далее представлен подход к расчету полей температурных напряжений, заключающийся в представлении ступенчатых распределений констант материала в сплошном слое при помощи кусочно-линейных аппроксимаций.
Возникает вопрос, каким образом аппроксимировать распределения параметров Ламе и коэффициента линейного расширения, чтобы получить решения для температурных напряжений, описывающих напряженно-деформированное состояние функционально-градиентного материала (наименее отличающихся от точных решений).
Рассмотрим трехслойный материал сферической формы ($i = 1..3$). Пусть в каждом слое константы материала могут иметь различные значения. Для удобства предположим, что каждый слой имеет одинаковую толщину, а каждая константа материала может изменяться на одинаковое значение при последовательном переходе от слоя к слою. В качестве референциальных значений констант материала используются следующие:
(3.1)
$\begin{gathered} {{\lambda }_{0}} = 91 \times {{10}^{9}}\;{\text{Па}},\quad {{\mu }_{0}} = 42 \times {{10}^{9}}\;{\text{Па}},\quad {{\alpha }_{0}} = 17 \times {{10}^{{ - 6}}}\;{{{\text{K}}}^{{ - 1}}} \\ {{R}_{0}} = 0.2\;{\text{м}},\quad {{T}_{0}} = 300\; {\text{K}},\quad {{k}_{0}} = 300 \times {{10}^{6}}\;{\text{Па}} \\ \end{gathered} $С целью проанализировать два максимально отличающихся друг от друга напряженно-деформированных состояния материала примем для констант материала в i-м слое два различных способа задания их значений в зависимости от номера слоя. Первый способ определяет увеличение констант материала при увеличении номера слоя:
(3.2)
$\begin{array}{*{20}{c}} {{{R}_{i}}{\text{/}}{{R}_{0}} = i + 1,\quad {{\mu }_{i}}{\text{/}}{{\mu }_{0}} = {{\lambda }_{i}}{\text{/}}{{\lambda }_{0}} = i,\quad {{\alpha }_{i}}{\text{/}}{{\alpha }_{0}} = i,\quad {{k}_{i}} = {{k}_{0}}} \end{array}$Второй способ определяет уменьшение значений констант материала при увеличении номера слоя:
(3.3)
$\begin{array}{*{20}{c}} {{{\mu }_{i}}{\text{/}}{{\mu }_{0}} = {{\lambda }_{i}}{\text{/}}{{\lambda }_{0}} = 4 - i,\quad {{\alpha }_{i}}{\text{/}}{{\alpha }_{0}} = 4 - i,\quad {{k}_{i}} = {{k}_{0}}} \end{array}$При построении непрерывных функций для констант материала используется линейная аппроксимация, проходящая через значения констант (3.2), (3.3), принадлежащих свободным поверхностям сферического слоя R0, Rn. В качестве примера запишем линейную аппроксимацию коэффициента линейного теплового расширения.
(3.4)
$\mathop \alpha \limits^q = (1 + {{w}_{q}}){{\alpha }_{n}}\frac{{r - {{R}_{0}}}}{{{{R}_{n}} - {{R}_{0}}}} + (1 - {{w}_{q}}){{\alpha }_{1}}\frac{{r - {{R}_{n}}}}{{{{R}_{0}} - {{R}_{n}}}}$Здесь и далее индексом q над соответствующей функцией обозначен способ аппроксимации параметров материала, который используется при вычислении данной функции. wq – отклонение значений аппроксимаций констант материала от соответствующих им дискретных аналогов (3.2), (3.3), заданных на свободных поверхностях сферического слоя. Значения wq и способы задания констант (3.2), (3.3) определяют различия в аппроксимациях (3.4). Для констант материала (3.2) параметры в формуле (3.4) запишем в форме
(3.5)
$\begin{gathered} q = 1,\quad {{w}_{1}} = 0,\quad {{\alpha }_{1}} = {{\alpha }_{0}},\quad {{\alpha }_{n}} = n{{\alpha }_{0}} \\ q = 2,\quad {{w}_{2}} = 0.5,\quad {{\alpha }_{1}} = {{\alpha }_{0}},\quad {{\alpha }_{n}} = n{{\alpha }_{0}} \\ q = 3,\quad {{w}_{3}} = 0.25,\quad {{\alpha }_{1}} = {{\alpha }_{0}},\quad {{\alpha }_{n}} = n{{\alpha }_{0}} \\ \end{gathered} $Для констант материала (3.3) параметры в формуле (3.4) примут вид:
(3.6)
$\begin{gathered} q = 4{\text{:}}\quad {{w}_{4}} = 0,\quad {{\alpha }_{1}} = n{{\alpha }_{0}},\quad {{\alpha }_{n}} = {{\alpha }_{0}} \\ q = 5{\text{:}}\quad {{w}_{5}} = 0.5,\quad {{\alpha }_{1}} = n{{\alpha }_{0}},\quad {{\alpha }_{n}} = {{\alpha }_{0}} \\ q = 6{\text{:}}\quad {{w}_{6}} = 0.25,\quad {{\alpha }_{1}} = n{{\alpha }_{0}},\quad {{\alpha }_{n}} = {{\alpha }_{0}} \\ \end{gathered} $4. Расчеты. В настоящем разделе представлены результаты расчетов при условии непрерывного распределения параметров материала и сравнение с результатами расчетов, выполненных в рамках подхода со слоистым представлением материала. В качестве критерия наилучшего соответствия численных решений для напряжений точным решениям выбрано следующее условие:
(4.1)
$I({{\mathop \sigma \limits^q }_{{ij}}}) = \sum\limits_{v = 1}^3 \;\int\limits_{{{R}_{{v - 1}}}}^{{{R}_{v}}} {{\text{|}}\sigma _{{ij}}^{{(v)}} - {{{\mathop \sigma \limits^q }}_{{ij}}}{\text{|}}dr} \to \min $Таблица 1
| ${{\alpha }_{1}} < {{\alpha }_{2}} < {{\alpha }_{3}}$ | ${{\alpha }_{1}} > {{\alpha }_{2}} > {{\alpha }_{3}}$ | |||||
|---|---|---|---|---|---|---|
| q = 1 | q = 2 | q = 3 | q = 4 | q = 5 | q = 6 | |
| $I({{\mathop \sigma \limits^q }_{{rr}}})$ | 0.301 | 0.132 | 0.194 | 0.482 | 0.212 | 0.120 |
| $I({{\mathop \sigma \limits^q }_{{\varphi \varphi }}})$ | 1.126 | 0.8223 | 0.808 | 1.539 | 1.238 | 1.061 |
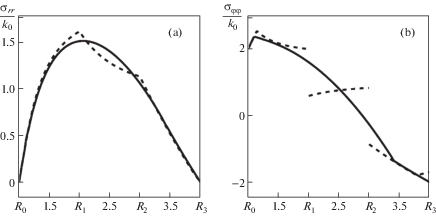
5. Обсуждение результатов. При проведении расчетов в рамках термоупругого равновесия установлено, что наилучшая аппроксимация констант для двух рассмотренных функционально-градиентных материалов достигается при q = 2 и q = 5 соответственно. При таком выборе параметров, описывающих непрерывное распределение констант, достигается наименьшее значение интеграла (4.1). В случае учета нелинейных эффектов, таких как пластическое течение на межслойных поверхностях контакта, выбор аппроксимации зависит от закономерностей распределения констант материала и размеров областей необратимого деформирования. Для материала, описываемого набором констант (1.2), (увеличение значений констант материала в направлении увеличения радиуса) наилучшей аппроксимацией является q = 2 при оценке радиального напряжения ${{\sigma }_{{rr}}}$ и q = 3 для окружного напряжения ${{\sigma }_{{\varphi \varphi }}}$, (рис. 1). Для материала, описываемого набором констант (1.3) наилучшей аппроксимацией констант является q = 6 (рис. 2). Данная аппроксимация позволяет получать минимальную разницу между всеми компонентами тензора напряжений, рассчитываемыми аналитически для многослойного материала и напряжениями, полученными численно. Отметим, что увеличение температуры и как следствие увеличение зон необратимого деформирования при наборе констант (1.3) приводит к уменьшению разницы между двумя рассматриваемыми способами расчета напряжений, а при наборе констант (1.2) наоборот к ее увеличению. Это связано с тем, что в многослойном материале пластическое течение в рамках кусочно-постоянных распределений параметров материала всегда начинается на меньшем радиусе слоя и развивается в направлении большего радиуса. При этом использование непрерывных распределений констант материала в одних случаях так же приводит к возникновению течений на внутренней поверхности сферического слоя, а в других, наоборот, к появлению течения на внешней поверхности. Данные особенности обуславливают уменьшение или увеличения разницы между напряжениями по мере развития пластических течений. Простейший вариант решения задачи для трех слоев позволяет указать наилучшие аппроксимации констант в зависимости от закономерностей их распределения в многослойном материале с целью использования таких аппроксимаций для описания функционально-градиентных материалов и сплавов с большим количеством слоев.
Заключение. В работе рассмотрена последовательность решений одномерных задач о необратимом деформировании функционально-градиентного материала в условиях неравномерного теплового расширения. Получены численные решения задач о нагреве упругопластической сферы, константы материала которой являются линейными функциями радиуса, и точные решения, в котором константы материала аппроксимированы ступенчатыми функциями. Показано, что деформирование функционально-градиентного упругопластического материала, в котором константы материала заданы кусочно-постоянными распределениями, может быть качественно описано численными решениями, в которых константы материала являются непрерывными аппроксимациями соответствующих ступенчатых функций. Установлено, что среди возможных линейных аппроксимаций констант существуют такие, при которых достигается минимальная разница между напряженно-деформированным состоянием многослойного материала и сплошного материала с непрерывным изменением его физических характеристик.
Благодарности. Работа выполнена в рамках государственного задания (№ госрегистрации АААА-А20-120011690132-4) и при поддержке Российского фонда фундаментальных исследований проекты № 19-51-60001, № 20-01-00666.
Список литературы
Mahamood R.M. et al. Scanning velocity influence on microstructure, microhardness and wear resistance performance of laser deposited Ti6Al4V/TiC composite // Materials & design. 2013. V. 50. P. 656–666.
Mahamood R.M., Akinlabi E.T. Types of functionally graded materials and their areas of application // Functionally Graded Materials. Springer, Cham, 2017. P. 9–21.
Mahamood R.M., Akinlabi E.T. Laser metal deposition of functionally graded Ti6Al4V/TiC // Materials & Design. 2015. V. 84. P. 402–410.
Mahamood R.M., Akinlabi E.T. Effect of laser power and powder flow rate on the wear resistance behaviour of laser metal deposited TiC/Ti6Al4 V composites // Materials Today: Proceedings. 2015. V. 2. № 4–5. P. 2679–2686.
Boley B., Weiner J. Theory of Thermal Stresses. N.Y.; L.: Wiley, 1960 = Боли Б., Уэйнер Дж. Теория температурных напряжений. М.: Мир, 1964. 512 с.
Ивлев Д.Д. К определению перемещений в задаче Л.А. Галина // Прикладная математика и механика. 1957. Т. 27. № 5. С. 716–718.
Дац Е.П., Мурашкин Е.В., Велмуруган Р. Вычисление необратимых деформаций в полом упругопластическом шаре в условиях нестационарного температурного воздействия // Вестник Чувашского государственного педагогического университета им. И.Я. Яковлева. Серия: Механика предельного состояния. 2015. № 3. С. 168–175.
Буренин А.А., Дац Е.П., Мокрин С.Н., Мурашкин Е.В. Пластическое течение и разгрузка полого цилиндра в процессе “нагрева-охлаждения” // Вестник Чувашского государственного педагогического университета им. И. Я. Яковлева. Серия: Механика предельного состояния. 2013. № 2. С. 22–28.
Дац Е.П., Мокрин С.Н., Мурашкин Е.В. Расчет накопленной остаточной деформации в процессе “нагрева-охлаждения” упругопластического шара // Вестник Чувашского государственного педагогического университета им. И.Я. Яковлева. Серия: Механика предельного состояния. 2012. № 4. С. 123–132.
Буренин А.А., Дац Е.П., Мурашкин Е.В. Формирование поля остаточных напряжений в условиях локального теплового воздействия // Известия РАН. Механика твердого тела. 2014. Т. 49. № 2. С. 124–131.
Dats E., Mokrin S., Murashkin E. Calculation of the Residual Stress Field of the Thin Circular Plate under Unsteady Thermal Action // Key Engineering Materials. 2016. T. 685. P. 37–41.
Orcan Y., Gamer U. Elastic-plastic deformation of a centrally heated cylinder // Acta Mech. 1991. V. 90. P. 61–80.
Dats E., Murashkin E. On Unsteady Heat Effect in Center of the Elastic-Plastic Disk // Proceedings of The World Congress on Engineering. 2016. P. 69–72.
Дац Е.П., Мурашкин Е.В., Ткачева А.В., Щербатюк Г.А. Температурные напряжения в упругопластической трубе в зависимости от выбора условия пластичности // Изв. РАН. МТТ. 2018. № 1. С. 32–43.
Dats E.P., Murashkin E.V., Gupta N.K. On Yield Criterion Choice in Thermoelastoplastic Problems // Procedia IUTAM. 2017. V. 23. № 2. P. 187–200.
Murashkin E., Dats E. Thermal Stresses Computation in Donut // Engineering Letters. 2019. V. 27 № 3. P. 1–4.
Мурашкин Е.В., Дац Е.П. Термоупругопластическое деформирование многослойного шара // Изв. РАН. МТТ. 2017. № 5. С. 30–36.
Bengeri M., Mack W. The influense of the temperature dependence of the yield stress on the stress distribution in a thermally assembled elastic-plastic snrink fit // Acta Mech. 1994. V. 103. P. 243–257.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела